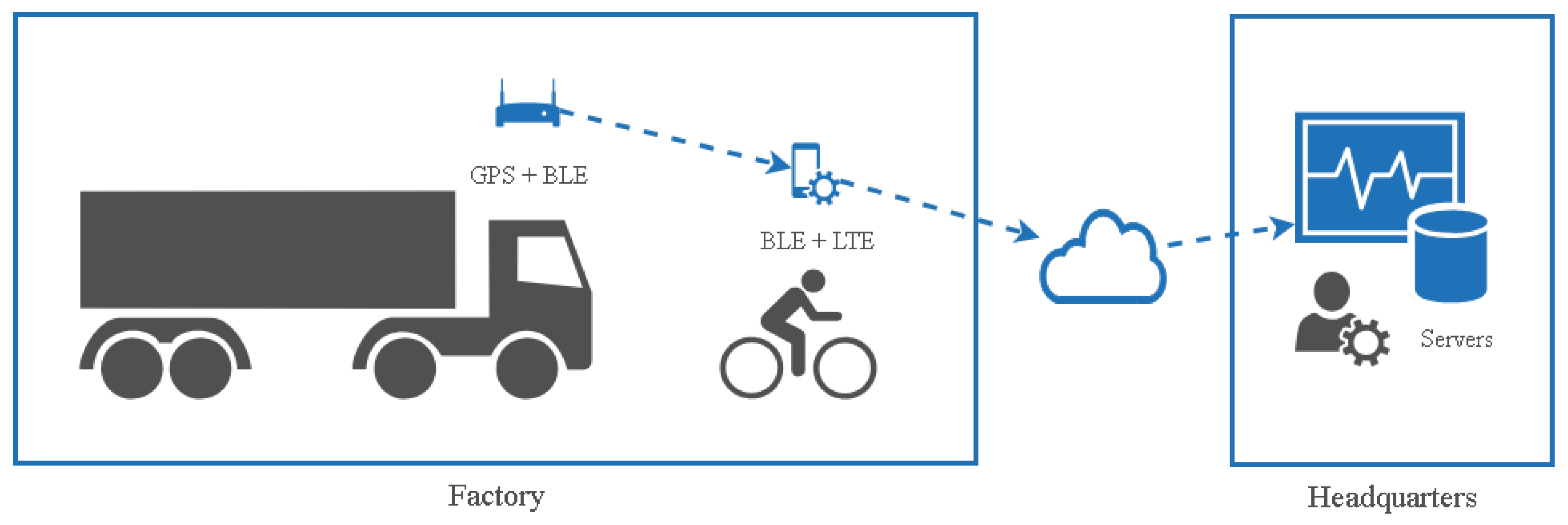
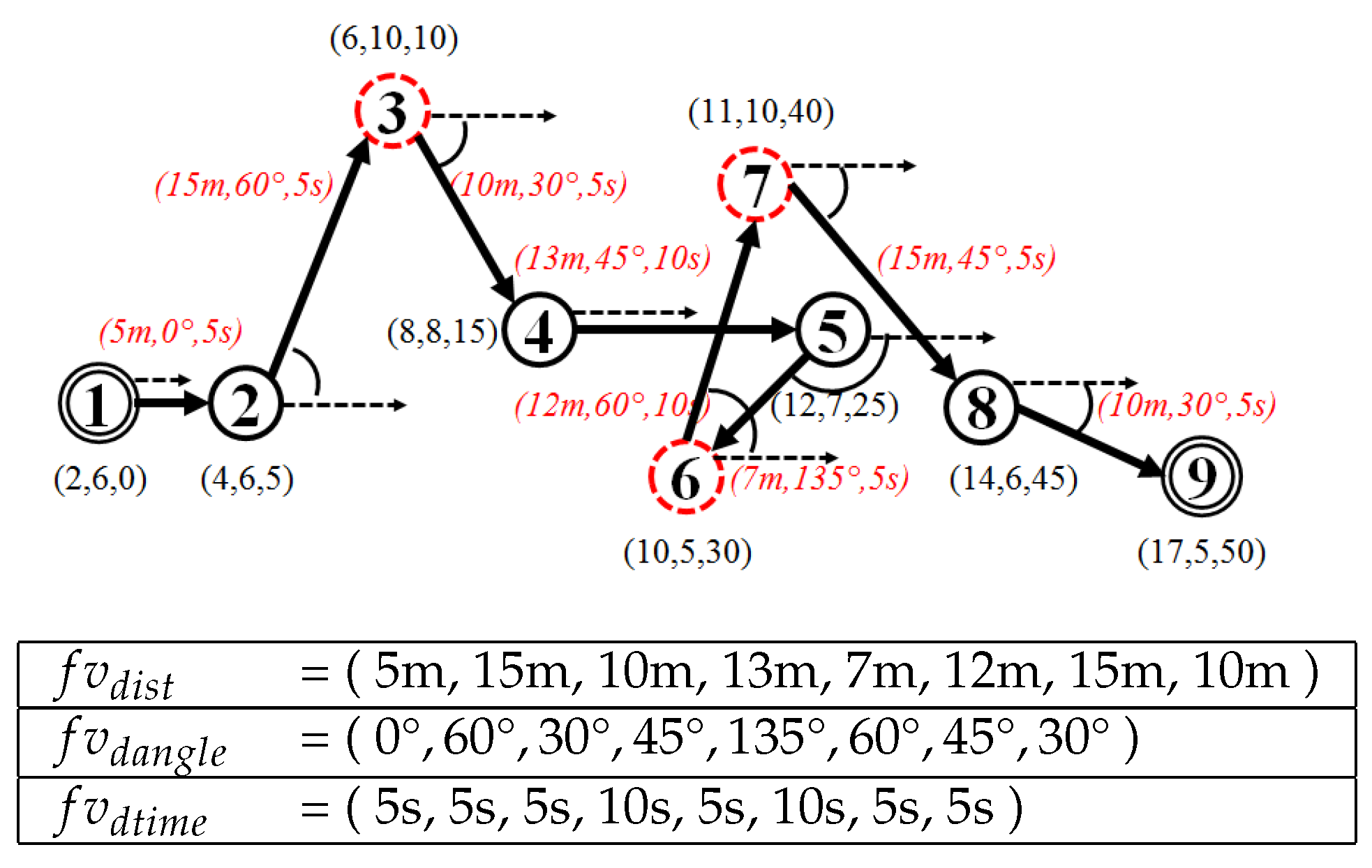
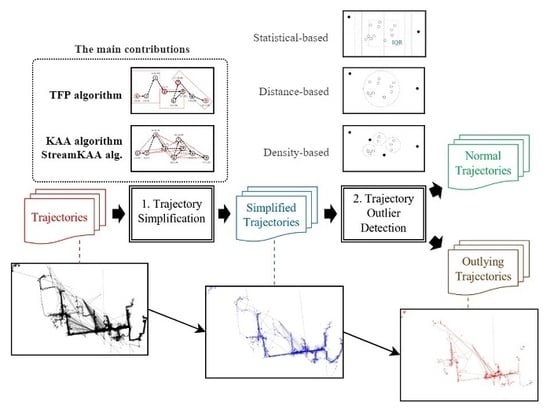
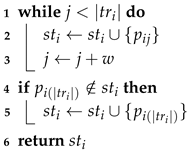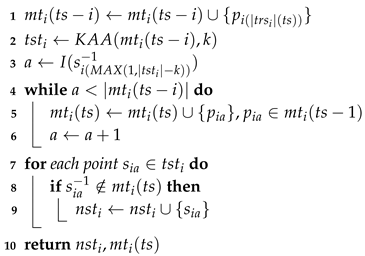5.1. Data
We verified the proposed approach by performing experiments using a real-world case study of a shipyard in South Korea. The dataset employed contains 284 trajectories with a total of 15,012 point-locations of block transporter movement. The data was taken from an actual block transporter movement based on a weekly scheduled movement. Since the planning recurs in a weekly time horizon, we considered that a weekly observation (in this case, 5 working days) was sufficient for our case study. In our dataset, 21 trajectories (7%) are the outlying-trajectories according to the domain expert. The domain expert in our case should have the following qualifications:
Doctor of Electrical Engineering or Control System Engineering;
an expert on developing logistics analysis and optimization system of shipyard; and
at least 2-years of experience in automation research in heavy industry.
The actual domain expert that work on this manuscript has all-of-the-above qualifications with the addition of an 18-years of experience in the automation research particularly in heavy industry.
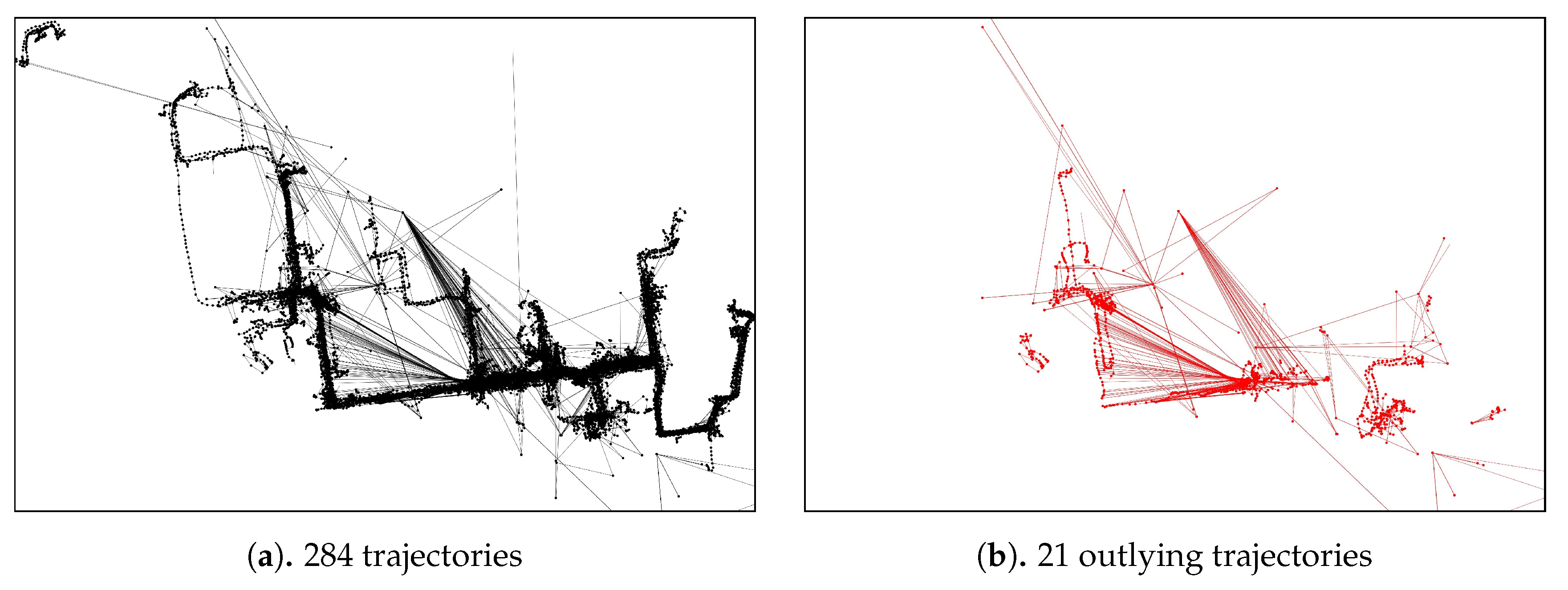
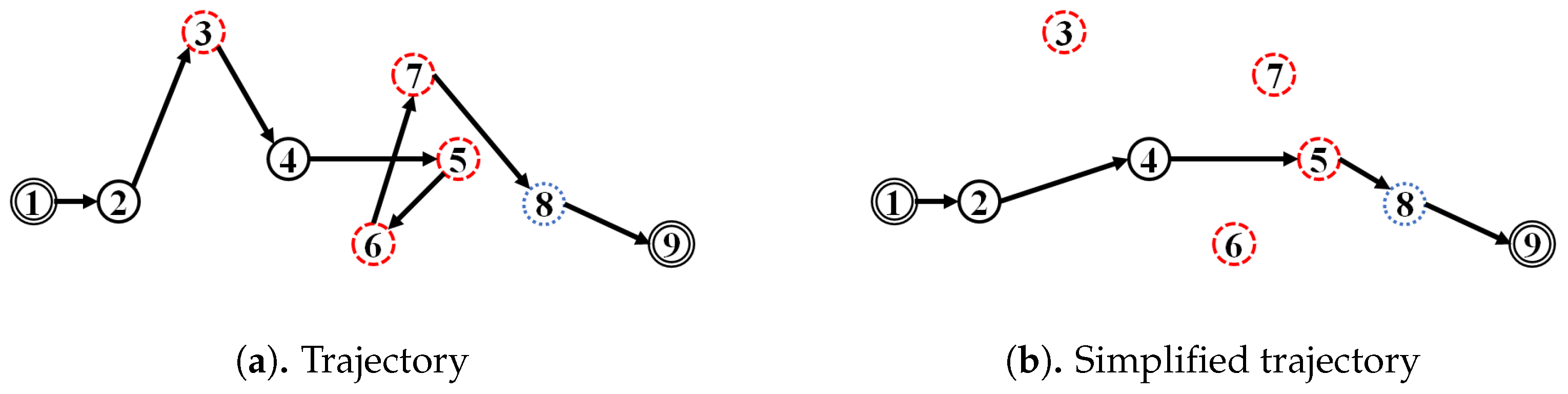
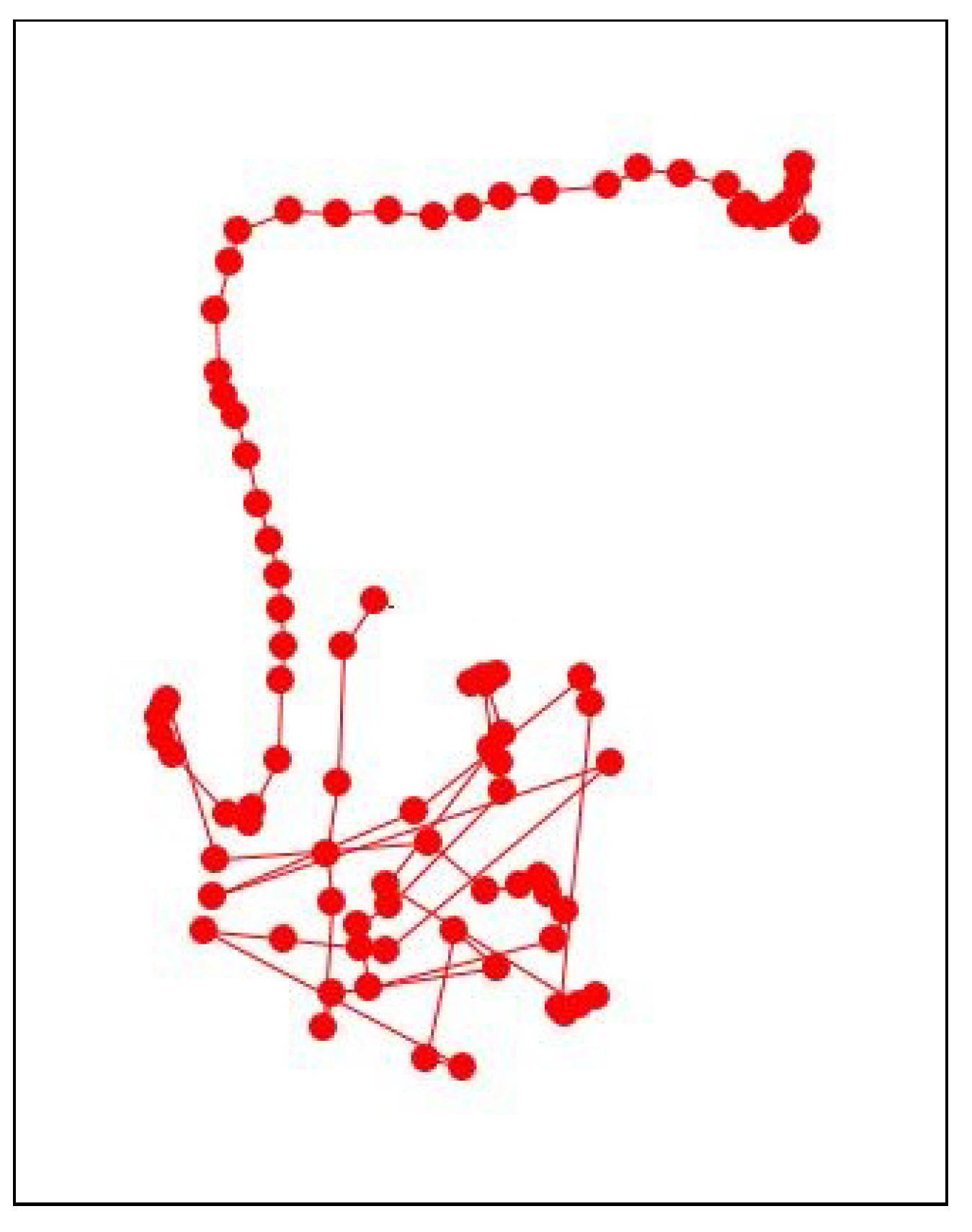
Figure 11 and, in the appendix section,
Figure A1 show an example of an outlying-trajectory, and the overall trajectories and outlying trajectories from the data identified by the domain expert, respectively.
5.2. Sensitivity Analysis
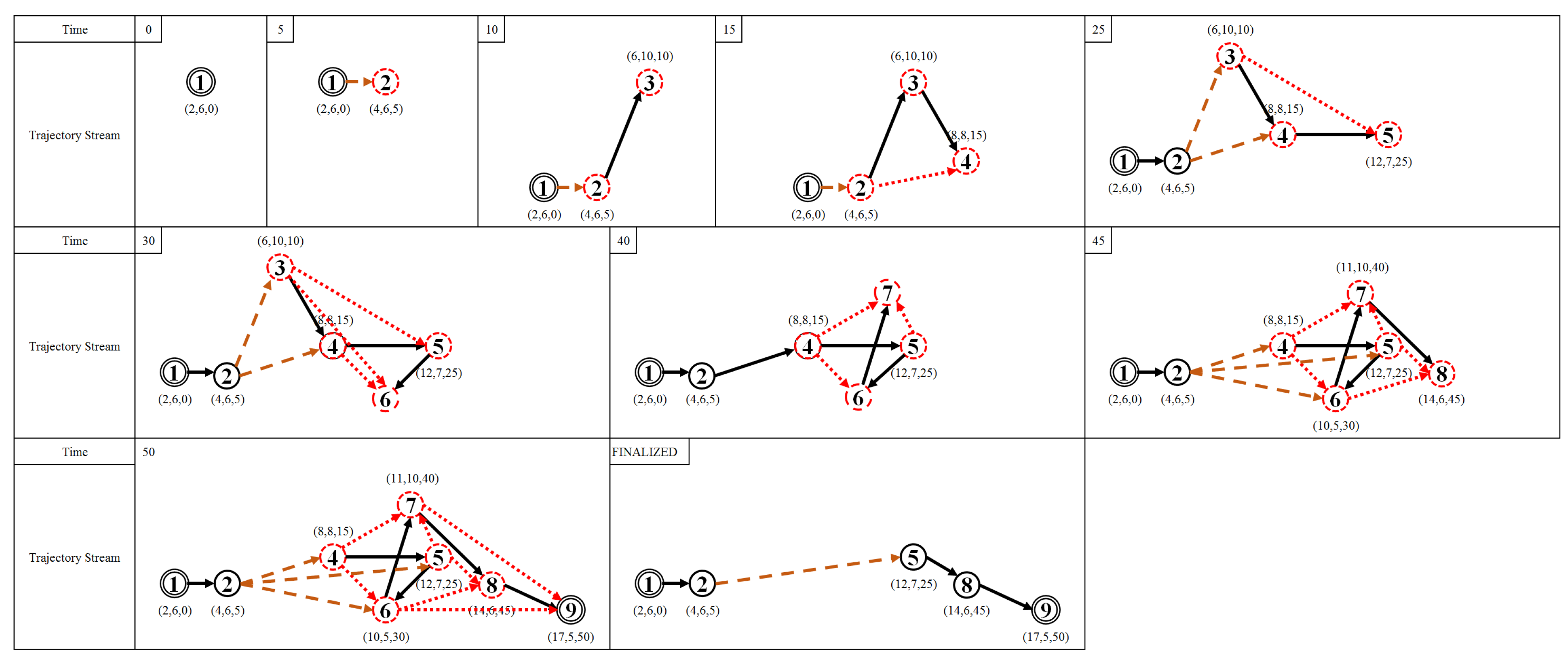
The first experiments tested the sensitivity of the t parameter of the TFP algorithm and the k parameter of the KAA algorithm for simplifying raw trajectories, under two scenarios:
absolute number scenario, with the t parameter of the TFP algorithm (TFP-ABS) and the k parameter of the KAA algorithm (KAA-ABS) is tuned within the 5–15 range notwithstanding the length of the trajectory; and
relative number scenario, with the t parameter of the TFP algorithm (TFP-REL) and the k parameter of the KAA algorithm (KAA-REL) tuned within the 5– range relative to the length of the trajectory.
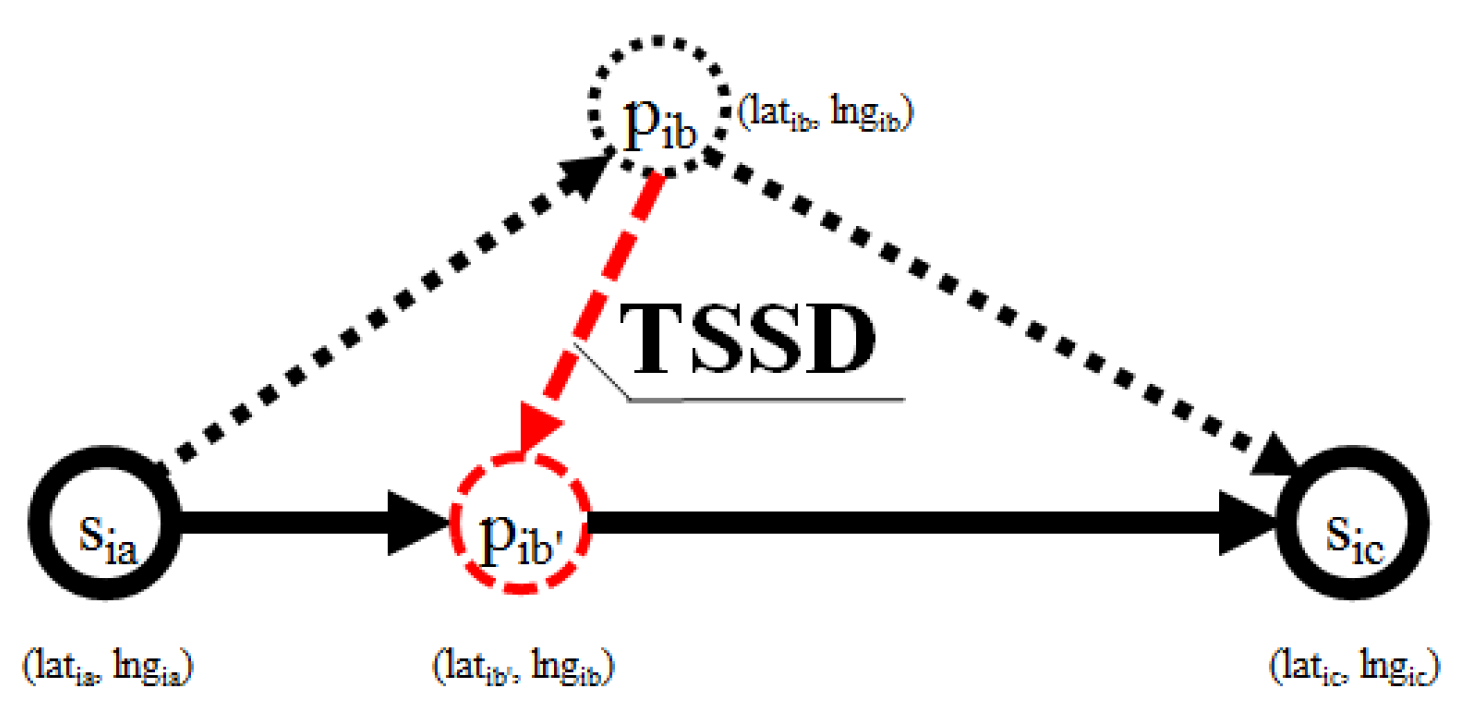
Then, a sensitivity analysis measured the compression ratio and the distance-reduced ratio between the raw and simplified trajectory. The Douglas-Peucker (DP) and the Direction-Preserving Trajectory-Simplification (DPTS) trajectory-simplification algorithm also were employed in our experiments. We varied the epsilon parameter of the DP trajectory-simplification algorithm within the 0– range, and the angular direction threshold within 5–15 degrees for the DPTS trajectory-simplification algorithm. Additionally, the StreamKAA algorithm is included by simulating each trajectory in a trajectory-stream scenario.
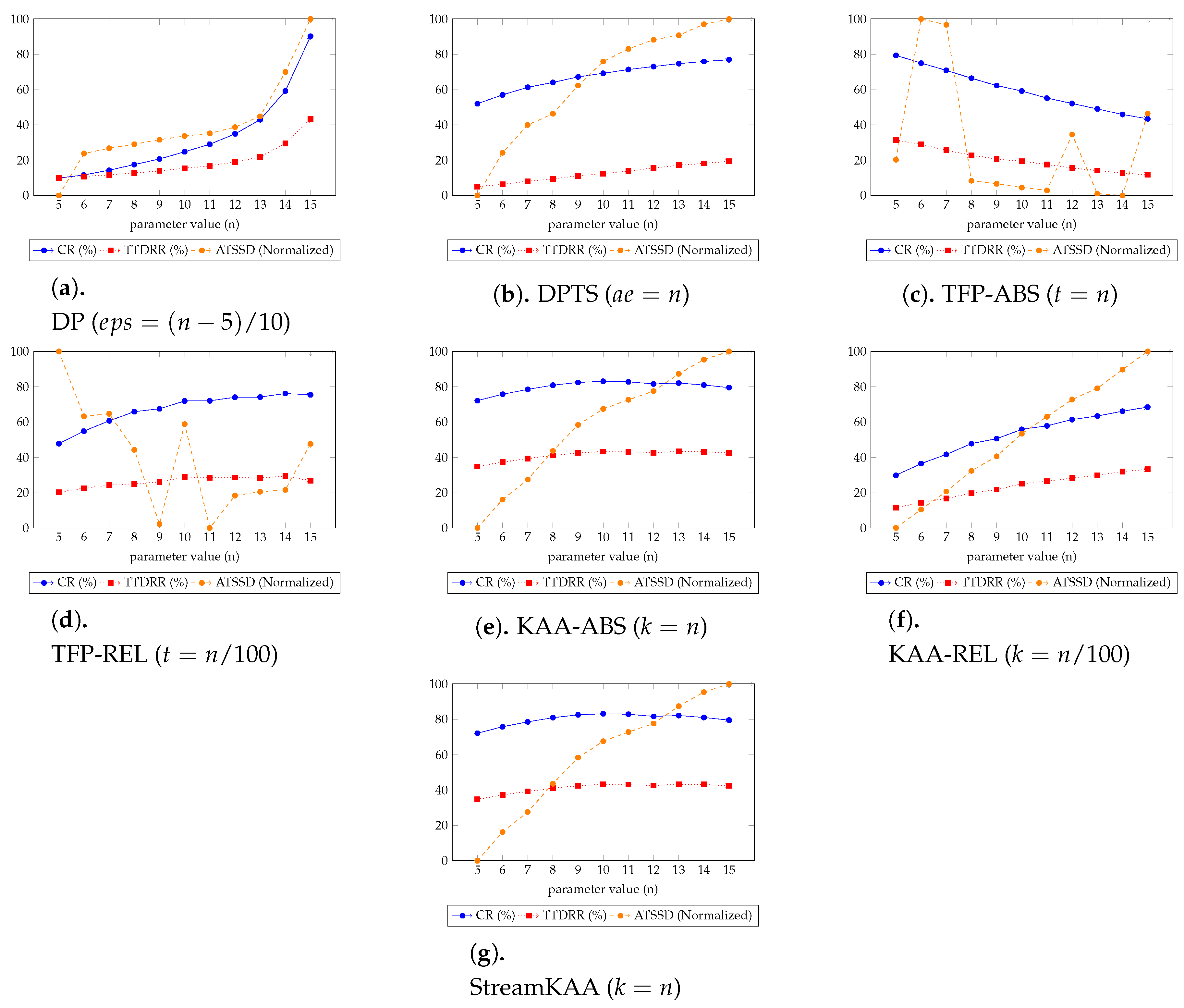
Figure 12 shows the overall experiment scenario for varying each of the input parameters. Here we try to balance the three-score metrics of CR, TTDRR, and ATSSD. The value of CR and TTDRR should lie closest to 100%, while ATSSD value should lie closest to 0 m. In
Figure 12, the value of ATSSDs are normalized into range between 0 and 100 percentage such that the values closest to 0% are considered best unless stated otherwise. The numerical version of
Figure 12 is presented in
Table A1,
Table A2 and
Table A3 (
Appendix A) for DP and DPTS algorithms, TFP algorithms, and KAA algorithms, respectively. We tried to determine, for our dataset, the
k and
t parameter that can balance the maximum compression ratio with the maximum total travel distance reduction ratio and minimum average time synchronized spatial distance.
In
Figure 12, we can categorize into three types of trends for each algorithm. For DP, DPTS and TFP-ABS algorithms, by increasing the parameter value n, all of the metrics for the simplification algorithms are having an increasing trend. While the KAA-ABS and the StreamKAA algorithms have the value of CR and TTDRR that are relatively stagnant compare to the increasing value of ATSDD; and, the TFP-ABS and the TFP-REL algorithms shows radical fluctuations for the ATSSD and a decreasing trend for CR and TTDRR metrics. The first category shows that finding the optimal parameter can be exhaustive search, the optimal parameter may lie at the end of the positive integer. The second category, we can see the convergence of CR and TTDRR regardless of the increasing trends of ATSSD values. The last category, however, the fluctuations of ATSSD can cause an unreliable selection of the parameter unless we check every possible value of ATSSD. We consider the second category as the most stable algorithm among others.
We summarized the best parameters of each algorithm in
Figure 12 in
Table 1 to determine, for our dataset, the
k and
t parameter that can balance the maximum compression ratio with the maximum total travel distance reduction ratio and minimum average time synchronized spatial distance. Based on our experiments, the balanced conditions for the DP algorithm occurred at
while the DPTS algorithm is balanced at
. For the TFP algorithm, they occurred at
and
for the absolute number and relative scenario, respectively. For the KAA algorithm, the balanced conditions occurred at
and
for the absolute number and relative scenario, respectively. In this case, the StreamKAA algorithm performs really close to KAA with absolute parameter
(KAA-ABS).
If we take a look at the individual score, the best algorithm for the CR and TTDRR metrics, having a value closest to 100%, is KAA for absolute value and the streaming KAA with value . Otherwise, TFP with an absolute value has the best score for ATTSD, having the value closest to 0 meters. This significantly improved the previous algorithms by and for the CR metrics for the DP and DPTS algorithms, respectively. For TTDRR, the improvement is and for the DP and DPTS algorithms, respectively, and there was a and decrease in terms of ATSSD for the DP and DPTS algorithms, respectively. Therefore, the percentage decreases of our algorithms compared with the previous work are considered to be improvements. Moreover, the overall best score, however, shows that KAA for absolute value is the best, whereby both CR and TTDRR are maximized and also its ATSSD is minimized among the other algorithms.
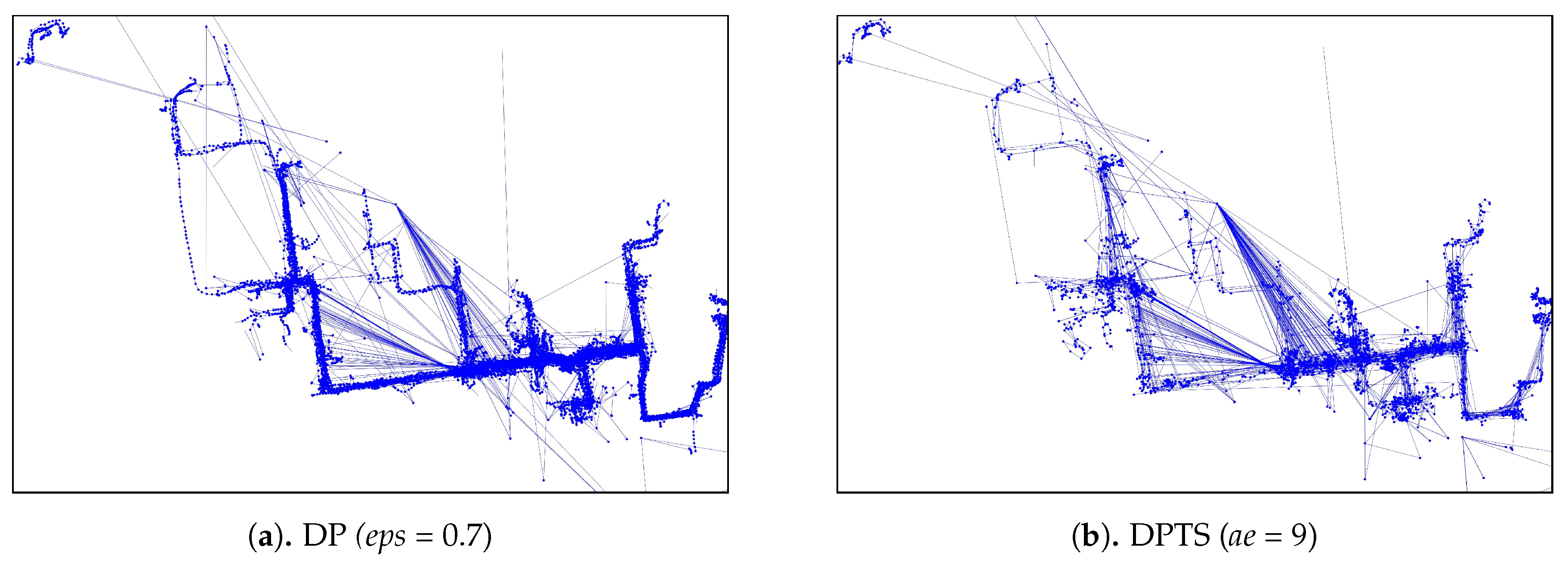
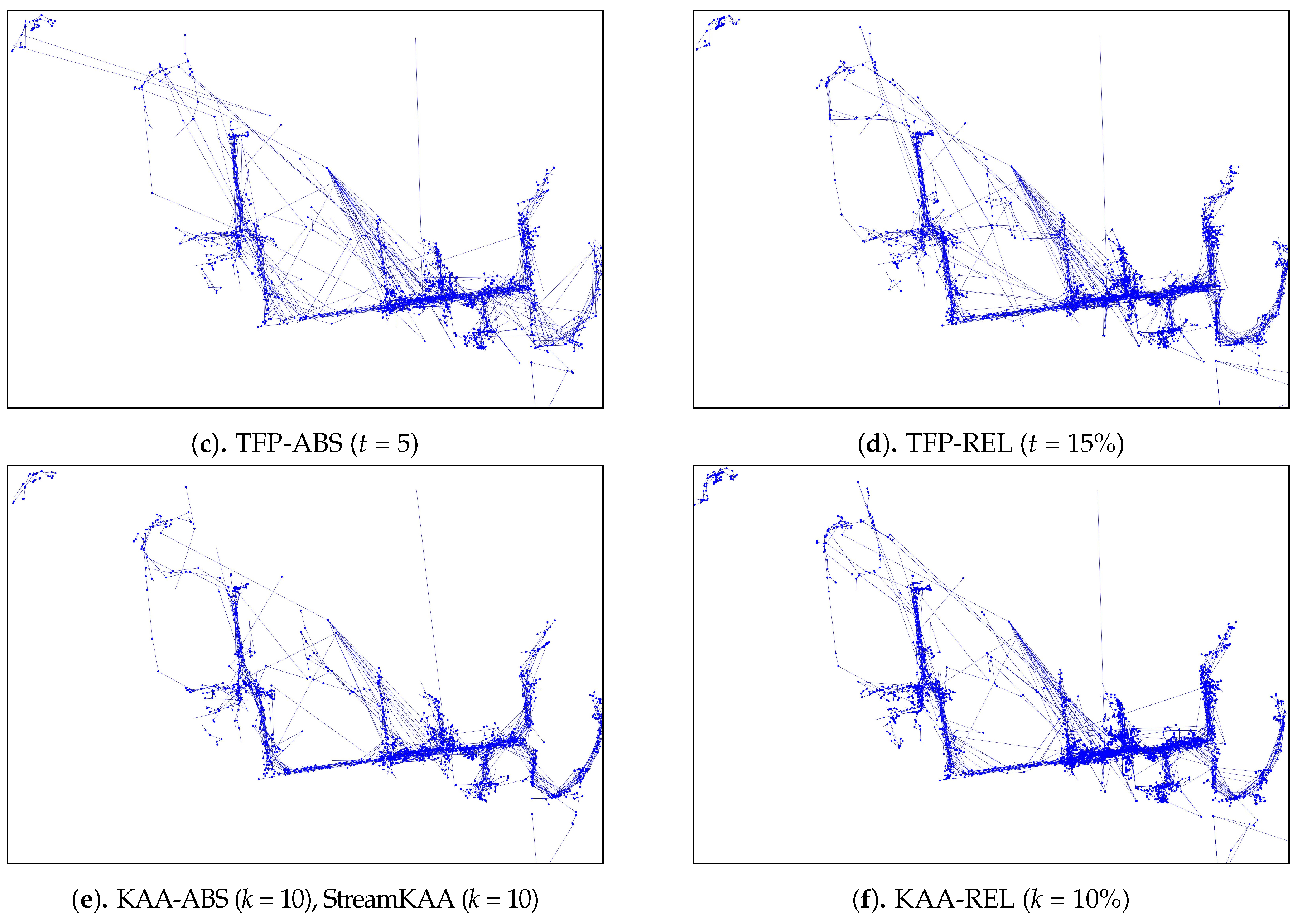
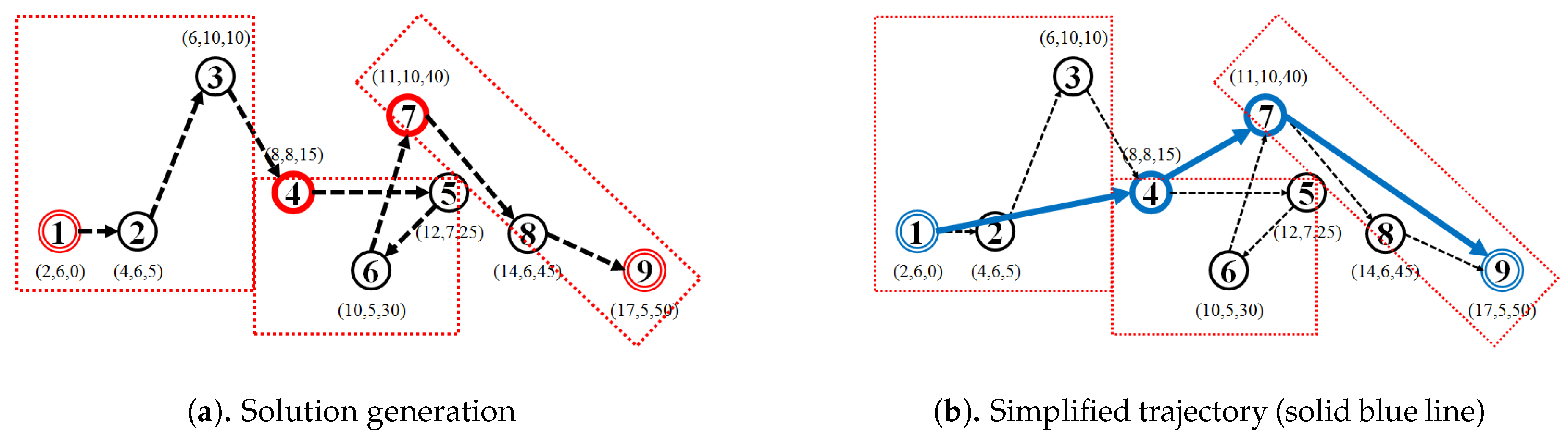
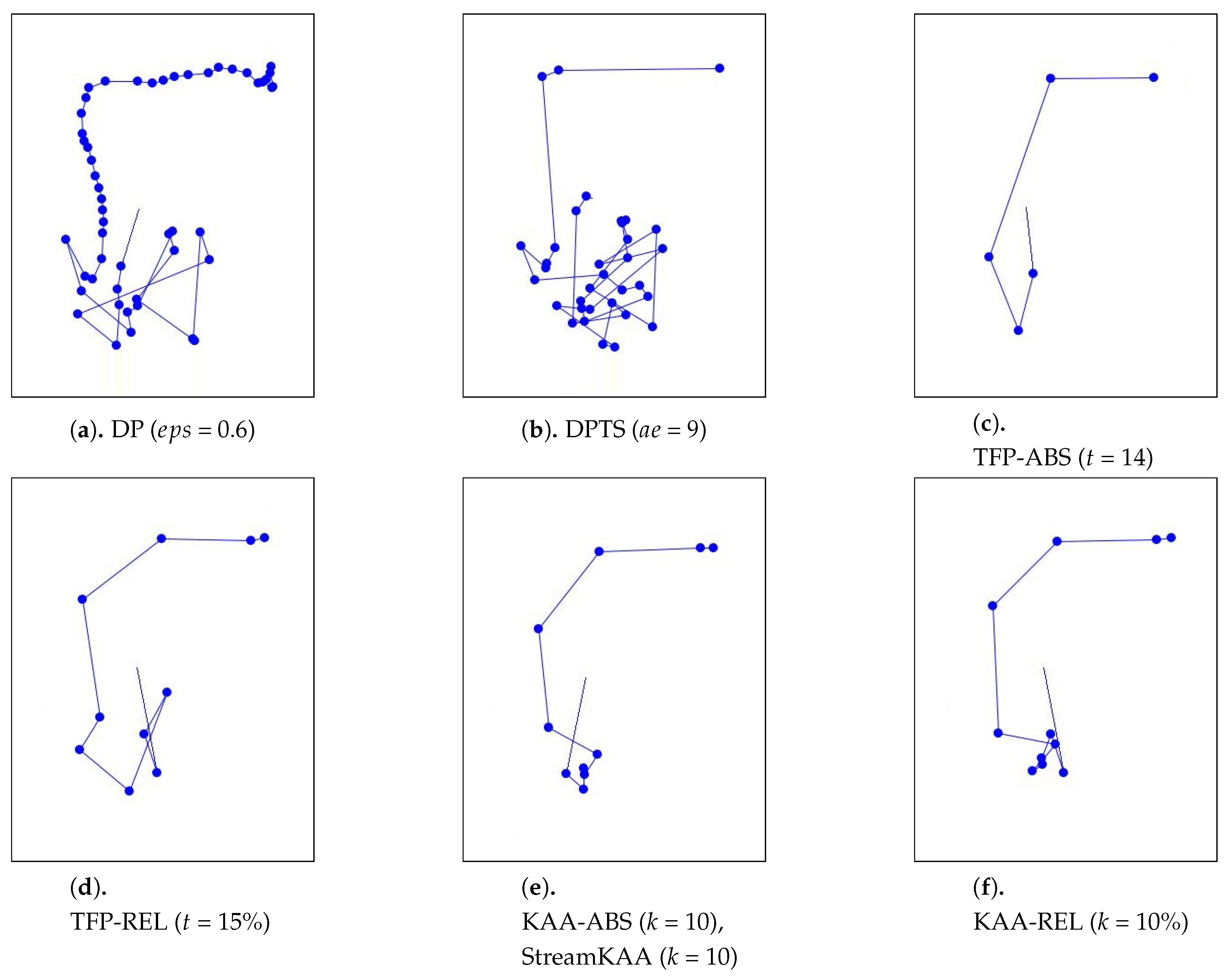
As for the visual comparison,
Figure 13 and
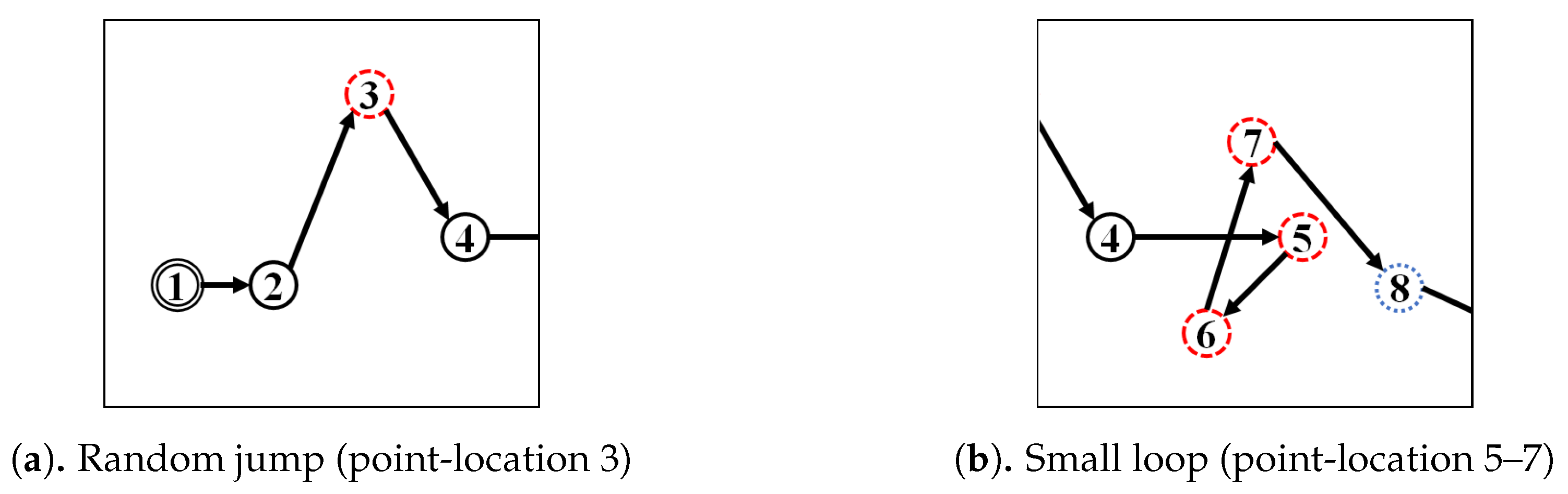
Figure A2 illustrate the corresponding simplified trajectory from trajectory-simplification algorithm at its best parameter values. The DP and DPTS trajectory-simplification algorithms had good compression scores and total travel distance reduction ratios. However, it has a relatively high score for the average time synchronized spatial distance error; and in fact, the visual comparison result clarified the fact that it is not robust against noise. Meanwhile, according to the visual comparison results, our algorithm is more robust against noise and at the same time gives a moderate compression ratio. The visual comparison results also shows that our algorithms outperformed previous algorithms, since it considered several points at a time to anticipate the occurrence of random jumps and small loops in a trajectory. Additionally, the previous works used error rates as input parameters, such that they sometimes failed to avoid noise in the form of point-locations far from their ‘true’ locations.
5.3. Outlier-Detection
After applying the trajectory-simplification algorithm, we tested the following three outlier-detection algorithms against the configurations respectively specified:
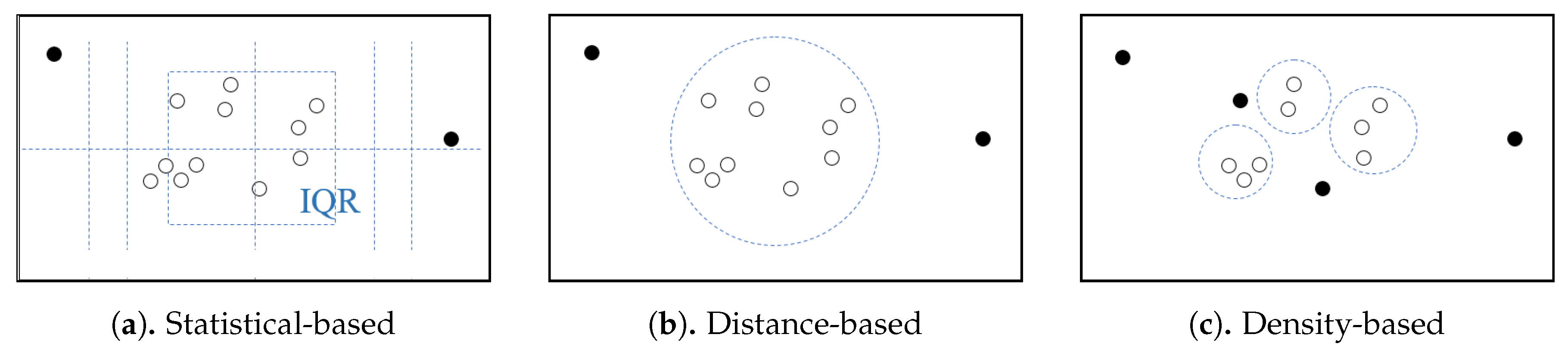
Statistics-based outlier-detection: Based on the recommendation of the original work called Tukey’s Boxplot [
28], we use the following parameters settings: Outlier factor set to
and extreme value factor set to
. Using this parameters settings, if the value of the feature vector is either three times or more above the third quartile or three times or more below the first quartile it will qualify as an outlier, while the value of feature vector is either 1.5 or more above the third quartile or 1.5 or more below the first quartile is called suspected outlier;
distance-based outlier-detection (): Given the idea that an outlier should be far from most of the population, and the domain expert is able to identify 7% of trajectories are outlying-trajectories, we assumed that normal trajectories are trajectory that have a maximum normalized distance of 0.5 () to 90% of the total number of trajectories (); and
density-based outlier-detection (): Following the distance-based outlier-detection, we assumed that a maximum local density of a trajectory cluster are 10% of the total number of trajectories, then we set , where denotes the total number of trajectories in set TR (our dataset contained 284 trajectories). So, we could use the 28th (0.1 × 284) nearest neighbors from a trajectory to determine the local density of a trajectory cluster.
The statistics-based outlier-detection is used to detect an outlying point-location from single trajectory. The distance-based and density-based outlier-detection detects a trajectory that significantly different from others trajectory, if the length of feature-vector of a trajectory is different, a dynamic time warp approach [
32] is used. We use the input parameter of
and
for statistic-based outlier detection,
and
for distance-based outlier detection, and
for density based outlier detection. We use the domain expert’s manual trajectory classification (whether a trajectory is outlier or not) as the target class, and, comparing our outlier detection result with the target class using precision and recall metrics. The precision is calculated by dividing the number of the true positive observation with the sum of the true and the false positive observations, while the recall is calculated by dividing the number of the true positive observation with the sum of the true positive and the false negative observations.
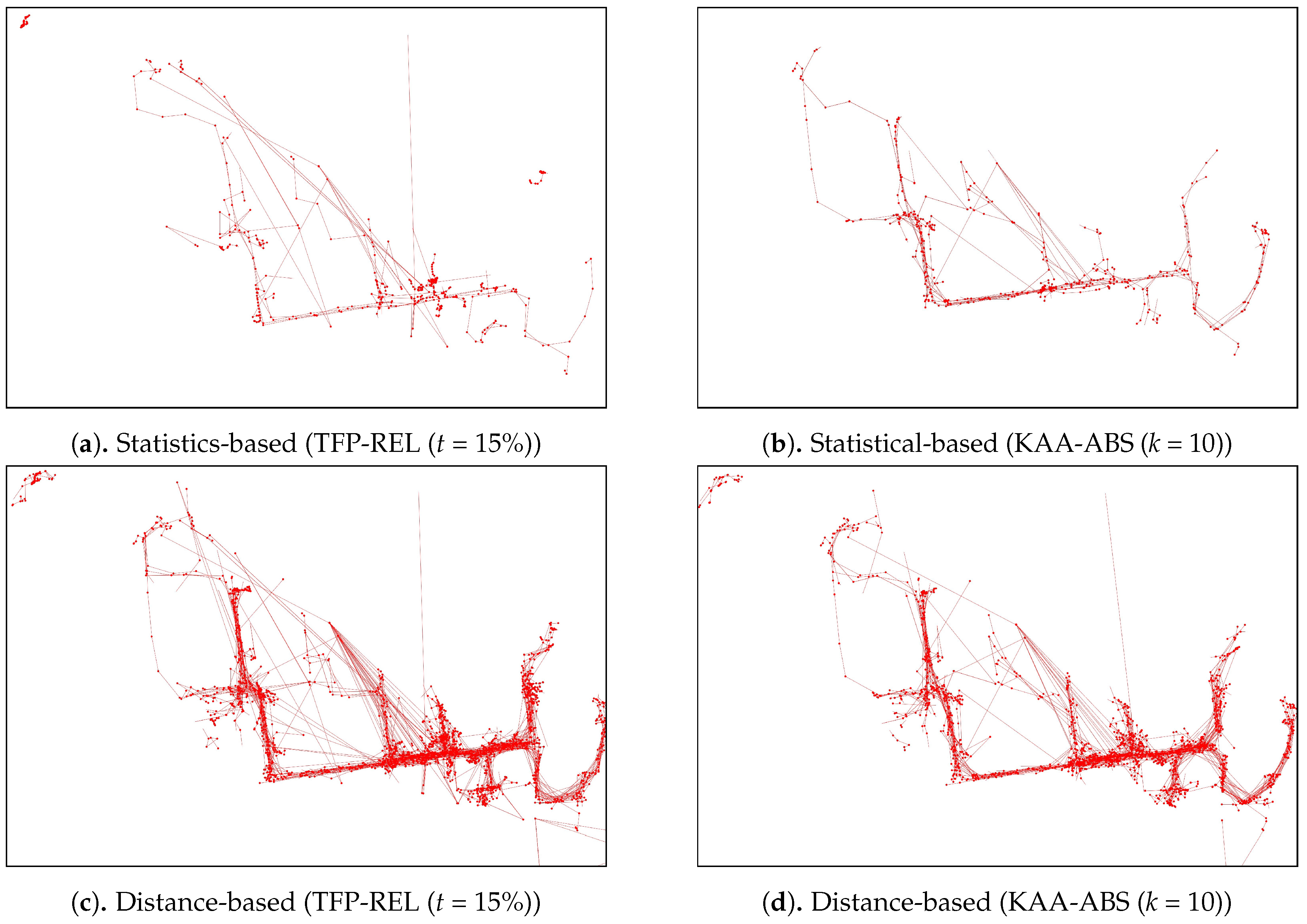
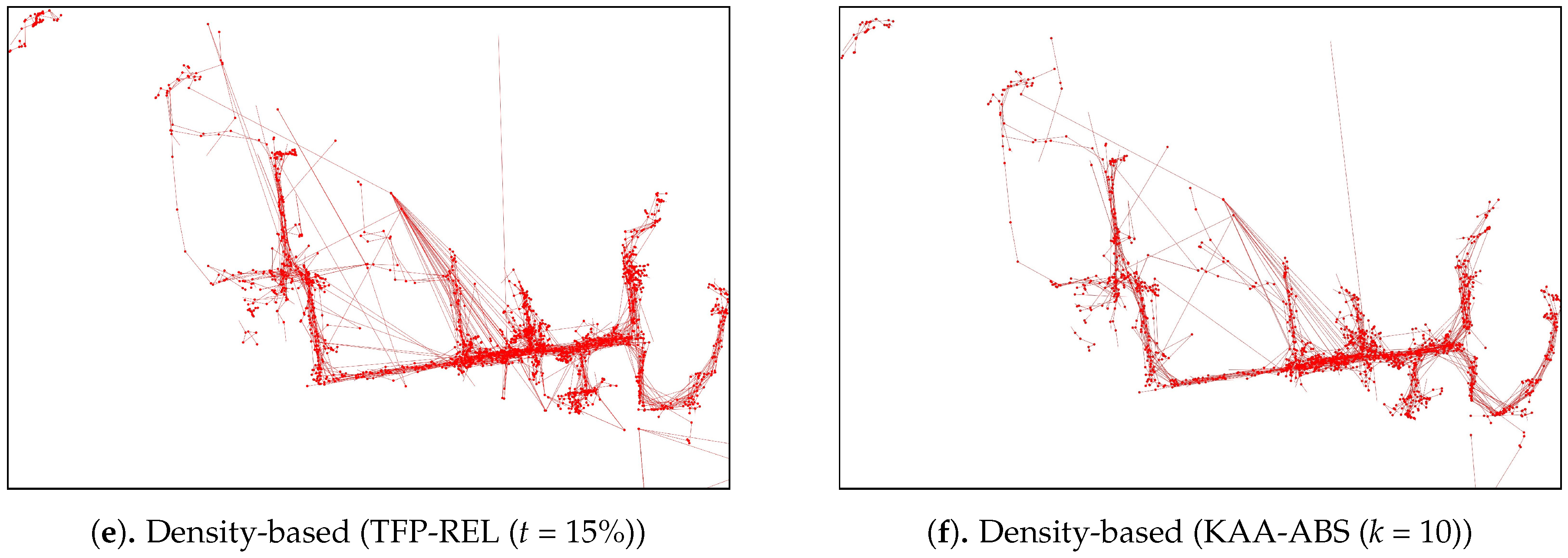
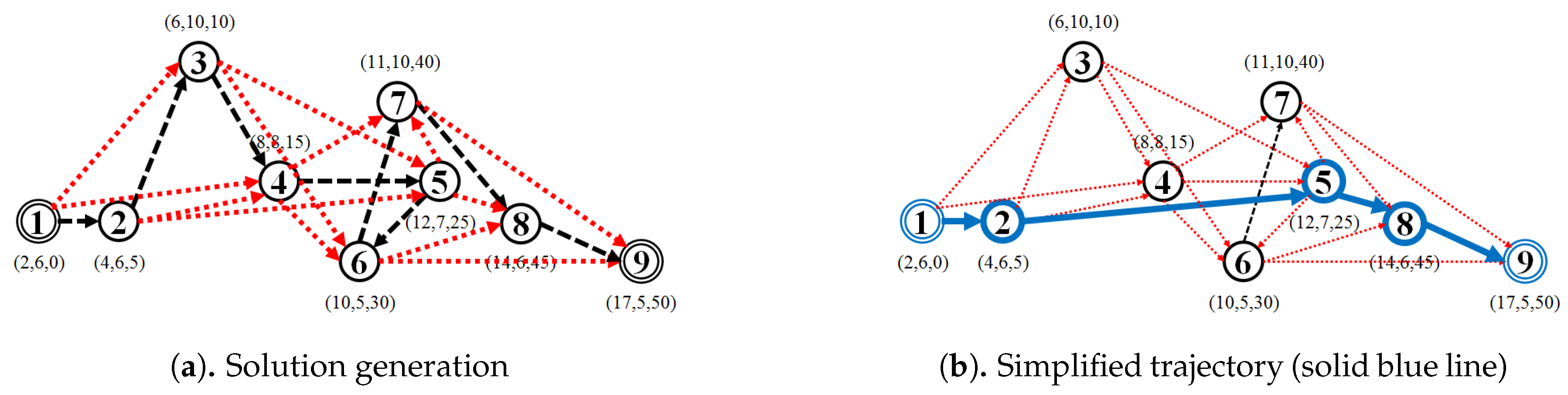
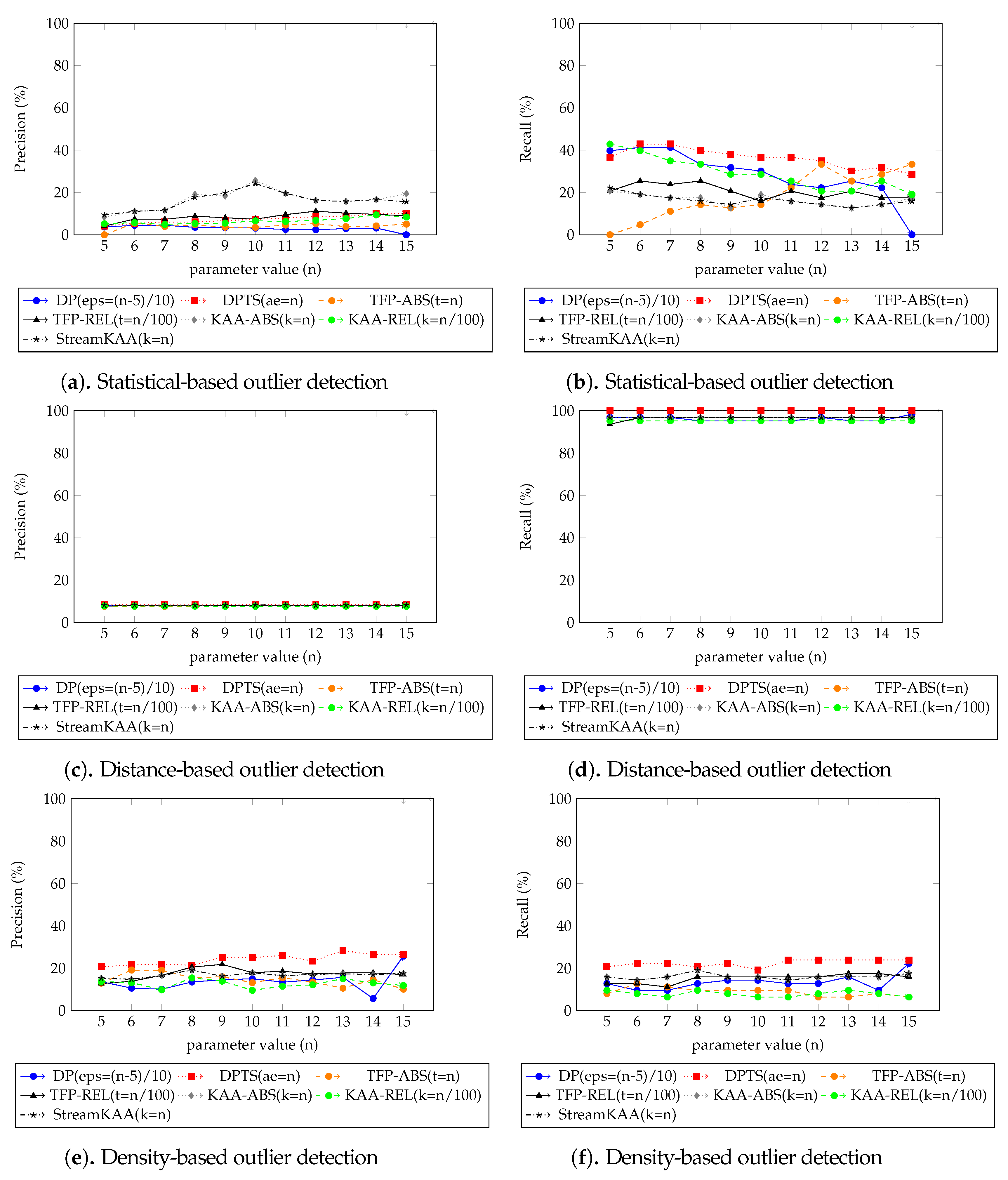
Figure 14 plots the performance results from the various outlier-detection algorithms. As for the visual comparison results,
Figure A3 illustrate the corresponding TFP and KAA-simplified trajectories, respectively, for the best parameter values. The outlier detection results after applying the trajectory-simplification algorithms are quite interesting. The statistics-based outlier detection precision improved when we increased the parameter of the trajectory-simplification algorithm; however, the recall value varies. The distance-based outlier detection precision and recall are somewhat similar for all trajectory-simplification algorithms regardless of parameter values. The density-based outlier detection precision and recall are quite similar for all trajectory-simplification algorithms.
We summarized our outlier-detection algorithm results of each outlier-detection algorithm shown in
Figure 14 in
Table 2 from the best parameter of each trajectory-smoothing algorithm shown in
Figure 12, for our dataset, which outlier-detection algorithm is performed best corresponds to the result of trajectory-simplification algorithms. The statistics-based outlier-detection precision is almost similar throughout all trajectory-simplification algorithms with KAA algorithm with
followed TFP algorithm with
is performed best with
and
precision, respectively; however, the DPTS algorithm with
and TFP with
is having better recall value. For the distance-based and the density-based outlier detections, the DPTS algorithm with
is performed best followed by the KAA algorithm with
in both precision and recall. However, due to the small number of outlying trajectories in our dataset, i.e., around 7%, the value of precision and recall seem very low since it does not even exceed 30% mark except for recall value on distance-based outlier detection algorithm. The overall best score, however, shows that DPTS algorithm with
is still performing at best followed by our KAA algorithm with
.