A GIS Tool for Mapping Dam-Break Flood Hazards in Italy
Abstract
1. Introduction
2. The methodological Framework
2.1. Dam-Break Outflow Hydrograph Calculator
2.2. Flood Propagation Calculator
2.3. DEM-Based Dam-break Hazard Mapping Calculator
2.4. The Implementation of the Tool: Libraries and Components
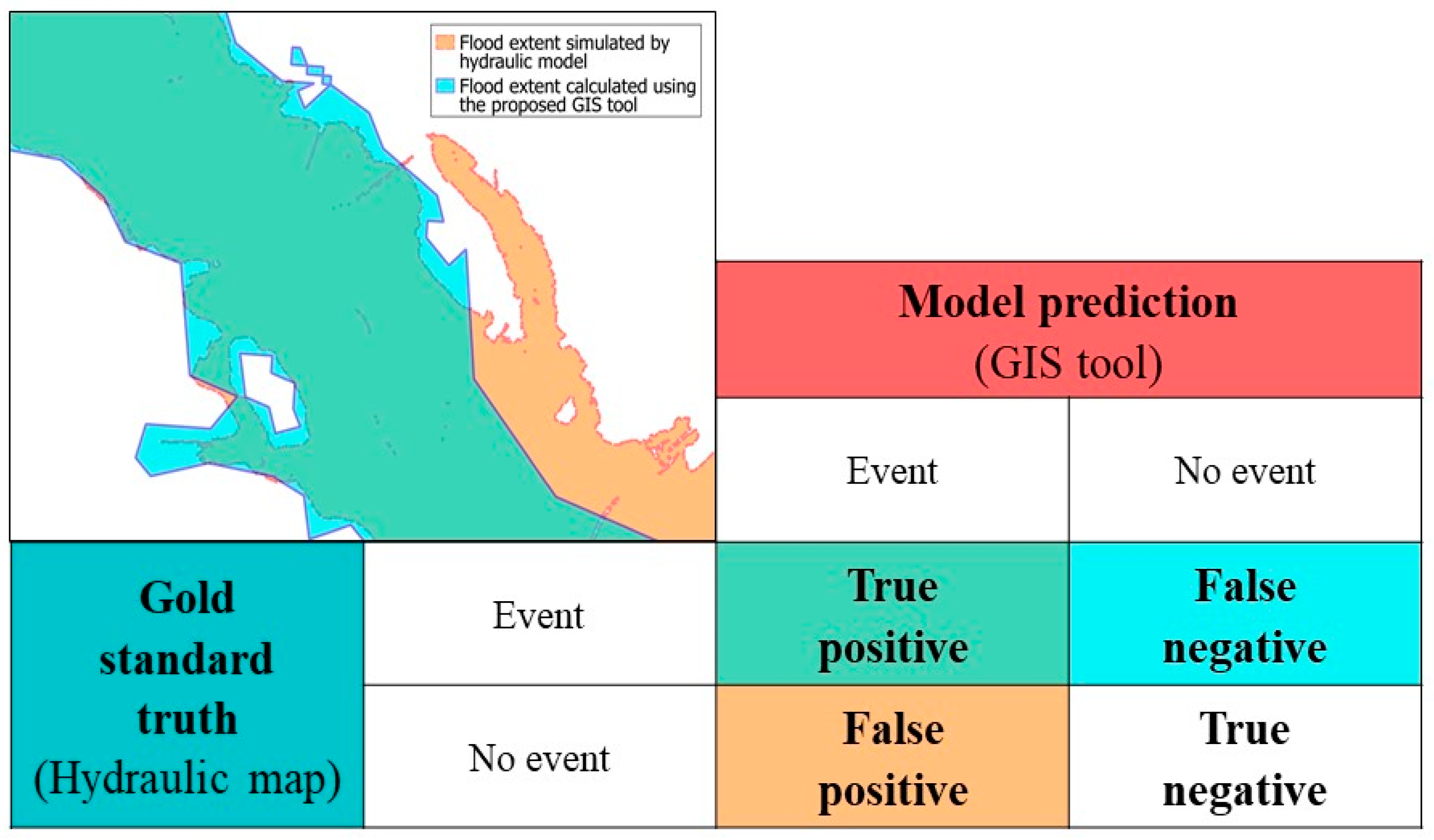
2.5. Validation
3. Case Studies
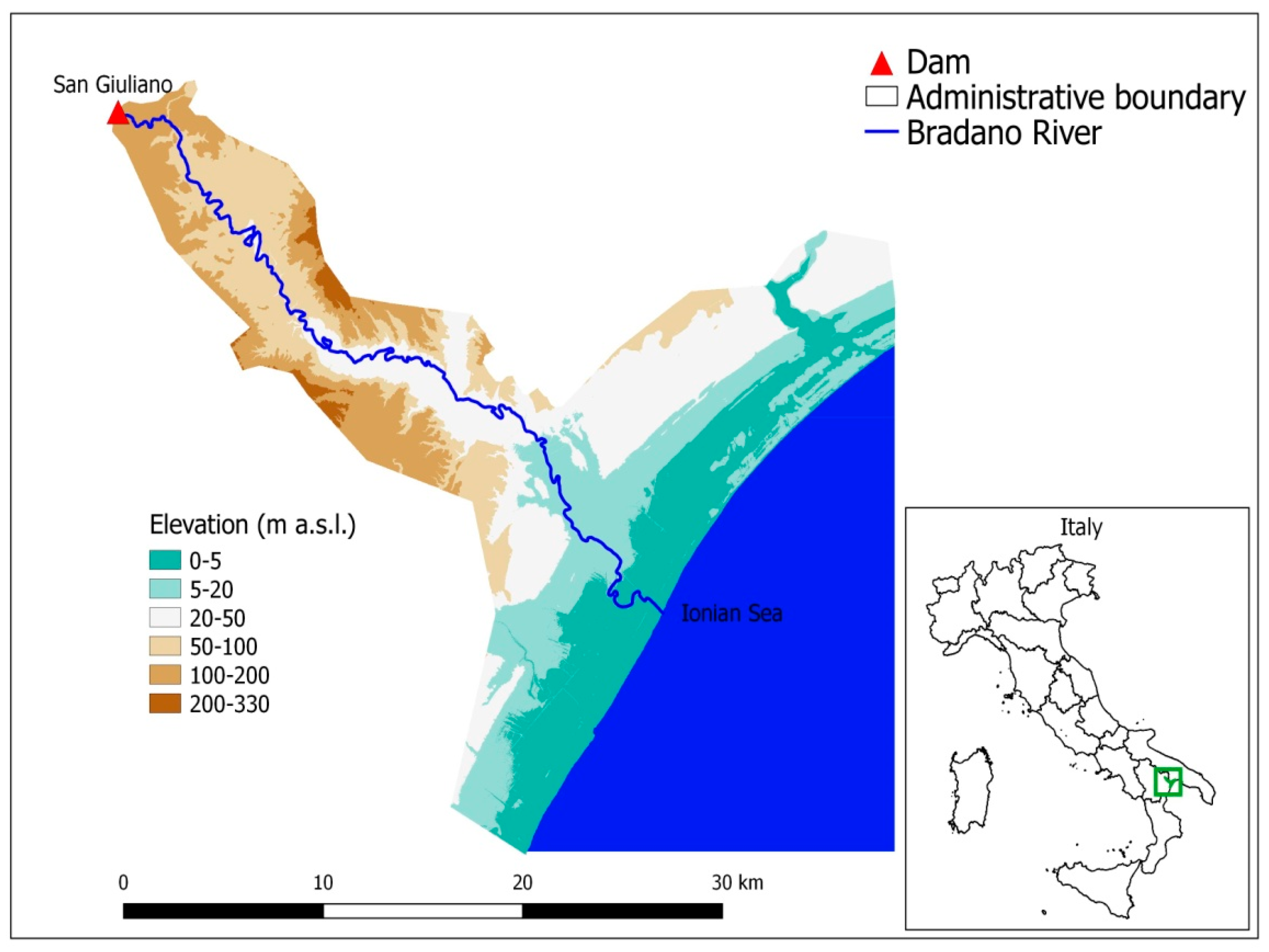
3.1. The San Giuliano Dam test case
3.1.1. 1D Hydrodynamic Study
3.1.2. 2D Hydrodynamic Modelling
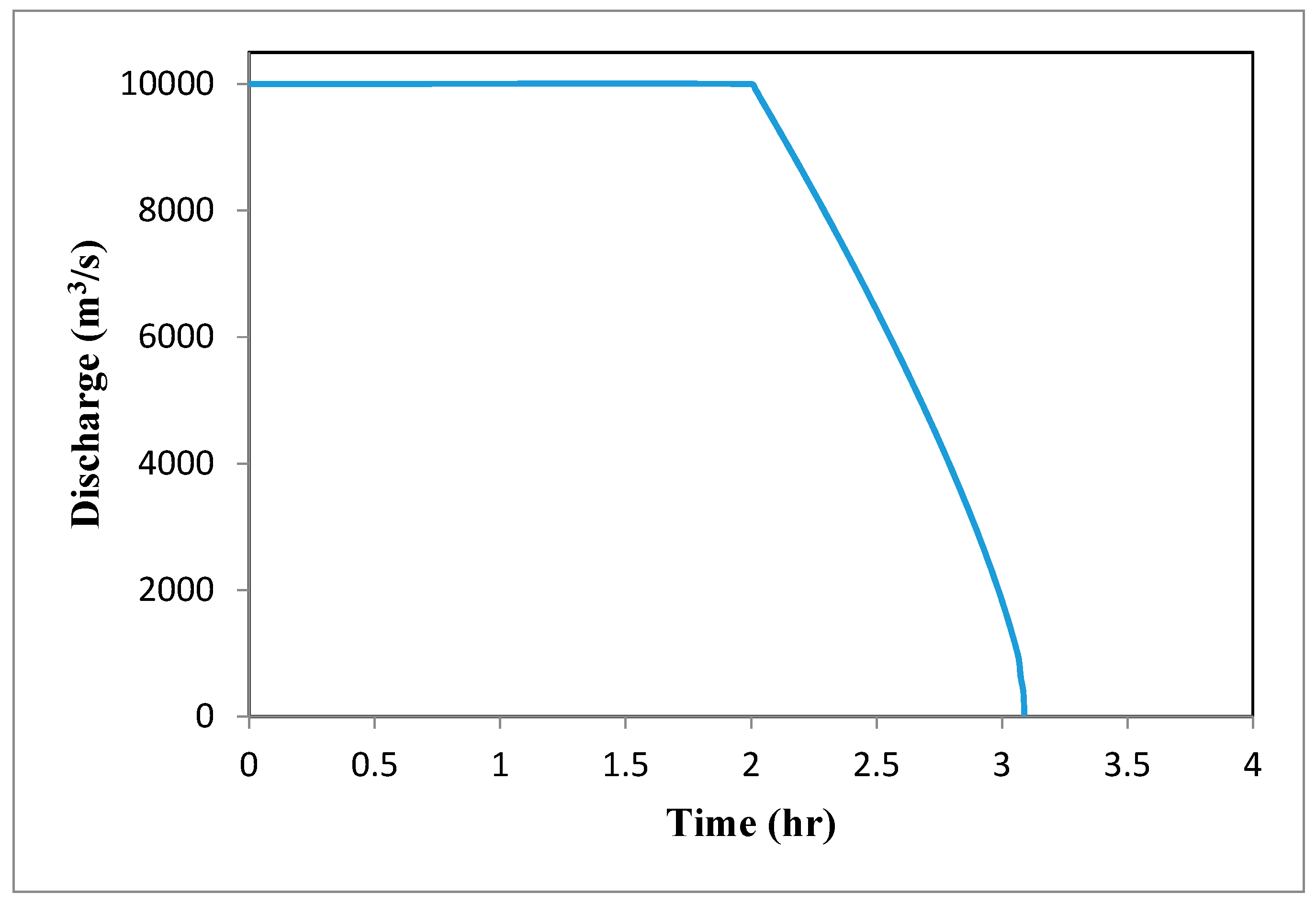
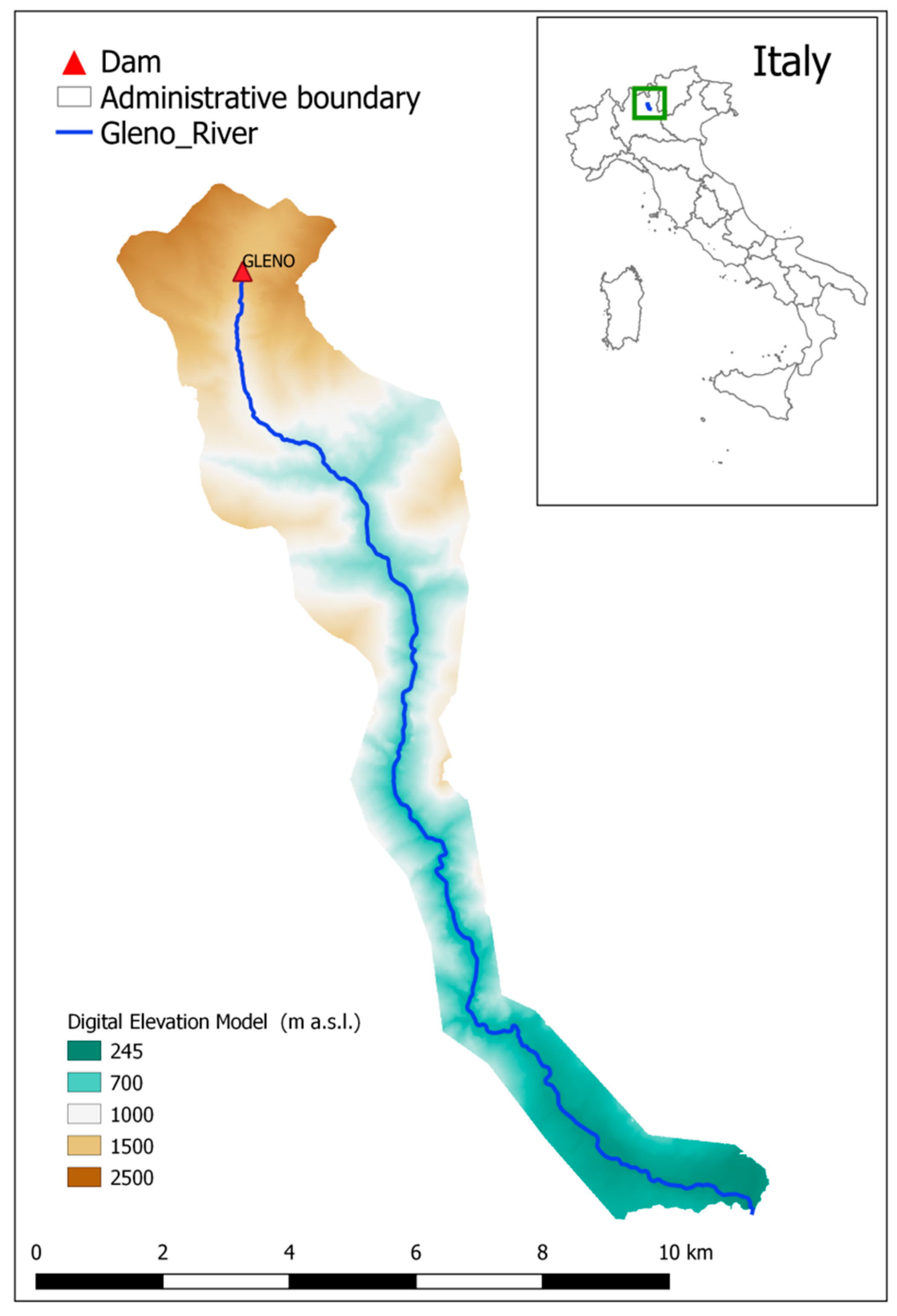
3.2. The Gleno Dam-Break Case Study
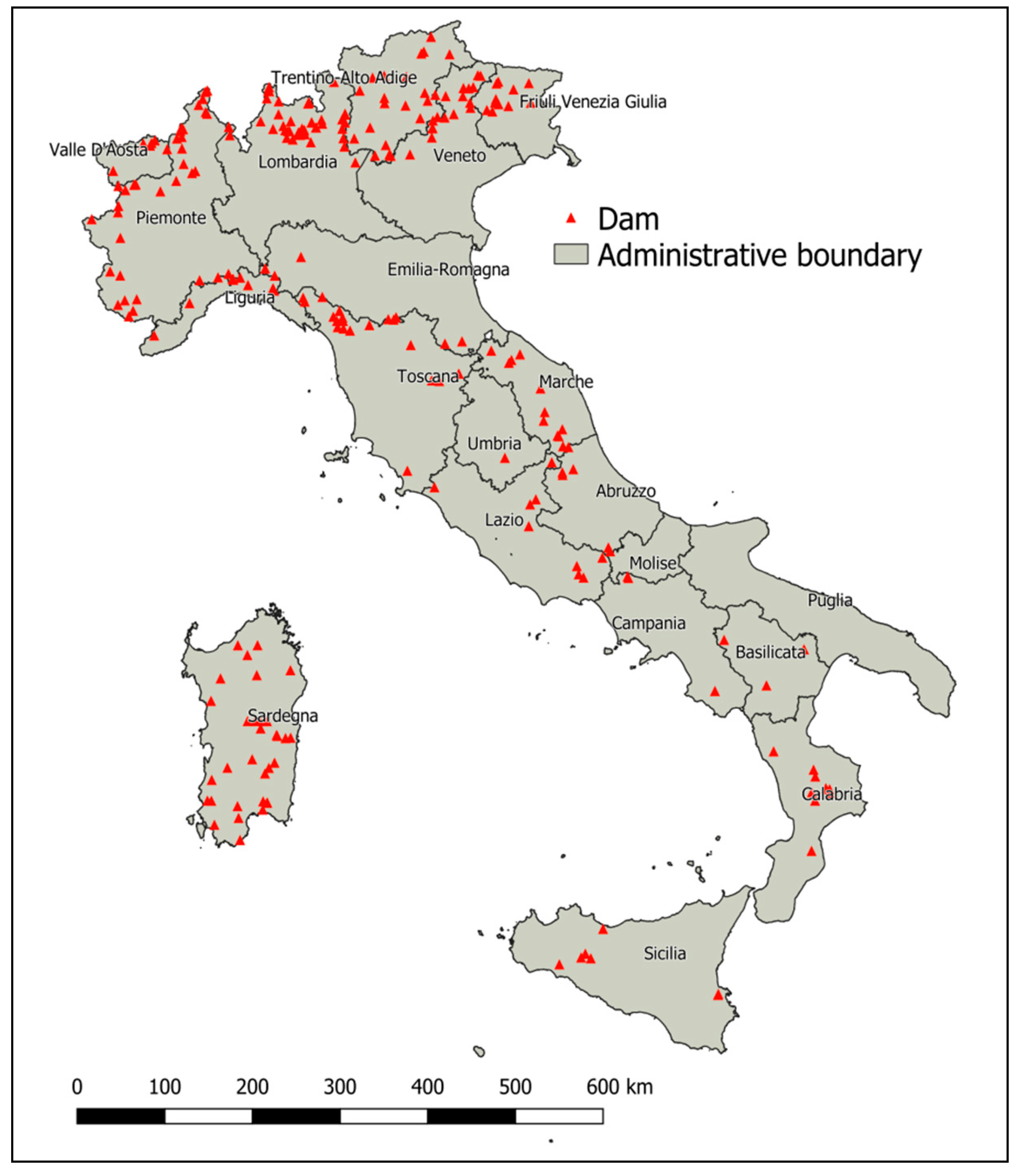
3.3. Example Application of Structural Failure for the 250 Existing Italian Masonry Arch and Gravity Dams
4. Results
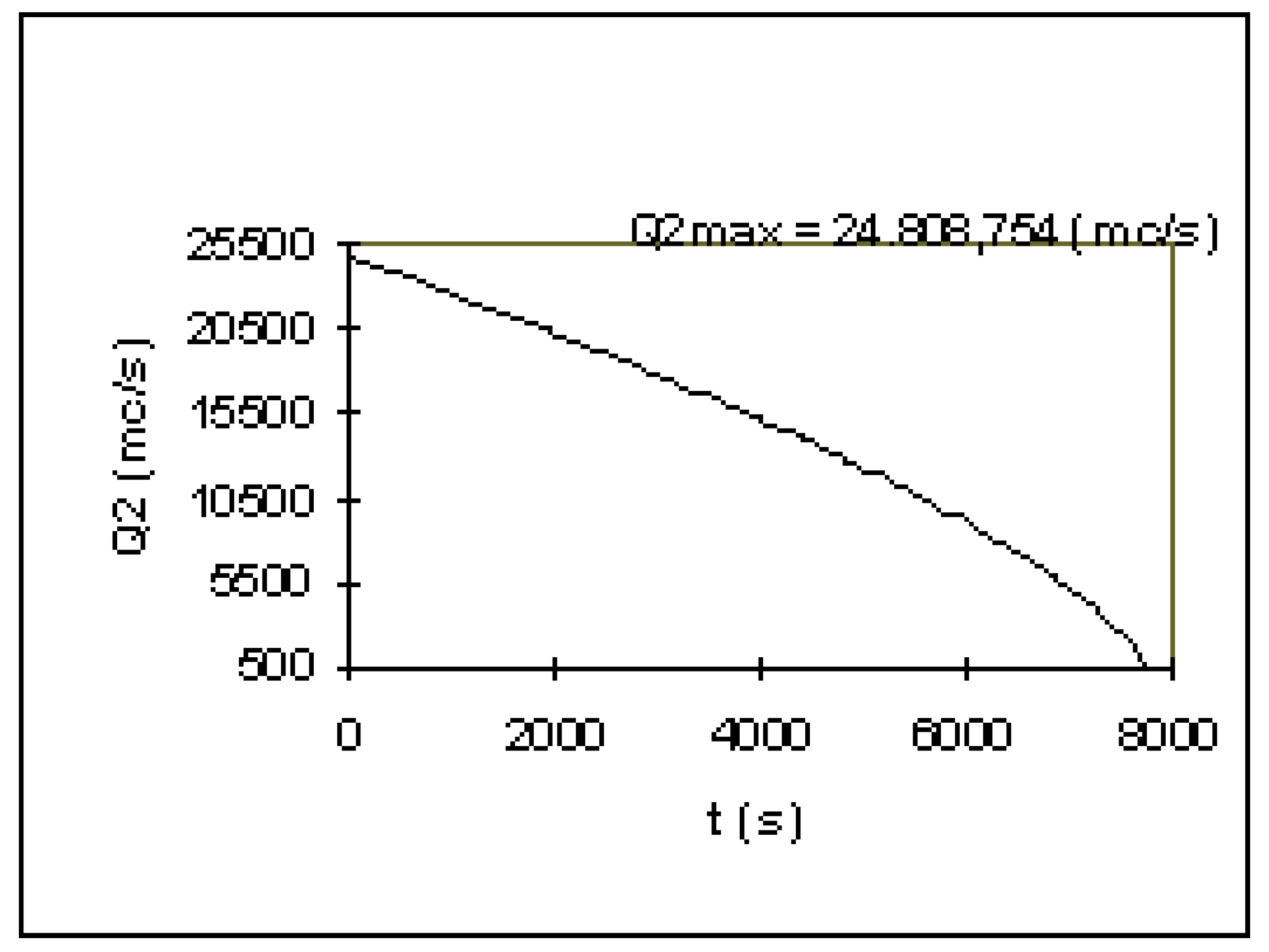
4.1. The Application on the San Giuliano Dam Case Study
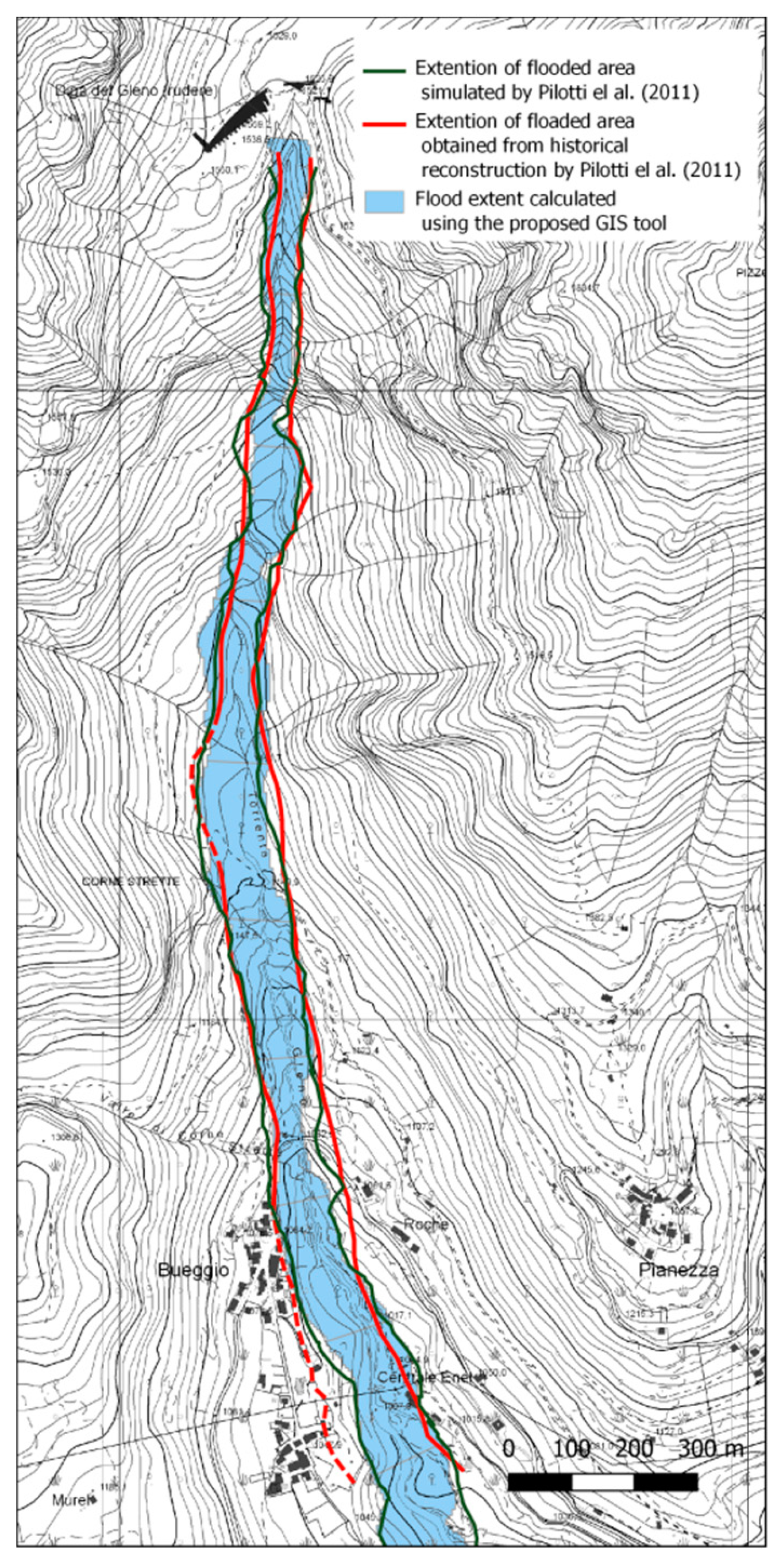
4.2. Validation on the 1923 Gleno Dam-Break
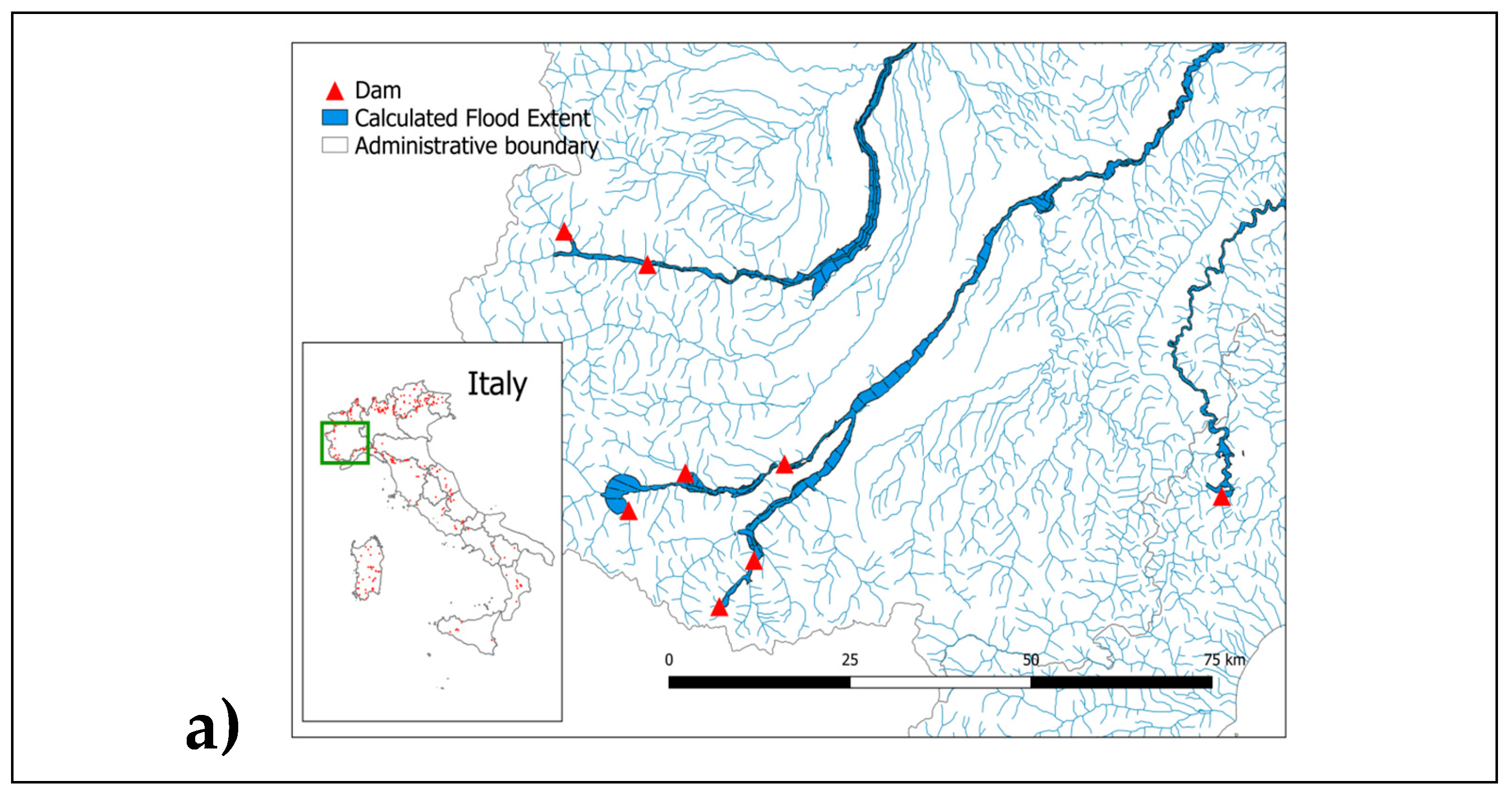
4.3. Computational Performance on Large Number of Dam-Break Cases
5. Discussion and Conclusion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fluixá-Sanmartín, J.; Altarejos-García, L.; Morales-Torres, A.; Escuder-Bueno, I. Review article: Climate change impacts on dam safety. Nat. Hazards Earth Syst. Sci. 2018, 18, 2471–2488. [Google Scholar] [CrossRef]
- Bonafè, A.; Mancusi, L.; Chieppa, V. The outlets vulnerability in the assessment of the safety of the dams/La vulnerabilità degli scarichi nella valutazione della sicurezza idraulica delle dighe. L’Acqua 2018, 6, 73–81. [Google Scholar]
- Falcucci, E.; Gori, S.; Bignami, C.; Pietrantonio, G.; Melini, D.; Moro, M.; Sarolli, M.; Galadini, F. The Campotosto Seismic Gap in Between the 2009 and 2016–2017 Seismic Sequences of Central Italy and the Role of Inherited Lithospheric Faults in Regional Seismotectonic Settings. Tectonics 2018, 37, 2425–2445. [Google Scholar] [CrossRef]
- De Moel, H.; Bouwer, L.M.; Aerts, J.C.J.H. Uncertainty and sensitivity of flood risk calculations for a dike ring in the south of the Netherlands. Sci. Total Environ. 2014, 473–474, 224–234. [Google Scholar] [CrossRef] [PubMed]
- Collenteur, R.A.; de Moel, H.; Jongman, B. The failed-levee effect: Do societies learn from flood disasters? Nat Hazards 2015, 76, 373. [Google Scholar] [CrossRef]
- Pu, J.H.; Shao, S.; Huang, Y.; Hussain, K. Evaluations of SWEs and SPH numerical modelling techniques for dam break flows. Eng. Appl. Comput. Fluid Mech. 2013, 7, 544–563. [Google Scholar]
- Lin, G.F.; Lai, J.S.; Guo, W.D. Performance of high-resolution TVD schemes for 1D dam-break simulations. J. Chin. Inst. Eng. 2005, 28, 771–782. [Google Scholar] [CrossRef]
- Manenti, E.; Pierobon, M.; Gallati, S.; Sibilla D’Alpaos, L.; Macchi, E.G.; Todeschini, S. Vajont Disaster: Smoothed Particle Hydrodynamics Modelling of the Postevent 2D Experiments. J. Hydraul. Eng. 2016, 142, 05015007. [Google Scholar] [CrossRef]
- Albano, R.; Mirauda, D.; Sole, A.; Adamowski, J. Modelling Large Floating Bodies in Urban Floods via a Smoothed Particle Hydrodynamics Model. J. Hydrol. 2016, 541 Pt A, 344–358. [Google Scholar] [CrossRef]
- George, A.C.; Nair, T.B. Dam Break analysis Using BOSS DAMBRK. Acquat. Procedia 2015, 4, 853–860. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Zhang, S.H.; Xia, Z.X.; Yuan, R.; Jiang, S.M. Parallel computation of a dam-break flow model using OpenMP on a multi-core computer. J. Hydrol. 2014, 512, 126–133. [Google Scholar] [CrossRef]
- Samela, C.; Albano, R.; Sole, A.; Manfreda, S. An open source GIS software tool for cost effective delineation of flood prone areas. Comput. Environ. Urban Syst. 2018, 70, 43–52. [Google Scholar] [CrossRef]
- Albano, R.; Craciun, I.; Mancusi, L.; Sole, A.; Ozunu, A. Flood damage assessment and uncertainity analysis: The case study of 2006 flood in Ilisua Basin in Romania. Carpath. J. Earth Environ. Sci. 2017, 12, 335–346. [Google Scholar]
- Seyedashraf, O.; Rezaei, A.; Akhtari, A.A. Dam break flow solution using artificial neural network. Ocean Eng. 2017, 142, 125–132. [Google Scholar] [CrossRef]
- Seyedashraf, O.; Mehrabi, M.; Akhtari, A.A. Novel approach for dam break flow modelling using computational intelligence. J. Hydrol. 2018, 559, 1028–1038. [Google Scholar] [CrossRef]
- Albano, R.; Mancusi, L.; Sole, A.; Adamowski, J. Sustainable and collaborative strategies for EU flood risk management: FOSS and Geospatial Tools—Challenge and opportunities for operative risk analysis. ISPRS Int. J. Geo-Inf. 2015, 4, 2704–2727. [Google Scholar] [CrossRef]
- Ritter, A. Die Fortpflanzung der Wasserwelle (Generation of the water wave). Z. Ver. Dtsch. Ing. 1982, 36, 947–954. (In German) [Google Scholar]
- Ven Te Chow. Open-Channel Hydraulics; McGraw-Hill Companies: New York, NY, USA, 1959. [Google Scholar]
- CGIAR-CSI Shuttle Radar Topography Mission DEM. Available online: http://srtm.csi.cgiar.org/ (accessed on 10 April 2017).
- Registro Italiano Dighe. Available online: www.registroitalianodighe.it (accessed on 10 July 2015).
- ANIDEL. Le dighe di ritenuta degli impianti idroelettrici italiani—Tecnica delle dighe di ritenuta in Italia; Associazione Nazionale Imprese Produttrici e Distributrici di Energia Elettrica: Roma, Italy, 1961. [Google Scholar]
- ENEL. Dighe di ritenuta degli impianti idroelettrici italiani, Le dighe appartenenti all’ENEL di costruzione posteriore al 1953; ENEL: Roma, Italy, 1970. [Google Scholar]
- Geoportale Nazionale—Ministero dell’Ambiente e della Tutela del Territorio e del Mare (Italia). Available online: http://www.pcn.minambiente.it/mattm/ (accessed on 10 March 2018).
- PostGIS—Spatial and Geographic objects for PostgreSQL. Available online: https://postgis.net/ (accessed on 20 April 2018).
- Marchi, E.; Rubatta, A. Meccanica dei Fluidi; UTET: Torino, Italy, 1981. [Google Scholar]
- Hunt, B. A perturbation solution of the flood-routing problem. J. Hydraul. Res. 1987, 25, 215–234. [Google Scholar] [CrossRef]
- Molinaro, P.; Fenaroli, G. Discussione dell’articolo di Hunt B. J. Hydraul. Res. 1988, 3, 26. [Google Scholar]
- Albano, R.; Sole, A.; Adamowski, J.; Perrone, A.; Inam, A. Using FloodRisk GIS freeware for uncertainty analysis of direct economic flood damages in Italy. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 220–229. [Google Scholar] [CrossRef]
- Albano, R.; Mancusi, L.; Sole, A.; Adamowski, J. FloodRisk: A collaborative, free and open-source software for flood risk analysis. Geomat. Nat. Hazards Risk 2017, 8, 1812–1832. [Google Scholar] [CrossRef]
- GDAL/OGR (Geospatial Data Abstraction) Python Library. Available online: https://www.gdal.org/ (accessed on 15 January 2018).
- NumPy Python Library. Available online: http://www.numpy.org/ (accessed on 7 May 2019).
- QGIS Desktop GIS. Available online: https://www.qgis.org/it/site/ (accessed on 7 May 2019).
- ScriptRunner QGIS Plugin. Available online: Github.com/g-sherman/Script-Runner (accessed on 7 May 2019).
- SQLite Database. Available online: https://www.sqlite.org/index.html (accessed on 7 May 2019).
- Pilotti, M.; Maranzoni, A.; Tomirotti, M.; Valerio, G. 1923 Gleno Dam Break: Case Study and Numerical Modelling. J. Hydraul. Eng. 2011, 137, 480–492. [Google Scholar] [CrossRef]
- Sole, A.; Crisci, A.; Scuccimarra, V. Studio dell’onda di sommersione conseguente all’ipotetico collasso e a manovre agli organi di scarico della diga si S. Giuliano; Pubblicazione interna DIFA Unibas: Potenza, Italy, 1997. [Google Scholar]
- Scarpino, S.; Albano, R.; Cantisani, A.; Mancusi, L.; Sole, A.; Milillo, G. Multitemporal SAR Data and 2D Hydrodynamic Model Flood Scenario Dynamics Assessment. ISPRS Int. J. Geo-Inf. 2018, 7, 105. [Google Scholar] [CrossRef]
- Chapi, K.; Singh, V.P.; Shrizadi, A.; Shahabi, H.; Bui, D.T.; Pham, B.T.; Khorsravi, K. A novel hybrid artificial intelligence approach for flood susceptibility assessment. Environ. Model. Softw. 2017, 95, 229–245. [Google Scholar] [CrossRef]
- Cantisani, A.; Giosa, L.; Mancusi, L.; Sole, A. FLORA-2D: A New Model to Simulate the Inundation in Areas Covered by Flexible and Rigid Vegetation. Int. J. Eng. Innov. Technol. 2014, 3, 179–186. [Google Scholar]
- Sole, A.; Giosa, L.; Albano, R.; Cantisani, A. The laser scan data as a key element in the hydraulic flood modelling in urban areas. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences—ISPRS Archive, London, UK, 29–31 May 2013. [Google Scholar]
- HEC-RAS—Hydrologic Engineering Center. Available online: https://www.hec.usace.army.mil/software/hec-ras/ (accessed on 15 June 2017).
- RSDI—Geoportale Basilicata—Regione Basilicata. Available online: https://rsdi.regione.basilicata.it/ (accessed on 30 August 2018).
- GNDCI—Progetto VAPI. Available online: http://www.gndci.cnr.it/it/vapi/welcome_it.htm (accessed on 20 August 2018).
- Benoist, G. Les études d’ondes de submersion des grands barrages d’EDF. La Houille Blanche 1989, 1, 43–54. (In French) [Google Scholar] [CrossRef][Green Version]
- Tsakiris, G. Flood risk assessment: Concepts, modelling, applications. Nat. Hazards Earth Syst. Sci. 2014, 14, 1361–1369. [Google Scholar] [CrossRef]
- Tsai, C.W.; Yeh, J.-J.; Huang, C.-H. Development of probabilistic inundation mapping for dam failure induced floods. Stoch. Environ. Res. Risk Assess. 2019, 33, 91–110. [Google Scholar] [CrossRef]
- Peter, S.J.; Siviglia, A.; Nagel, J.; Marelli, S.; Boes, R.M.; Vetsch, D.; Sudret, B. Development of Probabilistic Dam Breach Model Using Bayesian Inference. Water Resour. Res. 2018, 54, 4376–4400. [Google Scholar] [CrossRef]
- Wahl, T.L. Uncertainty of predictions of embankment dam breach parameters. J. Hydraul. Eng. 2004, 130, 389–397. [Google Scholar] [CrossRef]
- Froehlich, D.C. Embankment dam breach parameters and their uncertainties. J. Hydraul. Eng. 2008, 134, 1708–1721. [Google Scholar] [CrossRef]
- Ahmadisharaf, E.; Kalyanapu, A.J.; Thames, B.A.; Lillywhite, J. A probabilistic framework for comparison of dam breach parameters and outflow hydrograph generated by different empirical prediction methods. Environ. Model. Softw. 2016, 86, 248–263. [Google Scholar] [CrossRef]
- Ahmadisharaf, E.; Bhuyian, M.-N.M.; Kalyanapu, A.J. Impact of spatial resolution on downstream flood hazard due to dam break events using probabilistic flood modelling. In Proceedings of the 5th Dam Safety Conference, Providence, RI, USA, 16–20 September 2012; pp. 263–276. [Google Scholar]
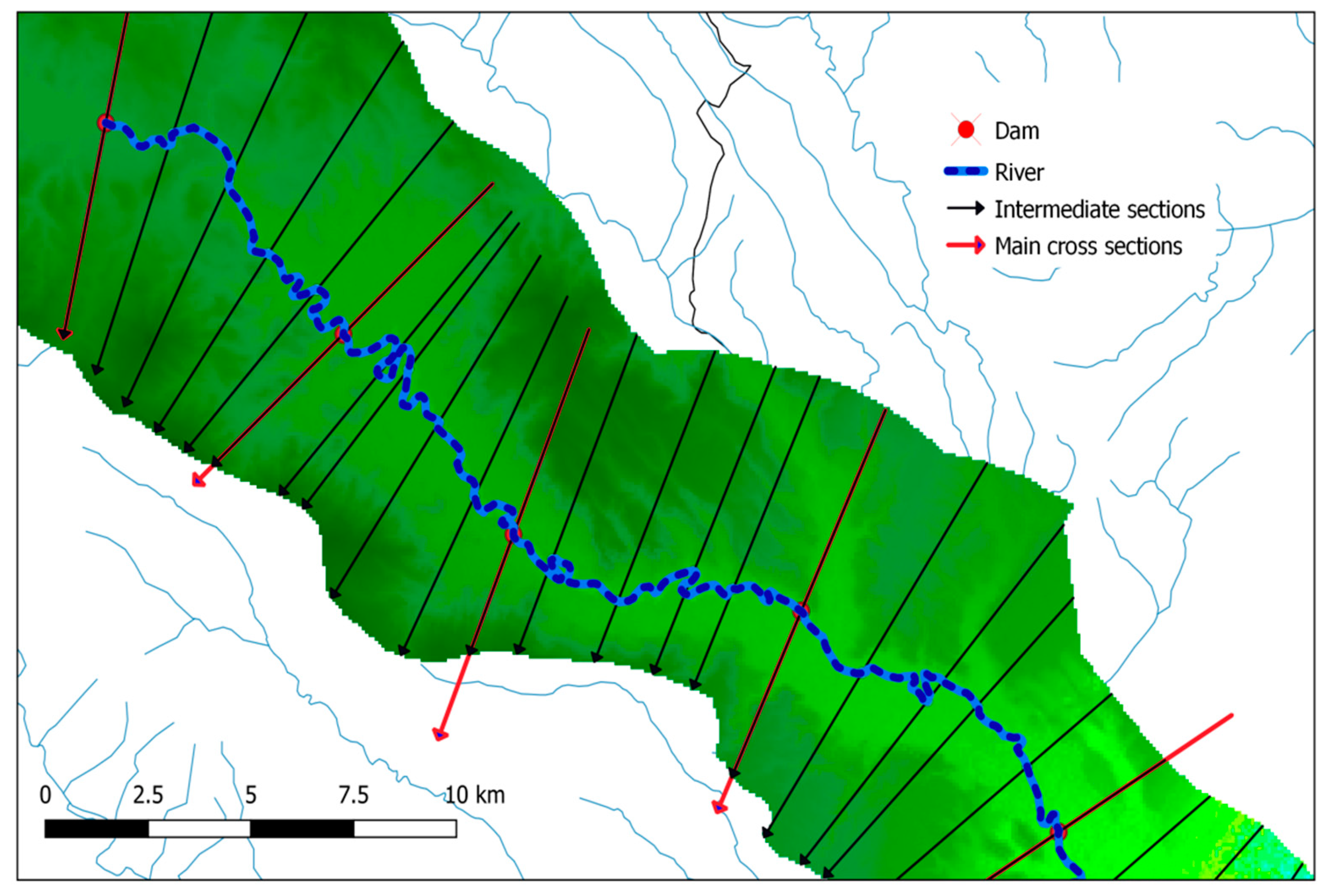
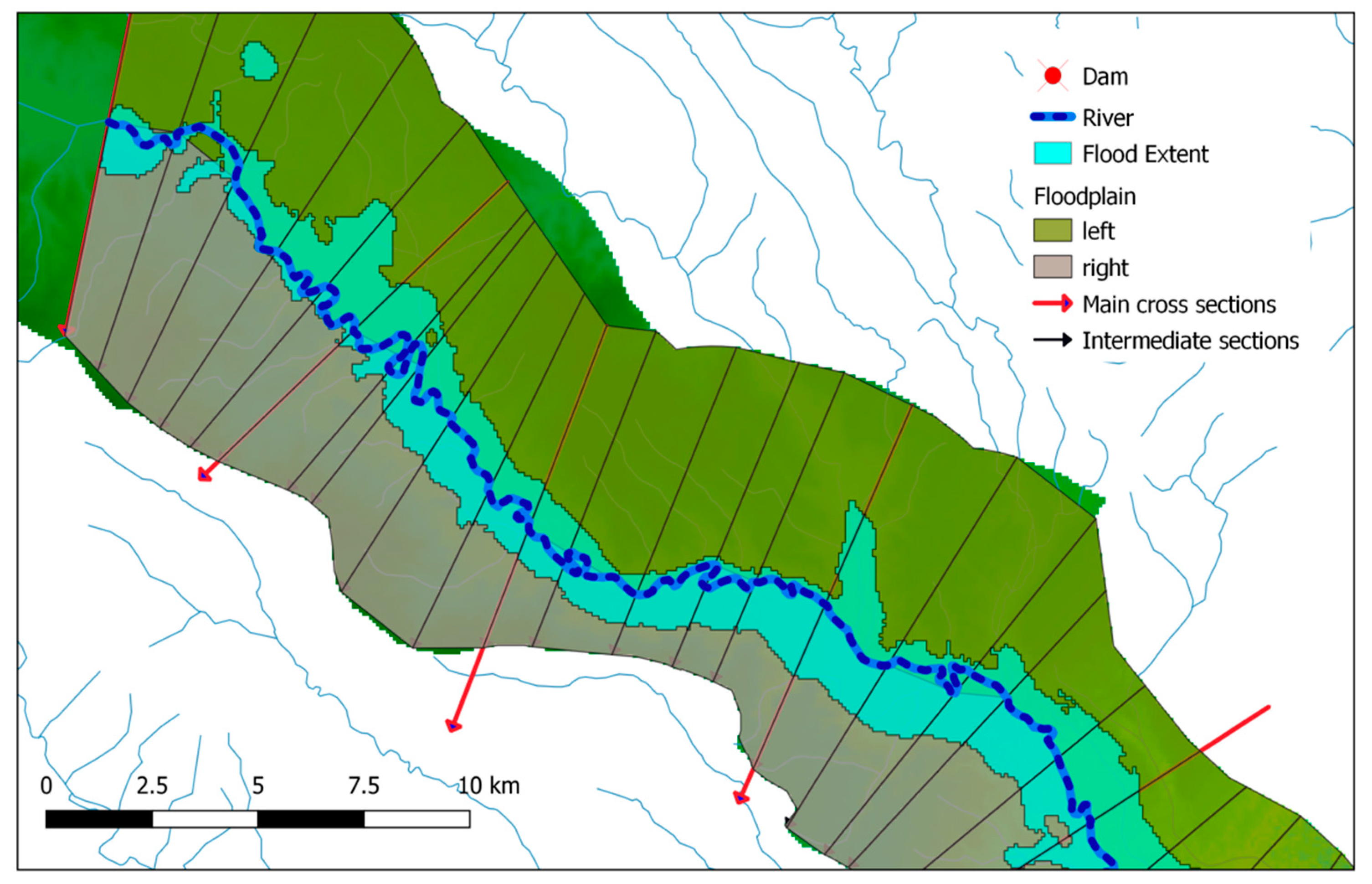
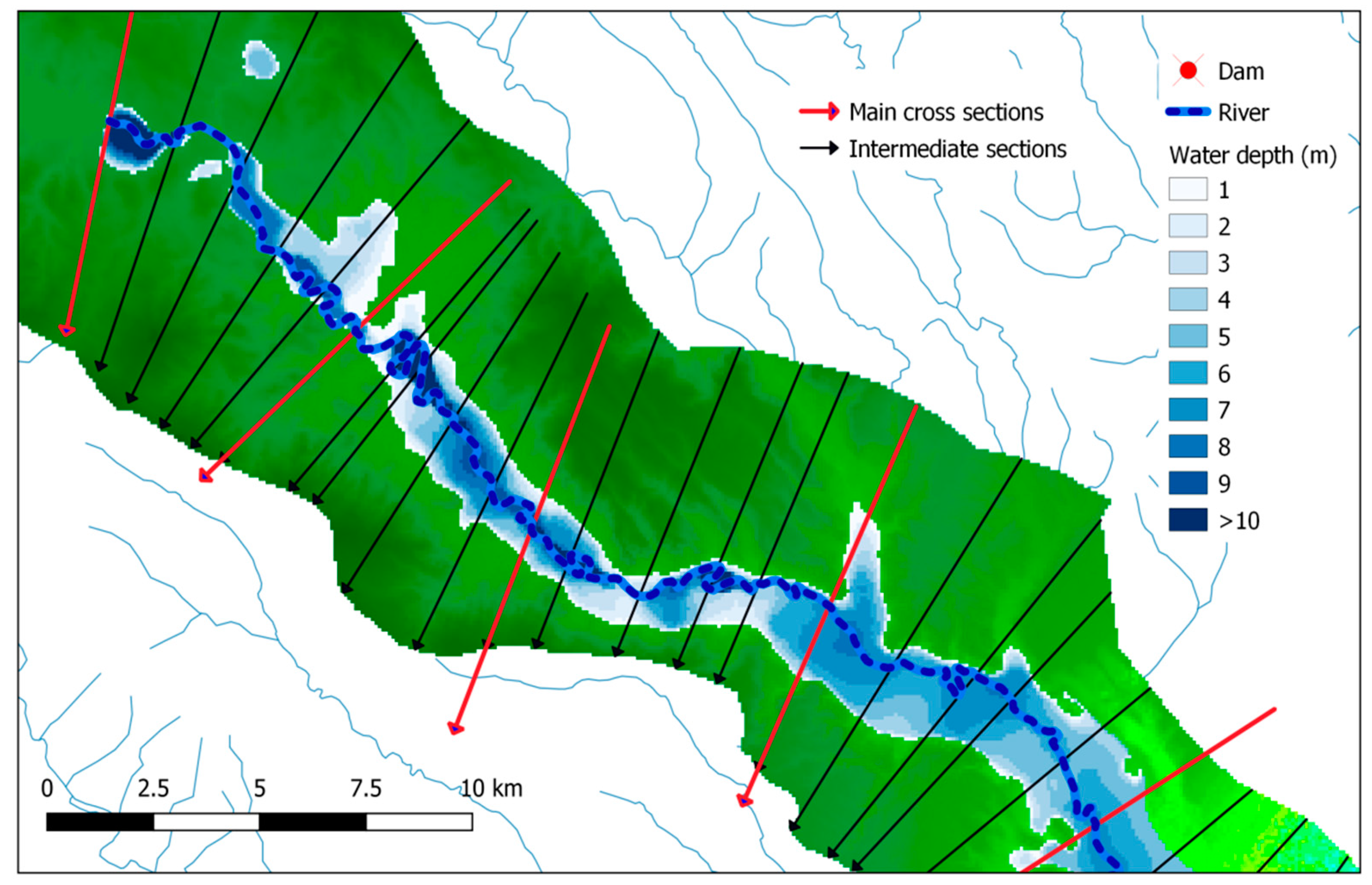
| Method | Spatial Resolution | Initial Conditions | Upstream Boundary Condition | Downstream Boundary Condition | Manning's Coefficient |
|---|---|---|---|---|---|
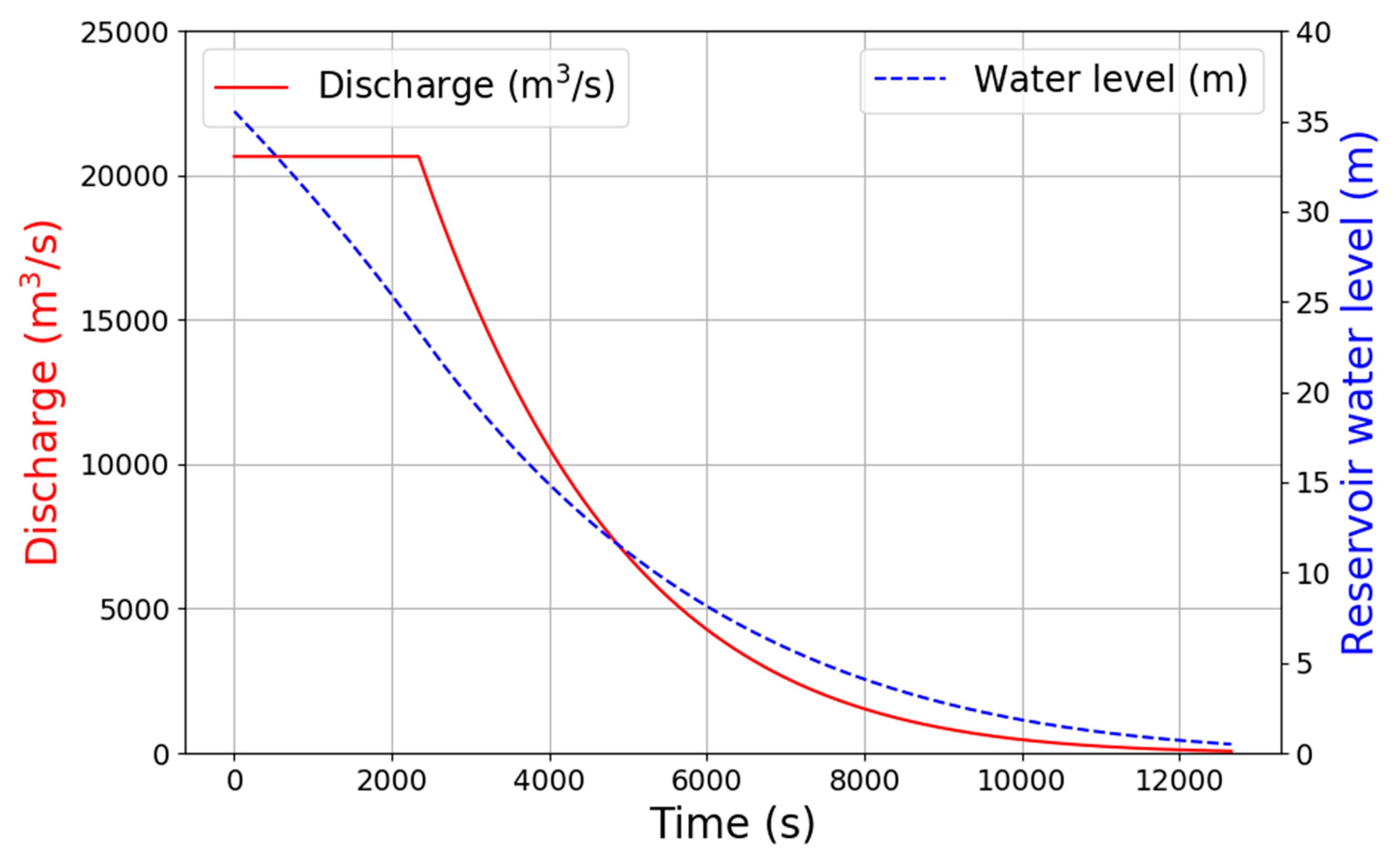
| The proposed GIS tool | 0.5 cross section per km | Dry | Dam-break outflow hydrograph of fig. 1 | None | 0.06 m-1/3s |
| Sole et al. [37] | 1 cross section per km | Discharge of 1 m3/s | Dam-break outflow hydrograph of fig. 7 | Sea level | 0.028 m-1/3s |
| 2D hydrodynamic modelling | 10 m DEM | Dry | Dam-break outflow hydrograph of fig. 8 | Critical water depth | Spatial variation |
| rfp | rtp | Accuracy | Sensitivity | Specificity | |
|---|---|---|---|---|---|
| 2D propagation model [40] | 10.1 | 78.5 | 86.5 | 75.5 | 89.9 |
| Sole et al. [37] | 19.9 | 59.7 | 74.2 | 57.7 | 80.1 |
| rfp | rtp | Accuracy | Sensitivity | Specificity | |
|---|---|---|---|---|---|
| Historical reconstruction of flooded area | 2.2 | 78.7 | 94.8 | 78.7 | 97.9 |
| Flooded area simulated by hydrodynamic model | 1.5 | 86.9 | 96.8 | 86.9 | 98.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albano, R.; Mancusi, L.; Adamowski, J.; Cantisani, A.; Sole, A. A GIS Tool for Mapping Dam-Break Flood Hazards in Italy. ISPRS Int. J. Geo-Inf. 2019, 8, 250. https://doi.org/10.3390/ijgi8060250
Albano R, Mancusi L, Adamowski J, Cantisani A, Sole A. A GIS Tool for Mapping Dam-Break Flood Hazards in Italy. ISPRS International Journal of Geo-Information. 2019; 8(6):250. https://doi.org/10.3390/ijgi8060250
Chicago/Turabian StyleAlbano, Raffaele, Leonardo Mancusi, Jan Adamowski, Andrea Cantisani, and Aurelia Sole. 2019. "A GIS Tool for Mapping Dam-Break Flood Hazards in Italy" ISPRS International Journal of Geo-Information 8, no. 6: 250. https://doi.org/10.3390/ijgi8060250
APA StyleAlbano, R., Mancusi, L., Adamowski, J., Cantisani, A., & Sole, A. (2019). A GIS Tool for Mapping Dam-Break Flood Hazards in Italy. ISPRS International Journal of Geo-Information, 8(6), 250. https://doi.org/10.3390/ijgi8060250








