An Application of the Spatial Autocorrelation Method on the Change of Real Estate Prices in Taitung City
Abstract
1. Introduction
2. Autocorrelation
2.1. Spatial Regression Analysis Model
2.2. Spatial Regression Analysis Model Establishment
2.2.1. Hedonic Price Method
2.2.2. Spatial Lag Model (SLM)
2.2.3. Spatial Error Model (SEM)
3. Spatial Dependence Test
4. Results and Discussion
4.1. Data Sources and Variable Selection
4.2. Comparison of the Spatial Autoregressive Model
4.2.1. Comparisons between the Hedonic Price Method and Spatial Autoregressive Model
4.2.2. Using R² Values to Express the Explanatory Power of the Models for Real Estate Prices
4.2.3. Using R² Values to Explain Real Estate Prices
4.3. Spatial Autocorrelation Analysis
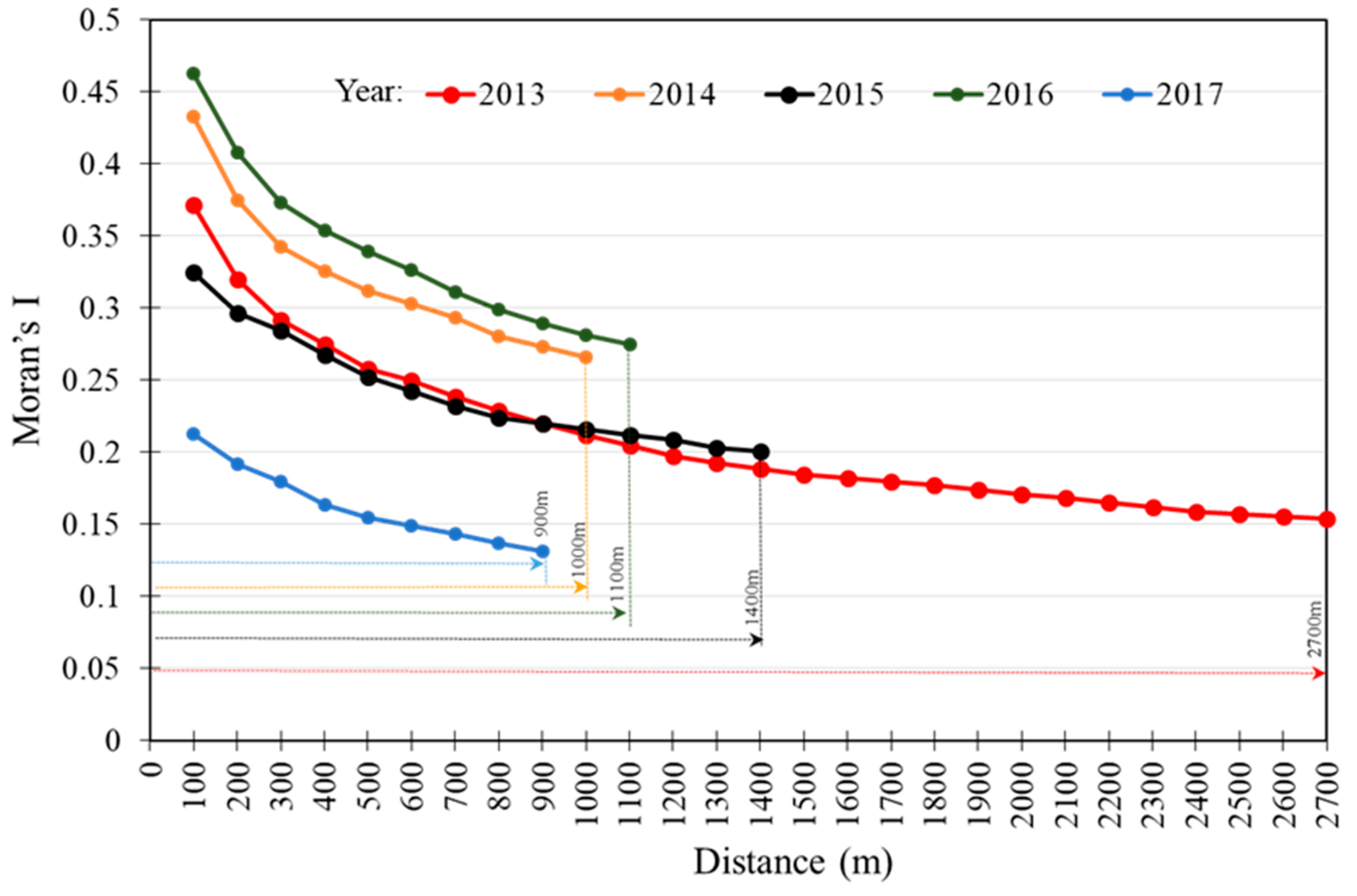
4.3.1. Global Moran’s I
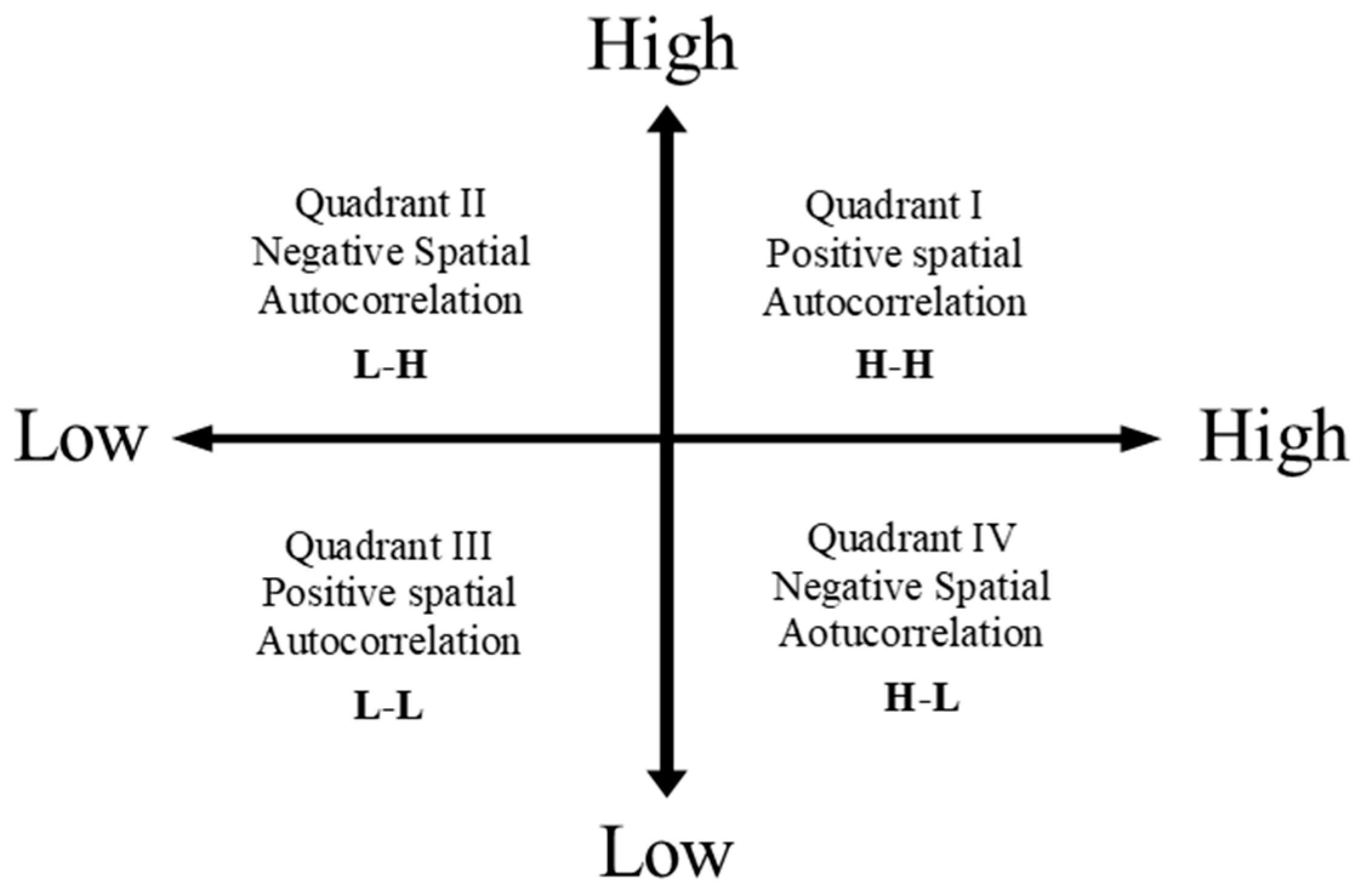
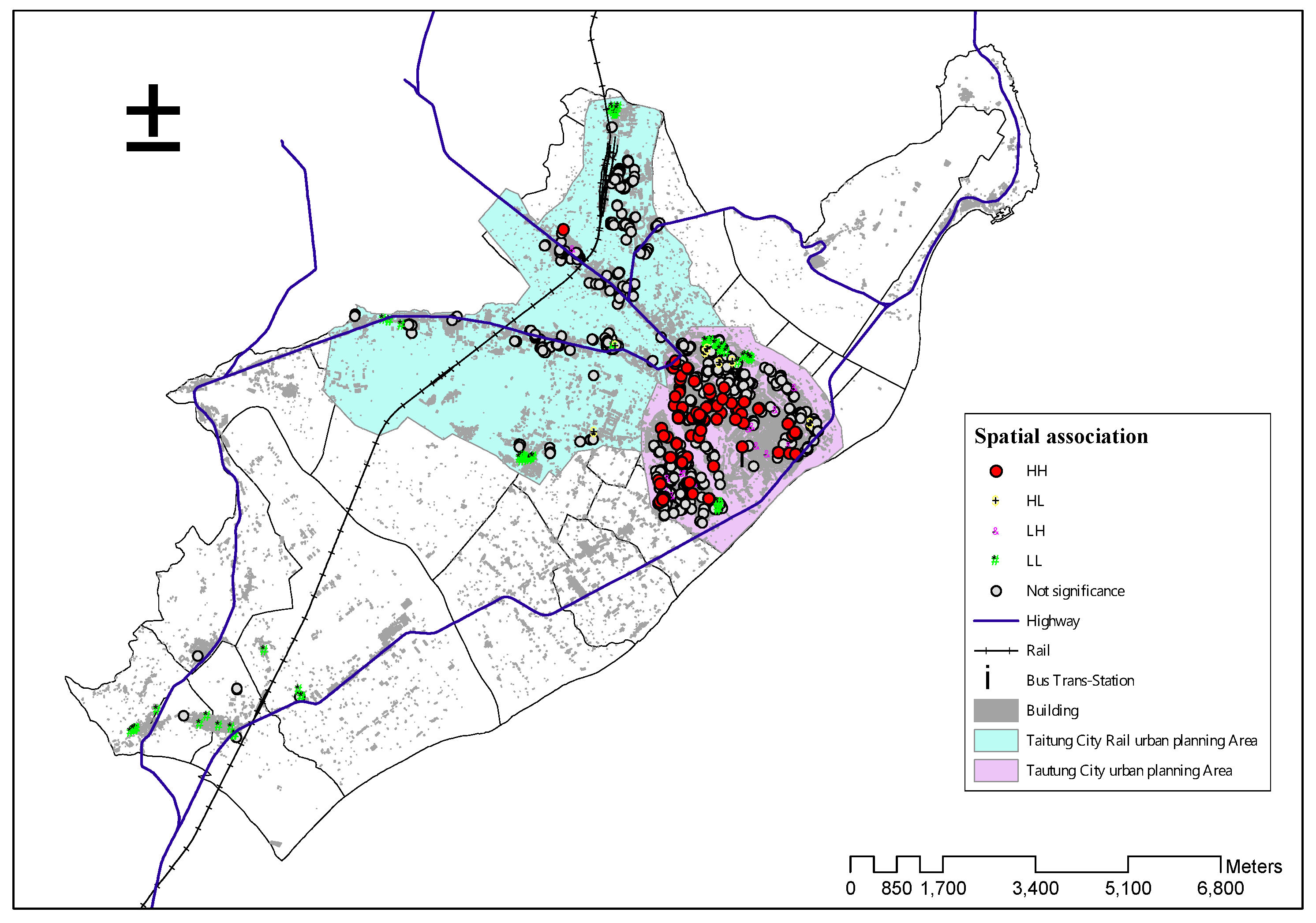
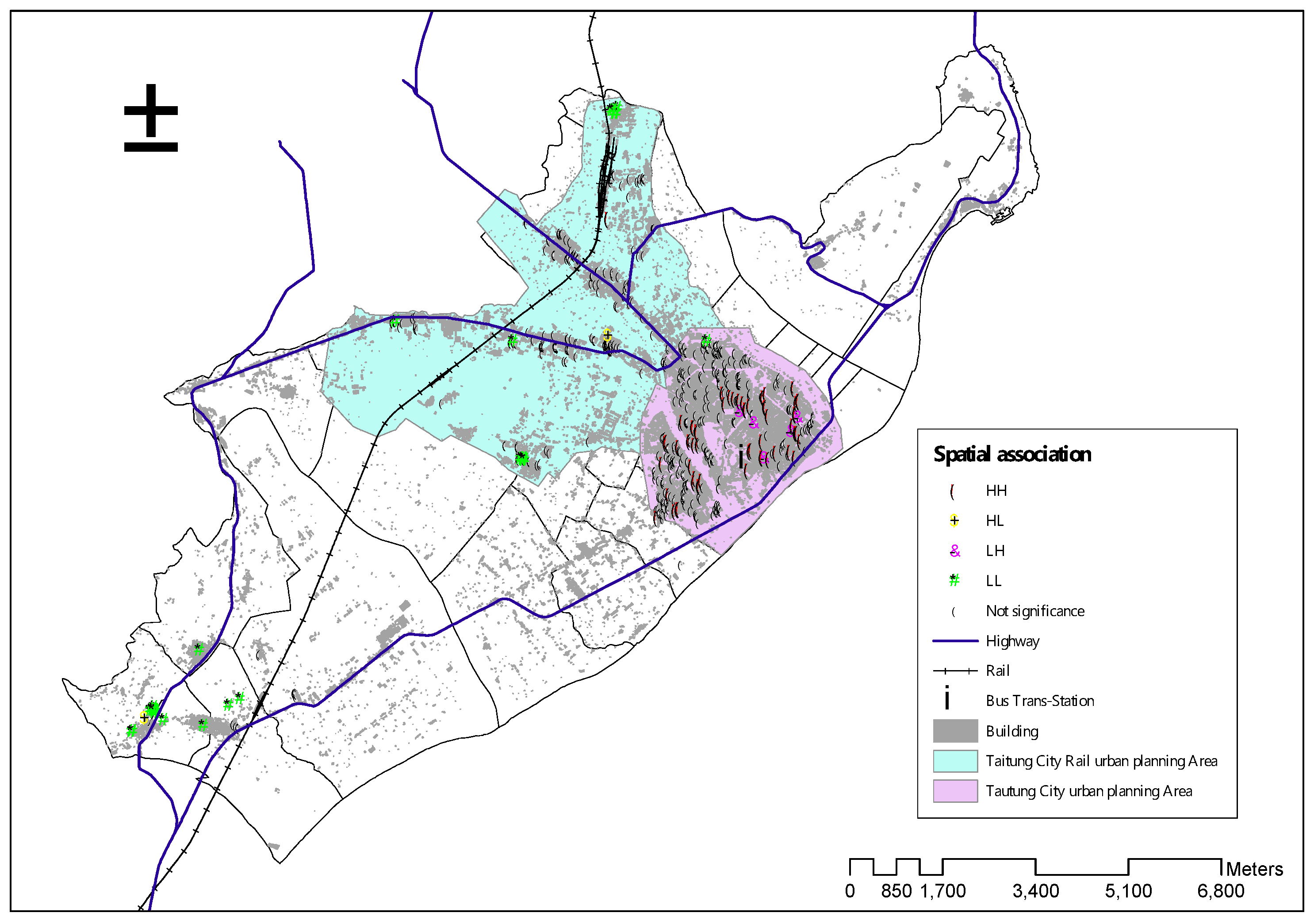
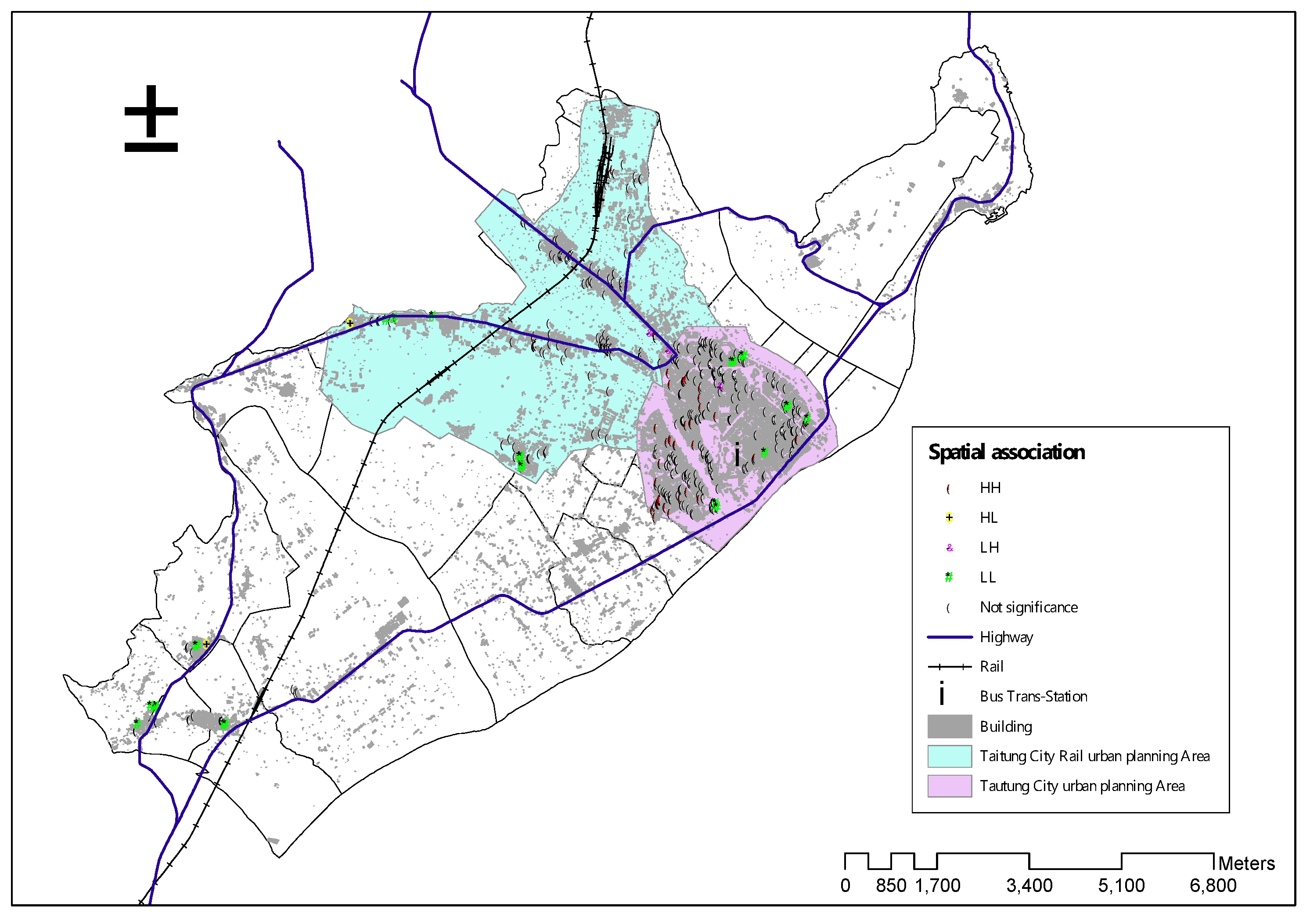
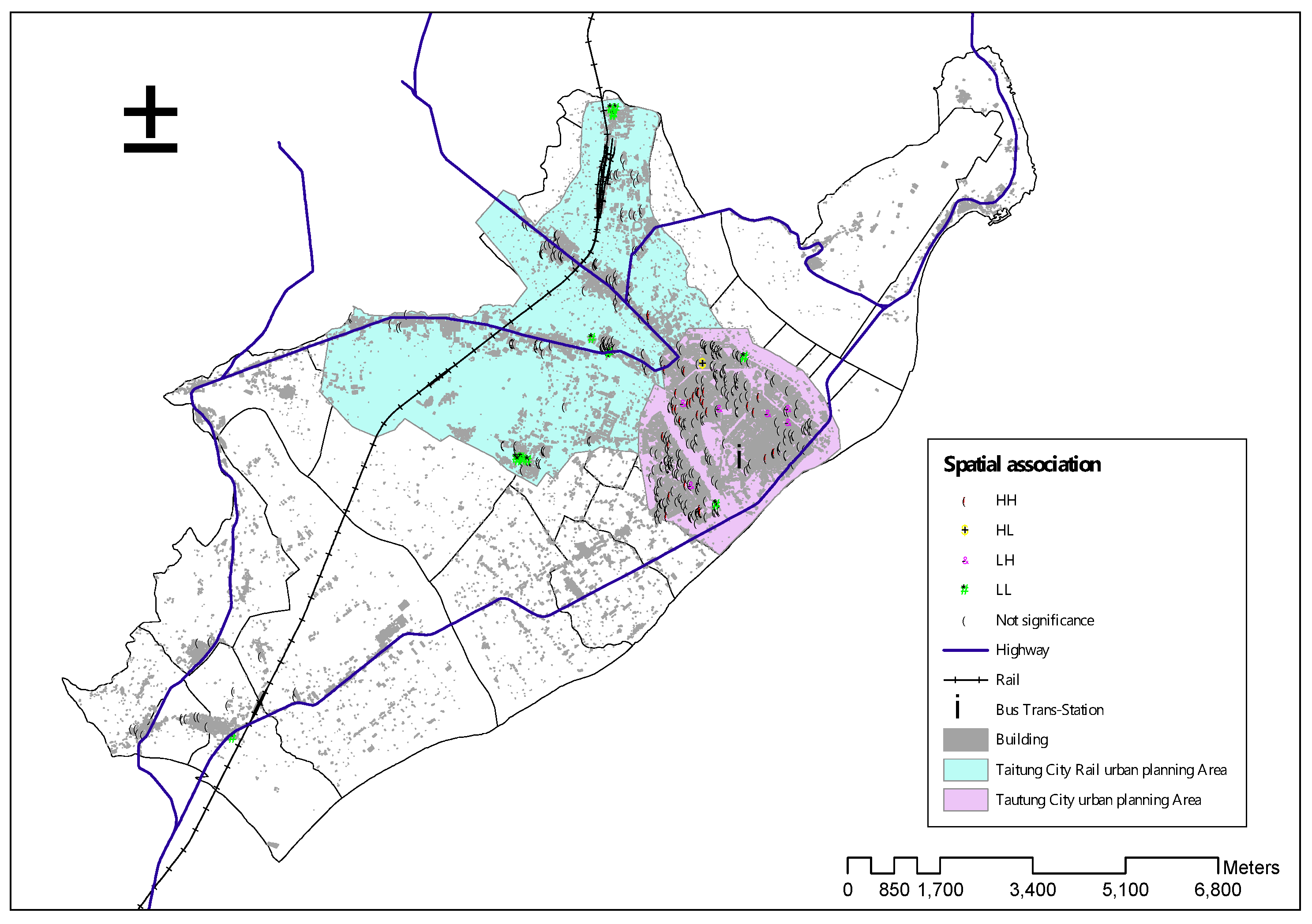
4.3.2. LISA and Spatial Change
4.4. Expected Effects of the Variables and Verification of the Analysis Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, S.T. Income, money and house prices: An observation of Taipei area for the past two decades. J. Hous. Stud. 1994, 2, 49–65. [Google Scholar] [CrossRef]
- Wang, J.C. Research on Estimation Platform Prototype for Trends in Housing Prices in Taipei. Master’s Thesis, National Taiwan University, Taipei, Taiwan, 2016. [Google Scholar]
- Chu, F.N.; Chang, C.O.; Chen, S.M. Comparative analysis of the housing purchase decision making processes of home-buyers and potential home-buyers: The difference between revealed preference and stated preference. J. City Plan. 2008, 35, 339–359. [Google Scholar]
- Goodman, A.C.; Thibodeau, T.G. Housing market segmentation and hedonic prediction accuracy. J. Hous. Econ. 2003, 12, 181–201. [Google Scholar] [CrossRef]
- Cervero, R.; Duncan, M. Transit’s value-added effects: Light and commuter rail services and commercial land values. Transp. Res. Rec. J. Transp. Res. Board 2002, 1805, 8–15. [Google Scholar] [CrossRef]
- Goodman, A.C. A dynamic equilibrium model of housing demand and mobility with transaction cost. J. Hous. Econ. 1995, 4, 307–327. [Google Scholar] [CrossRef]
- Bajic, V. The effects of a new subway line on housing prices in metropolitan Toronto. Urban Stud. 1983, 20, 147–158. [Google Scholar] [CrossRef]
- Damm, D.; Lerman, S.R.; Lerner-Lam, E.; Young, J. Response of urban real estate values in anticipation of the Washington Metro. J. Transp. Econ. Policy 1980, 14, 315–336. [Google Scholar]
- Rosen, S. Hedonic prices and implicit markets: Product differentiation in pure competition. J. Polit. Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Asabere, P.K.; Huffman, F.E.; Mehdian, S. Mispricing and optimal time on the market. J. Real Estate Res. 1993, 8, 149–156. [Google Scholar]
- Jim, C.-Y.; Chen, W.Y. Impacts of urban environmental elements on residential housing prices in Guangzhou (China). Landsc. Urban Plan. 2006, 78, 422–434. [Google Scholar] [CrossRef]
- Huh, S.; Kwak, S.J. The choice of functional and variables in the hedonic price model in Seoul. Urban Stud. 1997, 34, 989–998. [Google Scholar] [CrossRef]
- Laurice, J.; Bhattacharya, R. Prediction performance of a hedonic pricing model for housing. Apprais. J. 2005, 73, 198–209. [Google Scholar]
- Adair, A.S.; Berry, J.N.; McGreal, W.S. Hedonic modeling, housing submarkets and residential valuation. J. Prop. Res. 1996, 13, 67–83. [Google Scholar] [CrossRef]
- Can, A. Specification and estimation of hedonic housing price models. Reg. Sci. Urban Econ. 1992, 22, 453–474. [Google Scholar] [CrossRef]
- Hui, E.C.; Chau, C.K.; Pun, L.; Law, M.Y. Measuring the neighboring and environmental effects on residential property value: Using spatial weighting matrix. Build. Environ. 2007, 42, 2333–2343. [Google Scholar] [CrossRef]
- Lancaster, K. A new approach to consumer theory. J. Polit. Econ. 1966, 74, 132–157. [Google Scholar] [CrossRef]
- Dubin, R.; Pace, K.; Thibodeau, T. Spatial autoregression techniques for real estate data. J. Real Estate Lit. 1999, 7, 79–95. [Google Scholar] [CrossRef]
- Dubin, R.A. Predicting house prices using multiple listings data. J. Real Estate Financ. Econ. 1998, 17, 35–59. [Google Scholar] [CrossRef]
- Case, K.E.; Mayer, C.J. Housing price dynamics within a metropolitan area. Reg. Sci. Urban Econ. 1996, 26, 387–407. [Google Scholar] [CrossRef]
- Basu, S.; Thibodeau, T.G. Analysis of spatial autocorrelation in house prices. J. Real Estate Financ. Econ. 1998, 17, 61–85. [Google Scholar] [CrossRef]
- Can, A. GIS and spatial analysis of housing and mortgage markets. J. Hous. Res. 1998, 9, 61–86. [Google Scholar]
- Chang, S.L. The Study of Integrating Space Statistics Technique into Land Mass Assessment Approach. Master’s Thesis, National ChengKung University, Tainan, Taiwan, 2001. [Google Scholar]
- Spielman, S.E.; Thill, J.C. Social area analysis, data mining and GIS. Comput. Environ. Urban Syst. 2008, 32, 110–122. [Google Scholar] [CrossRef]
- Clapp, J.M.; Rodriguez, M.; Thrall, G. How GIS can put urban economic analysis on the map. J. Hous. Econ. 1997, 6, 368–386. [Google Scholar] [CrossRef]
- Mustafa, A.; Rompaey, A.V.; Cools, M.; Saadi, I.; Teller, J. Addressing the determinants of built-up expansion and densification processes at the regional scale. Urban Stud. 2018, 55, 3279–3298. [Google Scholar] [CrossRef]
- Griffith, D.A. Simplifying the normalizing factor in spatial autoregressions for irregular lattices. Pap. Reg. Sci. 1992, 71, 71–86. [Google Scholar] [CrossRef]
- Unwin, D.J. GIS, spatial analysis and spatial statistics. Prog. Hum. Geogr. 1996, 20, 540–551. [Google Scholar] [CrossRef]
- Pace, K.B.; Sirmans, C.F. Spatial statistics and real estate. J. Real Estate Financ. Econ. 1998, 17, 5–13. [Google Scholar] [CrossRef]
- Wong, S.T. Spatial Autoregressive Analysis of Housing Price in Tainan City. Master’s Thesis, National ChengKung University, Tainan, Taiwan, 2003. [Google Scholar]
- Ronald, B.; Pace, R.K. Kriging with large data sets using sparse matrix techniques. Commun. Stat. Comput. Simul. 1997, 26, 619–629. [Google Scholar]
- Anselin, L.; Getis, A. Spatial statistical analysis and geographic information systems. Ann. Reg. Sci. 1992, 26, 19–33. [Google Scholar] [CrossRef]
- Cliff, A.D.; Ord, J.K. Spatial Autocorrelation; Classics in Human Geography Revisited; Pion: London, UK, 1973. [Google Scholar] [CrossRef]
- Aurelia, B.M. A hedonic valuation of urban green areas. Landsc. Urban Plan. 2003, 66, 35–41. [Google Scholar] [CrossRef]
- Brasington, D.M.; Hite, D. Demand for environmental quality: A spatial hedonic analysis. Reg. Sci. Urban Econ. 2005, 35, 57–82. [Google Scholar] [CrossRef]
- Cliff, A.D.; Ord, J.K. Spatial Processes: Models and Applications; Pion: London, UK, 1981; Volume 266, ISBN 08-85086-081-4. [Google Scholar]
- Anselin, L. Local indicators of spatial association: LISA. Geogr. Anal. 1995, 93, 93–115. [Google Scholar] [CrossRef]
- Overmars, K.P.; de Koning, G.H.-J.; Veldkamp, A. Spatial autocorrelation in multi-scale landuse models. Ecol. Model. 2003, 164, 257–270. [Google Scholar] [CrossRef]
- Can, A. The measurement of neighborhood dynamics in urban house prices. Econ. Geogr. 1990, 66, 254–272. [Google Scholar] [CrossRef]
- Lin, J.H. Investigation of the Spatial Relation between the Disadvantaged Minority and Disaster Prevention by Spatial Autocorrelation and Network Analyst—A Case Study of Flooding. Master’s Thesis, National Taiwan Normal University, Taipei, Taiwan, 2018. [Google Scholar]
- Sklar, F.H.; Costanza, R. The development of dynamic spatial models for landscape ecology: A review and prognosis. In Quantitative Methods in Landscape Ecology; Turner, M.G., Gardner, R.H., Eds.; Ecological Studies 82; Springer: Berlin, Germany, 1991; pp. 239–288. [Google Scholar]
- Lambin, E.F. Modelling Deforestation Processes: A Review. Trees, Tropical Ecosystem Environment Observation by Satellites; Research Report No.1; European Commission Joint Research Centre: Brussels, Belgium; European Space Agency: Paris, France, 1994; p. 113. [Google Scholar]
- Riebsame, W.E.; Parton, W.J.; Galvin, K.A.; Burke, I.C.; Bohren, L.; Young, R.; Knop, E. Integrated modeling of land use and cover change: A conceptual scheme for applying an integration strategy to agricultural land use on the US Great Plains. Bioscience 1994, 44, 350–356. [Google Scholar] [CrossRef]
- Kaimowitz, D.; Angelsen, A. Economic Models of Tropical Deforestation: A Review; Center for International Forestry Research (CIFOR): Bogor, Indonesia, 1998; ISBN 979-8764-17-X. [Google Scholar]
- Lambin, E.F.; Rounsevell, M.D.A.; Geist, H.J. Are agricultural land-use models able to predict changes in land-use intensity? Agric. Ecosyst. Environ. 2000, 82, 321–331. [Google Scholar] [CrossRef]
- Veldkamp, A.; Lambin, E.F. Editorial: Predicting land-use change. Agric. Ecosyst. Environ. 2001, 85, 1–6. [Google Scholar] [CrossRef]
- Chen, T.J. A Spatial Autocorrelation Function Approach to Medical Image Quality Evaluation. Ph.D. Thesis, National TsingHua University, Hsinchu, Taiwan, 2003. [Google Scholar]
- Bae, C.C.; Jun, M.J.; Park, H. The impact of Seoul’s subway Line 5 on residential property values. Transp. Policy 2003, 10, 85–94. [Google Scholar] [CrossRef]
- Andresen, M.A. Crime measures and the spatial analysis of criminal activity. Br. J. Criminol. 2006, 46, 258–285. [Google Scholar] [CrossRef]
- Chan, Y.T. Application of Spatial Statistical Analysis on the Change of Farmland Transaction and the Farmhouse—A Case of Beinan Township in Taitung County. Master’s Thesis, National Taitung University, Taitung City, Taiwan, 2016. [Google Scholar]
- Batty, M.; Couclelis, H.; Eichen, M. Urban systems as cellular automata. Environ. Plan. B Plan. Des. 1997, 24, 159–305. [Google Scholar] [CrossRef]
- Batty, M.; Xie, Y.; Sun, Z. Modeling urban dynamics through GIS-based cellular automata. Comput. Environ. Urban Syst. 1999, 23, 205–233. [Google Scholar] [CrossRef]
- Clarke, K.C.; Hoppen, S.; Gaydos, L. A self-modifying cellular automata model of historical urbanization in the San Francisco Bay area. Environ. Plan. B Plan. Des. 1997, 24, 247–261. [Google Scholar] [CrossRef]
- White, R.; Engelen, G. Cellular automata and fractal urban form: A cellular modeling approach to the evolution of urban land use patterns. Environ. Plan. A 1993, 25, 1175–1199. [Google Scholar] [CrossRef]
- Lay, J.G.; Yap, K.H.; Wang, W. Exploring Land Use Changes and Spatial Dependence—A Case Study of Settlement Changes in the Taipei Basin. J. Taiwan Geogr. Inf. Sci. 2004, 1, 29–40. [Google Scholar]
- White, R.; Engelen, G. Cellular automata as the basis of integrated dynamic regional modelling. Environ. Plan. B Plan. Des. 1997, 24, 235–246. [Google Scholar] [CrossRef]
- Mustafa, A.; Rienow, A.; Saadi, I.; Cools, M.; Teller, J. Comparing support vector machines with logistic regression for calibrating cellular automata land use change models. Eur. J. Remote Sens. 2018, 51, 391–401. [Google Scholar] [CrossRef]
- Eisenlauer, J.F. Mass versus individual appraisals. Apprais. J. 1968, 36, 532–540. [Google Scholar]
- Blettner, R.A. Mass appraisals via multiple regression analysis. Apprais. J. 1969, 37, 513–521. [Google Scholar]
- Mohammady, M.; Moradi, H.R.; Zeinivand, H.; Temme, A.J.; Yazdani, M.R.; Pourghasemi, H.R. Modeling and assessing the effects of land use changes on runoff generation with the CLUE-s and WetSpa models. Theor. Appl. Climatol. 2018, 133, 459–471. [Google Scholar] [CrossRef]
- Kelejian, H.; Prucha, I. A generalized spatial two-stage least-squares procedure for estimating a spatial autoregressive model with autoregressive disturbances. J. Real Estate Financ. Econ. 1998, 17, 99–121. [Google Scholar] [CrossRef]
- Duncan, C.; Jones, K. Using multilevel models to model heterogeneity: Potential and pitfalls. Geogr. Anal. 2000, 32, 279–305. [Google Scholar] [CrossRef]
- Jones, K. Specifying and estimating multilevel models for geographical research. Trans. Inst. Br. Geogr. 1991, 16, 148–159. [Google Scholar] [CrossRef]
- Cleveland, W.; Devlin, S. Locally weighted regression: An approach to regression analysis by local fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
- Crespo, R.; Grêt-Regamey, A. Local hedonic house-price modelling for urban planners: Advantages of using local regression techniques. Environ. Plan. B Plan. Des. 2013, 40, 664–682. [Google Scholar] [CrossRef]
- Lin, Y.C. Neighborhood Effect and Housing Prices: A Case Study in Taipei, Taiwan. Master’s Thesis, National Taiwan University, Taipei, Taiwan, 2013. [Google Scholar]
- Anselin, L. Spatial Econometrics: Methods and Models; Springer Science & Business Media: Dordrecht, The Netherlands, 1988; ISBN 978-94-015-7799-1. [Google Scholar]
- Anselin, L. Spatial Econometrics. 1999. Available online: http://www.csiss.org/aboutus/presentations/files/baltchap.pdf (accessed on 1 December 2018).
- De Koning, G.H.J.; Veldkamp, A.; Fresco, L.O. Land use in Ecuador: A statistical analysis at different aggregation levels. Agric. Ecosyst. Environ. 1998, 70, 231–247. [Google Scholar] [CrossRef]
- Poelmans, L.; Van Rompaey, A. Complexity and performance of urban expansion models. Comput. Environ. Urban Syst. 2010, 34, 17–27. [Google Scholar] [CrossRef]
- Knegt, H.J.; Langevelde, F.; Coughenour, M.B.; Skidmore, A.K.; Boer, W.F.; Heitkönig, I.M.A.; Knox, N.M.; Slotow, R.; Waal, C.; Prins, H.H.T. Spatial autocorrelation and the scaling of species–environment relationships. Ecology 2010, 91, 2455–2465. [Google Scholar] [CrossRef]

| Year of Data | Access Data Count | Data Adopted Count |
|---|---|---|
| 2013 | 1011 | 913 |
| 2014 | 878 | 810 |
| 2015 | 824 | 738 |
| 2016 | 591 | 546 |
| 2017 | 603 | 526 |
| Total data | 3907 | 3533 |
| Variable | Y2013 | Y2014 | Y2015 | Y2016 | Y2017 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Coefficient | t-Value | Coefficient | t-Value | Coefficient | t-Value | Coefficient | t-Value | Coefficient | t-Value | |
| Total floor area | −0.0317 | −5.609 | −0.0512 | −7.876 | −0.0547 | −6.697 | −0.0300 | −3.130 | −0.0316 | −2.363 |
| Floor level | −0.0728 | −1.023 | −0.0258 | −0.371 | −0.1681 | −1.656 | −0.1181 | −1.092 | −0.0103 | −0.072 |
| Building type | 3.6234 | 11.724 | 4.2304 | 13.121 | 4.8005 | 9.960 | 3.9038 | 7.343 | 5.6861 | 7.782 |
| Building age | −0.0751 | −8.769 | −0.0839 | −9.317 | −0.1170 | −8.460 | −0.0344 | −2.351 | −0.0392 | −1.928 |
| Facing road width | 0.0459 | 2.271 | 0.0161 | 0.824 | 0.0934 | 2.767 | 0.1119 | 3.549 | −0.0062 | −0.127 |
| Distance to major road | −0.0020 | −1.721 | 2.0459 | 0.187 | −0.0072 | −2.195 | −0.0258 | −2.234 | −0.0142 | −1.899 |
| Distance to park | −1.6287 | −0.155 | 0.0002 | 1.688 | 2.8806 | 0.153 | 0.0003 | 1.621 | −9.1883 | −0.313 |
| Distance to elementary school | −0.0002 | −1.392 | −7.2894 | −0.342 | 0.0007 | 1.912 | −8.0024 | −0.213 | −0.0002 | −0.409 |
| Distance to junior school | −0.0002 | −2.634 | −0.0004 | −3.207 | −0.0005 | −2.330 | −0.0006 | −2.349 | −0.0003 | −0.911 |
| Distance to train station | −7.5787 | −1.887 | −0.0002 | −3.913 | 8.2500 | 1.210 | −1.3468 | −0.202 | −5.6660 | −0.622 |
| Distance to transfer station | −0.0004 | −6.132 | −0.0006 | −8.787 | −0.0007 | −7.034 | −0.0006 | −5.282 | −0.0005 | −3.031 |
| Spatial correlation coefficient | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| R² | 0.3511 | 0.4223 | 0.3671 | 0.2515 | 0.221905 | |||||
| Adj-R² | 0.3431 | 0.4143 | 0.3575 | 0.2361 | 0.2053 | |||||
| F-test | 44.3207 | 53.0273 | 38.2855 | 16.3094 | 13.3261 | |||||
| AIC | 4434.69 | 3967.83 | 4233.61 | 3021.82 | 3231.22 | |||||
| LR test | NA | NA | NA | NA | NA | |||||
| LM lag | 7.6927 | 7.3702 | 0.1729 | 1.1201 | 0.0004 | |||||
| LM error | 4.9943 | 4.6535 | 3.8405 | 0.2934 | 0.0670 | |||||
| Data | 913 | 810 | 738 | 546 | 526 | |||||
| Variable | Y2013 | Y2014 | Y2015 | Y2016 | Y2017 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Coefficient | z-Value | Coefficient | z-Value | Coefficient | z-Value | Coefficient | z-Value | Coefficient | z-Value | |
| Total floor area | −0.0306 | −5.6522 | −0.0518 | −8.066 | −0.0546 | −6.744 | −0.0305 | −3.227 | −0.0316 | −2.389 |
| Floor level | −0.0738 | −1.049 | −0.0246 | −0.3567 | −0.1685 | −1.674 | −0.1101 | −1.032 | −0.0104 | −0.074 |
| Building type | 3.4104 | 10.737 | 4.0444 | 12.140 | 4.8312 | 9.872 | 3.8068 | 7.233 | 5.6861 | 7.866 |
| Building age | −0.0737 | −8.654 | −0.0834 | −9.359 | −0.1172 | −8.520 | −0.0325 | −2.249 | −0.0392 | −1.949 |
| Facing road width | 0.0473 | 2.362 | 0.0172 | 0.893 | 0.0942 | 2.811 | 0.1125 | 3.618 | −0.0062 | −0.128 |
| Distance to major road | −0.0021 | −1.754 | 2.7396 | 0.253 | −0.0072 | −2.201 | −0.0277 | −2.431 | −0.0142 | −1.919 |
| Distance to park | −4.3562 | −0.042 | 0.0002 | 1.628 | 2.3272 | 0.125 | 0.0003 | 1.537 | −9.2752 | −0.319 |
| Distance to elementary school | −0.0002 | −1.355 | 8.3174 | 0.039 | 0.0007 | 1.852 | −6.8294 | −0.184 | −0.0002 | −0.413 |
| Distance to junior school | −0.0002 | −2.166 | −0.0004 | −3.223 | −0.0005 | −2.290 | −0.0005 | −2.305 | −0.0003 | −0.918 |
| Distance to train station | −6.4052 | −1.603 | −0.0002 | −3.386 | 8.1699 | 1.208 | −1.3848 | −0.021 | −5.6311 | −0.620 |
| Distance to transfer station | −0.0003 | −5.146 | −0.0005 | −6.954 | −0.0007 | −6.630 | −0.0005 | −5.116 | −0.0005 | −3.065 |
| Spatial correlation coefficient | 0.1618 | 2.455 | 0.1458 | 2.093 | −0.0326 | −0.409 | 0.1981 | 1.645 | −0.0052 | −0.037 |
| R² | 0.3569 | 0.4271 | 0.3673 | 0.2560 | 0.221907 | |||||
| Adj-R² | NA | NA | NA | NA | NA | |||||
| F檢定 | NA | NA | NA | NA | NA | |||||
| AIC | 4430.15 | 3964.34 | 4235.44 | 3021.14 | 3233.22 | |||||
| LR test | 6.5398 | 5.4933 | 0.1711 | 2.6824 | 0.0012 | |||||
| LM lag | NA | NA | NA | NA | NA | |||||
| LM error | NA | NA | 0.3673 | NA | NA | |||||
| Data | 913 | 810 | 738 | 546 | 526 | |||||
| Variable | Y2013 | Y2014 | Y2015 | Y2016 | Y2017 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Coefficient | z-Value | Coefficient | z-Value | Coefficient | z-Value | Coefficient | z-Value | Coefficient | z-Value | |
| Total floor area | −0.0311 | −5.703 | −0.0517 | −7.968 | −0.0555 | −6.845 | −0.0313 | −3.308 | −0.0321 | −2.433 |
| Floor level | −0.0747 | −1.053 | −0.0279 | −0.402 | −0.1653 | −1.629 | −0.1116 | −1.045 | −0.0092 | −0.066 |
| Building type | 3.5782 | 11.391 | 4.2177 | 12.887 | 4.9740 | 10.158 | 3.8446 | 7.305 | 5.7134 | 7.901 |
| Building age | −0.0758 | −8.802 | −0.0838 | −9.341 | −0.1203 | −8.689 | −0.0328 | −2.267 | −0.0388 | −1.926 |
| Facing road width | 0.0490 | 2.387 | 0.0189 | 0.960 | 0.0907 | 2.690 | 0.1117 | 3.577 | −0.0083 | −0.171 |
| Distance to major road | −0.0020 | −1.685 | 3.5054 | 0.324 | −0.0069 | −2.125 | −0.0283 | −2.462 | −0.0145 | −1.954 |
| Distance to park | −2.7155 | −0.237 | 0.0002 | 1.530 | 3.8439 | 0.184 | 0.0003 | 1.576 | −8.7546 | −0.302 |
| Distance to elementary school | −0.0002 | −1.371 | −4.6471 | −0.208 | 0.0008 | 2.056 | −9.5953 | −0.259 | −0.0002 | −0.431 |
| Distance to junior school | −0.0002 | −1.706 | −0.0004 | −2.844 | −0.0005 | −2.272 | −0.0005 | −2.3644 | −0.0003 | −0.919 |
| Distance to train station | −7.3536 | −1.615 | −0.0002 | −3.476 | 8.1308 | 1.030 | −7.4117 | −0.112 | −5.5035 | −0.605 |
| Distance to transfer station | −0.0004 | −5.4536 | −0.0006 | −7.981 | −0.0007 | −6.346 | −0.0005 | −5.185 | −0.0005 | −3.073 |
| Spatial correlation coefficient | 0.1547 | 1.884 | 0.1353 | 1.5612 | 0.1660 | 1.844 | 0.1882 | 1.173 | 0.0746 | 0.494 |
| R² | 0.3551 | 0.4254 | 0.3713 | 0.2539 | 0.222378 | |||||
| Adj-R² | NA | NA | NA | NA | NA | |||||
| F檢定 | NA | NA | NA | NA | NA | |||||
| AIC | 4430.64 | 3964.57 | 4230.13 | 3020.58 | 3231.01 | |||||
| LR test | 4.0472 | 3.2606 | 3.4755 | 1.2407 | 0.2095 | |||||
| LM lag | NA | NA | NA | NA | NA | |||||
| LM error | NA | NA | NA | NA | NA | |||||
| Data | 913 | 810 | 738 | 546 | 526 | |||||
| Spatial Autocorrelation | Year | Count | Count Average | Median | Standard Deviation | Maximum Price | Minimum Price |
|---|---|---|---|---|---|---|---|
| H-H | 2013 | 125 | 13.97 | 12.91 | 3.7 | 29.05 | 10.42 |
| 2014 | 109 | 15.68 | 14.38 | 4.25 | 46.73 | 11.87 | |
| 2015 | 61 | 21.81 | 18.4 | 10.32 | 63.59 | 13.04 | |
| 2016 | 48 | 19.38 | 17.74 | 4.6 | 35.09 | 14.4 | |
| 2017 | 32 | 23.15 | 21.07 | 7.84 | 51.07 | 16.4 | |
| L-L | 2013 | 91 | 4.75 | 4.67 | 1.2 | 6.74 | 1.86 |
| 2014 | 84 | 5.33 | 5.86 | 1.68 | 8.28 | 1.8 | |
| 2015 | 39 | 4.25 | 4.01 | 1.48 | 7.14 | 2.16 | |
| 2016 | 33 | 5.62 | 5.88 | 1.4 | 8.18 | 2.55 | |
| 2017 | 16 | 5.67 | 5.43 | 1.28 | 8.46 | 3.95 |
| Variables | Expected Correlation | Correlation by Model Analysis | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Y2013 | Y2014 | Y2015 | Y2016 | Y2017 | ||||||||||||
| Hedonic Price Method | Spatial Lag Model | Spatial Error Model | Hedonic Price Method | Spatial Lag Model | Spatial Error Model | Hedonic Price Method | Spatial Lag Model | Spatial Error Model | Hedonic Price Method | Spatial Lag Model | Spatial Error Model | Hedonic Price Method | Spatial Lag Model | Spatial Error Model | ||
| Total floor area | ||||||||||||||||
| Floors level | ||||||||||||||||
| Building type | ||||||||||||||||
| Building age | ||||||||||||||||
| Facing road width | ||||||||||||||||
| Distance to major road | ||||||||||||||||
| Distance to park | ||||||||||||||||
| Distance to elementary school | ||||||||||||||||
| Distance to junior school | ||||||||||||||||
| Distance to train station | ||||||||||||||||
| Distance to transfer station | ||||||||||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.-C.; Chang, Y.-J.; Wang, H.-C. An Application of the Spatial Autocorrelation Method on the Change of Real Estate Prices in Taitung City. ISPRS Int. J. Geo-Inf. 2019, 8, 249. https://doi.org/10.3390/ijgi8060249
Wang W-C, Chang Y-J, Wang H-C. An Application of the Spatial Autocorrelation Method on the Change of Real Estate Prices in Taitung City. ISPRS International Journal of Geo-Information. 2019; 8(6):249. https://doi.org/10.3390/ijgi8060249
Chicago/Turabian StyleWang, Wen-Ching, Yu-Ju Chang, and Hsueh-Ching Wang. 2019. "An Application of the Spatial Autocorrelation Method on the Change of Real Estate Prices in Taitung City" ISPRS International Journal of Geo-Information 8, no. 6: 249. https://doi.org/10.3390/ijgi8060249
APA StyleWang, W.-C., Chang, Y.-J., & Wang, H.-C. (2019). An Application of the Spatial Autocorrelation Method on the Change of Real Estate Prices in Taitung City. ISPRS International Journal of Geo-Information, 8(6), 249. https://doi.org/10.3390/ijgi8060249





