A Convenient Tool for District Heating Route Optimization Based on Parallel Ant Colony System Algorithm and 3D WebGIS
Abstract
:1. Introduction
1.1. District Heating Optimization
1.2. Intelligent Algorithms
1.3. GIS Tools for Designers
2. Materials and Methods
2.1. Study Area
2.2. DH Route Planning Indicator (DHRPI) Definition
2.3. Data Preparation
2.4. Parallel ACS Algorithm
2.4.1. Parameter Initialization
2.4.2. Route Searching
2.4.3. Pheromone Updating
2.5. Interactive 3D WebGISTool
3. Results and Discussion
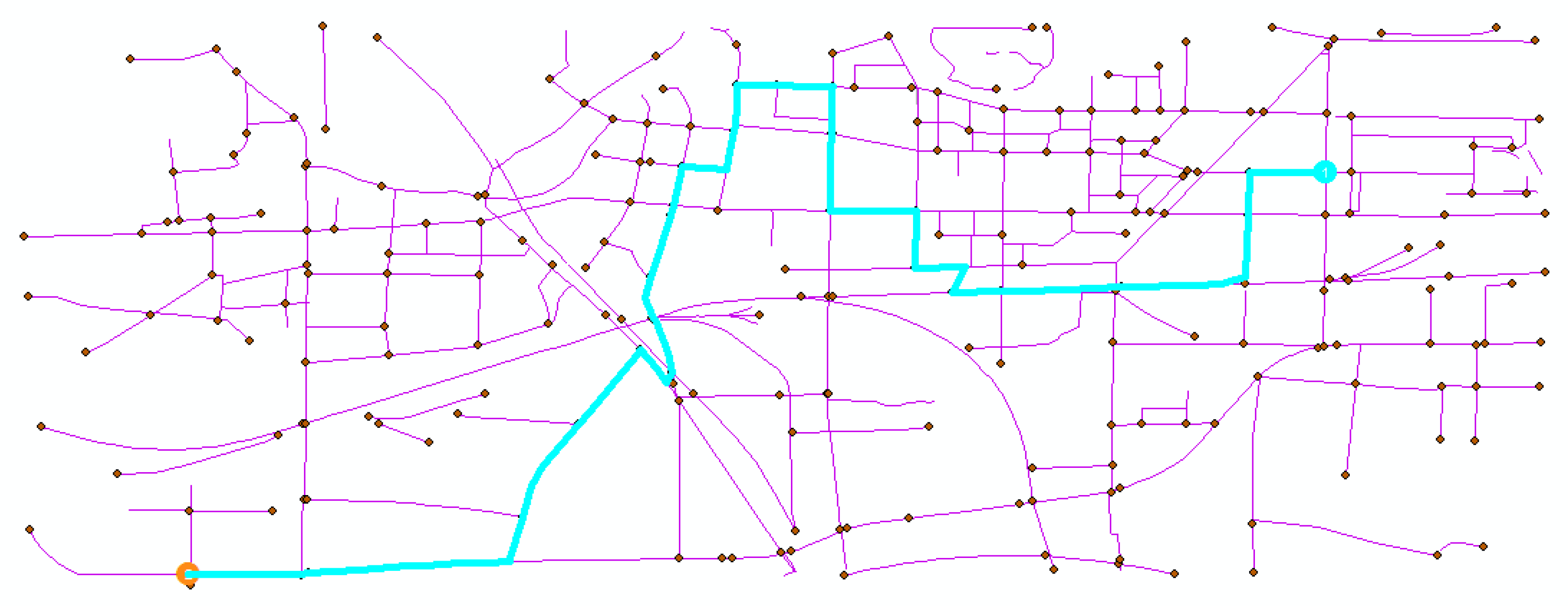
3.1. Comparation with the Manually Designed Route
3.2. Comparation with the Corresponding Sequential Algorithm
3.3. Comparation with ArcGIS Network Analyst Tool
3.4. Interactive Design Results of the 3D WebGIS Tool
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Full Name |
| 3D | three-dimensional |
| ABC | artificial bee colony |
| ACO | ant colony optimization |
| ACS | ant colony system |
| AS | ant system |
| ASrank | rank-based ant system |
| CS | cuckoo search |
| CVRP | capacitated vehicle routing problem |
| DH | district heating |
| DHRPI | district heating route planning indicator |
| GA | genetic algorithm |
| GIS | Geographic Information System |
| GPUs | graphics processing units |
| ID | identification numbers |
| IWD | intelligent water drops algorithm |
| MMAS | max–min ant system |
| OSM | OpenStreetMap |
| PSO | particle swarm optimization |
| SI | Swarm intelligence |
| TSP | traveling salesman problem |
Nomenclature
| Symbol | Description | Equation |
| ci,j | the cost between node i and node j | (1) |
| IRp | IR is thebinary image of road.For the exact pixel p, if p is the road pixel, IRp is set to 1; else, if p is not the road pixel, IRp is set to 0. | (1) |
| IBLp | IBL is thebinary image of bare land. For the exact pixel p, if p is the bare land pixel, IBLp is set to 1; else, if p is not the bare land pixel, IBLp is set to 0. | (2) |
| IVp | IV is thebinary image of vegetable. For the exact pixel p, if p is the vegetable pixel, IVp is set to 1; else, if p is not the vegetable pixel, IVp is set to 0. | (2) |
| IBp | IB is thebinary image of building. For the exact pixel p, if p is the building pixel, IBp is set to 1; else, if p is not the building pixel, IBp is set to 0. | (2) |
| IWp | IW is thebinary image of water. For the exact pixel p, if p is the water pixel, IWp is set to 1; else, if p is not the water pixel, IWp is set to 0. | (2) |
| wr | the weight of the road pixel | (2) |
| wbl | the weight of the bare land pixel | (2) |
| wv | the weight of the vegetation pixel | (2) |
| wb | the weight of the building pixel | (2) |
| ww | the weight of the water pixel | (2) |
| C | the cost matrix | (3) |
| Dn,n+1 | Dn,n+1 is the cost of the specific segment that composed a candidate route. It can be traced to ci,j by the index of the node. | (4) |
| find | the function of the DH route planning indicator | (2) |
| the initial value of pheromone | ||
| m | the number of ants | |
| Sp | the start point of the route | |
| Ep | the end point of the route | |
| Tabu | a matrix that storesthe index of visited nodes | |
| visited | a vector that stores the index of the visited nodes for the current ant | |
| allowed | a vector that stores the index of the candidate nodes for the current ant | |
| Nallowed | the size of the allowed vector | (6) |
| one of the candidate nodes from the allowed vector | (6) | |
| the current visited node | (6) | |
| the previous visited node | (6) | |
| sub_allowed | a subset of the allowed vector after the angle screening step | |
| q | a random number | (7) |
| qo | a constant | (7) |
| the intensity of the pheromone between node i and node j at time t | (7) | |
| the heuristic information between node i and node j at time t | (7) | |
| α | a constant that can be described as the weighted value of the pheromone () | (7) |
| β | a constant that can be described as the weighted value of the heuristic information () | (7) |
| a probability | (7) | |
| ρ | a parameter for the local updating rule | (8) |
| α | a parameter for the global updating rule | (9) |
| We set the same as the initial value of pheromone () | (8) | |
| the DH route planning indicator of the best route | (10) |
References
- Li, H.; Svendsen, S. District heating network design and configuration optimization with genetic algorithm. J. Sustain. Dev. Energy Water Environ. Syst. 2013, 1, 291–303. [Google Scholar] [CrossRef]
- Bloomquist, R.G. Geothermal district energy system analysis, design, and development. Available online: https://pangea.stanford.edu/ERE/pdf/IGAstandard/ISS/2001Romania/bloomquist_dh.pdf (accessed on 15 April 2019).
- Yildirim, N.; Toksoy, M.; Gokcen, G. Piping network design of geothermal district heating systems: Case study fora university campus. Energy 2010, 35, 3256–3262. [Google Scholar] [CrossRef]
- Dobersek, D.; Goricanec, D. Optimization of tree path pipe network with nonlinear optimization method. Appl. Therm. Eng. 2009, 29, 1584–1591. [Google Scholar] [CrossRef]
- Li, X.; Duanmu, L.; Shu, H. Optimal design of district heating and cooling pipe network of seawater-source heat pump. Energy Build. 2010, 42, 100–104. [Google Scholar] [CrossRef]
- Valdimarsson, P. PipeLab 3.18 Software. NuonTechnischBedrijf; University ofIceland: Reykjavík, Iceland, 2002. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colomi, A. The Ant System: An Autocatalytic Optimizing Process. Available online: http://citeseerx.ist.psu.edu/viewdoc/citations;jsessionid=C806753D4246E244F6BF5A5B82397014?doi=10.1.1.51.4214 (accessed on 15 April 2019).
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.714.4934 (accessed on 15 April 2019).
- Yang, X.-S.; Deb, S. Cuckoo Search Via Lévy Flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Shah-Hosseini, H. The intelligent water drops algorithm: A nature-inspired swarm-based optimization algorithm. Int. J. Bio-Inspired Comput. 2009, 1, 71–79. [Google Scholar] [CrossRef]
- Lawler, E.L.; Lenstra, J.K.; Kan, A.R.; Shmoys, D.B. The Traveling Salesman Problem: AguidedTour of Combinatorial Optimization; Wiley: Chichester, UK, 1985. [Google Scholar]
- Zhang, Y.; Zhao, H.; Cao, Y.; Liu, Q.; Shen, Z.; Wang, J.; Hu, M. A hybrid ant colony and cuckoo search algorithm for route optimization of Heating engineering. Energies 2018, 11, 2675. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man. Cybern. Part B 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Bullnheimer, B.; Hartl, R.F.; Strauss, C. A new rank-based version of the ant system: A computational study. Cent. Eur. J. Oper. Res. Econ. 1999, 7, 25–38. [Google Scholar]
- Stützle, T.; Hoos, H. MAX–MIN Ant System and Local Search for the Traveling Salesman Problem. In Proceedings of the 1997 IEEE International Conference on Evolutionary Computation (ICEC’97), Indianapolis, IN, USA, 13–16 April 1997; pp. 309–314. [Google Scholar]
- Dorigo, M.; Gambardella, L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Yu, B.; Yang, Z.-Z.; Yao, B. An improved ant colony optimization for vehicle routing problem. Eur. J. Oper. Res. 2009, 196, 171–176. [Google Scholar] [CrossRef]
- Tuba, M.; Jovanovic, R. Improved ACO algorithm with pheromone correction strategy for the traveling salesman problem. Int. J. Comput. Commun. 2013, 8, 477–485. [Google Scholar] [CrossRef]
- Dorigo, M.; Stützle, T. Ant Colony Optimization: Overview and Recent Advances. In Handbook of Metaheuristics; Gendreau, M., Potvin, J.Y., Eds.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Gambardella, L.M.; Taillard, E.D.; Agazzi, G. MACS-VRPTW: A Multiple Ant ColonySystem for Vehicle Routing Problems with Time Windows. In New Ideas in Optimization; Corne, D., Dorigo, M., Glover, F., Eds.; McGraw Hill: London, UK, 1999; pp. 63–76. [Google Scholar]
- Mahi, M.; Baykan, Ö.K.; Kodaz, H. A new hybrid method based on particle swarm optimization, ant colony optimization and 3-opt algorithms for traveling salesman problem. Appl. Soft Comput. 2015, 30, 484–490. [Google Scholar] [CrossRef]
- Tsutsui, S.; Fujimoto, N. Parallel Ant colony optimization algorithm on a multi-core processor. In Proceedings of the 7th International Conference onSwarm Intelligence, Brussels, Belgium, 8–10 September 2010; pp. 488–495. [Google Scholar]
- Delévacq, A.; Delisle, P.; Gravel, M.; Krajecki, M. Parallel ant colony optimization on graphics processing units. J. Parallel Distrib. Comput. 2013, 73, 52–61. [Google Scholar] [CrossRef]
- Pedemonte, M.; Nesmachnow, S.; Cancela, H. A survey on parallel ant colony optimization. Appl. Soft Comput. 2011, 11, 5181–5197. [Google Scholar] [CrossRef]
- Arcgis Online. Available online: www.arcgis.com (accessed on 15 April 2019).
- Kallel, A.; Serbaji, M.M.; Zairi, M. Using GIS-based tools for the optimization of solid waste collection and transport: Case study of Sfax City, Tunisia. J. Eng. 2016, 10, 1–7. [Google Scholar] [CrossRef]
- Abousaeidi, M.; Fauzi, R.; Muhamad, R. Geographic Information System (GIS) modeling approach to determine the fastest delivery routes. Saudi J. Biol. Sci. 2016, 23, 555–564. [Google Scholar] [CrossRef] [PubMed]
- Alazab, A.; Venkatraman, S.; Abawajy, J.; Alazab, M. An Optimal Transportation Routing Approach Using GIS-Based Dynamic Traffic Flows. In Proceedings of the International Conference on Management Technology and Applications, Singapore, 10–12 September 2010; pp. 172–178. [Google Scholar]
- Baufumé, S.; Grüger, F.; Grube, T.; Krieg, D.; Linssen, J.; Weber, M.; Stolten, D. GIS-based scenario calculations for a nationwide German hydrogen pipeline infrastructure. Int. J. Hydrog. Energy. 2013, 38, 3813–3829. [Google Scholar] [CrossRef]
- Google Earth. Available online: http://earth.google.com (accessed on 15 April 2019).
- Skyline. Available online: http://www.skylineglobe.cn/ (accessed on 15 April 2019).
- Website of Super map. Available online: http://www.supermap.com/cn/ (accessed on 15 April 2019).
- Website of EV-Globe. Available online: http://www.ev-image.com/products/l-3852968750166. html (accessed on 15 April 2019).
- NASA WorldWind Project Suspension Update. Available online: https://worldwind.arc.nasa.gov/ (accessed on 15 April 2019).
- Website of Cesium. Available online: http://cesiumjs.org/ (accessed on 15 April 2019).
- Torres-Martínez, J.A.; Seddaiu, M.; Rodríguez-Gonzálvez, P.; Hernández-López, D.; González-Aguilera, D. A Multi-Data Source and Multi-Sensor Approach for the 3D Reconstruction and Visualization of a Complex Archaelogical Site: The Case Study of Tolmo De Minateda. Int. Arch. Photogramm.Remote Sens. 2015, XL-5/W4, 37–44. [Google Scholar]
- Gobakis, K.; Mavrigiannaki, A.; Kalaitzakis, K.; Kolokotsa, D.-D. Design and Development of a Web Based GIS Platform for Zero energy Settlements Monitoring. In Proceedings of the 9th International Conference on Sustainability in Energy and Buildings, Chania, Greece, 5–7 July 2017; pp. 48–60. [Google Scholar]
- People’s Republic of China Ministry of Housing and Urban-Rural Development. Design Code for City Heating Network; CJJ 34-2010; China Building Industry Press: Beijing, China, 2011.
- Dalkey, N.; Helmer, O. An experimental application of the Delphi method to the use of experts. Manag. Sci. 1963, 9, 458–467. [Google Scholar] [CrossRef]
- Rowe, G.; Wright, G. The Delphi technique as a forecasting tool: Issues and analysis. Int. J. Forecast. 1999, 15, 353–375. [Google Scholar] [CrossRef]
- Website of ENVI/IDL. Available online: http://www.enviidl.com/ (accessed on 15 April 2019).
- Website of ENVI. Available online: https://www.harrisgeospatial.com/ (accessed on 15 April 2019).
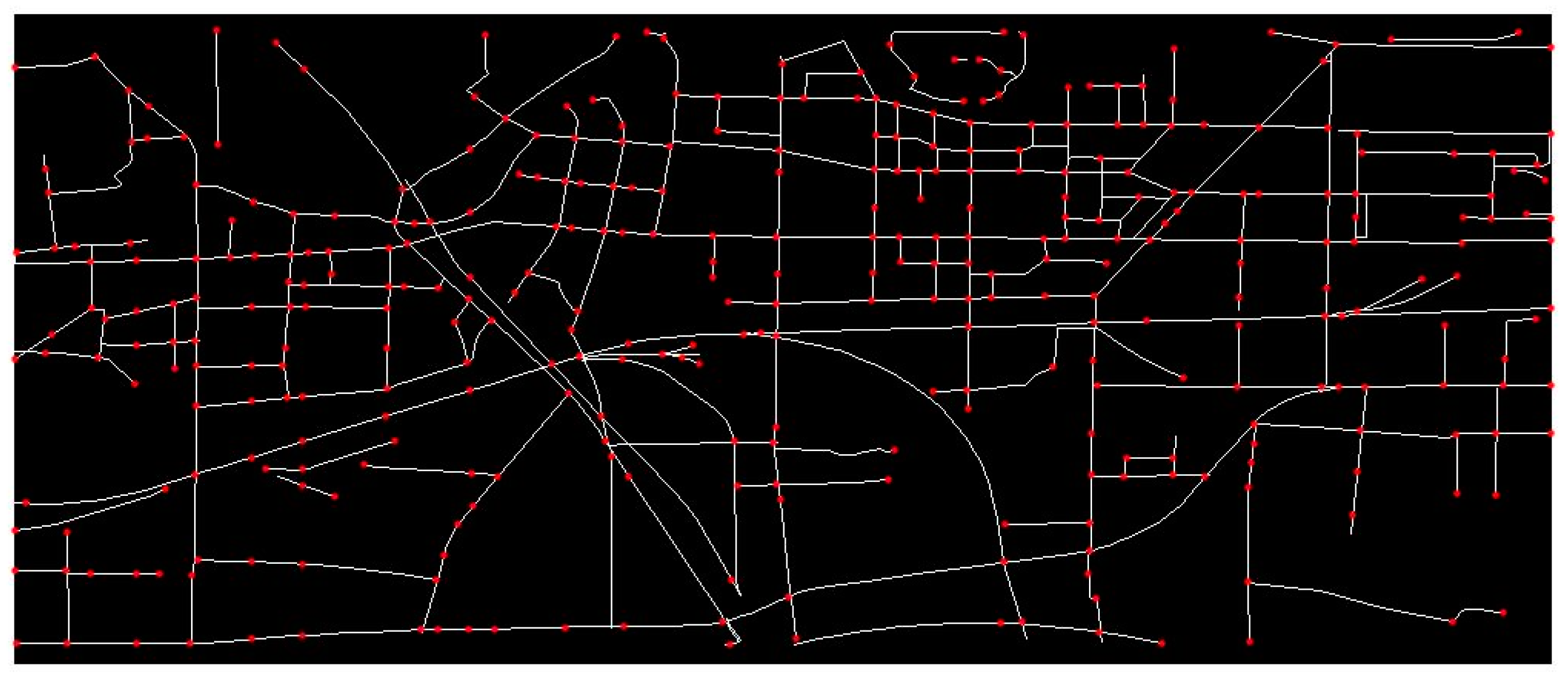

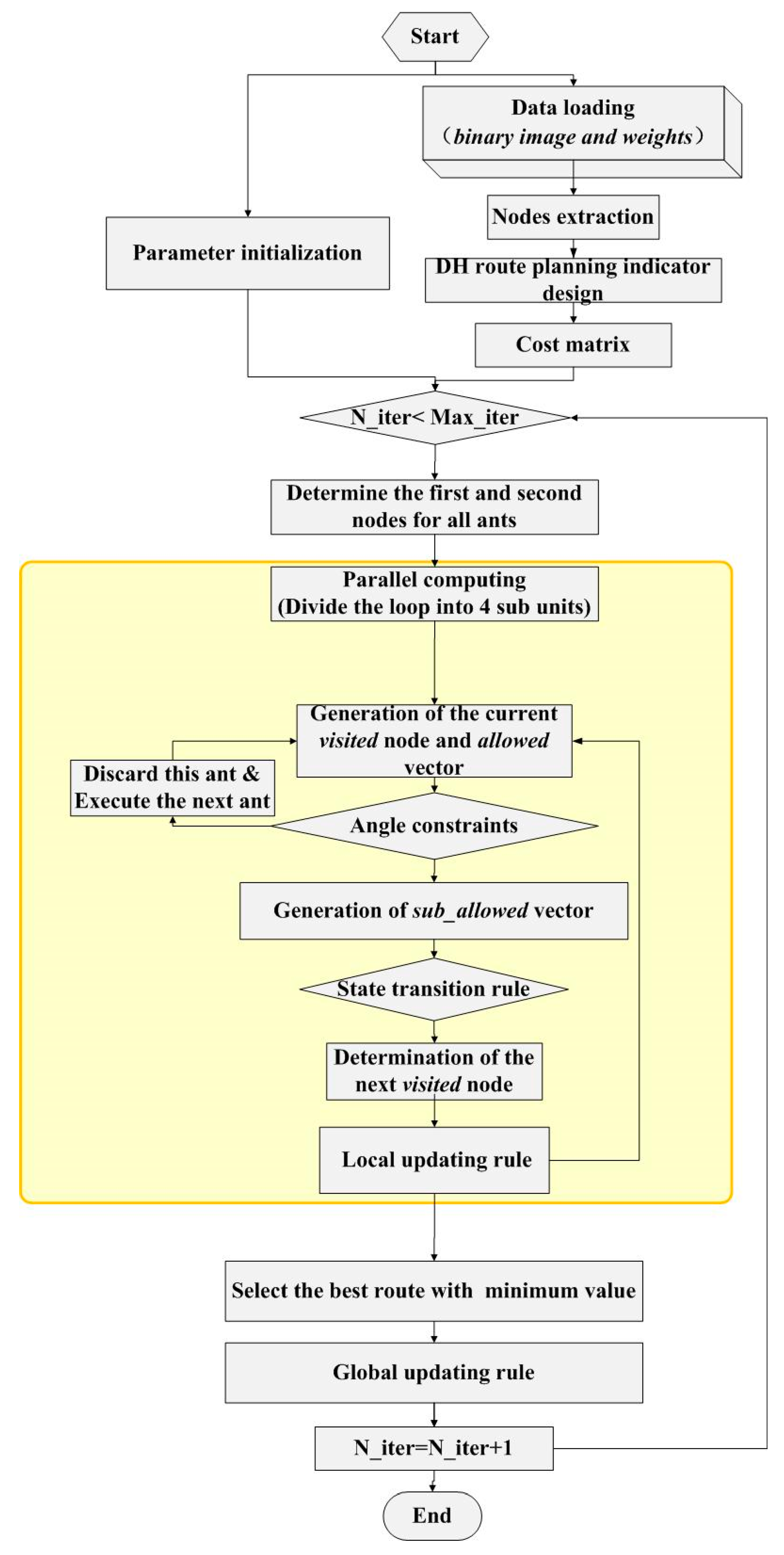
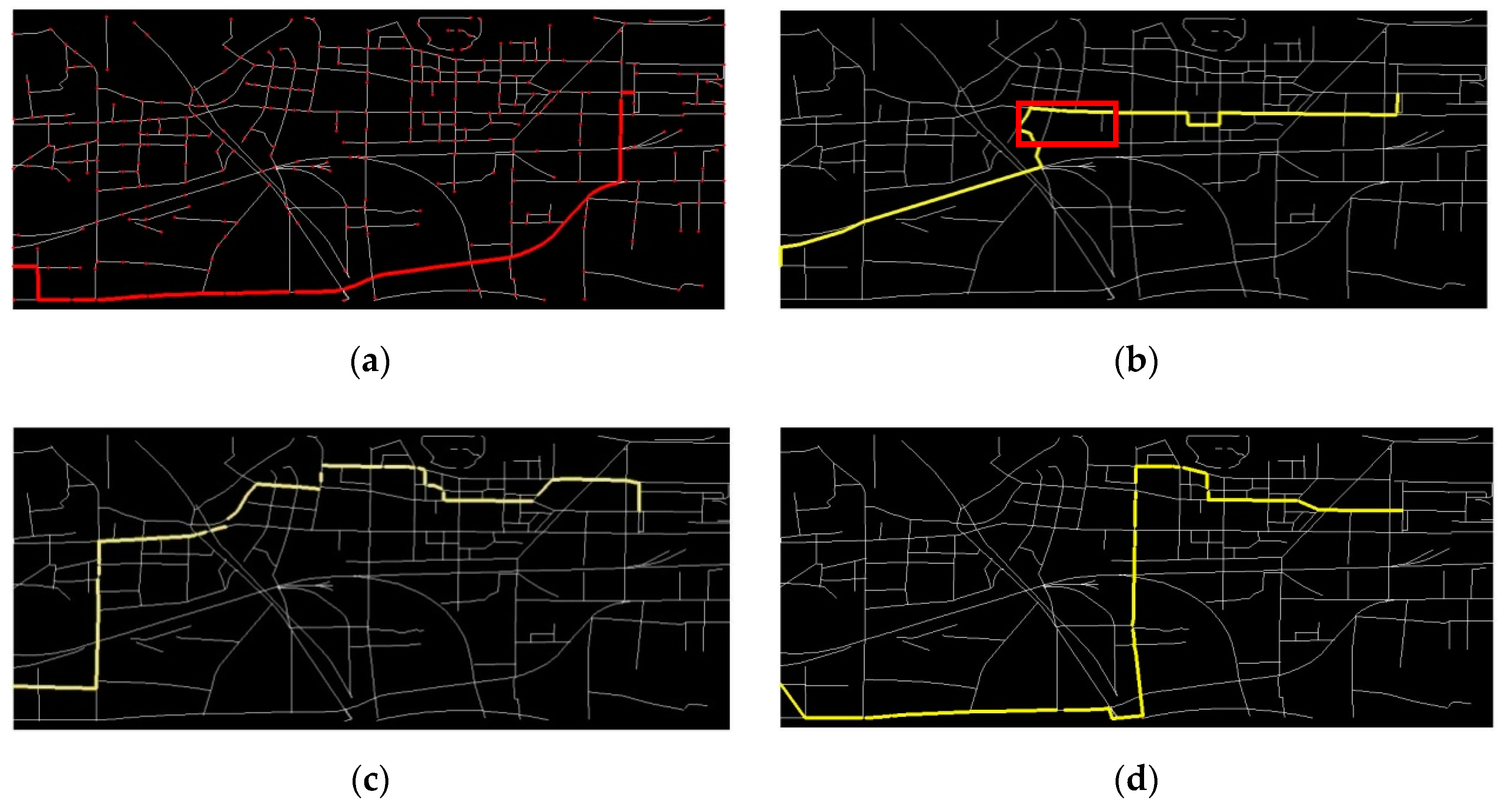
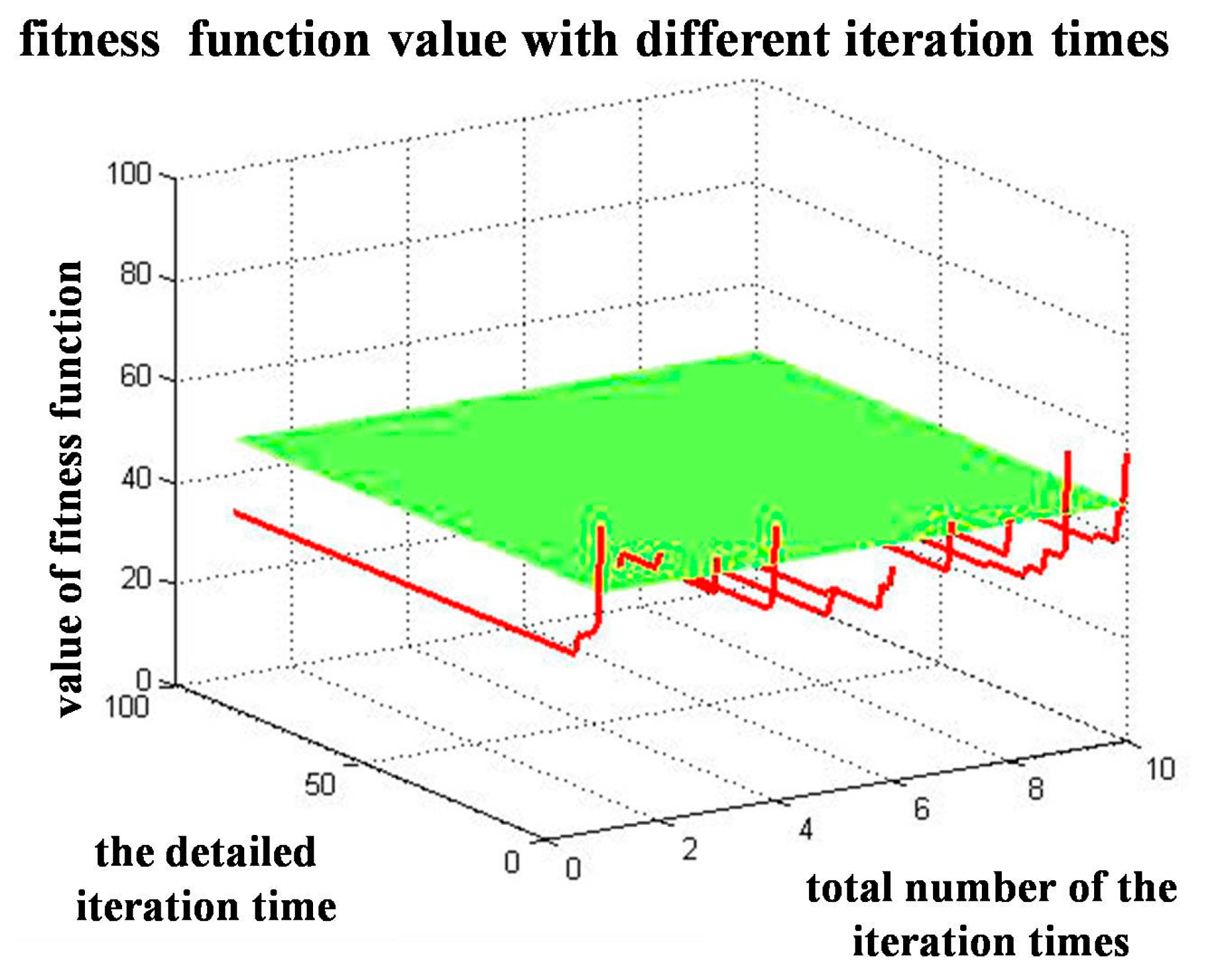
| No. | Indicators | No. | Indicators | No. | Indicators |
|---|---|---|---|---|---|
| 1 | 29.2184 | 11 | 36.5449 | 21 | 38.8374 |
| 2 | 30.2141 | 12 | 36.7126 | 22 | 39.1459 |
| 3 | 30.7896 | 13 | 36.9894 | 23 | 39.8428 |
| 4 | 31.9826 | 14 | 37.1286 | 24 | 39.905 |
| 5 | 32.0779 | 15 | 37.2763 | 25 | 41.9456 |
| 6 | 32.3144 | 16 | 37.4986 | 26 | 42.3429 |
| 7 | 32.6468 | 17 | 37.9436 | 27 | 44.4666 |
| 8 | 33.5068 | 18 | 38.231 | 28 | 45.2416 |
| 9 | 36.2242 | 19 | 38.5003 | 29 | 47.052 |
| 10 | 36.3235 | 20 | 38.6646 | 30 | 48.335 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, G.; Zhao, H.; Cao, Y.; Liu, Q.; Shen, Z.; Li, A. A Convenient Tool for District Heating Route Optimization Based on Parallel Ant Colony System Algorithm and 3D WebGIS. ISPRS Int. J. Geo-Inf. 2019, 8, 225. https://doi.org/10.3390/ijgi8050225
Zhang Y, Zhang G, Zhao H, Cao Y, Liu Q, Shen Z, Li A. A Convenient Tool for District Heating Route Optimization Based on Parallel Ant Colony System Algorithm and 3D WebGIS. ISPRS International Journal of Geo-Information. 2019; 8(5):225. https://doi.org/10.3390/ijgi8050225
Chicago/Turabian StyleZhang, Yang, Guoyong Zhang, Huihui Zhao, Yuming Cao, Qinhuo Liu, Zhanfeng Shen, and Aimin Li. 2019. "A Convenient Tool for District Heating Route Optimization Based on Parallel Ant Colony System Algorithm and 3D WebGIS" ISPRS International Journal of Geo-Information 8, no. 5: 225. https://doi.org/10.3390/ijgi8050225
APA StyleZhang, Y., Zhang, G., Zhao, H., Cao, Y., Liu, Q., Shen, Z., & Li, A. (2019). A Convenient Tool for District Heating Route Optimization Based on Parallel Ant Colony System Algorithm and 3D WebGIS. ISPRS International Journal of Geo-Information, 8(5), 225. https://doi.org/10.3390/ijgi8050225






