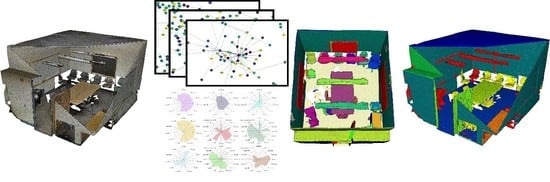
Voxel-based 3D Point Cloud Semantic Segmentation: Unsupervised Geometric and Relationship Featuring vs Deep Learning Methods
Abstract
:1. Introduction
- a new interoperable point cloud data clustering approach that account variability of domains for higher-end applications;
- a novel point cloud voxel-based featuring developed to accurately and robustly characterize a point cloud with local shape descriptors and topology pointers. It is robust to noise, resolution variation, clutter, occlusion, and point irregularity; and,
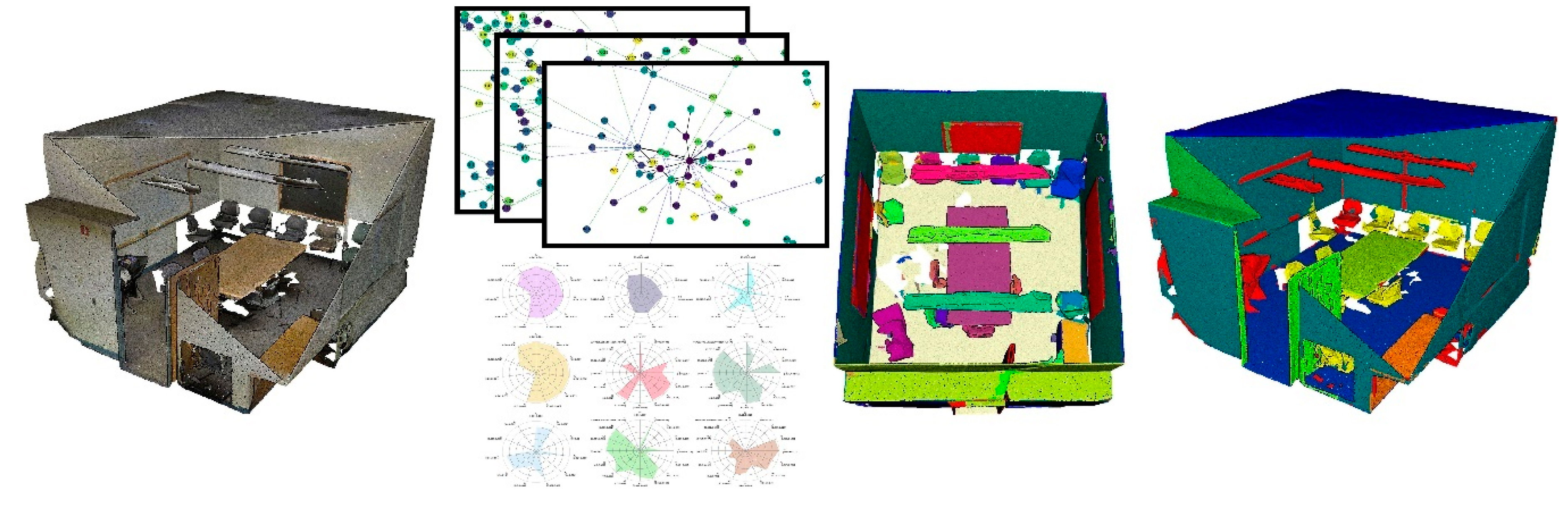
- a semantic segmentation framework to efficiently decompose large point clouds in related Connected Elements (unsupervised) that are specialized through a graph-based approach: it is fully benchmarked against state-of-the-art deep learning methods. We specifically looked at parallelization-compatible workflows.
2. Related Works
2.1. Point Cloud Feature Extraction
2.2. Semantic Segmentation Applied to Point Clouds
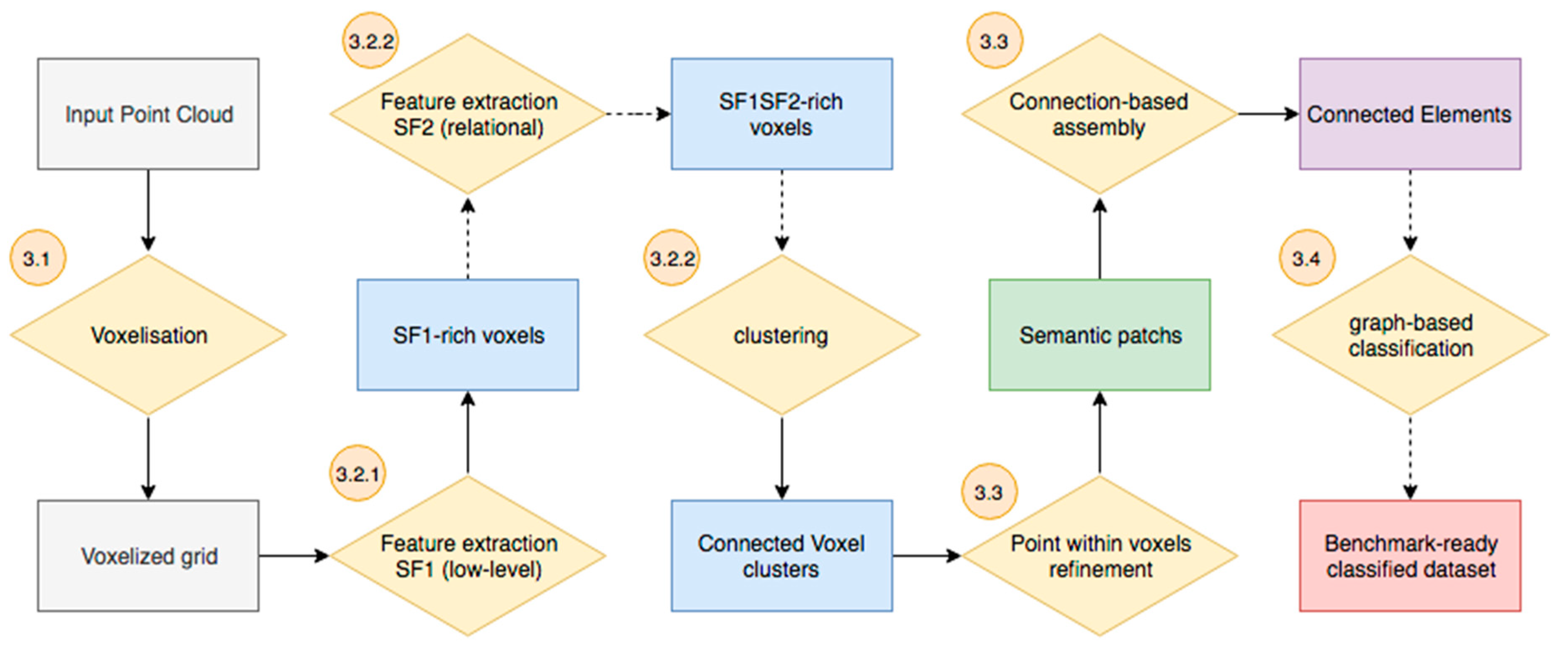
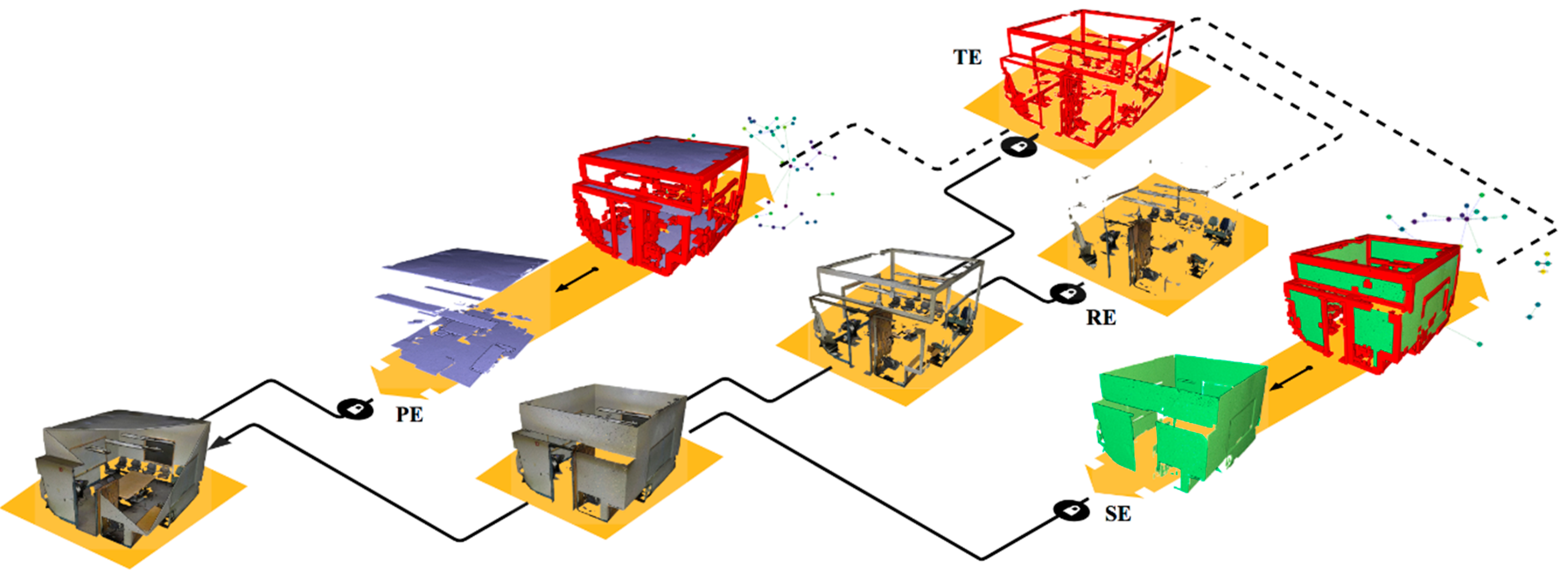
3. Materials and Methods
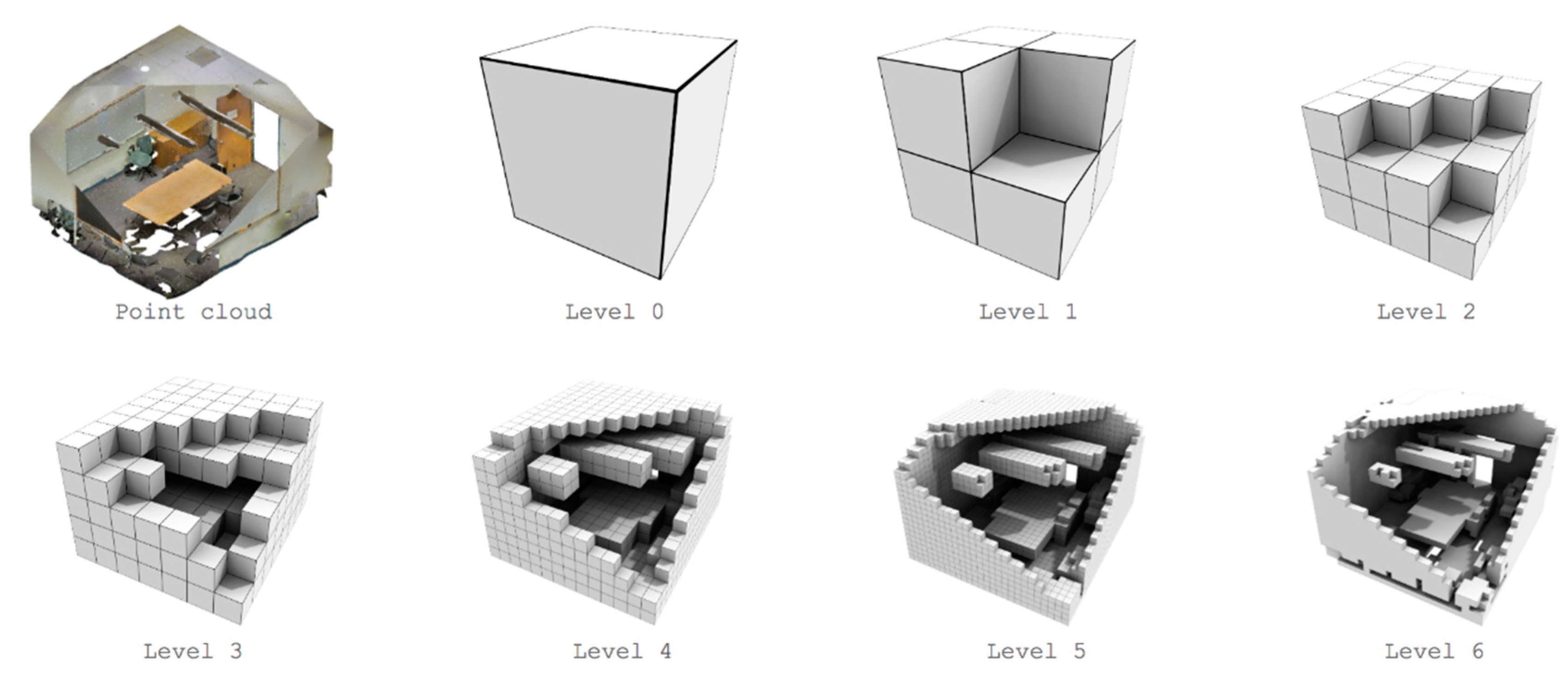
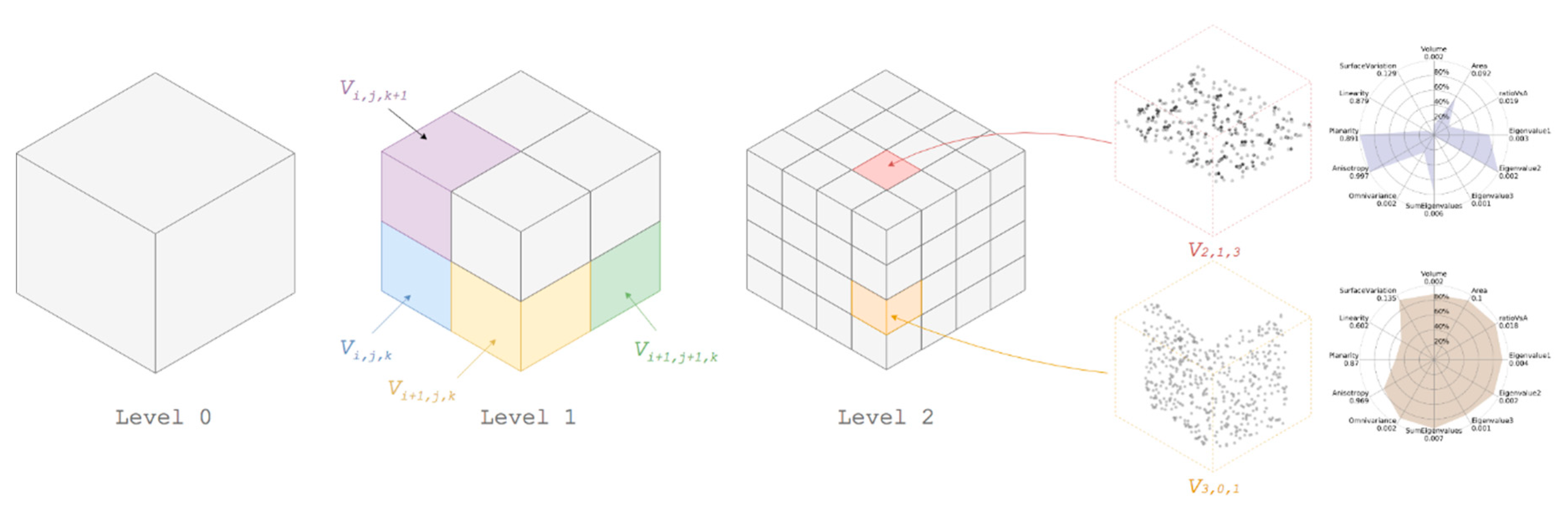
3.1. Voxelisation Grid Constitution
3.2. Feature Extraction
3.2.1. Low-Level Shape-Based Features (SF1)
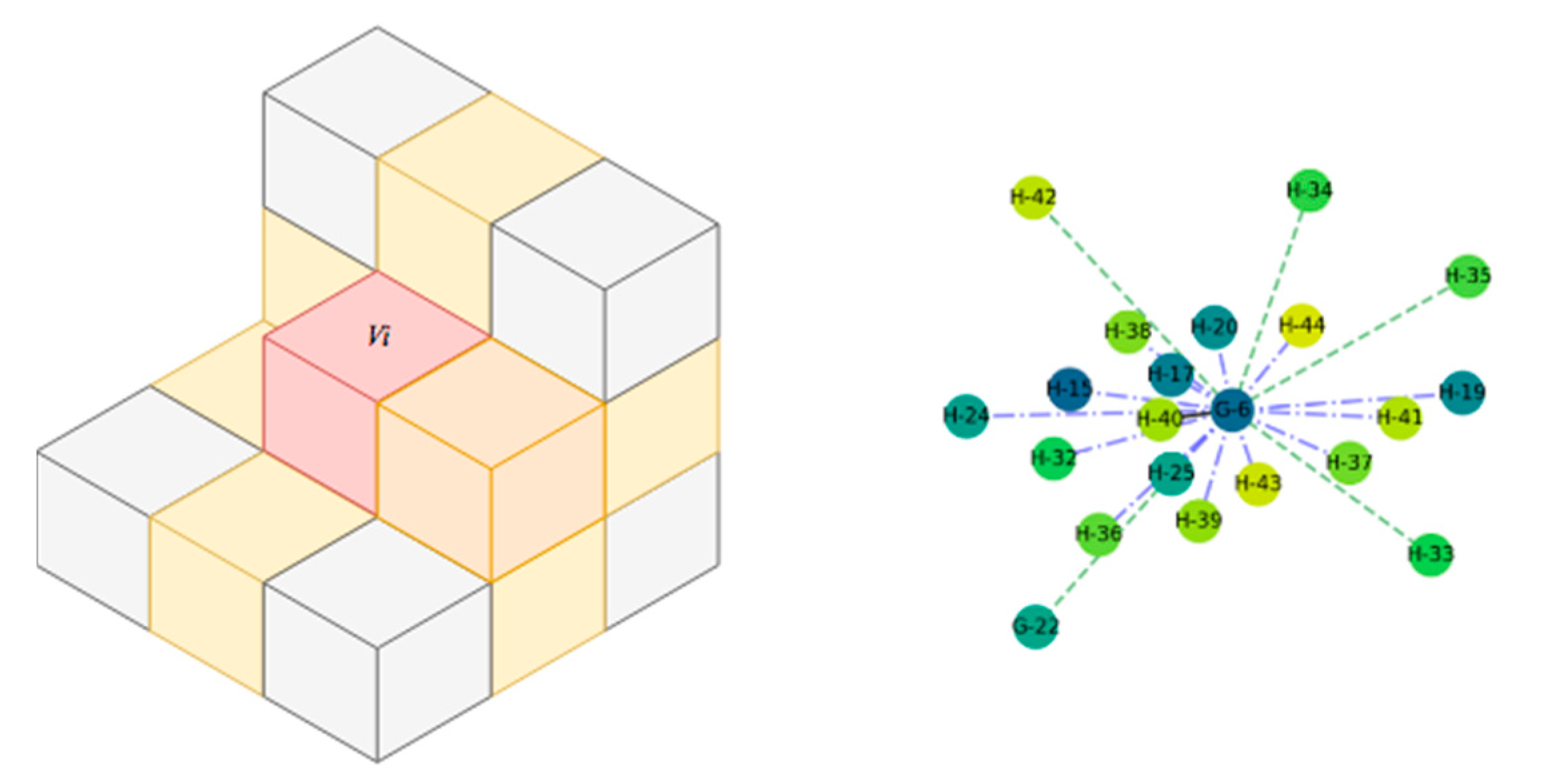
3.2.2. Connectivity and Relationship Features (SF2)
| Algorithm 1. Voxel Relation Convexity/Concavity Tagging |
| Require: A voxel and its direct vicinity expressed as a graph . |
| 1. For each do 2. angle between normal of voxels 3. if then 4. edge between and is tagged as Concave 5. else edge between and is tagged as Convex 6. end if 7. end for 8. end 9. return |
- Pure Horizontal relationship: For , if an adjacent voxel has a colinear to the main direction (vertical in gravity-based scenes), then the edge is tagged . If two adjacent nodes and hold an relationship and both are not colinear, they are connected by a directed edge, , where is the starting node. In practice, voxels that are near horizontal surfaces hold this relationship.
- Pure Vertical relationship: For , if an adjacent voxel has a orthogonal to the main direction (vertical in gravity-based scenes), then the edge is tagged . If two adjacent nodes and are connected through and both are coplanar but not colinear, then they are connected by a directed edge, . In the case that we are in a gravity-based scenario, they are further refined following and axis. These typically includes voxels that are near vertical surfaces.
- Mixed relationship: For , if within its 26-connectivity neighbours, the node presents and edges, then is tagged as . In practice, voxels near both horizontal and vertical surfaces hold this relationship.
- Neighbouring relationship. If two voxels do not hold one of these former constraining relationships but are neighbours, then the associated nodes are connected by an undirected edge without tags.
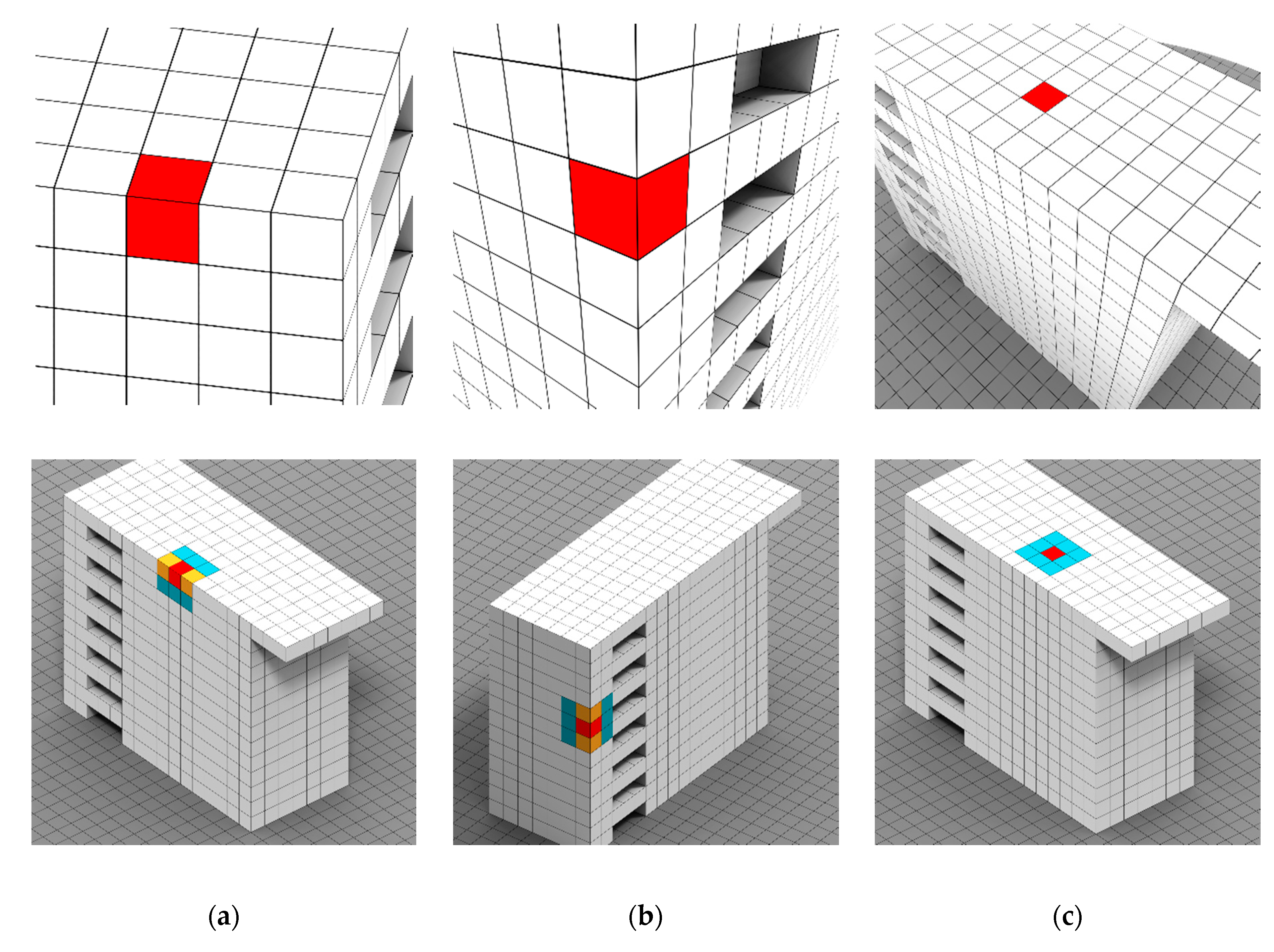
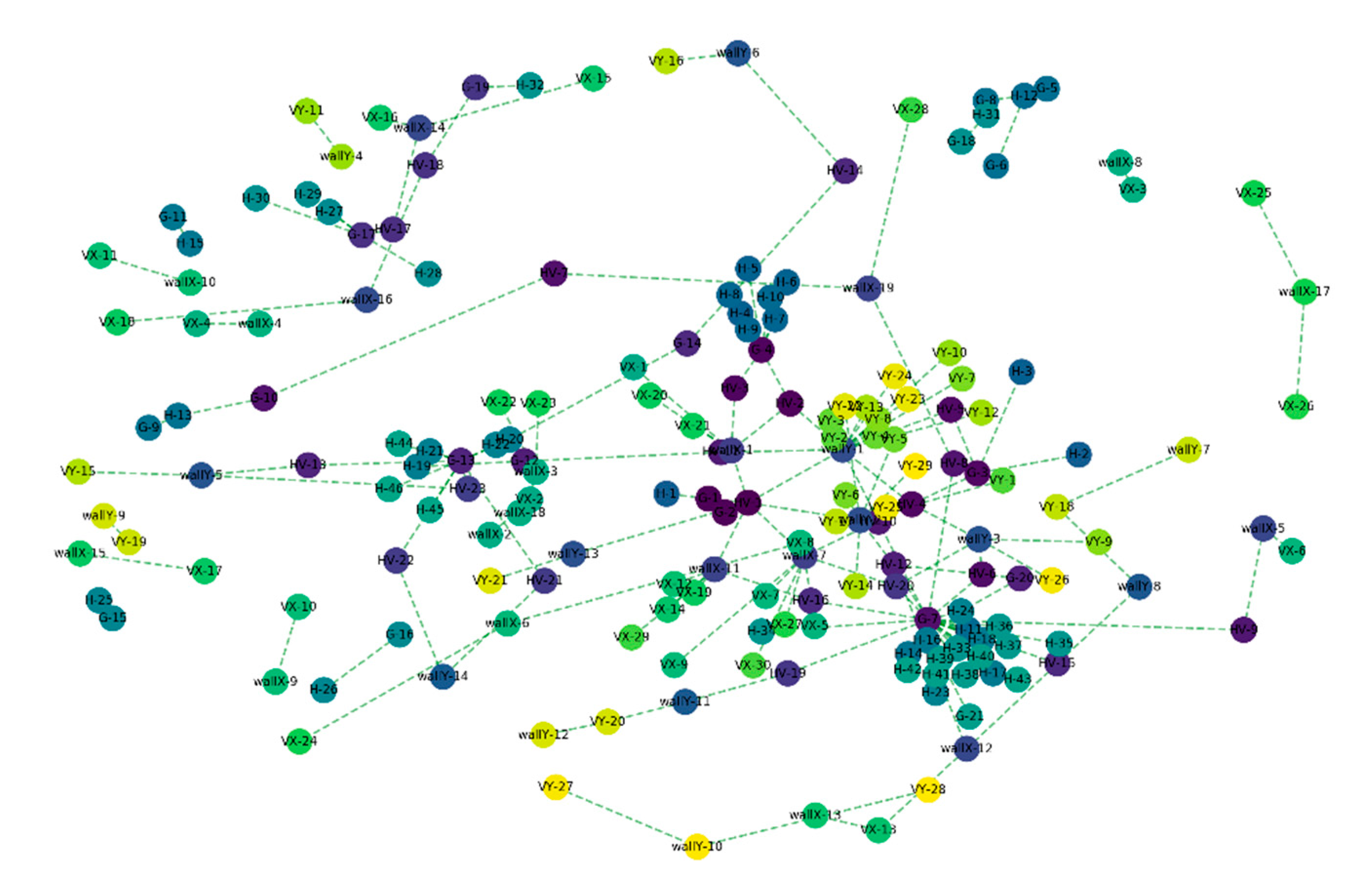
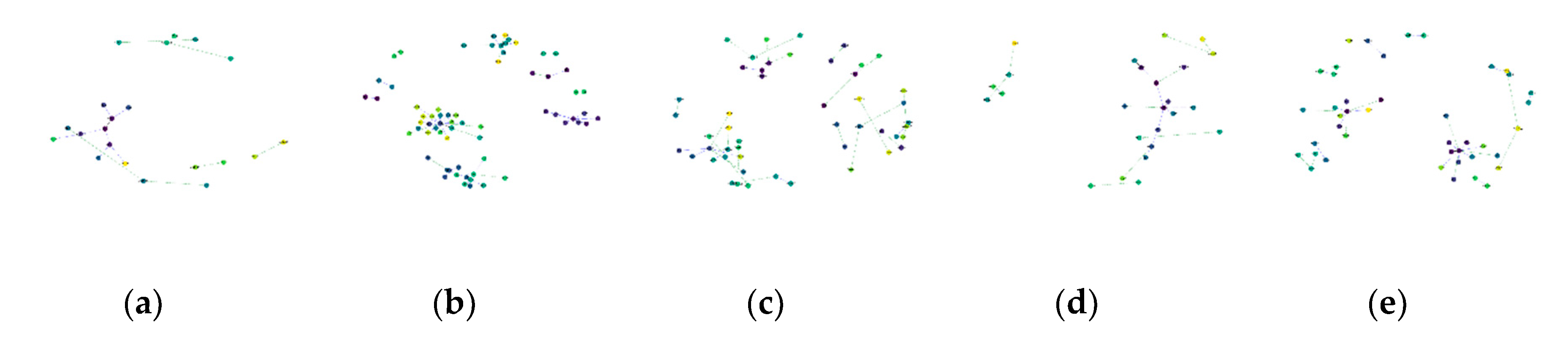
3.3. Connected Element Constitution and Voxel Refinement
3.4. Graph-based Semantic Segmentation
4. Dataset
5. Results
5.1. Metrics
- True Positive (TP): Observation is positive and is predicted to be positive.
- False Negative (FN): Observation is positive but is predicted negative.
- True Negative (TN): Observation is negative and is predicted to be negative.
- False Positive (FP): Observation is negative but is predicted positive.
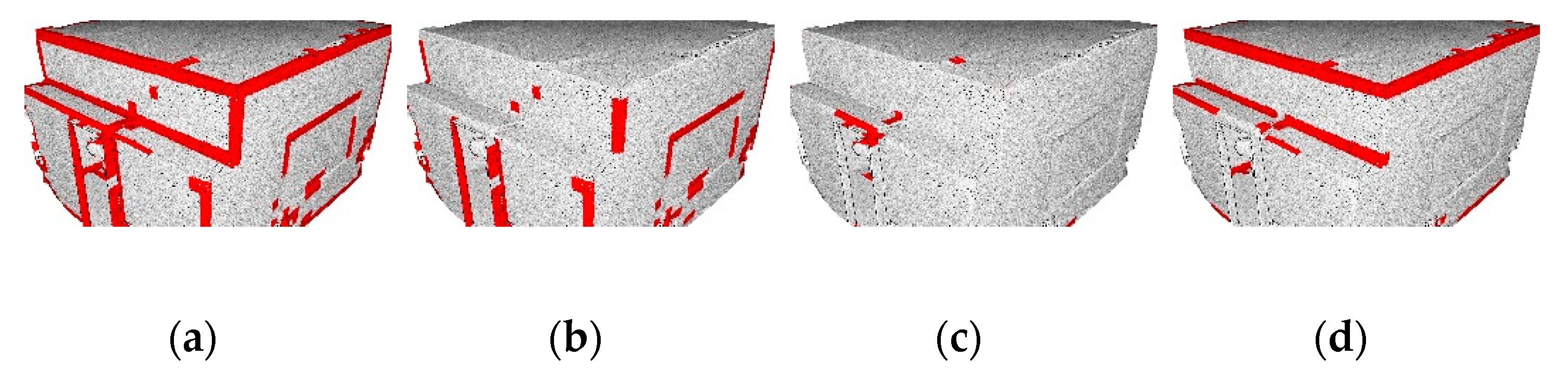
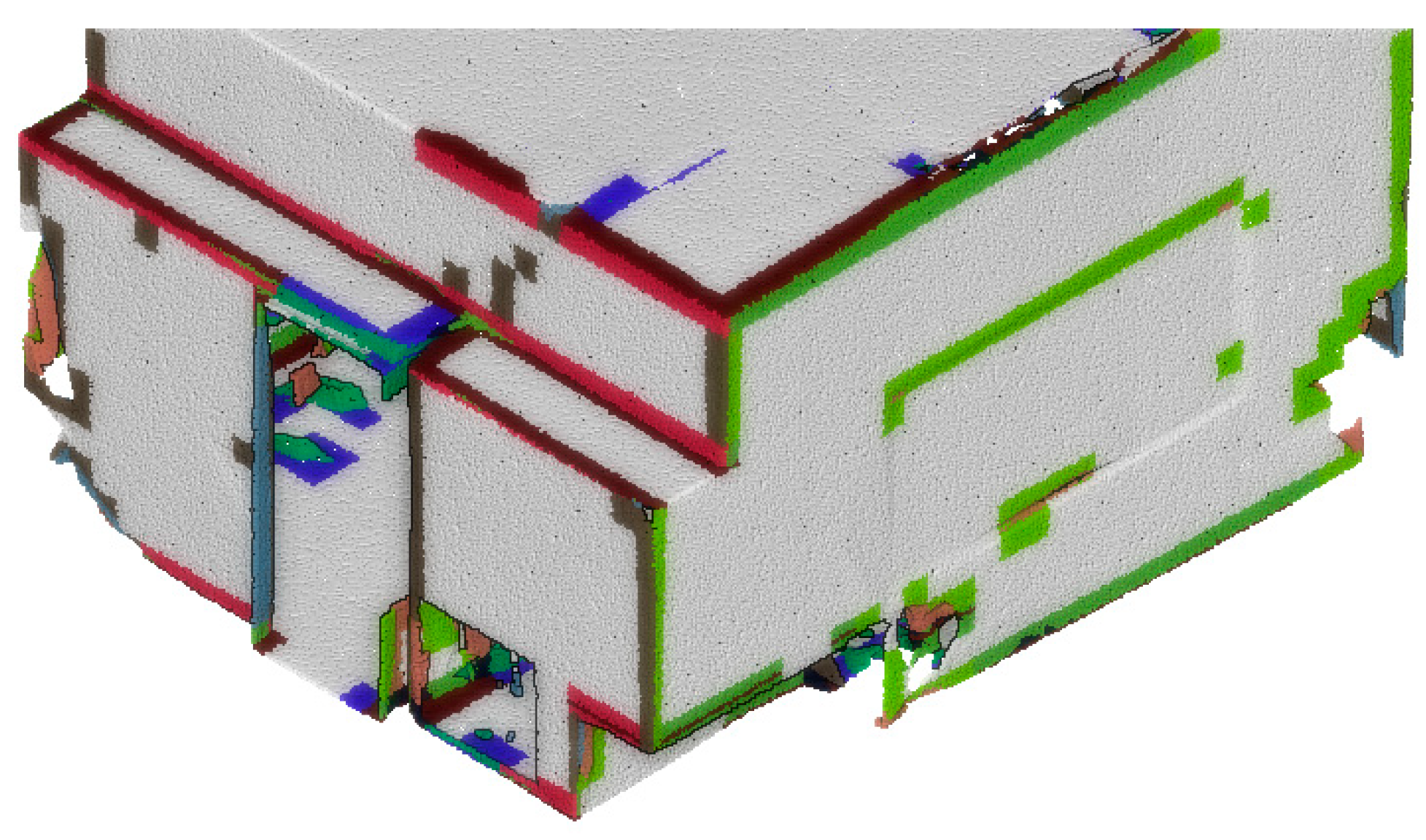
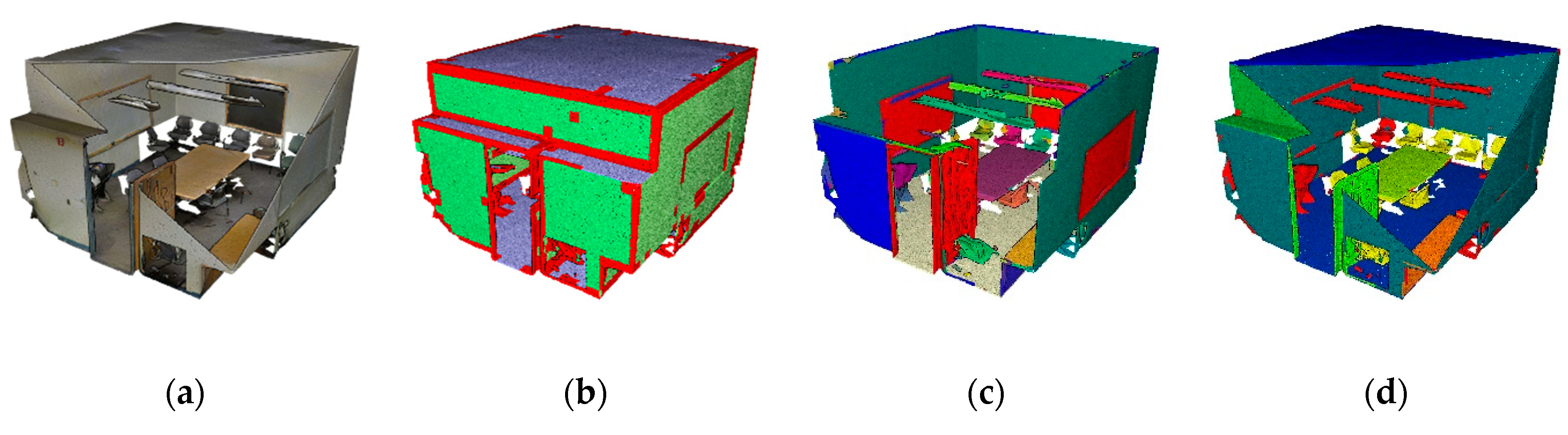
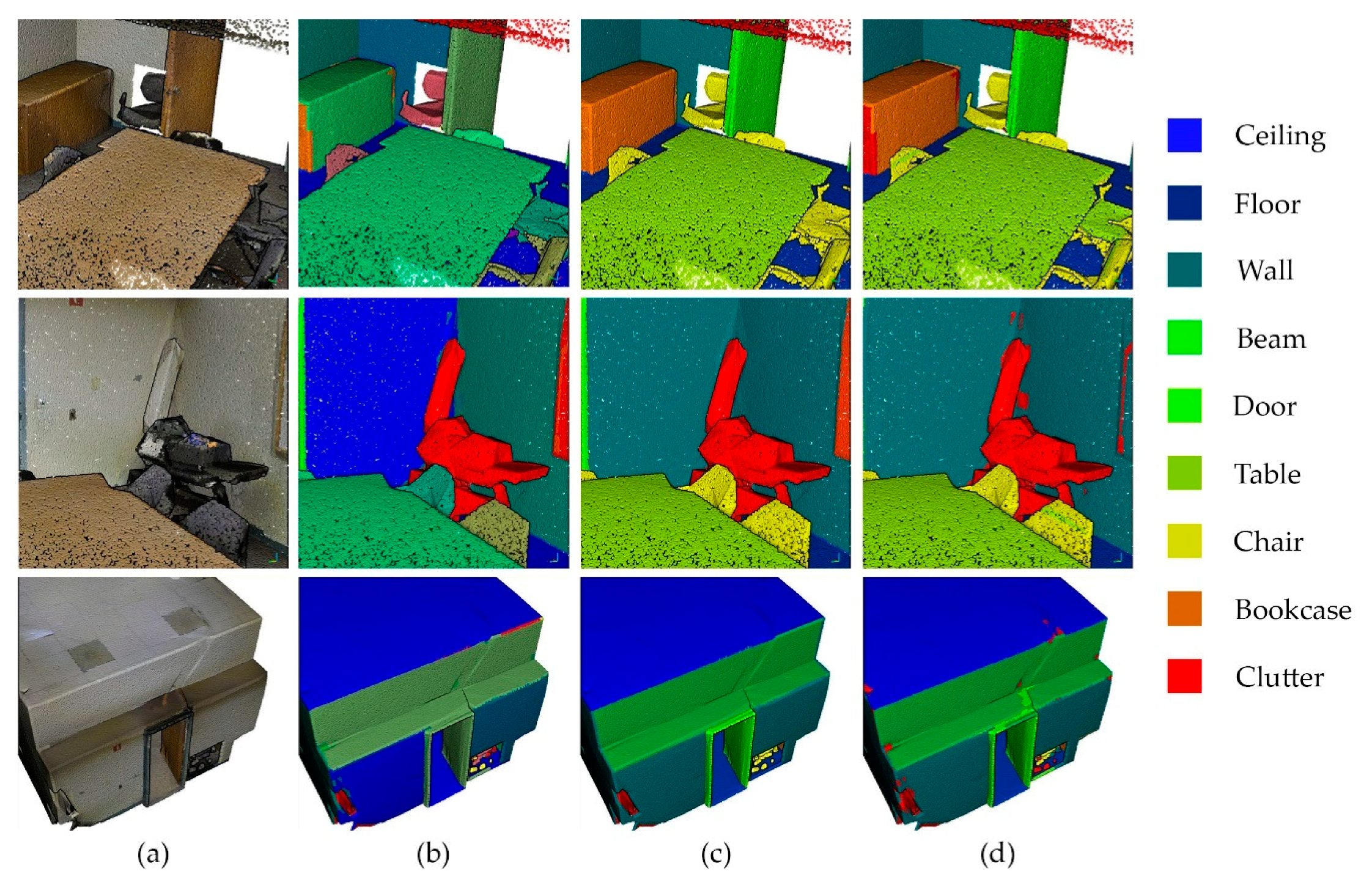
5.2. Quantitative and Qualitative Assessments
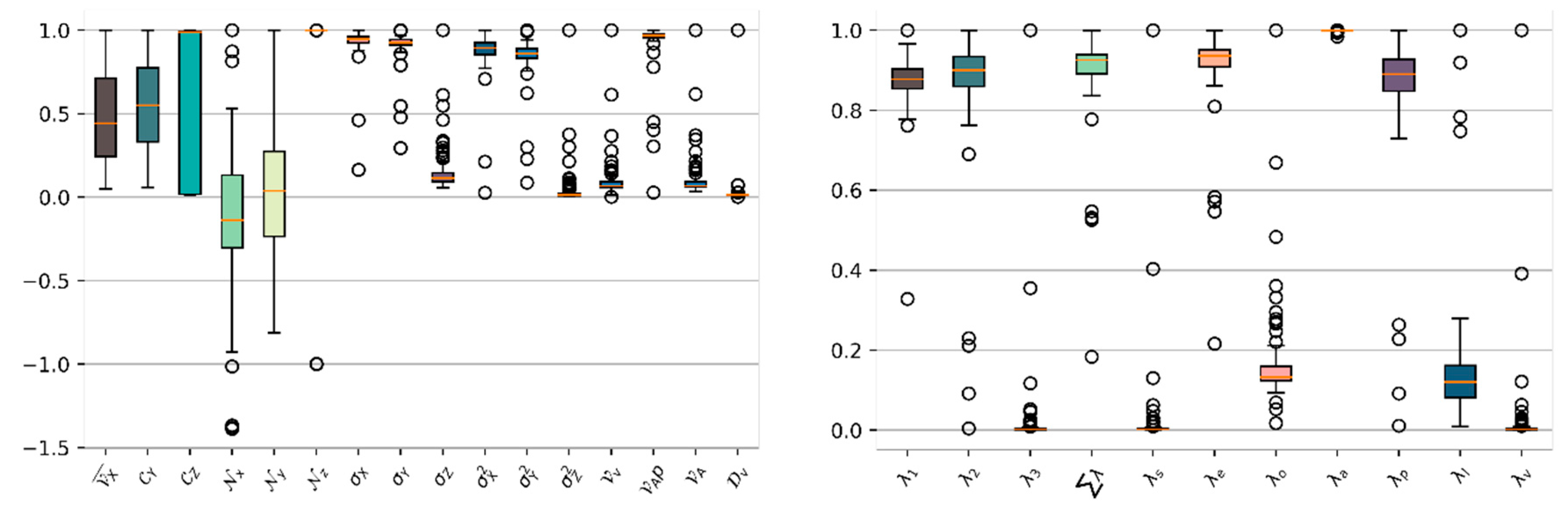
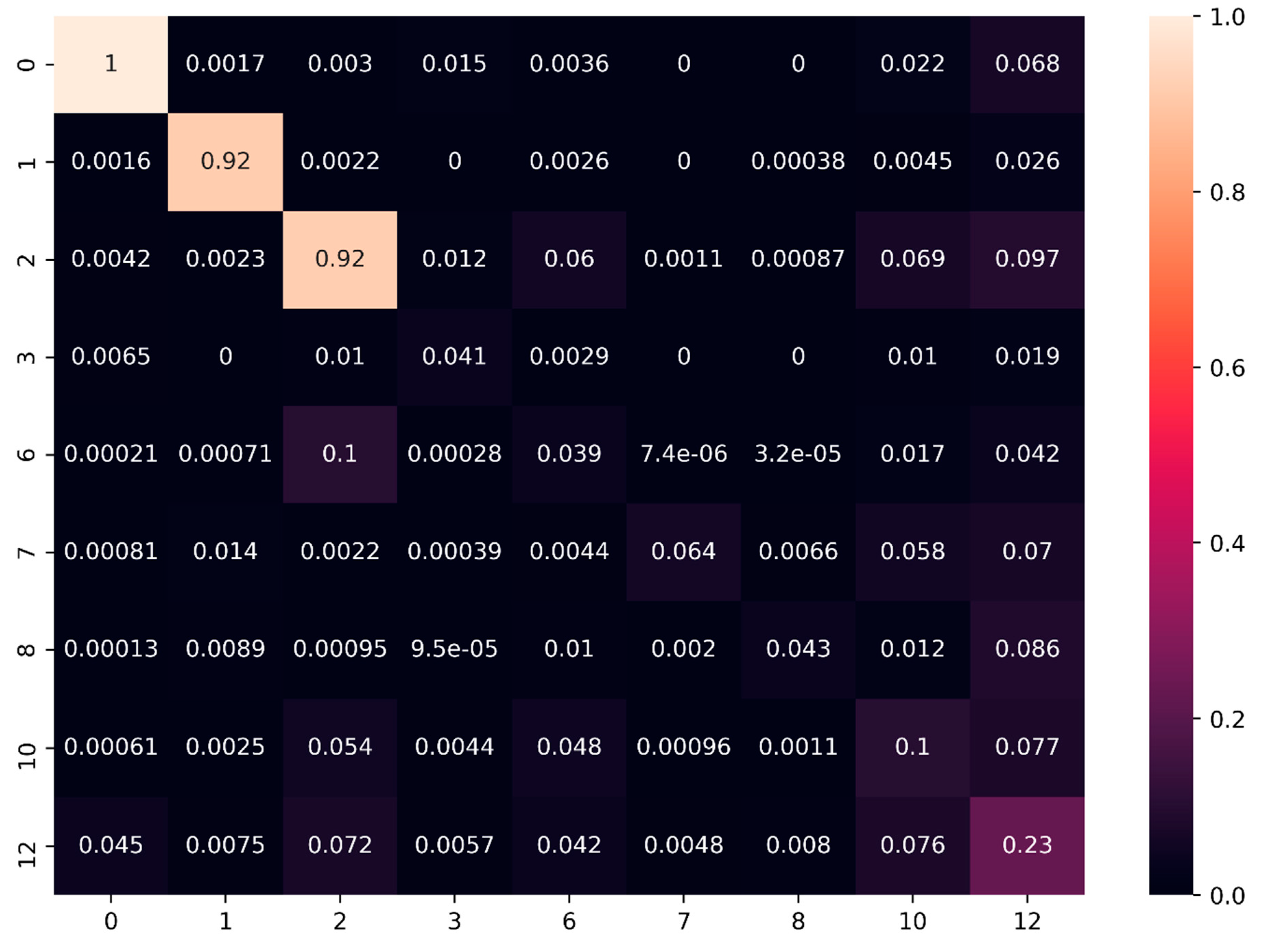
5.2.1. Feature Influence
5.2.2. Full S3DIS Benchmark
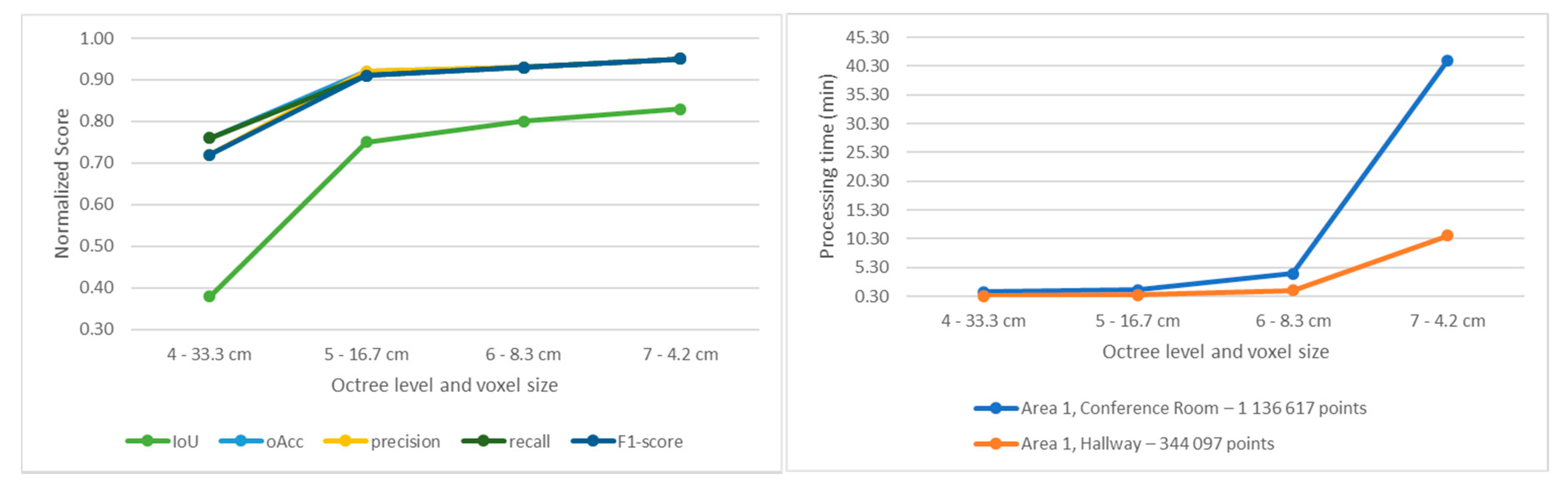
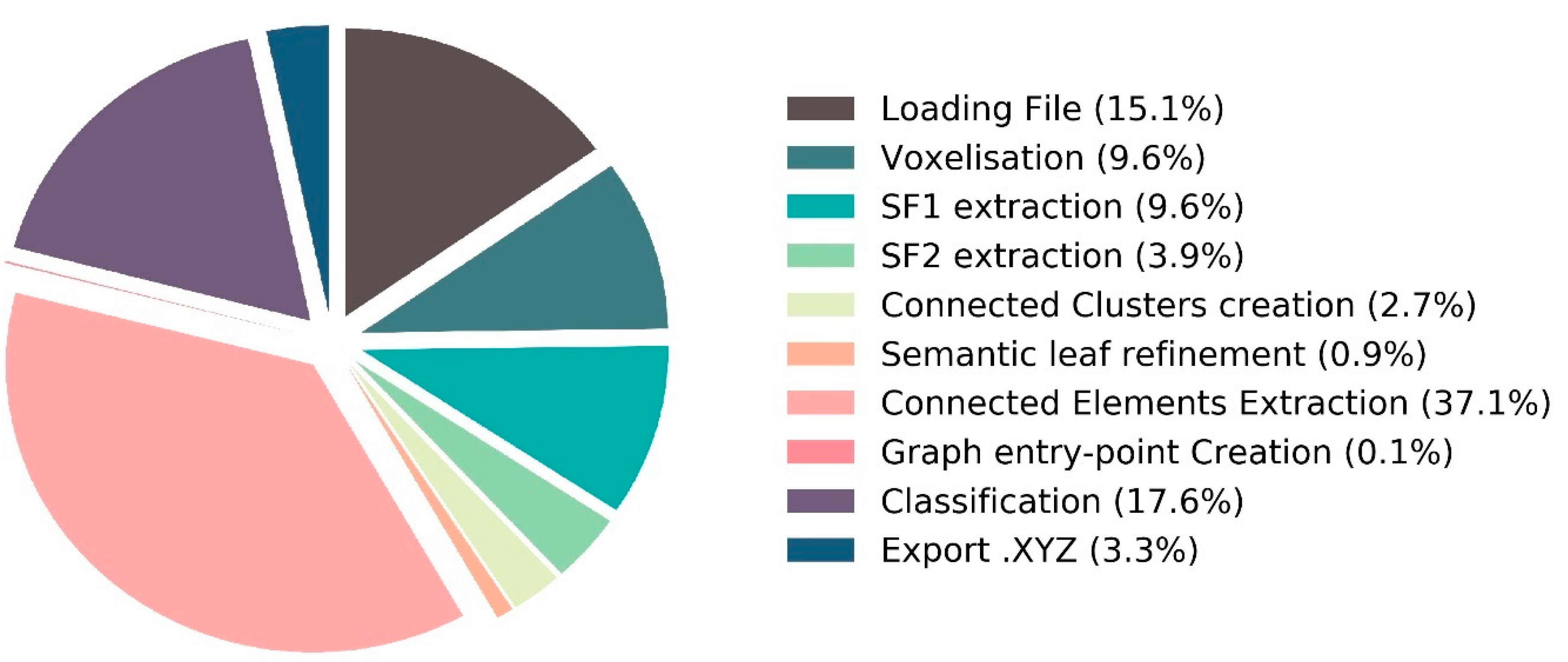
5.3. Implementation and Performances Details
6. Discussion
6.1. Strengths
6.2. Limitations and Research Directions
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| IoU for Area-5 | Ceiling | Floor | Wall | Beam | Door | Table | Chair | Bookcase | Clutter |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 6 | 7 | 8 | 10 | 12 | |
| PointNet [25] | 88.8 | 97.33 | 69.8 | 0.05 | 10.76 | 58.93 | 52.61 | 40.28 | 33.22 |
| SegCloud [48] | 90.06 | 96.05 | 69.86 | 0 | 23.12 | 70.4 | 75.89 | 58.42 | 41.6 |
| SPG [49] | 91.49 | 97.89 | 75.89 | 0 | 52.29 | 77.4 | 86.35 | 65.49 | 50.67 |
| Ours | 85.78 | 92.91 | 71.32 | 0 | 7.54 | 31.15 | 29.02 | 23.48 | 21.91 |
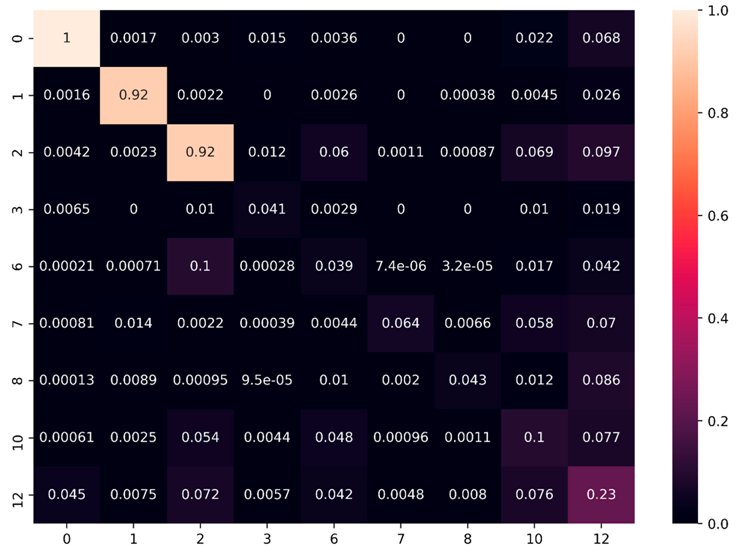
Appendix B

Appendix C
| F1-score | Ceiling | Floor | Wall | Beam | Door | Table | Chair | Bookcase | Clutter |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 6 | 7 | 8 | 10 | 12 | |
| Area-1 | 0.97 | 0.96 | 0.80 | 0.66 | 0.24 | 0.48 | 0.48 | 0.26 | 0.47 |
| Area-2 | 0.85 | 0.94 | 0.70 | 0.15 | 0.22 | 0.11 | 0.12 | 0.26 | 0.32 |
| Area-3 | 0.98 | 0.98 | 0.78 | 0.61 | 0.21 | 0.41 | 0.61 | 0.38 | 0.50 |
| Area-4 | 0.90 | 0.97 | 0.78 | 0.00 | 0.12 | 0.25 | 0.40 | 0.24 | 0.35 |
| Area-5 | 0.92 | 0.96 | 0.83 | 0.00 | 0.14 | 0.48 | 0.45 | 0.38 | 0.36 |
| Area-6 | 0.95 | 0.97 | 0.78 | 0.58 | 0.24 | 0.54 | 0.53 | 0.28 | 0.43 |
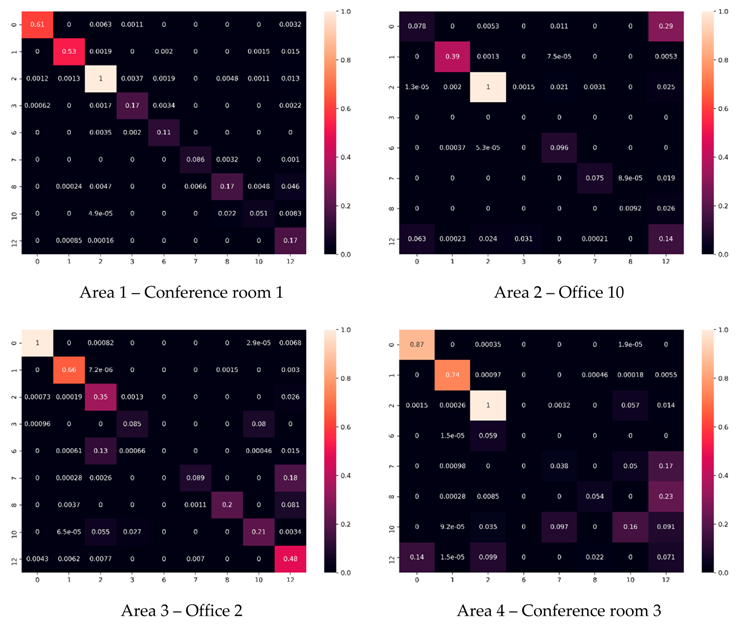
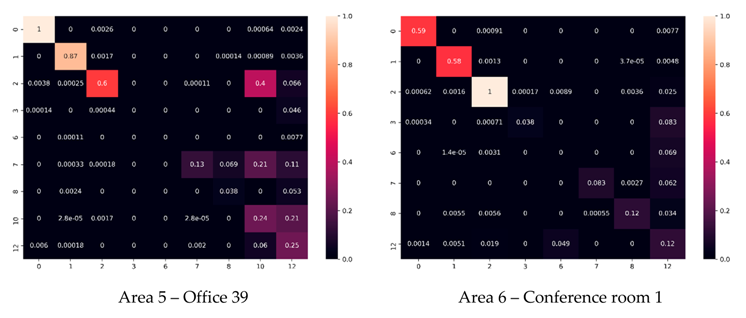
References
- Koffka, K. Principles of Gestalt Psychology; Routledge: Abingdon-on-Thames, UK, 2013. [Google Scholar]
- Poux, F.; Billen, R. A Smart Point Cloud Infrastructure for intelligent environments. In Laser Scanning: An Emerging Technology in Structural Engineering; Lindenbergh, R., Belen, R., Eds.; ISPRS Book Series; Taylor & Francis Group/CRC Press: Bocaton, FL, USA, 2019; in press. [Google Scholar]
- Yang, B.; Luo, W.; Urtasun, R. PIXOR: Real-time 3D Object Detection from Point Clouds. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 7652–7660. [Google Scholar]
- Rostami, R.; Bashiri, F.S.; Rostami, B.; Yu, Z. A Survey on Data-Driven 3D Shape Descriptors. Comput. Graph. Forum 2018, 38, 1–38. [Google Scholar] [CrossRef]
- Su, H.; Jampani, V.; Sun, D.; Maji, S.; Kalogerakis, E.; Yang, M.H.; Kautz, J. SPLATNet: Sparse Lattice Networks for Point Cloud Processing. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 2530–2539. [Google Scholar]
- Boulch, A.; Le Saux, B.; Audebert, N. Unstructured point cloud semantic labeling using deep segmentation networks. In Proceedings of the Eurographics Workshop on 3D Object Retrieval; EUROGRAPHICS: Lyon, France, 2017. [Google Scholar]
- Liao, Y.; Donné, S.; Geiger, A. Deep Marching Cubes: Learning Explicit Surface Representations. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 2916–2925. [Google Scholar]
- Thomas, H.; Goulette, F.; Deschaud, J.E.; Marcotegui, B.; Gall, Y. Le Semantic classification of 3d point clouds with multiscale spherical neighborhoods. In Proceedings of the International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 390–398. [Google Scholar]
- Jiang, M.; Wu, Y.; Lu, C. PointSIFT: A SIFT-like Network Module for 3D Point Cloud Semantic Segmentation. Comput. Vis. Pattern Recognit. 2018, arXiv:1807.00652. [Google Scholar]
- Nguyen, C.; Starek, M.J.; Tissot, P.; Gibeaut, J. Unsupervised clustering method for complexity reduction of terrestrial lidar data in marshes. Remote Sens. 2018, 10, 133. [Google Scholar] [CrossRef]
- Behl, A.; Paschalidou, D.; Donné, S.; Geiger, A. PointFlowNet: Learning Representations for 3D Scene Flow Estimation from Point Clouds. Comput. Vis. Pattern Recognit. 2018, arXiv:1806.02170. [Google Scholar]
- Engelmann, F.; Kontogianni, T.; Schult, J.; Leibe, B. Know What Your Neighbors Do: 3D Semantic Segmentation of Point Clouds. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Li, J.; Chen, B.M.; Lee, G.H. SO-Net: Self-Organizing Network for Point Cloud Analysis. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Guerrero, P.; Kleiman, Y.; Ovsjanikov, M.; Mitra, N.J. PCPNet learning local shape properties from raw point clouds. Comput. Graph. Forum 2018, 37, 75–85. [Google Scholar] [CrossRef]
- Boulch, A.; Guerry, J.; Le Saux, B.; Audebert, N. SnapNet: 3D point cloud semantic labeling with 2D deep segmentation networks. Comput. Graph. 2018, 71, 189–198. [Google Scholar] [CrossRef]
- Armeni, I.; Sener, O.; Zamir, A.R.; Jiang, H.; Brilakis, I.; Fischer, M.; Savarese, S. 3D Semantic Parsing of Large-Scale Indoor Spaces. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1534–1543. [Google Scholar]
- Ni, H.; Lin, X.; Zhang, J.; Ni, H.; Lin, X.; Zhang, J. Classification of ALS Point Cloud with Improved Point Cloud Segmentation and Random Forests. Remote Sens. 2017, 9, 288. [Google Scholar] [CrossRef]
- Ghorpade, V.K.; Checchin, P.; Malaterre, L.; Trassoudaine, L. 3D shape representation with spatial probabilistic distribution of intrinsic shape keypoints. EURASIP J. Adv. Signal Process. 2017, 2017, 52. [Google Scholar] [CrossRef]
- Bueno, M.; Martínez-Śanchez, J.; Gonźalez-Jorge, H.; Lorenzo, H. Detection of geometric keypoints and its application to point cloud coarse registration. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences - ISPRS Archives; ISPRS: Prague, Czech Republic, 2016; Volume 41, pp. 187–194. [Google Scholar]
- Vetrivel, A.; Gerke, M.; Kerle, N.; Nex, F.; Vosselman, G. Disaster damage detection through synergistic use of deep learning and 3D point cloud features derived from very high resolution oblique aerial images, and multiple-kernel-learning. ISPRS J. Photogramm. Remote Sens. 2018, 140, 45–59. [Google Scholar] [CrossRef]
- Poux, F.; Neuville, R.; Hallot, P.; Van Wersch, L.; Jancsó, A.L.; Billen, R. Digital investigations of an archaeological smart point cloud: A real time web-based platform to manage the visualisation of semantical queries. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. - ISPRS Arch. 2017, XLII-5/W1, 581–588. [Google Scholar] [CrossRef]
- Blomley, R.; Weinmann, M.; Leitloff, J.; Jutzi, B. Shape distribution features for point cloud analysis—A geometric histogram approach on multiple scales. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences; ISPRS: Zurich, Switzerland, 2014; Volume 2, pp. 9–16. [Google Scholar]
- Feng, C.C.; Guo, Z. Automating parameter learning for classifying terrestrial LiDAR point cloud using 2D land cover maps. Remote Sens. 2018, 10, 1192. [Google Scholar] [CrossRef]
- Shen, Y.; Feng, C.; Yang, Y.; Tian, D. Mining Point Cloud Local Structures by Kernel Correlation and Graph Pooling. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 4548–4557. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21 June–26 July 2017; pp. 77–85. [Google Scholar]
- Nurunnabi, A.; Belton, D.; West, G. Robust Segmentation for Large Volumes of Laser Scanning Three-Dimensional Point Cloud Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4790–4805. [Google Scholar] [CrossRef]
- Lawin, F.J.; Danelljan, M.; Tosteberg, P.; Bhat, G.; Khan, F.S.; Felsberg, M. Deep projective 3D semantic segmentation. In Proceedings of the Computer Analysis of Images and Patterns (CAIP), Ystad, Sweden, 22–24 August 2017; pp. 95–107. [Google Scholar]
- Mahmoudabadi, H.; Shoaf, T.; Olsen, M.J. Superpixel clustering and planar fit segmentation of 3D LIDAR point clouds. In Proceedings of the 4th International Conference on Computing for Geospatial Research and Application, (COM.Geo), New York, NY, USA, 22–24 July 2013; pp. 1–7. [Google Scholar]
- Ioannou, Y.; Taati, B.; Harrap, R.; Greenspan, M. Difference of normals as a multi-scale operator in unorganized point clouds. In Proceedings of the 3D Imaging, Modeling, Processing, Visualization and Transmission (3DIMPVT); IEEE: Zurich, Switzerland, 2012; pp. 501–508. [Google Scholar]
- Vosselman, G.; Gorte, B.G.H.; Sithole, G.; Rabbani, T. Recognising structure in laser scanner point clouds. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences-ISPRS Archives; ISPRS: Freiburg, Germany, 2003; Volume 46, pp. 33–38. [Google Scholar]
- Song, T.; Xi, F.; Guo, S.; Ming, Z.; Lin, Y. A comparison study of algorithms for surface normal determination based on point cloud data. Precis. Eng. 2015, 39, 47–55. [Google Scholar] [CrossRef]
- Weber, C.; Hahmann, S.; Hagen, H. Sharp feature detection in point clouds. In Proceedings of the International Conference on Shape Modeling and Applications; IEEE: Washington, DC, USA, 2010; pp. 175–186. [Google Scholar]
- Ni, H.; Lin, X.; Ning, X.; Zhang, J. Edge Detection and Feature Line Tracing in 3D-Point Clouds by Analyzing Geometric Properties of Neighborhoods. Remote Sens. 2016, 8, 710. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for Point Cloud Shape Detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Hackel, T.; Wegner, J.D.; Schindler, K. Joint classification and contour extraction of large 3D point clouds. ISPRS J. Photogramm. Remote Sens. 2017, 130, 231–245. [Google Scholar] [CrossRef]
- Son, H.; Kim, C. Semantic as-built 3D modeling of structural elements of buildings based on local concavity and convexity. Adv. Eng. Inf. 2017, 34, 114–124. [Google Scholar] [CrossRef]
- Wang, J.; Lindenbergh, R.; Menenti, M. SigVox—A 3D feature matching algorithm for automatic street object recognition in mobile laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2017, 128, 111–129. [Google Scholar] [CrossRef]
- Liu, Y.-S.; Ramani, K. Robust principal axes determination for point-based shapes using least median of squares. Comput. Aided Des. 2009, 41, 293–305. [Google Scholar] [CrossRef]
- Xu, Y.; Tuttas, S.; Hoegner, L.; Stilla, U. Voxel-based segmentation of 3D point clouds from construction sites using a probabilistic connectivity model. Pattern Recognit. Lett. 2018, 102. [Google Scholar] [CrossRef]
- Xu, Y.; Hoegner, L.; Tuttas, S.; Stilla, U. Voxel- and Graph-Based Point Cloud Segmentation of 3D Scenes Using Perceptual Grouping Laws. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences; ISPRS: Hannover, Germany, 2017; Volume 4, pp. 43–50. [Google Scholar]
- Zhu, Q.; Li, Y.; Hu, H.; Wu, B. Robust point cloud classification based on multi-level semantic relationships for urban scenes. ISPRS J. Photogramm. Remote Sens. 2017, 129, 86–102. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, L.; Chen, Y.; Wu, Y.; Li, M. Building point detection from vehicle-borne LiDAR data based on voxel group and horizontal hollow analysis. Remote Sens. 2016, 8, 419. [Google Scholar] [CrossRef]
- Ben-Shabat, Y.; Avraham, T.; Lindenbaum, M.; Fischer, A. Graph based over-segmentation methods for 3D point clouds. Comput. Vis. Image Underst. 2018, 174, 12–23. [Google Scholar] [CrossRef]
- Ben-Shabat, Y.; Lindenbaum, M.; Fischer, A. 3D Point Cloud Classification and Segmentation Using 3D Modified Fisher Vector Representation for Convolutional Neural Networks. Available online: http://arxiv.org/abs/1711.08241 (accessed on 31 October 2018).
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast Point Feature Histograms (FPFH) for 3D registration. In Proceedings of the International Conference on Robotics and Automation (ICRA); IEEE: Kobe, Japan, 2009; pp. 3212–3217. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 24 January 2019. [Google Scholar]
- Tchapmi, L.P.; Choy, C.B.; Armeni, I.; Gwak, J.; Savarese, S. SEGCloud: Semantic Segmentation of 3D Point Clouds. In Proceedings of the International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017. [Google Scholar]
- Landrieu, L.; Simonovsky, M. Large-Scale Point Cloud Semantic Segmentation with Superpoint Graphs. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 4558–4567. [Google Scholar]
- Poux, F.; Neuville, R.; Hallot, P.; Billen, R. MODEL FOR SEMANTICALLY RICH POINT CLOUD DATA. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, IV-4/W5, 107–115. [Google Scholar] [CrossRef]
- Engelmann, F.; Kontogianni, T.; Hermans, A.; Leibe, B. Exploring Spatial Context for 3D Semantic Segmentation of Point Clouds. In Proceedings of the International Conference on Computer Vision (ICCV); IEEE: Istanbul, Turkey, 2018; pp. 716–724. [Google Scholar]
- Poux, F.; Hallot, P.; Neuville, R.; Billen, R. SMART POINT CLOUD: DEFINITION AND REMAINING CHALLENGES. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, IV-2/W1, 119–127. [Google Scholar] [CrossRef]
- Truong-Hong, L.; Laefer, D.F.; Hinks, T.; Carr, H. Flying Voxel Method with Delaunay Triangulation Criterion for Façade/Feature Detection for Computation. J. Comput. Civ. Eng. 2012, 26, 691–707. [Google Scholar] [CrossRef]
- Quan, S.; Ma, J.; Hu, F.; Fang, B.; Ma, T. Local voxelized structure for 3D binary feature representation and robust registration of point clouds from low-cost sensors. Inf. Sci. (Ny). 2018, 444, 153–171. [Google Scholar] [CrossRef]
- Poux, F.; Neuville, R.; Hallot, P.; Billen, R. Point clouds as an efficient multiscale layered spatial representation. In Proceedings of the Eurographics Workshop on Urban Data Modelling and Visualisation; Vincent, T., Biljecki, F., Eds.; The Eurographics Association: Liège, Belgium, 2016. [Google Scholar]
- Nourian, P.; Gonçalves, R.; Zlatanova, S.; Ohori, K.A.; Vu Vo, A. Voxelization algorithms for geospatial applications: Computational methods for voxelating spatial datasets of 3D city models containing 3D surface, curve and point data models. MethodsX 2016, 3, 69–86. [Google Scholar] [CrossRef]
- Weinmann, M.; Jutzi, B.; Hinz, S.; Mallet, C. Semantic point cloud interpretation based on optimal neighborhoods, relevant features and efficient classifiers. ISPRS J. Photogramm. Remote Sens. 2015, 105, 286–304. [Google Scholar] [CrossRef]
- De Lathauwer, L.; De Moor, B.; Vandewalle, J. A Multilinear Singular Value Decomposition. SIAM J. Matrix Anal. Appl. 2003, 21, 1253–1278. [Google Scholar] [CrossRef]
- Poux, F.; Neuville, R.; Nys, G.-A.; Billen, R. 3D Point Cloud Semantic Modelling: Integrated Framework for Indoor Spaces and Furniture. Remote Sens. 2018, 10, 1412. [Google Scholar] [CrossRef]
- Clementini, E.; Di Felice, P. Approximate topological relations. Int. J. Approx. Reason. 1997, 16, 173–204. [Google Scholar] [CrossRef]
- He, L.; Ren, X.; Gao, Q.; Zhao, X.; Yao, B.; Chao, Y. The connected-component labeling problem: A review of state-of-the-art algorithms. Pattern Recognit. 2017, 70, 25–43. [Google Scholar] [CrossRef]
- Krijnen, T.; Beetz, J. An IFC schema extension and binary serialization format to efficiently integrate point cloud data into building models. Adv. Eng. Inform. 2017, 33, 473–490. [Google Scholar] [CrossRef]
- Lehtola, V.; Kaartinen, H.; Nüchter, A.; Kaijaluoto, R.; Kukko, A.; Litkey, P.; Honkavaara, E.; Rosnell, T.; Vaaja, M.; Virtanen, J.-P.; et al. Comparison of the Selected State-Of-The-Art 3D Indoor Scanning and Point Cloud Generation Methods. Remote Sens. 2017, 9, 796. [Google Scholar] [CrossRef]
- Neuville, R.; Pouliot, J.; Poux, F.; Billen, R. 3D Viewpoint Management and Navigation in Urban Planning: Application to the Exploratory Phase. Remote Sens. 2019, 11, 236. [Google Scholar] [CrossRef]
- Neuville, R.; Pouliot, J.; Poux, F.; de Rudder, L.; Billen, R. A Formalized 3D Geovisualization Illustrated to Selectivity Purpose of Virtual 3D City Model. ISPRS Int. J. Geo-Inf. 2018, 7, 194. [Google Scholar] [CrossRef]
- Belongie, S.; Malik, J.; Puzicha, J. Shape matching and object recognition using shape contexts. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 509–522. [Google Scholar] [CrossRef]
- Liu, S.; Xie, S.; Chen, Z.; Tu, Z. Attentional ShapeContextNet for Point Cloud Recognition. Conf. Comput. Vis. Pattern Recognit. 2018, 4606–4615. [Google Scholar]
- Poux, F.; Neuville, R.; Van Wersch, L.; Nys, G.-A.; Billen, R. 3D Point Clouds in Archaeology: Advances in Acquisition, Processing and Knowledge Integration Applied to Quasi-Planar Objects. Geosciences 2017, 7, 96. [Google Scholar] [CrossRef]

| Eigen-Based Feature | Description | |
|---|---|---|
| Eigen values of where |  | |
| Respective Eigen vectors of | ||
| Normal vector of | ||
| Anisotropy of voxel | ||
| Eigen entropy of voxel | ||
| Linearity of voxel | ||
| Omnivariance of voxel | ||
| Planarity of voxel | ||
| Sphericity of voxel | ||
| Surface variation of voxel | ||
| Geometrical Feature | Description | |
|---|---|---|
| Mean value of points in respectively along |  | |
| Variance of points in voxel | ||
| Area of points in along () | ||
| Area of points in along | ||
| Number of points in | ||
| Volume occupied by points in | ||
| point density within voxel | ||
| Relational Feature | Description |
|---|---|
| Graph of voxel entity and its neighbours retaining voxel topology (vertex.touch, edge.touch, face.touch) | |
| Geometrical difference | |
| retaining Convex/Concave tags. | |
| retaining planarity tags (). |
| Area-1 | Area-2 | Area-3 | Area-4 | Area-5 | Area-6 | |
|---|---|---|---|---|---|---|
 | ||||||
| #Points | 43 956 907 | 470 023 210 | 18 662 173 | 43 278 148 | 78 649 818 | 41 308 364 |
| Area (m²) | 965 | 1100 | 450 | 870 | 1700 | 935 |
| Rooms (nb) | 44 | 40 | 23 | 47 | 68 | 48 |
| Method | Ceiling | Floor | Wall | Beam | Door | Table | Chair | Bookcase | Others |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 6 | 7 | 8 | 10 | 12 | |
| Area 1 | 56 | 45 | 235 | 62 | 87 | 70 | 156 | 91 | 123 |
| Area 2 | 82 | 51 | 284 | 62 | 94 | 47 | 546 | 49 | 92 |
| Area 3 | 38 | 24 | 160 | 14 | 38 | 31 | 68 | 42 | 45 |
| Area 4 | 74 | 51 | 281 | 4 | 108 | 80 | 160 | 99 | 106 |
| Area 5 | 77 | 69 | 344 | 4 | 128 | 155 | 259 | 218 | 183 |
| Area 6 | 64 | 50 | 248 | 69 | 94 | 78 | 180 | 91 | 127 |
| Full S3DIS | 391 | 290 | 1552 | 215 | 549 | 461 | 1369 | 590 | 676 |
| Method | Zone | Time (min) | CEL number | mIOU | oAcc | F1-score |
|---|---|---|---|---|---|---|
| SF1 | Room | 0.7 | 214 | 0.53 | 0.73 | 0.77 |
| Area 1 | 42.4 | 10105 | 0.35 | 0.58 | 0.63 | |
| SF1SF2 | Room | 1.0 | 125 | 0.83 | 0.95 | 0.95 |
| Area 1 | 55.0 | 5489 | 0.47 | 0.75 | 0.75 |
| CEL Number | Ceiling | Floor | Wall | Beam | Door | Table | Chair | Bookcase |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 6 | 7 | 8 | 10 | |
| Room 1 | 1 | 1 | 4 | 1 | 1 | 1 | 13 | 1 |
| Tagged CEL | 1 | 1 | 4 | 1 | 1 | 1 | 11 | 1 |
| Area 1 | 56 | 44 | 235 | 62 | 87 | 70 | 156 | 91 |
| Tagged CEL | 52 | 44 | 146 | 47 | 23 | 67 | 129 | 70 |
| Global Metrics Area-1 | Ceiling | Floor | Wall | Beam | Door | Table | Chair | Bookcase | Clutter |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 6 | 7 | 8 | 10 | 12 | |
| SF1 IoU | 0.81 | 0.75 | 0.61 | 0.39 | 0.10 | 0.24 | 0.06 | 0.02 | 0.14 |
| SF1 Precision | 0.99 | 0.99 | 0.84 | 0.67 | 0.11 | 0.96 | 0.09 | 0.15 | 0.32 |
| SF1 Recall | 0.82 | 0.75 | 0.69 | 0.48 | 0.57 | 0.25 | 0.14 | 0.03 | 0.20 |
| SF1 F-1 score | 0.90 | 0.86 | 0.76 | 0.56 | 0.18 | 0.39 | 0.11 | 0.05 | 0.24 |
| SF1SF2 IoU | 0.95 | 0.92 | 0.67 | 0.49 | 0.14 | 0.32 | 0.32 | 0.15 | 0.31 |
| SF1SF2 Precision | 0.98 | 0.95 | 0.79 | 0.88 | 0.29 | 0.9 | 0.69 | 0.2 | 0.41 |
| SF1SF2 Recall | 0.97 | 0.97 | 0.82 | 0.53 | 0.2 | 0.33 | 0.37 | 0.37 | 0.56 |
| SF1SF2 F-1 score | 0.97 | 0.96 | 0.8 | 0.66 | 0.24 | 0.48 | 0.48 | 0.26 | 0.47 |
| Ceiling | Floor | Wall | Beam | Door | Table | Chair | Bookcase | Clutter | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 6 | 7 | 8 | 10 | 12 | |
| PointNet [25] | 88 | 88.7 | 69.3 | 42.4 | 51.6 | 54.1 | 42 | 38.2 | 35.2 |
| MS+CU(2) [51] | 88.6 | 95.8 | 67.3 | 36.9 | 52.3 | 51.9 | 45.1 | 36.8 | 37.5 |
| SegCloud [48] | 90.1 | 96.1 | 69.9 | 0 | 23.1 | 75.9 | 70.4 | 40.9 | 42 |
| G+RCU [51] | 90.3 | 92.1 | 67.9 | 44.7 | 51.2 | 58.1 | 47.4 | 39 | 41.9 |
| SPG [49] | 92.2 | 95 | 72 | 33.5 | 60.9 | 65.1 | 69.5 | 38.2 | 51.3 |
| KWYND [12] | 92.1 | 90.4 | 78.5 | 37.8 | 65.4 | 64 | 61.6 | 51.6 | 53.7 |
| Ours | 85.4 | 92.4 | 65.2 | 32.4 | 10.5 | 27.8 | 23.7 | 18.5 | 23.9 |
| Method | Ceiling | Floor | Wall | Beam | Door | Table | Chair | Bookcase | Clutter |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 6 | 7 | 8 | 10 | 12 | |
| PointNet | 84 | 87.2 | 57.9 | 37 | 35.3 | 51.6 | 42.4 | 26.4 | 25.5 |
| MS+CU(2) | 86.5 | 94.9 | 58.8 | 37.7 | 36.7 | 47.2 | 46.1 | 30 | 31.2 |
| Ours | 85.4 | 92.4 | 65.2 | 32.4 | 10.5 | 27.8 | 23.7 | 18.5 | 23.9 |
| S3DIS Class Metrics | Ceiling | Floor | Wall | Beam | Door | Table | Chair | Bookcase | Clutter | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 6 | 7 | 8 | 10 | 12 | ||
| Precision | 0.94 | 0.96 | 0.79 | 0.53 | 0.19 | 0.88 | 0.72 | 0.28 | 0.33 | 0.75 |
| Recall | 0.90 | 0.96 | 0.79 | 0.46 | 0.19 | 0.29 | 0.26 | 0.36 | 0.47 | 0.72 |
| F1-score | 0.92 | 0.96 | 0.79 | 0.49 | 0.19 | 0.43 | 0.38 | 0.31 | 0.39 | 0.72 |
| Overall Precision | Ceiling | Floor | Wall | Beam | Door | Table | Chair | Bookcase |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 6 | 7 | 8 | 10 | |
| Baseline (no colour) [16] | 0.48 | 0.81 | 0.68 | 0.68 | 0.44 | 0.51 | 0.12 | 0.52 |
| Baseline (full) [16] | 0.72 | 0.89 | 0.73 | 0.67 | 0.54 | 0.46 | 0.16 | 0.55 |
| Ours | 0.94 | 0.96 | 0.79 | 0.53 | 0.19 | 0.88 | 0.72 | 0.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poux, F.; Billen, R. Voxel-based 3D Point Cloud Semantic Segmentation: Unsupervised Geometric and Relationship Featuring vs Deep Learning Methods. ISPRS Int. J. Geo-Inf. 2019, 8, 213. https://doi.org/10.3390/ijgi8050213
Poux F, Billen R. Voxel-based 3D Point Cloud Semantic Segmentation: Unsupervised Geometric and Relationship Featuring vs Deep Learning Methods. ISPRS International Journal of Geo-Information. 2019; 8(5):213. https://doi.org/10.3390/ijgi8050213
Chicago/Turabian StylePoux, Florent, and Roland Billen. 2019. "Voxel-based 3D Point Cloud Semantic Segmentation: Unsupervised Geometric and Relationship Featuring vs Deep Learning Methods" ISPRS International Journal of Geo-Information 8, no. 5: 213. https://doi.org/10.3390/ijgi8050213
APA StylePoux, F., & Billen, R. (2019). Voxel-based 3D Point Cloud Semantic Segmentation: Unsupervised Geometric and Relationship Featuring vs Deep Learning Methods. ISPRS International Journal of Geo-Information, 8(5), 213. https://doi.org/10.3390/ijgi8050213