A 25-Intersection Model for Representing Topological Relations between Simple Spatial Objects in 3-D Space
Abstract
:1. Introduction
2. Methodology
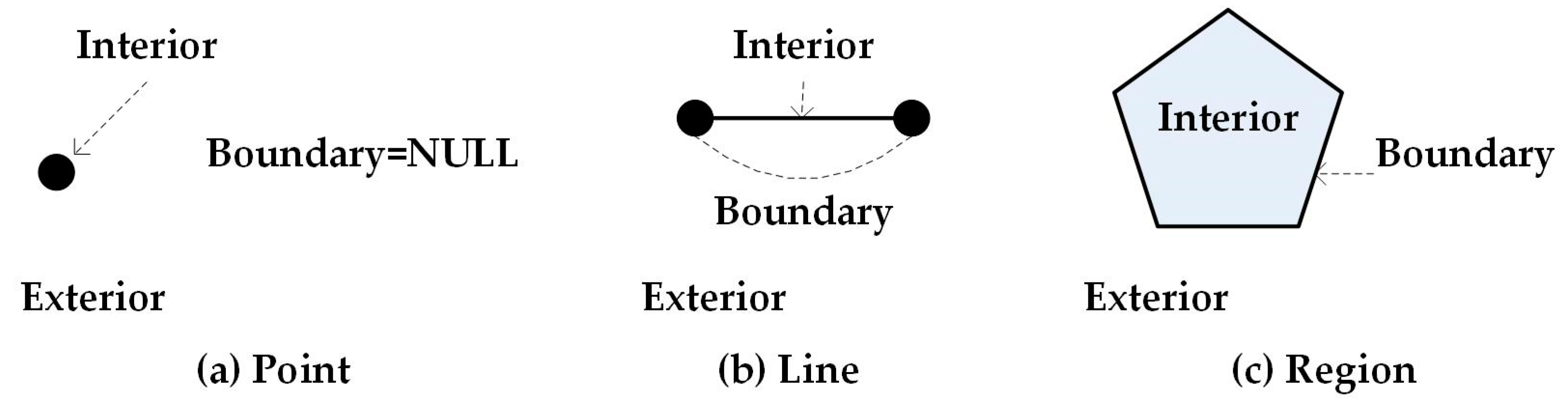
2.1. Definition of Spatial Objects in Three-Dimensional Space
2.2. 25-Intersection Model
- Let Q be the universal set, and .
- A’s vertex, edge, face, interior, and exterior are represented by , , , , and , respectively.
- A’s boundary , A’s closure +, and A’s exterior .
- The exterior , interior , face and edge are open sets, and the vertex set is a closed set.
- The value of an intersection is 0 or 1, where 0 denotes that the intersection is empty, and 1 denotes that the intersection is non-empty.
3. Results
- A/B is a body if any value of the 4th row/column is non-empty.
- A/B is a region if all the values of the 4th row/column are empty and any value of the 3rd row/column is non-empty.
- A/B is a line if all the values of the 3rd and 4th rows/columns are empty and any value of the 2nd row/column is non-empty.
- A/B is a point if all the values of the 2nd, 3rd, and 4th rows/columns are empty.
3.1. Body/Body Relations
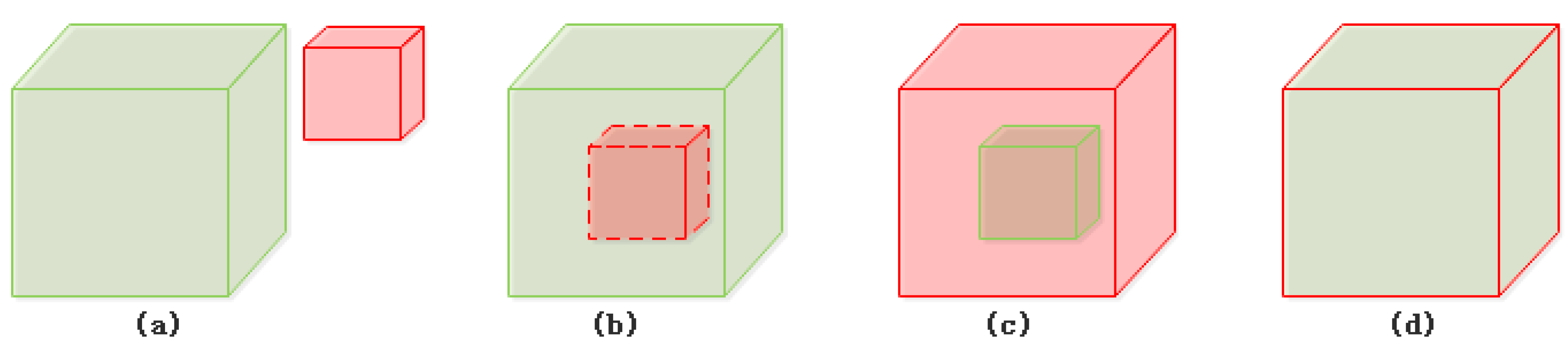
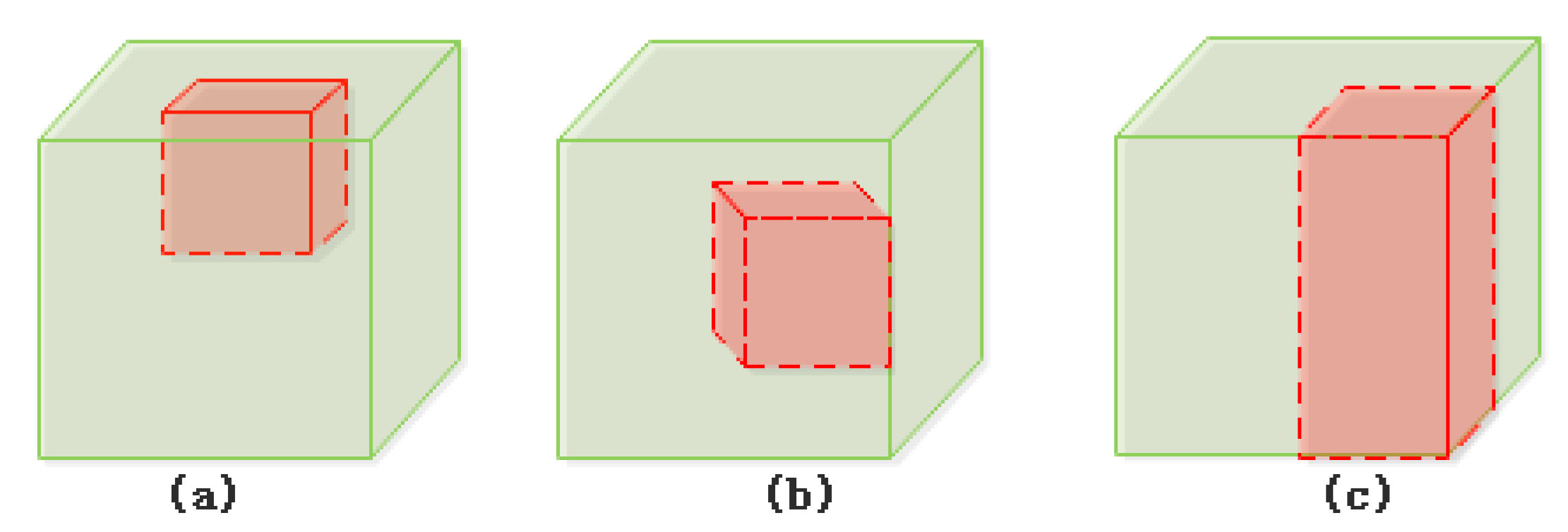
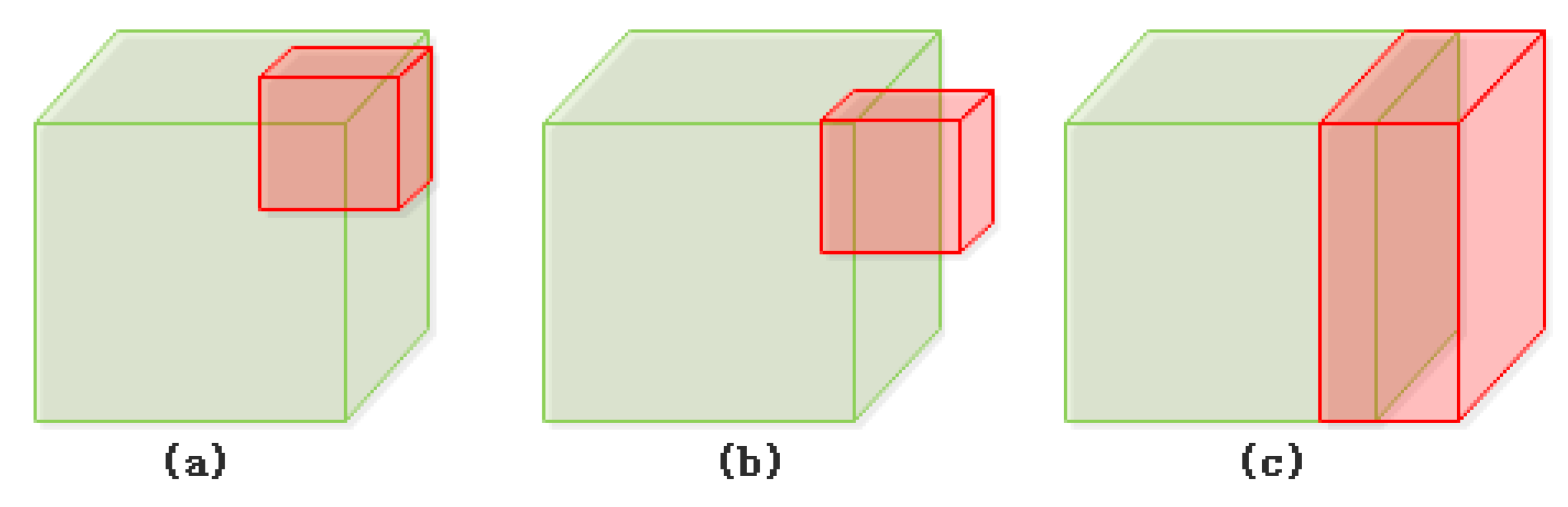
- Disjoint (Figure 5a): A body/body disjoint relation means that body B locates in the exterior of body A. If the intersection of A’s closure and B’s closure is empty, then body A disjoints from body B. There is only one body/body disjoint relation that can be realized based on the 25IM.
- Contain: A body/body contain relation means that body B is inside the interior of body A. If the intersection of A’s interior and B’s closure is equal to B’s closure, then A contains B. There are two body/body contain relations that can be realized based on the 25IM: A contains B (Figure 5b) and B contains A (Figure 5c). No more details like this will be repeated below.
- 3.
- Equal (Figure 5d): A body/body equal relation means that body A and body B are spatially the same. If a topological part of body A only intersects with the same topological part of body B, then A is equal to B. There is only one body/body equal relation that can be realized based on the 25IM.
- 4.
- Meet: A body/body meet relation means that body B touches body A at a vertex, edge, or face, and B’s interior is located in A’s exterior. If the intersection of A’s interior and B’s interior is empty, and the intersection of A’s boundary and B’s boundary is non-empty, then body A meets body B. There are three situations for the body/body meet relation.
- (1)
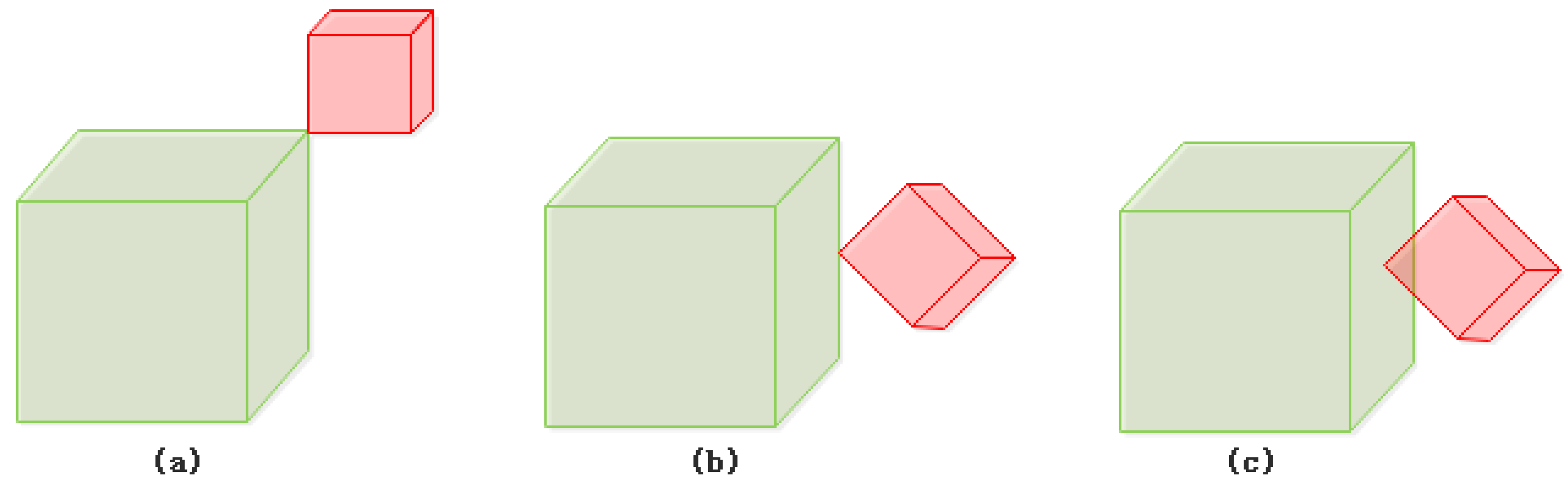
- Meet at vertex (Figure 6): Body B’s interior is inside body A’s exterior. One or more of B’s vertices touch A’s vertex, edge, or face. However, no edge or face of B touches A’s closure. There are 1 + 2 + 4 + 4 + 2 = 13 body/body meet-at-vertex relations that can be realized based on the 25IM.
- (2)
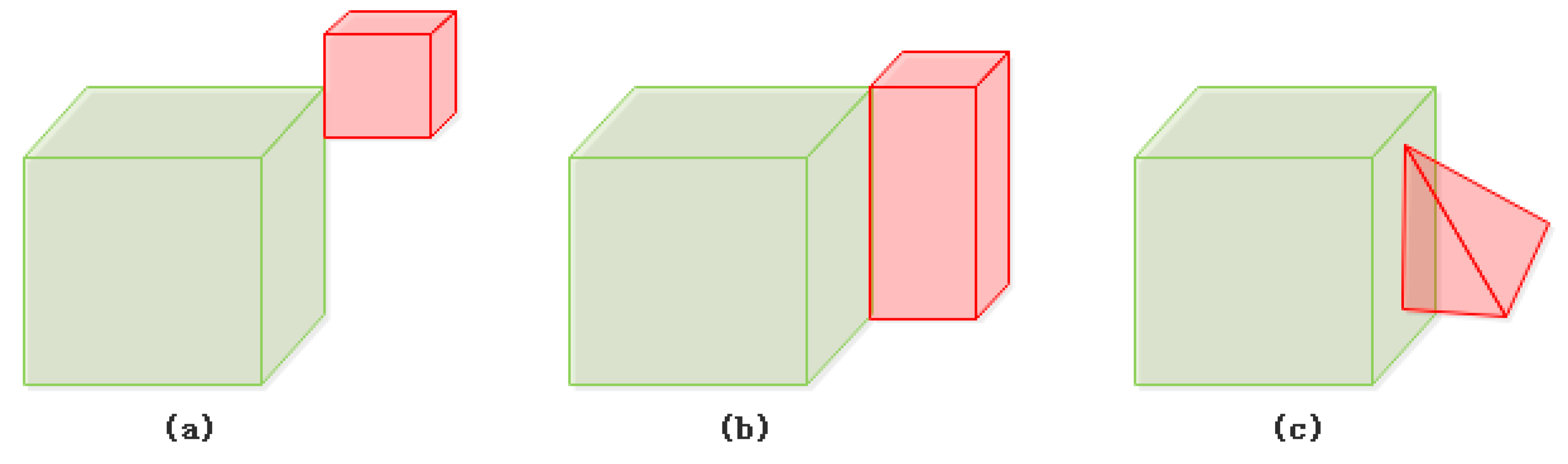
- Meet at edge (Figure 7): Body B’s interior is inside body A’s exterior. One or more of B’s edges touches A’s edges or faces. A and B may share common vertices, but no face of B touches A’s face. There are body/body meet-at-edge relations that can be realized based on the 25IM.
- (3)
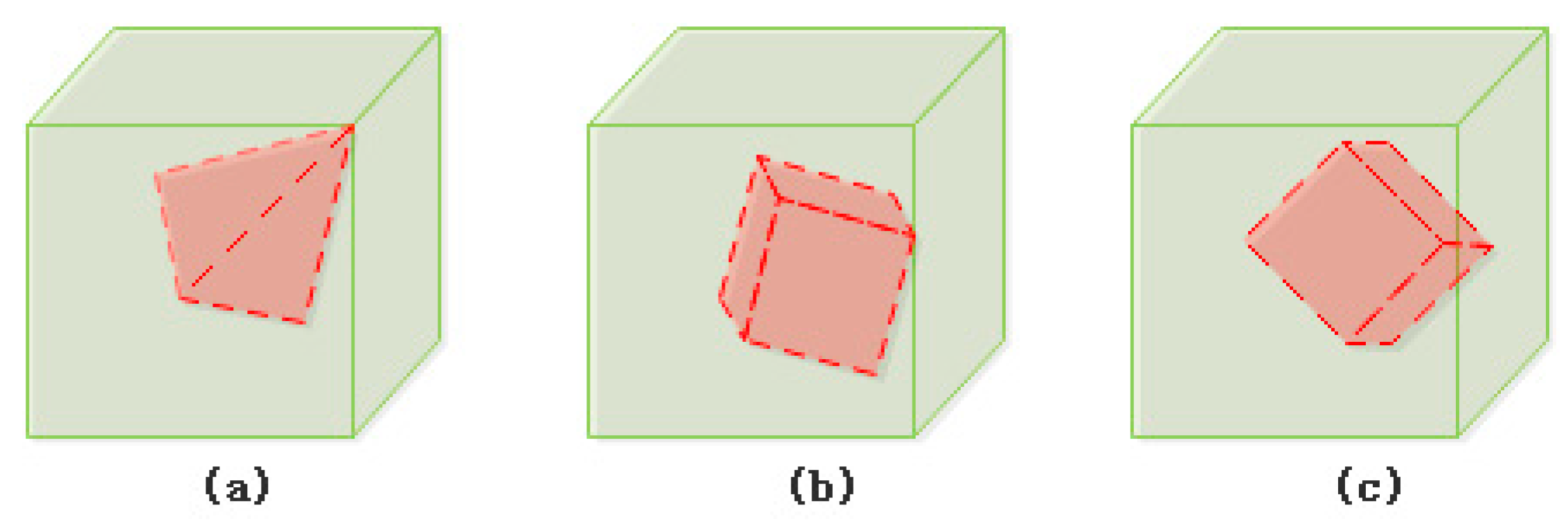
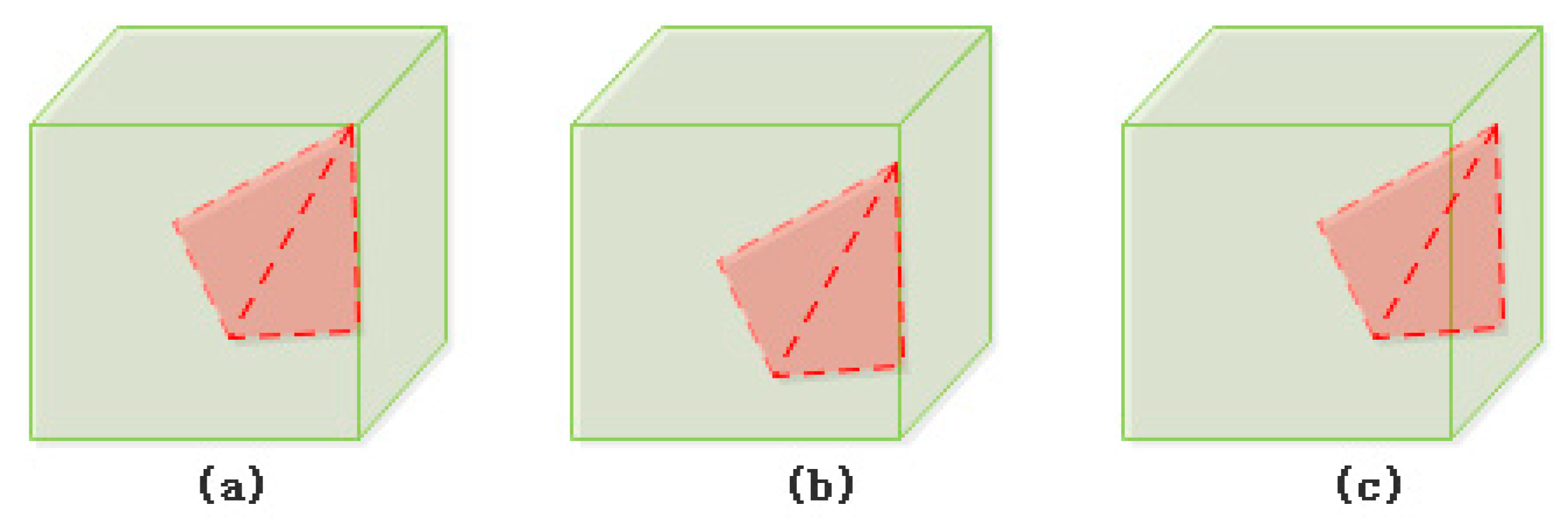
- Meet at face (Figure 3): Body B’s interior is inside body A’s exterior. B’s face touches A’s face. A and B may share common vertices or edges. There are body/body meet-at-face relations that can be realized based on the 25IM.
- 5.
- Cover: A body/body cover relation means that body B’s interior is inside body A’s closure and body B touches body A at a vertex, edge, or face. If the intersection of A’s closure and B’s closure is equal to B’s closure, the intersection of A’s exterior and B’s closure is empty, the intersection of A’s interior and B’s boundary is non-empty, and the intersection of A’s boundary and B’s boundary is non-empty, then A covers B. There are three situations for the body/body cover relation.Theorem 3.If body A cover body B, there must be a B’s vertex on A’s boundary.
- (1)
- Cover at vertex (Figure 8): Body B’s interior is inside body A’s closure. One or more of B’s vertices touches A’s vertex, edge, or face. However, no edge or face of B touches A’s boundary. There are body/body cover-at-vertex relations that can be realized based on the 25IM.
- (2)
- Cover at edge (Figure 9): Body B’s interior is inside body A’s closure. One or more B’s edges touch body A’s edge or face. A and B may share common vertices, but no face of B touches A’s boundary. There are body/body cover-at-edge relations that can be realized based on the 25IM.
- (3)
- Cover at face (Figure 10): Body B’s interior is inside body A’s closure. B’s face touches A’s faces. A and B may share common vertex or edge. There are body/body cover-at-face relations that can be realized based on the 25IM.
- 6.
- Overlap (Figure 11): A body/body overlap relation means that body A’s interior intersects with body B’s interior, but A does not contain, does not cover, or is not equal to B. If the intersection of A’s interior and B’s interior is non-empty, the intersection of A’s interior and B’s boundary is non-empty, and the intersection of A’s boundary and B’s boundary is non-empty, then A overlaps B.
3.2. Body/Region Relations
- Disjoint: There are two body/region disjoint relations that can be realized based on the 25IM.
- Contain: There are two body/region contain relations that can be realized based on the 25IM.
- Meet:
- (1)
- Meet at vertex: There are body/region meet-at-vertex relations that can be realized based on the 25IM.
- (2)
- Meet at edge: There are body/region meet-at-edge relations that can be realized based on the 25IM.
- (3)
- Meet at face: There are body/region meet-at-face relations that can be realized based on the 25IM.
- 4.
- Cover:
- (1)
- Cover at vertex: There are body/region cover-at-vertex relations that can be realized based on the 25IM.
- (2)
- Cover at edge: There are body/region cover-at-edge relations that can be realized based on the 25IM.
- (3)
- Cover at face: There are body/region cover-at-face relations that can be realized based on the 25IM.
- 5.
- Overlap: There are body/region cover relations that can be realized based on the 25IM.
3.3. Body/Line Relations
- Disjoint: There are two body/line disjoint relations that can be realized based on the 25IM.
- Contain: There are two body/line contain relations that can be realized based on the 25IM.
- Meet:
- (1)
- Meet at vertex: There are body/line meet-at-vertex relations that can be realized based on the 25IM.
- (2)
- Meet at edge: There are body/line meet-at-edge relations that can be realized based on the 25IM.
Therefore, there are 14 + 80 = 94 body/line meet relations that can be realized based on the 25IM. - Cover: The body/line cover at edge relations are included in body/line meet-at-edge relations. Thus, only the expressions of body/line cover-at-vertex relations are listed here. There are body/line cover relations that can be realized based on the 25IM.
- Overlap: There are body/line overlap relations that can be realized based on the 25IM.
3.4. Body/Point Relations
- Disjoint: There are two body/point disjoint relations that can be realized based on the 25IM.
- Contain: There are two body/point contain relations that can be realized based on the 25IM.
- Meet: The body/point meet relations mean that point B is on body A’s vertex, edge, or face. There are six body/point meet relations that can be realized based on the 25IM.Therefore, there are 2 + 2 + 6 = 10 body/point relations that can be realized based on the 25IM.
3.5. Region/Region Relations
- Disjoint: There is only one region/region disjoint relation that can be realized based on the 25IM.
- Contain: There are two region/region contain relations that can be realized based on the 25IM.
- Equal: There is only one region/region equal relation that can be realized based on the 25IM.
- Meet:
- (1)
- Meet at vertex: There are 1 + 2 + 4 + 4 + 2 = 13 region/region meet-at-vertex relations that can be realized based on the 25IM.
- (2)
- Meet at edge: There are region/region meet-at-edge relations that can be realized based on the 25IM.
- 5.
- Cover: If region A covers region B, then A and B are on the same plane.
- (1)
- Cover at vertex: There are region/region cover-at-vertex relations that can be realized based on the 25IM.
- (2)
- Cover at edge: There are region/region cover-at-edge relations that can be realized based on the 25IM.
- 6.
- Overlap: There are region/region overlap relations that can be realized based on the 25IM.
3.6. Region/Line Relations
- Disjoint: There are two region/line disjoint relations that can be realized based on the 25IM.
- Contain: There are two region/line contain relations that can be realized based on the 25IM.
- Meet:
- (1)
- Meet at vertex: There are region/line meet-at-vertex relations that can be realized based on the 25IM.
- (2)
- Meet at edge: There are region/line meet-at-edge relations that can be realized based on the 25IM.
Therefore, there are 14 + 16 = 30 region/line meet relations that can be realized based on the 25IM. - Cover: The region/line cover-at-edge relations are included in the region/line meet-at-edge relations. Thus, only the expressions of region/line cover-at-vertex relations are listed here. There are region/line cover relations that can be realized based on the 25IM.
- Overlap: There are region/line overlap relations that can be realized based on the 25IM.
3.7. Region/Point Relations
- Disjoint: There are two region/point disjoint relations that can be realized based on the 25IM.
- Contain: There are two region/line contain relations that can be realized based on the 25IM.
- Meet: A region/point meet relation means that point B is on the vertex or edge of body A. There are four body/point meet relations that can be realized based on the 25IM.Therefore, there are 2 + 2 + 4 = 8 region/point relations that can be realized based on the 25IM.
3.8. Line/line relations
- Disjoint: There is only one line/line disjoint relation that can be realized based on the 25IM.
- Contain: There are two region/line contain relations that can be realized based on the 25IM.
- Equal: There is only one line/line equal relation that can be realized based on the 25IM.
- Meet: Line/line meet-at-edge relations are included in line/line overlap relations. Therefore, only line/line meet-at-vertex relations are listed here. There are 1 + 2 + 2 = 5 line/line meet-at-vertex relations that can be realized based on the 25IM.
- Cover: There are two line/line cover relations that can be realized based on the 25IM.
- Overlap: There are line/line overlap relations that can be realized based on the 25IM.
3.9. Line/Point Relations
- Disjoint: There are two line/point disjoint relations that can be realized based on the 25IM.
- Contain: Line A contains point B when B is on A’s edge. There are two line/point contain relations that can be realized based on the 25IM.
- Meet: Line A meets point B when B is the vertex of A. There are two line/point meet relations that can be realized based on the 25IM.Therefore, there are 2 + 2 + 2 = 6 line/point relations that can be realized based on the 25IM.
3.10. Point/Point Relations
- Disjoint: There is only one point/point disjoint relation that can be realized based on the 25IM.
- Equal: There is only one point/point equal relation that can be realized based on the 25IM.Therefore, there are two line/point relations that can be realized based on the 25IM.
4. Discussion
5. Conclusions
- The 25IM refines the 9IM by subdividing the topological part “boundary” into vertex, edge, and face.
- The classification of topological relations is simplified by merging contain/inside and cover/coveredby because “A is covered by B” is equal to “B covers A” and “A is inside B” is equal to “B contains A”. The matrix of “A is covered by B” is the transposed matrix of “A covers B”, and the matrix of “A is inside B” is the transposed matrix of “A contains B”.
- The 25IM expressions of topological relations that exist in reality are listed. The 25IM can totally distinguish 6259 relations that exist in the real world:
- 2651 body/body relations (one disjoint relation, two contain relations, one equal relation, 461 meet relations, 138 cover relations, and 2048 overlap relations),
- 2588 body/region relations (two disjoint relations, two contain relations, 910 meet relations, 138 cover relations, and 1536 overlap relations),
- 368 body/line relations (two disjoint relations, two contain relations, 94 meet relations, 14 cover relations, and 256 overlap relations),
- 10 body/point relations (two disjoint relations, two contain relations, and six meet relations),
- 497 region/region relation (one disjoint relation, two contain relations, one equal relation, 213 meet relations, 24 cover relations, and 256 overlap relations),
- 110 region/line relations (two disjoint relations, two contain relations, 30 meet relations, 12 cover relations, and 64 overlap relations),
- 8 region/point relations (two disjoint relations, two contain relations, and four meet relations),
- 19 line/line relations (one disjoint relation, two contain relations, one equal relation, five meet relations, two cover relations, and eight overlap relations),
- 6 line/point relations (two disjoint relations, two contain relations, and two meet relations) and
- two point/point relations (one disjoint relation and one equal relation).
- The 25IM is demonstrated to be more expressive than the 9IM and the DE-9IM, especially in distinguishing the details of situations of meet, cover, and overlap (e.g., two bodies meet/cover at a vertex, edge, or face).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sharma, J. Integrated Spatial Reasoning in Geographic Information Systems: Combining Topology and Direction. Ph.D. Thesis, University of Maine, Orono, ME, USA, 1996. [Google Scholar]
- Worboys, M.F.; Bofakos, P. A canonical model for a class of areal spatial objects. In Proceedings of the International Symposium on Spatial Databases, Singapore, 23–25 June 1993; pp. 36–52. [Google Scholar]
- Egenhofer, M.J.; Mark, D.M. Naive geography. In Proceedings of the International Conference on Spatial Information Theory, Semmering, Austria, 21–23 September 1995; pp. 1–15. [Google Scholar]
- Dube, M.P. Topological augmentation: A step forward for qualitative partition reasoning. J. Spat. Inf. Sci. 2017, 2017, 1–29. [Google Scholar] [CrossRef]
- Egenhofer, M.J.; Franzosa, R.D. Point-set topological spatial relations. Int. J. Geogr. Inf. Syst. 1991, 5, 161–174. [Google Scholar] [CrossRef]
- Egenhofer, M.J.; Herring, J. Categorizing Binary Topological Relations between Regions, Lines, and Points in Geographic Databases; University of Maine: Orono, ME, USA, 1991; p. 28. [Google Scholar]
- Clementini, E.; Di Felice, P.; Van Oosterom, P. A small set of formal topological relationships suitable for end-user interaction. In Proceedings of the International Symposium on Spatial Databases, Singapore, 23–25 June 1993; pp. 277–295. [Google Scholar]
- Deng, M.; Cheng, T.; Chen, X.; Li, Z. Multi-level topological relations between spatial regions based upon topological invariants. GeoInformatica 2007, 11, 239–267. [Google Scholar] [CrossRef]
- Liu, K.; Shi, W. Extended model of topological relations between spatial objects in geographic information systems. Int. J. Appl. Earth Observ. Geoinf. 2007, 9, 264–275. [Google Scholar] [CrossRef]
- Kurata, Y. The 9+-intersection: A universal framework for modeling topological relations. In Proceedings of the International Conference on Geographic Information Science, Park City, UT, USA, 23–26 September 2008; pp. 181–198. [Google Scholar]
- Alboody, A.; Sedes, F.; Inglada, J. Modeling topological relations between uncertain spatial regions in geo-spatial databases: Uncertain intersection and difference topological model. In Proceedings of the 2010 Second International Conference on Advances in Databases, Knowledge, and Data Applications, Menuires, France, 11–16 April 2010; pp. 7–15. [Google Scholar]
- Shen, J.; Zhou, T.; Chen, M. A 27-intersection model for representing detailed topological relations between spatial objects in two-dimensional space. ISPRS Int. J. Geo-Inf. 2017, 6, 37. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, L.; Chen, M. Topological relations between spherical spatial regions with holes. Int. J. Digit. Earth 2018, 1–28. [Google Scholar] [CrossRef]
- Kurata, Y. From three-dimensional topological relations to contact relations. In Developments in 3D Geo-Information Sciences; Springer: Berlin/Heidelberg, Germany, 2010; pp. 123–142. [Google Scholar]
- Zlatanova, S. On 3D topological relationships. In Proceedings of the 11th International Workshop on Database and Expert Systems Applications, London, UK, 4–8 September 2000; pp. 913–919. [Google Scholar]



| Relation | Figure | 9IM | DE-9IM | 25IM | |
|---|---|---|---|---|---|
| Disjoint | Figure 5a | ||||
| Contain | Figure 5b | ||||
| Equal | Figure 5d | ||||
| Meet | Meet at vertex | Figure 6a | |||
| Figure 6b | |||||
| Figure 6c | |||||
| Meet at edge | Figure 7a | ||||
| Figure 7b | |||||
| Figure 7c | |||||
| Meetatface | Figure 3a | ||||
| Figure 3b | |||||
| Figure 3c | |||||
| Cover | Cover at vertex | Figure 8a | |||
| Figure 8b | |||||
| Figure 8c | |||||
| Cover at edge | Figure 9a | ||||
| Figure 9b | |||||
| Figure 9c | |||||
| Cover at face | Figure 10a | ||||
| Figure 10b | |||||
| Figure 10c | |||||
| Overlap | Figure 11a | ||||
| Figure 11b | |||||
| Figure 11c | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, M.; Guan, Q. A 25-Intersection Model for Representing Topological Relations between Simple Spatial Objects in 3-D Space. ISPRS Int. J. Geo-Inf. 2019, 8, 182. https://doi.org/10.3390/ijgi8040182
Zhou M, Guan Q. A 25-Intersection Model for Representing Topological Relations between Simple Spatial Objects in 3-D Space. ISPRS International Journal of Geo-Information. 2019; 8(4):182. https://doi.org/10.3390/ijgi8040182
Chicago/Turabian StyleZhou, Mengyun, and Qingfeng Guan. 2019. "A 25-Intersection Model for Representing Topological Relations between Simple Spatial Objects in 3-D Space" ISPRS International Journal of Geo-Information 8, no. 4: 182. https://doi.org/10.3390/ijgi8040182
APA StyleZhou, M., & Guan, Q. (2019). A 25-Intersection Model for Representing Topological Relations between Simple Spatial Objects in 3-D Space. ISPRS International Journal of Geo-Information, 8(4), 182. https://doi.org/10.3390/ijgi8040182






