Distance-Decay Effect in Probabilistic Time Geography for Random Encounter
Abstract
1. Introduction
2. Background
2.1. Probabilistic Time Geography and Random Encounter
2.1.1. Probabilistic Time Geography
2.1.2. Random Encounter in Probabilistic Time Geography
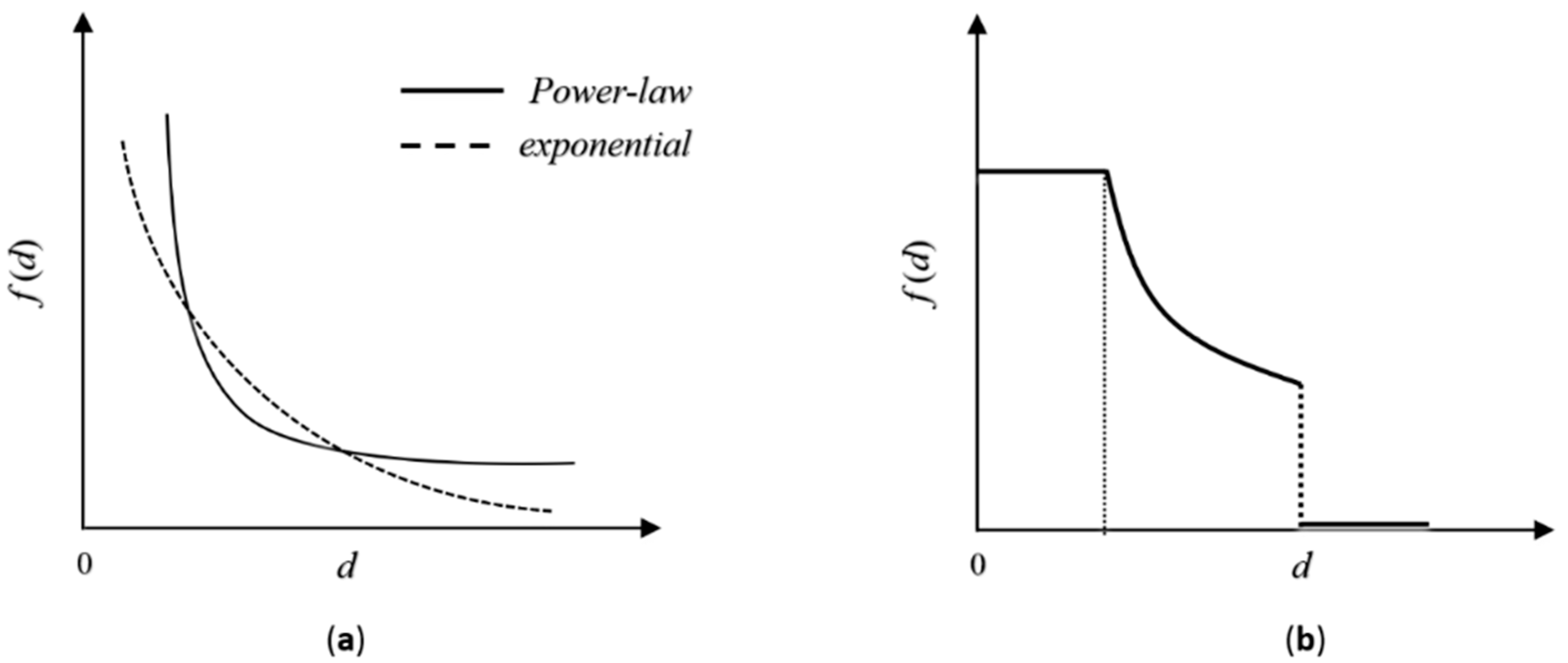
2.2. Distance-Decay Effect and Distance-Decay Function
3. Random Encounter Model under Distance-Decay Effect
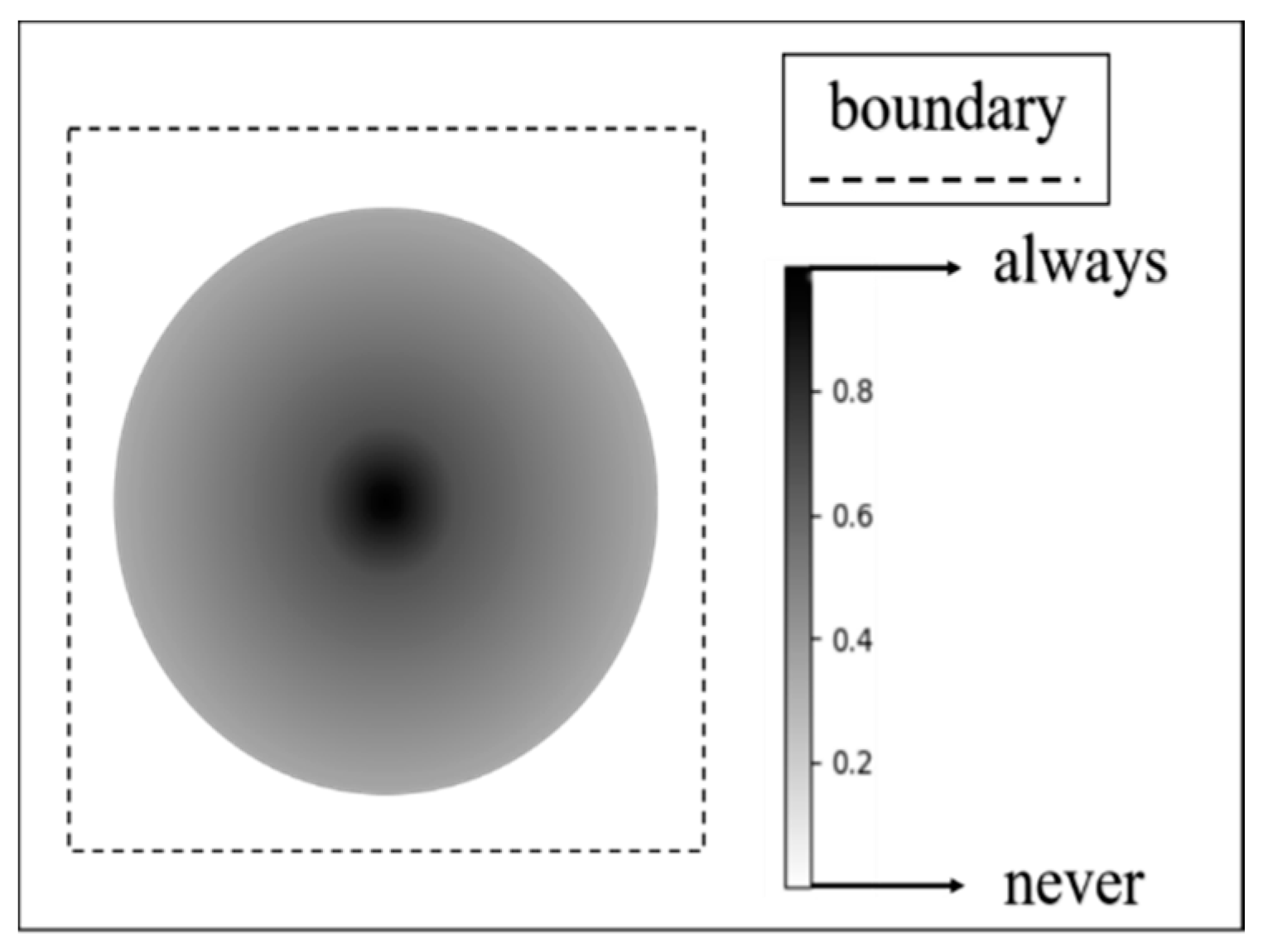
3.1. Construction of Encounter Event Based on the Distance Decay Effect
3.2. Quantifying Distance-Decay Effect
3.3. Encounter Probability Model Based on the Distance-Decay Effect
- = According to formula (3)
- = Multiplication rule for independent events
- = =
- According to Formula (3)
- Addition rule for mutually exclusive events
- According to Formula (5)
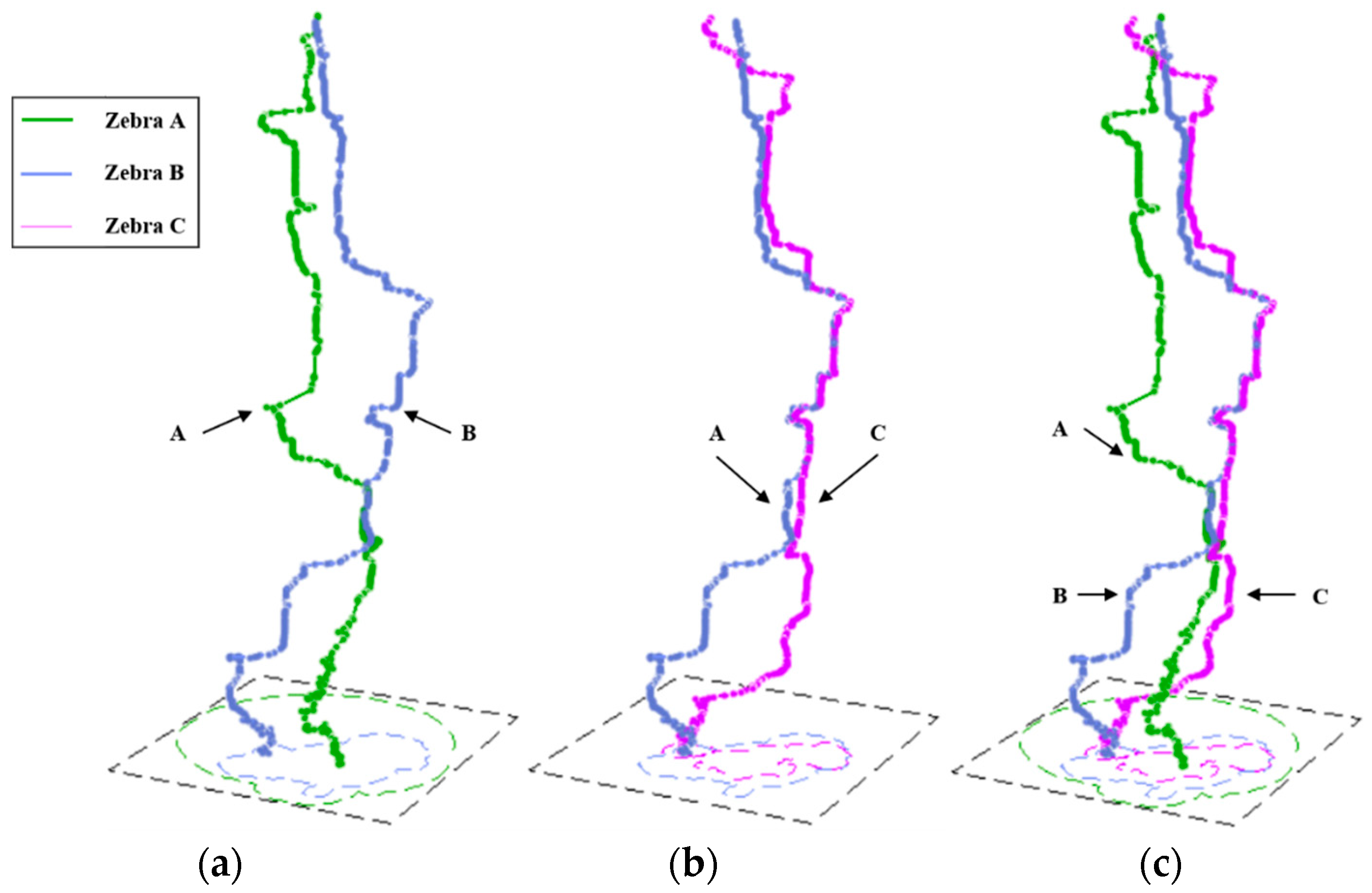
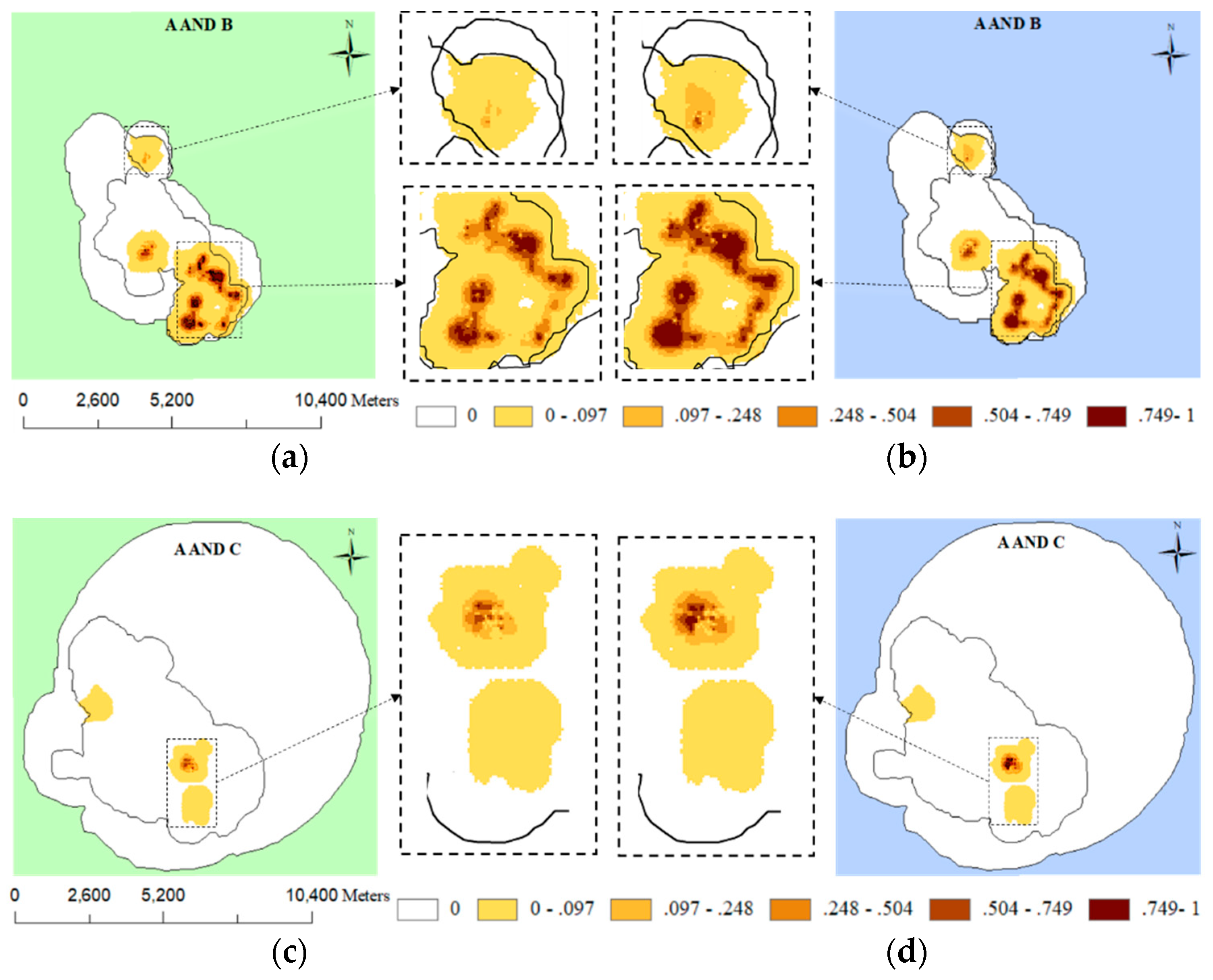
4. Application
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Winter, S.; Yin, Z.C. The elements of probabilistic time geography. GeoInformatica 2011, 15, 417–434. [Google Scholar] [CrossRef]
- Winter, S.; Yin, Z.C. Directed movements in probabilistic time geography. Int. J. Geogr. Inf. Sci. 2010, 24, 1349–1365. [Google Scholar] [CrossRef]
- Downs, J.A.; Horner, M.W. Voxel-based probabilistic space-time prisms for analysing animal movements and habitat use. Int. J. Geogr. Inf. Sci. 2014, 28, 875–890. [Google Scholar] [CrossRef]
- Yin, Z.C.; Wu, Y.; Winter, S. Random encounters in probabilistic time geography. Int. J. Geogr. Inf. Sci. 2018, 1–17. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Yu, W.H.; Chen, Y.G. Regional co-location pattern scoping on a street network considering distance decay effects of spatial interaction. PLoS ONE 2017, 12, e0181959. [Google Scholar] [CrossRef] [PubMed]
- Miller, H.J.; Bridwell, S.A. A field-based theory for time geography. Ann. Assoc. Am. Geogr. 2009, 99, 49–75. [Google Scholar] [CrossRef]
- Song, Y.; Miller, H.J. Simulating visit probability distributions within planar space-time prisms. Int. J. Geogr. Inf. Sci. 2014, 28, 104–125. [Google Scholar] [CrossRef]
- Song, Y.; Miller, H.J. Modeling visit probabilities within network-time prisms using markov techniques. Geogr. Anal. 2016, 48, 18–42. [Google Scholar] [CrossRef]
- Downs, J.A.; Horner, M.W. Probabilistic potential path trees for visualizing and analyzing vehicle tracking data. J. Transp. Geogr. 2012, 23. [Google Scholar] [CrossRef]
- Abi-Zeid, I.; Frost, J.R. SARPlan: A decision support system for canadian search and rescue operations. Eur. J. Oper. Res. 2005, 162, 630–653. [Google Scholar] [CrossRef]
- Demvsar, U.; Buchin, K. Analysis and visualisation of movement: An interdisciplinary review. Mov. Ecol. 2015, 3, 1–24. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, L. Quantifying the distance effect in spatial interactions. Acta Sci. Nat. Univ. Pekin. 2014, 50, 526–534. [Google Scholar] [CrossRef]
- Hipp, J.R.; Boessen, A. The shape of mobility: Measuring the distance decay function of household mobility. Prof. Geogr. 2016, 69, 1–13. [Google Scholar] [CrossRef]
- McLaren, Z.M.; Ardington, C. Distance decay and persistent health care disparities in South Africa. BMC Health Serv. Res. 2014, 14, 541. [Google Scholar] [CrossRef]
- Fotheringham, A.S. Spatial structure and distance-decay parameters. Ann. Assoc. Am. Geogr. 2010, 71, 425–436. [Google Scholar] [CrossRef]
- Halás, M.; Klapka, P. Distance-decay functions for daily travel-to-work flows. J. Transp. Geogr. 2014, 35, 107–119. [Google Scholar] [CrossRef]
- Östh, J.; Lyhagen, J. A new way of determining distance decay parameters in spatial interaction models with application to job accessibility analysis in Sweden. Eur. J. Transp. Infrastruct. Res. 2016, 16, 344–363. [Google Scholar] [CrossRef]
- Nijkamp, P.; Rietveld, P. Exponential or power distance-decay for commuting? An alternative specification. Environ. Plan. A 2004, 41, 461–480. [Google Scholar] [CrossRef][Green Version]
- Stȩpniak, M.; Jacobs-Crisioni, C. Reducing the uncertainty induced by spatial aggregation in accessibility and spatial interaction applications. J. Transp. Geogr. 2017, 61, 17–29. [Google Scholar] [CrossRef]
- Ladau, J.; Green, J.L. The geometry of the distance-decay of similarity in ecological communities. bioRxiv 2017. [Google Scholar] [CrossRef]
- Soininen, J.; Mcdonald, R. The distance decay of similarity in ecological communities. Ecography 2007, 30, 3–12. [Google Scholar] [CrossRef]
- Hélène, M.; Chuyong, G. A general framework for the distance–decay of similarity in ecological communities. Ecol. Lett. 2008, 11, 904–917. [Google Scholar] [CrossRef]
- Liu, Y.; Sui, Z.W. Uncovering patterns of inter-urban trip and spatial interaction from social media check-in data. PLoS ONE 2014, 9, e86026. [Google Scholar] [CrossRef]
- Luncz, L.V.; Proffitt, T. Distance-decay effect in stone tool transport by wild chimpanzees. Proc. R. Soc. B Biol. Sci. 2016, 283. [Google Scholar] [CrossRef]
- Requia, W.J.; Roig, H.L. Mapping distance-decay of cardiorespiratory disease risk related to neighborhood environments. Environ. Res. 2016, 151, 203–215. [Google Scholar] [CrossRef]
- Requia, W.J.; Petros, K. Mapping distance-decay of premature mortality attributable to PM2.5-related traffic congestion. Environ. Pollut. 2018, 243, 9–16. [Google Scholar] [CrossRef]
- Long, J.A.; Webb, S.L. Mapping areas of spatial-temporal overlap from wildlife tracking data. Mov. Ecol. 2015, 3, 38. [Google Scholar] [CrossRef]
- Zhang, P.D.; Beernaerts, J. A hybrid approach combining the multi-temporal scale spatio-temporal network with the continuous triangular model for exploring dynamic interactions in movement data: A case study of football. Isprs Int. J. Geo-Inf. 2018, 7, 31. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Z.-C.; Jin, Z.-H.-N.; Ying, S.; Liu, H.; Li, S.-J.; Xiao, J.-Q. Distance-Decay Effect in Probabilistic Time Geography for Random Encounter. ISPRS Int. J. Geo-Inf. 2019, 8, 177. https://doi.org/10.3390/ijgi8040177
Yin Z-C, Jin Z-H-N, Ying S, Liu H, Li S-J, Xiao J-Q. Distance-Decay Effect in Probabilistic Time Geography for Random Encounter. ISPRS International Journal of Geo-Information. 2019; 8(4):177. https://doi.org/10.3390/ijgi8040177
Chicago/Turabian StyleYin, Zhang-Cai, Zhang-Hao-Nan Jin, Shen Ying, Hui Liu, San-Juan Li, and Jia-Qiang Xiao. 2019. "Distance-Decay Effect in Probabilistic Time Geography for Random Encounter" ISPRS International Journal of Geo-Information 8, no. 4: 177. https://doi.org/10.3390/ijgi8040177
APA StyleYin, Z.-C., Jin, Z.-H.-N., Ying, S., Liu, H., Li, S.-J., & Xiao, J.-Q. (2019). Distance-Decay Effect in Probabilistic Time Geography for Random Encounter. ISPRS International Journal of Geo-Information, 8(4), 177. https://doi.org/10.3390/ijgi8040177




