A Variant of the Planchon and Darboux Algorithm for Filling Depressions in Raster Digital Elevation Models
Abstract
:1. Introduction
2. Review of the Improved Implementation of the P&D Algorithm and the W&T Variant
| Algorithm 1. Pseudo-code of the W&T variant. | |
| 1. | Let DEM be the input DEM; |
| 2. | Let W be the covered water layer and converging to the output DEM; |
| 3. | Let m be a huge positive number and ε be a very small positive number; |
| 4. | Let S1 and S2 be two empty stack; |
| 5. | Let minNeighbors(W(c)) be a procedure which finds the minimum water elevation of the neighbors of cell c; |
| 6. | Let swapStack(S1, S2) be a procedure that switches stack S1 and stack S2; |
| 7. | Stage 1: Initialization of the surface to m |
| 8. | For (each cell c of the DEM){ |
| 9. | If (c is a border cell) W(c) = DEM(c); |
| 10. | Else { |
| 11. | W(c) = m; |
| 12. | Push c into S1; |
| 13. | } |
| 14. | } |
| 15. | Stage 2: Removing excess water |
| 16. | Do{ |
| 17. | For (each cell c of in S1){ |
| 18. | If (W(c) > DEM(c)){ |
| 19. | mN = minNeighbors(W(c)); |
| 20. | If (DEM(c)> = mN+ε) W(c) = DEM(c); |
| 21. | Else{ |
| 22. | if (W(c)>mN+ε) W(c) = mN+ε; |
| 23. | Push c into S2; |
| 24. | } |
| 25. | } |
| 26. | } |
| 27. | swapStack(S1, S2); |
| 28. | } |
| 29. | While (any cell is changed) |
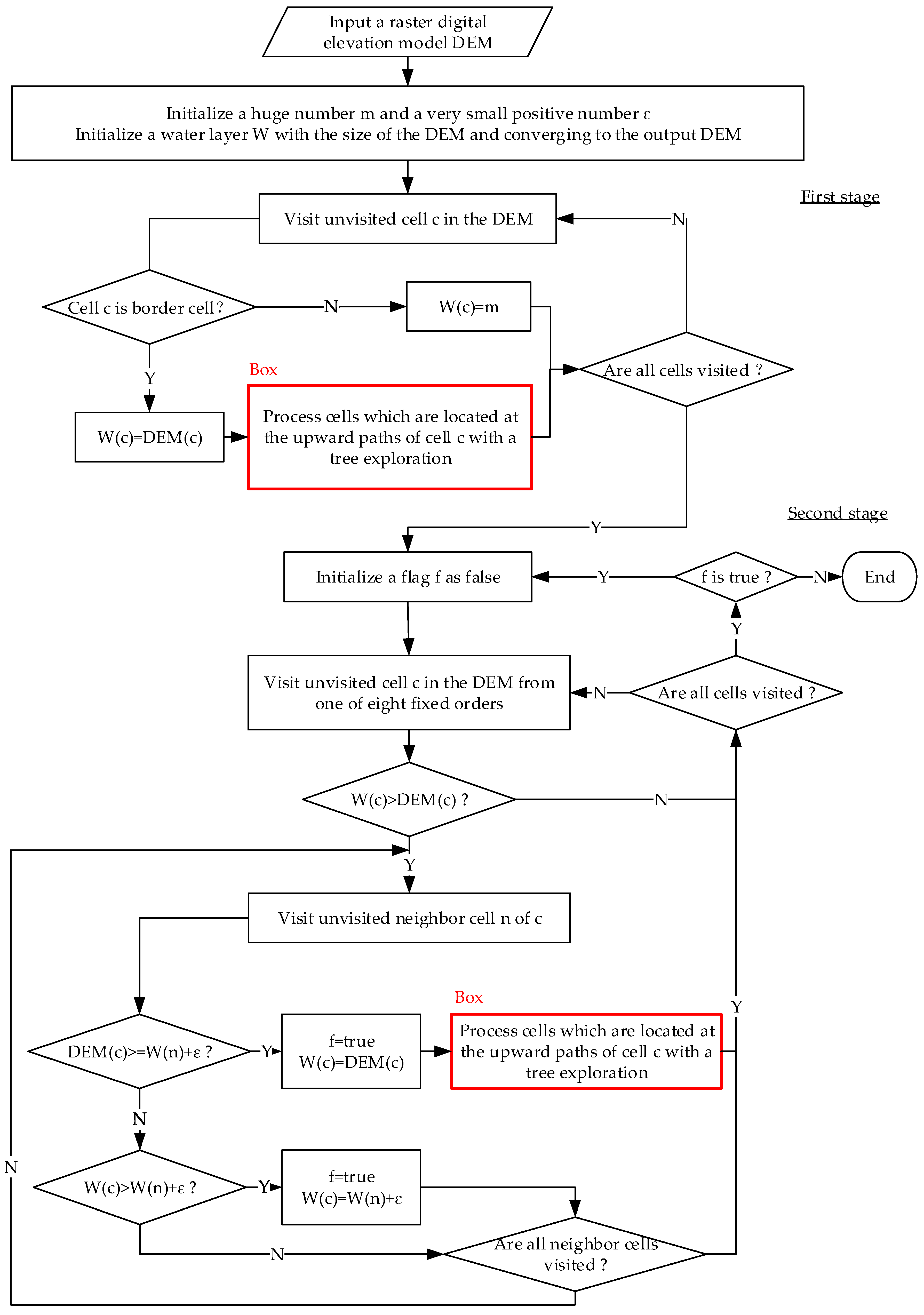
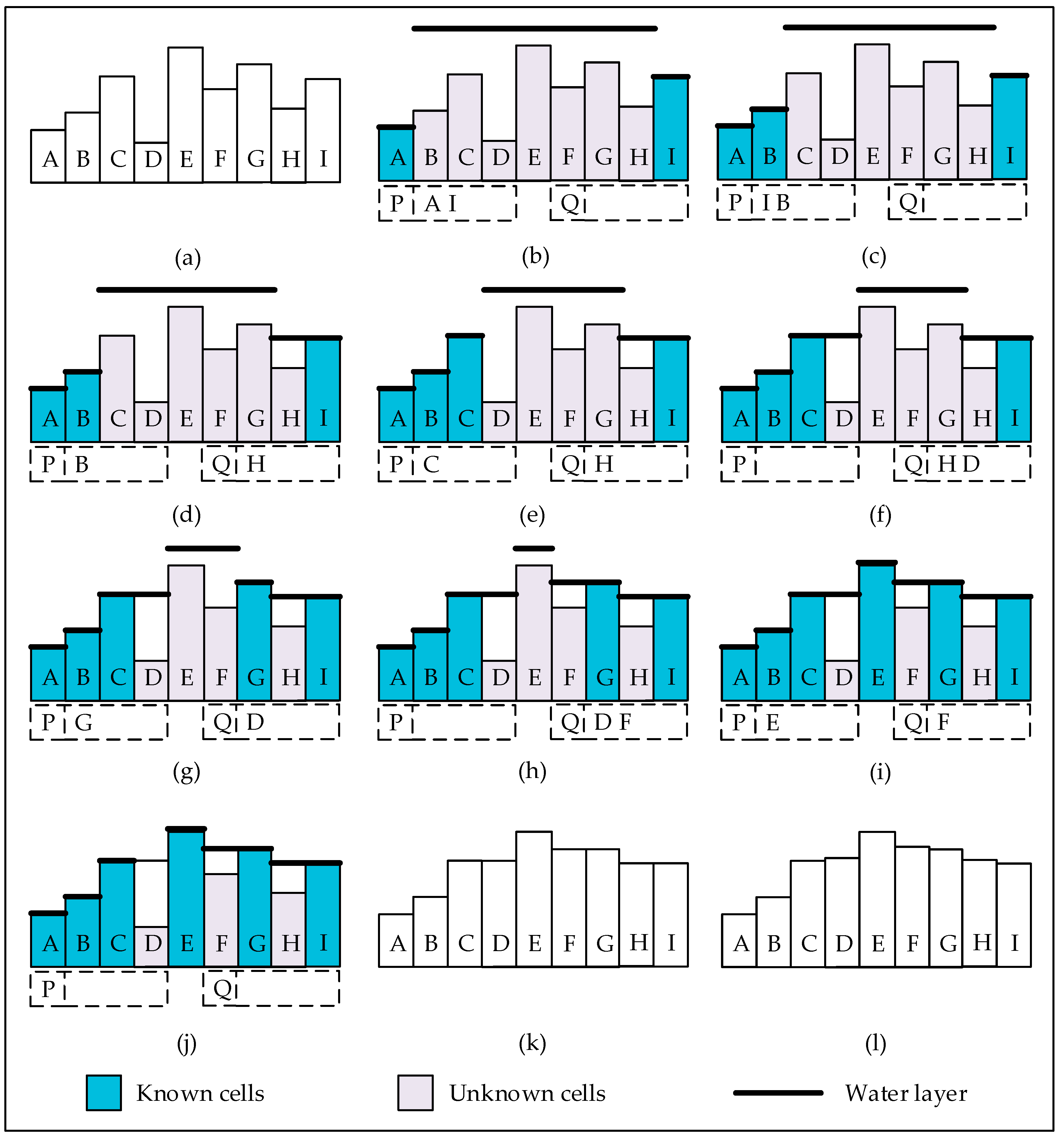
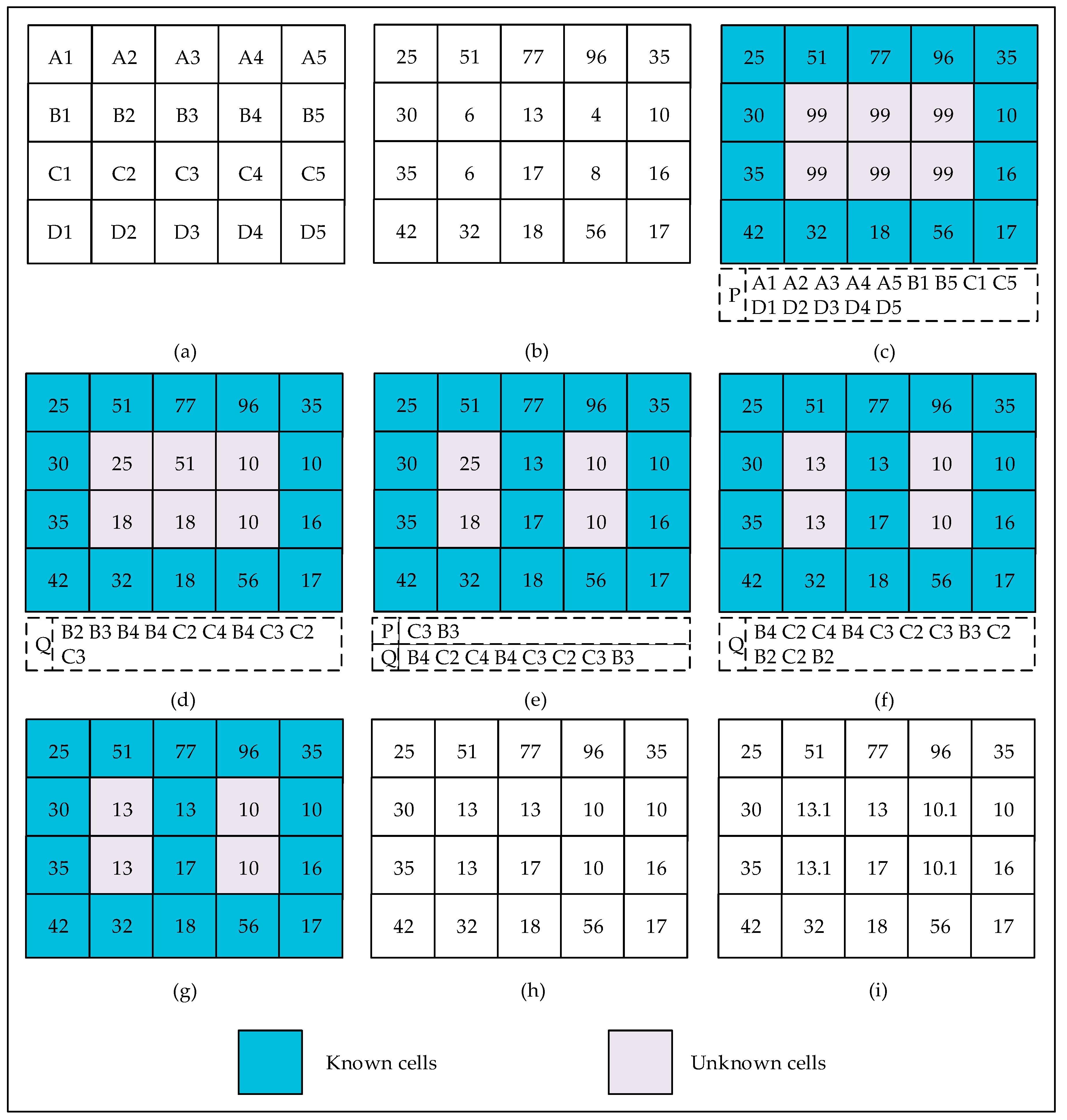
3. Proposed Variant of the P&D Algorithm
| Algorithm 2. Pseudo-code of our variant. | |
| 1. | Let DEM be the input DEM; |
| 2. | Let W be the covered water layer and converging to output DEM; |
| 3. | Let ε be a very small positive number and m be a huge positive number. |
| 4. | Let P and Q be two empty plain queue; |
| 5. | Function dryCell(n){ |
| 6. | W(n) = DEM(n); |
| 7. | Push n into P; |
| 8. | } |
| 10. | Stage 1: Initialization of the surface to m |
| 11. | For (each cell c in the DEM){ |
| 12. | If (c is a border cell) dryCell(c); |
| 13. | Else W(c) = m; |
| 14. | } |
| 15. | Stage 2: Removing of excess water |
| 16. | While (P is not empty or Q is not empty){ |
| 17. | If (P is not empty) Pop cell c off P; |
| 18. | Else { |
| 19. | Pop cell c off Q; |
| 20. | If (DEM(c) ≥ W(c)) continue; |
| 21. | } |
| 22. | For (each existing neighbor cell n of c){ |
| 23. | If (DEM(n) ≥ W(n)) continue; |
| 24. | If (DEM(n) ≥ W(c)+ε) dryCell(n); |
| 25. | Else if (W(n) > W(c)+ε){ |
| 26. | W(n) = W(c)+ε; |
| 27. | Push n into Q; |
| 28. | } |
| 29. | } |
| 30. | } |
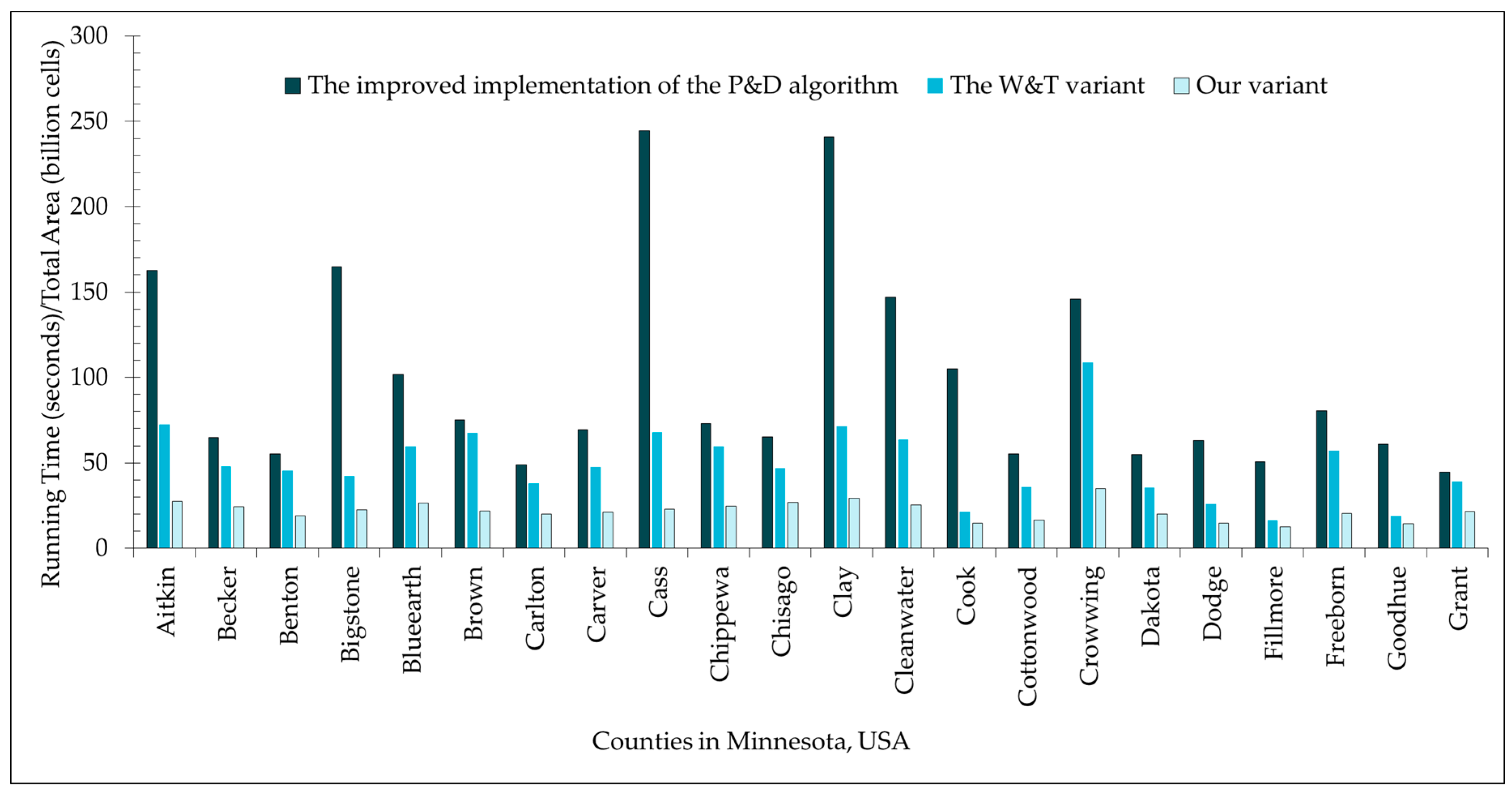
4. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, L.; Liu, H. An efficient method for identifying and filling surface depressions in digital elevation models for hydrologic analysis and modelling. Int. J. Geogr. Inf. Sci. 2006, 20, 193–213. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, H.; Peng, C.; Zhang, W.; Qiao, F.; Chen, C. A new treatment of depression for drainage network extraction based on DEM. J. Mt. Sci. 2009, 6, 311–319. [Google Scholar] [CrossRef]
- Nobre, A.D.; Cuartas, L.A.; Hodnett, M.; Rennó, C.D.; Rodrigues, G.; Silveira, A.; Waterloo, M.; Saleska, S. Height above the nearest drainage–a hydrologically relevant new terrain model. J. Hydrol. 2011, 404, 13–29. [Google Scholar] [CrossRef]
- Xiong, L.; Tang, G.; Yan, S.; Zhu, S. Landform-oriented flow-routing algorithm for the dual-structure loess terrain based on digital elevation models. Hydrol. Process. 2014, 28, 1756–1766. [Google Scholar] [CrossRef]
- Qin, C.; Zhu, A.; Pei, T.; Li, B.; Zhou, C.; Yang, L. An adaptive approach to selecting a flow-partition exponent for a multiple-flow-direction algorithm. Int. J. Geogr. Inf. Sci. 2007, 21, 443–458. [Google Scholar] [CrossRef]
- Liu, X.; Wang, N.; Shao, J.; Chu, X. An automated processing algorithm for flat areas resulting from DEM filling and interpolation. ISPRS Int. J. Geo-Inf. 2017, 6, 376. [Google Scholar] [CrossRef]
- Zhou, G.; Liu, X.; Fu, S.; Sun, Z. Parallel identification and filling of depressions in raster digital elevation models. Int. J. Geogr. Inf. Sci. 2017, 31, 1061–1078. [Google Scholar] [CrossRef]
- Jenson, K.; Domingue, O. Extracting topographic structure from digital elevation Data for geographic system analysis. Photogramm. Eng. Remote Sens. 1988, 54, 1593–1600. [Google Scholar]
- Planchon, O.; Darboux, F. A fast, simple and versatile algorithm to fill the depressions of digital elevation models. CATENA 2002, 46, 0–176. [Google Scholar] [CrossRef]
- Barnes, R.; Lehman, C.; Mulla, D. Priority-Flood: An Optimal Depression-Filling and Watershed-Labeling Algorithm for Digital Elevation Models. Comput. Geosci. 2014, 62, 117–127. [Google Scholar] [CrossRef]
- Bai, R.; Li, T.; Huang, Y.; Li, J.; Wang, G. An efficient and comprehensive method for drainage network extraction from DEM with billions of pixels using a size-balanced binary search tree. Geomorphology 2015, 238, 56–67. [Google Scholar] [CrossRef]
- Zhou, G.; Sun, Z.; Fu, S. An efficient variant of the Priority-Flood algorithm for filling depressions in raster digital elevation models. Comput. Geosci. 2016, 90, 87–96. [Google Scholar] [CrossRef]
- Wei, H.; Zhou, G.; Fu, S. Efficient Priority-Flood depression filling in raster digital elevation models. Int. J. Digit. Earth 2018, 1–13. [Google Scholar] [CrossRef]
- Zhu, D.; Ren, Q.; Xuan, Y.; Chen, Y.; Cluckie, I.D. An effective depression filling algorithm for DEM-based 2-D surface flow modelling. Hydrol. Earth Syst. Sci. 2013, 17, 495–505. [Google Scholar] [CrossRef]
- Rieger, W. A phenomenon-based approach to upslope contributing area and depressions in DEMs. Hydrol. Process. 1998, 12, 857–872. [Google Scholar] [CrossRef]
- Soille, P. Optimal removal of spurious pits in grid digital elevation models. Water Resour. Res. 2004, 40, 229–244. [Google Scholar] [CrossRef]
- Lindsay, J.B. Efficient hybrid breaching-filling sink removal methods for flow path enforcement in digital elevation models. Hydrol. Process. 2016, 30, 846–857. [Google Scholar] [CrossRef]
- Zhu, Q.; Tian, Y.; Zhao, J. An efficient depression processing algorithm for hydrologic analysis. Comput. Geosci. 2006, 32, 615–623. [Google Scholar] [CrossRef]
- Berends, C.J.; van de Wal, R.S. A computationally efficient depression-filling algorithm for digital elevation models, applied to proglacial lake drainage. Geosci. Model. Dev. 2016, 9, 4451–4460. [Google Scholar] [CrossRef]
- Wallis, C.; Wallace, D.; Tarboton, D.G.; Schreuders, K. Hydrologic terrain processing using parallel computing. In Proceedings of the 18th World IMACS Congress and MODSIM09 International Congress on Modelling and Simulation, Modelling and Simulation Society of Australia and New Zealand and International Association for Mathematics and Computers in Simulation, Cairns, Australia, 13–17 July 2009; pp. 2540–2545. [Google Scholar]
- Tarboton, D.G. Terrain Analysis Using Digital Elevation Models (TauDEM). Utah Water Research Laboratory, Utah State University, 2017. Available online: http://hydrology.usu.edu/taudem/taudem5/index.html (accessed on 31 January 2019).
- Gong, J.; Xie, J. Extraction of drainage networks from large terrain datasets using high throughput computing. Comput. Geosci. 2009, 35, 337–346. [Google Scholar] [CrossRef]
- Qin, C.; Zhan, L. Parallelizing flow-accumulation calculations on graphics processing units—From iterative DEM preprocessing algorithm to recursive multiple-flow-direction algorithm. Comput. Geosci. 2012, 43, 7–16. [Google Scholar] [CrossRef]
- Yıldırım, A.A.; Watson, D.; Tarboton, D.G.; Wallace, R. A virtual tile approach to raster-based calculations of large digital elevation models in a shared-memory system. Comput. Geosci. 2015, 82, 78–88. [Google Scholar] [CrossRef]
- Barnes, R. Parallel Priority-Flood depression filling for trillion cell digital elevation models on desktops or clusters. Comput. Geosci. 2016, 96, 56–68. [Google Scholar] [CrossRef]
- Shahzad, F.; Gloaguen, R. TecDEM: A MATLAB based toolbox for tectonic geomorphology, Part 1: Drainage network preprocessing and stream profile analysis. Comput. Geosci. 2011, 37, 250–260. [Google Scholar] [CrossRef]
- Tesfa, T.K.; Tarboton, D.G.; Watson, D.W.; Schreuders, K.A.T. Extraction of hydrological proximity measures from DEMs using parallel processing. Environ. Model. Softw. 2011, 26, 1696–1709. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, H.; Zhou, G.; Dong, W. A Variant of the Planchon and Darboux Algorithm for Filling Depressions in Raster Digital Elevation Models. ISPRS Int. J. Geo-Inf. 2019, 8, 164. https://doi.org/10.3390/ijgi8040164
Wei H, Zhou G, Dong W. A Variant of the Planchon and Darboux Algorithm for Filling Depressions in Raster Digital Elevation Models. ISPRS International Journal of Geo-Information. 2019; 8(4):164. https://doi.org/10.3390/ijgi8040164
Chicago/Turabian StyleWei, Hongqiang, Guiyun Zhou, and Wenyan Dong. 2019. "A Variant of the Planchon and Darboux Algorithm for Filling Depressions in Raster Digital Elevation Models" ISPRS International Journal of Geo-Information 8, no. 4: 164. https://doi.org/10.3390/ijgi8040164
APA StyleWei, H., Zhou, G., & Dong, W. (2019). A Variant of the Planchon and Darboux Algorithm for Filling Depressions in Raster Digital Elevation Models. ISPRS International Journal of Geo-Information, 8(4), 164. https://doi.org/10.3390/ijgi8040164




