A New, Score-Based Multi-Stage Matching Approach for Road Network Conflation in Different Road Patterns
Abstract
1. Introduction
2. Materials and Methods
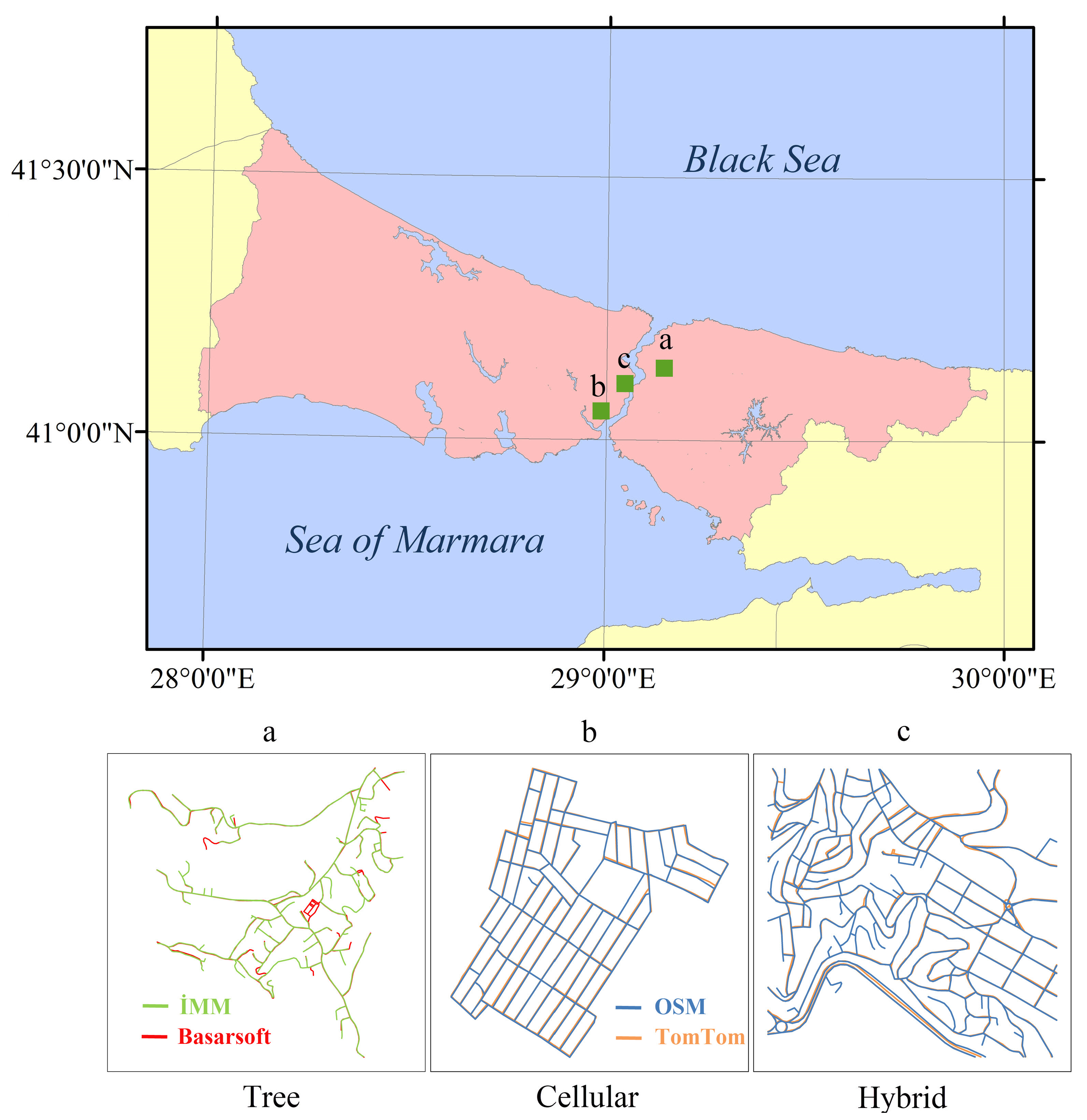
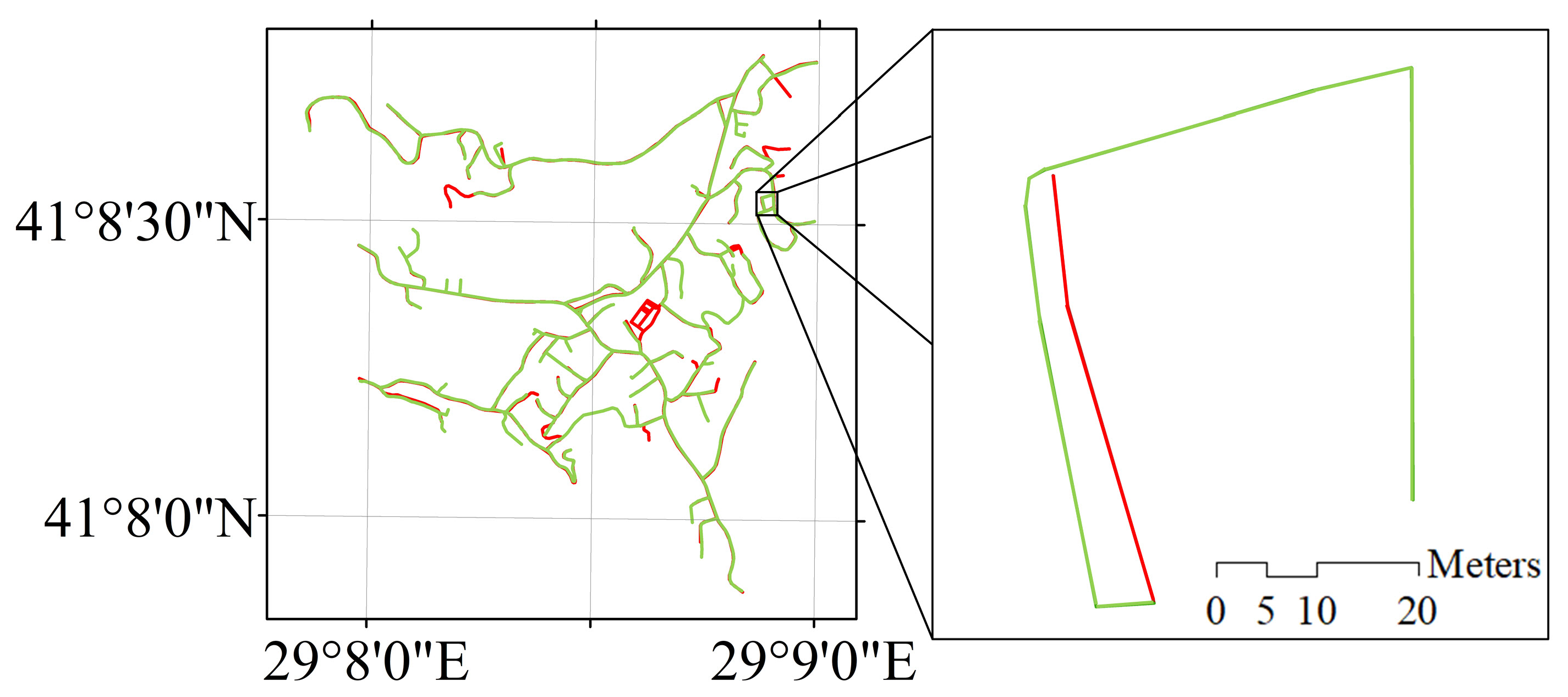
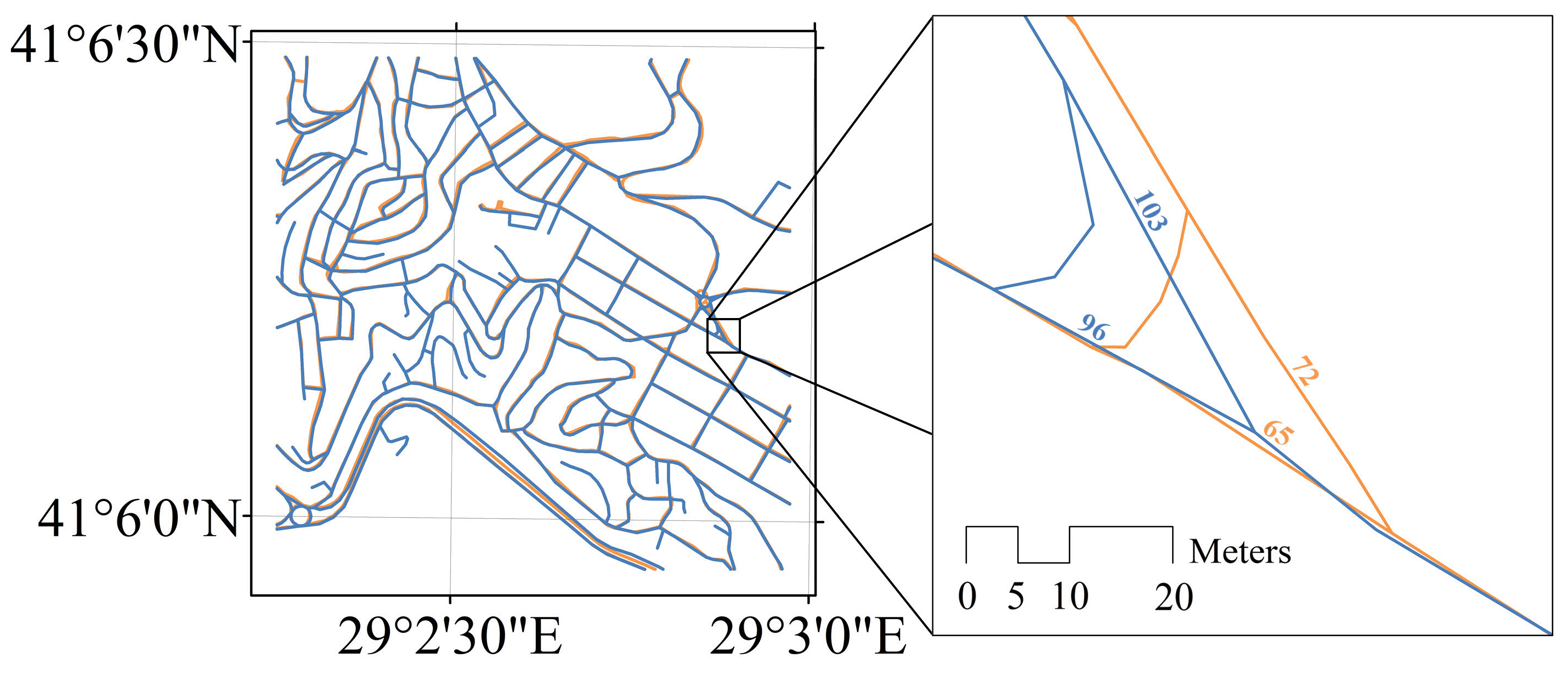
2.1. Study Area, Road Data, and Road Patterns
2.2. Similarity Measures
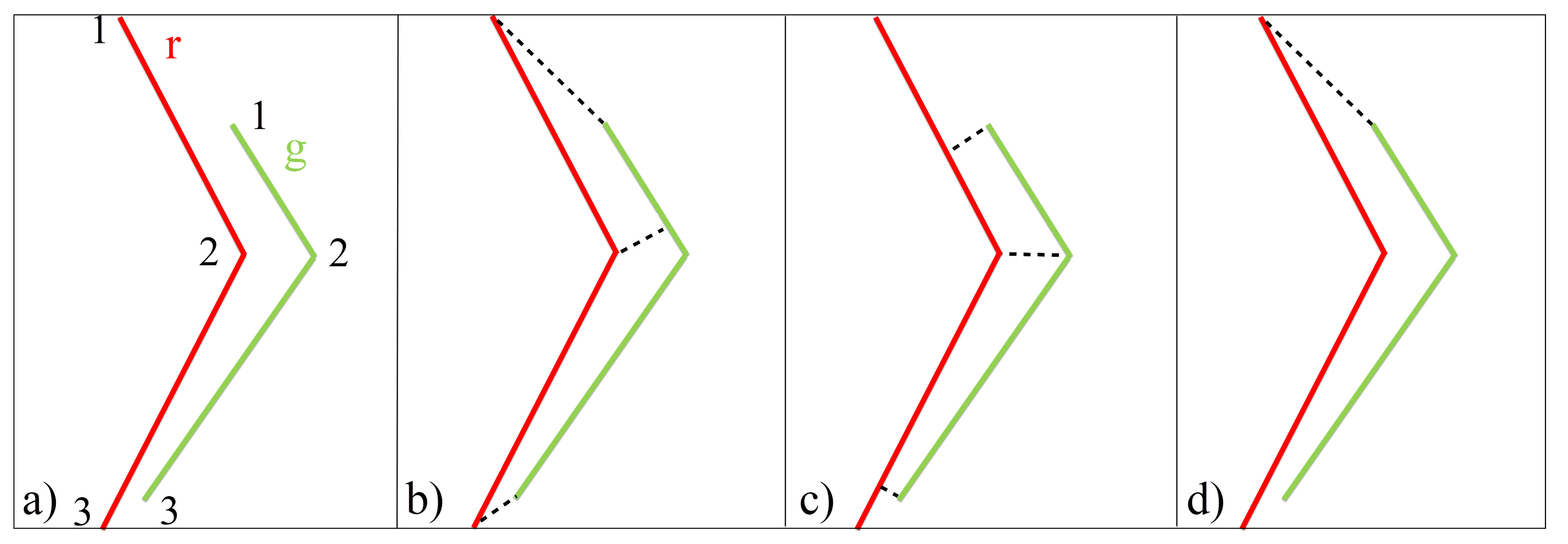
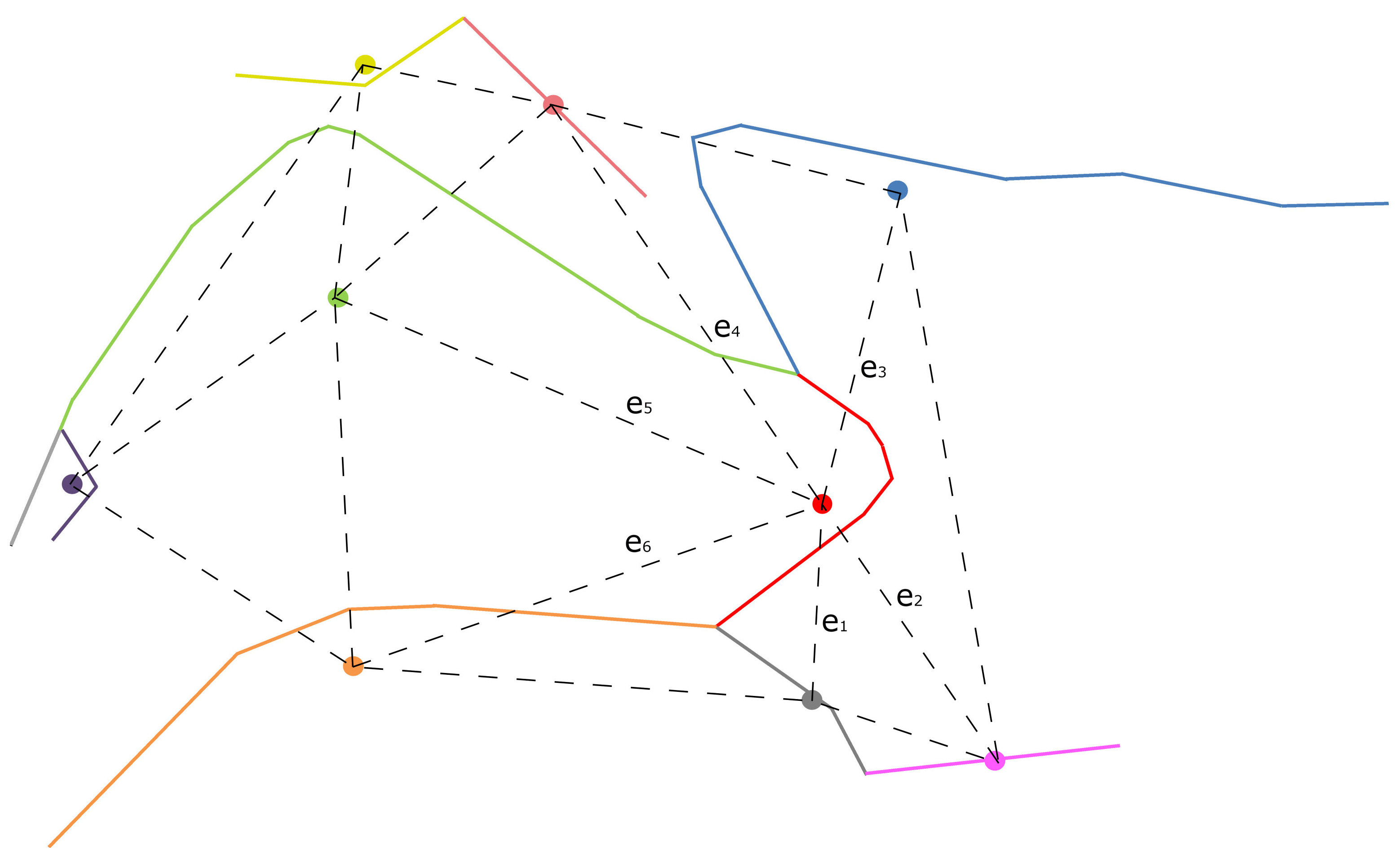
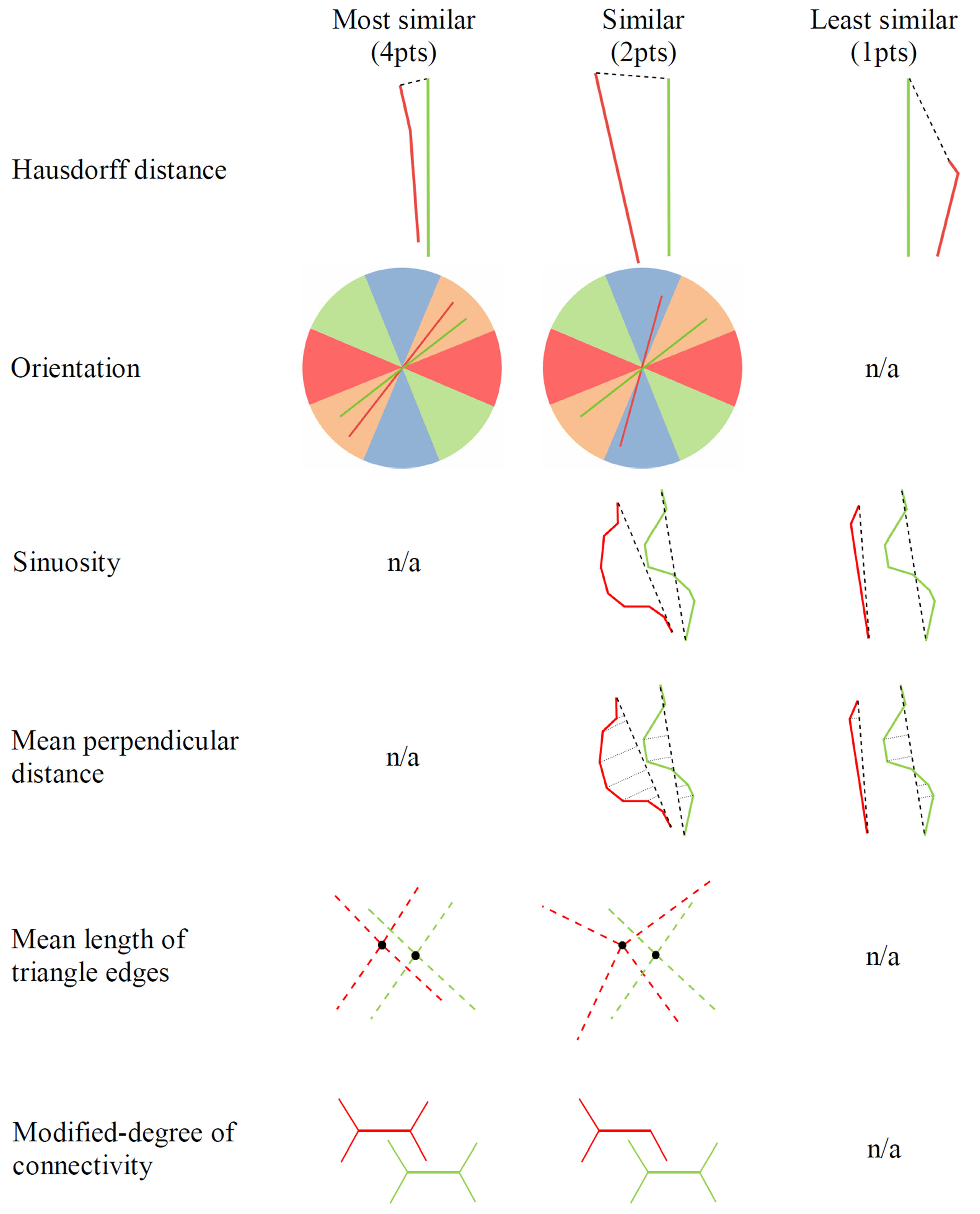
2.2.1. Hausdorff Distance
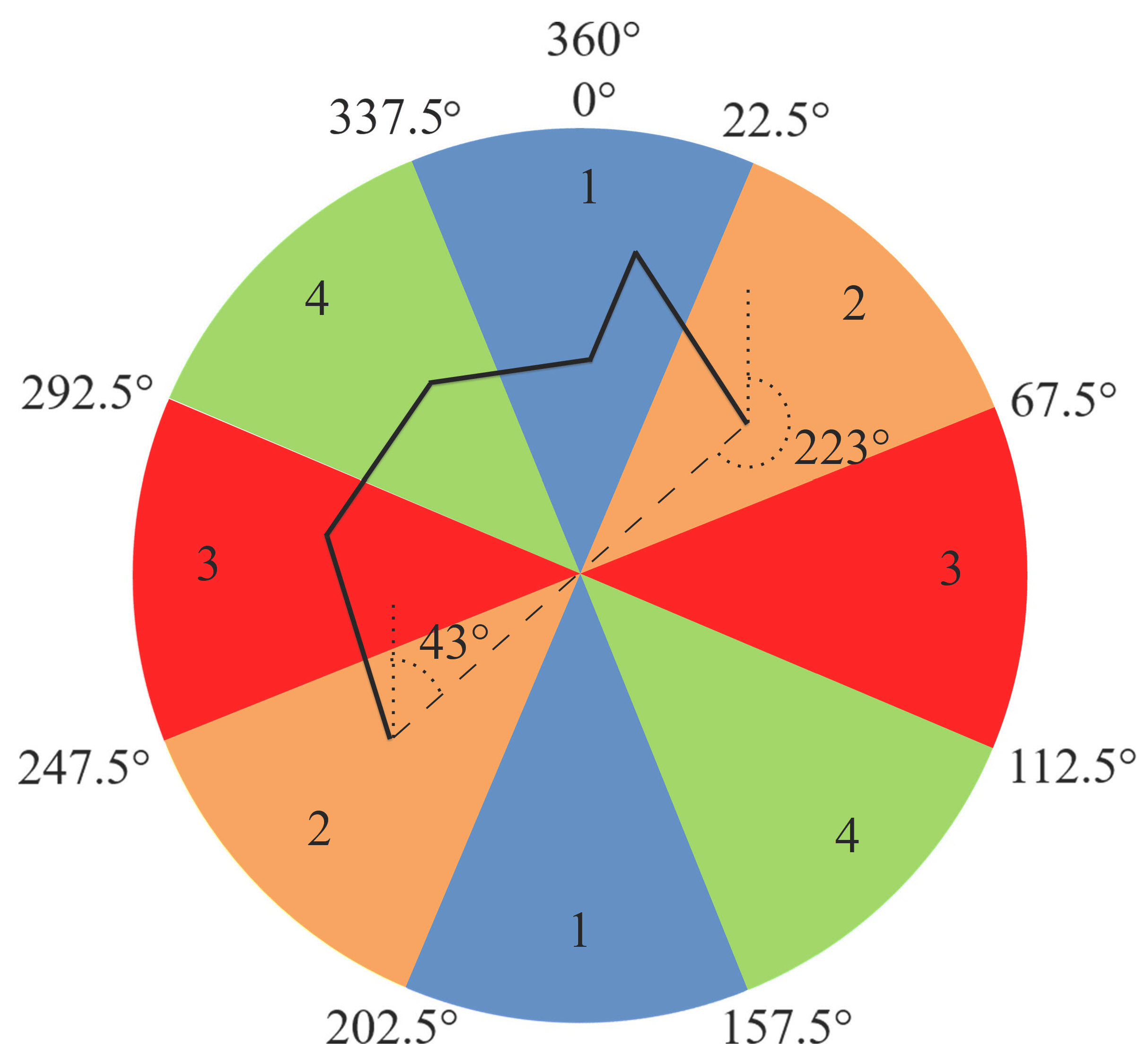
2.2.2. Orientation
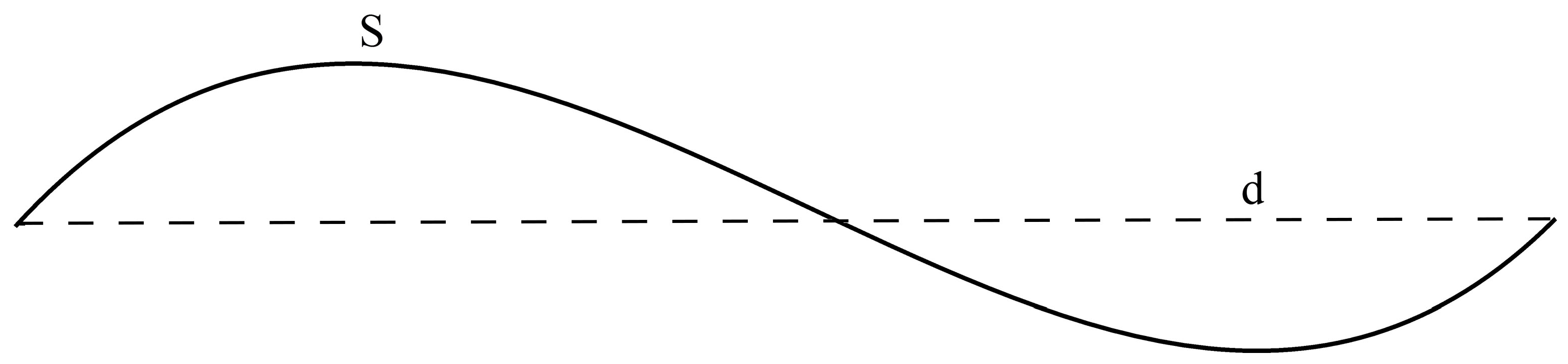
2.2.3. Sinuosity
2.2.4. Mean Perpendicular Distance
2.2.5. Mean Length of Triangle Edges
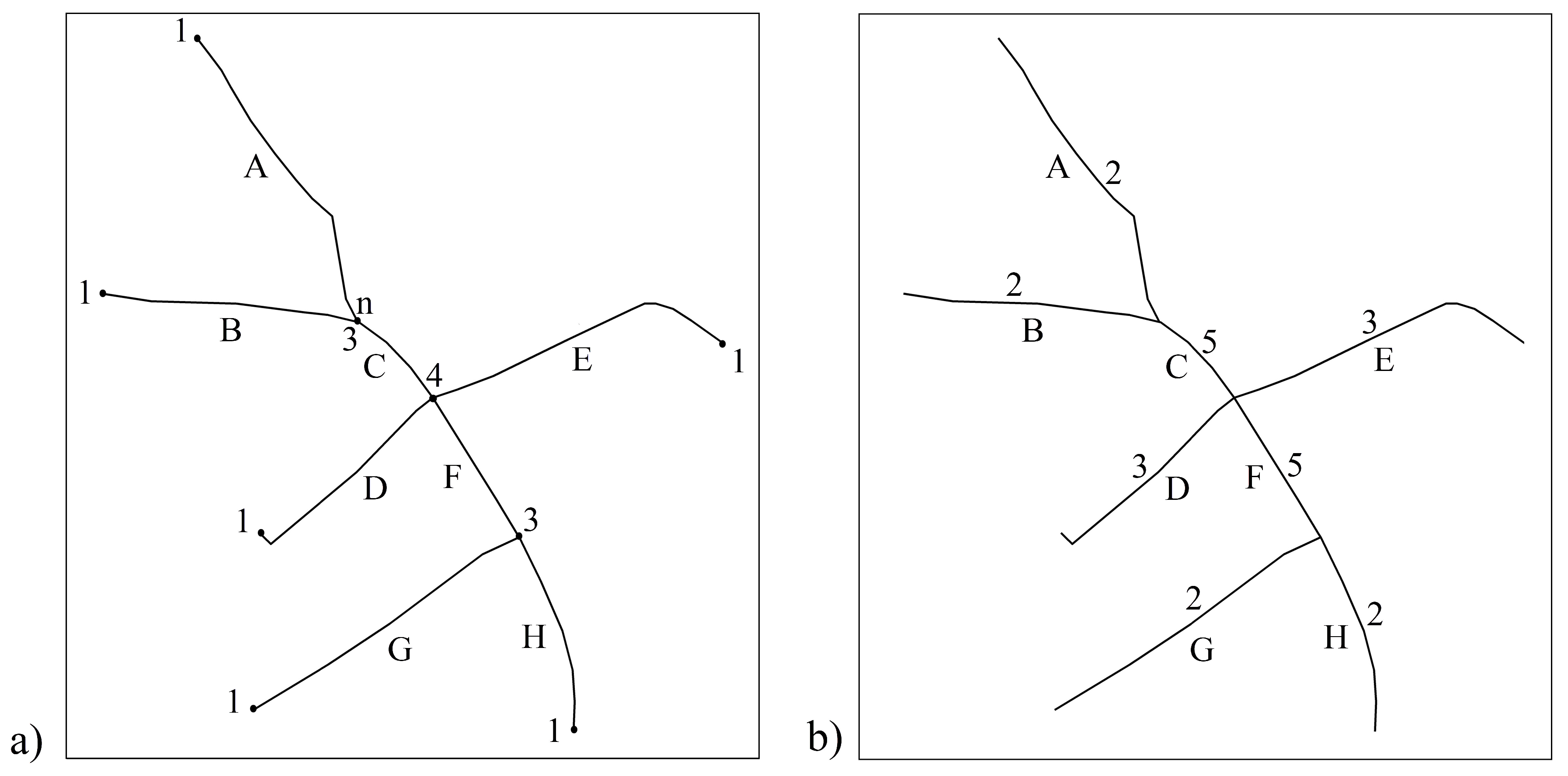
2.2.6. Modified Degree of Connectivity
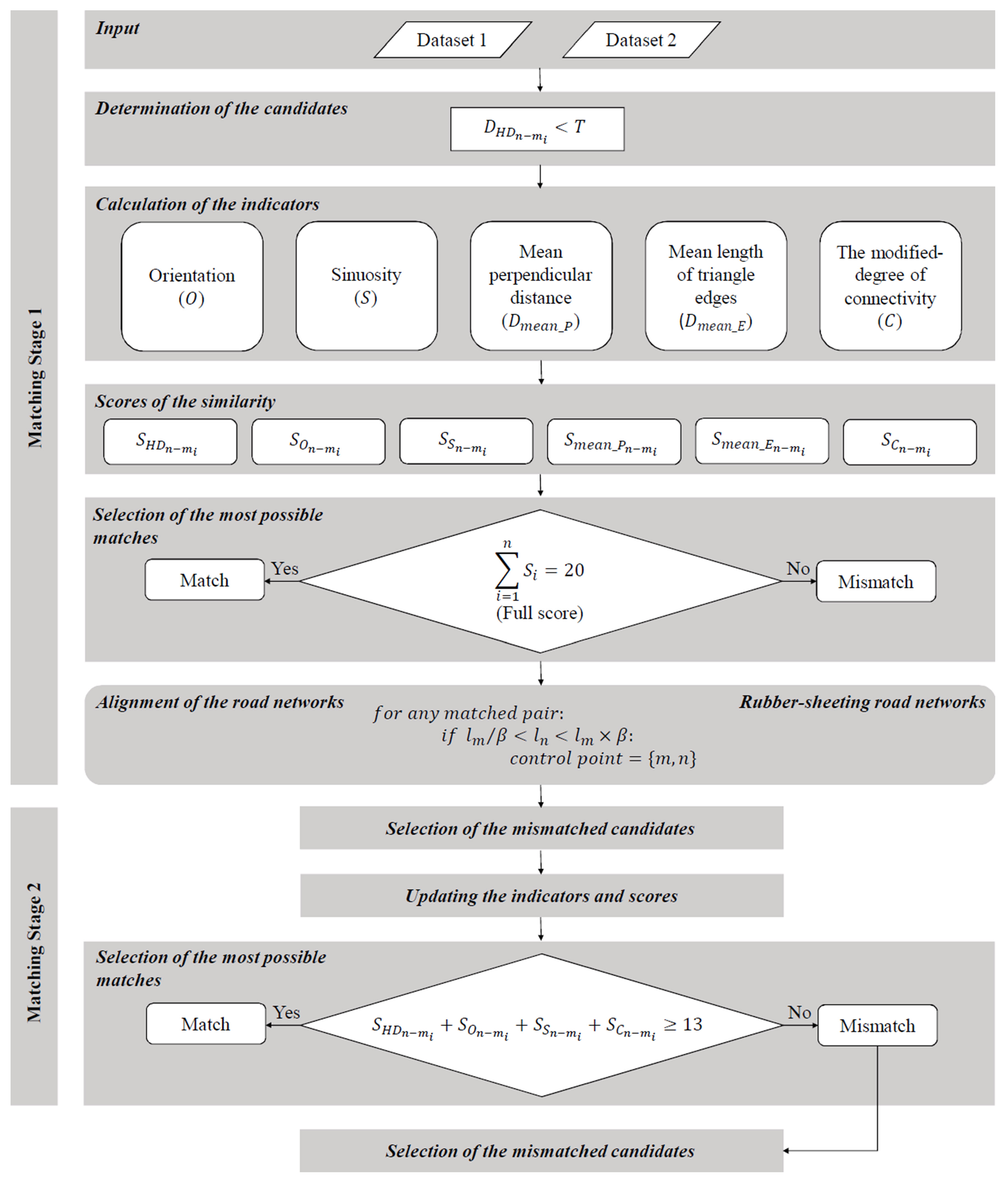
2.3. The Proposed Method: Score-Based Matching
2.3.1. Scores with Respect to the Indicators
- Hausdorff distances from a line to its candidates are sorted ascendingly. The first three of the closest candidate matches are the first three minimum distances between Line n, which is any road line in the first dataset, and Line m, which is the matching candidate of Line n in the other dataset; they are scored as , , and , respectively. If there are more than three candidates, then the fourth and others are scored as .
- The difference between orientation classes where the candidate pair belong ( and ) helps to determine the orientation score (). Candidate pairs in the same class are scored as . If the difference between the classes is one (i.e., if they are in adjacent classes), the score is assigned as . Otherwise, the score is assigned as .
- The rules for sinuosity scores () for Line n in dataset 1 and Line m in dataset 2 are as follows:
- and , then
- and , then
- and , then
- and , then
- and , then
- and , then
- and , then
- and , then
- and , then
- In order to determine the score with respect to mean perpendicular distances, the standard deviation of all mean perpendicular distances () is computed first. If the difference between the mean perpendicular distances of Line n and Line m is less than or equal to , then this matching is scored as . If the difference between the mean perpendicular distances of Line n and Line m is greater than and less than or equal to , then this matching is scored as . Otherwise, this matching is scored as .
- In order to determine the score with respect to the mean length of triangle edges, the standard deviation of all mean lengths of triangle edges () is computed first. If the difference between the mean length of triangle edges of Line n and Line m is less than or equal to , then this matching is scored as . If the difference between the mean length of triangle edges of Line n and Line m is greater than and less than or equal to , then this matching is scored as . Otherwise, this matching is scored as .
- The difference between the modified degree values of Line n and Line m ( and ) helps to determine the score of connectivity. If the candidates have the same degree, then this matching is scored as . If there is a just one degree of difference between the candidates, then this matching is scored as . Otherwise, this matching is scored as .
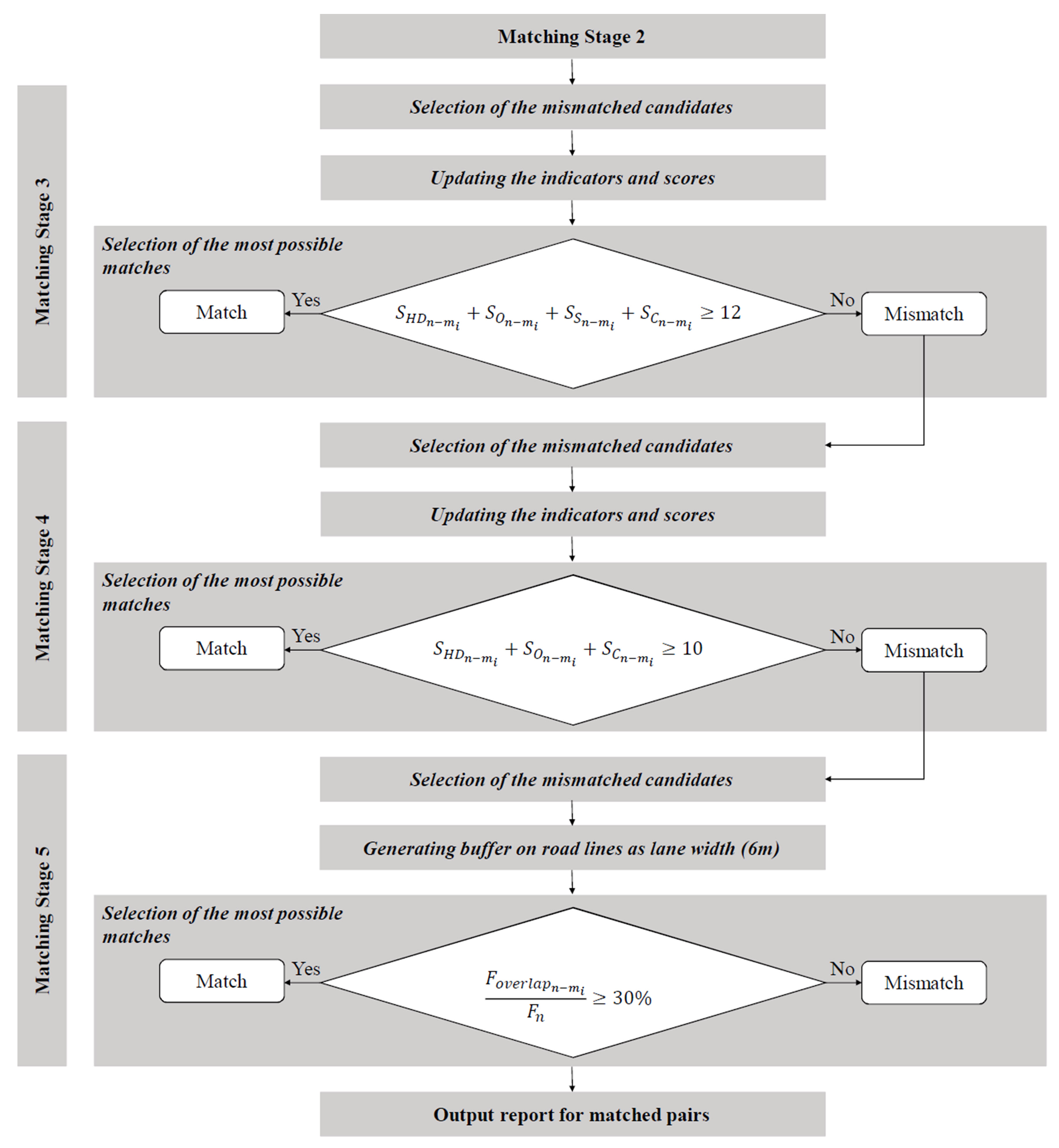
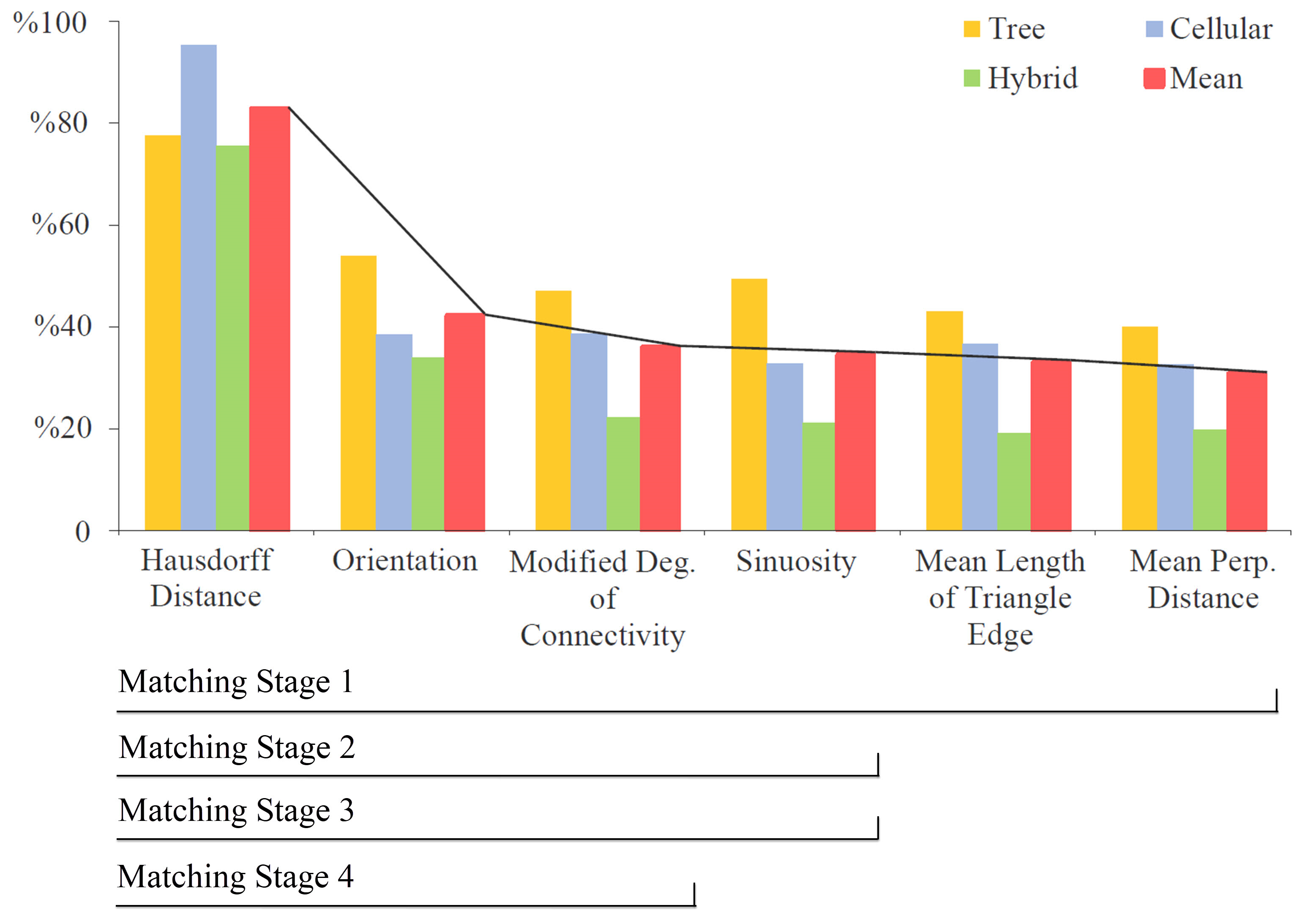
2.3.2. The Stages of the Approach
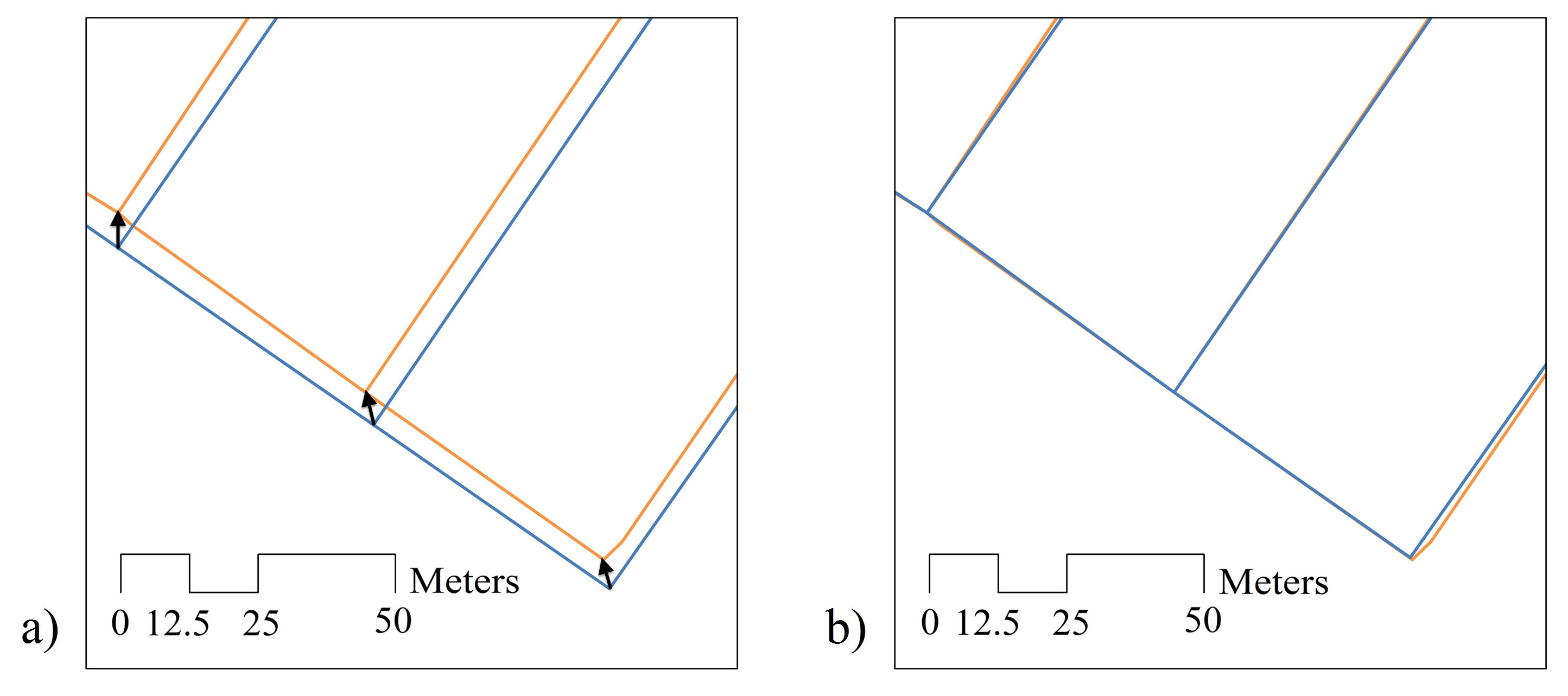
3. Results of the Experimental Testing
4. Evaluation of the Results
Experimental Results and Evaluation on Large Datasets
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lynch, M.; Saalfeld, A. Conflation: Automated map compilation—A video game approach. In Proceedings of the Autocarto 7, Washington, DC, USA, 11–14 March 1985; pp. 343–352. [Google Scholar]
- Rosen, B.; Saalfeld, A. Match criteria for automatic alignment. In Proceedings of the Autocarto 7, Washington, DC, USA, 11–14 March 1985; pp. 1–20. [Google Scholar]
- Lupien, A.; Moreland, W. A general approach to map conflation. In Proceedings of the Autocarto 8, Baltimore, MD, USA, 29 March–3 April 1987; pp. 630–639. [Google Scholar]
- Saalfeld, A. Conflation automated map compilation. Int. J. Geogr. Inf. Syst. 1988, 2, 217–228. [Google Scholar] [CrossRef]
- Cobb, M.A.; Chung, M.J.; Foley, H., III; Petry, F.E.; Shaw, K.B.; Miller, H.V. A rule-based approach for the conflation of attributed vector data. GeoInformatica 1998, 2, 7–35. [Google Scholar] [CrossRef]
- Ruiz-Lendinez, J.J.; Ariza-López, F.J.; Ureña-Cámara, M.A.; Blázquez, E. Digital Map Conflation: A Review of the Process and a Proposal for Classification. Int. J. Geogr. Inf. Sci. 2011, 25, 1439–1466. [Google Scholar] [CrossRef]
- Yuan, S.; Tao, C. Development of conflation components. In Proceedings of the Geoinformatics’99 Conference, Ann Arbor, MI, USA, 19–21 June 1999; pp. 1–13. [Google Scholar]
- Samal, A.; Seth, S.; Cueto, K. A feature-based approach to conflation of geospatial sources. Int. J. Geogr. Inf. Sci. 2004, 18, 459–489. [Google Scholar] [CrossRef]
- Kim, J.O.; Yu, K.; Heo, J.; Lee, W.H. A new method for matching objects in two different geospatial datasets based on the geographic context. Comput. Geosci. 2010, 36, 1115–1122. [Google Scholar] [CrossRef]
- Neis, P.; Zipf, A. Analyzing the Contributor Activity of a Volunteered Geographic Information Project—The Case of OpenStreetMap. ISPRS Int. J. Geo-Inf. 2012, 1, 146–165. [Google Scholar] [CrossRef]
- Koukoletsos, T.; Haklay, M.; Ellul, C. Assessing data completeness of VGI through an automated matching procedure for linear data. Trans. GIS 2012, 16, 477–498. [Google Scholar] [CrossRef]
- Corcoran, P.; Mooney, P.; Bertolotto, M. Analysing the growth of OpenStreetMap networks. Spat. Stat. 2013, 3, 21–32. [Google Scholar] [CrossRef]
- Zhao, P.; Jia, T.; Qin, K.; Shan, J.; Jiao, C. Statistical analysis on the evolution of OpenStreetMap road networks in Beijing. Physica A 2015, 420, 59–72. [Google Scholar] [CrossRef]
- Hacar, M.; Kılıç, B.; Şahbaz, K. Analyzing OpenStreetMap Road Data and Characterizing the Behavior of Contributors in Ankara, Turkey. ISPRS Int. J. Geo-Inf. 2018, 7, 400. [Google Scholar] [CrossRef]
- Doytsher, Y.; Filin, S.; Ezra, E. Transformation of datasets in a linear-based map conflation framework. Surv. Land Inf. Syst. 2001, 61, 159–169. [Google Scholar]
- Xiong, D.; Sperling, J. Semiautomated matching for network database integration. ISPRS J. Photogramm. 2004, 59, 35–46. [Google Scholar] [CrossRef]
- Haunert, J.H. Link based conflation of geographic datasets. In Proceedings of the 8th ICA Workshop on Generalisation and Multiple Representation, Coruña, Spain, 7–8 July 2005. [Google Scholar]
- Volz, S. An iterative approach for matching multiple representations of street data. In Proceedings of the ISPRS Workshop on Multiple Representation and Interoperability of Spatial Data, Hannover, Germany, 22–24 February 2006; pp. 101–110. [Google Scholar]
- Zhang, M.; Meng, L. An iterative road-matching approach for the integration of postal data. Comput. Environ. Urban 2007, 31, 597–615. [Google Scholar] [CrossRef]
- Mustière, S.; Devogele, T. Matching networks with different levels of detail. GeoInformatica 2008, 12, 435–453. [Google Scholar] [CrossRef]
- Li, L.; Goodchild, M.F. An optimisation model for linear feature matching in geographical data conflation. Int. J. Image Data 2011, 2, 309–328. [Google Scholar] [CrossRef]
- López-Vázquez, C.; Manso Callejo, M.A. Point-and curve-based geometric conflation. Int. J. Geogr. Inf. Sci. 2013, 27, 192–207. [Google Scholar] [CrossRef]
- Kang, B.; Scully, J.Y.; Stewart, O.; Hurvitz, P.M.; Moudon, A.V. Split-match-aggregate (SMA) algorithm: Integrating sidewalk data with transportation network data in GIS. Int. J. Geogr. Inf. Sci. 2015, 29, 440–453. [Google Scholar] [CrossRef]
- Foley, H.; Petry, F. Fuzzy knowledge-based system for performing conflation in geographical information systems. In Intelligent Problem Solving. Methodologies and Approaches; Logananthara, R., Palm, G., Ali, M., Eds.; IEA/AIE 2000; Lecture Notes in Computer Science; Springer: Heidelberg, Berlin, 2000; Volume 1821, pp. 260–269. [Google Scholar]
- Rahimi, S.; Cobb, M.; Ali, D.; Paprzycki, M.; Petry, F. A knowledge-based multi-agent system for geospatial data conflation. J. Geogr. Inf. Decis. Anal. 2002, 6, 67–81. [Google Scholar]
- Walter, V.; Fritsch, D. Matching spatial data sets: A statistical approach. Int. J. Geogr. Inf. Sci. 1999, 13, 445–473. [Google Scholar] [CrossRef]
- Yang, B.; Luan, X.; Zhang, Y. A pattern-based approach for matching nodes in heterogeneous urban road networks. Trans. GIS 2014, 18, 718–739. [Google Scholar] [CrossRef]
- Pourabdollah, A.; Morley, J.; Feldman, S.; Jackson, M. Towards an authoritative OpenStreetMap: Conflating OSM and OS OpenData national maps’ road network. ISPRS Int. J. Geo-Inf. 2013, 2, 704–728. [Google Scholar] [CrossRef]
- Fan, H.; Yang, B.; Zipf, A.; Rousell, A. A polygon-based approach for matching OpenStreetMap road networks with regional transit authority data. Int. J. Geogr. Inf. Sci. 2016, 30, 748–764. [Google Scholar] [CrossRef]
- Marshall, S. Streets and Patterns; Routledge: London, UK, 2005. [Google Scholar]
- Hausdorff, F. Dimension und äußeres Maß. Mathematische Annalen 1918, 79, 157–179. [Google Scholar] [CrossRef]
- Mueller, J.E. An introduction to the hydraulic and topographic sinuosity indexes. Ann. Assoc. Am. Geogr. 1968, 58, 371–385. [Google Scholar] [CrossRef]
- Haynes, R.; Jones, A.; Kennedy, V.; Harvey, I.; Jewell, T. District variations in road curvature in England and Wales and their association with road-traffic crashes. Environ. Plan. A 2007, 39, 1222–1237. [Google Scholar] [CrossRef]
- Transport Infrastructure. National Road Network Sinuosity Index: Ireland. 2018. Available online: https://data.gov.ie/dataset/national-road-network-sinuosity-index (accessed on 31 December 2018).
- Hacar, M.; Gökgöz, T. Usage of Variance in Determination of Sinuosity Intervals for Road Matching. SUJEST 2018, 6, 779–786. [Google Scholar] [CrossRef]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartogr. Int. J. Geogr. Inf. Geovisualization 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Jones, C.B.; Ware, J.M. Proximity search with a triangulated spatial model. Comput. J. 1998, 41, 71–83. [Google Scholar] [CrossRef]
- Song, W.; Keller, J.M.; Haithcoat, T.L.; Davis, C.H. Relaxation-based point feature matching for vector map conflation. Trans. GIS 2011, 15, 43–60. [Google Scholar] [CrossRef]

| Orientation Interval | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 |
| Sinuosity Index | Intervals |
|---|---|
| Low | <1.0001 |
| Mid | ≥1.0001 and < |
| High | ≥ |
| Control Points | ||
|---|---|---|
| Tree | 1.06612 | 41 |
| Cellular | 1.02218 | 49 |
| Hybrid | 1.11479 | 66 |
| Tree | Cellular | Hybrid | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Cor. 1 | Incor. 2 | Mis. 3 | Cor. | Incor. | Mis. | Cor. | Incor. | Mis. | |
| Manual matching | 116 | - | - | 150 | - | - | 262 | - | - |
| Matching Stage 1 | 42 | - | 74 | 65 | - | 85 | 64 | 2 | 196 |
| Matching Stage 2 | 22 | 2 | 50 | 68 | - | 17 | 66 | 1 | 129 |
| Matching Stage 3 | 12 | 2 | 36 | 9 | - | 8 | 26 | 6 | 97 |
| Matching Stage 4 | 6 | 1 | 29 | 1 | - | 7 | 20 | 9 | 68 |
| Matching Stage 5 | 15 | - | 14 | 4 | - | 3 | 36 | 1 | 31 |
| Final | 97 | 5 | 14 | 147 | - | 3 | 212 | 19 | 31 |
| Tree | Cellular | Hybrid | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Prec. 4 (%) | Rec. 5 (%) | F-val. 6 (%) | Prec. (%) | Rec. (%) | F-val. (%) | Prec. (%) | Rec. (%) | F-val. (%) | |
| Matching Stage 1 | 100 | - | - | 100 | - | - | 97.0 | - | - |
| Matching Stage 2 | 91.7 | - | - | 100 | - | - | 98.5 | - | - |
| Matching Stage 3 | 85.7 | - | - | 100 | - | - | 81.3 | - | - |
| Matching Stage 4 | 85.7 | - | - | 100 | - | - | 69.0 | - | - |
| Matching Stage 5 | 100 | - | - | 100 | - | - | 97.3 | - | - |
| Final | 95.1 | 87.4 | 91.1 | 100 | 98.0 | 99.0 | 91.8 | 87.2 | 89.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hacar, M.; Gökgöz, T. A New, Score-Based Multi-Stage Matching Approach for Road Network Conflation in Different Road Patterns. ISPRS Int. J. Geo-Inf. 2019, 8, 81. https://doi.org/10.3390/ijgi8020081
Hacar M, Gökgöz T. A New, Score-Based Multi-Stage Matching Approach for Road Network Conflation in Different Road Patterns. ISPRS International Journal of Geo-Information. 2019; 8(2):81. https://doi.org/10.3390/ijgi8020081
Chicago/Turabian StyleHacar, Müslüm, and Türkay Gökgöz. 2019. "A New, Score-Based Multi-Stage Matching Approach for Road Network Conflation in Different Road Patterns" ISPRS International Journal of Geo-Information 8, no. 2: 81. https://doi.org/10.3390/ijgi8020081
APA StyleHacar, M., & Gökgöz, T. (2019). A New, Score-Based Multi-Stage Matching Approach for Road Network Conflation in Different Road Patterns. ISPRS International Journal of Geo-Information, 8(2), 81. https://doi.org/10.3390/ijgi8020081






