Shoreline Detection using Optical Remote Sensing: A Review
Abstract
1. Introduction
2. Coastline Indicators
3. Pre-Processing
4. Land-Sea Segmentation
- the edge detection approaches, which treat the extraction of shoreline as an edge detection problem;
- the band thresholding methods, in which a thresholding value is selected either by man-machine interaction or by a local adaptive strategy;
- the classification approaches, which aim to separate the image into land and water components, and then take the boundary line between them as the shoreline.
4.1. Thesholding
4.2. Classification
4.2.1. Pixel-Based Classification
4.2.2. Object-Based Classification
4.3. Morphological Segmentation
5. Edge Detection
6. Discussion
7. Conclusions
Funding
Conflicts of Interest
References
- De Ruiter, A.; Bertacchini, Y. l’intelligence territoriale: l’eau, un enjeu fédérateur dans l’émergence du pole «mer» en région Paca? 4e Tic & Territoire: Quels développements? Journée sur les systèmes d’information élaborée, ile Rouss. 2005. Available online: http://isdm.univ-tln.fr/PDF/isdm22/isdm22_ruiter.pdf (accessed on 20 October 2017).
- Dolan, R.; Hayden, B.P.; May, P.; May, S.K. The reliability of shoreline change measurements from aerial photo-graphs. Shore Beach 1980, 48, 22–29. [Google Scholar]
- Bird, E.C.F. Coastline Changes: A Global Review; John Wiley and Sons: Hoboken, NJ, USA, 1985; p. 219. [Google Scholar]
- Davidson-Arnott, R. An Introduction to Coastal Processes and Geomorphology; Cambridge University Press: Cambridge, UK, 2010; p. 442. [Google Scholar]
- CMRC. Methodology for Coastal Monitoring Programme at Portrane; Technical Report for Fingal County Council; Rush Beaches, Co.: Dublin, Ireland, 2009. [Google Scholar]
- Mallet, C.; Michot, A.; de De La Torre, Y.; Lafon, V.; Robin, M.; Prevoteaux, B. Synthèse de référence des techniques de suivi du trait de côte. 2012. Available online: http://infoterre.brgm.fr/rapports/RP-60616-FR.pdf (accessed on 15 September 2017).
- NOAA. What Is Remote Sensing? National Ocean Service Website. Available online: https://oceanservice.noaa.gov/facts/remotesensing.html (accessed on 7 June 2017).
- Boak, E.H.; Turner, I.L. Shoreline Definition and Detection: A Review. J. Coast. Res. 2005, 21, 688–703. [Google Scholar] [CrossRef]
- Faye, B.N. Dynamique du trait de côte sur les littoraux sableux de la Mauritanie à la Guinée-Bissau (Afrique de l’Ouest): Approches régionale et locale par photo-interprétation, traitement d’images et analyse de cartes anciennes, These de l’universite de Bretagne occidentale. soutenue le 15 février 2010. Available online: https://tel.archives-ouvertes.fr/tel-00472200/PDF/DYNAMIQUE-DU-TRAIT-DE-COTE-EN-AFRIQUE-DE-L_OUEST-MAURITANIE-GUINEE-BISSAU-VOLUME1.pdf (accessed on 5 January 2015).
- Sorensen, R.M. Basic Coastal Engineering, 3rd ed.; Springer Science + Business Media: New York, NY, USA, 2006. [Google Scholar]
- Firoozfar, A.; Neshaei, M.A.L.; Dykes, A. Beach Profiles and Sediments, a Case of Caspian Sea. Int. J. Mar. Sci. 2014, 4, 1–9. [Google Scholar]
- Baiocchi, V.; Brigante, R.; Radicioni, F.; Dominicin, D. Détermination de la ligne de côte par des images multi-spectrales haute résolution. Géomatique Expert—N° 86—Mai-Juin 2012. Available online: http://www.geomag.fr/sites/default/files/pdf/geo86_pp28-35_topo-traitsdecote.pdf (accessed on 7 April 2017).
- Lentz, E.E.; Hapke, C.J. Geologic Framework Influences on the geomorphology of an anthropogenically modified barrier island: Assessment of dune/beach changes at Fire Island, New York. Geomorphology 2011, 126, 82–96. [Google Scholar] [CrossRef]
- Young, A.P.; Guza, R.T.; Dickson, M.E.; O’Reilly, W.C.; Flick, R.E. Ground motions on rocky, cliffed, and sandy shorelines generated by ocean waves. J. Geophys. Res. Oceans 2013, 18, 2169–9275. [Google Scholar] [CrossRef]
- Barone, D.A.; Mckenna, K.K.; Farrell, S.C.; Sandy, H. Beach-dune performance at New Jersey Beach Profile Network sites. Shore Beach 2014, 82, 13–23. [Google Scholar]
- Dissanayake, P.; Brown, J.; Wisse, P.; Karunarathna, H. Comparison of storm cluster vs isolated event impacts on beach/dune morphodynamics. Estuar. Coast. Shelf Sci. 2015, 164, 301–312. [Google Scholar] [CrossRef]
- Keijsers, J.G.; Giardino, A.; Poortinga, A.; Mulder, J.P.; Riksen, M.J.; Santinelli, G. Adaptation strategies to maintain dunes as flexible coastal flood defense in The Netherlands. Mitig. Adapt. Strateg. Glob. Chang. 2010, 20, 913–928. [Google Scholar] [CrossRef]
- Wernette, P.; Houser, C.; Bishop, M.P. An automated approach for extracting Barrier Island morphology from digital elevation models. Geomorphology 2016, 262, 1–7. [Google Scholar] [CrossRef]
- Pye, K.; Blot, S.J. Assessment of beach and dune erosion and accretion using lidar: Impact of the stormy 2013–14 winter and longer term trends on the Sefton Coast, UK. Geomorphology 2016, 266, 146–167. [Google Scholar] [CrossRef]
- Thornton, E.B.; Sallenger, A.; Sesto, J.C.; Egley, L.; Mcgee, T.; Parsons, R. Sand mining impacts on long-term dune erosion in southern Monterey Bay. Mar. Geol. 2006, 229, 45–58. [Google Scholar] [CrossRef]
- Palmsten, M.L.; Holman, R.A. Laboratory investigation of dune erosion using stereo video. Coast. Eng. 2006, 60, 123–135. [Google Scholar] [CrossRef]
- Pajak, M.J.; Leatherman, S. The high water line as shoreline indicator. J. Coast. Res. 2002, 18, 329–337. [Google Scholar]
- Zuzek, P.J.; Nairn, R.B.; Thieme, S. Spatial and temporal considerations for calculating shoreline change rates in the Great Lakes basin. J. Coast. Res. 2003, 38, 125–146. [Google Scholar]
- Stockdon, H.F.; Doran, K.S.; Sallenger, A.H. Extraction of lidar based dune crest elevations for use in examining the vulnerability of beaches to inundation during hurricanes. Coast. Res. 2009, 25, 59–65. [Google Scholar] [CrossRef]
- Hapke, C.J.; Reid, D. National Assessment of Shoreline Change, Part 4: Historical Coastal Cliff Retreat along the California Coast; Open-file Report; U.S. Geological Survey: Washington, DC, USA, 2007; 51p.
- Isla, F.I.; Cortizoc, L.C. Sediment input from fluvial sources and cliff erosion to the continental shelf of Argentina. J. Integr. Coast. Zone Manag. 2014, 14, 541–552. [Google Scholar] [CrossRef]
- Kuhn, D.; Prüfer, S. Coastal cliff monitoring and analysis of mass wasting processes with the application of terrestrial laser scanning: A case study of Rügen, Germany. Geomorphology 2014, 213, 153–165. [Google Scholar] [CrossRef]
- Erikson, L.; O’Neill, A. Patrick Barnard, Sean Vitousek, Patrick Limber, Climate Change-Driven Cliff and Beach Evolution at Decadal to Centennial Time Scales; Paper No. 210; Coastal Dynamics 2017: Helsingør, Danmark.
- Young, A.P. Decadal-scale coastal cliff retreat in southern and central California. Geomorphology 2018, 300, 164–175. [Google Scholar] [CrossRef]
- Le Berre, I.; Henaff, A.; Devogele, T.; Mascret, A.; Wenzel, F. Spot 5: Un outil pertinent pour le suivi du trait de côte? Norois 2005, 196, 23–35. [Google Scholar] [CrossRef]
- Tsuguo, S. Rocky coast processes: With special reference to the recession of soft rock cliffs. Proc. Jpn. Acad. Ser. B 2015, 91, 481–500. [Google Scholar]
- Davidson-.Arnott, R. Erosion of Cohesive Bluff Shorelines A discussion paper on processes controlling erosion and recession of cohesive shorelines with particular reference to the Ausable Bayfield Conservation Authority (ABCA) shoreline north of Grand Bend. 2016. Available online: https://www.abca.on.ca/downloads/Discussion-Paper-on-Erosion-of-Cohesive-Bluff-Shorelines-FINAL.pdf (accessed on 3 August 2018).
- Young, A.P.; Guza, R.T.; Dickson, M.E.; O’Reilly, W.C.; Flick, R.E. Observations of coastal cliff base waves, sand levels, and cliff top shaking. Earth Surf. Process. Landf. 2016, 41, 1564–1573. [Google Scholar] [CrossRef]
- Priest, G.R. Coastal shoreline change study northern and central Lincoln county, Oregon. J. Coast. Res. 1999, 28, 140–157. [Google Scholar]
- Bonnot-Courtois, C.; Levasseur, J.E. Reconnaissance de la Limite Terrestre du Domaine Maritime. Intérêt et Potentialités de Critàres Morpho-Sédimentaires et Botaniques; Rapport Ministàre de l’équipement CETMEF/Rivages: France, 2002; 160p. [Google Scholar]
- Bonnot-Courtois, C.; Levasseur, J.E. Recherche d’indicateurs “naturalistes” de la limite supérieure du domaine maritime. Cah. Nantais 2003, 59, 47–56. [Google Scholar]
- Robin, M. Télédétection et modélisation du trait de côte et de sa cinématique. In Le Littoral, Regards, Pratiques et Savoirs; Baron-Yelles, N., Goeldner-Gionella, L., Velut, S., Eds.; Etudes Offertes à Fernand Verger Edition Rue d’Ulm; Presses Universitaires de l’Ecole Normale Supérieure: Paris, France, 2002; pp. 95–115. [Google Scholar]
- Morton, R.A.; Speed, M.F. Evaluation of shorelines and legal boundaries controlled by water levels on sandy beaches. J. Coast. Res. 1998, 14, 1373–1384. [Google Scholar]
- Coyne, M.A.; Fletcher, C.H.; Richmond, B.M. Mapping coastal erosion hazard areas in Hawaii: Observations and errors. J. Coast. Res. 1999, 28, 171–184. [Google Scholar]
- Moore, L.J.; Benumof, B.J.; Griggs, G.B. Coastal erosion hazards in Santa Cruz and San Diego. J. Coast. Res. 1999, 28, 121–130. [Google Scholar]
- Guy, D.E. Erosion hazard area mapping, Lake County, Ohio. J. Coast. Res. 1999, 28, 185–196. [Google Scholar]
- Natesan, U.; Subramanian, S.P. Identification of Erosion-Accretion regimes along the Tamilnadu coast, India. J. Coast. Res. 1994, 10, 203–205. [Google Scholar]
- Kraus, N.C.; Rosati, J.D. Interpretation of shoreline–Position data for coastal engineering analysis. Coastal Engineering Technical Note, CETN II-39 (12/97). 1997. Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/a591274.pdf (accessed on 8 August 2018).
- Morton, R.A.; Mckenna, K.K. Analysis and projection of erosion hazard areas in Brazoria and Galveston counties, Texas. J. Coast. Res. 1999, 28, 106–120. [Google Scholar]
- Pandian, P.K.; Ramesh, S.; Murthy, M.V.R.; Ramachandran, S.; Thayumanavan, S. Shoreline changes and near shore processes along Ennore Coast, East Coast of South India. J. Coast. Res. 2004, 20, 828–845. [Google Scholar] [CrossRef]
- Norcross, Z.M.; Fletcher, C.H.; Merrifield, M. Annual and interannual changes on a reef-fringed pocket beach: Kailua Bay, Hawaii. Mar. Geol. 2002, 190, 553–580. [Google Scholar] [CrossRef]
- Fletcher, C.H.; Rooney, J.J.; Barbee, M.; Lim, S.C.; Richmond, B. Mapping shoreline change using digital orthophotogrammetry on Maui, Hawaii. J. Coast. Res. 2003, 38, 106–124. [Google Scholar]
- Genz, A.S.; Fletcher, C.H.; Dunn, R.A.; Frazer, L.N.; Rooney, J.J. The predictive accuracy of shoreline rate methods and alongshore beach variation on Maui, Hawaii. J. Coast. Res. 2007, 23, 87–105. [Google Scholar] [CrossRef]
- Leatherman, S. Shoreline change mapping and management along the US East Coast. J. Coast. Res. 2003, 38, 5–13. [Google Scholar]
- O’connel, J.F. The art and science of mapping and interpreting shoreline change data: The Massachusetts experience. In Proceedings of the 13th Biennial Coastal Zone Conference, Baltimore, MD, USA, 13–17 July 2003; 6p. [Google Scholar]
- Dehouck, A. Morphodynamique des Plages Sableuses de la mer d’Iroise (Finistàre). Ph.D. Thesis, Université de Bretagne Occidentale, Brest, France, 2006; 262p. [Google Scholar]
- Ferreira, O.; Garcia, T.; Matias, A.; Tabordac, R.; Dias, J.A. An Integrated Method For The Determination Of Set-Back Lines For Coastal Erosion Hazards On Sandy Shores. Cont. Shelf Res. 2006, 26, 1030–1044. [Google Scholar] [CrossRef]
- Morton, R.A.; Paine, J.G. Beach and Vegetation-Line Changes at Galveston Island, Texas: Erosion, Deposition, And Recovery from Hurricane Alicia. Geol. Circ. 1985, 85, 39. [Google Scholar]
- Paine, J.G.; Morton, R.A. Shoreline and Vegetation-Line Movement, Texas Gulf Coast, 1974 To 1982. Geol. Circ. 1989, 89, 50. [Google Scholar]
- Trepanier, I.; Dubois, J.M.M.; Bonn, F. Suivi de l’évolution du trait de côte à partir d’images HRV (XS) de SPOT: Application au delta du fleuve rouge, Viêtnam. Int. J. Remote Sens. 2002, 23, 917–937. [Google Scholar] [CrossRef]
- Thieler, E.R.; O’connel, J.F.; Schupp, C.A. The Massachusetts Shoreline Change Project: 1800s To 1994; Technical Report; USGS: Woods Hole, MA, USA, 2001; 39p.
- Foody, G.M.; Muslim, A.M.; Atkinson, P.M. Super-Resolution Mapping of The Waterline From Remotely Sensed Data. Int. J. Remote Sens. 2005, 26, 5381–5392. [Google Scholar] [CrossRef]
- Gopinath, G.; Seralathan, P. Rapid Erosion of The Coast of Sagar Island, West Bengal-India. Environ. Geol. 2005, 48, 1058–1067. [Google Scholar] [CrossRef]
- Guariglia, A.; Buonamassa, A.; Losurdo, A.; Saladino, R.; Trivigno, M.L.; Zaccagnino, A.; Colangelo, A. A Multisource Approach for Coastline Mapping and Identification of Shoreline Changes. Ann. Geophys. 2006, 41, 295–304. [Google Scholar]
- Muslim, A.M.; Foody, G.M.; Atkinson, P.M. Localized Soft Classification for Super Resolution Mapping of The Shoreline. Int. J. Remote Sens. 2006, 27, 2271–2285. [Google Scholar] [CrossRef]
- Muslim, A.M.; Foody, G.M.; Atkinson, P.M. Shoreline Mapping from Coarse-Spatial Resolution Remote Sensing Imagery of Seberang Takir, Malaysia. J. Coast. Res. 2007, 23, 1399–1408. [Google Scholar] [CrossRef]
- Ruiz, L.A.; Pardo, J.E.; Almonacid, J.; RodríGuez, B. Coastline Automated Detection and Multiresolution Evaluation Using Satellite Images. In Proceedings of the Coastal Zone 07, Portland, OR, USA, 22–26 July 2007; 5p. [Google Scholar]
- Ekercin, S. Coastline Change Assessment at The Aegean Sea Coasts in Turkey Using Multitemporal Landsat Imagery. J. Coast. Res. 2007, 23, 691–698. [Google Scholar] [CrossRef]
- Hoeke, R.K.; Zarillo, G.A.; Synder, M. A Gis Based Tool for Extracting Shoreline Positions From Aerial Imagery (Beachtools); Coastal and Hydraulics Engineering Technical Note Chetn-Iv-37; U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 2001; 12p. [Google Scholar]
- Robertson, W.; Whitman, D.; Zhang, Z.; Leatherman, S.P. Mapping Shoreline Position Using Airborne Laser Altimetry. J. Coast. Res. 2004, 20, 884–892. [Google Scholar] [CrossRef]
- Zhang, K.; Huang, W.; Douglas, B.C.; Leatherman, S.P. Shoreline Position Variability and Long Term Trend Analysis. Shore Beach 2002, 70, 31–35. [Google Scholar]
- Makota, V.; Sallema, R.; Mahika, C. Monitoring Shoreline Change Using Remote Sensing And Gis: A Case Study Of Kunduchi Area, Tanzania. West. Indian Ocean J. Mar. Sci. 2004, 3, 1–10. [Google Scholar]
- Zhang, K.; Douglas, B.C.; Leatherman, S.P. Global Warming and Coastal Erosion. Clim. Chang. 2004, 64, 41–58. [Google Scholar] [CrossRef]
- Moore, L.J.; Ruggiero, P.; List, J.H. Comparing Mean High Water and High Water Line Shorelines: Should Proxy-Datum Offsets Be Incorporated Into Shoreline Change Analysis? J. Coast. Res. 2006, 22, 894–905. [Google Scholar] [CrossRef]
- Romagnoli, C.; Mancini, C.; Brunelli, R. Historical Shoreline Changes At An Active Island Volcano: Stromboli, Italy. J. Coast. Res. 2006, 22, 739–749. [Google Scholar] [CrossRef]
- Ruggiero, P.; Kaminsky, G.M.; Gelfenbaum, G. Linking Proxy-Based and Datum-Based Shorelines on A High-Energy Coastline: Implications for Shoreline Change Analyses. J. Coast. Res. 2006, 38, 57–82. [Google Scholar]
- Langley, S.K.; Alexander, C.R.; Bush, D.M.; Jackson, C.W. Modernizing Shoreline Change Analysis in Georgia Using Topographic Survey Sheets in A Gis Environment. J. Coast. Res. 2003, 38, 168–177. [Google Scholar]
- Chang, J.; Liu, G.; Huang, C.; Xu, L. Remote Sensing Monitoring On Coastline Evolution In The Yellow River Delta Since 1976. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Seoul, Korea, 29 July 2005; Volume 3, pp. 2161–2164. [Google Scholar]
- Horikawa, K. (Ed.) Nearshore Dynamics and Coastal Processes. Theory, Measurement and Predictive Model; University of Tokyo Press: Tokyo, Japan, 1988; 522p. [Google Scholar]
- Aagaard, T.; Davidson-Arnott, R.; Greenwood, B.; Nielsen, J. Sediment Supply from Shoreface To Dunes: Linking Sediment Transport Measurements and Long-Term Morphological Evolution. Geomorphology 2004, 60, 205–224. [Google Scholar] [CrossRef]
- Morton, R.A.; Miller, T.L. National Assessment of Shoreline Change: Part 2. Historical Shoreline Changes and Associated Coastal Land Loss along The, U.S. Southeast Atlantic Coast; Open-File Report 2005-1401; U.S. Geological Survey: Washington, DC, USA, 2005; 35p.
- Hapke, C.J.; Reid, D.; Richmond, B.M.; Ruggiero, P.; List, J. National Assessment of Shoreline Change Part 3: Historical Shoreline Change and Associated Coastal Land Loss along Sandy Shorelines of the California Coast; U.S. Geological Survey: Washington, DC, USA, 2006; 72p.
- Liu, H.; Sherman, D.; Gu, G. Automated extraction of shorelines from airborne light detection and ranging data and accuracy assessment based on Monte Carlo simulation. J. Coast. Res. 2007, 23, 1359–1369. [Google Scholar] [CrossRef]
- Farris, A.S.; List, J.H. Shoreline change as a Proxy for subaerial beach volume change. J. Coast. Res. 2007, 23, 740–748. [Google Scholar] [CrossRef]
- Miller, J.K.; Dean, R.G. Shoreline variability via empirical orthogonal function analysis: Part I temporal and spatial characteristics. Coast. Eng. 2007, 54, 111–131. [Google Scholar] [CrossRef]
- Stive, M.J.F.; Aarninkhof, S.G.J.; Hamm, L.; Hanson, H.; Larson, M.; Wijnberg, K.M.; Nicholls, R.J.; Capobianco, M. Variability of shore and shoreline evolution. Coast. Eng. 2002, 47, 211–255. [Google Scholar] [CrossRef]
- Reeve, D.E.; Spivack, M. Evolution of shoreline position moments. Coast. Eng. 2004, 51, 661–673. [Google Scholar] [CrossRef]
- Allan, J.C.; Komar, P.D.; Priest, G.R. Shoreline variability on the high-energy Oregon coast and its usefulness in erosion-hazard assessments. J. Coast. Res. 2003, 38, 83–105. [Google Scholar]
- Reeve, D.E.; Fleming, C.A. A statistical-dynamical method for predicting long term coastal evolution. Coast. Eng. 1997, 30, 259–280. [Google Scholar] [CrossRef]
- Aurrocoechea, I.; Pethick, J.S. The coastline, its physical and legal definition. Int. J. Coast. Estuar. Law 1986, 1, 29–42. [Google Scholar] [CrossRef]
- Lafon, V.; Froidefond, J.-M.; Castaing, P. Méthode d’analyse de l’évolution morphodynamique d’une embouchure tidale par imagerie satellite. Exemple du bassin d’Arcachon (France). Comptes Rendus Académie des Sciences Paris. Series IIA- Earth and Planetary Science 2000, 331, 373–378. [Google Scholar]
- Lafon, V.; Dupuis, H.; Howa, H.; Froidefond, J.-M. Mesure du déplacement des barres et baïnes parallèlement au trait de côte à l’aide de l’imagerie spatiale Spot. Oceanol. Acta 2002, 25, 149–158. [Google Scholar] [CrossRef]
- Plant, N.G.; Holman, R.A. Intertidal beach profile estimation using video images. Mar. Geol. 1997, 140, 1–24. [Google Scholar] [CrossRef]
- Plant, N.G.; Aarninkhof, S.G.J.; Turner, I.L.; Kingston, K.S. The performance of shoreline detection models applied to video imagery. J. Coast. Res. 2007, 23, 658–670. [Google Scholar] [CrossRef]
- Aarninkhof, S.G.J. Nearshore Bathymetry Derived from Video Imagery. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2003; 175p. [Google Scholar]
- Robin, M. Cinématique d’un littoral par squelettisation de formes. Photo-Interprétation 1990, 29, 65–67. [Google Scholar]
- Anfuso, G.; Martinez Del Pozo, J.A. Towards management of coastal erosion problems and human structure impacts using GIS tools: Case study in Ragusa Province, Southern Sicily, Italy. Environ. Geol. 2005, 48, 646–659. [Google Scholar] [CrossRef]
- Kochel, R.C.; Kahn, J.H.; Dolan, R.; Hayden, B.P.; May, P.F.U.S. Mid-Atlantic Barrier Island Geomorphology. J. Coast. Res. 1985, 1, 1–9. [Google Scholar]
- Dolan, R.; Hayden, B. Patterns and Prediction of Shoreline Change. In CRC Handbook of Coastal Processes and Erosion; Komar, P.D., Ed.; CRC Series in Marine Science; CRC Press: Boca Raton, FL, USA, 1983; pp. 123–149. [Google Scholar]
- Pinot, P. Vocabulaire de Géomorphologie; Document, Électronique; Institut Océanographique: Paris, France, 2001; Available online: www.oceano.org/io/voca (accessed on 2 March 2016).
- Parker, B. The difficulties in measuring a consistently defined shoreline–The problem of vertical referencing. J. Coast. Res. 2003, 38, 44–56. [Google Scholar]
- Rees, W.G.; Satchell, M.J.F. The effect of median filtering on synthetic aperture radar images. Int. J. Remote Sens. 1997, 18, 2887–2893. [Google Scholar] [CrossRef]
- Liu, H.; Wang, L.; Sherman, D.J.; Wu, Q.; Su, H. Algorithmic Foundation and Software Tools for Extracting Shoreline Features from Remote Sensing Imagery and lidar Data. J. Geogr. Inf. Syst. 2011, 3, 99–119. [Google Scholar] [CrossRef]
- Tewari, K.; Tiwari, M.V. Efficient Removal of Impulse Noise in Digital Images. Int. J. Sci. Res. Publ. 2010, 2, 1–7. [Google Scholar]
- Lee, J.S. Speckle Suppression and Analysis for Synthetic Aperture Radar Images. Opt. Eng. 1986, 25, 255636. [Google Scholar] [CrossRef]
- Frost, V.S.; Stiles, J.A.; Shanmugan, K.S.; Holtzman, J.C. model for radar images and its application to adaptive digital filtering of multiplicative noise. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 4, 157–165. [Google Scholar] [CrossRef]
- Louati, M.; Zargouni, F. Évolution Du Trait De Côte Du Littoral Du Delta De Medjerda Par Imagerie Landsat Et Sig. 2012. Available online: http://www.geosp.net/wp-content/uploads/2013/07/Mourad-Louati-Fouad-Zargouni.pdf (accessed on 10 October 2017).
- Pardo-Pascual, J.E.; Almonacid-Caballer, J.; Ruiz, L.A.; Palomar-Vázquez, J. Automatic extraction of shorelines from Landsat TM and ETM+ multi-temporal images with subpixel precision. Remote Sens. Environ. 2012, 123, 1–11. [Google Scholar] [CrossRef]
- Chaaban, F. Apport potentiel des Systèmes d’Informations Géographiques (SIG) pour une meilleure gestion d’un littoral dans une optique de développement durable, approches conceptuelles et méthodologiques appliquées dans le Nord de la France. Ph.D. Thesis, Présentée Pour l’obtention du titre de Docteur de l’Université Lille Sciences et Technologies, Villeneuve-d’Ascq, France, 21 October 2011. [Google Scholar]
- Zhang, T.; Yang, X.; Xu, S.; Su, F. Extraction of Coastline in Aquaculture Coast from Multispectral Remote Sensing Images: Object-Based Region Growing Integrating Edge Detection. Remote Sens. 2013, 5, 4470–4487. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from grey scale histogram. IEEE Trans. Syst. Man Cyber. 1979, 1, 62–66. [Google Scholar] [CrossRef]
- Jishuang, Q.; Chao, W.C. A multi-threshold based morphological approach for extracting coastal line feature in remote sensed images, Pecora 15/Land Satellite Information IV/ISPRS Commission I/FIEOS 2002 Conference Proceedings. Available online: https://pdfs.semanticscholar.org/52f2/4efb7af14ac3ccfb00e1c130cd55ef70b983.pdf (accessed on 12 January 2017).
- Aedla, R.; Dwarakish, G.S.; Reddy, V.D. Automatic Shoreline Detection and Change Detection Analysis of Netravati-gurpurrivermouth Using Histogram Equalization and Adaptive Thresholding Techniques. Aquat. Procedia 2015, 4, 563–570. [Google Scholar] [CrossRef]
- Kuleli, T.; Guneroglu, A.; Karsli, F.; Dihkan, M. Automatic detection of shoreline change on coastal Ramsar wetlands of Turkey. Ocean Eng. 2011, 38, 1141–1149. [Google Scholar] [CrossRef]
- Liu, H.; Jezek, K.C. Automated extraction of coastline from satellite imagery by integrating Canny edge detection and locally adaptive thresholding methods. Int. J. Remote Sens. 2004, 25, 937–958. [Google Scholar] [CrossRef]
- Levenberg, K. A Method for the Solution of Certain Non-linear Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for the Least-Squares Estimation of Nonlinear Parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Zeng, R.; Wu, J.; Shao, Z.; Chen, Y.; Chen, B.; Senhadji, L.; Shu, H. Color image classification via quaternion principal component analysis network. Neurocomputing 2016, 216, 416–428. [Google Scholar] [CrossRef]
- García-Rubio, G.; Huntley, D.; Russell, P. Evaluating shoreline identification using optical satellite images. Mar. Geol. 2015, 359, 96–105. [Google Scholar] [CrossRef]
- Rasuly, A.; Naghdifarb, R.; Rasoli, M. Monitoring of Caspian Sea Coastline Changes Using Object-Oriented Techniques. International Society for Environmental Information Sciences 2010 Annual Conference. Procedia Environ. Sci. 2010, 2, 416–426. [Google Scholar] [CrossRef]
- Gao, B.-C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Mcfeeters, S.K. Using the Normalized Difference Water Index (NDWI) within a Geographic Information System to Detect Swimming Pools for Mosquito Abatement: A Practical Approach. Remote Sens. 2013, 5, 3544–3561. [Google Scholar] [CrossRef]
- Ozturk, D.; Sesli, F.A. Shoreline change analysis of the Kizilirmak Lagoon Series. Ocean Coast. Manag. 2015, 118, 90–308. [Google Scholar] [CrossRef]
- Sharma, R.C.; Tateishi, R.; Hara, K.; Nguyen, L.V. Developing Superfine Water Index (SWI) for Global Water Cover Mapping Using MODIS Data. Remote Sens. 2015, 7, 13807–13841. [Google Scholar] [CrossRef]
- Ghoneim, E.; Mashaly, J.; Gamble, D.; Halls, J.; Abubakr, M. Nile Delta exhibited a spatial reversal in the rates of shoreline retreat on the Rosetta promontory comparing pre- and post-beach protection. Geomorphology 2015, 228, 1–14. [Google Scholar] [CrossRef]
- Thao, P.T.P.; Duan, H.D.; To, D.V. Integrated Remote Sensing and Gis For Calculating Shoreline Change in Phan-Thiet Coastal Area. In Proceedings of the International Symposium on Geoinformatics for Spatial Infrastructure Development in Earth and Allied Sciences, Hanoi, Vietnam, 4–6 December 2008. [Google Scholar]
- Dewi, R.S.; Bijker, W.; Stein, A.; Marfai, M.A. Fuzzy Classification for Shoreline Change Monitoring in a Part of the Northern Coastal Area of Java, Indonesia. Remote Sens. 2016, 8, 190. [Google Scholar] [CrossRef]
- Masria, A.; Nadaoka, K.; Negm, A.; Iskander, M. Detection of Shoreline and Land Cover Changes around Rosetta Promontory, Egypt, Based on Remote Sensing Analysis. Land 2015, 4, 216–230. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, Q.; Xu, J. Coastline Extraction Using Support Vector Machine from Remote Sensing Image. J. Multimedia 2013, 8. [Google Scholar] [CrossRef]
- Tsekouras, G.E.; Trygonis, V.; Maniatopoulos, A.; Rigos, A.; Chatzipavlis, A.; Tsimikas, J.; Mitianoudi, N.; Velegrakis, A.F. A Hermite Neural Network Incorporating Artificial Bee Colony Optimization to Model Shoreline Realignment at a Reef-Fronted Beach. Neurocomputing 2018, 280, 32–45. [Google Scholar] [CrossRef]
- Kerh, T.; Lu, H.; Saunders, R. Shoreline Change Estimation from Survey Image Coordinates and Neural Network Approximation. Int. J. Civil Environ. Eng. 2014, 8, 381–386. [Google Scholar]
- Foody, G.M. Pattern Recognition and Classification of Remotely Sensed Images by Artificial Neural Networks. In Ecological Informatics; Springer: Berlin, Germany, 2006; pp. 459–477. [Google Scholar]
- Bayram, B.; Janpaule, I.; Avşar, Ö.; Oğurlu, M.; Bozkurt, S.; Reis, H.C.; Seker, D.Z. Shoreline Extraction and Change Detection using 1:5000 Scale Orthophoto Maps: A Case Study of Latvia-Riga. Int. J. Environ. Geoinform. 2015, 2, 1–6. [Google Scholar] [CrossRef]
- Bagli, S.; Soille, P. Automatic delineation of shoreline and lake boundaries from Landsat satellite images. In Proceedings of the initial ECO-IMAGINE GI and GIS for Integrated Coastal Management, Seville, Spain, 13–15 May 2004. [Google Scholar]
- Adams, R.; Bischof, L. Seeded region growing. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 641–647. [Google Scholar] [CrossRef]
- Mehnert, A.; Jackway, P. An improved seeded region growing algorithm. Pattern Recognit. Lett. 1997, 18, 1065–1071. [Google Scholar] [CrossRef]
- Yu, S.; Mou, Y.; Xu, D.; You, X.; Zhou, L.; Zeng, W. A New Algorithm for Shoreline Extraction from Satellite Imagery with Non-Separable Wavelet and Level Set Method. Int. J. Mach. Learn. Comput. 2013, 3, 158–163. [Google Scholar] [CrossRef]
- Taha, L.G.; Elbeih, S.F. Investigation of fusion of SAR and Landsat data for shoreline super resolution mapping: The northeastern Mediterranean Sea coast in Egypt. Appl. Geomat. 2010, 2, 177–186. [Google Scholar] [CrossRef]
- Giannini, M.B.; Parente, C. An object based approach for coastline extraction from Quickbird multispectral images. Int. J. Eng. Technol. (IJET) 2015, 6, 2698–2704. [Google Scholar]
- Tonyé, E.; Akono, A.; Nyoungui, A.N.; Nlend, C.; Rudant, J.P. Cartographie des traits de côte par analyse texturale d’images radar à synthèse d’ouverture ERS-1 et E-SA. 2000. Available online: https://www.researchgate.net/publication/272510492_Cartographie_des_traits_de_cote_par_analyse_texturale_d’images_radar_a_synthese_d’ouverture_ERS-1_et_E-SAR (accessed on 2 February 2015).
- Heene, G.; Gautama, S. Optimisation of a coastline extraction algorithm for object-oriented matching of multisensor satellite imagery. In Proceedings of the IEEE 2000 International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 24–28 July 2000. [Google Scholar]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active Contour Models. Int. J. Comput. Vis. 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Klinger, T.; Ziems, M.; Heipke, C.; Hannover Schenke, H.W.; Ott, H.; Bremerhaven. Antarctic Coastline Detection using Snakes Extended version of a paper published in The International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2010, 6, 421–434. [Google Scholar]
- Chong, J.; Ouyang, Y.; Zhu, M. Two Coastline Detection Methods Based on Improved Level Set Algorithm in Synthetic Aperture Radar Images. Proc. Dragon 1 Program Final Results 2004–2007, Beijing, P.R. China 21–25 April 2008 (ESA SP-655, April 2008). Available online: https://www.researchgate.net/profile/Jinsong_Chong/publication/233165295_Two_coastline_detection_methods_in_Synthetic_Aperture_Radar_imagery_based_on_Level_Set_Algorithm/links/55bd5a2d08aec0e5f44459f5.pdf (accessed on 25 May 2015).
- Li, C.; Xu, C. Distance regularized level set evolution and its application to image segmentation. IEEE Trans. Image Process. 2010, 19, 3243–3254. [Google Scholar] [PubMed]
- Toure, S.; Diop, O.; Kpalma, K.; Maiga, A.S. Coastline detection using fusion of over segmentation and distance regularization level set evolution. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-3/W4, 513–518. [Google Scholar]
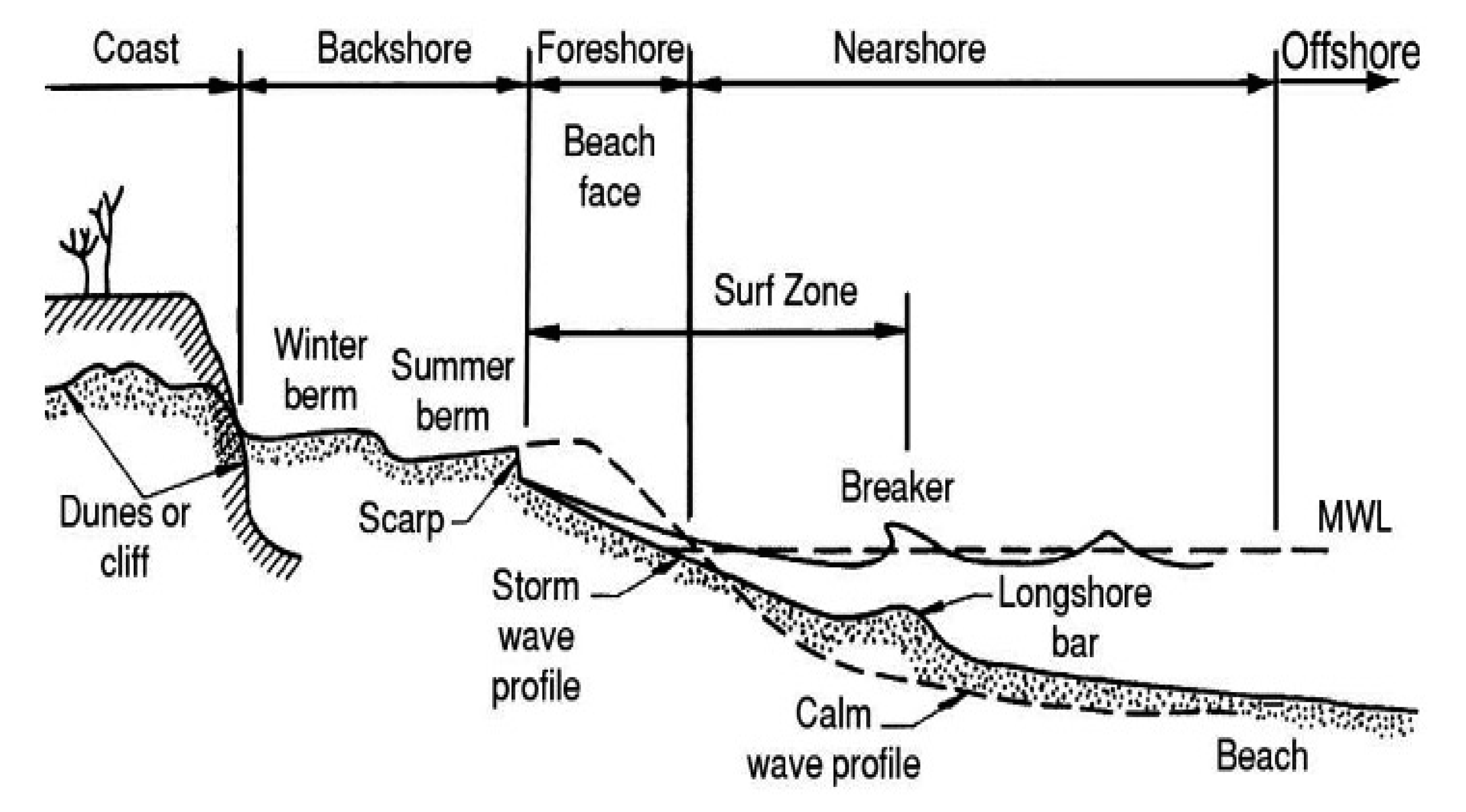
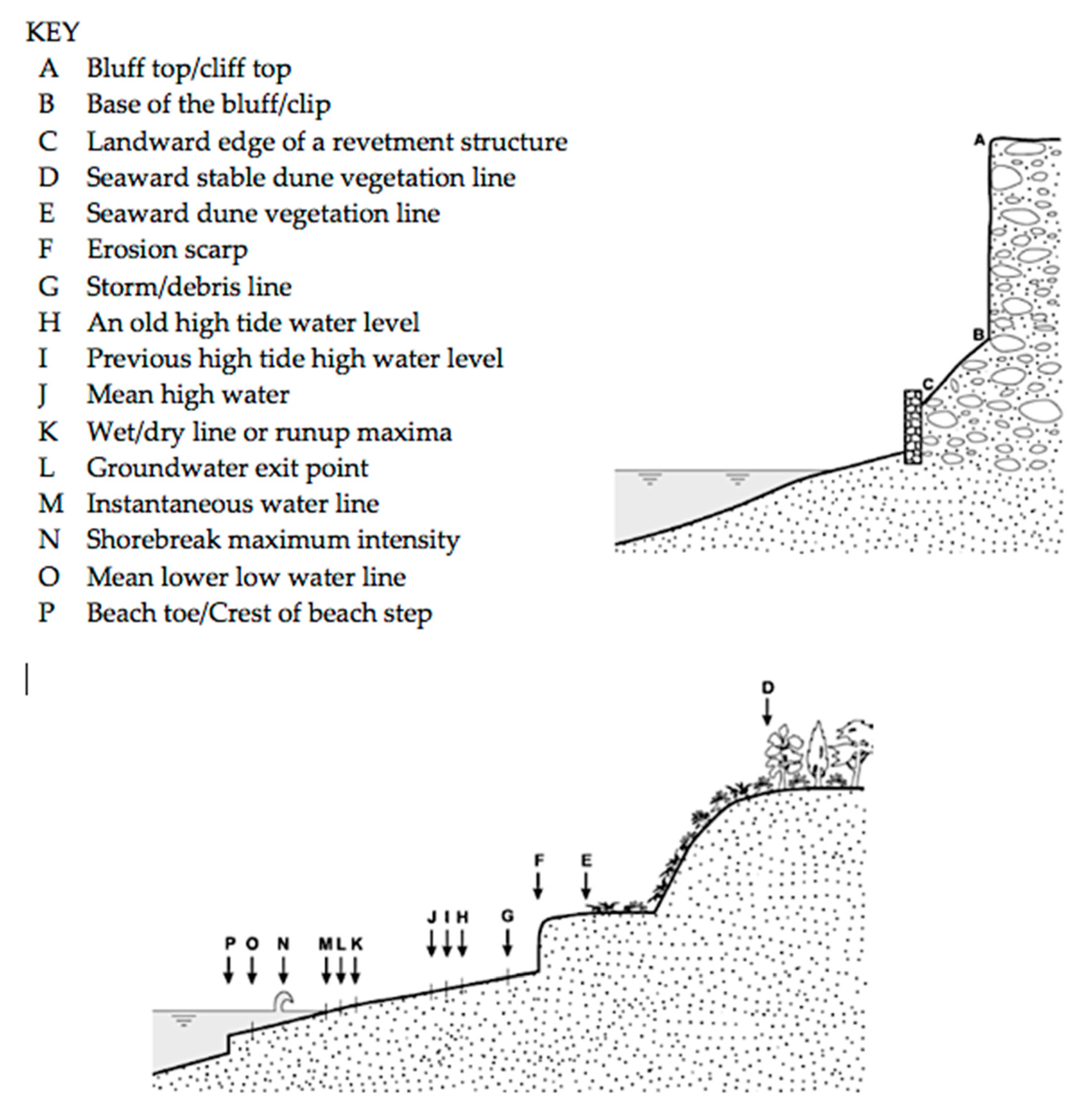
| Kinds of Indicator | Indicators | Description | References | |
|---|---|---|---|---|
| Morphological reference lines | Coastal dunes | Dune foot (dune toe, dune line) | The dune foot or dune toe is the outline from elevation and slope changes observed landward of the berm [13]. | [13,14,15,16,17,18,19] |
| Dune top edge | The sliding of material on the dune front can create a scree deck at its base and thus hide the foot of dune. In this case, it is possible to use the top edge of the dune which may also correspond to a vegetation limit | [14,20,21] | ||
| Kinds of Indicator | Indicators | Description | References | |
|---|---|---|---|---|
| Morphological reference lines | Coastal dunes | Dune crest line | The dune crest is the highest elevation peak, where the slope changes sign from positive (landward facing) to negative (seaward facing) [23]. | [18,22,23,24] |
| Cliffs and backed beach | Bluff top, cliff top, top of the cliff | The bluff top (cliff top) refers to the top edge of the cliff | [14,25,26,27,28,29] | |
| Base of the bluff, cliff toe, bluff toe | In areas with sharp cliffs, with no notches, regularly beaten by the waves and cleared of fallen materials, the base of the cliff is an optimal alternative to the cliff top. | [14,30,31,32,33] | ||
| In case of scree at the cliff’s toe | Top of the landslide headwall | This indicator is only used in [34], on bluffed shores in areas with mass movement, for example, earth flows, landslides, among others [8] | [34] | |
| Base of the scree | The base of the scree is an indicator that may be chosen when the cliff is affected by mass movements. | [35,36] | ||
| Contour of the tear scar | Like the base of the scree, the contour of the tear scar may be used in case of cliff mass movements | [37] | ||
| In case of a protected seafront | Seaward-most edge of hardening structures | On beaches with hardening structures, a tree kind of indictor may be used: the seaward most edge of hardening structures, the landward edge of shoreline protection structures and crest of the shore-protection structure. These reference lines are not able to show shoreline evolution in this type of beach since they are intended to freeze the shoreline and can be modified at any time [8] | [38,39] | |
| Landward edge of shoreline protection structures | [40] | |||
| Crest of the shore- protection structure | [41] | |||
| Berm crest | The berm crest is the morphological feature that separates the steeper forebeach from the gentler sloping backbeach. It is a depositional feature constructed by runup of normal waves (generally summer conditions) and a destruction feature when eroded by waves at abnormally high water levels (generally winter conditions) [38] | [22,38,41,42,43,44,45] | ||
| Kinds of Indicator | Indicators | Description | References |
|---|---|---|---|
| Berm toe | It is the base of the foreshore extending from the dune crest to the low tide terrace | [39,45,47,48] | |
| Vegetation limits | Vegetation line, seaward edge of dune vegetation | The vegetation line is a biological indicator of the limits of regular flooding by high water and therefore it represents a nearly ideal indicator of shoreline movement [35]. | [22,30,49,50,51,52] |
| Line of permanent (stable, long-term) vegetation | The vegetation line is a natural line formed by the plants in the beach. It is easily identifiable, even on older photographs that cannot be used for beach toe identification. | [34,39,41,53,54,55] | |
| Bound between Ammophila arenaria and Agropyrum junceum in tempered coastal dunes | Ammophila arenaria and Agropyrum junceum are plants used to stop coastal dunes movements in tempered zones. | [35,36] | |
| Upper limit of algae or marine lichen on the walls of rocky cliffs | The upper limit of algae or lichen may be used in a case of rocky cliff | [30,35,36,56] | |
| Instant tidal levels and wetting limits | Water line (swash line, swash terminus) | The water line is the interface between the body of water and the slope of the beach. It refers to the limit of the foam of the swash (the rush of seawater up the beach after the breaking of a wave). | [57,58,59,60,61,62,63] |
| Wet/dry line (wet/dry boundary, wetted bound, wet/sand line) | It is the end of the swash at high tide and during the ebb tide; it migrates to the sea and marks the land side limit of the sands darkened by the breaking of a wave. | [50,56,64,65] | |
| High water line | It is defined as the level of the last high tide and therefore corresponds to the upper wetting limit of the foreshore by the previous open sea. The instantaneous high water line is commonly mapped on aerial photographs as the shoreline proxy because it is easily identified. | [22,49,66,67,68,69,70] | |
| High tide wrack line | The high tide wrack line is the line of debris left on the beach by high tide. It is usually made up of eelgrass, or others kinds of litter. | [56,50] |
| Kinds of Indicator | Indicators | Description | References |
|---|---|---|---|
| Instant tidal levels and wetting limits | Usual or mean high water line (average high water line) | It is supposed to represent the average position of the full seas. There is a correlation between the instantaneous high water line and the mean high water line, but the mean high water line it is not quite a tide datum because its definition takes into account other criteria that include, among others, the vegetation limit. | [71,72,73] |
| Tidal datums | Mean sea level | The rise and fall of the tides along the coast is a complex process that influences the establishment of a shoreline indicator. The tidal datums refer essentially to high tide or low tide. Different tidal data are used successfully as shoreline indicators. We can cite the mean sea level, the mean high water line, and the mean spring high water line, among others. | [74,75] |
| Mean high water line | [76,77,78,79,80] | ||
| Mean spring high water line, mean high water spring tide | [81,82] | ||
| Mean higher high water line | [83] | ||
| Mean low water line | [81,84] | ||
| Mean low water spring tide mark | [85] | ||
| Lowest astronomical sea level | [86,87] | ||
| Virtual reference lines | Shoreline maximum intensity | It is the line of maximum light intensity. Like all virtual reference lines, this line is a digital reference line resulting from image processing | [88,89] |
| Shoreline extracted from colour and luminance distinction on colour averaged video images | These features represent an average position of the instantaneous shoreline for about ten minutes. | [89,90] | |
| Skeleton of beach | It corresponds to the median line of the form described by the contours of the beach circumscribed by the vegetative limit or the foot of the dune and the wetting line of foreshore or “visible high seas” [91]. | [91] |
| Kinds of Indicator | Indicators | Description | References |
|---|---|---|---|
| Beach contours | Beach width | It defines the variations of the width of the range between an upstream limit and a downstream limit. The upstream limit is set at the foot of the dune or the lower limit of vegetation whereas the position of the downstream limit varies according to the authors. | [64,46,92] |
| Storm lines | Storm-surge penetration line (overwash penetration boundary) | In [93] the overwash penetration distance is defined as the width of the “active” sand zone; that is, the distance between the ocean shoreline and the zone of dense vegetation that typically extends to the seaward face of barrier foredunes. | [94,95] |
| Crest of washover terrace | Washover terraces are deposited where beaches are highly erosional and adjacent ground elevations are lower than the highest storm surges. The crest of the washover terrace forms the highest beach elevation and is the best indicator of shoreline movement for these types of beaches [38]. | [38,44,53,54,96] |
| Approaches | Advantages/Disadvantages | References |
|---|---|---|
| Thresholding | It is the simplest segmentation method with a rapid implementation. Since thresholding uses only the image histogram, the image should be of good quality. | [107,109,108,110]; |
| K-means/ISODATA | K-means and ISODATA are the most popular classification methods. They are easy to implement and they give good results when they are applied to images in which the different regions are easily separable | [114,115] |
| Neural network | The Artificial Neural Network (ANN) is easy to use and can perform complex segmentation and object recognition problems | [130,131] |
| Region growing | The region growing methods are fast and conceptually simple, but they are very sensitive to the distribution of the objects in the image. | [124,129] |
| Watershed transform | Watershed transform is fast in computation time but often provides a very large number of regions that will be merged to obtain a correct segmentation of the objects in the image. | [125,129] |
| Wavelet transform | The wavelet transform is computationally fast and offers a simultaneous localization in time and frequency domain. | [132] |
| Super resolution mapping | The advantages of this technique are simplicity of integrating two images and good for highlighting urban features. Its drawback is that it does not retain the radiometry of the input multispectral image [133]. | [133] |
| Principal Component Analysis | The PCA allows the use of smaller databases and reduction of noise | [124,120] |
| Object-oriented classification | It reduces salt-and-pepper effects commonly noted in pixel-based remote sensing image classification. | [120,128,134] |
| Texture analysis-based methods | Texture analysis groups together a set of techniques allowing quantifying the different grey-levels present in an image in terms of intensity and distribution in order to calculate a number of parameters characteristic of the texture to be studied. It is a very important task, which is useful for image segmentation and object detection. | [135] |
| Approaches | Advantages | Disadvantages | References |
|---|---|---|---|
| Canny Edges detection | Good results can be obtained for images in some spectral bands | Due to the Gaussian smoothing: the location of the edges might be off, depending on the size of the Gaussian kernel. | [110,135] |
| Snakes | Snakes can adapt to differences and noise in stereo matching and motion tracking. Additionally, the method can find illusory contours in the image by ignoring missing boundary information | Snakes are sensitive to local minima states, which can be counteracted by simulated annealing techniques. Minute features are often ignored during energy minimization over the entire contour. Their accuracy depends on the convergence policy | [138] |
| Level Set Algorithm | Compared to the Snake method, the Level Set Algorithm also to improve the edge detection speed. | The procedure using LSA requires a lot of time when applied to high-resolution images | [132,139,141] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toure, S.; Diop, O.; Kpalma, K.; Maiga, A.S. Shoreline Detection using Optical Remote Sensing: A Review. ISPRS Int. J. Geo-Inf. 2019, 8, 75. https://doi.org/10.3390/ijgi8020075
Toure S, Diop O, Kpalma K, Maiga AS. Shoreline Detection using Optical Remote Sensing: A Review. ISPRS International Journal of Geo-Information. 2019; 8(2):75. https://doi.org/10.3390/ijgi8020075
Chicago/Turabian StyleToure, Seynabou, Oumar Diop, Kidiyo Kpalma, and Amadou Seidou Maiga. 2019. "Shoreline Detection using Optical Remote Sensing: A Review" ISPRS International Journal of Geo-Information 8, no. 2: 75. https://doi.org/10.3390/ijgi8020075
APA StyleToure, S., Diop, O., Kpalma, K., & Maiga, A. S. (2019). Shoreline Detection using Optical Remote Sensing: A Review. ISPRS International Journal of Geo-Information, 8(2), 75. https://doi.org/10.3390/ijgi8020075





