Modeling Spatio-Temporal Evolution of Urban Crowd Flows
Abstract
1. Introduction
2. Related Work
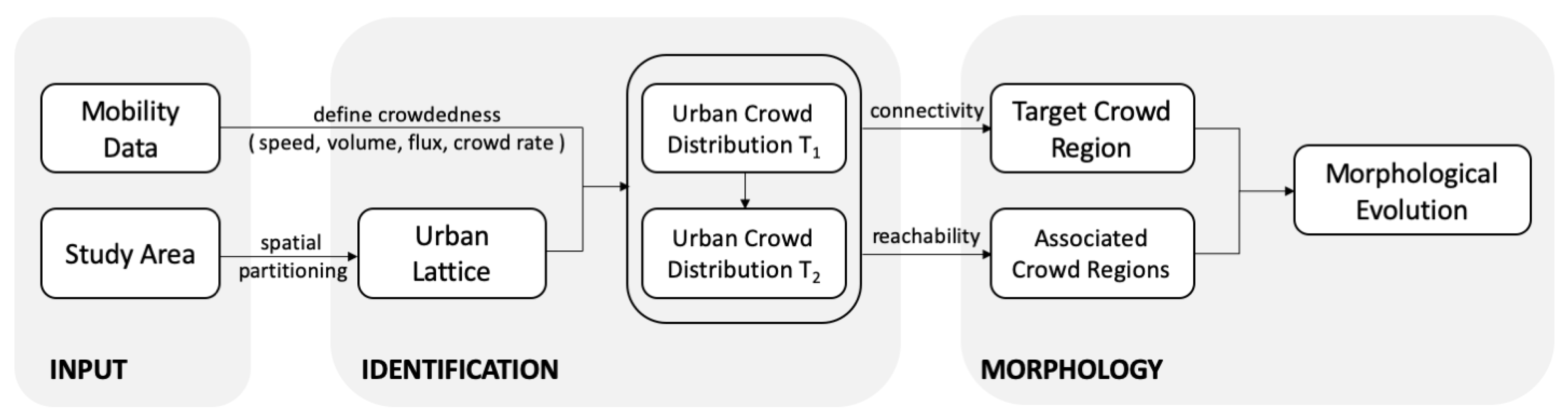
3. Methodology
3.1. Urban Lattice
3.1.1. Spatial Partition
3.1.2. Crowd Level
- Speed
- Volume (or density)where the operator counts the cardinality of the input set (e.g., the number of unique individuals that have ever appeared in the cell during the given time period).
- Flux
- Crowd rate
- Free flow: for ;
- Slowed flow: for and ;
- Crowded flow: for and ;
3.2. Urban Crowd Hotspot
3.2.1. Connectivity
3.2.2. Connected Component
3.2.3. Crowd Region
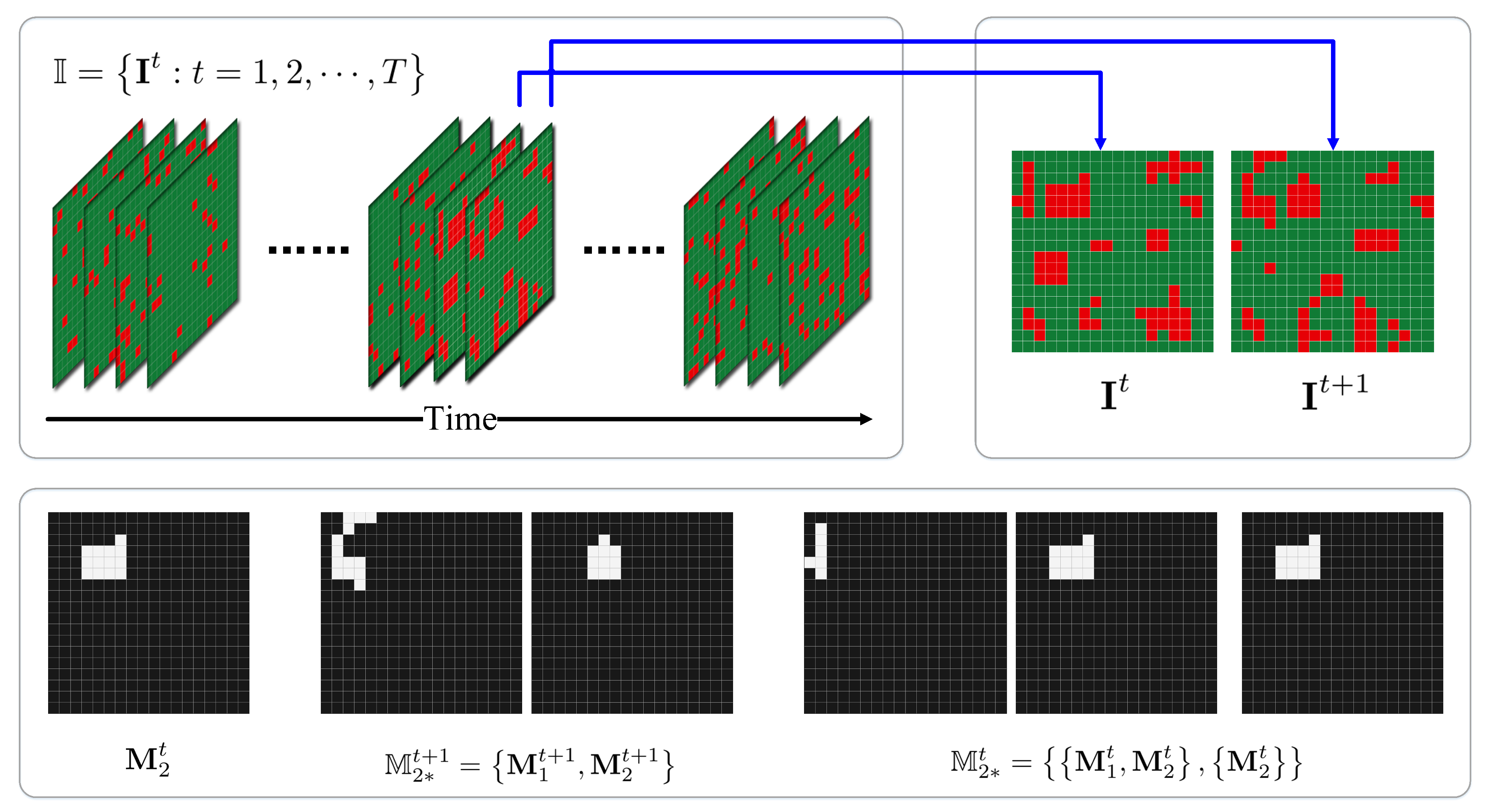
3.3. Spatio-Temporal Evolution
3.3.1. Mask Region
3.3.2. Crowd Morphology
| Algorithm 1: Morphological analysis. |
 |
3.3.3. Nested Crowd Evolution
| Algorithm 2: Nested morphological analysis. |
 |
4. Case Study
4.1. Scenario I: Simulation
4.1.1. Synthetic Data
4.1.2. Pattern Assignments
4.2. Scenario II: Real Observation
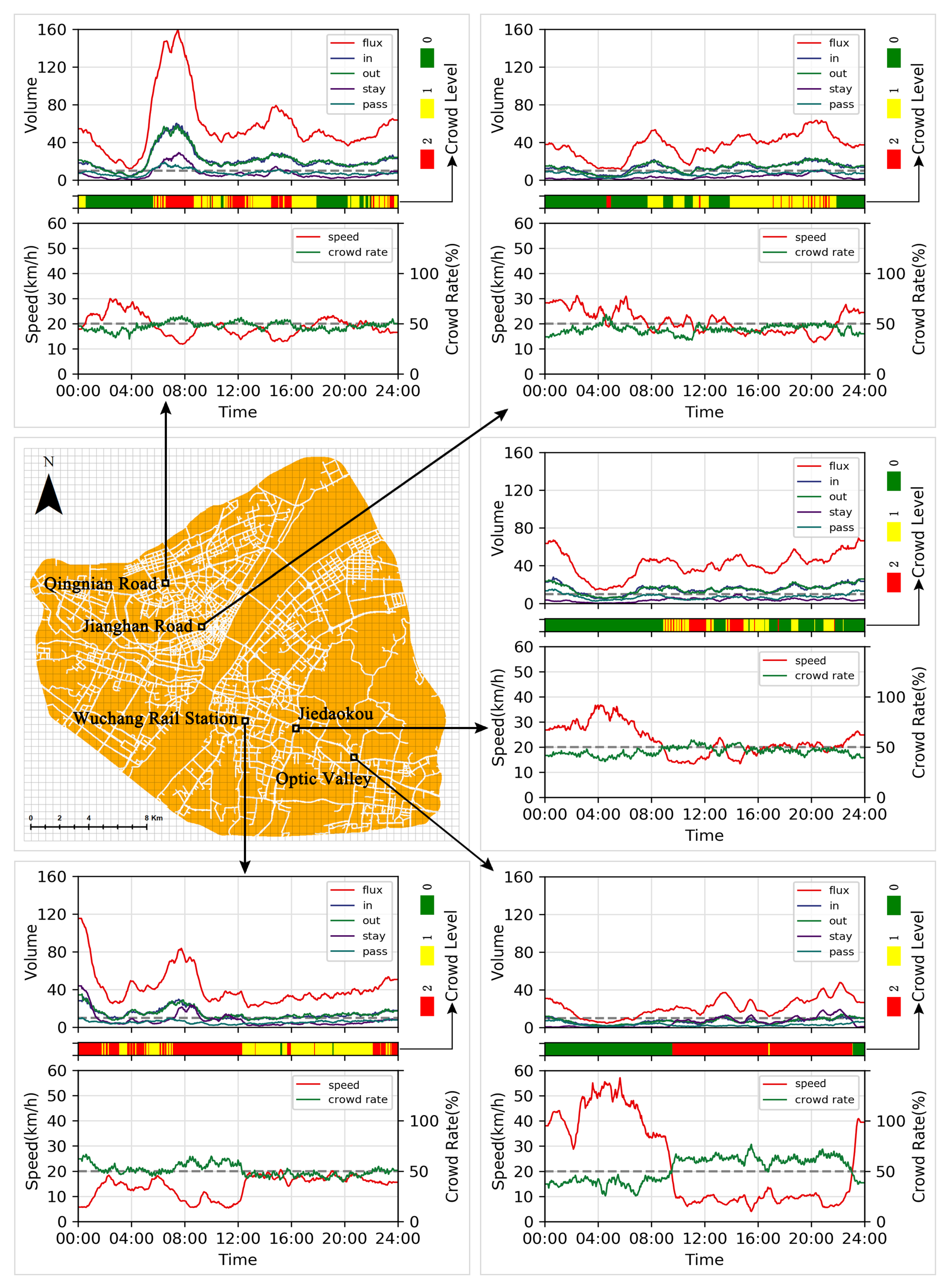
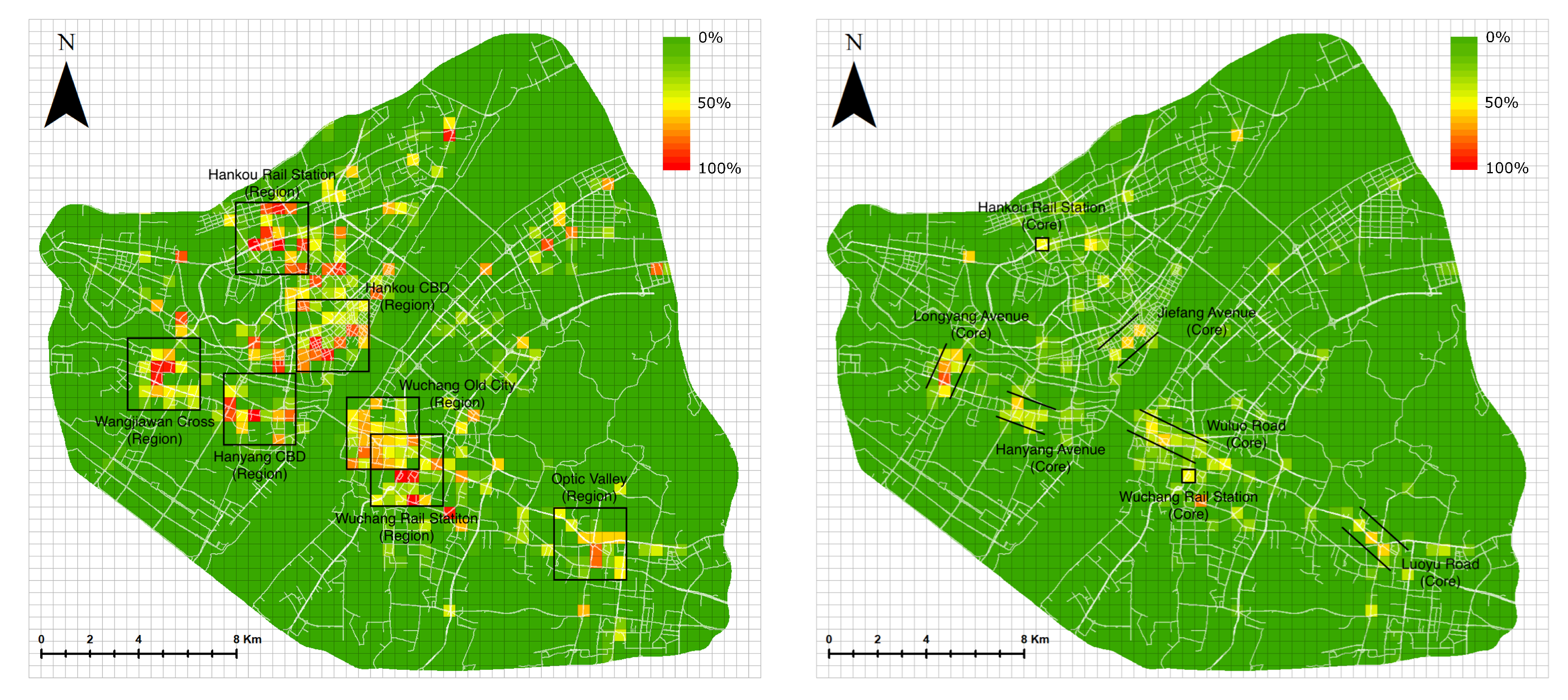
4.2.1. Case Study Area
4.2.2. Citywide Crowd Hotspots
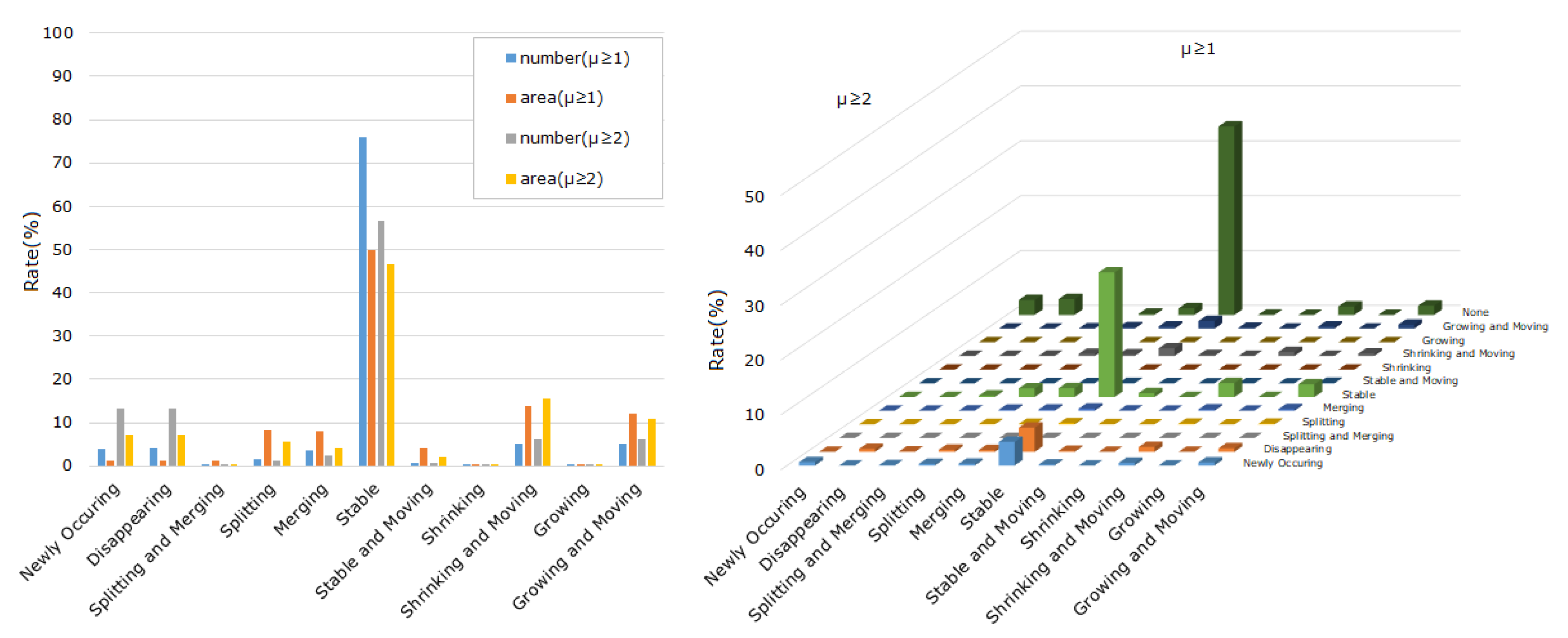
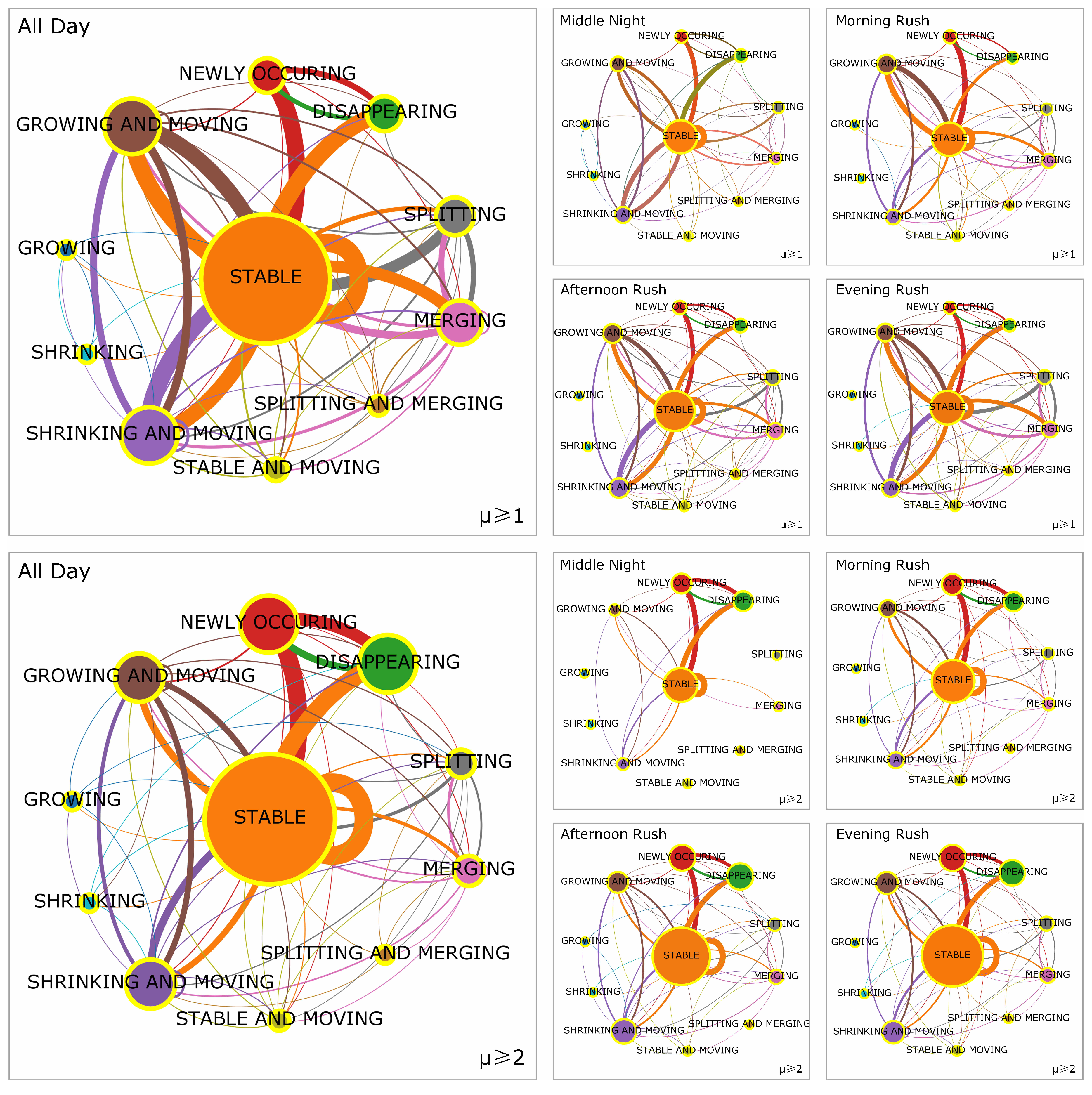
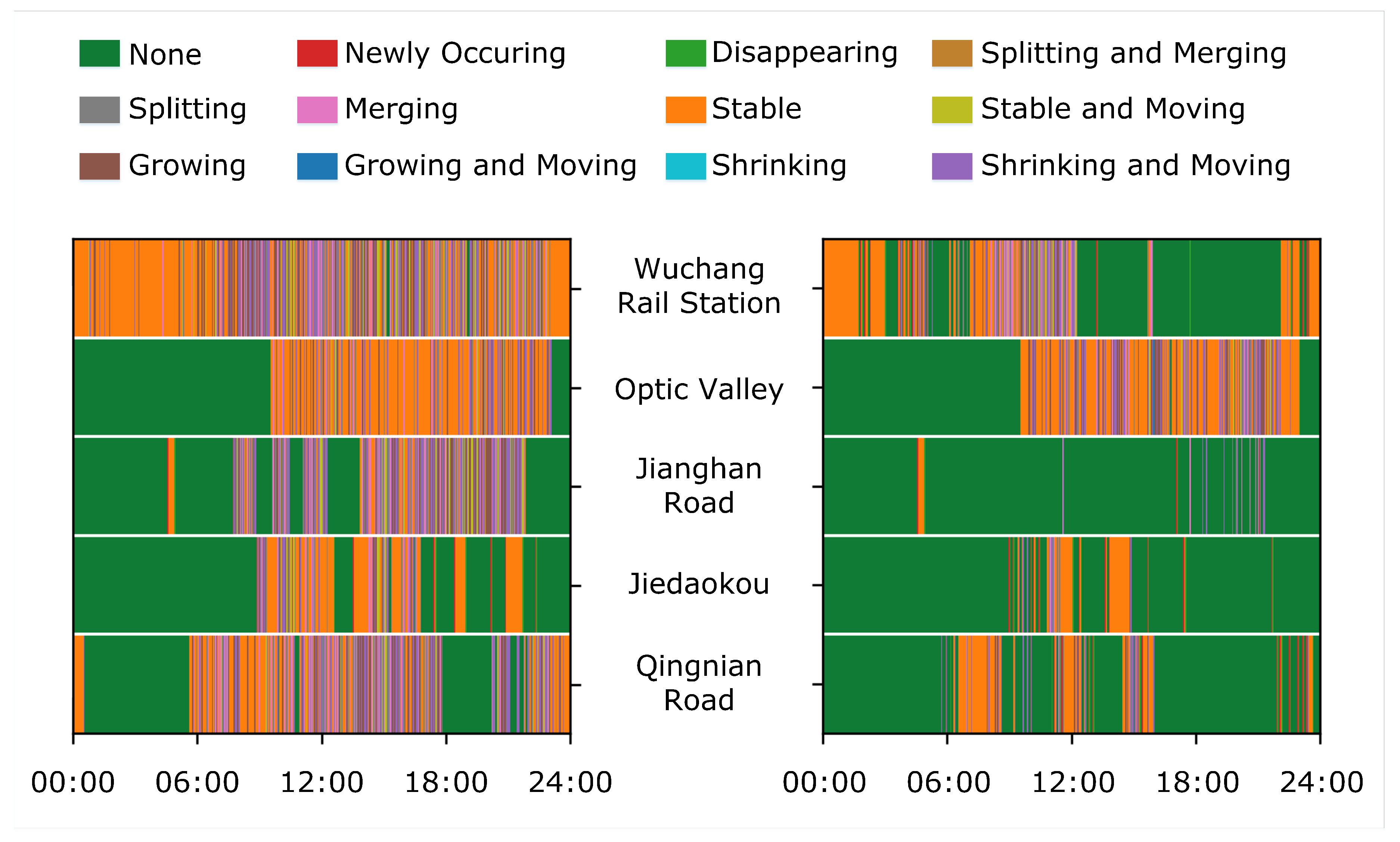
4.2.3. Morphological Evolutionary Patterns
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barthelemy, M. A global take on congestion in urban areas. Environ. Plan. B Plan. Des. 2016, 43, 800–804. [Google Scholar] [CrossRef]
- Batty, M. The New Science of Cities; MIT Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Kerner, B.S. Breakdown in Traffic Networks: Fundamentals of Transportation Science; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Liu, Y.; Liu, X.; Gao, S.; Gong, L.; Kang, C.; Zhi, Y.; Chi, G.; Shi, L. Social Sensing: A New Approach to Understanding Our Socioeconomic Environments. Ann. Assoc. Am. Geogr. 2015, 105, 512–530. [Google Scholar] [CrossRef]
- Zheng, Y.; Capra, L.; Wolfson, O.; Yang, H. Urban Computing: Concepts, Methodologies, and Applications. ACM Trans. Intell. Syst. Technol. 2014, 5, 38. [Google Scholar] [CrossRef]
- Kang, C.; Qin, K. Understanding Operation Behaviors of Taxicabs in Cities by Matrix Factorization. Comput. Environ. Urban Syst. 2016, 60, 79–88. [Google Scholar] [CrossRef]
- Rao, A.M.; Rao, K.R. Measuring Urban Traffic Congestion-A Review. Int. J. Traffic Transp. Eng. 2012, 2, 286–305. [Google Scholar]
- Stathopoulos, A.; Karlaftis, M.G. Modeling Duration of Urban Traffic Congestion. J. Transp. Eng. 2002, 128, 587–590. [Google Scholar] [CrossRef]
- Sweet, M. Does Traffic Congestion Slow the Economy? J. Plan. Lit. 2011, 26, 391–404. [Google Scholar] [CrossRef]
- Kan, Z.; Tang, L.; Kwan, M.P.; Ren, C.; Liu, D.; Li, Q. Traffic congestion analysis at the turn level using Taxis’ GPS trajectory data. Comput. Environ. Urban Syst. 2019, 74, 229–243. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Y.; Qi, D. Deep Spatio-Temporal Residual Networks for Citywide Crowd Flows Prediction. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 1655–1661. [Google Scholar]
- Gidófalvi, G.; Yang, C. Scalable Detection of Traffic Congestion from Massive Floating Car Data Streams. In Proceedings of the 1st International ACM SIGSPATIAL Workshop on Smart Cities and Urban Analytics, Bellevue, WA, USA, 3–6 November 2015; ACM: New York, NY, USA, 2015; pp. 114–121. [Google Scholar] [CrossRef]
- Kaiser, M.S.; Lwin, K.T.; Mahmud, M.; Hajializadeh, D.; Chaipimonplin, T.; Sarhan, A.; Hossain, M.A. Advances in Crowd Analysis for Urban Applications Through Urban Event Detection. IEEE Trans. Intell. Transp. Syst. 2017, 19, 3092–3112. [Google Scholar] [CrossRef]
- Maurin, B.; Masoud, O.; Papanikolopoulos, N.P. Tracking all traffic: Computer vision algorithms for monitoring vehicles, individuals, and crowds. IEEE Robot. Autom. Mag. 2005, 12, 29–36. [Google Scholar] [CrossRef]
- Kang, C.; Liu, Y.; Ma, X.; Wu, L. Towards estimating urban population distributions from mobile call data. J. Urban Technol. 2012, 19, 3–21. [Google Scholar] [CrossRef]
- Domínguez, D.R.; Redondo, R.P.D.; Vilas, A.F.; Khalifa, M.B. Sensing the city with Instagram: Clustering geolocated data for outlier detection. Expert Syst. Appl. 2017, 78, 319–333. [Google Scholar] [CrossRef]
- Cheng, T.; Tanaksaranond, G.; Brunsdon, C.; Haworth, J. Exploratory visualisation of congestion evolutions on urban transport networks. Transp. Res. Part C Emerg. Technol. 2013, 36, 296–306. [Google Scholar] [CrossRef]
- Ma, Y.; Lin, T.; Cao, Z.; Li, C.; Wang, F.; Chen, W. Mobility viewer: An Eulerian approach for studying urban crowd flow. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2627–2636. [Google Scholar] [CrossRef]
- Wu, F.; Zhu, M.; Wang, Q.; Zhao, X.; Chen, W.; Maciejewski, R. Spatial-temporal visualization of city-wide crowd movement. J. Vis. 2017, 20, 183–194. [Google Scholar] [CrossRef]
- Wirz, M.; Franke, T.; Roggen, D.; Mitleton-Kelly, E.; Lukowicz, P.; Tröster, G. Probing crowd density through smartphones in city-scale mass gatherings. EPJ Data Sci. 2013, 2, 5. [Google Scholar] [CrossRef]
- Calabrese, F.; Colonna, M.; Lovisolo, P.; Parata, D.; Ratti, C. Real-time urban monitoring using cell phones: A case study in Rome. IEEE Trans. Intell. Transp. Syst. 2011, 12, 141–151. [Google Scholar] [CrossRef]
- Ben Khalifa, M.; Redondo, R.P.D.; Vilas, A.F.; Rodríguez, S.S. Identifying urban crowds using geo-located Social media data: A Twitter experiment in New York City. J. Intell. Inf. Syst. 2017, 48, 287–308. [Google Scholar] [CrossRef]
- Zhu, X.; Guo, D. Mapping large spatial flow data with hierarchical clustering. Trans. GIS 2014, 18, 421–435. [Google Scholar] [CrossRef]
- Chen, W.; Guo, F.; Wang, F.Y. A survey of traffic data visualization. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2970–2984. [Google Scholar] [CrossRef]
- Helbing, D.; Johansson, A.; Al-Abideen, H.Z. Dynamics of crowd disasters: An empirical study. Phys. Rev. E 2007, 75, 046109. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Liu, Y.; Ni, L.; Li, M.; Fan, J. Detecting crowdedness spot in city transportation. IEEE Trans. Veh. Technol. 2013, 62, 1527–1539. [Google Scholar] [CrossRef]
- D’Andrea, E.; Marcelloni, F. Detection of traffic congestion and incidents from GPS trace analysis. Expert Syst. Appl. 2017, 73, 43–56. [Google Scholar] [CrossRef]
- Fan, Z.; Pei, T.; Ma, T.; Du, Y.; Song, C.; Liu, Z.; Zhou, C. Estimation of urban crowd flux based on mobile phone location data: A case study of Beijing, China. Comput. Environ. Urban Syst. 2018, 69, 114–123. [Google Scholar] [CrossRef]
- Hadjieleftheriou, M.; Kollios, G.; Gunopulos, D.; Tsotras, V.J. On-Line Discovery of Dense Areas in Spatio-temporal Databases. In Advances in Spatial and Temporal Databases; Hadzilacos, T., Manolopoulos, Y., Roddick, J., Theodoridis, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 306–324. [Google Scholar]
- Tao, Y.; Kollios, G.; Considine, J.; Li, F.; Papadias, D. Spatio-temporal aggregation using sketches. In Proceedings of the 20th International Conference on Data Engineering, Boston, MA, USA, 30 March–2 April 2004; pp. 214–225. [Google Scholar] [CrossRef]
- Jensen, C.S.; Lin, D.; Ooi, B.C.; Zhang, R. Effective Density Queries on Continuously Moving Objects. In Proceedings of the 22nd International Conference on Data Engineering, Atlanta, GA, USA, 3–7 April 2006; p. 71. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, W.; Zhao, X.; Li, Y. Modeling the hourly distribution of population at a high spatiotemporal resolution using subway smart card data: A case study in the central area of Beijing. ISPRS Int. J. Geo-Inf. 2017, 6, 128. [Google Scholar] [CrossRef]
- Fan, Z.; Song, X.; Shibasaki, R.; Adachi, R. CityMomentum: An online approach for crowd behavior prediction at a citywide level. In Proceedings of the 2015 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Osaka, Japan, 7–11 September 2015; pp. 559–569. [Google Scholar]
- Khezerlou, A.V.; Zhou, X.; Li, L.; Shafiq, Z.; Liu, A.X.; Zhang, F. A Traffic Flow Approach to Early Detection of Gathering Events: Comprehensive Results. ACM Trans. Intell. Syst. Technol. 2017, 8, 74:1–74:24. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Y.; Qi, D.; Li, R.; Yi, X.; Li, T. Predicting Citywide Crowd Flows Using Deep Spatio-Temporal Residual Networks. Artif. Intell. 2018, 259, 147–166. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, M.; Yuan, X.; Zhang, J.; Van De Wetering, H. Visual traffic jam analysis based on trajectory data. IEEE Trans. Vis. Comput. Graph. 2013, 19, 2159–2168. [Google Scholar] [CrossRef]
- Hoang, M.X.; Zheng, Y.; Singh, A.K. FCCF: Forecasting citywide crowd flows based on big data. In Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Burlingame, CA, USA, 31 October–3 November 2016; p. 6. [Google Scholar]
- Yang, D.; Guo, Z.; Rundensteiner, E.A.; Ward, M.O. CLUES: A Unified Framework Supporting Interactive Exploration of Density-Based Clusters in Streams. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management, Glasgow, Scotland, UK, 24–28 October 2011; pp. 815–824. [Google Scholar]
- An, S.; Yang, H.; Wang, J.; Cui, N.; Cui, J. Mining urban recurrent congestion evolution patterns from GPS-equipped vehicle mobility data. Inf. Sci. 2016, 373, 515–526. [Google Scholar] [CrossRef]
- Rudomín, I.; Solar, G.V.; Oviedo, J.E.; Pérez, H.; Martini, J.L.Z. Modelling Crowds in Urban Spaces. Comput. Y Sist. 2017, 21, 57–66. [Google Scholar] [CrossRef]
- An, S.; Yang, H.; Wang, J. Revealing Recurrent Urban Congestion Evolution Patterns with Taxi Trajectories. ISPRS Int. J. Geo-Inf. 2018, 7, 128. [Google Scholar]
- Wang, Y.; Cao, J.; Li, W.; Gu, T.; Shi, W. Exploring traffic congestion correlation from multiple data sources. Pervasive Mob. Comput. 2017, 41, 470–483. [Google Scholar] [CrossRef]
- Fang, Z.; Yang, X.; Xu, Y.; Shaw, S.L.; Yin, L. Spatiotemporal model for assessing the stability of urban human convergence and divergence patterns. Int. J. Geogr. Inf. Sci. 2017, 31, 2119–2141. [Google Scholar] [CrossRef]
- Ji, Y.; Luo, J.; Geroliminis, N. Empirical observations of congestion propagation and dynamic partitioning with probe data for large-scale systems. Transp. Res. Rec. J. Transp. Res. Board 2014, 2422, 1–11. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, Y.; Huang, L.; Wang, E.; Li, D. Discovering Urban Traffic Congestion Propagation Patterns With Taxi Trajectory Data. IEEE Access 2018, 6, 69481–69491. [Google Scholar] [CrossRef]
- Yuan, M. Modeling semantic, spatial and temporal information in GIS. In Geographic Information Research: Bridging the Atlantic; CRC Press: Boca Raton, FL, USA, 1996; pp. 334–347. [Google Scholar]
- Nadi, S.; Reza Delavar, M. Spatio-Temporal Modeling of Dynamic Phenomena in GIS. In Proceedings of the 9th Scandinavian Research Conference on Geographical Information Science, Espoo, Finland, 4–6 June 2003; pp. 215–225. [Google Scholar]
- Claramunt, C.; Thériault, M. Managing Time in GIS An Event-Oriented Approach. In Recent Advances in Temporal Databases; Clifford, J., Tuzhilin, A., Eds.; Springer: London, UK, 1995; pp. 23–42. [Google Scholar]
- Yuan, M. Temporal GIS and spatio-temporal modeling. In Proceedings of the Third International Conference Workshop on Integrating GIS and Environment Modeling, Sante Fe, NM, USA, 21–25 January 1996; Volume 33, pp. 1–13. [Google Scholar]
- Yuan, M. Representing complex geographic phenomena in GIS. Cartogr. Geogr. Inf. Sci. 2001, 28, 83–96. [Google Scholar] [CrossRef]
- Hornsby, K.; Egenhofer, M. Identify-based change: A foundation for spatio- temporal knowledge representation. Int. J. Geogr. Inf. Sci. 2000, 14, 207–224. [Google Scholar] [CrossRef]
- Grenon, P.; Smith, B. SNAP and SPAN: Towards dynamic spatial ontology. Spat. Cogn. Comput. 2004, 4, 69–104. [Google Scholar] [CrossRef]
- Worboys, M. Event-oriented approaches to geographic phenomena. J. Geogr. Inf. Sci. 2005, 19, 1–28. [Google Scholar] [CrossRef]
- Benenson, I.; Torrens, P.M.; Torrens, P. Geosimulation: Automata-Based Modeling of Urban Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Ester, M.; Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, Oregon, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Horn, R.A. The Hadamard product. In Proceedings of Symposia in Applied Mathematics; Johnson, C.R., Ed.; American Mathematical Society: Providence, RI, USA, 1990; Volume 40, pp. 87–169. [Google Scholar]
- Scherf, N.; Herberg, M.; Thierbach, K.; Zerjatke, T.; Kalkan, T.; Humphreys, P.; Smith, A.; Glauche, I.; Roeder, I. Imaging, quantification and visualization of spatio-temporal patterning in mESC colonies under different culture conditions. Bioinformatics 2012, 28, i556–i561. [Google Scholar] [CrossRef][Green Version]
- Hu, M.K. Visual pattern recognition by moment invariants. IRE Trans. Inf. Theory 1962, 8, 179–187. [Google Scholar]
- Lenormand, M.; Louail, T.; Barthelemy, M.; Ramasco, J.J. Is spatial information in ICT data reliable? arXiv 2016, arXiv:1609.03375. [Google Scholar]
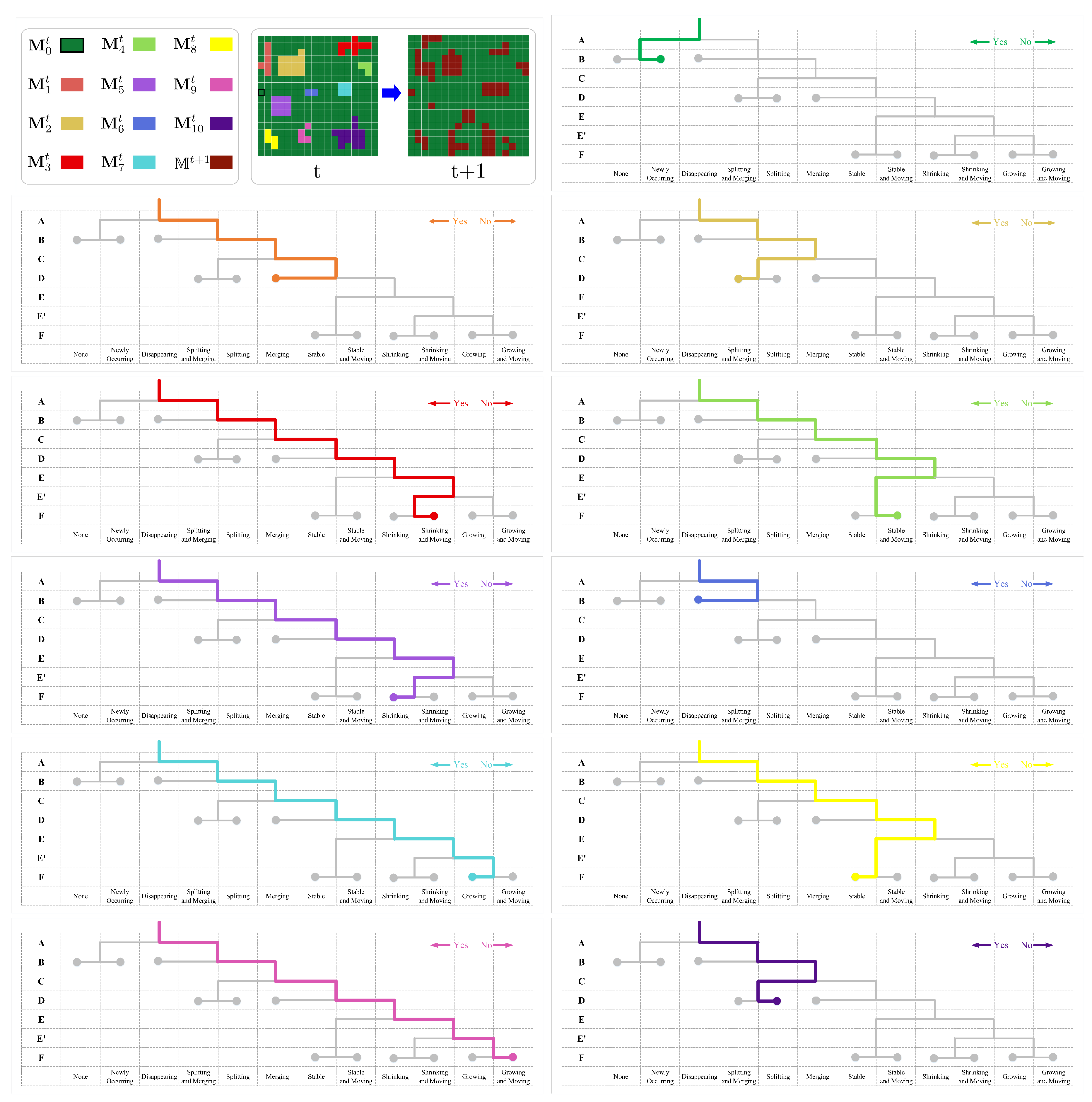
| Morphology (t → t+1) | ||
|---|---|---|
| Centroid (x, y) | Area (Number of Cells) | |
| Newly Occurring | None → Exist | Zero → Non-Zero |
| Disappearing | Exist → None | Non-Zero → Zero |
| Splitting and Merging | Multiple → Multiple | — |
| Splitting | Single → Multiple | — |
| Merging | Multiple → Single | — |
| Stable | No Change | No Change |
| Stable and Moving | Cell A → Cell B | No Change |
| Shrinking | No Change | Large → Small |
| Shrinking and Moving | Cell A → Cell B | Large → Small |
| Growing | No Change | Small → Large |
| Growing and Moving | Cell A → Cell B | Small → Large |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, K.; Xu, Y.; Kang, C.; Sobolevsky, S.; Kwan, M.-P. Modeling Spatio-Temporal Evolution of Urban Crowd Flows. ISPRS Int. J. Geo-Inf. 2019, 8, 570. https://doi.org/10.3390/ijgi8120570
Qin K, Xu Y, Kang C, Sobolevsky S, Kwan M-P. Modeling Spatio-Temporal Evolution of Urban Crowd Flows. ISPRS International Journal of Geo-Information. 2019; 8(12):570. https://doi.org/10.3390/ijgi8120570
Chicago/Turabian StyleQin, Kun, Yuanquan Xu, Chaogui Kang, Stanislav Sobolevsky, and Mei-Po Kwan. 2019. "Modeling Spatio-Temporal Evolution of Urban Crowd Flows" ISPRS International Journal of Geo-Information 8, no. 12: 570. https://doi.org/10.3390/ijgi8120570
APA StyleQin, K., Xu, Y., Kang, C., Sobolevsky, S., & Kwan, M.-P. (2019). Modeling Spatio-Temporal Evolution of Urban Crowd Flows. ISPRS International Journal of Geo-Information, 8(12), 570. https://doi.org/10.3390/ijgi8120570







