Multi-Scale Validation of MODIS LAI Products Based on Crop Growth Period
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data and Pre-Processing
2.3. Methods
2.3.1. Leaf area index Reference Maps Generated Using the PROSAIL Model
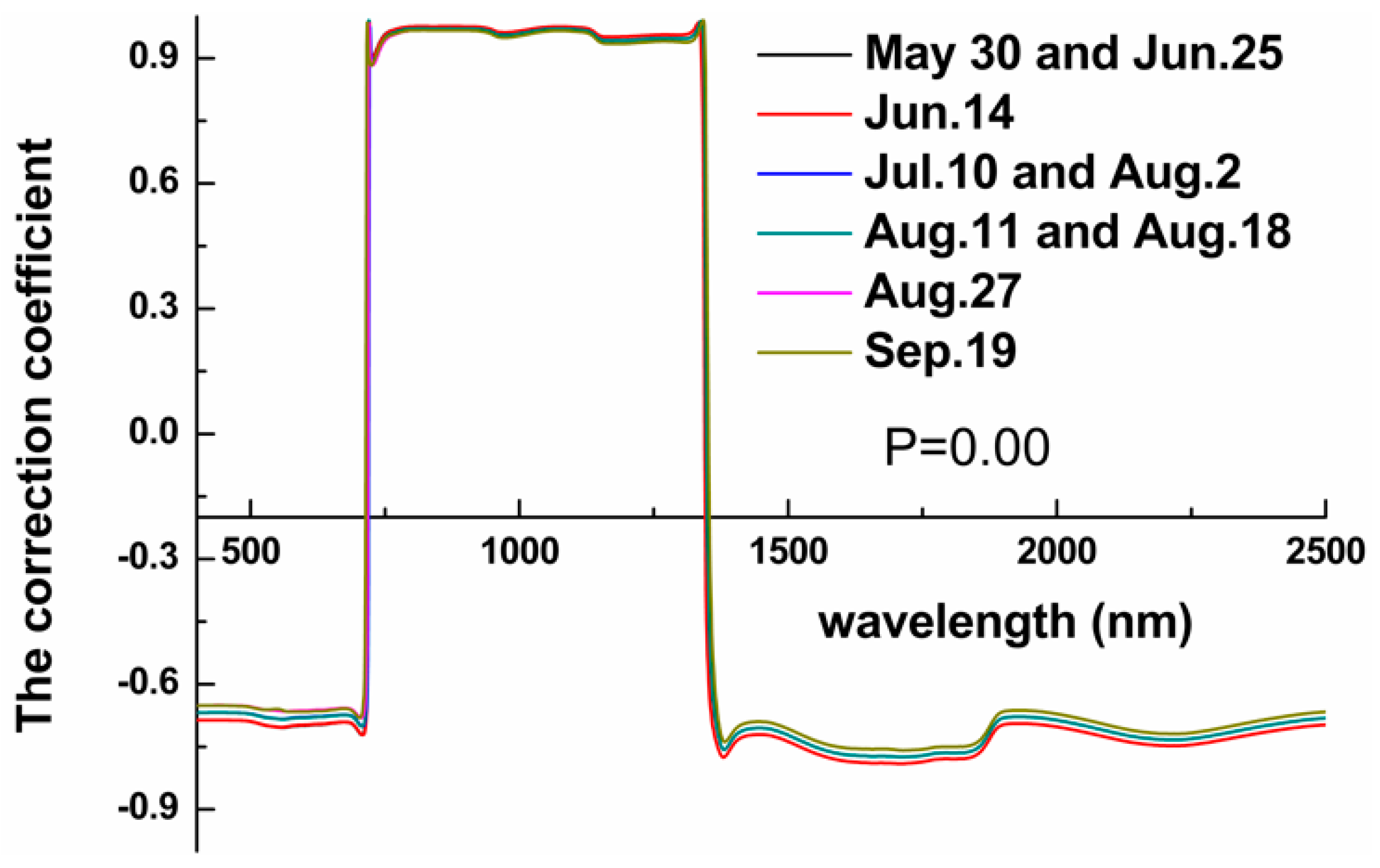
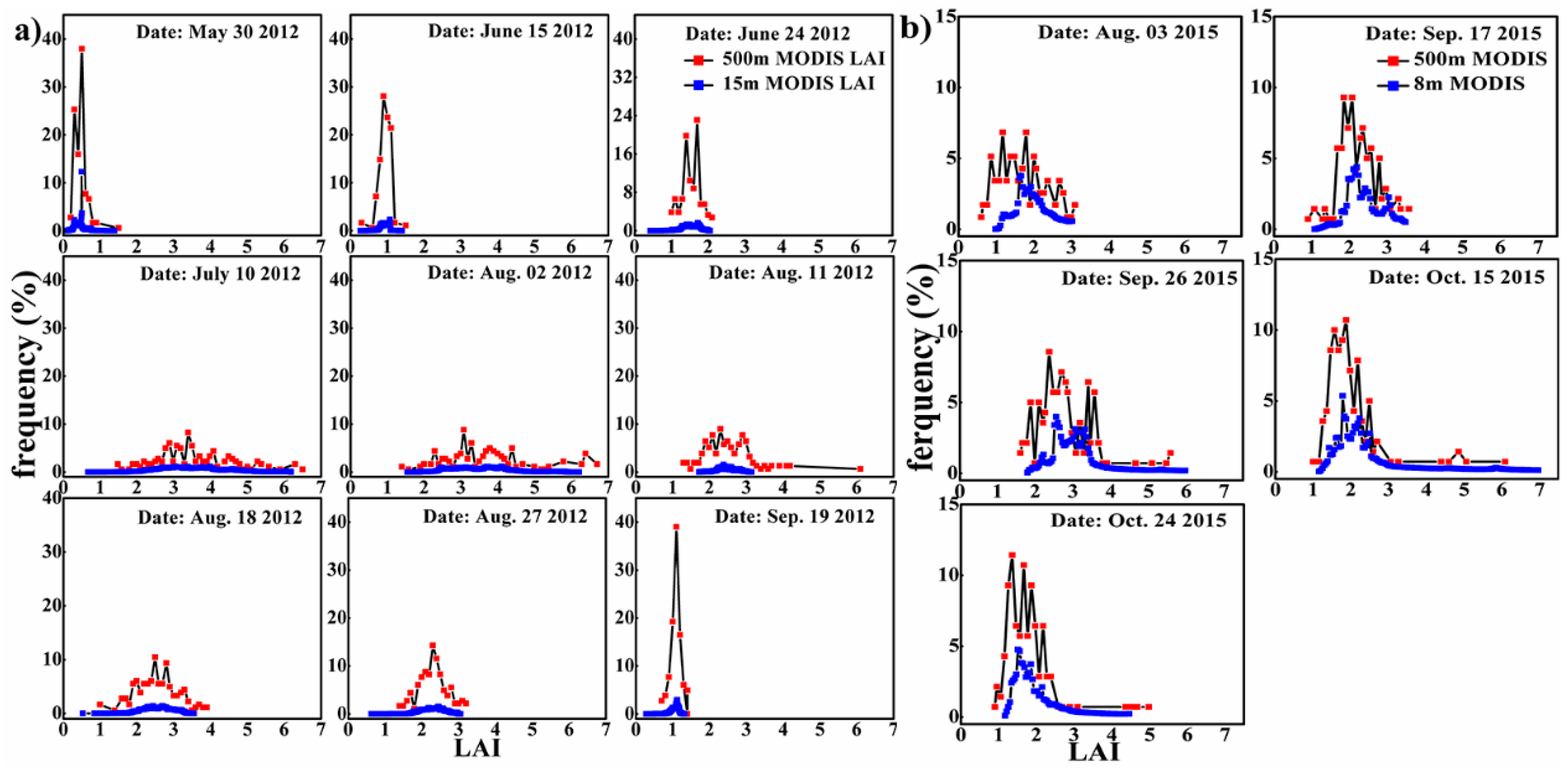
2.3.2. Validation of Multi-Scale MODIS LAI Products Based on the EBK Interpolation
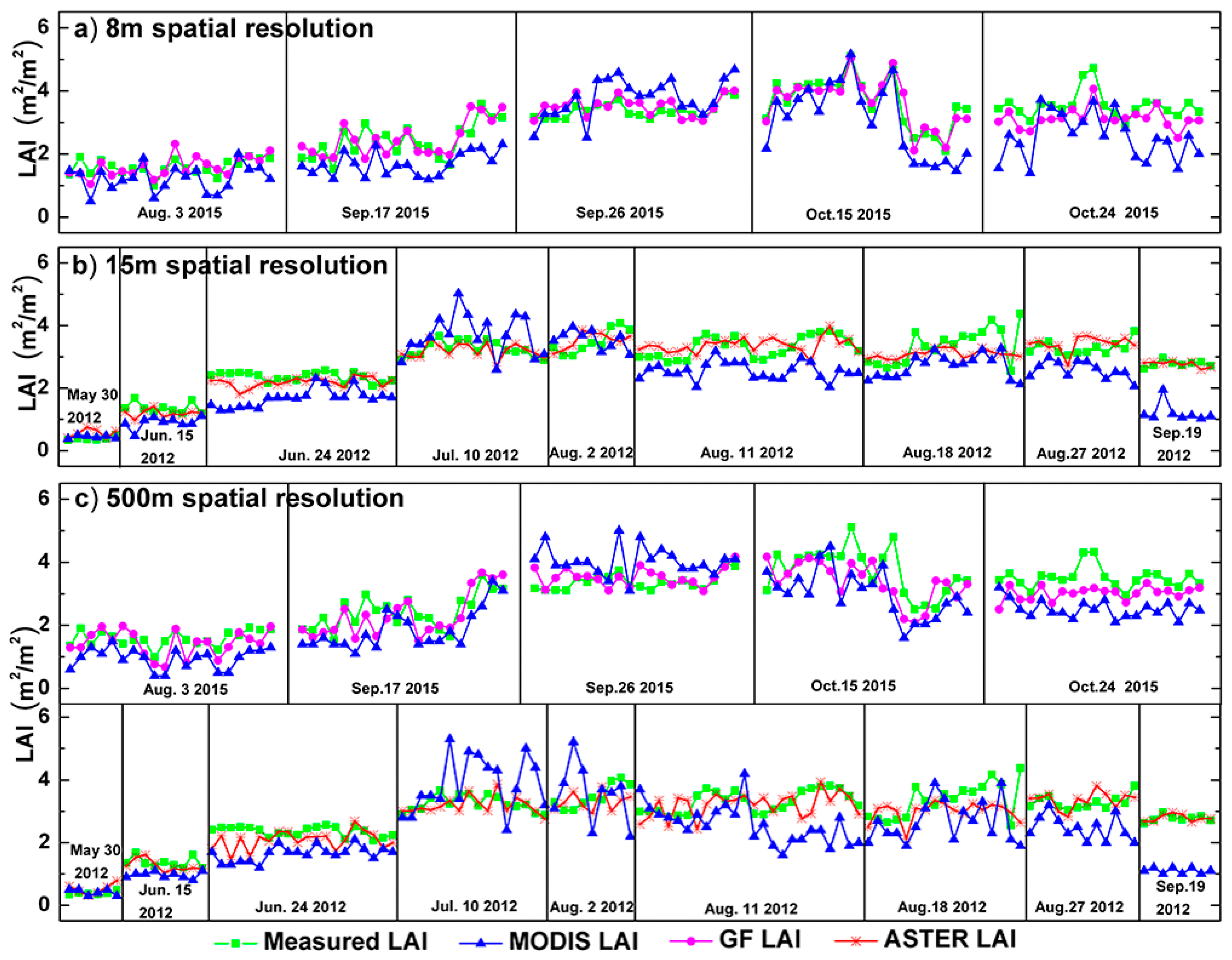
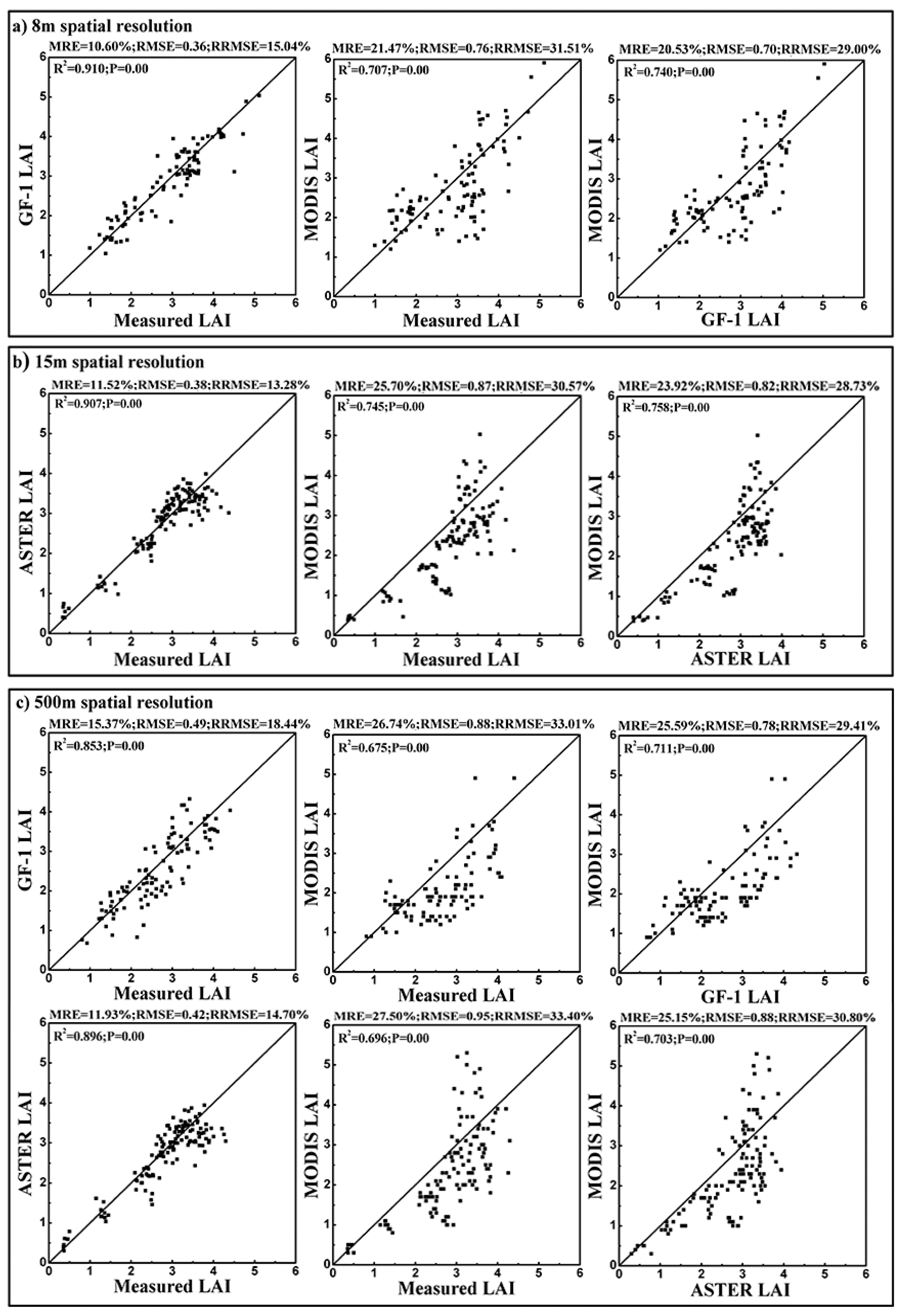
3. Results
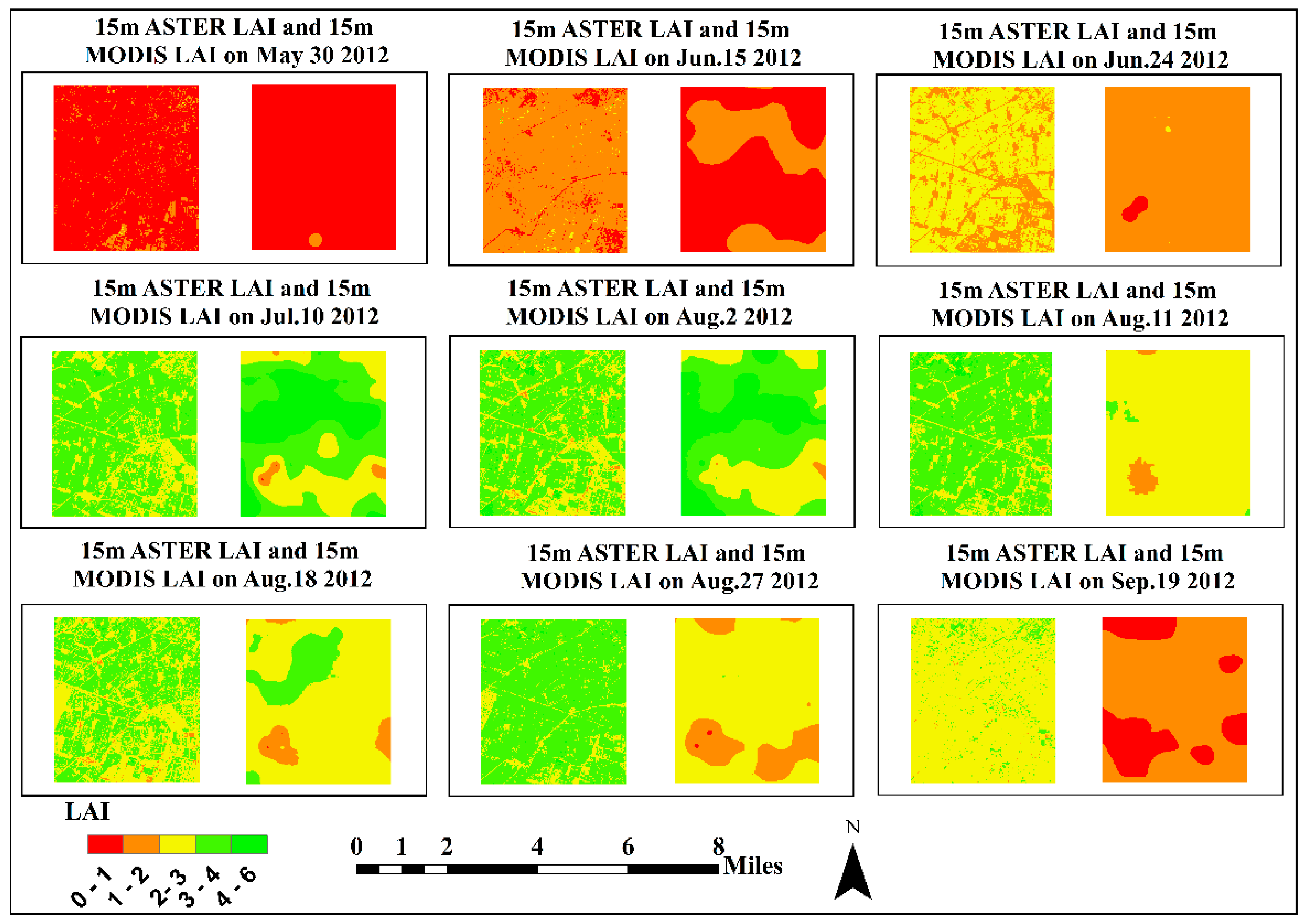
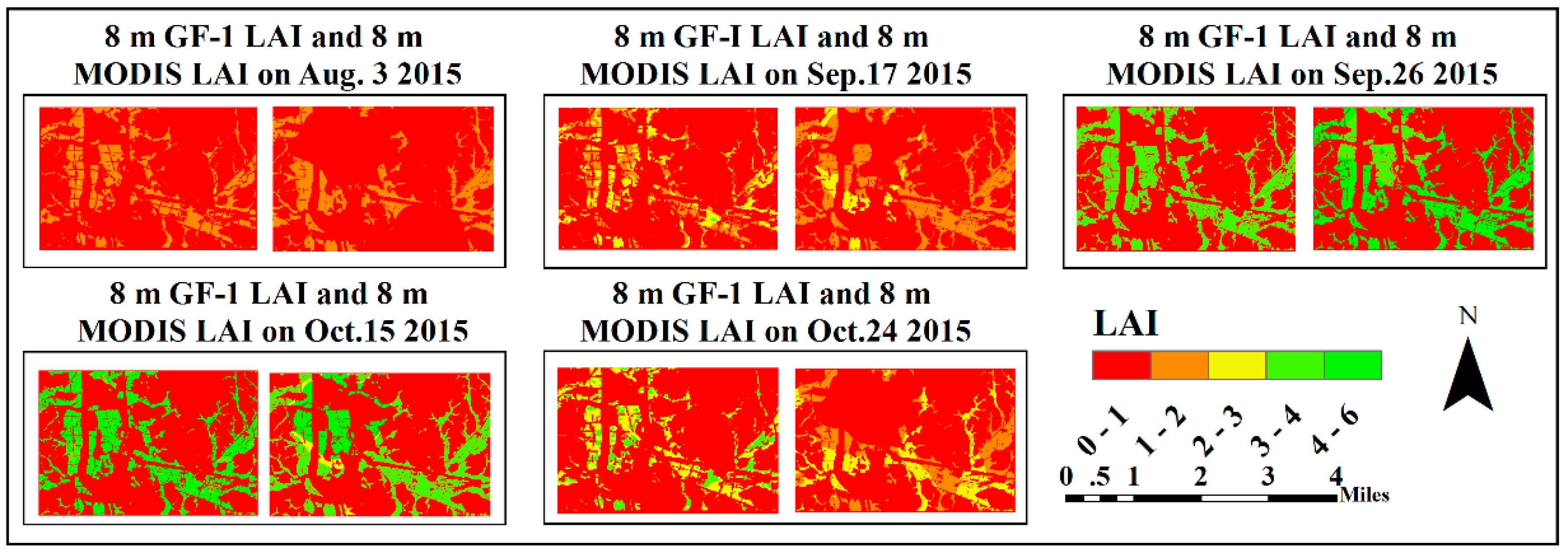
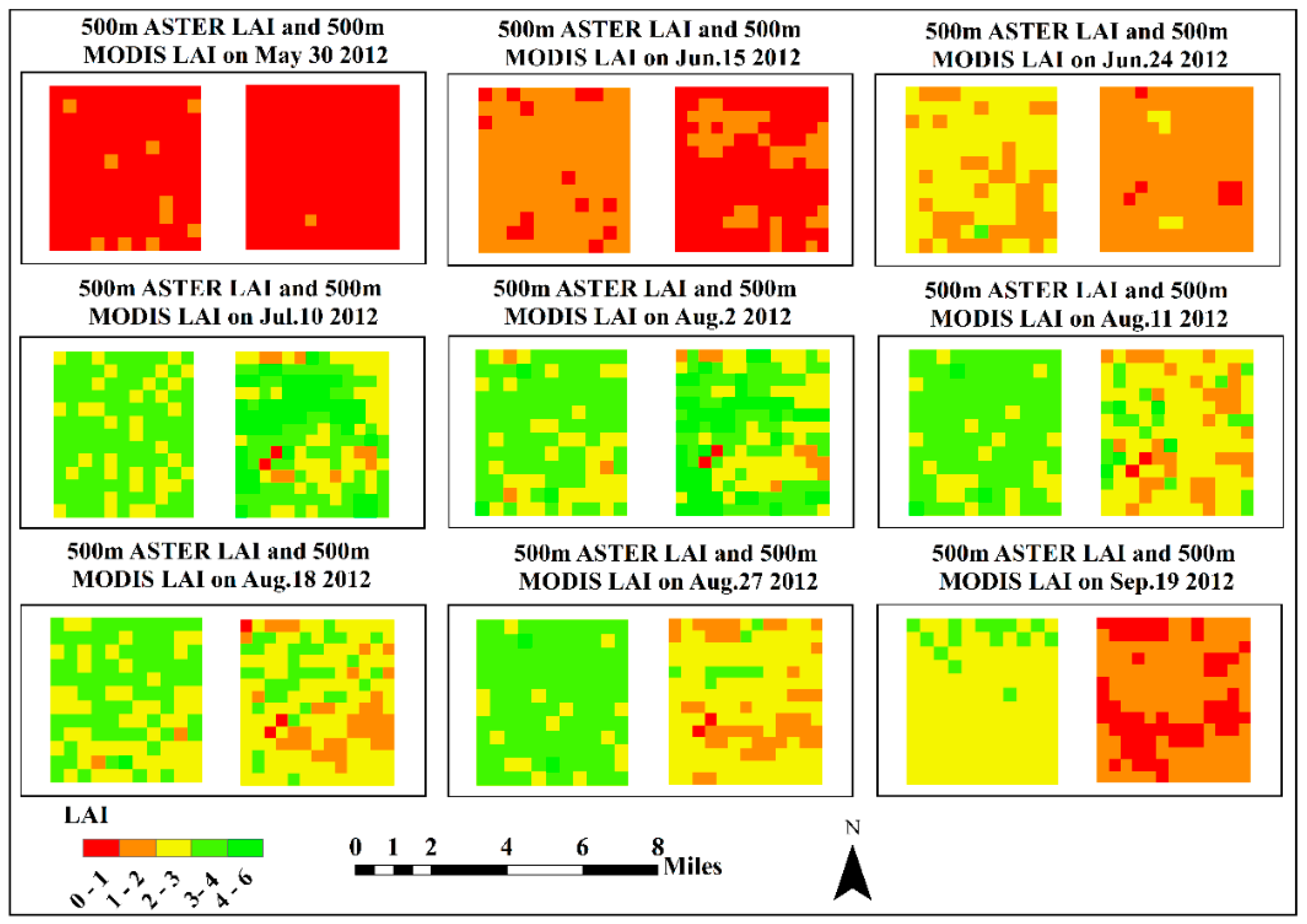
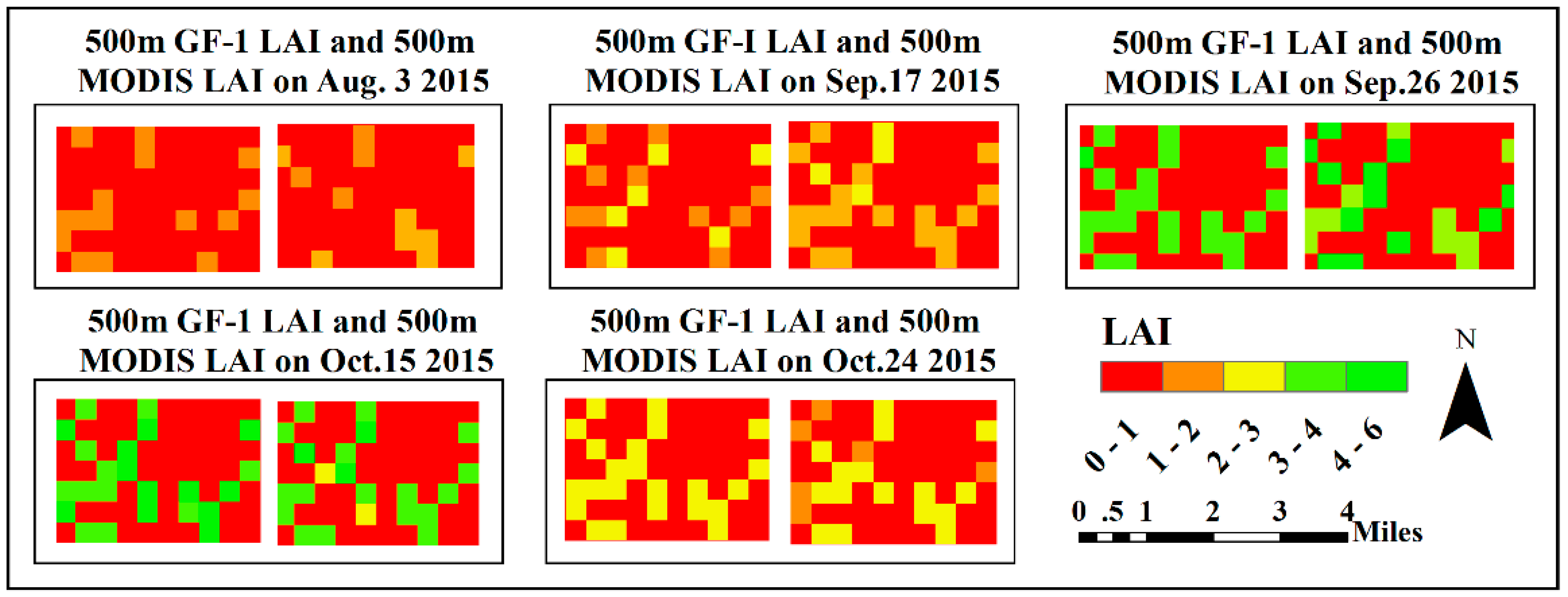
3.1. Distribution Map of Multi-Scale ASTER, GF-1, and MODIS LAI over Crop during Its Growth Cycle
3.2. Multi-Scale Validation of MODIS LAI Product
4. Discussion
4.1. Comparison with Other Similar Studies
4.2. Prospects for Future Studies
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moran, M.S.; Maas, S.J.; Pinter, P.J. Combining remote sensing and modeling for estimating surface evaporation and biomass production. Remote Sens. Rev. 1995, 12, 335–353. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Li, F.; Prueger, J.H.; Mecikalski, J.R. Effects of Vegetation Clumping on Two–Source Model Estimates of Surface Energy Fluxes from an Agricultural Landscape during SMACEX. J. Hydrometeorol. 2005, 6, 892–909. [Google Scholar] [CrossRef]
- Doraiswamy, P. Crop condition and yield simulations using Landsat and MODIS imagery. Remote Sens. Environ. 2004, 92, 548–559. [Google Scholar] [CrossRef]
- Sun, C.; Liu, L.; Guan, L.; Jiao, Q.; Peng, D. Validation and error analysis of the MODIS LAI product in Xilinhot grassland. J. Remote Sens. 2014, 18, 518–536. [Google Scholar]
- Morisette, J.T.; Baret, F.; Privette, J.L.; Myneni, R.B.; Nickeson, J.E.; Garrigues, S.; Shabanov, N.V.; Fernandes, R.A.; Leblanc, S.G.; Kalacska, M.; et al. Validation of global moderate-resolution LAI products: A framework proposed within the CEOS land product validation subgroup. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1804–1817. [Google Scholar] [CrossRef]
- Garrigues, S.; Lacaze, R.; Baret, F.; Morisette, J.T.; Weiss, M.; Nickeson, J.E.; Fernandes, R.; Plummer, S.; Shabanov, N.V.; Myneni, R.B.; et al. Validation and intercomparison of global Leaf Area Index products derived from remote sensing data. J. Geophys. Res. Biogeosciences 2008, 113. [Google Scholar] [CrossRef]
- Fang, H.; Wei, S.; Liang, S. Validation of MODIS and CYCLOPES LAI products using global field measurement data. Remote Sens. Environ. 2012, 119, 43–54. [Google Scholar] [CrossRef]
- Yang, Y.; Li, A.; Jin, H.; Yin, G.; Zhao, W.; Lei, G.; Bian, J. Intercomparison Among GEOV1, GLASS and MODIS LAI Products over Mountainous Area in Southwestern China. Remote Sens. Technol. Appl. 2016, 31, 438–450. [Google Scholar]
- Gessner, U.; Niklaus, M.; Kuenzer, C.; Dech, S. Intercomparison of leaf area index products for a gradient of sub-humid to arid environments in West Africa. Remote Sens. 2013, 5, 1235–1257. [Google Scholar] [CrossRef]
- Jin, H.; Li, A.; Bian, J.; Nan, X.; Zhao, W.; Zhang, Z.; Yin, G. Intercomparison and validation of MODIS and GLASS leaf area index (LAI) products over mountain areas: A case study in southwestern China. Int. J. Appl. Earth Obs. Geoinf. 2017, 55, 52–67. [Google Scholar] [CrossRef]
- Sea, W.B.; Choler, P.; Beringer, J.; Weinmann, R.A.; Hutley, L.B.; Leuning, R. Documenting improvement in leaf area index estimates from MODIS using hemispherical photos for Australian savannas. Agric. For. Meteorol. 2011, 151, 1453–1461. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, J.; Liu, Q. Review article: Global LAI ground validation dataset and product validation framework. Adv. Earth Sci. 2012, 27, 165–174. [Google Scholar]
- Liu, Y.; Wang, J.; Zhou, H.; Xue, H. Upscaling approach for validation of LAI products derived from remote sensing observation. J. Remote Sens. 2014, 18, 1189–1198. [Google Scholar]
- Yin, G.; Li, A.; Jin, H.; Zhao, W.; Bian, J.; Qu, Y.; Zeng, Y.; Xu, B. Derivation of temporally continuous LAI reference maps through combining the LAI Net observation system with CACAO. Agric. For. Meteorol. 2017, 233, 209–221. [Google Scholar] [CrossRef]
- Liu, L. Simulation and correction of spatialscaling effects for leaf area index. J. Remote Sens. 2014, 18, 1158–1168. [Google Scholar]
- Yang, J.; Chen, H.; Borjigin, N.; Zhao, M.; Zhou, Y.; Huang, Y. Validation of the MODIS LAI product in Qinghai Lake Basin combined with field measurements using Landsat 8 OLI data. Acta Ecol. Sin. 2017, 37, 322–331. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, R.; Hu, Y.; Fan, S.; Feng, P. Generating high spatiotemporal resolution LAI based on MODIS/GF-1 data and combined kriging-cressman interpolation. Int. J. Agric. Biol. Eng. 2016, 9, 120–131. [Google Scholar]
- Houborg, R.; Mccabe, M.F.; Gao, F. A Spatio-Temporal Enhancement Method for medium resolution LAI (STEM-LAI). Int. J. Appl. Earth Obs. Geoinf. 2016, 47, 15–29. [Google Scholar] [CrossRef]
- Qu, Y.; Zhu, Y.; Han, W.; Wang, J.; Ma, M. Crop leaf area index observations with a wireless sensor network and its potential for validating remote sensing products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 431–444. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Wang, W.; Hu, X.; Xu, Z.; Wen, J.; et al. A multiscale dataset for understanding complex eco-hydrological processes in a heterogeneous oasis system. Sci. Data 2017, 4, 170083. [Google Scholar] [CrossRef] [PubMed]
- Available online: http://www.heihedata.org (accessed on 10 October 2019).
- LP DAAC - MOD15A2H. Available online: https://lpdaac.usgs.gov/products/mod15a2hv006/ (accessed on 20 October 2019).
- Kancheva, R.; Georgiev, G. Assessing Cd-induced stress from plant spectral response. In Proceedings of the SPIE—The International Society for Optical Engineering, Amsterdam, The Netherlands, 22–25 September 2014; Volume 9239, pp. 1–12. [Google Scholar]
- Krzywinski, M.; Altman, N. Multiple linear regression. Nat. Methods 2015, 66, 1103–1104. [Google Scholar] [CrossRef] [PubMed]
- Feret, J.B.; François, C.; Asner, G.P.; Gitelsond, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Gu, C.; Du, H.; Zhou, G.; Han, N.; Xu, X.; Zhao, X.; Sun, X. Retrieval of leaf area index of Moso bamboo forest with Landsat Thematic Mapper image based on PROSAIL canopy radiative transfer model. Chin. J. Appl. Ecol. 2013, 24, 2248–2256. [Google Scholar]
- Li, H. Leaf Area Index Retrieval Based on Prospect, Liberty and Geosail Models. Sci. Silvae Sin. 2011, 47, 75–81. [Google Scholar]
- Krivoruchko, K.; Butler, K. Unequal Probability-Based Spatial Sampling; Esri: Redlands, CA, USA, 2013. [Google Scholar]
- Goovaerts, P. Kriging and Semivariogram Deconvolution in the Presence of Irregular Geographical Units. Math. Geosci. 2008, 40, 101–128. [Google Scholar] [CrossRef]
- Omre, H. Bayesian kriging-merging observations and qualified guesses in kriging. Math. Geol. 1987, 19, 25–39. [Google Scholar] [CrossRef]
- Fabijańczyk, P.; Zawadzki, J.; Magiera, T. Magnetometric assessment of soil contamination in problematic area using empirical Bayesian and indicator kriging: A case study in Upper Silesia, Poland. Geoderma 2017, 308, 69–77. [Google Scholar] [CrossRef]
- John, I.; Russell, C.; Timothy, L.; Andrew, P. Uncertainty Analysis in the Creation of a Fine-Resolution Leaf Area Index (LAI) Reference Map for Validation of Moderate Resolution LAI Products. Remote Sens. 2015, 7, 1397–1421. [Google Scholar]
- Claverie, M.; Weiss, M.; Frédéric, B.; Hagolle, O.; Demarez, V. Validation of coarse spatial resolution LAI and FAPAR time series over cropland in southwest France. Remote Sens. Environ. 2013, 139, 216–230. [Google Scholar] [CrossRef]
- Serbin, S.P.; Ahl, D.E.; Gower, S.T. Spatial and temporal validation of the MODIS LAI and FPAR products across a boreal forest wildfire chronosequence. Remote Sens. Environ. 2013, 133, 71–84. [Google Scholar] [CrossRef]
- Jia, S.; Ma, M.; Yu, W. Validation of the LAI Product in Heihe River Basin. Remote Sens. Technol. Appl. 2014, 29, 1037–1045. [Google Scholar]
- Qu, Y.; Han, W.; Ma, M. Retrieval of a Temporal High-Resolution Leaf Area Index (LAI) by Combining MODIS LAI and ASTER Reflectance Data. Remote Sens. 2015, 7, 195–210. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, R.; Chen, J.; Cheng, X.; Zheng, G. Current Status and Perspectives of Leaf Area Index Retrieval from Optical Remote Sensing Data. Geo-Inf. Sci. 2013, 15, 734. [Google Scholar] [CrossRef]
- Jing, W.; Yang, Y.; Yue, X.; Zhao, X. A Spatial Downscaling Algorithm for Satellite-Based Precipitation over the Tibetan Plateau Based on NDVI, DEM, and Land Surface Temperature. Remote Sens. 2016, 8, 655. [Google Scholar] [CrossRef]
- Im, J.; Park, S.; Rhee, J.; Baik, J.; Choi, M. Downscaling of AMSR-E soil moisture with MODIS products using machine learning approaches. Environ. Earth Sci. 2016, 75, 1120. [Google Scholar] [CrossRef]
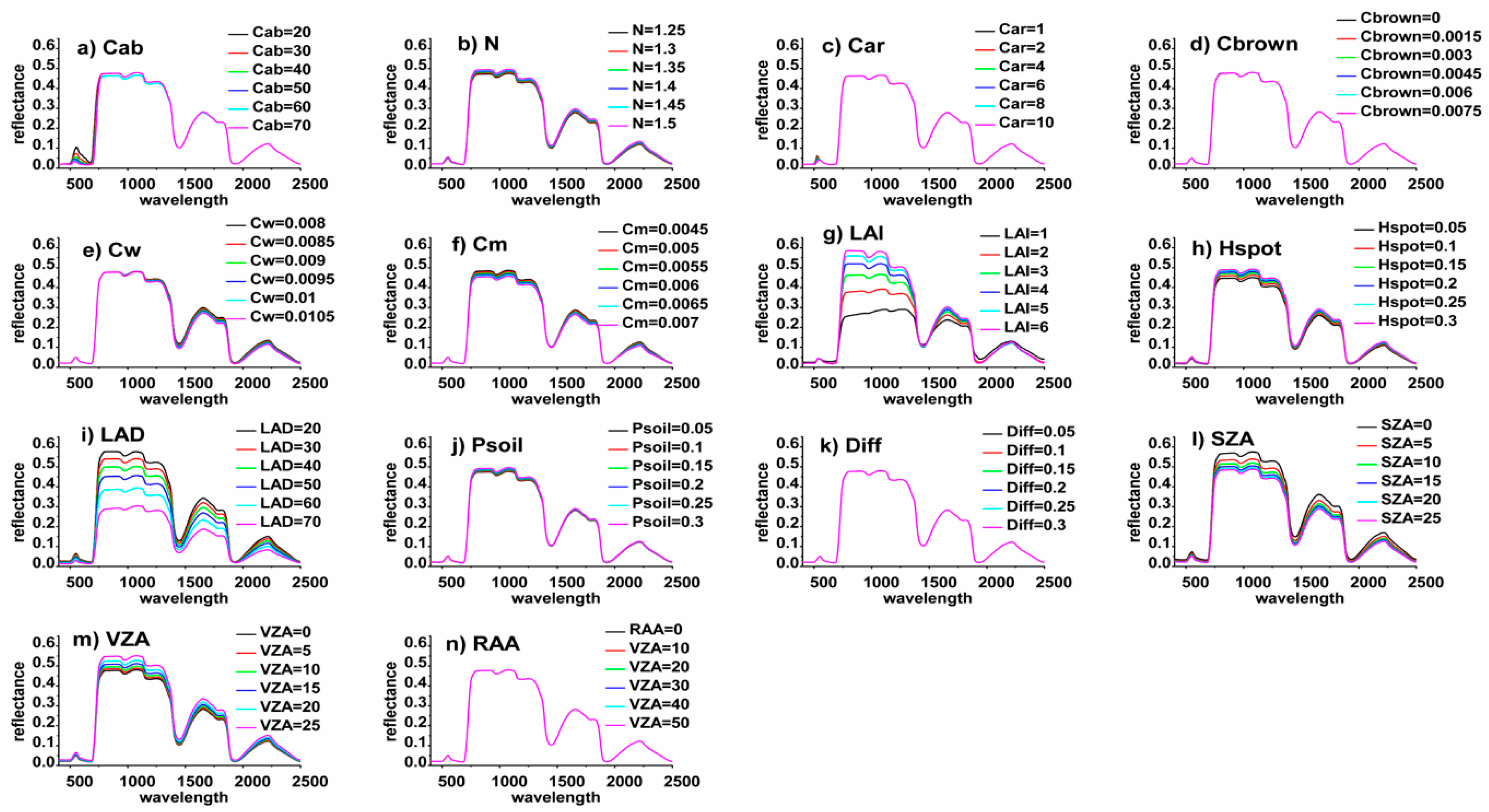
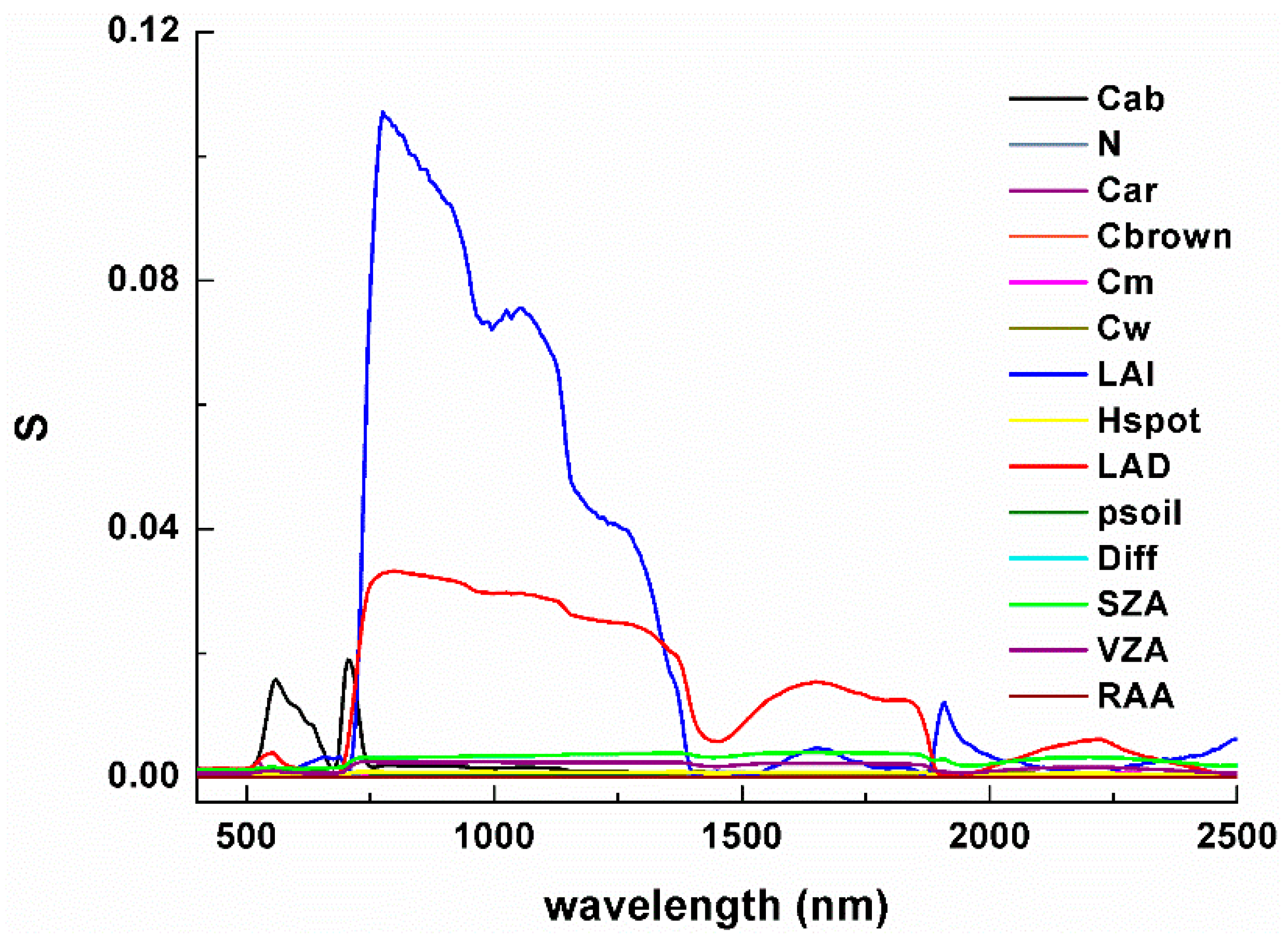
| Parameters | Units | Min | Max | Step |
|---|---|---|---|---|
| leaf structure index N | unitless | 1.3 | 1.3 | - |
| leaf chlorophyll content a + b Cab | (μg/cm2) | 20 | 70 | 5 |
| carotenoid content Car | (μg/cm2) | 8 | 8 | - |
| brown pigment Cbrown | (μg/cm2) | 0 | 0 | - |
| water content Cw | (g/cm2) | 0.0095 | 0.0095 | - |
| dry matter content Cm | (μg/cm2) | 0.0015 | 0.0015 | - |
| leaf area index LAI | (m2/m2) | 0.05 | 7 | 0.05 |
| hot parameter Hspot | (m2/m2) | 0.2 | 0.2 | - |
| leaf angle distribution LAD | (°) | 20 | 70 | 5 |
| diffuse reflection coefficient Diff | (fraction) | 0.2 | 0.2 | - |
| soil coefficient | unitless | 0.5 | 0.5 | - |
| Sun zenith angle SZA | (°) | 32 | 32 | - |
| view zenith angle VZA | (°) | 0 | 0 | - |
| Relative azimuth angle RAA | (°) | 0 | 0 | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Qu, Y.; Xia, Z.; Peng, Y.; Liu, Z. Multi-Scale Validation of MODIS LAI Products Based on Crop Growth Period. ISPRS Int. J. Geo-Inf. 2019, 8, 547. https://doi.org/10.3390/ijgi8120547
Wang T, Qu Y, Xia Z, Peng Y, Liu Z. Multi-Scale Validation of MODIS LAI Products Based on Crop Growth Period. ISPRS International Journal of Geo-Information. 2019; 8(12):547. https://doi.org/10.3390/ijgi8120547
Chicago/Turabian StyleWang, Ting, Yonghua Qu, Ziqing Xia, Yiping Peng, and Zhenhua Liu. 2019. "Multi-Scale Validation of MODIS LAI Products Based on Crop Growth Period" ISPRS International Journal of Geo-Information 8, no. 12: 547. https://doi.org/10.3390/ijgi8120547
APA StyleWang, T., Qu, Y., Xia, Z., Peng, Y., & Liu, Z. (2019). Multi-Scale Validation of MODIS LAI Products Based on Crop Growth Period. ISPRS International Journal of Geo-Information, 8(12), 547. https://doi.org/10.3390/ijgi8120547





