Using a Complex Network to Analyze the Effects of the Three Gorges Dam on Water Level Fluctuation in Poyang Lake
Abstract
1. Introduction
2. Materials and Methods
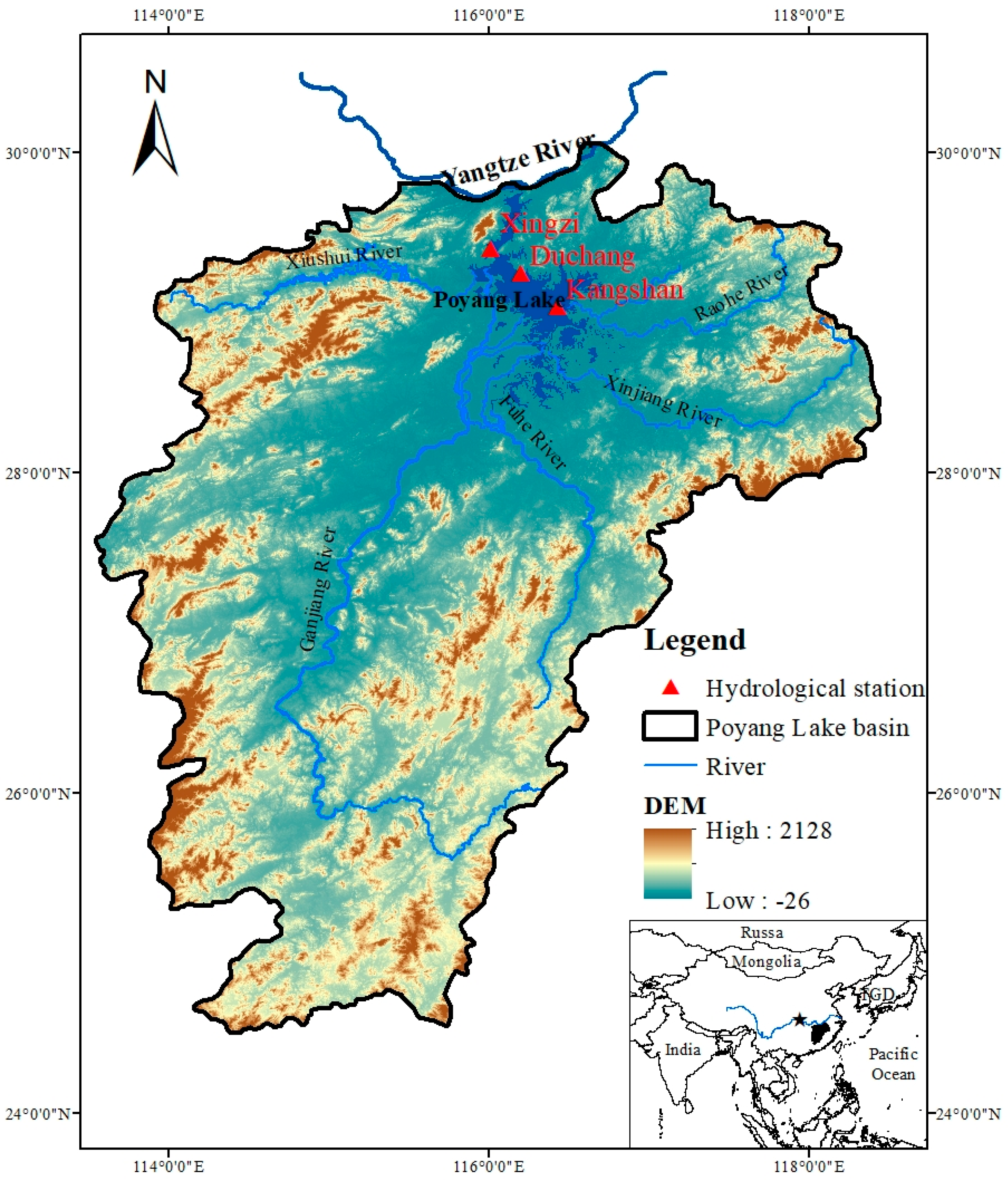
2.1. Study Area and Data
2.2. Methods
2.2.1. Change-Point Analysis
2.2.2. Complex Network Generated by Coarse-Graining Processing
2.2.3. The Measurement of Betweenness Centrality (BC) of Complex Network Topology Parameters
3. Results
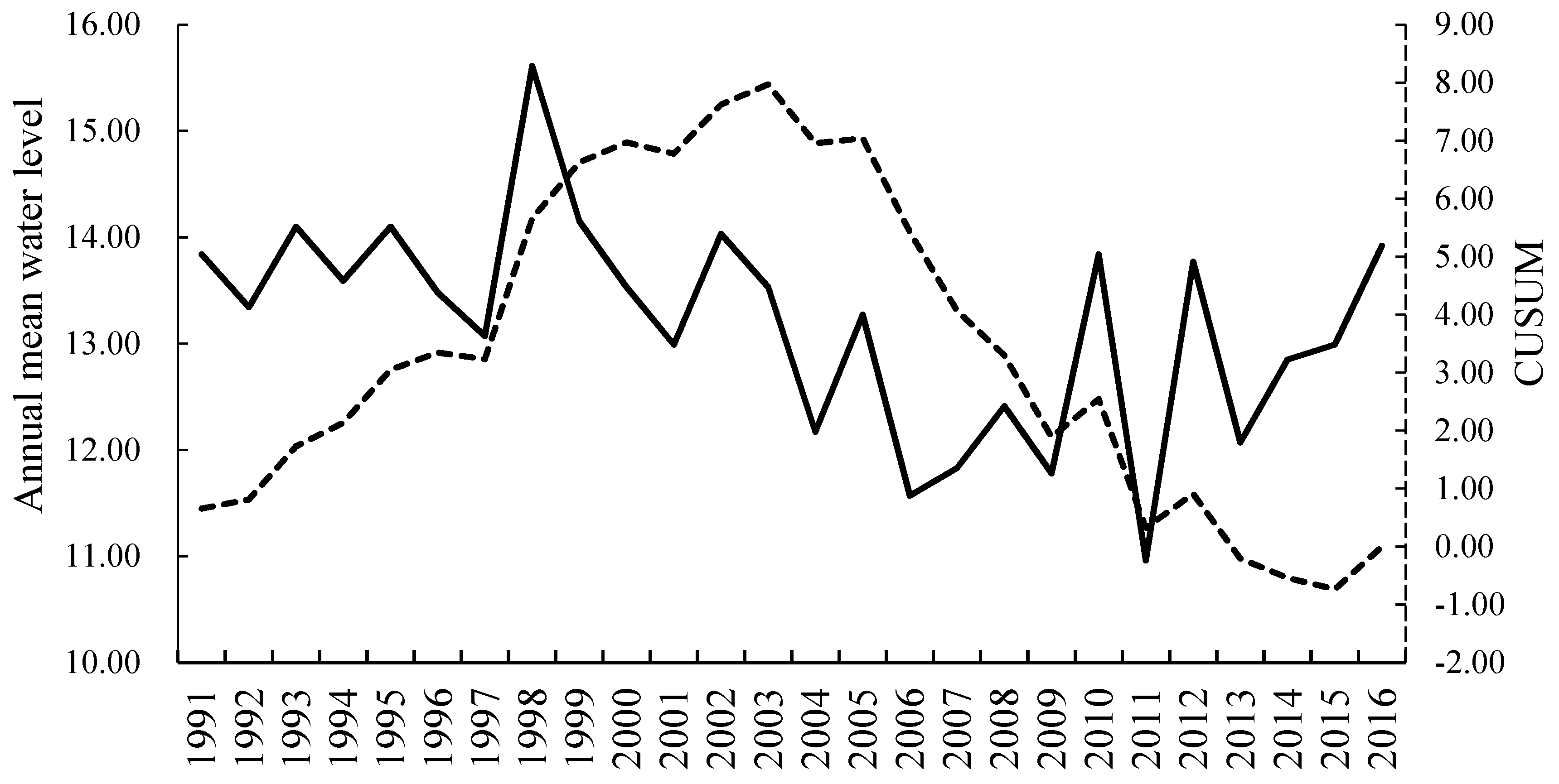
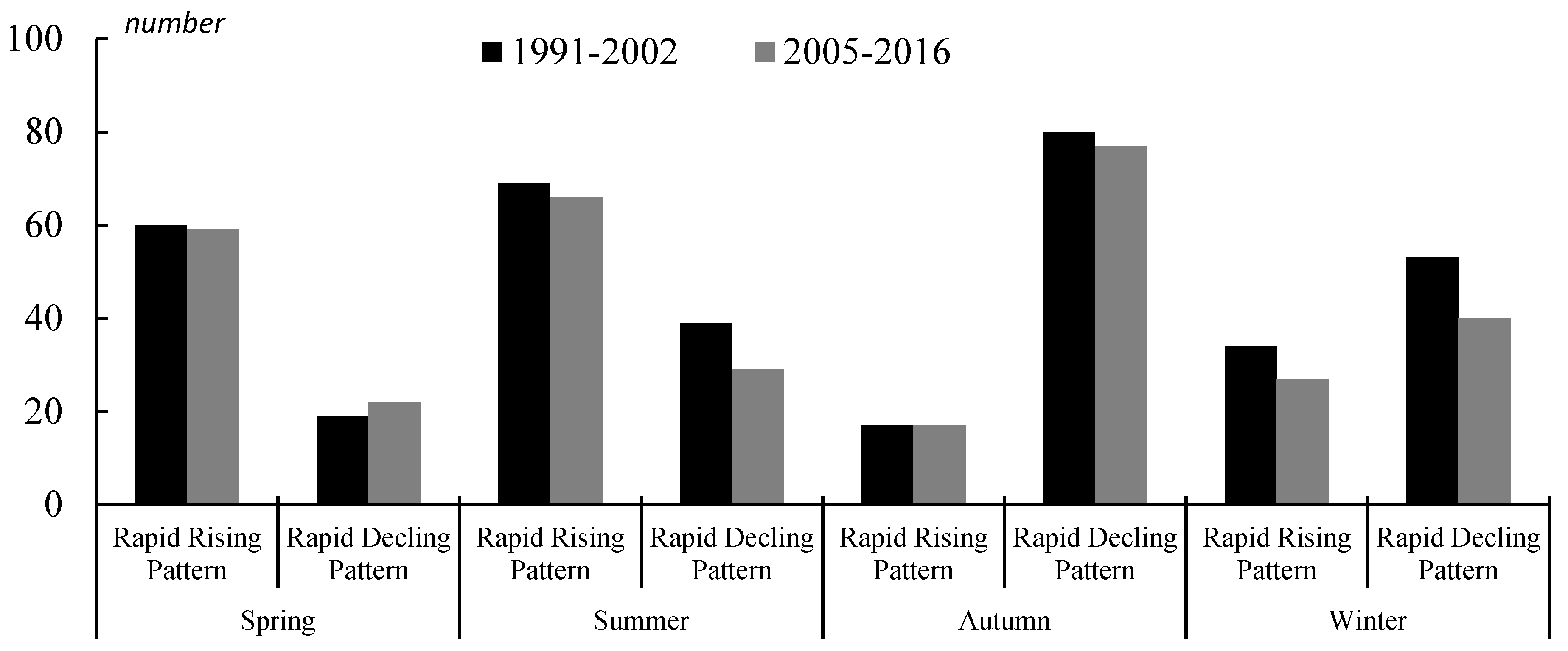
3.1. Change Point (CPA) Analysis
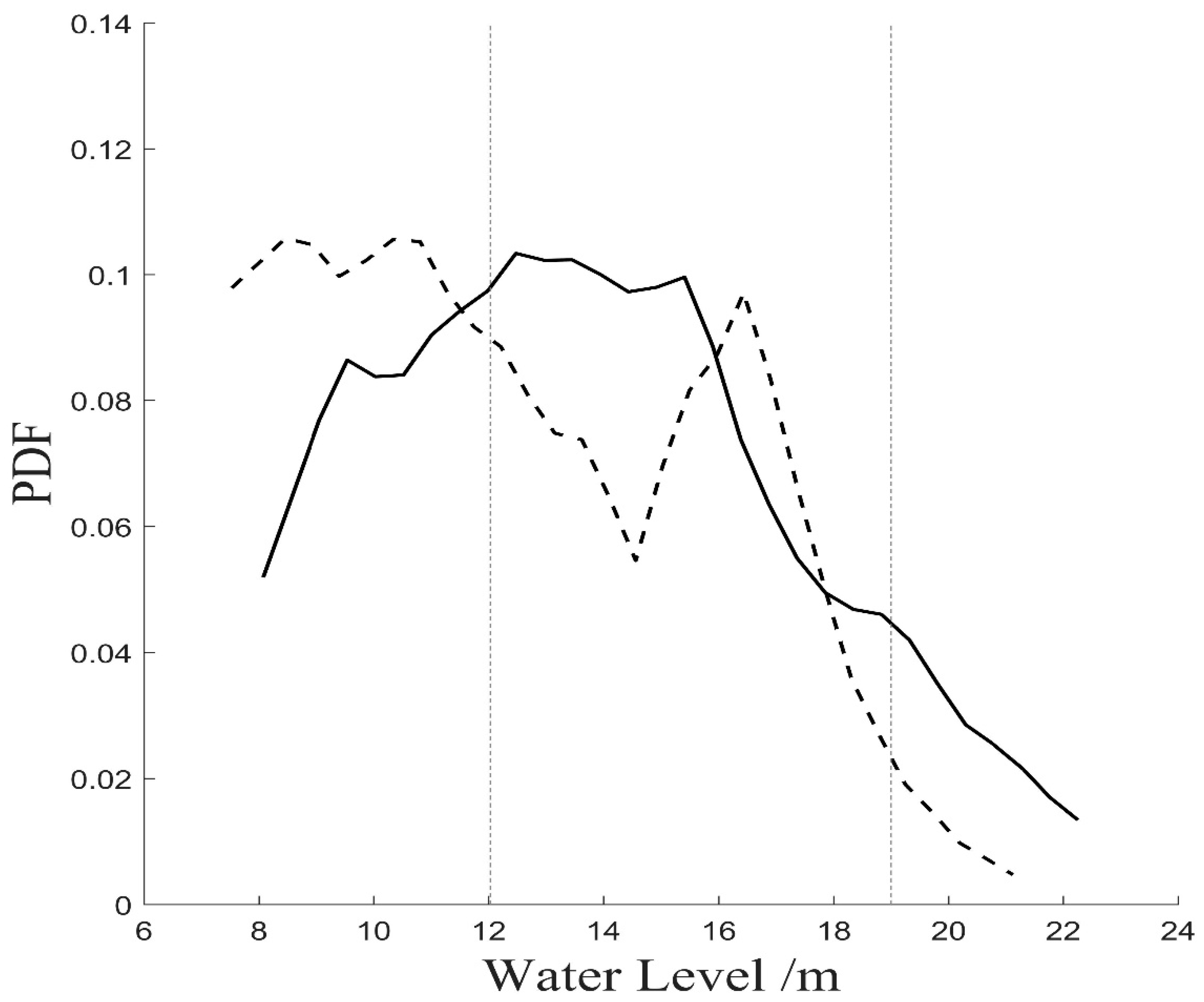
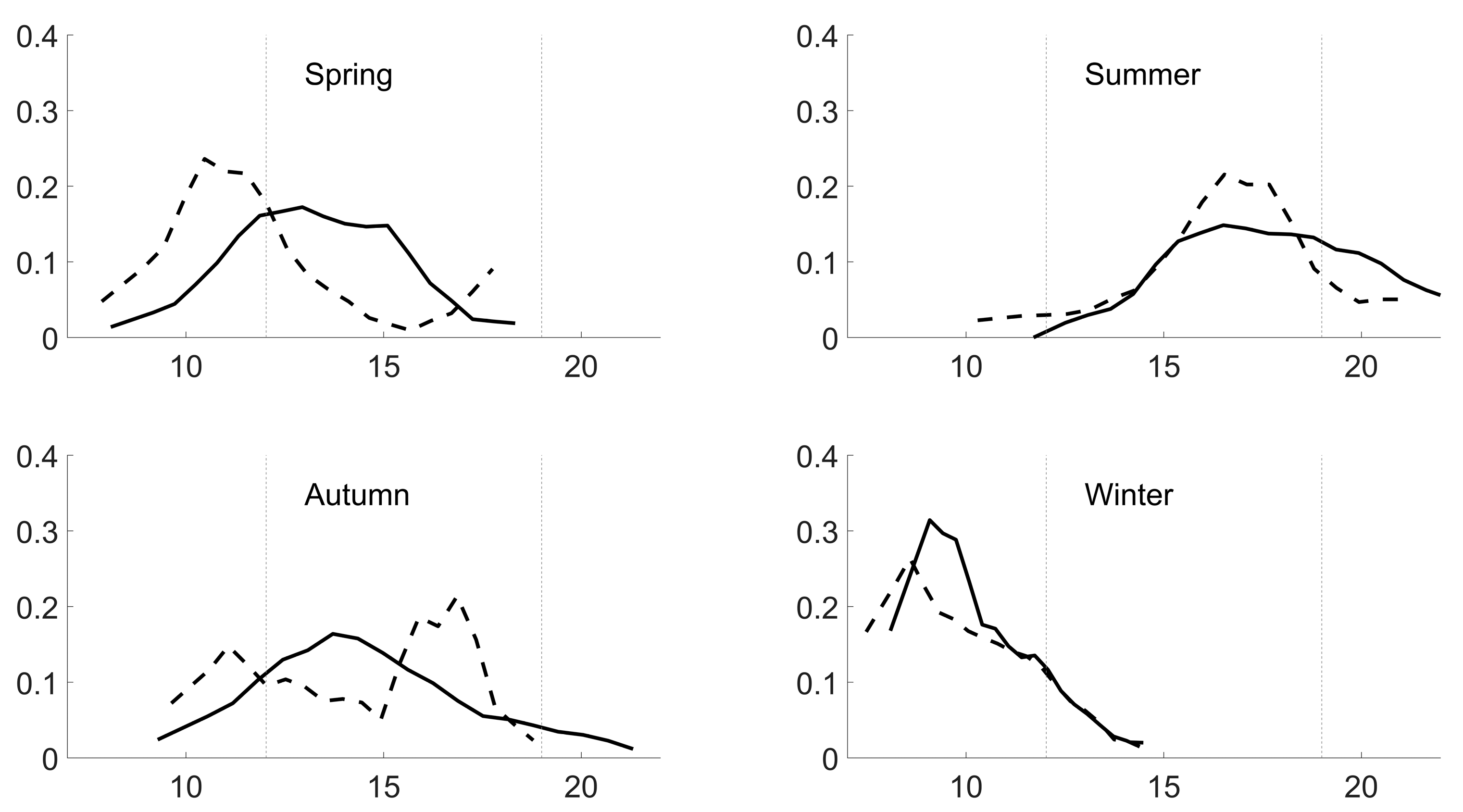
3.2. Distribution of the Water Level Using Frequency Distribution
3.3. Analysis of the Hydrological Complex Network of the Two Periods
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Wang, C.; Bai, W.; Wang, Z.; Tu, Y.; Yangjaen, D.G. Alpine wetlands in the Lhasa River basin, China. J. Geogr. Sci. 2010, 20, 375–388. [Google Scholar] [CrossRef]
- Brinson, M.M.; Malvárez, A.I. Temperate freshwater wetlands: Types, status, and threats. Environ. Conserv. 2002, 29, 115–133. [Google Scholar] [CrossRef]
- Ming, J.; Xian-Guo, L.; Lin-Shu, X.; Li-juan, C.; Shouzheng, T. Flood mitigation benefit of wetland soil—A case study in Momoge National Nature Reserve in China. Ecol. Econ. 2007, 61, 217–223. [Google Scholar] [CrossRef]
- Ouyang, X.; Lee, S.Y.; Connolly, R.M.; Kainz, M.J. Spatially-explicit valuation of coastal wetlands for cyclone mitigation in Australia and China. Sci. Rep. 2018, 8, 3035. [Google Scholar] [CrossRef]
- Verhoeven, J.T.; Meuleman, A.F. Wetlands for wastewater treatment: Opportunities and limitations. Ecol. Eng. 1999, 12, 5–12. [Google Scholar] [CrossRef]
- Erwin, K.L. Wetlands and global climate change: The role of wetland restoration in a changing world. Wetl. Ecol. Manag. 2009, 17, 71. [Google Scholar] [CrossRef]
- Birol, E.; Cox, V. Using choice experiments to design wetland management programmes: The case of severn estuary wetland, UK. J. Environ. Plan. Manag. 2007, 50, 363–380. [Google Scholar] [CrossRef]
- Berthou, S.; Mailler, S.; Drobinski, P.; Arsouze, T.; Bastin, S.; Béranger, K.; Flaounas, E.; Lebeaupin Brossier, C.; Somot, S.; Stéfanon, M. Influence of submonthly air–sea coupling on heavy precipitation events in the western mediterranean basin. Q. J. R. Meteorol. Soc. 2016, 142, 453–471. [Google Scholar] [CrossRef]
- Hulme, A.L.; Martin, J.E. Synoptic-and frontal-scale influences on tropical transition events in the atlantic basin. Part i: A six-case survey. Mon. Weather Rev. 2009, 137, 3605–3625. [Google Scholar] [CrossRef]
- Ma, K.; You, L.; Liu, J.; Zhang, M. A hybrid wetland map for China: A synergistic approach using census and spatially explicit datasets. PLoS ONE 2012, 7, e47814. [Google Scholar] [CrossRef][Green Version]
- Costanza, R.; d’Arge, R.; De Groot, R.; Farber, S.; Grasso, M.; Hannon, B.; Limburg, K.; Naeem, S.; O’neill, R.V.; Paruelo, J. The value of the world’s ecosystem services and natural capital. Nature 1997, 387, 253. [Google Scholar] [CrossRef]
- Carpenter, S.R.; Stanley, E.H.; Vander Zanden, M.J. State of the world’s freshwater ecosystems: Physical, chemical, and biological changes. Annu. Rev. Environ. Resour. 2011, 36, 75–99. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; McIntyre, P.B.; Gessner, M.O.; Dudgeon, D.; Prusevich, A.; Green, P.; Glidden, S.; Bunn, S.E.; Sullivan, C.A.; Liermann, C.R. Global threats to human water security and river biodiversity. Nature 2010, 467, 555. [Google Scholar] [CrossRef] [PubMed]
- Webb, E.L.; Friess, D.A.; Krauss, K.W.; Cahoon, D.R.; Guntenspergen, G.R.; Phelps, J. A global standard for monitoring coastal wetland vulnerability to accelerated sea-level rise. Nat. Clim. Chang. 2013, 3, 458. [Google Scholar] [CrossRef]
- Walling, D. Human impact on land–ocean sediment transfer by the world’s rivers. Geomorphology 2006, 79, 192–216. [Google Scholar] [CrossRef]
- Nilsson, C.; Reidy, C.A.; Dynesius, M.; Revenga, C. Fragmentation and flow regulation of the world’s large river systems. Science 2005, 308, 405–408. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.; Liu, G.; Pi, J.; Chen, G.; Li, C. On the river–lake relationship of the middle yangtze reaches. Geomorphology 2007, 85, 197–207. [Google Scholar] [CrossRef]
- Fu, B.-J.; Wu, B.-F.; Lü, Y.-H.; Xu, Z.-H.; Cao, J.-H.; Niu, D.; Yang, G.-S.; Zhou, Y.-M. Three gorges project: Efforts and challenges for the environment. Prog. Phys. Geogr. 2010, 34, 741–754. [Google Scholar] [CrossRef]
- Sun, Z.; Huang, Q.; Opp, C.; Hennig, T.; Marold, U. Impacts and implications of major changes caused by the three gorges dam in the middle reaches of the Yangtze River, China. Water Resour. Manag. 2012, 26, 3367–3378. [Google Scholar] [CrossRef]
- Xu, K.; Milliman, J.D. Seasonal variations of sediment discharge from the yangtze river before and after impoundment of the three gorges dam. Geomorphology 2009, 104, 276–283. [Google Scholar] [CrossRef]
- Gong, G.C.; Chang, J.; Chiang, K.P.; Hsiung, T.M.; Hung, C.C.; Duan, S.W.; Codispoti, L. Reduction of primary production and changing of nutrient ratio in the East China Sea: Effect of the three gorges dam? Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, J.; Xu, X. Influence of the three gorges dam on downstream delivery of sediment and its environmental implications, yangtze river. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Guo, H.; Hu, Q.; Zhang, Q.; Feng, S. Effects of the three gorges dam on yangtze river flow and river interaction with Poyang Lake, China: 2003–2008. J. Hydrol. 2012, 416, 19–27. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Chen, X.; Zhao, X. Dramatic inundation changes of China’s two largest freshwater lakes linked to the three gorges dam. Environ. Sci. Technol. 2013, 47, 9628–9634. [Google Scholar] [CrossRef]
- An, H.; Gao, X.; Fang, W.; Huang, X.; Ding, Y. The role of fluctuating modes of autocorrelation in crude oil prices. Phys. A Stat. Mech. Appl. 2014, 393, 382–390. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1998, 393, 440. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.-L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.; Watts, D.J. Renormalization group analysis of the small-world network model. Phys. Lett. A 1999, 263, 341–346. [Google Scholar] [CrossRef]
- Cheng, C.X.; Shi, P.J.; Song, C.Q.; Gao, J.B. Geographic big-data: A new opportunity for geography complexity study. Acta Geogr. Sin. 2018, 8, 1397–1406. [Google Scholar]
- Kaluza, P.; Kölzsch, A.; Gastner, M.T.; Blasius, B. The complex network of global cargo ship movements. J. R. Soc. Interface 2010, 7, 1093–1103. [Google Scholar] [CrossRef]
- Van den Heuvel, M.P.; Mandl, R.C.; Stam, C.J.; Kahn, R.S.; Pol, H.E.H. Aberrant frontal and temporal complex network structure in schizophrenia: A graph theoretical analysis. J. Neurosci. 2010, 30, 15915–15926. [Google Scholar] [CrossRef] [PubMed]
- Brockmann, D.; Helbing, D. The hidden geometry of complex, network-driven contagion phenomena. Science 2013, 342, 1337–1342. [Google Scholar] [CrossRef] [PubMed]
- Pagani, G.A.; Aiello, M. The power grid as a complex network: A survey. Phys. A Stat. Mech. Appl. 2013, 392, 2688–2700. [Google Scholar] [CrossRef]
- Wang, J.; Mo, H.; Wang, F.; Jin, F. Exploring the network structure and nodal centrality of China’s air transport network: A complex network approach. J. Transp. Geogr. 2011, 19, 712–721. [Google Scholar] [CrossRef]
- Yang, J.; Cheng, C.; Shen, S.; Yang, S. Comparison of complex network analysis software: Citespace, Sci 2 and Gephi. In Proceedings of the 2017 IEEE 2nd International Conference on Big Data Analysis (ICBDA), Beijing, China, 10–12 March 2017; pp. 169–172. [Google Scholar]
- Guo, Y.; Zhang, J.; Yang, Y.; Zhang, H. Modeling the fluctuation patterns of monthly inbound tourist flows to China: A complex network approach. Asia Pac. J. Tour. Res. 2015, 20, 942–953. [Google Scholar] [CrossRef]
- Li, P.; Wang, B.-H. Extracting hidden fluctuation patterns of hang seng stock index from network topologies. Phys. A Stat. Mech. Appl. 2007, 378, 519–526. [Google Scholar] [CrossRef]
- Garlaschelli, D.; Loffredo, M.I. Structure and evolution of the world trade network. Phys. A Stat. Mech. Appl. 2005, 355, 138–144. [Google Scholar] [CrossRef]
- Li, H.; An, H.; Gao, X.; Huang, J.; Xu, Q. On the topological properties of the cross-shareholding networks of listed companies in China: Taking shareholders’ cross-shareholding relationships into account. Phys. A Stat. Mech. Appl. 2014, 406, 80–88. [Google Scholar] [CrossRef]
- Shen, S.; Cheng, C.; Yang, J.; Yang, S. Visualized analysis of developing trends and hot topics in natural disaster research. PLoS ONE 2018, 13, e0191250. [Google Scholar] [CrossRef]
- Li, P.; Wang, B. An approach to hang seng index in Hong Kong stock market based on network topological statistics. Chin. Sci. Bull. 2006, 51, 624–629. [Google Scholar] [CrossRef]
- An, H.; Zhong, W.; Chen, Y.; Li, H.; Gao, X. Features and evolution of international crude oil trade relationships: A trading-based network analysis. Energy 2014, 74, 254–259. [Google Scholar] [CrossRef]
- Wang, M.; Tian, L. From time series to complex networks: The phase space coarse graining. Phys. A Stat. Mech. Appl. 2016, 461, 456–468. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Y.; Liang, D.; Deng, Y.; Pang, Y. 30+ year evolution of cu in the surface sediment of Lake Poyang, China. Chemosphere 2017, 168, 1604–1612. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Ye, X.-C.; Werner, A.D.; Li, Y.-L.; Yao, J.; Li, X.-H.; Xu, C.-Y. An investigation of enhanced recessions in Poyang Lake: Comparison of Yangtze River and local catchment impacts. J. Hydrol. 2014, 517, 425–434. [Google Scholar] [CrossRef]
- Ye, X.; Li, Y.; Li, X.; Zhang, Q. Factors influencing water level changes in China’s largest freshwater lake, Poyang Lake, in the past 50 years. Water Int. 2014, 39, 983–999. [Google Scholar] [CrossRef]
- Sheng, L.; Xiu-Ping, Z.; Rong-Fang, L.; Xiao-Hua, X.; Qun, F. Analysis the changes of annual for poyang lake wetland vegetation based on modis monitoring. Procedia Environ. Sci. 2011, 10, 1841–1846. [Google Scholar] [CrossRef]
- Li, X.; Yao, J.; Li, Y.; Zhang, Q.; Xu, C.-Y. A modeling study of the influences of yangtze river and local catchment on the development of floods in Poyang Lake, China. Hydrol. Res. 2016, 47, 102–119. [Google Scholar] [CrossRef]
- Buishand, T.A. Some methods for testing the homogeneity of rainfall records. J. Hydrol. 1982, 58, 11–27. [Google Scholar] [CrossRef]
- Radziejewski, M.; Bardossy, A.; Kundzewicz, Z.W. Detection of change in river flow using phase randomization. Hydrol. Sci. J. 2000, 45, 547–558. [Google Scholar] [CrossRef]
- Smadi, M.M.; Zghoul, A. A sudden change in rainfall characteristics in Amman, Jordan during the mid 1950s. Am. J. Environ. Sci. 2006, 2, 84–91. [Google Scholar] [CrossRef]
- Mavromatis, T.; Stathis, D. Response of the water balance in Greece to temperature and precipitation trends. Theor. Appl. Climatol. 2011, 104, 13–24. [Google Scholar] [CrossRef]
- Burdon, F.J.; McIntosh, A.R.; Harding, J.S. Habitat loss drives threshold response of benthic invertebrate communities to deposited sediment in agricultural streams. Ecol. Appl. 2013, 23, 1036–1047. [Google Scholar] [CrossRef] [PubMed]
- Tao, H.; Gemmer, M.; Bai, Y.; Su, B.; Mao, W. Trends of streamflow in the Tarim River basin during the past 50 years: Human impact or climate change? J. Hydrol. 2011, 400, 1–9. [Google Scholar] [CrossRef]
- Taylor, W.A. Change-Point Analysis: A Powerful New Tool for Detecting Changes. 2000. Available online: http://www.variation.com/cpa/tech/changepoint.html (accessed on 3 October 2018).
- Wackerbauer, R.; Witt, A.; Atmanspacher, H.; Kurths, J.; Scheingraber, H. A comparative classification of complexity measures. Chaos Solitons Fractals 1994, 4, 133–173. [Google Scholar] [CrossRef]
- Zhou, L.; Gong, Z.-Q.; Zhi, R.; Feng, G.-L. Study on the regional characteristics of the temperature changes in China based on complex network. Acta Phys. Sin. 2009, 58, 7351–7358. [Google Scholar]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef]
- Goh, K.-I.; Oh, E.; Kahng, B.; Kim, D. Betweenness centrality correlation in social networks. Phys. Rev. E 2003, 67, 017101. [Google Scholar] [CrossRef]
- Freeman, L.C.; Borgatti, S.P.; White, D.R. Centrality in valued graphs: A measure of betweenness based on network flow. Soc. Netw. 1991, 13, 141–154. [Google Scholar] [CrossRef]
- Gao, B.; Yang, D.; Yang, H. Impact of the three gorges dam on flow regime in the middle and lower yangtze river. Quat. Int. 2013, 304, 43–50. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Q.; Sun, P.; Gu, X.; Fang, Z. Minimun ecological water requirements of the poyang lake. Acta Sci. Nat. Univ. Sunyatseni 2014, 53, 149–153. [Google Scholar]
- Gan, X.Y. The Research about the Impact of Drought on Poyang Wetland; Nanchang University: Nanchang, China, 2011. [Google Scholar]
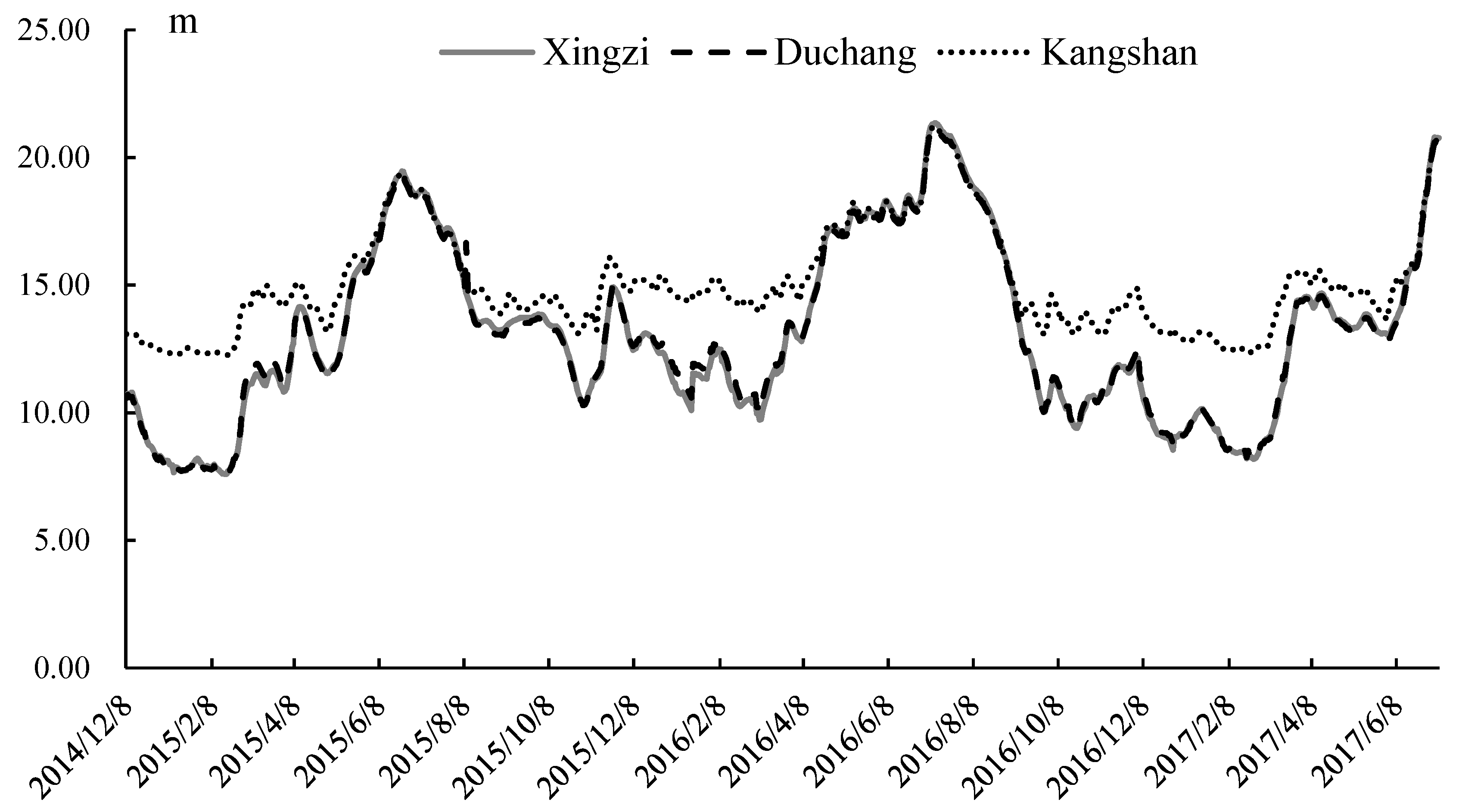


| Xingzi | Duchang | Kangshan | |
|---|---|---|---|
| Xingzi | 1 | 0.998 ** | 0.959 ** |
| Duchang | - | 1 | 0.966 ** |
| Kangshan | - | - | 1 |
| Periods | Rapid Rising Pattern | Slow Variation Pattern | Rapid Declining Pattern |
|---|---|---|---|
| 1991–2002 | 182 (24.9%) | 18 (2.5%) | 194 (26.6%) |
| 2005–2016 | 185 (25.3%) | 23 (3.2%) | 163 (22.3%) |
| 1991–2002 | Node | RRR | DDD | rrr | RRr | ddd | Rre | dDD | ede | rRR | rrR |
| BC(%) | 16.0% | 8.6% | 5.5% | 5.3% | 4.5% | 4.0% | 3.4% | 2.7% | 2.7% | 2.7% | |
| Rank | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 2005–2016 | Node | RRR | DDD | rRR | edd | rrr | eer | rre | der | RRr | eee |
| BC(%) | 9.9% | 9.4% | 5.5% | 5.0% | 4.9% | 4.8% | 4.3% | 4.2% | 4.1% | 3.7% | |
| Rank | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, L.; Zhou, Y.; Cheng, C.; Ye, S.; Shen, S. Using a Complex Network to Analyze the Effects of the Three Gorges Dam on Water Level Fluctuation in Poyang Lake. ISPRS Int. J. Geo-Inf. 2019, 8, 470. https://doi.org/10.3390/ijgi8110470
Ning L, Zhou Y, Cheng C, Ye S, Shen S. Using a Complex Network to Analyze the Effects of the Three Gorges Dam on Water Level Fluctuation in Poyang Lake. ISPRS International Journal of Geo-Information. 2019; 8(11):470. https://doi.org/10.3390/ijgi8110470
Chicago/Turabian StyleNing, Lixin, Yunkai Zhou, Changxiu Cheng, Sijing Ye, and Shi Shen. 2019. "Using a Complex Network to Analyze the Effects of the Three Gorges Dam on Water Level Fluctuation in Poyang Lake" ISPRS International Journal of Geo-Information 8, no. 11: 470. https://doi.org/10.3390/ijgi8110470
APA StyleNing, L., Zhou, Y., Cheng, C., Ye, S., & Shen, S. (2019). Using a Complex Network to Analyze the Effects of the Three Gorges Dam on Water Level Fluctuation in Poyang Lake. ISPRS International Journal of Geo-Information, 8(11), 470. https://doi.org/10.3390/ijgi8110470






