A Hybrid Framework for High-Performance Modeling of Three-Dimensional Pipe Networks
Abstract
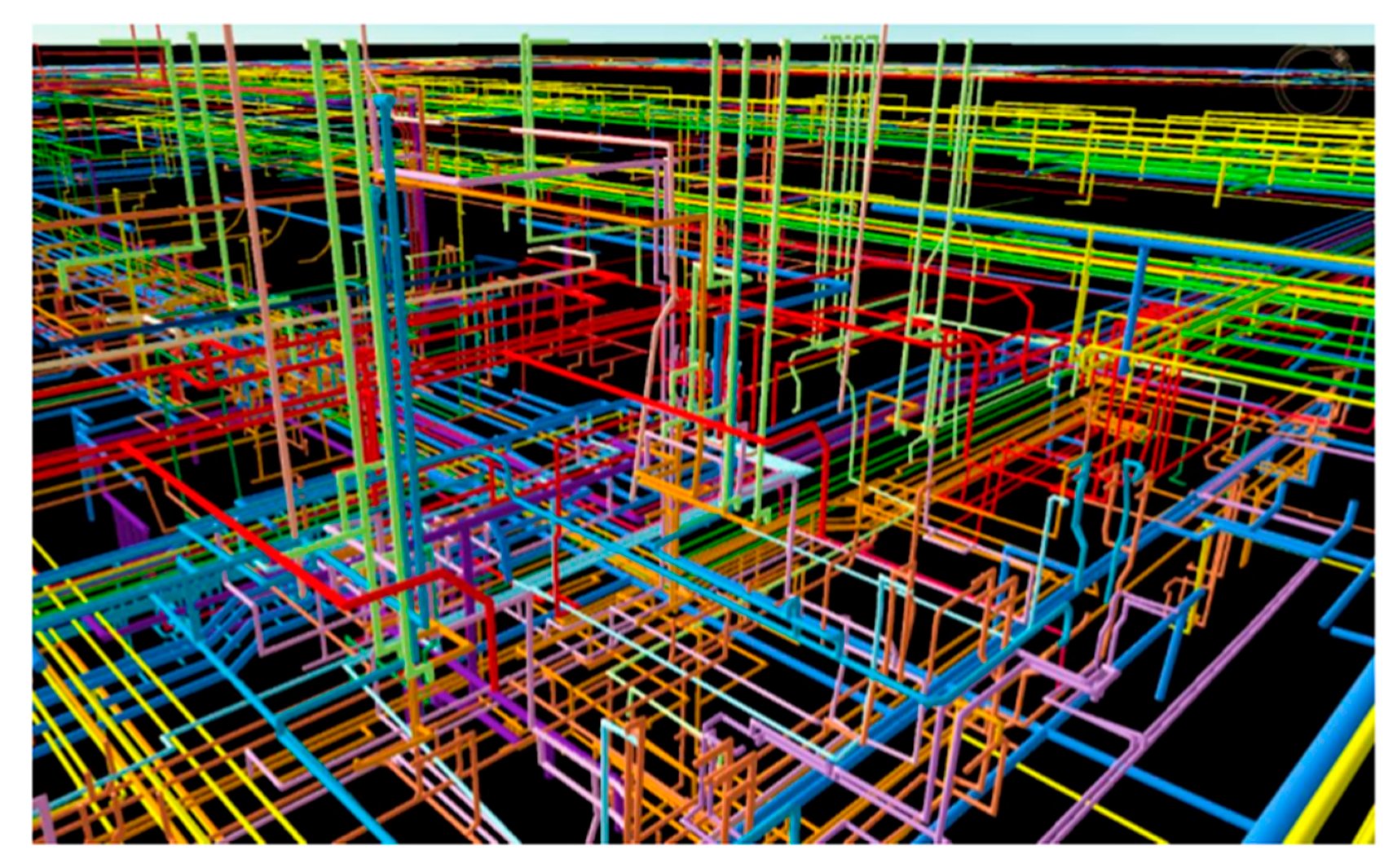
:1. Introduction
2. Pipe Network Data Model
2.1. Pipe Network Data Structure
2.2. Construction of Pipeline Model
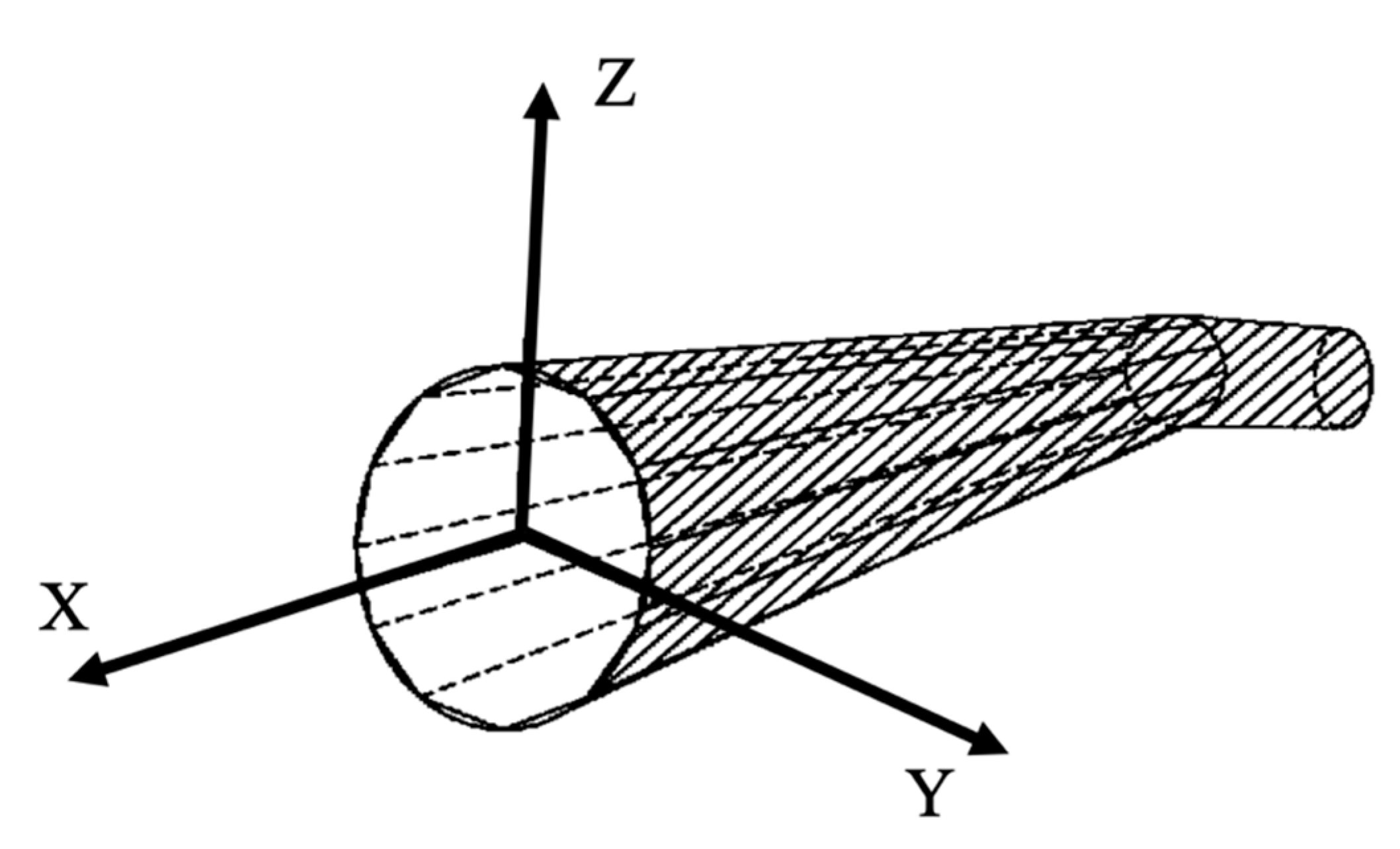
2.2.1. Coordinate Computation of Pipeline Network Model
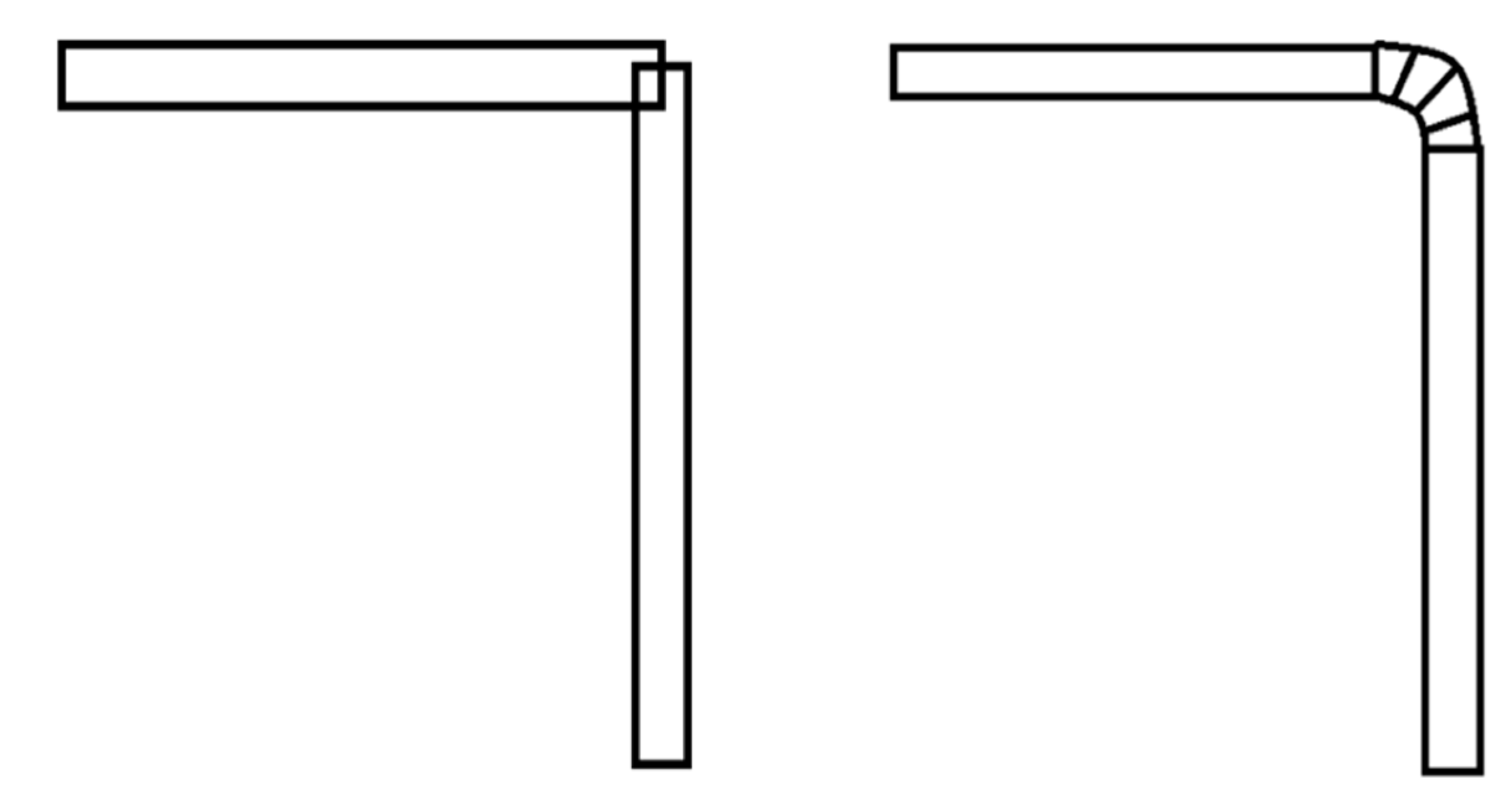
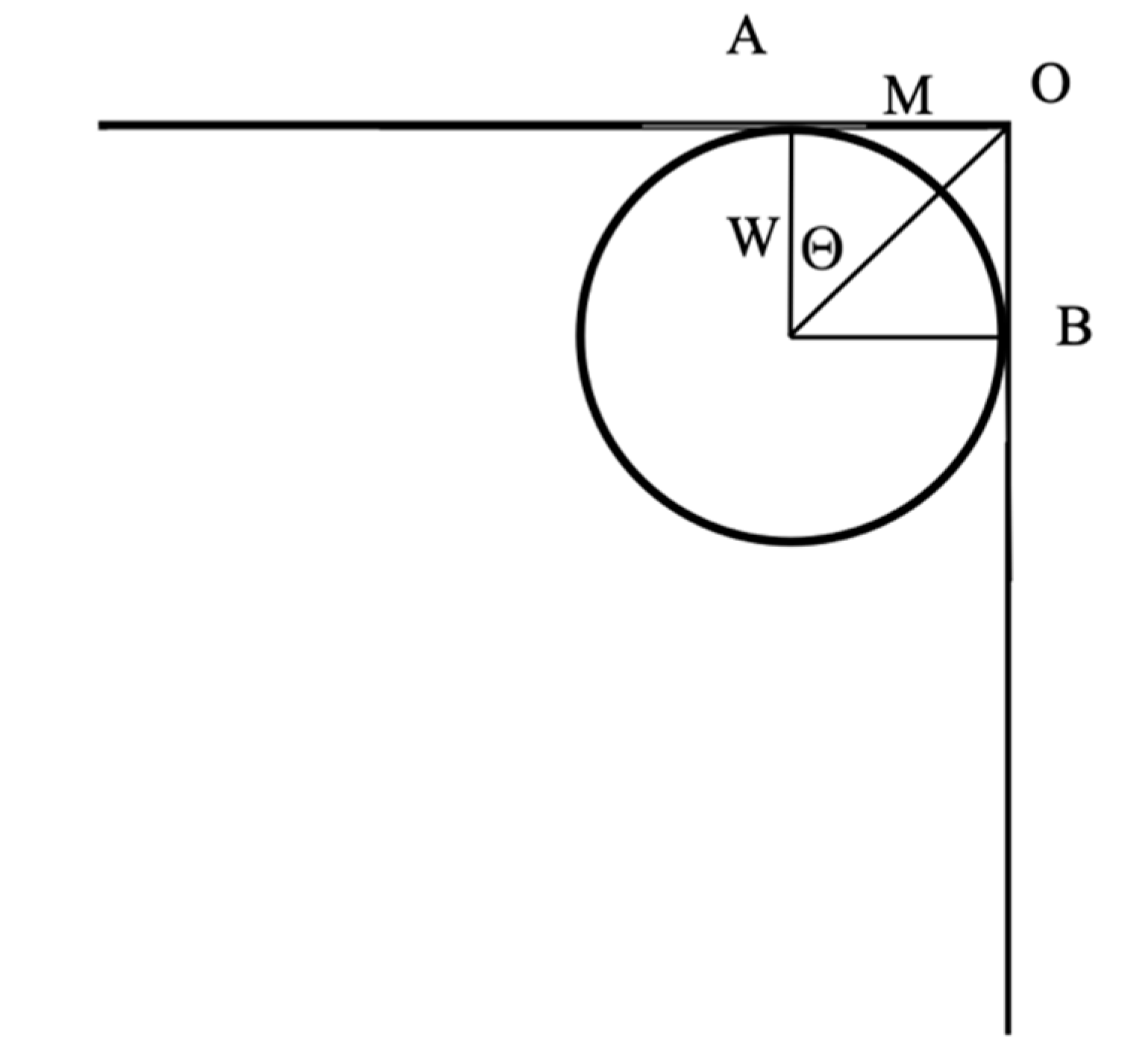
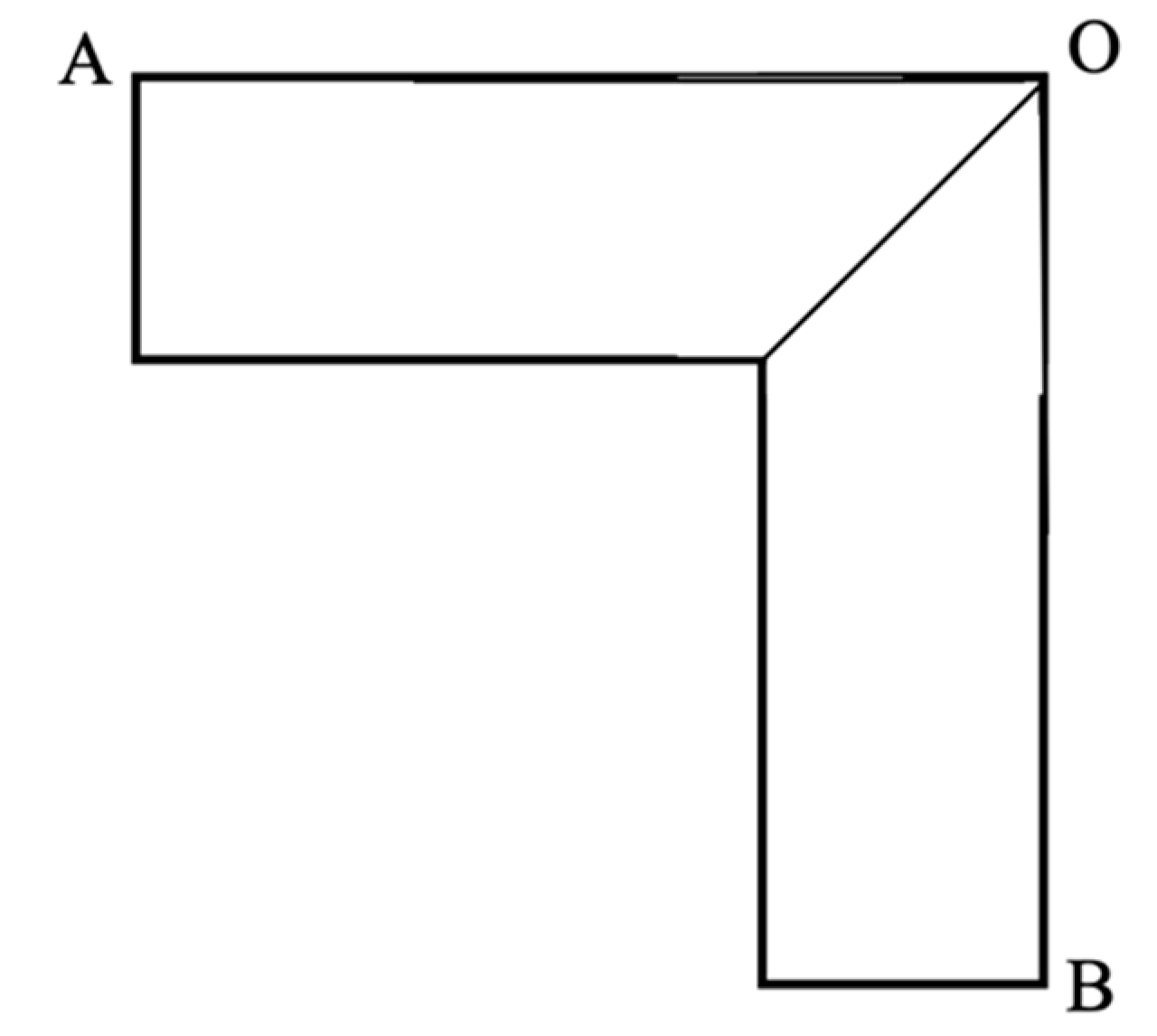
2.2.2. Smoothing of Pipeline Inflection Points
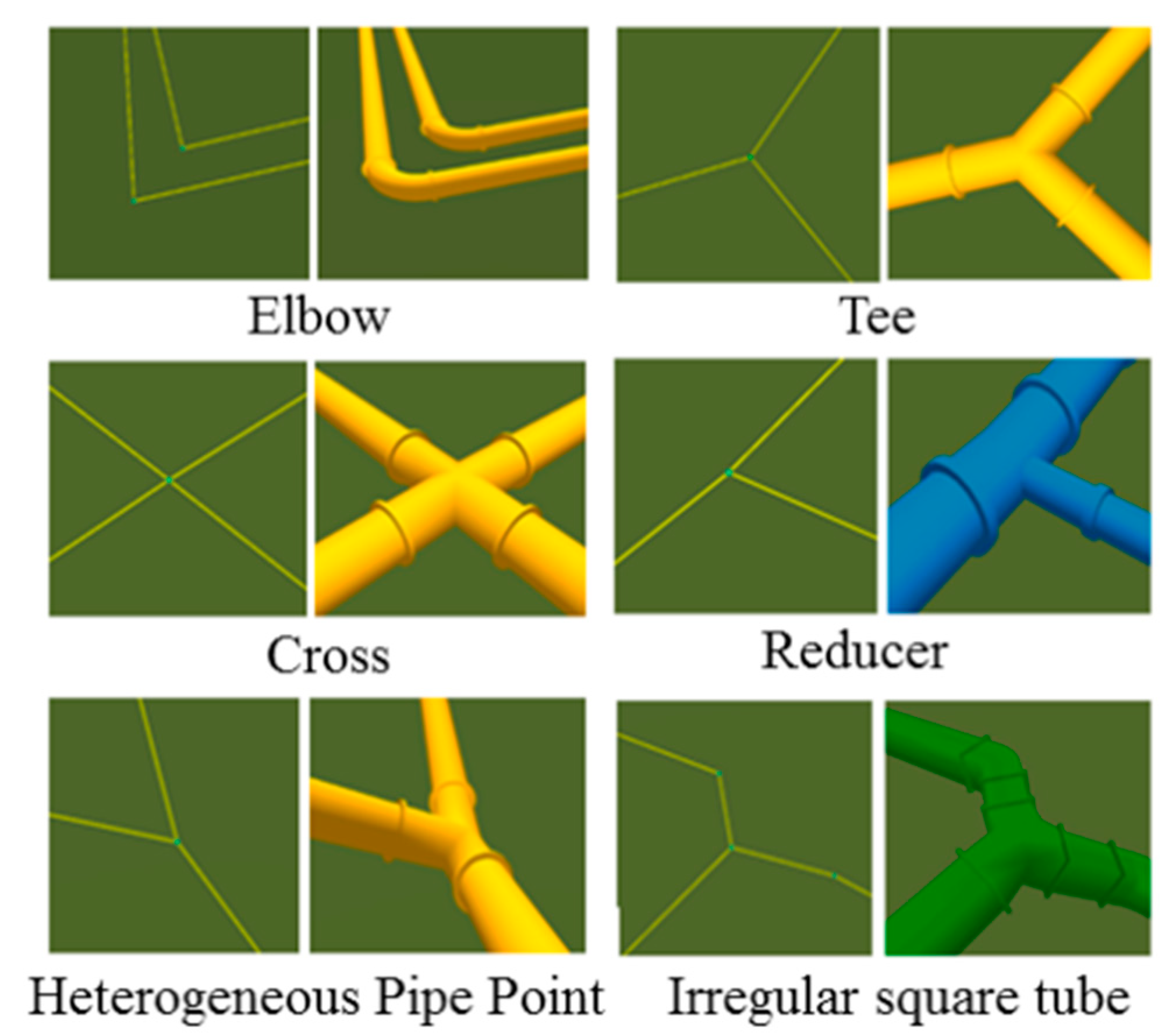
2.3. Construction of the Pipe Point Model
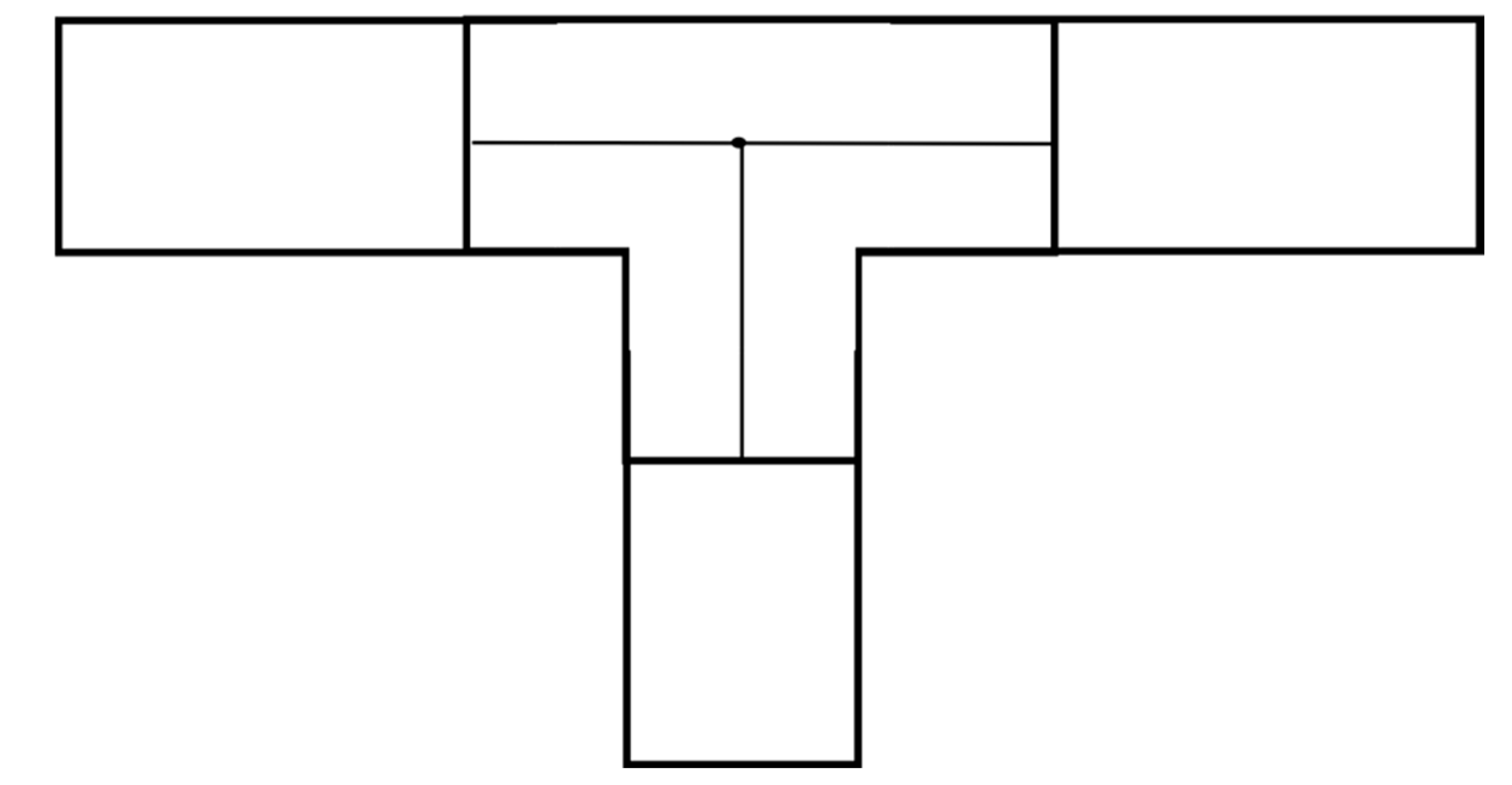
2.3.1. Constructing the Pipe Point Model
- (1)
- Traverse the points A, B on each of the two pipelines, calculate their plane P with the center point O;
- (2)
- Traverse the other pipeline points C except for A and B, calculate the position it projects onto P, and record whether the half pipe pairs of and the half pipe pairs of are required as the boolean variables bneedAtoB and bneedBtoA. The initial value is true;
- (3)
- Determine the relationship between and . If falls inside , then bneedAtoB = false; if falls outside , then bneedBtoA = false;
- (4)
- After traversing the other points except for A and B, if the needAtoB is true, the half pipe pair is recorded. If the bneedBtoA is true, the half pipe pair is recorded; back to (1).
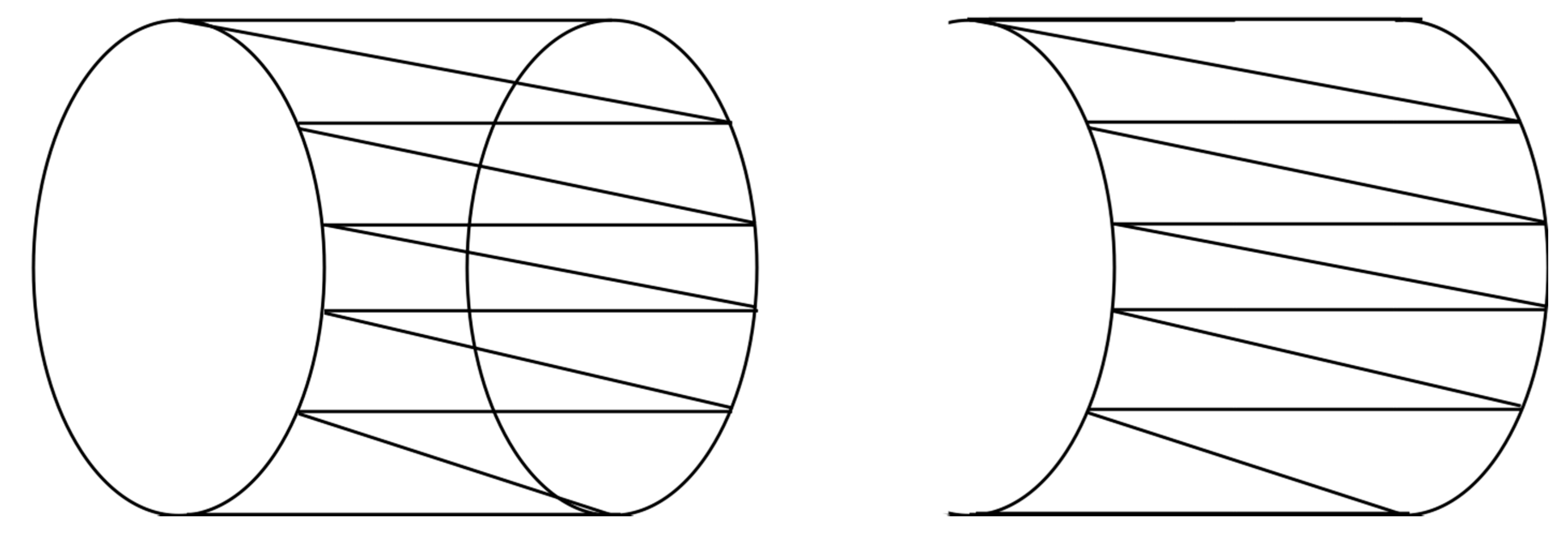
2.3.2. Matrix Computation of Half-Pipe
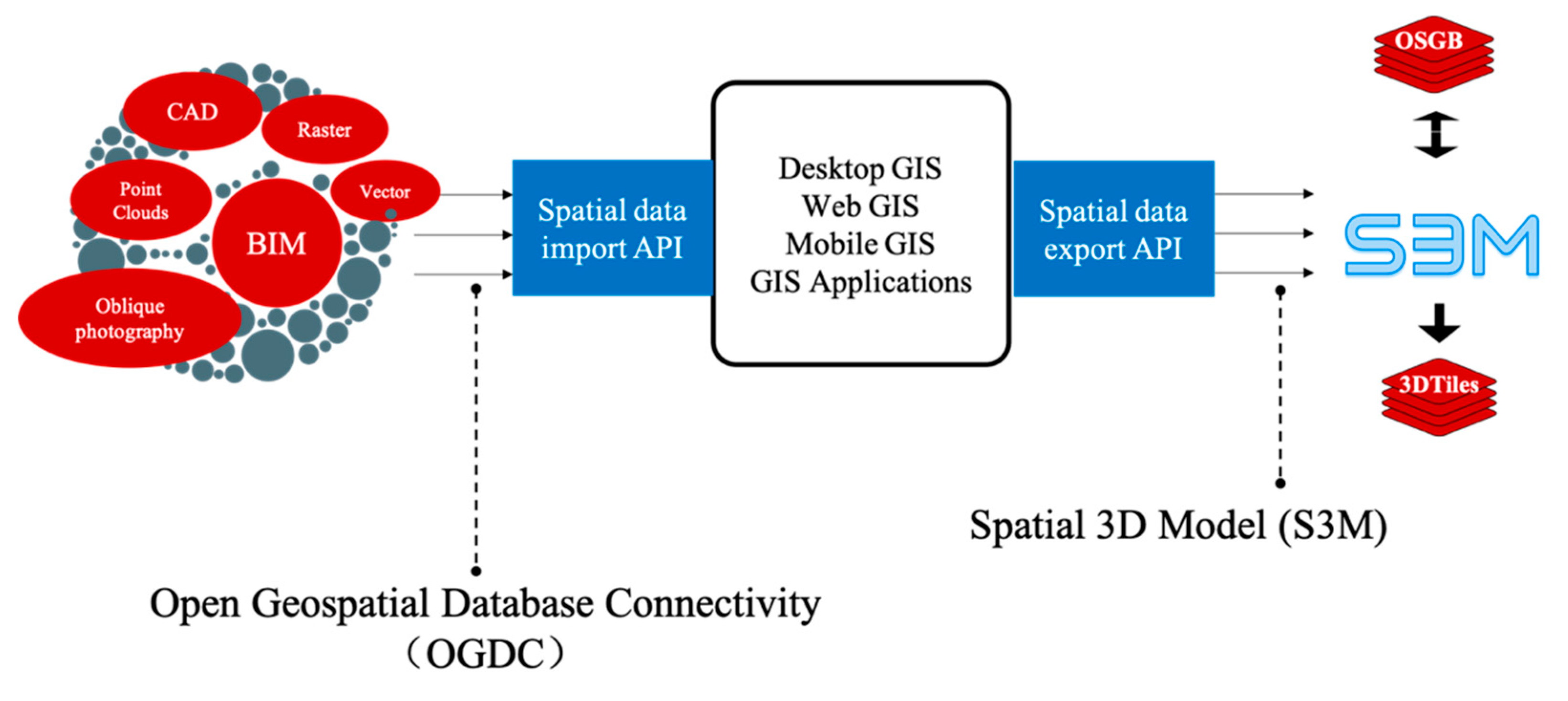
2.4. Integration Framework for 2D GIS and 3D GIS
3. High-Performance Modeling for 3D Pipe Networks
3.1. Spatial 3D Model (S3M)
3.2. Instantiation Rendering of Pipe Networks
3.3. Adaptive Rendering for Pipe Network Data
3.4. Combination Computing Framework with GPU and OpenMP
4. Experiments
5. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhong, E. Geocontrol and live geography: Some thoughts on the direction of gis. J. Geo-Inf. Sci. 2013, 15, 783–792. [Google Scholar]
- Anejionu, O.; Thakuriahab, P.; McHugh, A.; Sun, Y.; McArthur, D.; Mason, P.; Walpol, R. Spatial urban data system: A cloud-enabled big data infrastructure for social and economic urban analytics. Future Gener. Comput. Syst. 2019, 98, 18. [Google Scholar] [CrossRef]
- Biljecki, F.; Ledoux, H.; Stoter, J. An improved lod specification for 3D building models. Comput. Environ. Urban Syst. 2016, 59, 25–37. [Google Scholar] [CrossRef]
- Wang, S.; Zhong, Y.; Wang, E. An integrated gis platform architecture for spatiotemporal big data. Future Gener. Comput. Syst. 2019, 94, 160–172. [Google Scholar] [CrossRef]
- Yu, M.; Yang, C. A 3D multi-threshold, region-growing algorithm for identifying dust storm features from model simulations. Int. J. Geogr. Inf. Sci. 2017, 31, 939–961. [Google Scholar] [CrossRef]
- Wu, C.-L.; Chiang, Y.-C. A geodesign framework procedure for developing flood resilient city. Habitat Int. 2018, 75, 78–89. [Google Scholar] [CrossRef]
- Wang, S.; Zhong, E.; Cai, W.; Zhou, Q.; Lu, H.; Gu, Y.; Yun, W.; Hu, Z.; Long, L. A visual analytics framework for big spatiotemporal data. In Proceedings of the 2nd ACM SIGSPATIAL Workshop on Analytics for Local Events and News, Seattle, WA, USA, 6 November 2018; ACM: New York, NY, USA; p. 3. [Google Scholar]
- Borrmann, A.; Kolbe, T.H.; Donaubauer, A.; Steuer, H.; Jubierre, J.R.; Flurl, M. Multi-scale geometric-semantic modeling of shield tunnels for gis and bim applications. Comput. Aided Civ. Infrastruct. Eng. 2015, 30, 263–281. [Google Scholar] [CrossRef]
- Amirebrahimi, S.; Rajabifard, A.; Mendis, P.; Ngo, T. A framework for a microscale flood damage assessment and visualization for a building using bim–gis integration. Int. J. Digit. Earth 2016, 9, 363–386. [Google Scholar] [CrossRef]
- Bakalov, P.; Hoel, E.G.; Kim, S. A network model for the utility domain. In Proceedings of the 25th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Redondo Beach, CA, USA, 7–10 November 2017; ACM: New York, NY, USA; p. 32. [Google Scholar]
- Oliver, D.; Hoel, E.G. A trace framework for analyzing utility networks: A summary of results (industrial paper). In Proceedings of the 26th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 6–9 November 2018; ACM: New York, NY, USA; pp. 249–258. [Google Scholar]
- Alam, S.N.; Haas, Z.J. Coverage and connectivity in three-dimensional underwater sensor networks. Wirel. Commun. Mob. Comput. 2008, 8, 995–1009. [Google Scholar] [CrossRef]
- Hijazi, I.; Ehlers, M.; Zlatanova, S.; Isikdag, U. Ifc to citygml transformation framework for geo-analysis: A water utility network case. In Proceedings of the 4th International Workshop on 3D Geo-Information, Ghent, Belgium, 4–5 November 2009. [Google Scholar]
- Hijazi, I.; Ehlers, M.; Zlatanova, S.; Becker, T.; van Berlo, L. Initial investigations for modeling interior utilities within 3d geo context: Transforming ifc-interior utility to citygml/utilitynetworkade. In Advances in 3D Geo-Information Sciences; Springer: Berlin/Heidelberg, Germany, 2011; pp. 95–113. [Google Scholar]
- Becker, T.; Nagel, C.; Kolbe, T.H. Integrated 3d modeling of multi-utility networks and their interdependencies for critical infrastructure analysis. In Advances in 3D Geo-Information Sciences; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–20. [Google Scholar]
- Teo, T.-A.; Cho, K.-H. Bim-oriented indoor network model for indoor and outdoor combined route planning. Adv. Eng. Inform. 2016, 30, 268–282. [Google Scholar] [CrossRef]
- Li, X.; Yeh, A.G.-O. Modelling sustainable urban development by the integration of constrained cellular automata and gis. Int. J. Geogr. Inf. Sci. 2000, 14, 131–152. [Google Scholar] [CrossRef]
- Su, D.Z. Gis-based urban modelling: Practices, problems, and prospects. Int. J. Geogr. Inf. Sci. 1998, 12, 651–671. [Google Scholar] [CrossRef] [PubMed]
- Moghadam, S.T.; Toniolo, J.; Mutani, G.; Lombardi, P. A gis-statistical approach for assessing built environment energy use at urban scale. Sustain. Cities Soc. 2018, 37, 70–84. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, G.; Jiang, L.; Zhang, X.; Liu, Y.; Wang, Y.; Zhao, C. Analysis of spatial characteristics of digital signage in beijing with multi-source data. ISPRS Int. J. Geo-Inf. 2019, 8, 207. [Google Scholar] [CrossRef]
- Liu, K.; Gao, S.; Lu, F. Identifying spatial interaction patterns of vehicle movements on urban road networks by topic modelling. Comput. Environ. Urban Syst. 2019, 74, 50–61. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Tan, Y.; Wu, P.; Sutrisna, M.; Cheng, J.; Hampson, K. Trends and opportunities of bim-gis integration in the architecture, engineering and construction industry: A review from a spatio-temporal statistical perspective. ISPRS Int. J. Geo-Inf. 2017, 6, 397. [Google Scholar] [CrossRef]
- Zhu, J.; Wright, G.; Wang, J.; Wang, X. A critical review of the integration of geographic information system and building information modelling at the data level. ISPRS Int. J. Geo-Inf. 2018, 7, 66. [Google Scholar] [CrossRef]
- Kang, T.W.; Hong, C.H. A study on software architecture for effective bim/gis-based facility management data integration. Autom. Constr. 2015, 54, 25–38. [Google Scholar] [CrossRef]
- Liu, X.; Wang, X.; Wright, G.; Cheng, J.; Li, X.; Liu, R. A state-of-the-art review on the integration of building information modeling (bim) and geographic information system (gis). ISPRS Int. J. Geo-Inf. 2017, 6, 53. [Google Scholar] [CrossRef]
- Karan, E.P.; Irizarry, J.; Haymaker, J. Bim and gis integration and interoperability based on semantic web technology. J. Comput. Civ. Eng. 2015, 30, 04015043. [Google Scholar] [CrossRef]
- Bansal, V. Integrated cad and gis–based framework to support construction planning: Case study. J. Archit. Eng. 2017, 23, 05017005. [Google Scholar] [CrossRef]
- Quan, S.J.; Li, Q.; Augenbroe, G.; Brown, J.; Yang, P.P.-J. Urban data and building energy modeling: A gis-based urban building energy modeling system using the urban-epc engine. In Planning Support Systems and Smart Cities; Springer: Berlin/Heidelberg, Germany, 2015; pp. 447–469. [Google Scholar]
- Yu, L.-J.; Sun, D.-F.; Peng, Z.-R.; Zhang, J. A hybrid system of expanding 2D gis into 3D space. Cartogr. Geogr. Inf. Sci. 2012, 39, 140–153. [Google Scholar] [CrossRef]
- Hu, M.; Li, C. Design smart city based on 3S, internet of things, grid computing and cloud computing technology. In Internet of Things; Springer: Berlin/Heidelberg, Germany, 2012; pp. 466–472. [Google Scholar]
- Biljecki, F.; Stoter, J.; Ledoux, H.; Zlatanova, S.; Çöltekin, A. Applications of 3d city models: State of the art review. ISPRS Int. J. Geo-Inf. 2015, 4, 2842–2889. [Google Scholar] [CrossRef]
- Liang, J.; Gong, J.; Zhou, J.; Ibrahim, A.N.; Li, M. An open-source 3D solar radiation model integrated with a 3D geographic information system. Environ. Model. Softw. 2015, 64, 94–101. [Google Scholar] [CrossRef]
- Luo, F.; Zhong, E.; Cheng, J.; Huang, Y. Vgis-collide: An effective collision detection algorithm for multiple objects in virtual geographic information system. Int. J. Digit. Earth 2011, 4, 65–77. [Google Scholar] [CrossRef]
- Luo, F.; Zhong, E.; Cao, G.; Tellez, R.D.; Gao, P. Vgis-antijitter: An effective framework for solving jitter problems in virtual geographic information systems. Int. J. Digit. Earth 2013, 6, 28–50. [Google Scholar] [CrossRef]
- Ortega, L.; Rueda, A. Parallel drainage network computation on cuda. Comput. Geosci. 2010, 36, 171–178. [Google Scholar] [CrossRef]
- Wu, J.; Deng, L.; Paul, A. 3d terrain real-time rendering method based on cuda-opengl interoperability. IETE Tech. Rev. 2015, 32, 471–478. [Google Scholar] [CrossRef]
- Zhang, J.; You, S. Cudagis: Report on the design and realization of a massive data parallel gis on gpus. In Proceedings of the 3rd ACM SIGSPATIAL International Workshop on GeoStreaming, Redondo Beach, CA, USA, 6 November 2012; ACM: New York, NY, USA; pp. 101–108. [Google Scholar]
- Zhou, C.; Chen, Z.; Pian, Y.; Xiao, N.; Li, M. A parallel scheme for large-scale polygon rasterization on cuda-enabled gpus. Trans. GIS 2017, 21, 608–631. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, C.; Min, G.; Wu, Y.; Zuo, Y. Distributed machine learning in big data era for smart city. In From Internet of Things to Smart Cities; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017; pp. 151–177. [Google Scholar]
- Heitzler, M.; Lam, J.C.; Hackl, J.; Adey, B.T.; Hurni, L. Gpu-accelerated rendering methods to visually analyze large-scale disaster simulation data. J. Geovis. Spat. Anal. 2017, 1, 3. [Google Scholar] [CrossRef]
- Perelman, L.S.; Allen, M.; Preis, A.; Iqbal, M.; Whittle, A.J. Multi-level automated sub-zoning of water distribution systems. In Proceedings of the 7th Intl. Congress on Env. Modelling and Software, San Diego, CA, USA, 15–19 June 2014. [Google Scholar]
- SuperMap. Spatial 3d Model Project. Available online: https://github.com/SuperMap/s3m-spec (accessed on 20 July 2019).
- SuperMap. The Open Geospatial Database Connectivity Project. Available online: https://github.com/SuperMap/OGDC (accessed on 20 July 2019).
- SuperMap. The Idesktop-Cross Project. Available online: https://supermap-idesktop.github.io/SuperMap-iDesktop-Cross/ (accessed on 20 July 2019).
- Cai, W.; Wang, S.; Zhong, E.; Hu, C.; Liu, X. Design and implementation of a new cross-platform open source gis desktop software. Bull. Surv. Mapp. 2017, 1, 122–125. [Google Scholar]
- SuperMap. The Iclient-Javascript Project. Available online: https://github.com/SuperMap/iClient-JavaScript (accessed on 20 July 2019).
- SuperMap. The Iclient3d for Webgl Project. Available online: https://enonline.supermap.com/SuperMap_iClient3D_9.0.1_for_WebGL/ (accessed on 20 July 2019).
- SuperMap. Supermap Iearth for Webgl Project. Available online: http://www.supermapol.com/earth/ (accessed on 20 July 2019).
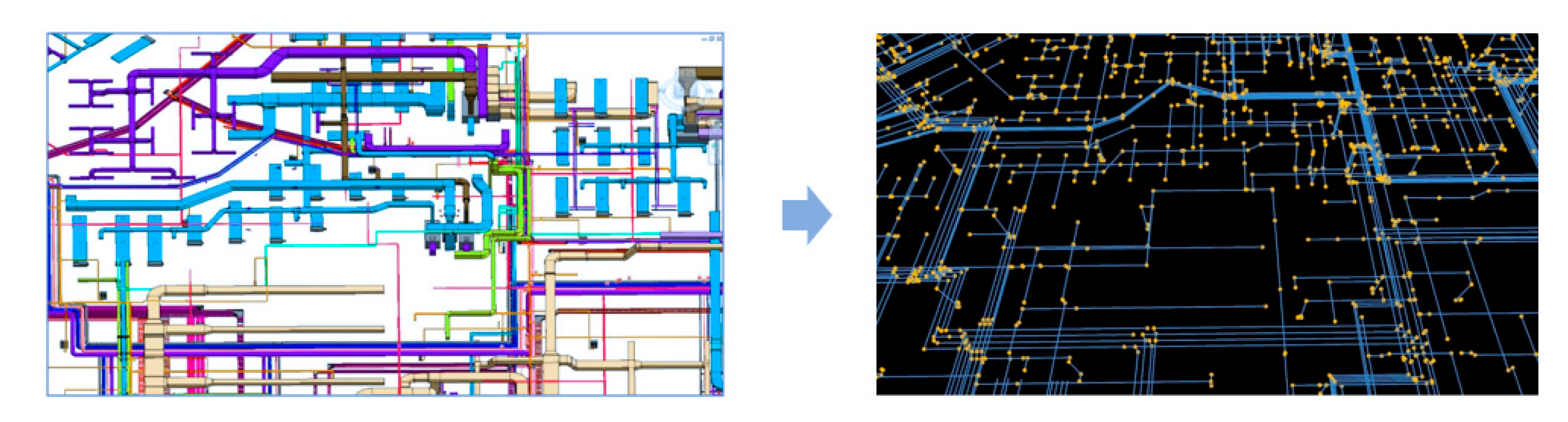

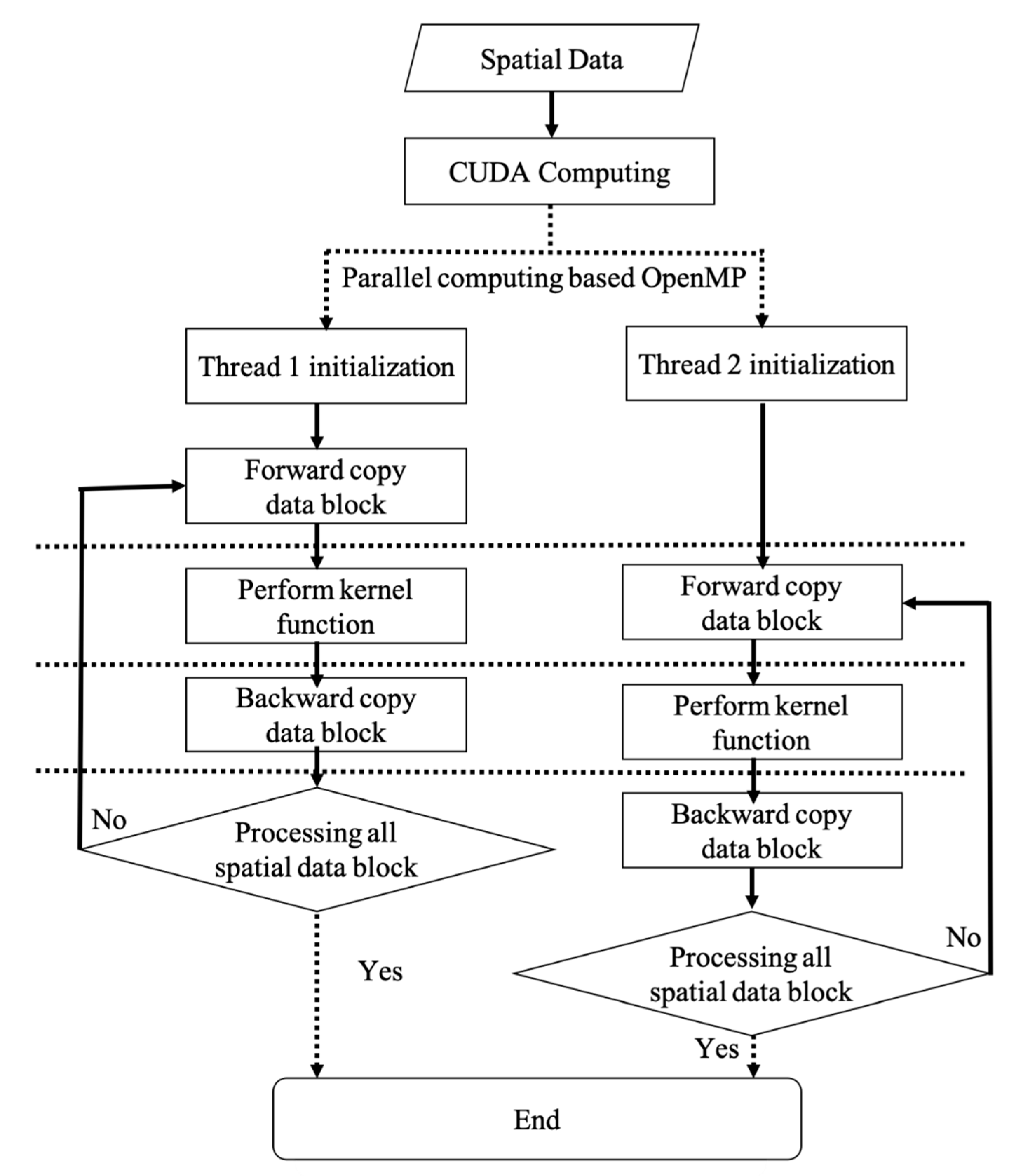
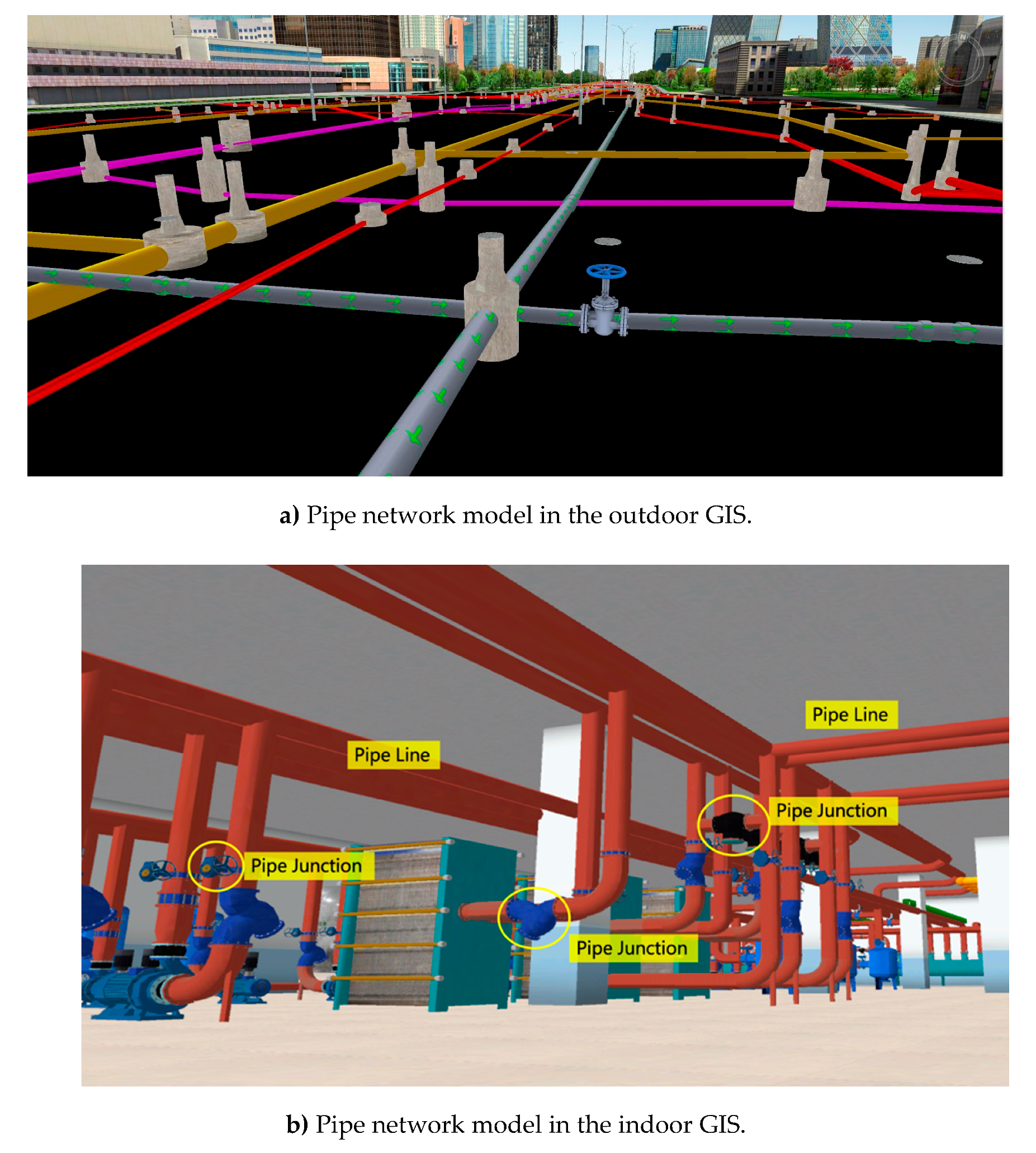
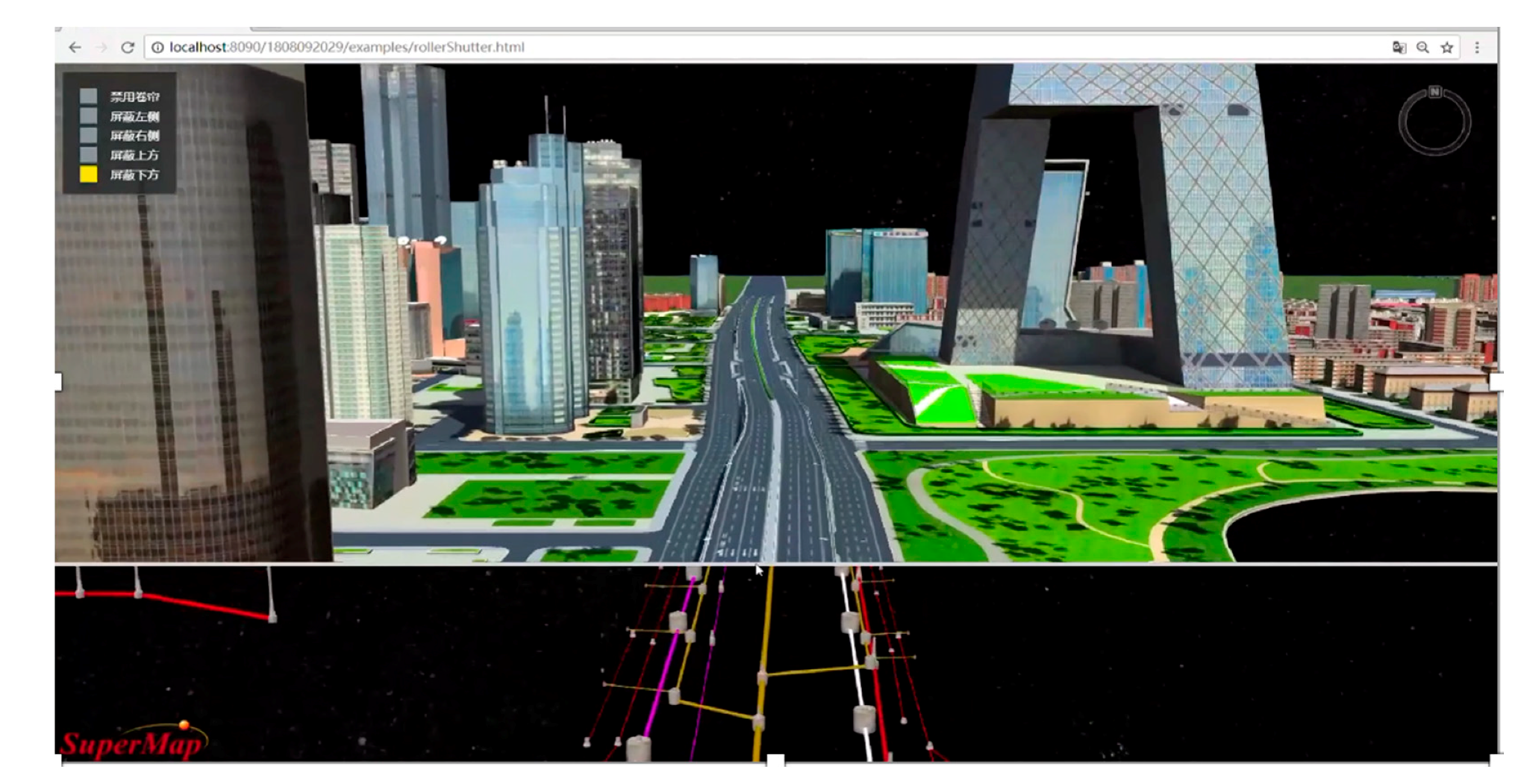
| ID Number | From Node | To Node | PrePoint | NextPoint | Geometry Information |
|---|---|---|---|---|---|
| 1 | 3 | 2 |
| ID Number | Geometry Information |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| … | … |
| n |
| Object | Storage Format | File Type | Description |
|---|---|---|---|
| TileTreeSetInfo | .scp | description file | description of the entire data |
| AttributeInfos | attribute .xml | attribute description file | description of each data set attribute in TileTreeSet |
| TileTree | Folder | data folder | store all data in the tile range |
| AttributeData | .xml | attribute data file | attribute data of all objects belong to the tile |
| IndexTree | .json | index tree file | all PagedLOD information belong to the tile |
| Tile | .s3mb | data file | a S3MB file stores data in a spatial division of the LOD layer |
| Experiment Type | Rendering Frame Rate | Percentage of CPU (%) | Physical Memory (MB) | Video Memory (MB) |
|---|---|---|---|---|
| Non-instantiation method | 32.44 | 32.29 | 580.39 | 340-550 |
| Instantiation method | 61.66 | 9.34 | 552.57 | 310-360 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Sun, Y.; Sun, Y.; Guan, Y.; Feng, Z.; Lu, H.; Cai, W.; Long, L. A Hybrid Framework for High-Performance Modeling of Three-Dimensional Pipe Networks. ISPRS Int. J. Geo-Inf. 2019, 8, 441. https://doi.org/10.3390/ijgi8100441
Wang S, Sun Y, Sun Y, Guan Y, Feng Z, Lu H, Cai W, Long L. A Hybrid Framework for High-Performance Modeling of Three-Dimensional Pipe Networks. ISPRS International Journal of Geo-Information. 2019; 8(10):441. https://doi.org/10.3390/ijgi8100441
Chicago/Turabian StyleWang, Shaohua, Yeran Sun, Yinle Sun, Yong Guan, Zhenhua Feng, Hao Lu, Wenwen Cai, and Liang Long. 2019. "A Hybrid Framework for High-Performance Modeling of Three-Dimensional Pipe Networks" ISPRS International Journal of Geo-Information 8, no. 10: 441. https://doi.org/10.3390/ijgi8100441
APA StyleWang, S., Sun, Y., Sun, Y., Guan, Y., Feng, Z., Lu, H., Cai, W., & Long, L. (2019). A Hybrid Framework for High-Performance Modeling of Three-Dimensional Pipe Networks. ISPRS International Journal of Geo-Information, 8(10), 441. https://doi.org/10.3390/ijgi8100441






