Integrating Geovisual Analytics with Machine Learning for Human Mobility Pattern Discovery
Abstract
1. Introduction
- (1)
- We develop an integrated geovisual analytics approach that integrates two advanced machine learning methods with interactive maps to characterize two types of high-level, complex transit travel behavior patterns, including a clustering algorithm to identify transit corridors and a graph-embedding algorithm to identify hierarchical mobility community structure.
- (2)
- We design novel integrated geovisual analytics interfaces for the discovered complex transit movement patterns, including specific views to visualize identified mobility communities and corridors, allowing regular users to examine and understand these ever-changing patterns at different scales and perspectives.
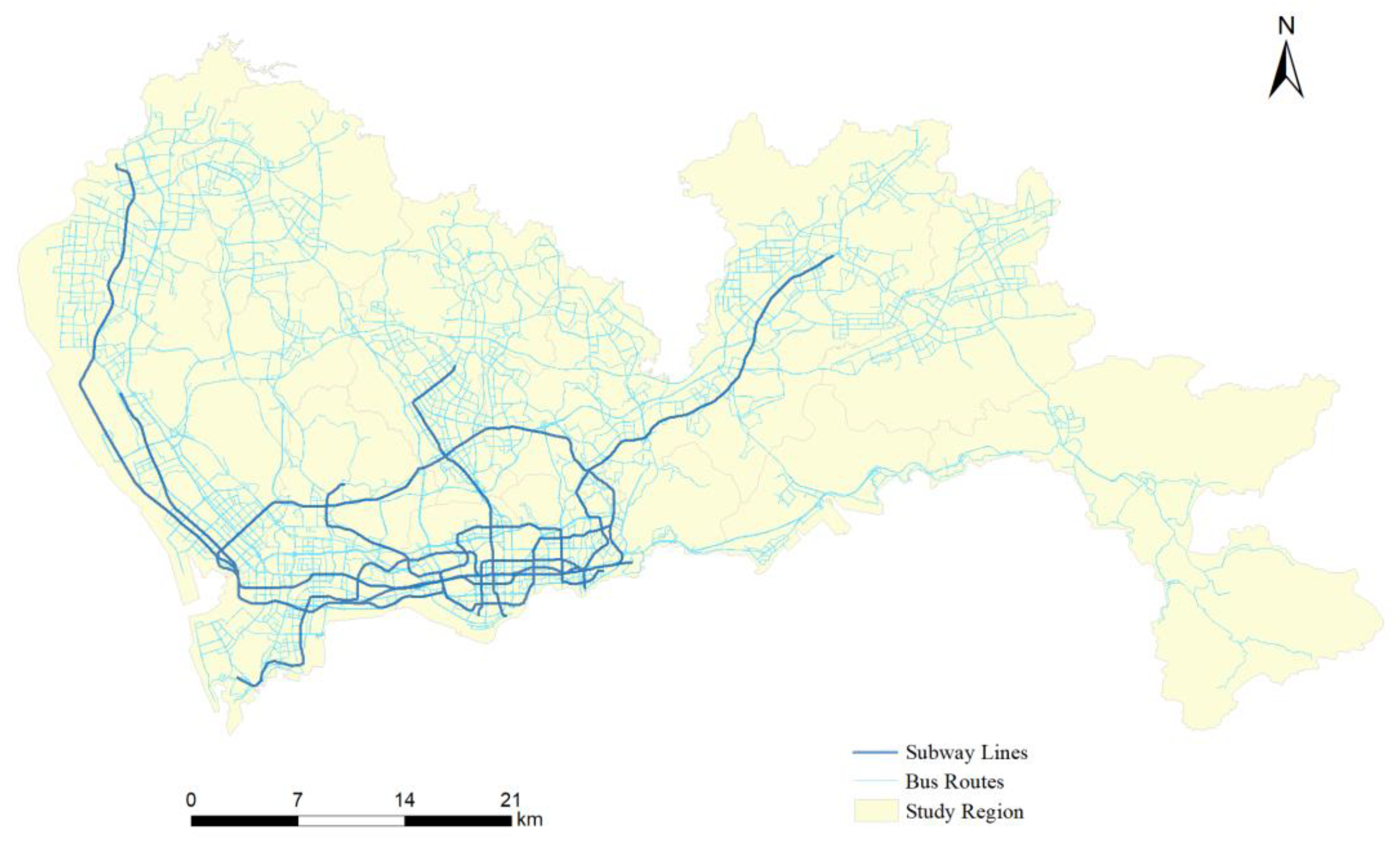
2. Data
3. Methodology
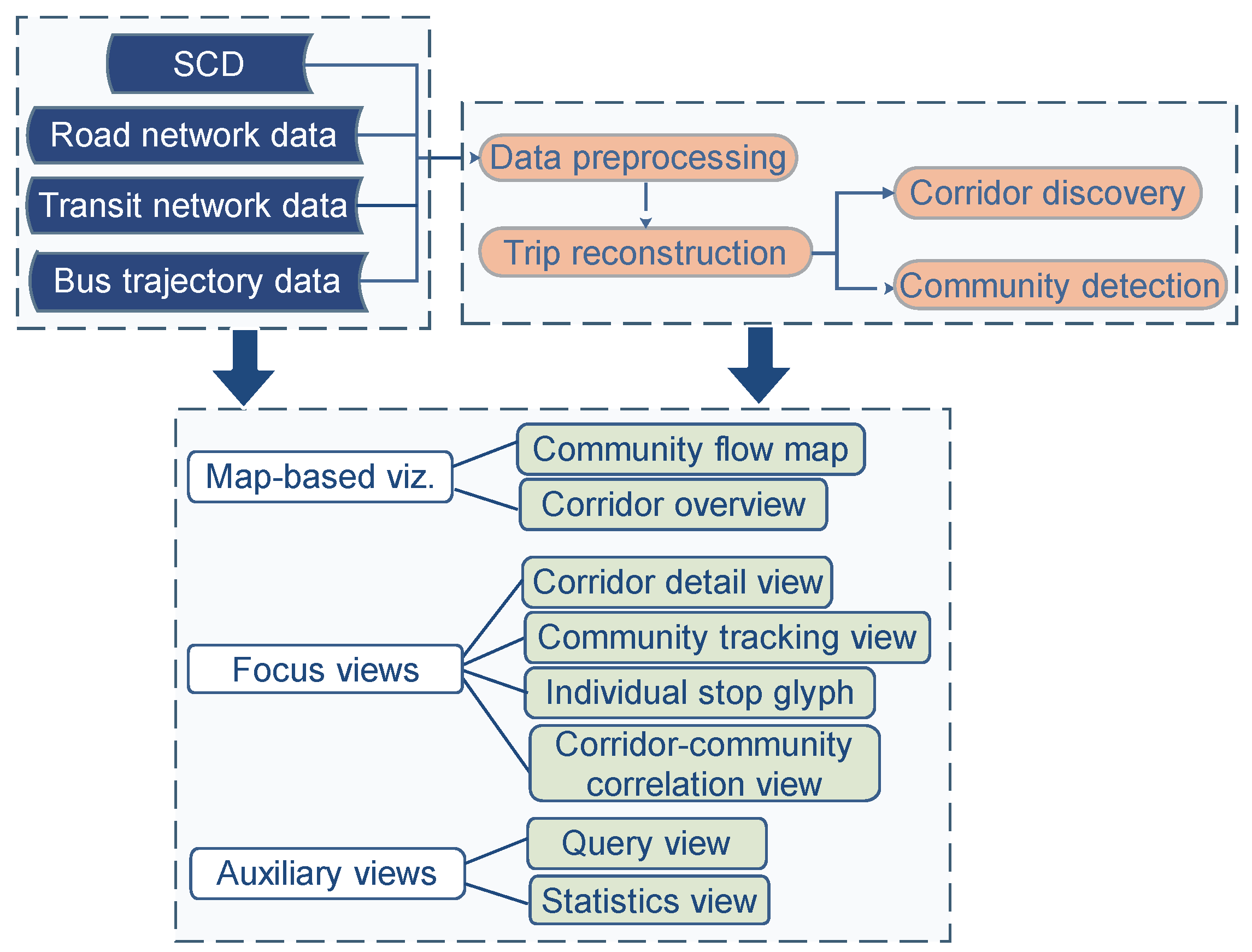
3.1. Methodology Overview
- (1)
- Global pattern discovery task 1: discover hierarchical mobility structure based on transit trip data and analyze their inter-correlations;
- (2)
- Global pattern discovery task 2: identify significant transit corridors for any specified time intervals;
- (3)
- Local pattern exploration task 1: explore the intrinsic information of identified individual transit corridors;
- (4)
- Local pattern exploration task 2: examine the temporal evolution of the discovered mobility community structure;
- (5)
- Comprehensive analysis task: design and implement linked or integrated views to visually analyze different components of public transit services (including corridors, community structures, and stops) and discovered travel patterns.
3.2. Data Pre-Processing and Trip Reconstruction
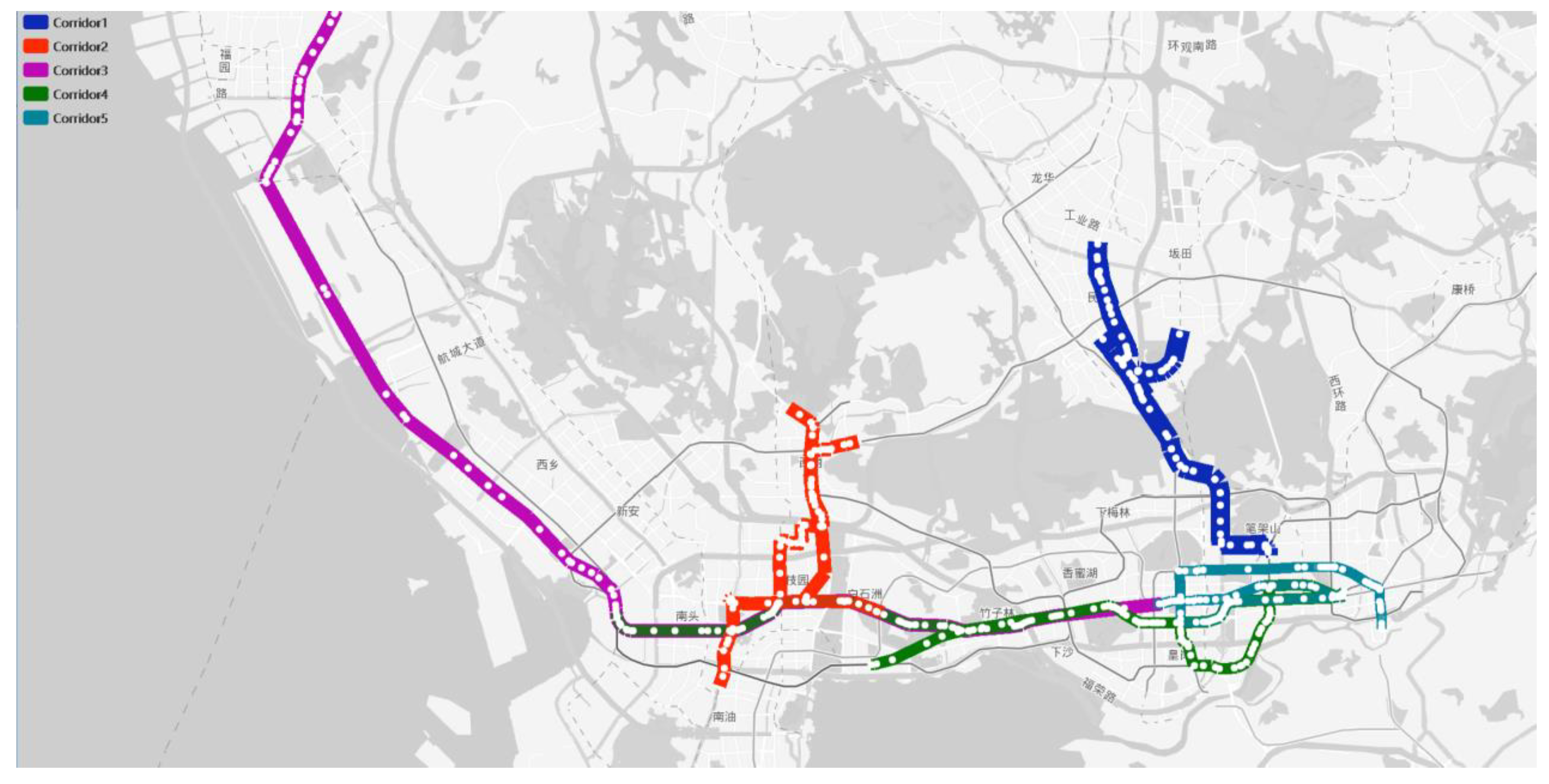
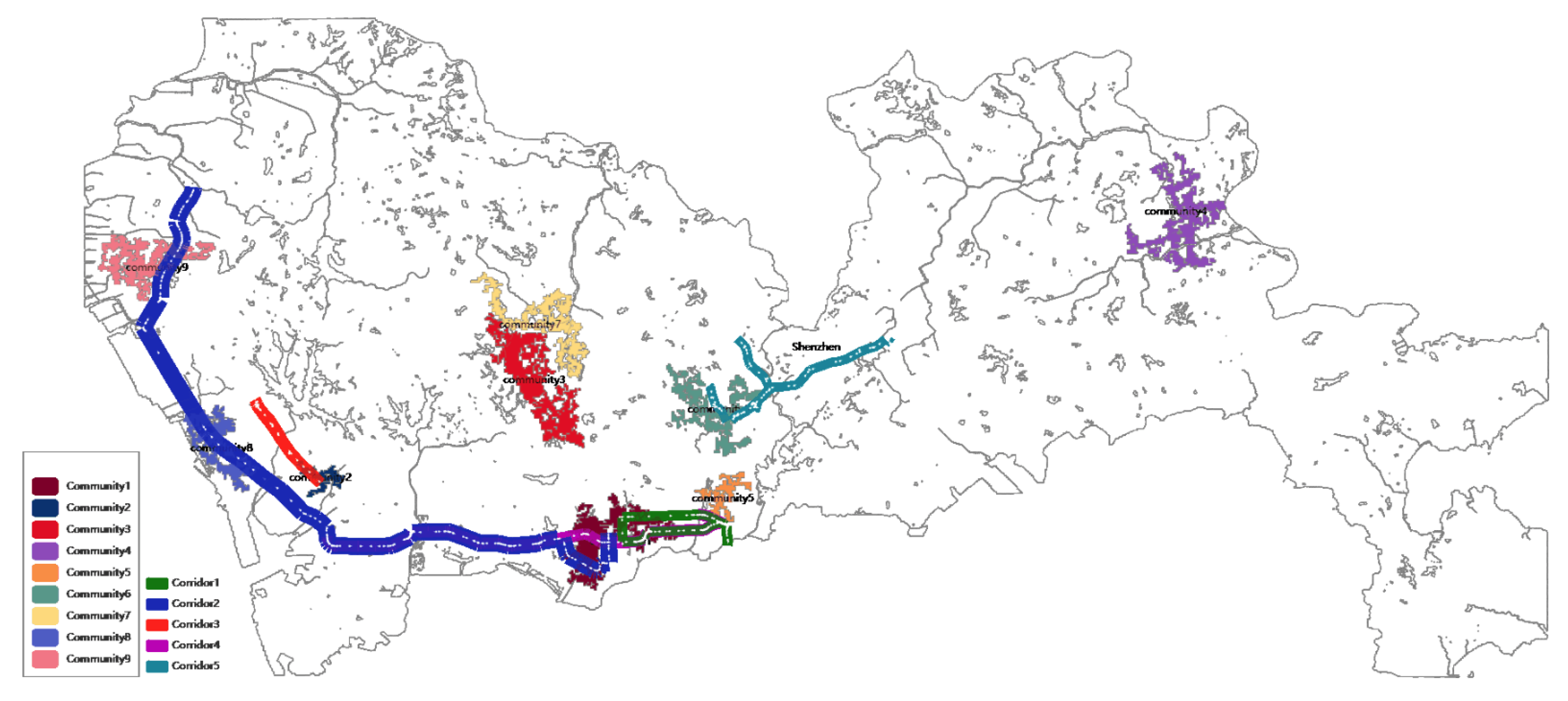
3.3. Extracting Transit Corridors
- (1)
- Network modeling. The public transit network can be modeled as a directed graph and is mapped to the road network G (V, E), where V denotes the sets of road intersections Vr and transit stops Vt (Vt have been projected into road links), E denotes road segments between road intersections and transit stops. We extract a small set of connected segments Ec whose end nodes have a large shared “accumulated transit flow” and identify them as transit corridors.
- (2)
- Computing accumulated transit flow. For each node v in Vt, the number of passengers who board at v or before it is recorded as nv. For each passenger, the number of stops she has passed after boarding is recorded until she exits from the vehicle. Then for each v, this number is used as the “accumulated transit flow” at(v).
- (3)
- Corridor initialization. We choose nodes with a significant number of accumulated transit flows as seeds to grow corridors.
- (4)
- Corridor expansion. The seed nodes are stacked into a priority queue, ranked by its accumulated transit flow. The one with highest at(v) is popped out and used as the initial seed s0 to expand a corridor. From s0, the algorithm searches for one adjacent stop, s1, that meets the criterion of significant “shared accumulated transit flow” between s0 and s1. “Shared accumulated transit flow” is defined as sa(0→1) = [at(1)− at(0)] /at(0), i.e., the change ratio of accumulated transit flow for the two adjacent stops/nodes. Meanwhile, the two nodes must meet another criterion, namely, “shared transit flow”, which is defined as st(0→1) = n0⋂n1. If the two nodes meet both criteria, the algorithm expands a corridor from node 0 to 1. This procedure repeats until no downstream nodes meet the two criteria. Then another seed in the queue is fetched to grow another corridor, until all seeds are popped.
- (5)
- Corridor pruning. We need to prune short corridors (with less than 4 stops) or non-significant corridors (transit flows are less than a pre-defined threshold).
- (6)
- Corridor merging. This final step is to merge corridors if they are already connected or overlapped.
3.4. Discovering Mobility Communities
3.5. Visual Analytics Design
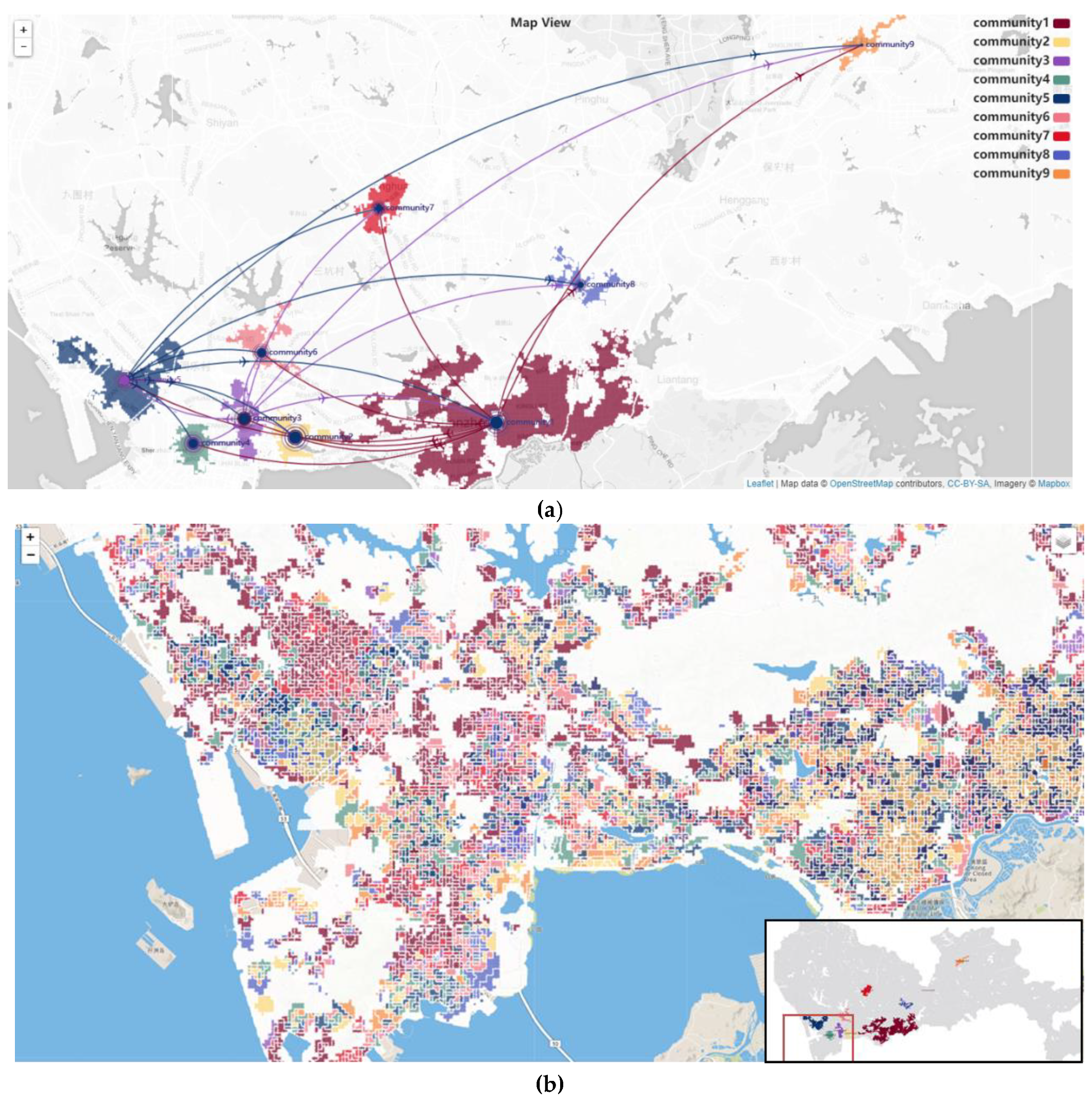
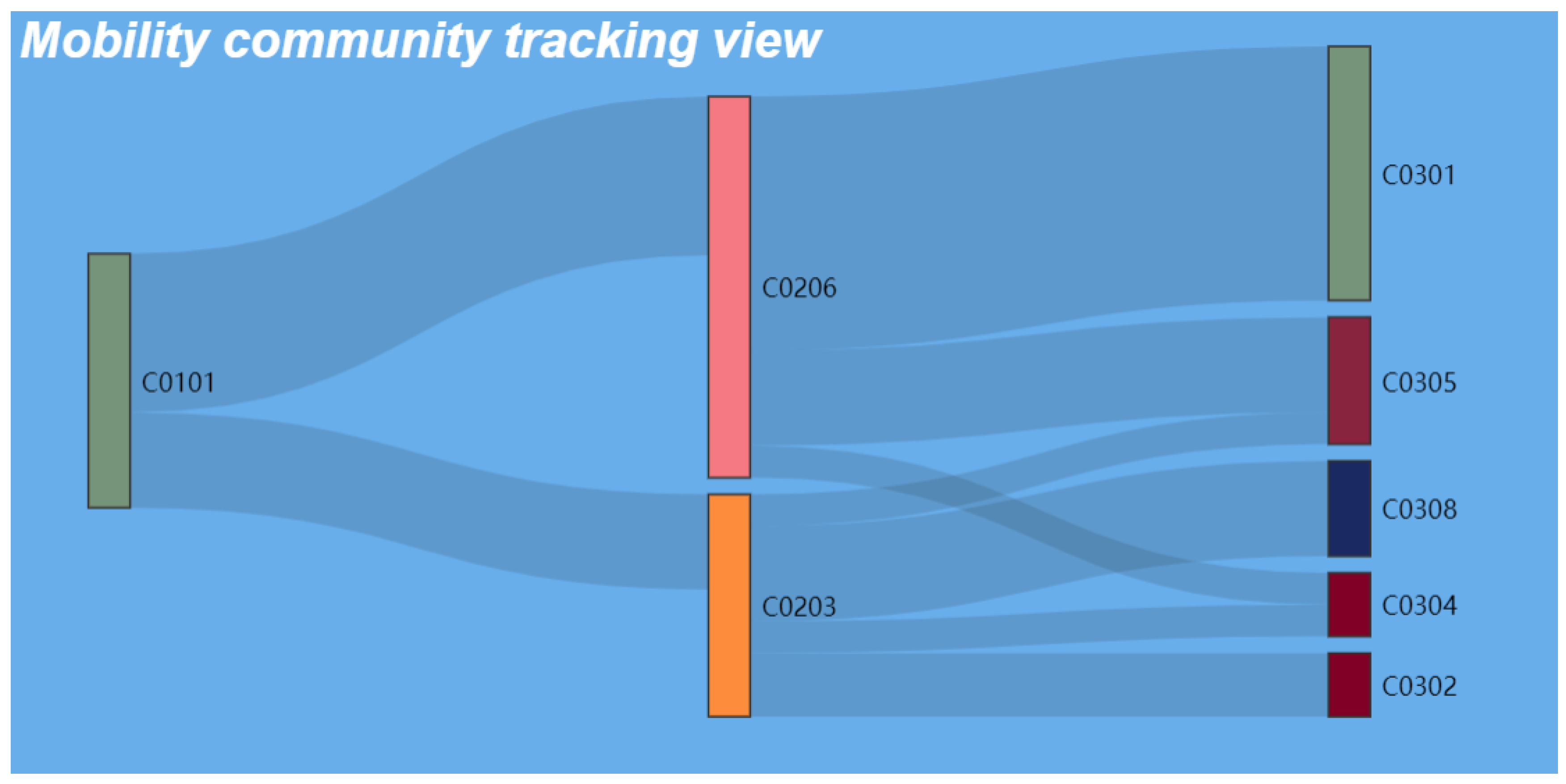
3.5.1. Mobility Communities
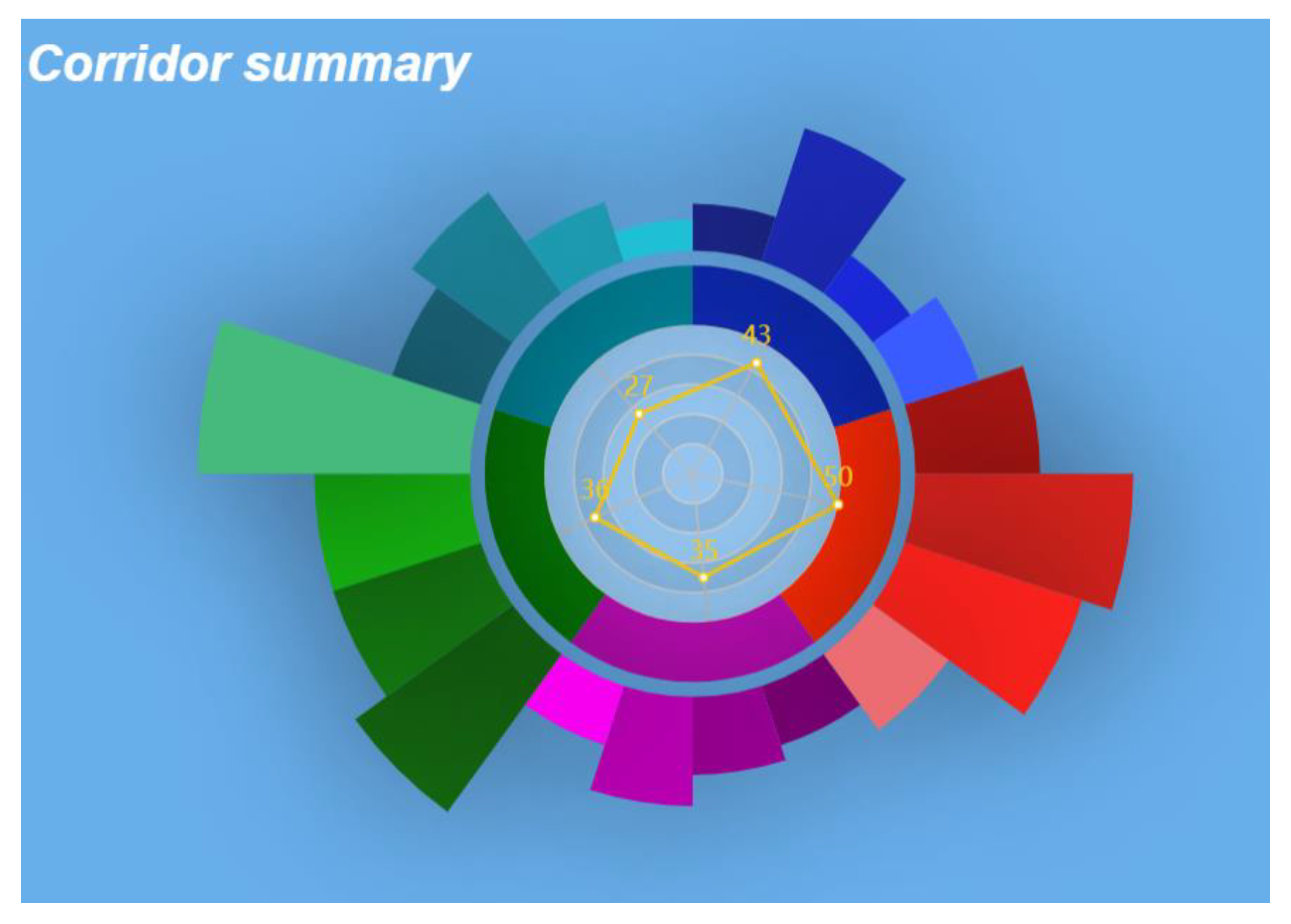
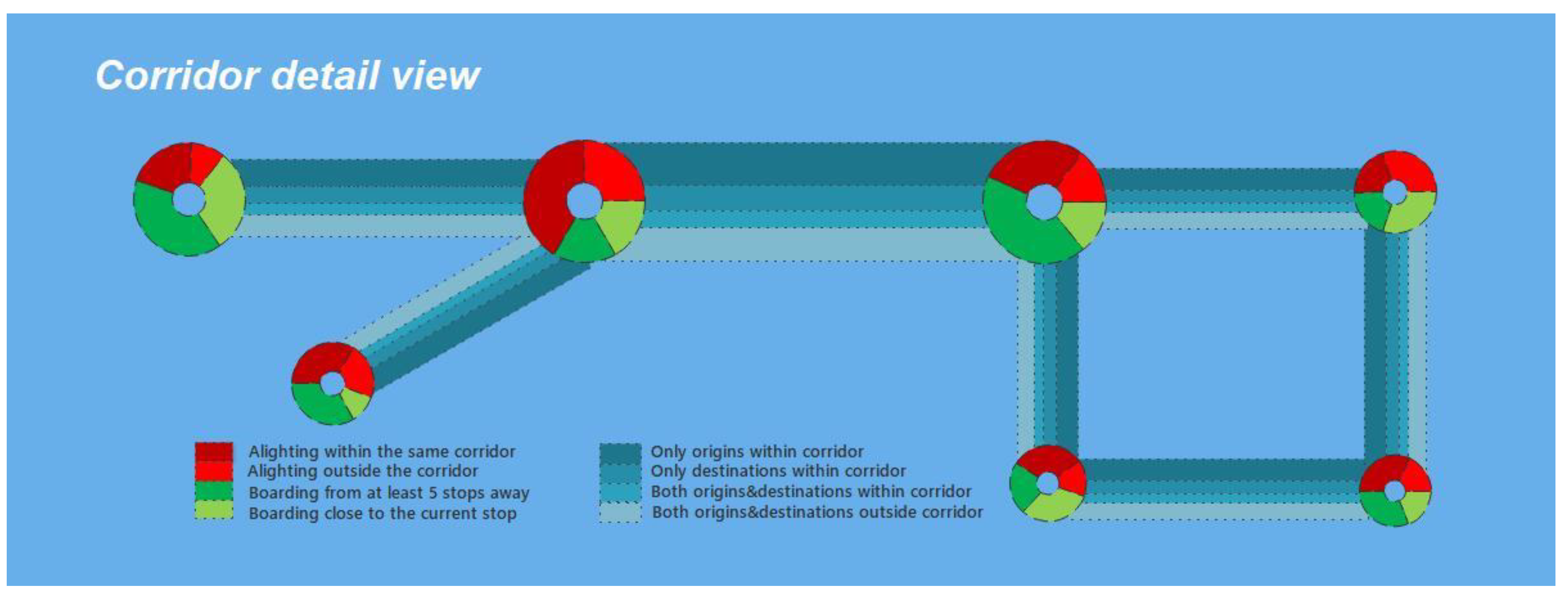
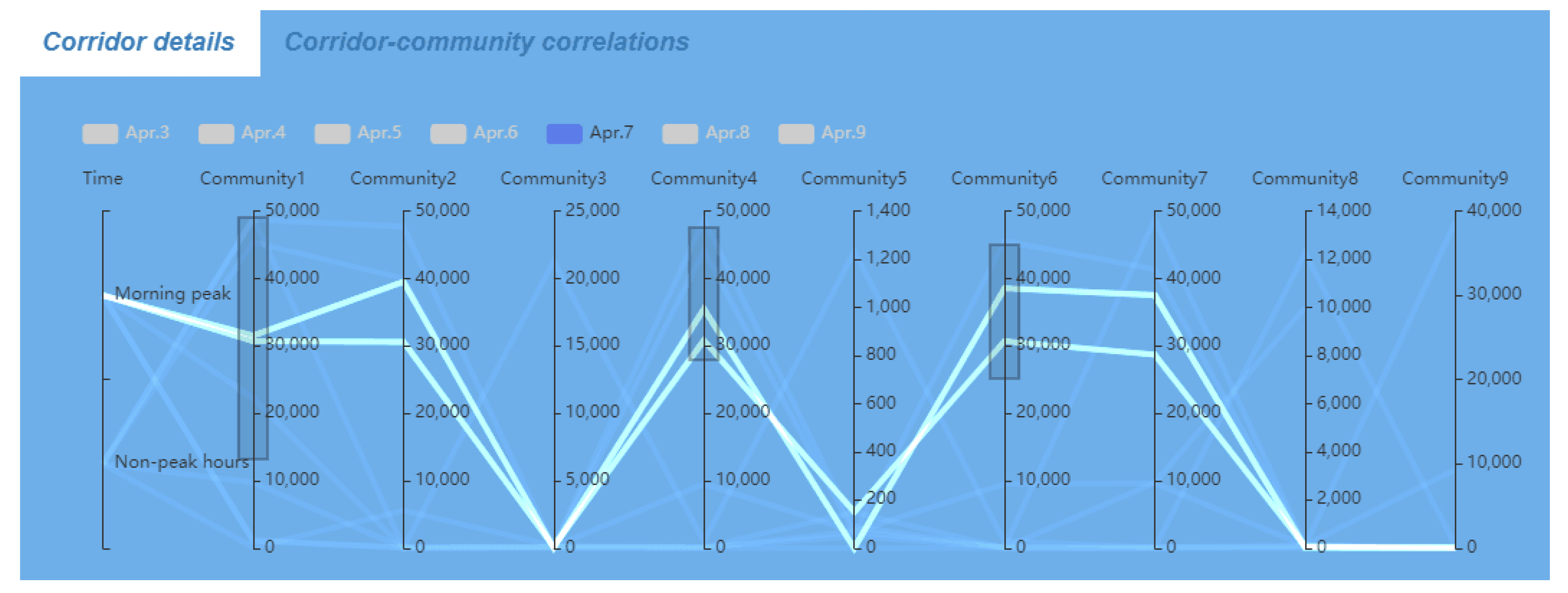
3.5.2. Corridors
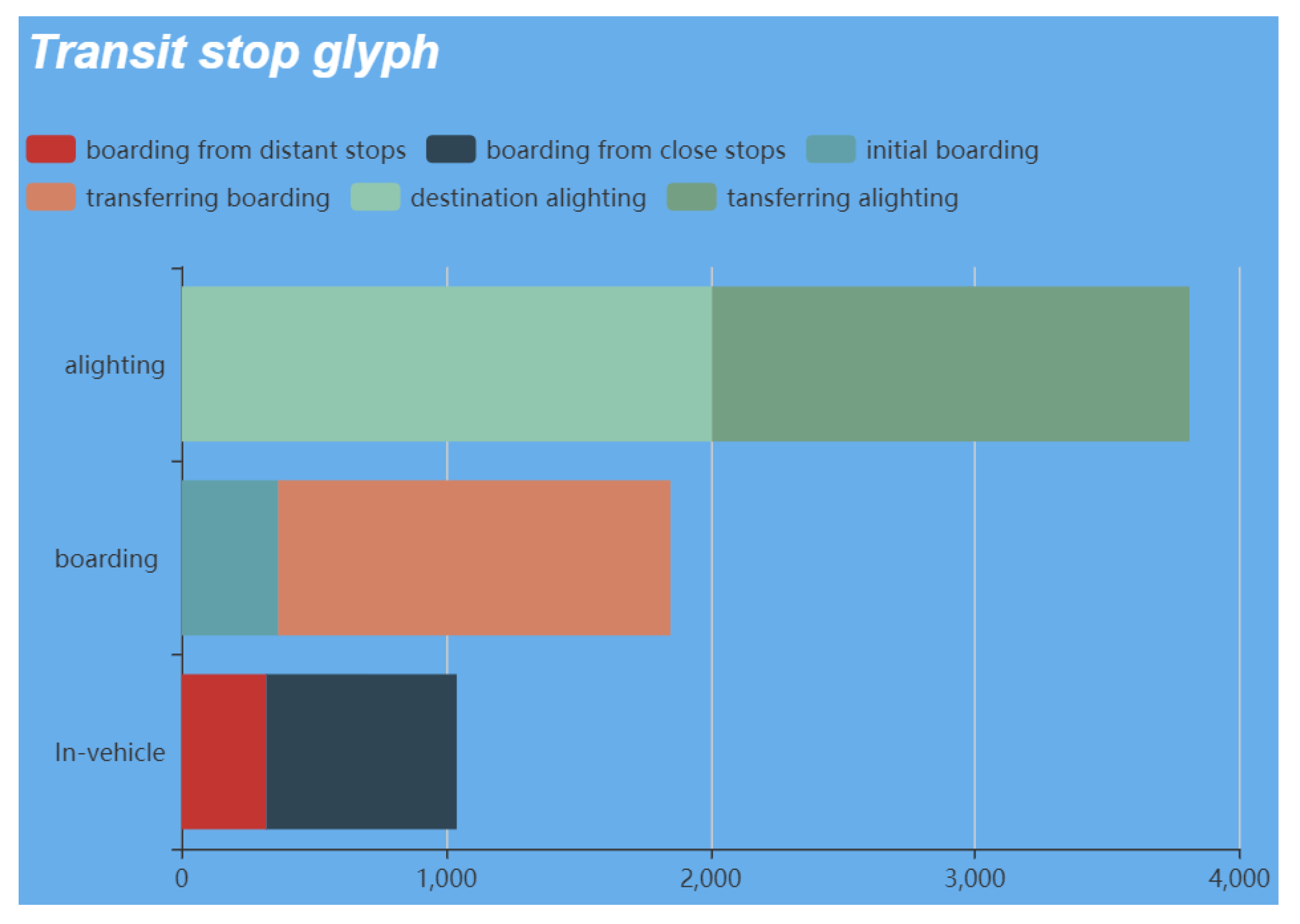
3.5.3. Transit Stops
3.5.4. Correlations between Corridors and Communities
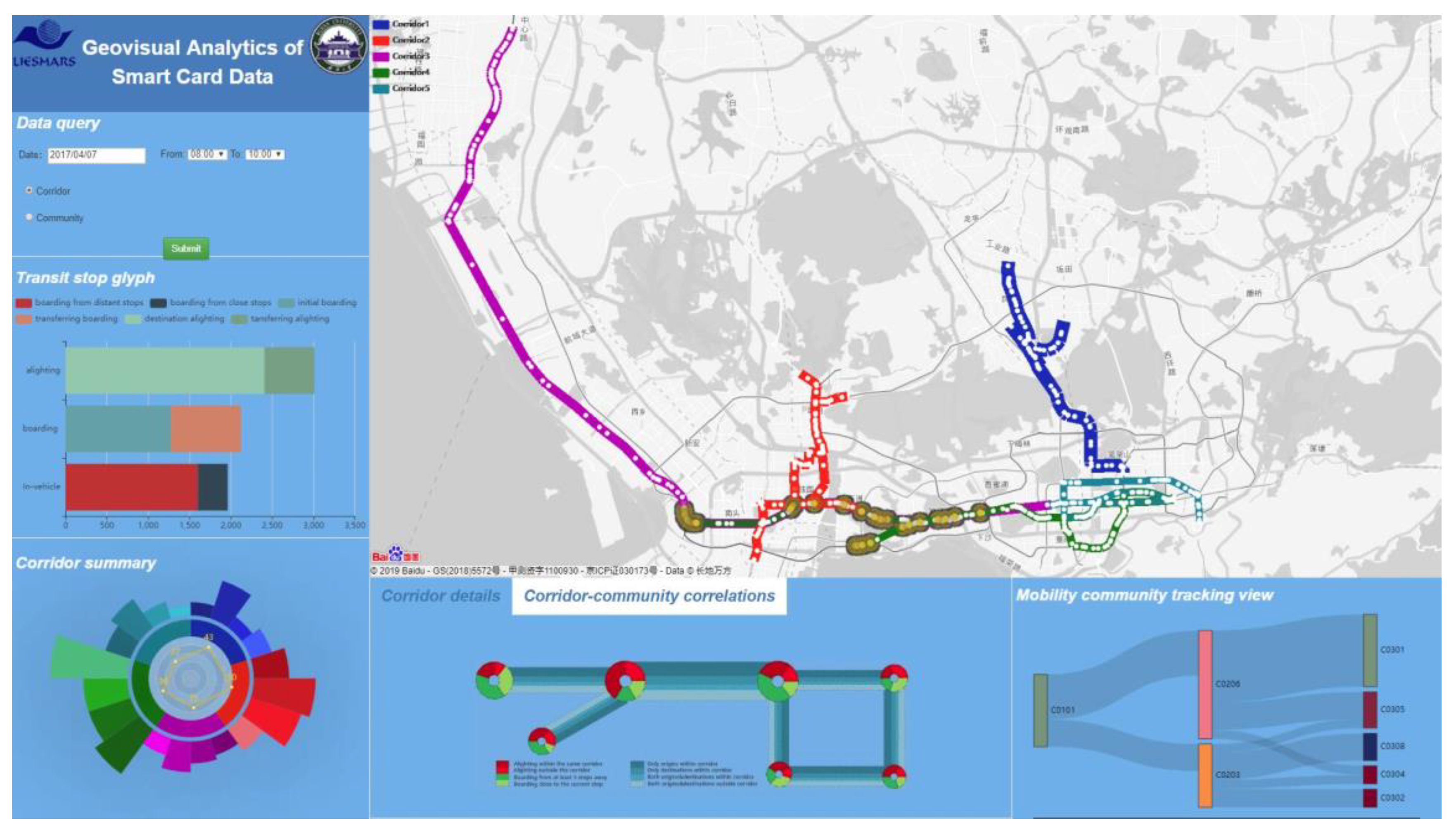
4. Implementation and Prototype
5. Analysis and Discussion
5.1. Geovisual Analytics Workflow and Examples
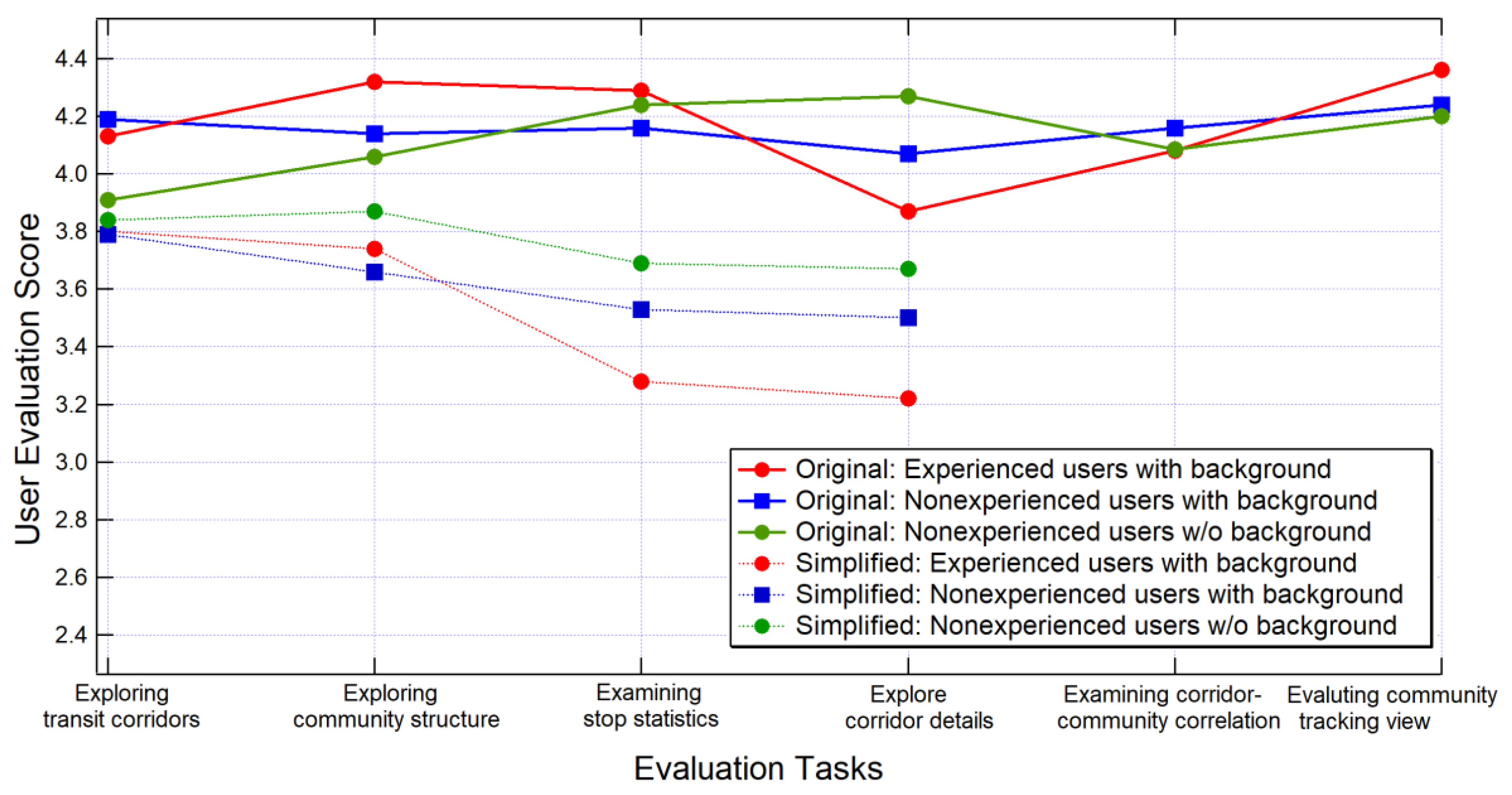
5.2. User Evaluation
5.3. Discussion
- (1)
- It offers an efficient and effective method to explore a massive amount of transit trips, which is otherwise challenging to analyze and visualize. Based on discovered corridors and mobility communities, we can focus on the most significant travel patterns while still having the capability to explore the details of any stop.
- (2)
- It delivers an intuitive user interface to combine multiple views that allows regular users to analyze complex transit travel behaviors from different perspectives. For example, corridors present high-level representations of concentrated trips based on road networks, whereas mobility communities are produced to synthesize similar travel characteristics over the partition of the study region.
- (3)
- It is beneficial for many transit management applications, such as demand modeling, transit planning, and daily operations, since they provide an applicable approach to highlight aggregated movement patterns at multiple spatial and temporal resolutions. The prototype can also be used by regular passengers to plan their transit trips and choose their residence or work place.
6. Conclusions and Further Work
Author Contributions
Funding
Conflicts of Interest
References
- Pelletier, M.-P.; Trepanier, M.; Morency, C. Smart card data use in public transit: A literature review. Transp. Res. Part C 2011, 19, 557–568. [Google Scholar] [CrossRef]
- Sun, L.; Axhausen, K. Understanding urban mobility patterns with a probabilistic tensor factorization framework. Transp. Res. Part B 2016, 91, 511–524. [Google Scholar] [CrossRef]
- Zhao, J.; Qu, Q.; Zhang, F.; Xu, C.; Liu, S. Spatio-temporal analysis of passenger travel patterns in massive smart card data. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3135–3146. [Google Scholar] [CrossRef]
- El Mahrsi, M.; Come, E.; Oukhellou, L.; Verleysen, M. Clustering smart card data for urban mobility analysis. IEEE Trans. Intell. Transp. Syst. 2017, 18, 712–728. [Google Scholar] [CrossRef]
- Kieu, L.; Ou, Y.; Cai, C. Large-scale transit market segmentation with spatial-behavioural features. Transp. Res. Part C 2018, 90, 97–113. [Google Scholar] [CrossRef]
- Trépanier, M.; Habib, K.; Morency, C. Are transit users loyal? Revelations from a hazard model based on smart card data. Can. J. Civ. Eng. 2012, 39, 610–618. [Google Scholar] [CrossRef]
- Li, T.; Sun, D.; Jing, P.; Yang, K. Smart card data mining of public transport destination: A literature review. Information 2018, 9, 18. [Google Scholar] [CrossRef]
- Wang, Y.; Correia, G.; Romph, E.; Timmermans, H. Using metro smart card data to model location choice of after-work activities: An application to Shanghai. J. Transp. Geogr. 2017, 63, 40–47. [Google Scholar] [CrossRef]
- Çolak, S.; Lima, A.; González, M.C. Understanding congested travel in urban areas. Nat. Commun. 2016, 7, 10793. [Google Scholar] [CrossRef]
- Toole, J.L.; Herrera-Yaqüe, C.; Schneider, C.M.; González, M.C. Coupling human mobility and social ties. J. R. Soc. Interface 2015, 12, 20141128. [Google Scholar] [CrossRef]
- Schneider, C.M.; Rudloff, C.; Bauer, D.; González, M.C. Daily travel behavior: Lessons from a week-long survey for the extraction of human mobility motifs related information. In Proceedings of the 2nd ACM SIGKDD International Workshop on Urban Computing, Chicago, IL, USA, 11 August 2013. Article No. 3. [Google Scholar]
- Hedayatifar, L.; Bar-Yam, Y.; Morales, A.J. Social fragmentation at multiple scales. arXiv 2018, arXiv:1809.07676. [Google Scholar]
- Mazimpaka, J.; Timpf, S. Trajectory data mining: A review of methods and applications. J. Spat. Inf. Sci. 2016, 13, 61–99. [Google Scholar] [CrossRef]
- Toch, E.; Lerner, B.; Ben-Zion, E.; Ben-Gal, I. Analyzing large-scale human mobility data: A survey of machine learning methods and applications. Knowl. Infor. Syst. 2019, 58, 501–523. [Google Scholar] [CrossRef]
- Xie, R.; Ji, Y.; Yue, Y.; Zuo, X. Mining individual mobility patterns from mobile phone data. In Proceedings of the 2011 International Workshop on Trajectory Data Mining and Analysis, Beijing, China, 18 September 2011; pp. 37–44. [Google Scholar]
- Khoroshevsky, F.; Lerner, B. Human mobility-pattern discovery and next-place prediction from GPS data. In Multimodal Pattern Recognition of Social Signals in Human-Computer-Interaction; Schwenker, F., Scherer, S., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; Volume 10183, pp. 24–35. [Google Scholar]
- Chen, X.; Shi, D.; Zhao, B.; Liu, F. Mining individual mobility patterns based on location history. In Proceedings of the IEEE First International Conference on Data Science in Cyberspace (DSC), Changsha, China, 13–16 June 2016. [Google Scholar]
- Ouyang, X.; Zhang, C.; Zhou, P.; Jiang, H. DeepSpace: An online deep learning framework for mobile big data to understand human mobility patterns. arXiv 2016, arXiv:1610.07009. [Google Scholar]
- Kim, D.; Song, H. Method of predicting human mobility patterns using deep learning. Neurocomputing 2018, 280, 56–64. [Google Scholar] [CrossRef]
- Wang, C.; Ma, L.; Li, R.; Durrani, T.; Zhang, H. Exploring trajectory prediction through machine learning methods. IEEE Access 2019, 7, 101441–101452. [Google Scholar] [CrossRef]
- Chen, R.; Chen, M.; Li, W.; Wang, J.; Yao, X. Mobility modes awareness from trajectories based on clustering and a convolutional neural network. ISPRS Int. J. Geo-Inf. 2019, 8, 208. [Google Scholar] [CrossRef]
- Ben-Zion, E.; Lerner, B. Identifying and predicting social lifestyles in people’s trajectories by neural networks. EPJ Data Sci. 2018, 7, 45. [Google Scholar] [CrossRef]
- Gonzalez, M.C. Transportation Model in the Boston Metropolitan Area from Origin Destination Matrices Generated with Big Data; New England University Transportation Center Year 24 Final Report (MITR24-5); Massachusetts Institute of Technology: Cambridge, MA, USA, 2016. [Google Scholar]
- Di Lorenzo, G.; Sbodio, M.; Calabrese, F.; Berlingerio, M.; Pinelli, F.; Nair, R. AllAbroad: Visual exploration of cellphone mobility data to optimise public transport. IEEE Trans. Vis. Comput. Graph. 2016, 22, 1036–1050. [Google Scholar] [CrossRef]
- Zhou, Z.; Yu, J.; Guo, Z.; Liu, Y. Visual exploration of urban functions via spatio-temporal taxi OD data. J. Vis. Lang. Comput. 2018, 48, 169–177. [Google Scholar] [CrossRef]
- Kim, S.; Jeong, S.; Woo, I.; Jang, Y.; Maciejewski, R.; Ebert, D. Data flow analysis and visualization for spatiotemporal statistical data without trajectory information. IEEE Trans. Vis. Comput. Graph. 2017, 24, 1287–1300. [Google Scholar] [CrossRef] [PubMed]
- Tao, S.; Rohde, D.; Corcoran, J. Examining the spatial-temporal dynamics of bus passenger travel behaviour using smart card data and the flow-comap. J. Transp. Geogr. 2014, 41, 21–36. [Google Scholar] [CrossRef]
- Zeng, W.; Fu, C.-W.; Arisona, S.; Schubiger, S.; Burkhard, R.; Ma, K.-L. Visualizing the relationship between human mobility and points of interest. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2271–2284. [Google Scholar] [CrossRef]
- Von Landesberger, T.; Brodkorb, F.; Roskosch, P.; Andrienko, N.; Andrienko, G.; Kerren, A. MobilityGraphs: Visual analysis of mass mobility dynamics via spatio-temporal graphs and clustering. IEEE Trans. Vis. Comput. Graph. 2016, 22, 11–20. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Shi, J.; Schonfeld, P. Identifying passenger flow characteristics and evaluating travel time reliability by visualizing AFC data: A case study of Shanghai Metro. Public Transp. 2016, 8, 341–363. [Google Scholar] [CrossRef]
- Palomo, C.; Guo, Z.; Silva, C.; Freire, J. Visually exploring transportation schedules. IEEE Trans. Vis. Comput. Graph. 2016, 22, 170–179. [Google Scholar] [CrossRef] [PubMed]
- Zeng, W.; Fu, C.-W.; Arisona, S.; Erath, A.; Qu, H. Visualizing mobility of public transportation system. IEEE Trans. Vis. Comput. Graph. 2014, 20, 1833–1842. [Google Scholar] [CrossRef]
- Song, Y.; Fan, Y.; Li, X.; Ji, Y. Multidimensional visualization of transit smartcard data using space-time plots and data cubes. Transportation 2018, 45, 311–333. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y.; Yang, H.; Cui, C.; Li, J.; Qiao, Q. Identifying primary public transit corridors using multi-source big transit data. Int. J. Geogr. Inf. Sci. 2019, 1–25. [Google Scholar] [CrossRef]
- Primerano, F.; Taylor, M.; Pitaksringkarn, L.; Tisato, P. Defining and understanding trip chaining behaviour. Transportation 2008, 35, 55–72. [Google Scholar] [CrossRef]
- Nassir, N.; Hickman, M.; Ma, Z. Activity detection and transfer identification for public transfer fare card data. Transportation 2015, 42, 683–705. [Google Scholar] [CrossRef]
- Carr, J.; Dixon, C.; Meyer, M. Guidebook for Corridor-Based Statewide Transportation Planning; Transportation Research Board: Washington, DC, USA, 2010. [Google Scholar]
- Yildirimoglu, M.; Kim, J. Identification of communities in urban mobility networks using multi-layer graphs of network traffic. Transp. Res. Part C 2018, 89, 254–267. [Google Scholar] [CrossRef]
- Newman, M. Communities, modules, and large-scale structure in networks. Nat. Phys. 2011, 8, 25–31. [Google Scholar] [CrossRef]
- Fortunato, S.; Hric, D. Community detection in networks: A user guide. Phys. Rep. 2016, 659, 1–44. [Google Scholar] [CrossRef]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Wang, D.; Cui, P.; Zhu, W. Structural deep network embedding. In Proceedings of the KDD ’16, 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Scheepens, R.; Hurter, C.; van de Wetering, H.; van Wijk, J. Visualization, selection, and analysis of traffic flows. IEEE Trans. Vis. Comput. Graph. 2016, 22, 379–388. [Google Scholar] [CrossRef] [PubMed]
- Guo, D. Regionalization with dynamically constrained agglomerative clustering and partitioning (REDCAP). Int. J. Geogr. Inf. Sci. 2008, 22, 801–823. [Google Scholar] [CrossRef]
- Newman, E.; Leicht, E. Mixture models and exploratory analysis in networks. Proc. Natl. Acad. Sci. USA 2007, 104, 9564–9569. [Google Scholar] [CrossRef] [PubMed]
- Newman, E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef]
- Long, Y.; Thill, J. Combining smart card data and household travel survey to analyze jobs–housing relationships in Beijing. Comput. Environ. Urban Syst. 2015, 53, 19–35. [Google Scholar] [CrossRef]
- Alsger, A.; Assemi, B.; Mesbah, M.; Ferreira, L. Validating and improving public transport origin-destination estimation algorithm using smart card fare data. Transp. Res. Part C 2016, 68, 490–506. [Google Scholar] [CrossRef]
| Weekdays | Weekends | |
|---|---|---|
| [44] | 0.0372 | 0.0707 |
| Ours | 0.0218 | 0.0229 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Wang, J.; Cui, C.; Li, Y.; He, W.; Lu, Y.; Qiao, Q. Integrating Geovisual Analytics with Machine Learning for Human Mobility Pattern Discovery. ISPRS Int. J. Geo-Inf. 2019, 8, 434. https://doi.org/10.3390/ijgi8100434
Zhang T, Wang J, Cui C, Li Y, He W, Lu Y, Qiao Q. Integrating Geovisual Analytics with Machine Learning for Human Mobility Pattern Discovery. ISPRS International Journal of Geo-Information. 2019; 8(10):434. https://doi.org/10.3390/ijgi8100434
Chicago/Turabian StyleZhang, Tong, Jianlong Wang, Chenrong Cui, Yicong Li, Wei He, Yonghua Lu, and Qinghua Qiao. 2019. "Integrating Geovisual Analytics with Machine Learning for Human Mobility Pattern Discovery" ISPRS International Journal of Geo-Information 8, no. 10: 434. https://doi.org/10.3390/ijgi8100434
APA StyleZhang, T., Wang, J., Cui, C., Li, Y., He, W., Lu, Y., & Qiao, Q. (2019). Integrating Geovisual Analytics with Machine Learning for Human Mobility Pattern Discovery. ISPRS International Journal of Geo-Information, 8(10), 434. https://doi.org/10.3390/ijgi8100434





