Road Extraction from VHR Remote-Sensing Imagery via Object Segmentation Constrained by Gabor Features
Abstract
1. Introduction
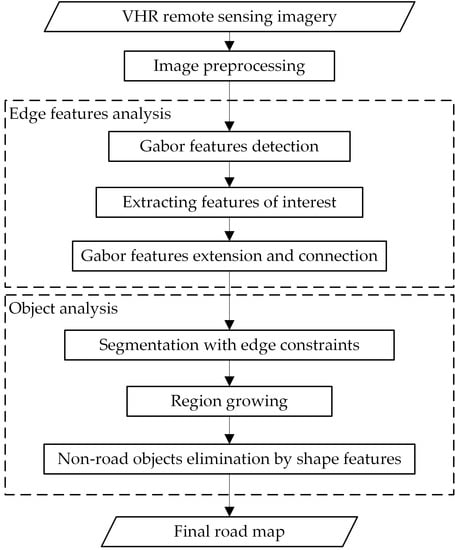
2. Methods
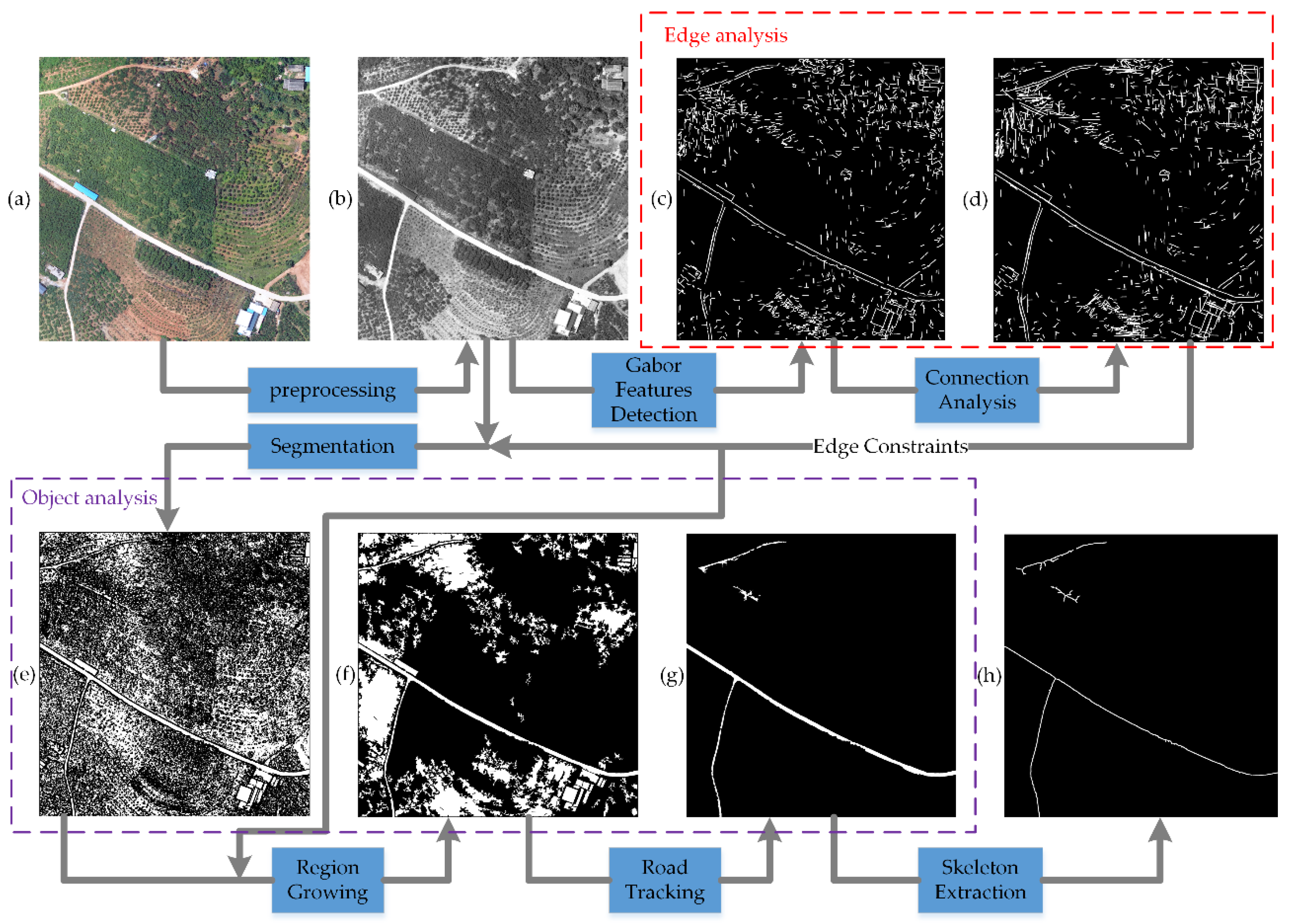
2.1. Image Preprocessing
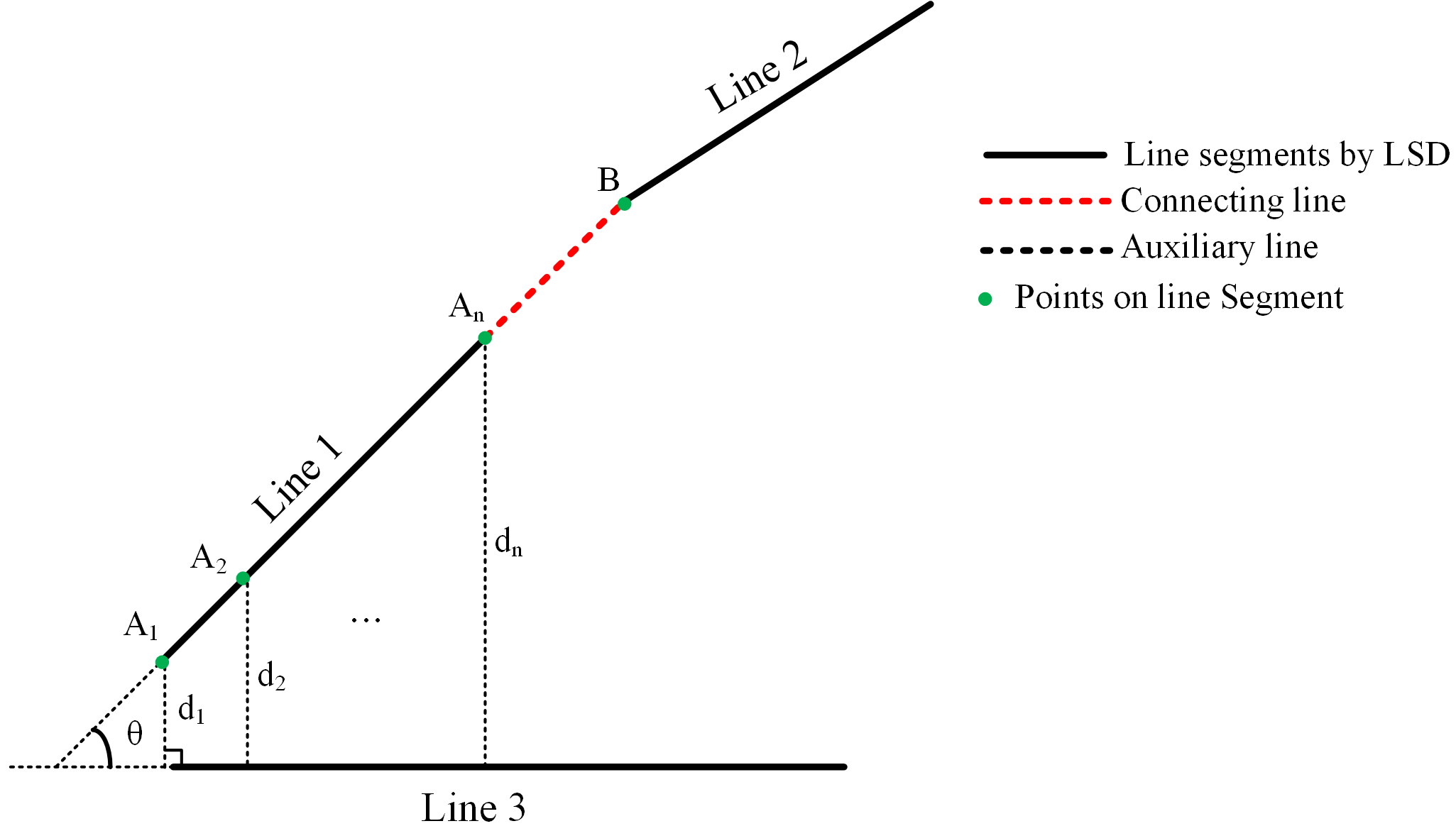
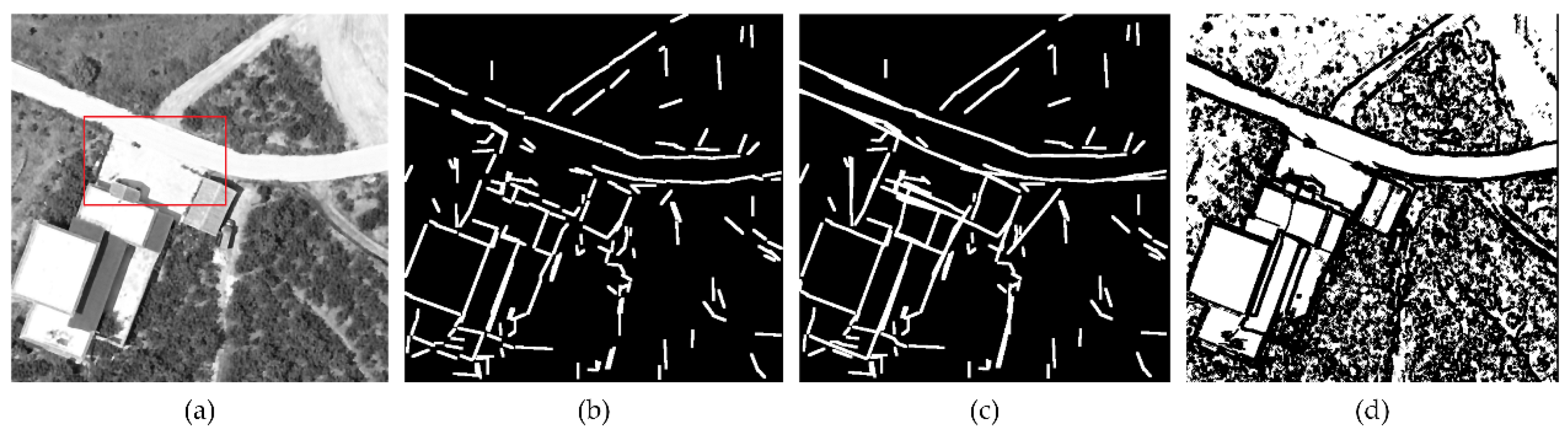
2.2. Gabor Feature Detection
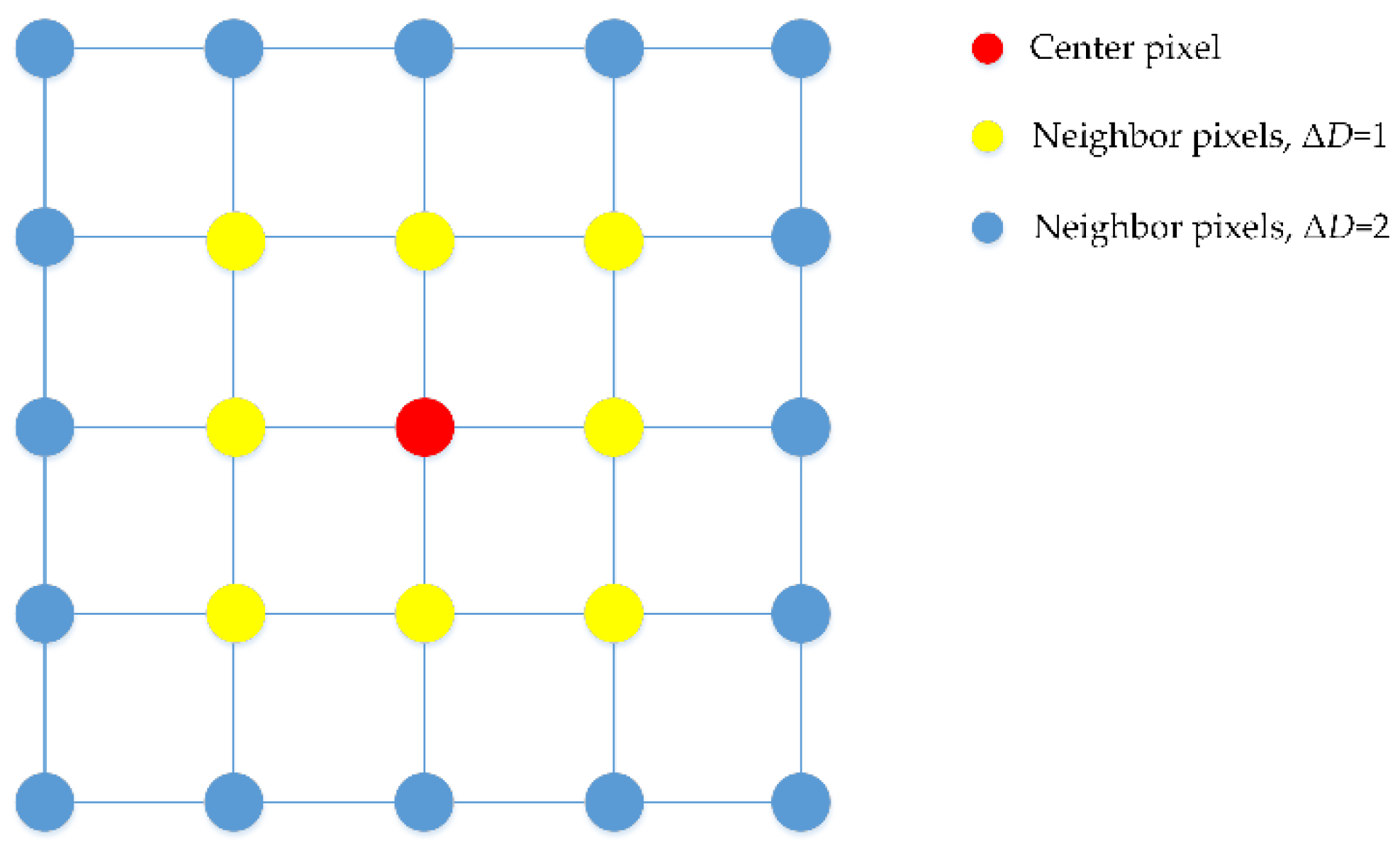
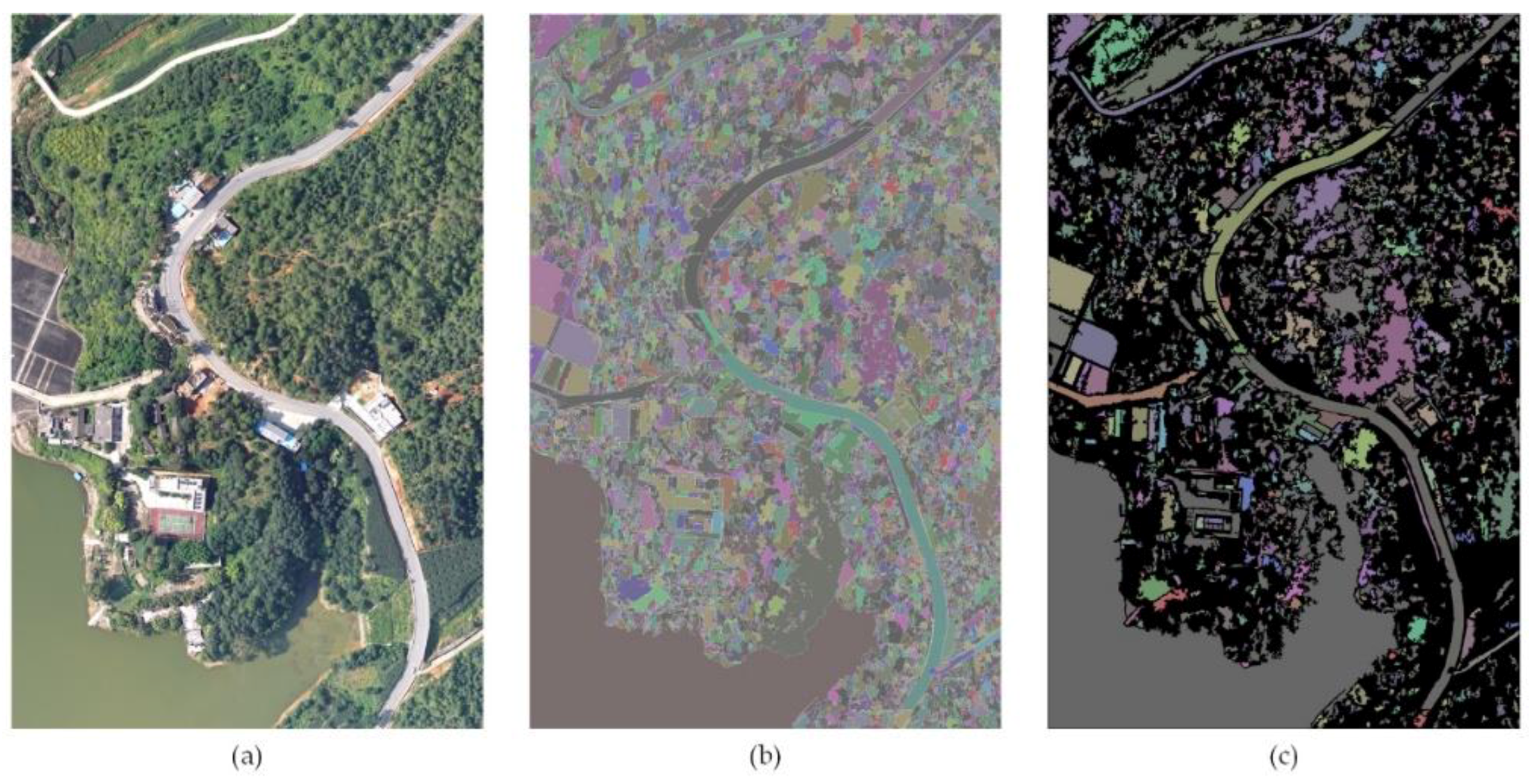
2.3. Object Segmentation and Region Growing with Edge Constraints
| Algorithm 1 Objects Segmentation |
| Input: Preprocessed color image and Gabor feature map. Output: Segmented objects map 1 divide color image to R, G, and B grayscale maps 2 foreach Pi, j(x, y) in three maps do 3 if all Pk within range ΔD meet Sk = Sr,k.+ Sg,k + Sb,k < ST then 4 its flagi, j = 1; 5 else 6 flagi, j = 0; 7 end 8 foreach Pi, j(x, y) in Gabor feature map do 9 if gray value of P’i, j(x, y) is greater than 0 then 10 its flagi, j = 0; 11 end |
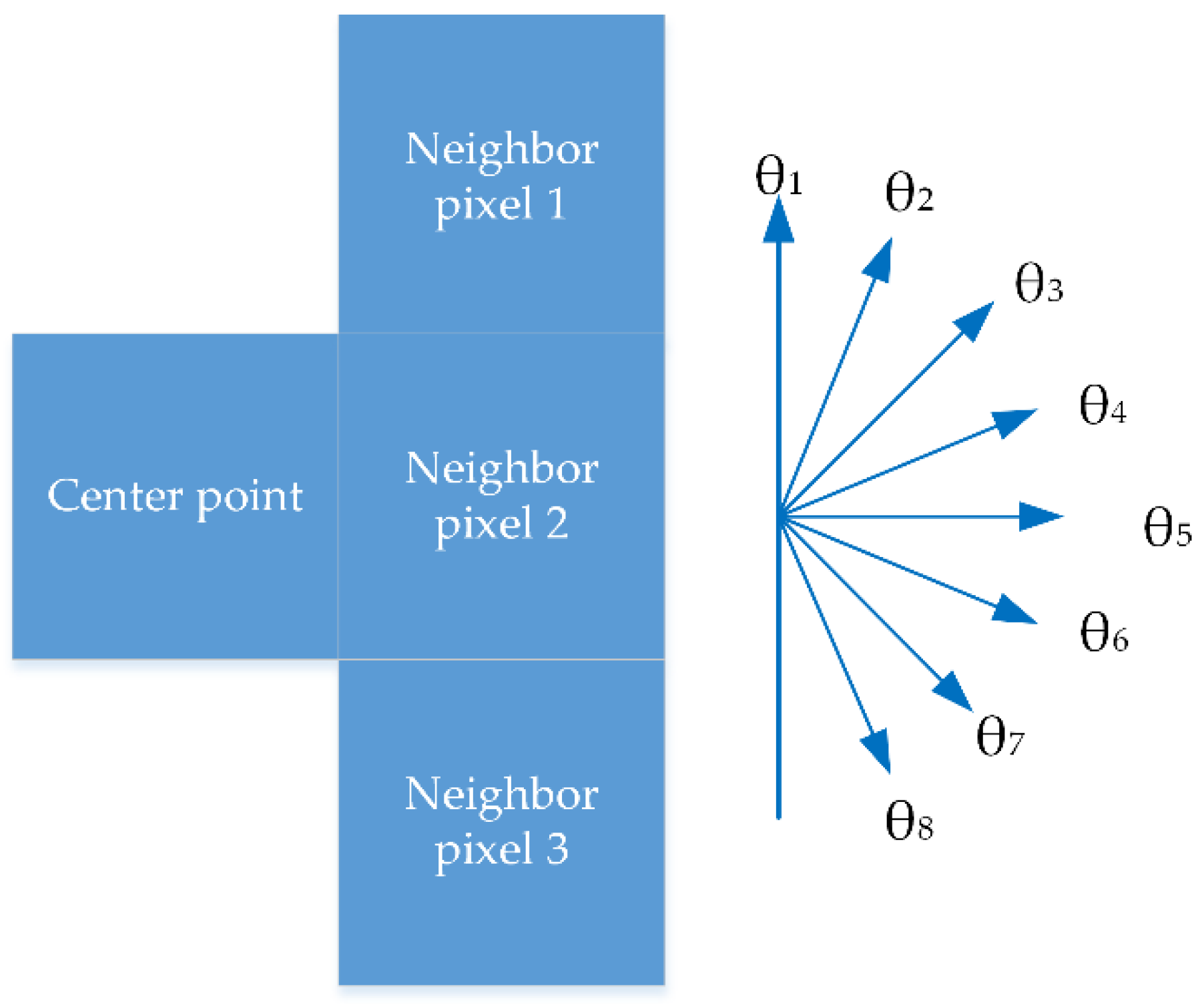
2.4. Road-Object Tracking by Shape Features
2.4.1. Area S
2.4.2. Shortest Inner Diameter D
2.4.3. Complex Rate C
2.4.4. Length–Width Ratio of Bounding Rectangle R
2.4.5. Fullness Ratio F
| Algorithm 2 Road-Object Tracking |
| Input: Segmented objects map Output: Road objects map 1 label each object by seed filling algorithm 2 foreach labeled object do 3 if && && then 4 remain the object 5 else 6 reject the object 7 end 8 foreach remanent object do 9 if R > 3 || F < 0.33 then 10 remain the object 11 end |
3. Results
3.1. Datasets
- Panzhihua Road dataset: The dataset consists of over 100 images covering a part of rural region of Panzhihua City, China. The size of all images is 5001 × 5001 pixels with a spatial resolution of 0.1 m per pixel. These are aerial images collected from a crossing research project. In this work Figure 11a and Figure 13a were cropped images from this dataset.
- Dingbian Road dataset: The dataset consists of about 200 images acquired from aerial photography, covering a part of rural region of Dingbian County, China. The size of all images is 2163 × 1532 pixels with spatial resolution of 0.4 m per pixel. The dataset was collected from a crossing research project. In this work, Figure 13b,c were cropped images from this dataset.
- VPLab Data: This dataset was collected by the QuickBird satellite and was downloaded from VPLab [40]. The dataset consists of images from urban, suburban, and rural regions. The size of all images is 512 × 512 pixels with a spatial resolution of 0.6 m per pixel. In this work, Figure 12a,e was from this dataset.
3.2. Experiment and Parameter Setting
3.3. Comparison and Discussion
4. Conclusions
Author Contributions
Funding
References
- Fortier, A.; Ziou, D.; Armenakis, C.; Wang, S. Survey of Work on Road Extraction in Aerial and Satellite Images; Technical Report; Center for Topographic Information Geomatics: Ontario, ON, Canada, 1999. [Google Scholar]
- Memon, I.; Chen, L.; Majid, A.; Lv, M.; Hussain, I.; Chen, G. Travel recommendation using geo-tagged photos in social media for tourist. Wirel. Pers. Commun. 2015, 80, 1347–1362. [Google Scholar] [CrossRef]
- Shifa, A.; Afgan, M.S.; Asghar, M.N.; Fleury, M.; Memon, I.; Abdullah, S.; Rasheed, N. Joint crypto-stego scheme for enhanced image protection with nearest-centroid clustering. IEEE Access 2018, 6, 16189–16206. [Google Scholar] [CrossRef]
- Memon, I.; Chen, L.; Arain, Q.A.; Memon, H.; Chen, G. Pseudonym changing strategy with multiple mix zones for trajectory privacy protection in road networks. Int. J. Commun. Syst. 2018, 31, e3437. [Google Scholar] [CrossRef]
- Gao, L.; Shi, W.; Miao, Z.; Lv, Z. Method based on edge constraint and fast marching for road centerline extraction from very high-resolution remote sensing images. Remote Sens. 2018, 10, 900. [Google Scholar] [CrossRef]
- Demir, I.; Koperski, K.; Lindenbaum, D.; Pang, G.; Huang, J.; Basu, S.; Hughes, F.; Tuia, D.; Raskar, R. Deepglobe 2018: A challenge to parse the earth through satellite images. arXiv, 2018; arXiv:1805.06561. [Google Scholar]
- Shi, W.; Miao, Z.; Debayle, J. An integrated method for urban main-road centerline extraction from optical remotely sensed imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3359–3372. [Google Scholar] [CrossRef]
- Poullis, C.; You, S. Delineation and geometric modeling of road networks. ISPRS J. Photogramm. Remote Sens. 2010, 65, 165–181. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, Z.; Xu, M. Road structure refined cnn for road extraction in aerial image. IEEE Geosci. Remote Sens. Lett. 2017, 14, 709–713. [Google Scholar] [CrossRef]
- Buslaev, A.; Seferbekov, S.S.; Iglovikov, V.I.; Shvets, A.A. Fully convolutional network for automatic road extraction from satellite imagery. arXiv, 2018; arXiv:1806.05182. [Google Scholar]
- Alshehhi, R.; Marpu, P.R.; Woon, W.L.; Dalla Mura, M. Simultaneous extraction of roads and buildings in remote sensing imagery with convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2017, 130, 139–149. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 679–698. [Google Scholar] [CrossRef]
- Von Gioi, R.G.; Jakubowicz, J.; Morel, J.-M.; Randall, G. Lsd: A fast line segment detector with a false detection control. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 722–732. [Google Scholar] [CrossRef] [PubMed]
- Zang, Y.; Wang, C.; Yu, Y.; Luo, L.; Yang, K.; Li, J. Joint enhancing filtering for road network extraction. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1511–1525. [Google Scholar] [CrossRef]
- Kaur, S.; Baghla, S. Automatic road detection of satellite images using improved edge detection. Int. J. Comput. Technol. 2013, 10, 1546–1552. [Google Scholar] [CrossRef][Green Version]
- Liu, W.; Zhang, Z.; Chen, X.; Li, S.; Zhou, Y. Dictionary learning-based hough transform for road detection in multispectral image. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2330–2334. [Google Scholar] [CrossRef]
- Shao, Y.; Guo, B.; Hu, X.; Di, L. Application of a fast linear feature detector to road extraction from remotely sensed imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 626–631. [Google Scholar] [CrossRef]
- Lisini, G.; Tison, C.; Cherifi, D.; Tupin, F.; Gamba, P. Improving Road Network Extraction in High-Resolution sar Images by Data Fusion. Presented at CEOS SAR Workshop, Ulm, Germany, 27–28 May 2004. [Google Scholar]
- Zang, Y.; Wang, C.; Cao, L.; Yu, Y.; Li, J. Road network extraction via aperiodic directional structure measurement. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3322–3335. [Google Scholar] [CrossRef]
- Yuan, J.; Tang, S.; Wang, F.; Zhang, H. A robust road segmentation method based on graph cut with learnable neighboring link weights. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 1644–1649. [Google Scholar]
- Akram, K.M.; Elahi, M.M.L.; Amin, M.A. Multiple level set region based single line road extraction. In Proceedings of the 2013 International Conference on Machine Learning and Cybernetics, Tianjin, China, 14–17 July 2013; pp. 1201–1206. [Google Scholar]
- Gaetano, R.; Masi, G.; Poggi, G.; Verdoliva, L.; Scarpa, G. Marker-controlled watershed-based segmentation of multiresolution remote sensing images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2987–3004. [Google Scholar] [CrossRef]
- Song, M.; Civco, D. Road extraction using svm and image segmentation. Photogramm. Eng. Remote Sens. 2004, 70, 1365–1371. [Google Scholar] [CrossRef]
- Maboudi, M.; Amini, J.; Hahn, M.; Saati, M. Object-based road extraction from satellite images using ant colony optimization. Int. J. Remote Sens. 2017, 38, 179–198. [Google Scholar] [CrossRef]
- Shi, W.; Miao, Z.; Wang, Q.; Zhang, H. Spectral-spatial classification and shape features for urban road centerline extraction. IEEE Geosci. Remote Sens. Lett. 2014, 11, 788–792. [Google Scholar]
- Xiaoqi, L.; Weixing, W.; Jun, L. A method of road extraction from high-resolution remote sensing images based on shape features. Acta Geod. Cartogr. Sin. 2016, 38, 457–465. [Google Scholar]
- Kumar, M.; Singh, R.; Raju, P.; Krishnamurthy, Y. Road network extraction from high resolution multispectral satellite imagery based on object oriented techniques. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 107. [Google Scholar] [CrossRef]
- Memon, M.H.; Li, J.-P.; Memon, I.; Arain, Q.A. Geo matching regions: Multiple regions of interests using content based image retrieval based on relative locations. Multimed. Tools Appl. 2017, 76, 15377–15411. [Google Scholar] [CrossRef]
- Memon, M.H.; Li, J.-P.; Memon, I.; Shaikh, R.A.; Mangi, F.A. Efficient object identification and multiple regions of interest using cbir based on relative locations and matching regions. In Proceedings of the 2015 12th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP), Chengdu, China, 18–20 December 2015; pp. 247–250. [Google Scholar]
- Alshehhi, R.; Marpu, P.R. Hierarchical graph-based segmentation for extracting road networks from high-resolution satellite images. ISPRS J. Photogramm. Remote Sens. 2017, 126, 245–260. [Google Scholar] [CrossRef]
- Zhao, W.; Luo, L.; Guo, Z.; Yue, J.; Yu, X.; Liu, H.; Wei, J. Road extraction in remote sensing images based on spectral and edge analysis. Guang Pu Xue Yu Guang Pu Fen Xi= Guang Pu 2015, 35, 2814–2819. [Google Scholar] [PubMed]
- Daugman, J.G. Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters. JOSA A 1985, 2, 1160–1169. [Google Scholar] [CrossRef]
- Kamarainen, J.-K.; Kyrki, V.; Kalviainen, H. Invariance properties of gabor filter-based features-overview and applications. IEEE Trans. Image Process. 2006, 15, 1088–1099. [Google Scholar] [CrossRef] [PubMed]
- Kamarainen, J.-K. Gabor features in image analysis. In Proceedings of the 2012 3rd International Conference on Image Processing Theory, Tools and Applications (IPTA), Istanbul, Turkey, 15–18 October 2012; pp. 13–14. [Google Scholar]
- Ilonen, J.; Kamarainen, J.-K.; Kalviainen, H. Fast extraction of multi-resolution gabor features. In Proceedings of the 14th International Conference on Image Analysis and Processing (ICIAP 2007), Modena, Italy, 10–14 September 2007; pp. 481–486. [Google Scholar]
- Sghaier, M.O.; Lepage, R. Road extraction from very high resolution remote sensing optical images based on texture analysis and beamlet transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1946–1958. [Google Scholar] [CrossRef]
- Shaikh, R.A.; Deep, S.; Li, J.-P.; Kumar, K.; Khan, A.; Memon, I. Contemporary integration of content based image retrieval. In Proceedings of the 2014 11th International Computer Conference on Wavelet Actiev Media Technology and Information Processing(ICCWAMTIP), Chengdu, China, 19–21 December 2014; pp. 301–304. [Google Scholar]
- Memon, M.H.; Khan, A.; Li, J.-P.; Shaikh, R.A.; Memon, I.; Deep, S. Content based image retrieval based on geo-location driven image tagging on the social web. In Proceedings of the 2014 11th International Computer Conference on Wavelet Actiev Media Technology and Information Processing(ICCWAMTIP), Chengdu, China, 19–21 December 2014; pp. 280–283. [Google Scholar]
- Liu, J.; Qin, Q.; Li, J.; Li, Y. Rural road extraction from high-resolution remote sensing images based on geometric feature inference. ISPRS Int. J. Geo Inf. 2017, 6, 314. [Google Scholar] [CrossRef]
- VPLab Data. Available online: http://www.cse.iitm.ac.in/~vplab/satellite.html (accessed on 16 April 2017).






| λ | σ | θ | φ | κ |
|---|---|---|---|---|
| λ1 = 2.2 | σ1 = 1.2 | θn = nπ/8, n = 0, 1, 2, …, 7 | φ = 0 | κ = 0.3 |
| λ2 = 3.0 | σ2 = 1.7 | |||
| λ3 = 4.2 | σ3 = 2.4 |
| Road Shape | Area S | Shortest Inner Diameter D | Complex Rate C | Length–Width Ratio of Bounding Rectangle R | Fullness Ratio F |
|---|---|---|---|---|---|
| Straight Line | 1000–50,000 | 30–50 | 100 | 3.5 | - |
| Curve Line | 1000–50,000 | 30–50 | 100 | - | 0.33 |
| Method | Image I | Image II | ||||
|---|---|---|---|---|---|---|
| Completeness | Correctness | Quality | Completeness | Correctness | Quality | |
| Lei et al. [26] | 0.9 | 0.71 | 0.66 | 0.89 | 0.86 | 0.77 |
| -proposed | 0.92 | 0.79 | 0.74 | 0.94 | 0.96 | 0.91 |
| Evaluation | Zang et al. [19] | Lei et al. [26] | Proposed |
|---|---|---|---|
| Image I | |||
| Completeness | 0.89 | 0.97 | 0.97 |
| Correctness | 0.47 | 0.86 | 0.97 |
| Quality | 0.44 | 0.84 | 0.95 |
| Image II | |||
| Completeness | 0.75 | 0.82 | 0.89 |
| Correctness | 0.43 | 0.69 | 0.97 |
| Quality | 0.38 | 0.6 | 0.87 |
| Image III | |||
| Completeness | 0.8 | 0.7 | 0.77 |
| Correctness | 0.47 | 0.92 | 0.96 |
| Quality | 0.42 | 0.66 | 0.75 |
| Method | Implementation Environment | Running Time for Image I | Running Time for Image II | Running Time for Image III |
|---|---|---|---|---|
| Zang et al. [19] | 2.6 GHz Intel Core i7-6700HQ CPU | 271 s | 335 s | 339 s |
| Lei et al. | 2.6 GHz Intel Core i7-6700HQ CPU | 38 s | 47 s | 56 s |
| Proposed | 2.6 GHz Intel Core i7-6700HQ CPU | 49 s | 62 s | 71 s |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Zhu, Q.; Xie, X.; Hu, H.; Zeng, H. Road Extraction from VHR Remote-Sensing Imagery via Object Segmentation Constrained by Gabor Features. ISPRS Int. J. Geo-Inf. 2018, 7, 362. https://doi.org/10.3390/ijgi7090362
Chen L, Zhu Q, Xie X, Hu H, Zeng H. Road Extraction from VHR Remote-Sensing Imagery via Object Segmentation Constrained by Gabor Features. ISPRS International Journal of Geo-Information. 2018; 7(9):362. https://doi.org/10.3390/ijgi7090362
Chicago/Turabian StyleChen, Li, Qing Zhu, Xiao Xie, Han Hu, and Haowei Zeng. 2018. "Road Extraction from VHR Remote-Sensing Imagery via Object Segmentation Constrained by Gabor Features" ISPRS International Journal of Geo-Information 7, no. 9: 362. https://doi.org/10.3390/ijgi7090362
APA StyleChen, L., Zhu, Q., Xie, X., Hu, H., & Zeng, H. (2018). Road Extraction from VHR Remote-Sensing Imagery via Object Segmentation Constrained by Gabor Features. ISPRS International Journal of Geo-Information, 7(9), 362. https://doi.org/10.3390/ijgi7090362