A Simple Line Clustering Method for Spatial Analysis with Origin-Destination Data and Its Application to Bike-Sharing Movement Data
Abstract
1. Introduction
2. Related Research
2.1. Point Clustering Method for OD Data
2.2. Trajectory Clustering Methods
3. SLCM Clustering Method
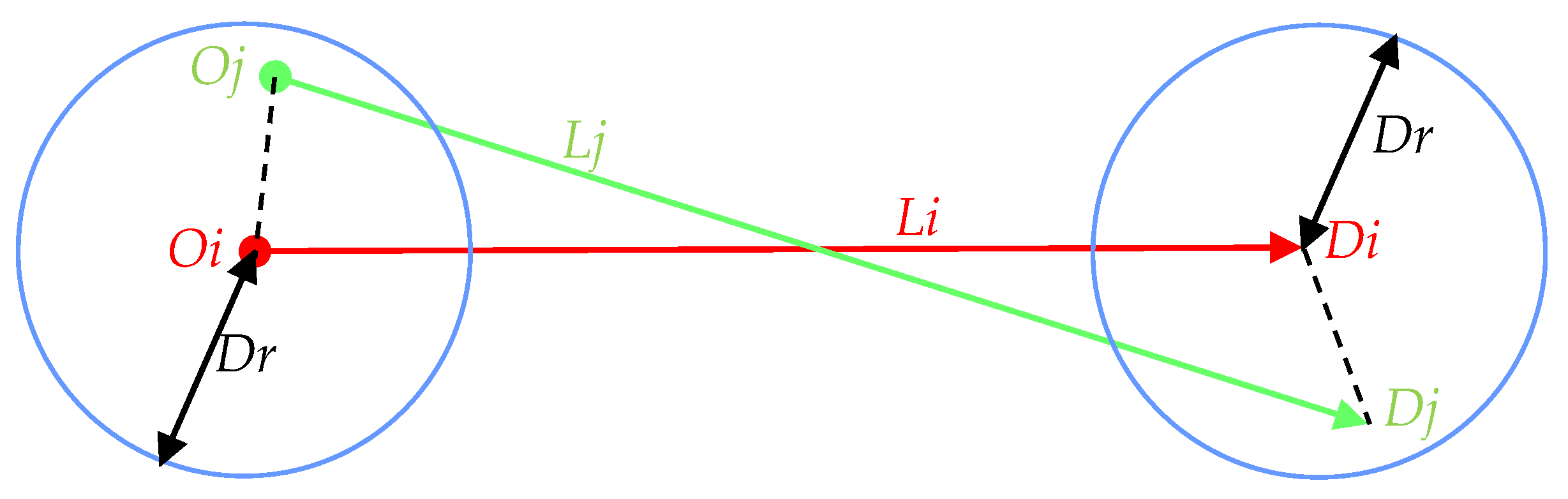
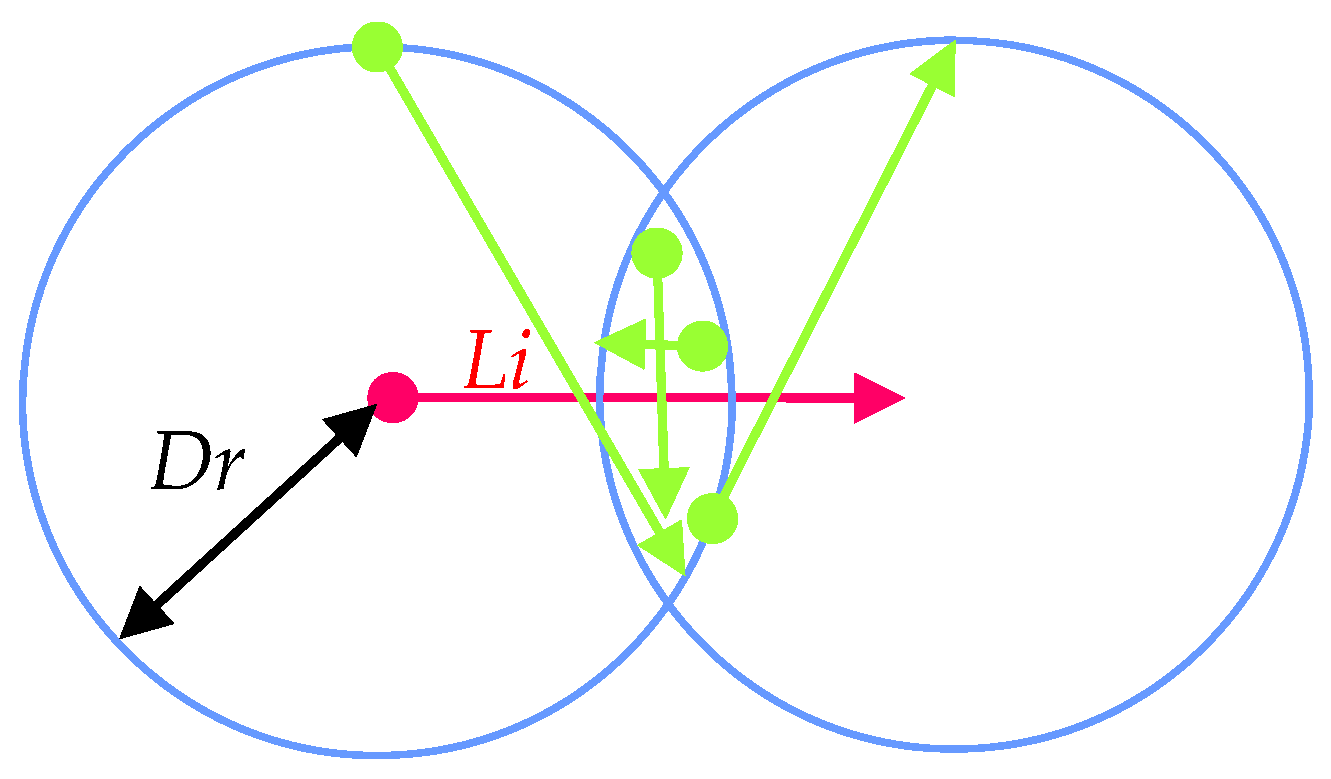
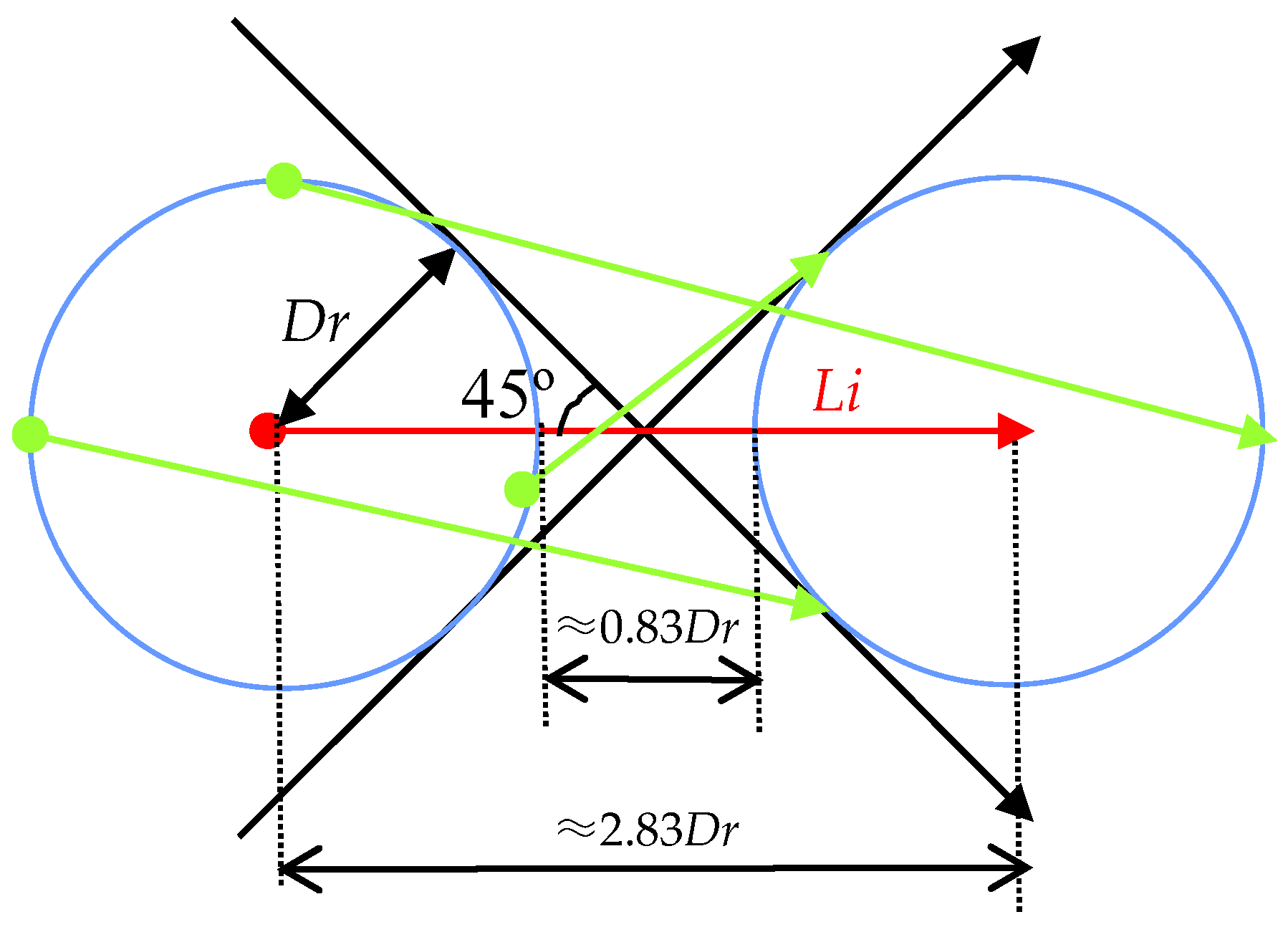
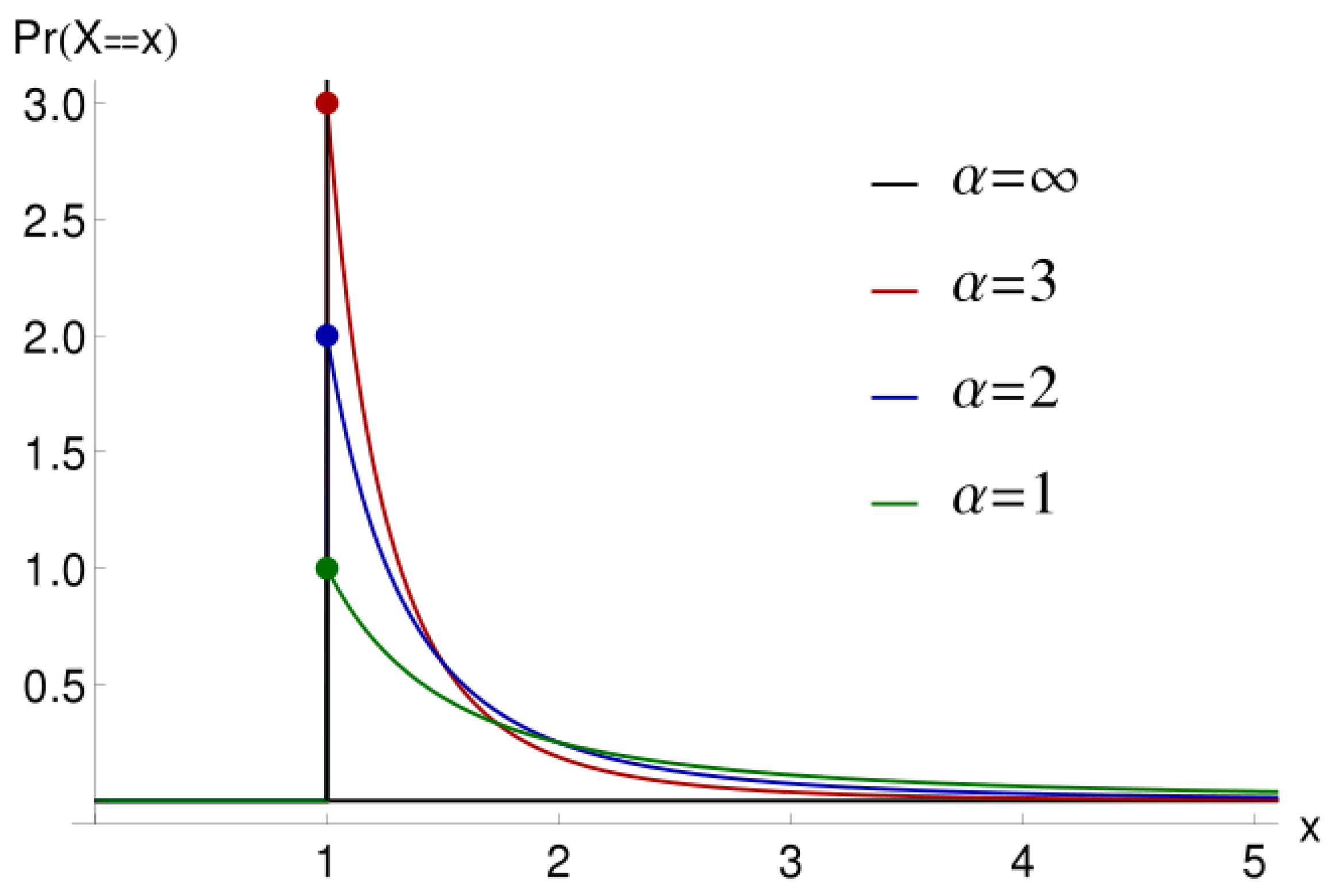
3.1. The Definitions
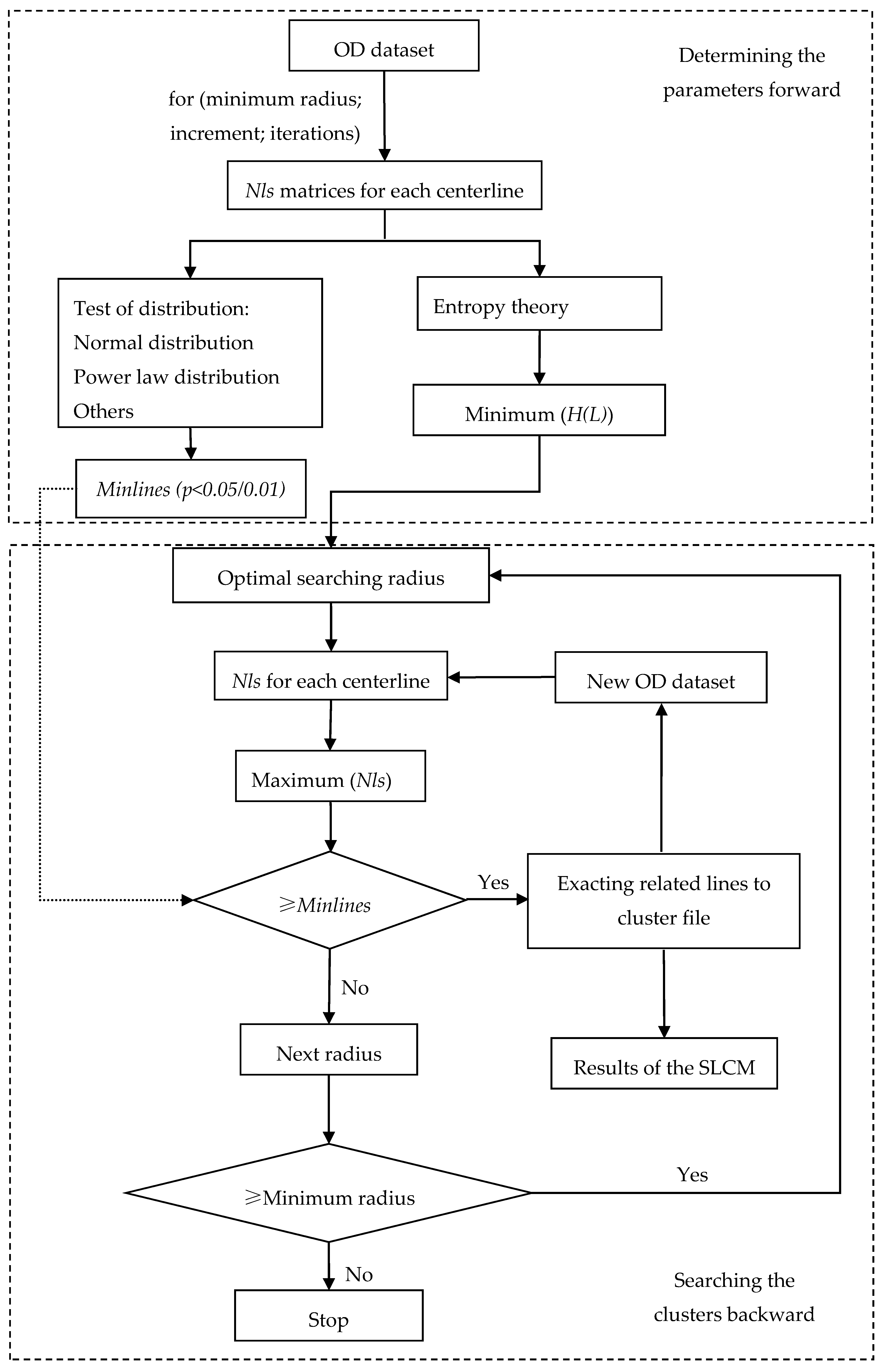
3.2. Determining the Parameters
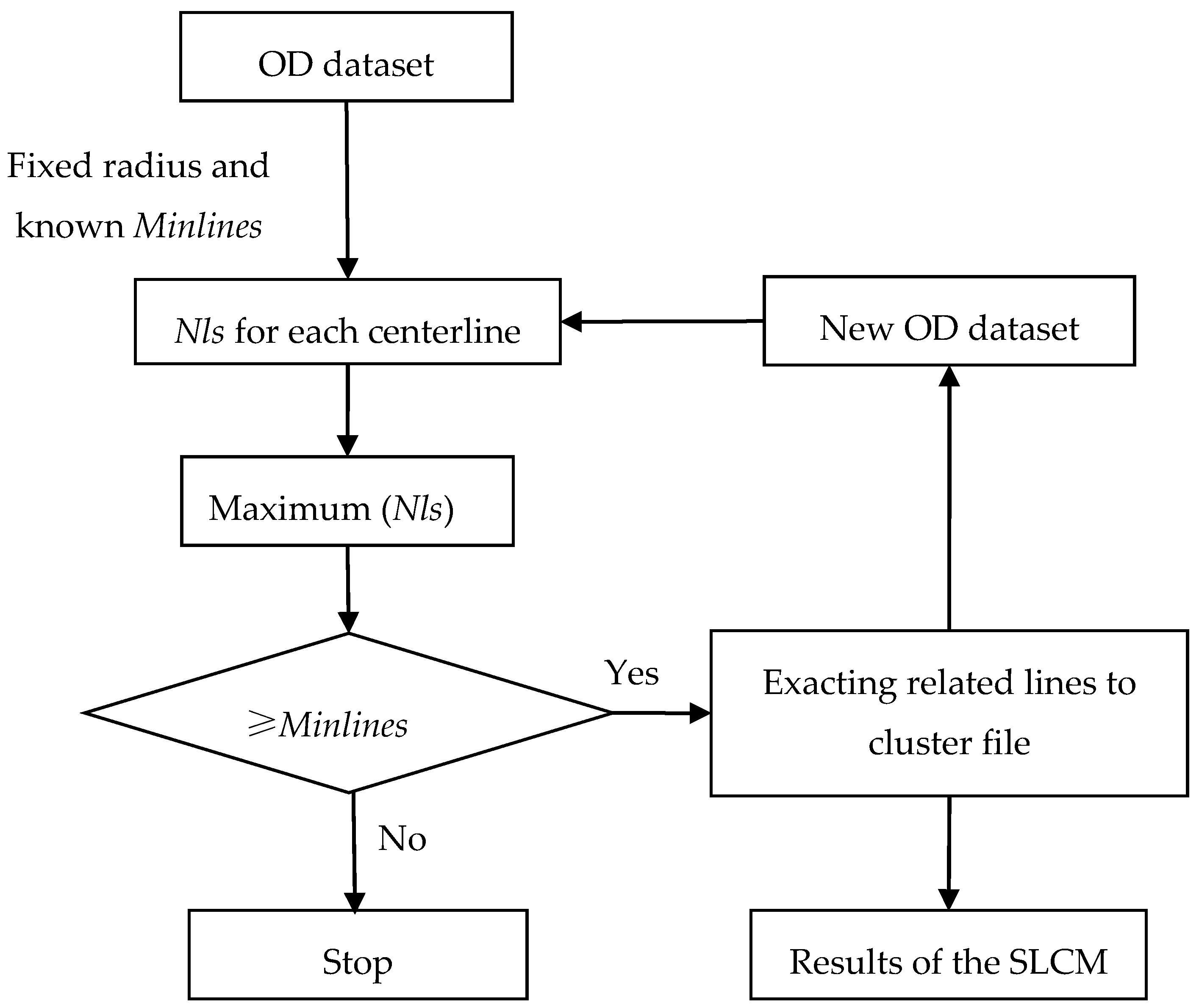
3.3. Clustering Process Flowchart
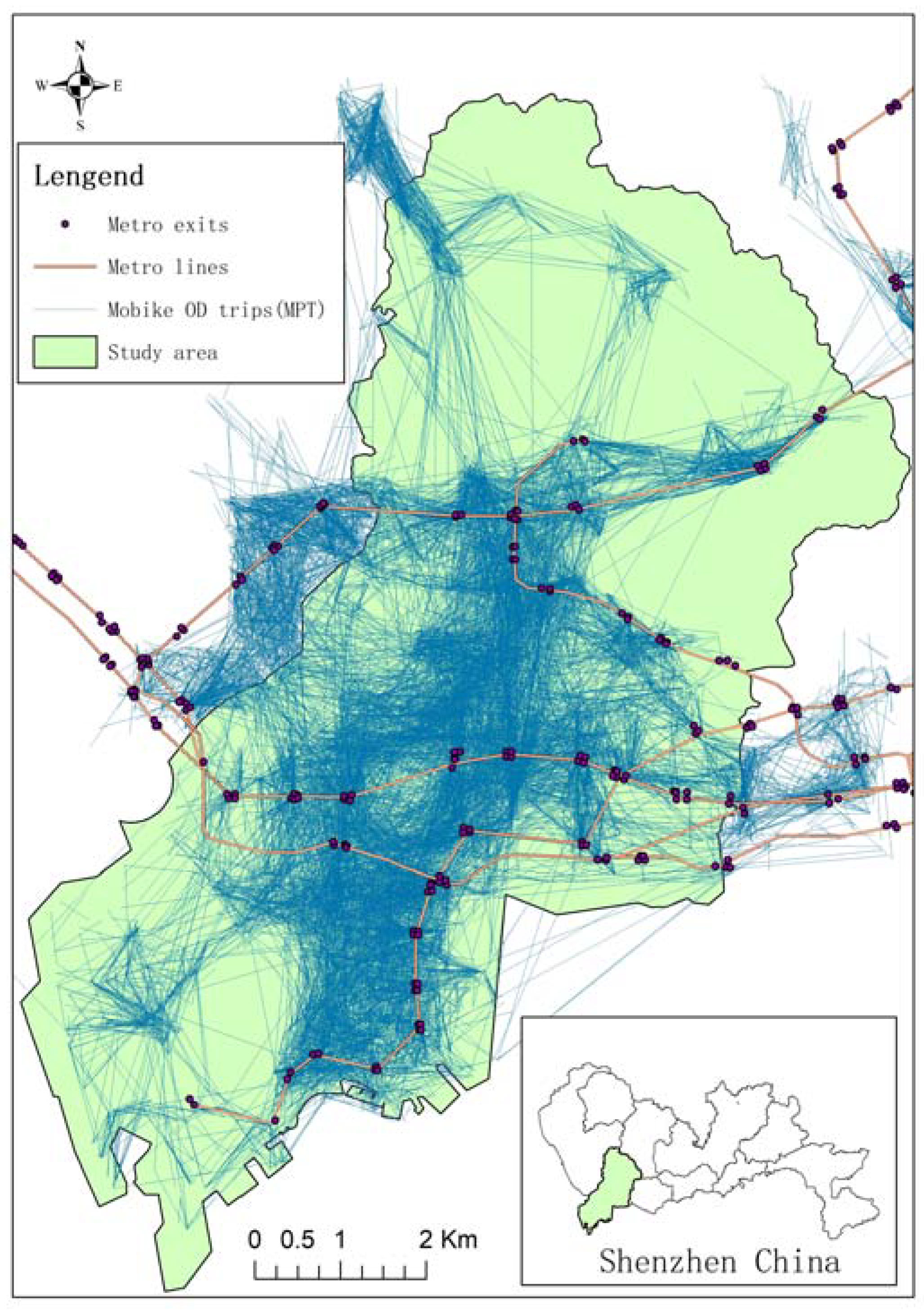
4. Case Study
4.1. The Parameter Determination
4.2. Clustering Process with a Fixed Radius
4.3. Clustering Results with Flexible Radius
5. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Calabrese, F.; Lorenzo, G.D.; Liu, L.; Ratti, C. Estimating Origin-Destination Flows Using Mobile Phone Location Data. IEEE Pervasive Comput. 2011, 10, 36–44. [Google Scholar] [CrossRef]
- Guo, D.; Zhu, X. Origin-Destination Flow Data Smoothing and Mapping. IEEE Trans. Vis. Comput. Graph. 2014, 20, 2043–2052. [Google Scholar] [CrossRef] [PubMed]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Adrienko, N.; Adrienko, G. Spatial Generalization and Aggregation of Massive Movement Data. IEEE Trans. Vis. Comput. Graph. 2011, 17, 205–219. [Google Scholar] [CrossRef] [PubMed]
- Andrienko, G.; Andrienko, N. Spatio-temporal aggregation for visual analysis of movements. In Proceedings of the IEEE Symposium on Visual Analytics Science and Technology, Columbus, OH, USA, 19–24 October 2008; Ebert, D., Ertl, T., Eds.; IEEE: Washington, DC, USA, 2008; pp. 51–58. [Google Scholar]
- Cui, W.; Zhou, H.; Qu, H.; Wong, P.C.; Li, X. Geometry-Based Edge Clustering for Graph Visualization. IEEE Trans. Vis. Comput. Graph. 2008, 14, 1277–1284. [Google Scholar] [CrossRef] [PubMed]
- Buchin, K.; Speckmann, B.; Verbeek, K. Flow Map Layout via Spiral Trees. IEEE Trans. Vis. Comput. Graph. 2011, 17, 2536–2544. [Google Scholar] [CrossRef] [PubMed]
- Holten, D.; Van Wijk, J.J. Force-Directed Edge Bundling for Graph Visualization. Comput. Graph. Forum 2009, 28, 983–990. [Google Scholar] [CrossRef]
- Guo, D.S.; Zhu, X.; Jin, H.; Gao, P.; Andris, C. Discovering spatial patterns in origin-destination mobility data. Trans. GIS 2012, 16, 411–429. [Google Scholar] [CrossRef]
- Zhu, X.; Guo, D. Mapping Large Spatial Flow Data with Hierarchical Clustering. Trans. GIS 2014, 18, 421–435. [Google Scholar] [CrossRef]
- Mao, F.; Ji, M.; Liu, T. Mining spatiotemporal patterns of urban dwellers from taxi trajectory data. Front. Earth Sci. 2016, 10, 205–221. [Google Scholar] [CrossRef]
- Lee, J.G.; Han, J.; Whang, K.Y. Trajectory clustering: A partition-and-group framework. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Beijing, China, 11–13 June 2007; pp. 593–604. [Google Scholar]
- Cao, H.; Mamoulis, N.; Cheung, D.W. Discovery of periodic patterns in spatiotemporal sequences. IEEE Trans. Knowl. Data Eng. 2007, 19, 453–467. [Google Scholar] [CrossRef]
- Ferrero, C.A.; Alvares, L.O.; Zalewski, W.; Bogorny, V. Movelets: Exploring Relevant Subtrajectories for Robust Trajectory Classification. In Proceedings of the 33rd ACM/SIGAPP Symposium on Applied Computing, Pau, France, 9–13 April 2018. [Google Scholar]
- Chen, J.; Leung, M.K.H.; Gao, Y. Noisy Logo Recognition Using Line Segment Hausdorff Distance. Pattern Recognit. 2003, 36, 943–955. [Google Scholar] [CrossRef]
- Lee, J.G.; Han, J.; Li, X.; Gonzalez, H. Traclass: Trajectory classification using hierarchical region-based and trajectory-based clustering. Proceedings of VLDB Endowment, Auckland, New Zealand, 23–28 August 2008; pp. 1081–1094. [Google Scholar]
- Yuan, G.; Xia, S.; Zhang, L.; Zhou, Y.; Ji, C. An efficient trajectory-clustering algorithm based on an index tree. Trans. Inst. Meas. Control. 2011, 34, 850–861. [Google Scholar] [CrossRef]
- Zhang, D.; Lee, K.; Lee, I.; Zhang, D.; Lee, K.; Lee, I. Hierarchical trajectory clustering for spatio-temporal periodic pattern mining. Expert Syst. Appl. 2018, 92, 1–11. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, K.; Chen, Y.; Zhao, P. Detecting anomalous trajectories and behavior patterns using hierarchical clustering from taxi GPS data. ISPRS Int. J. Geo-Inf. 2018, 7, 25. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, Y.; Li, Q.; Xie, X.; Ma, W.Y. Understanding transportation modes based on GPS data for web applications. ACM Trans. Web 2010, 4, 1–36. [Google Scholar] [CrossRef]
- Xiao, Z.; Wang, Y.; Fu, K.; Wu, F. Identifying different transportation modes from trajectory data using tree-based ensemble classifiers. ISPRS Int. J. Geo-Inf. 2017, 6, 57. [Google Scholar] [CrossRef]
- Campello, R.J.G.B.; Moulavi, D.; Sander, J. Density-based clustering based on hierarchical density estimates. In PAKDD 2013: Advances in Knowledge Discovery and Data Mining; Lecture Notes in Computer Science: Volume 7819; Pei, J., Tseng, V.S., Cao, L., Motoda, H., Xu, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 160–172. [Google Scholar]
- Dodge, S.; Weibel, R.; Forootan, E. Revealing the physics of movement: Comparing the similarity of movement characteristics of different types of moving objects. Comput. Environ. Urban Syst. 2009, 33, 419–434. [Google Scholar] [CrossRef]
- Tiakas, E.; Papadopoulos, A.N.; Nanopoulos, A.; Manolopoulos, Y.; Stojancivic, D.; DjordjevicKajan, S. Searching for similar trajectories in spatial networks. J. Syst. Softw. 2009, 82, 772–788. [Google Scholar] [CrossRef]
- Etemad, M.; Soares Júnior, A.; Matwin, S. Predicting Transportation Modes of GPS Trajectories Using Feature Engineering and Noise Removal. Adv. Artif. Intell. 2018, 259–264. [Google Scholar]
- Moreno, B.; Júnior, A.S.; Times, V.; Tedesco, P.; Matwin, S. Weka-SAT: A Hierarchical Context-Based Inference Engine to Enrich Trajectories with Semantics. In Advances in Artificial Intelligence. AI 2014; Lecture Notes in Computer Science, Volume 8436; Sokolova, M., van Beek, P., Eds.; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- ArcGIS Help. Available online: http://resources.arcgis.com/en/help/main/10.2/index.html#//005p00000006000000 (accessed on 30 July 2013).
- Yaneer, B.Y.; Concepts: Power Law. New England Complex Systems Institute. Available online: http://www.necsi.edu/guide/concepts/powerlaw.html (accessed on 18 August 2015).
- Barry, C.A. Pareto Distributions; International Co-Operative Publishing House: Fairland, MD, USA, 1983; ISBN 0-89974-012-X. [Google Scholar]
- Pareto Distribution. Available online: https://en.m.wikipedia.org/wiki/Pareto_distribution (accessed on 15 January 2018).
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law Distributions in Empirical Data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Shenzhen Statistical Yearbook 2017. Available online: http://www.sztj.gov.cn/xxgk/tjsj/tjnj/201712/W020171219625244452877.pdf (accessed on 19 December 2017)(In Chinese and English).
- Mobike Stays Ahead in Chinese Bike-Sharing Market, Analysis Says. 2017. Available online: http://www.chinadaily.com.cn/business/tech/2017-02/10/content_28163187.htm (accessed on 10 February 2017).
- 2017 Sharing Bike and Urban Development White Paper. 2017. Available online: http://news.cssn.cn/zx/bwyc/201704/t20170412_3484389.shtml (accessed on 12 April 2017). (In Chinese).
- Deng, L.F.; Xie, Y.F.; Huang, D.X. Bicycle-sharing facility planning based on riding spatiotemporal data. Planners 2017, 10, 82–88. [Google Scholar]
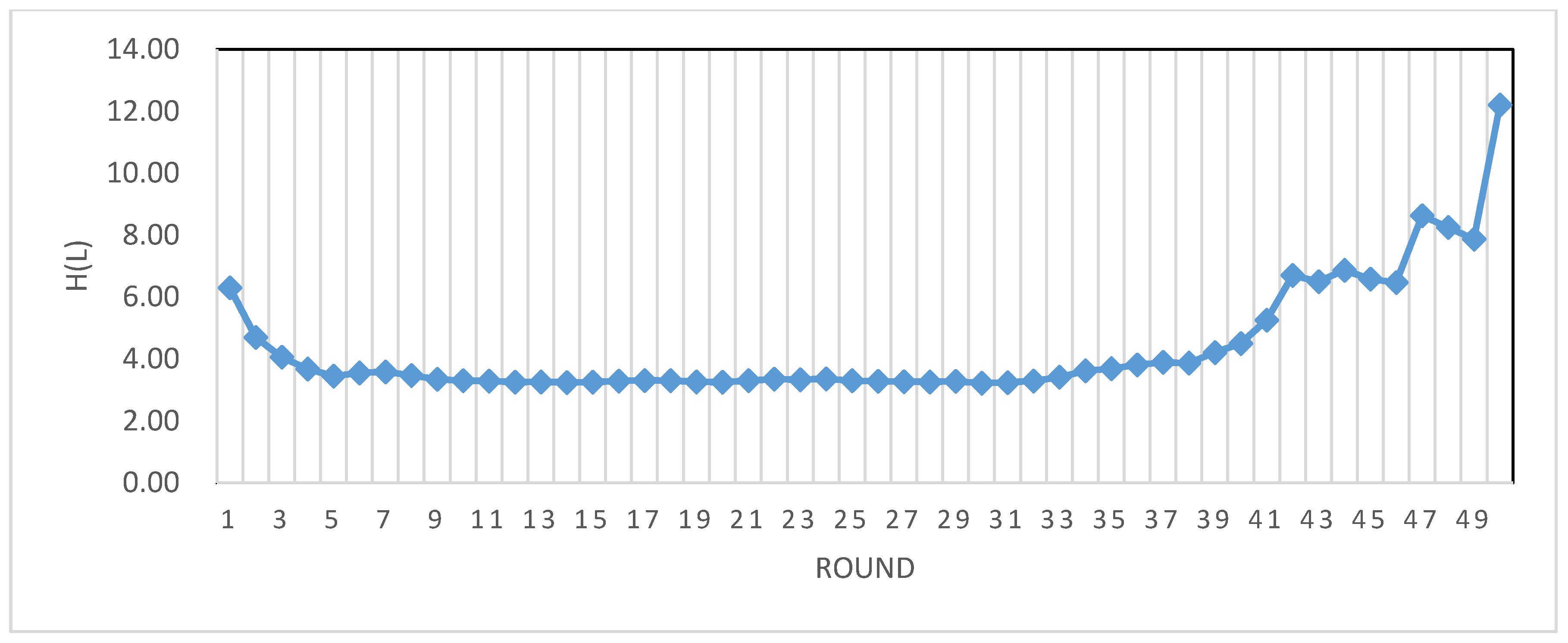

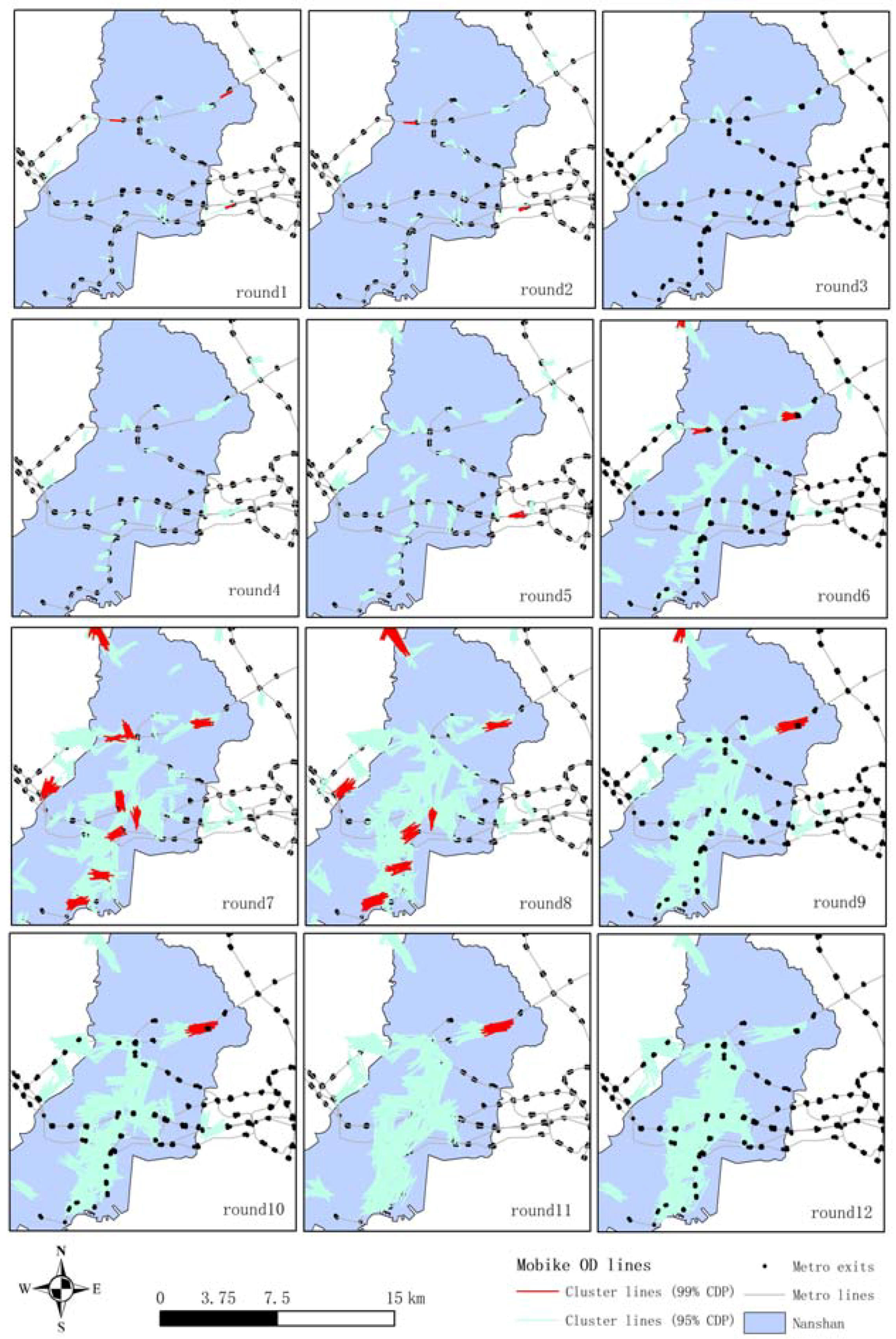
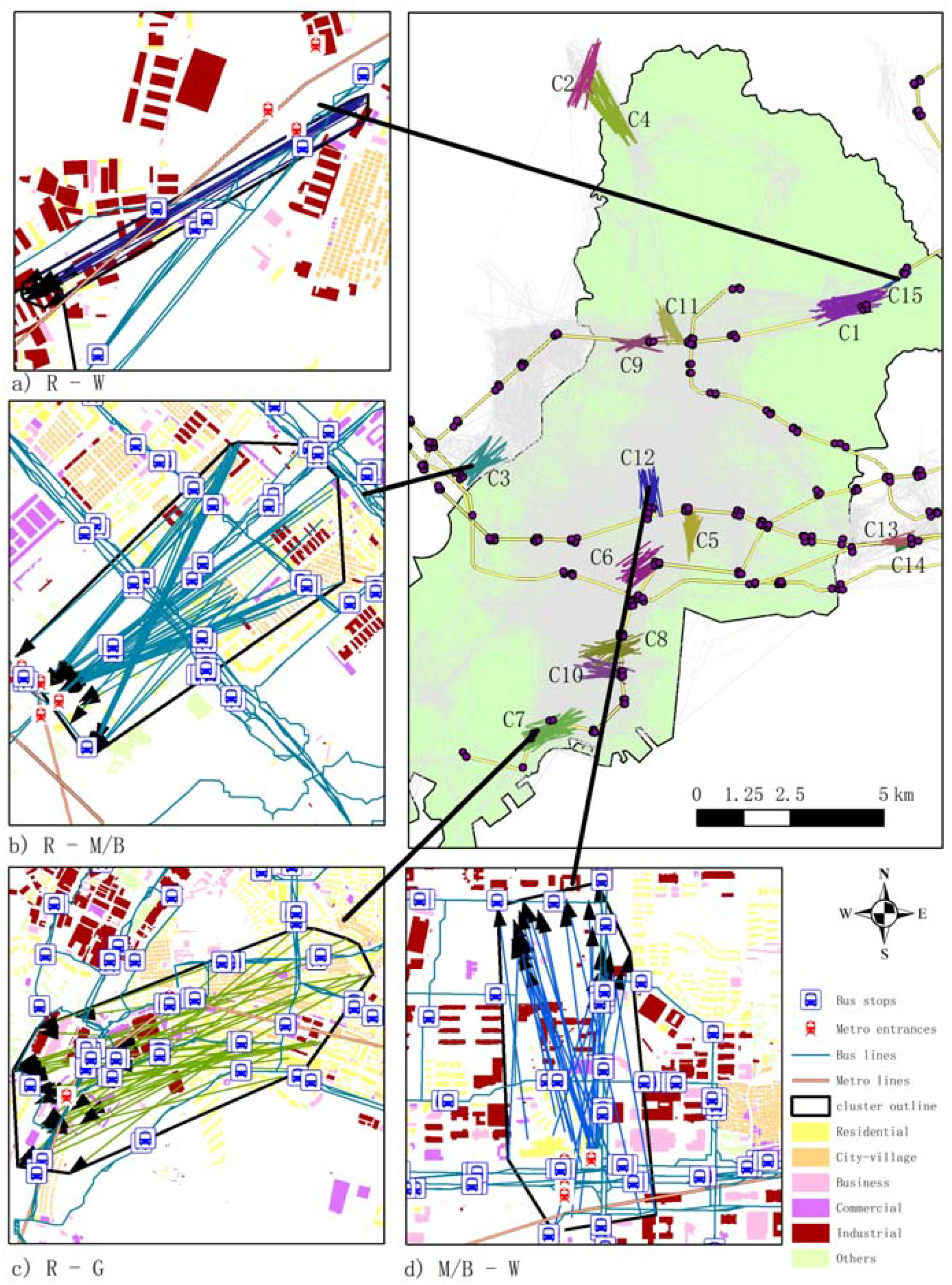
| Round | Dr (m) | R2 | α | Minlines (95% of CDP) | Minlines (99% of CDP) | Entropy | Max (Nls) |
|---|---|---|---|---|---|---|---|
| 1 | 50 | 0.914 | 1.685 | 6 | 16 | 6.30 | 24 |
| 2 | 100 | 0.893 | 1.397 | 9 | 28 | 4.70 | 31 |
| 3 | 150 | 0.919 | 1.175 | 13 | 51 | 4.06 | 33 |
| 4 | 200 | 0.911 | 1.124 | 15 | 61 | 3.68 | 42 |
| 5 | 250 | 0.886 | 1.172 | 15 | 51 | 3.45 | 51 |
| 6 | 300 | 0.952 | 1.238 | 13 | 42 | 3.55 | 55 |
| 7 | 350 | 0.930 | 1.359 | 10 | 30 | 3.59 | 55 |
| 8 | 400 | 0.902 | 1.296 | 11 | 35 | 3.47 | 63 |
| 9 | 450 | 0.917 | 1.152 | 14 | 55 | 3.35 | 84 |
| 10 | 500 | 0.923 | 1.066 | 17 | 76 | 3.30 | 103 |
| 11 | 550 | 0.918 | 1.046 | 18 | 82 | 3.29 | 98 |
| 12 | 600 | 0.909 | 1.005 | 20 | 98 | 3.25 | 84 |
| 13 | 650 | 0.895 | 0.980 | - | 3.26 | 80 | |
| 14 | 700 | 0.892 | 0.863 | - | 3.24 | 88 | |
| 15 | 750 | 0.899 | 0.801 | - | 3.25 | 92 |
| R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 | R10 | R11 | R12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of clusters | 37 | 37 | 29 | 35 | 45 | 76 | 150 | 139 | 95 | 69 | 58 | 55 |
| Number of total clustered lines | 733 | 492 | 560 | 793 | 1101 | 1594 | 2566 | 2607 | 2267 | 1937 | 1787 | 1784 |
| Average number of clustered lines | 20 | 13 | 19 | 23 | 24 | 21 | 17 | 19 | 24 | 28 | 31 | 32 |
| Length of centerline | 0.34 | 0.70 | 0.69 | 0.74 | 0.88 | 1.05 | 1.22 | 1.37 | 1.47 | 1.62 | 1.76 | 1.91 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Radius (m) | 550 | 450 | 400 | 400 | 400 | 400 | 400 | 400 | 350 | 350 | 350 | 350 | 250 | 200 | 150 |
| Length of centerline (km) | 1.6 | 1.3 | 1.1 | 1.7 | 1.2 | 1.1 | 1.3 | 1.2 | 1.0 | 1.0 | 1.0 | 1.0 | 0.7 | 0.5 | 0.7 |
| Number of clustered lines | 98 | 60 | 63 | 46 | 42 | 39 | 37 | 35 | 55 | 36 | 34 | 30 | 51 | 29 | 17 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, B.; Zhang, Y.; Chen, Y.; Gu, Z. A Simple Line Clustering Method for Spatial Analysis with Origin-Destination Data and Its Application to Bike-Sharing Movement Data. ISPRS Int. J. Geo-Inf. 2018, 7, 203. https://doi.org/10.3390/ijgi7060203
He B, Zhang Y, Chen Y, Gu Z. A Simple Line Clustering Method for Spatial Analysis with Origin-Destination Data and Its Application to Bike-Sharing Movement Data. ISPRS International Journal of Geo-Information. 2018; 7(6):203. https://doi.org/10.3390/ijgi7060203
Chicago/Turabian StyleHe, Biao, Yan Zhang, Yu Chen, and Zhihui Gu. 2018. "A Simple Line Clustering Method for Spatial Analysis with Origin-Destination Data and Its Application to Bike-Sharing Movement Data" ISPRS International Journal of Geo-Information 7, no. 6: 203. https://doi.org/10.3390/ijgi7060203
APA StyleHe, B., Zhang, Y., Chen, Y., & Gu, Z. (2018). A Simple Line Clustering Method for Spatial Analysis with Origin-Destination Data and Its Application to Bike-Sharing Movement Data. ISPRS International Journal of Geo-Information, 7(6), 203. https://doi.org/10.3390/ijgi7060203





