An Endmember Initialization Scheme for Nonnegative Matrix Factorization and Its Application in Hyperspectral Unmixing
Abstract
1. Introduction
2. Methodology
2.1. Linear Mixture Model
2.2. Nonnegative Matrix Factorization
2.3. Automatic Target Generation Process
- The observed pixel of the hyperspectral image is set to a vector , and the VD determined by the HFC algorithm is .
- Based on the convex geometry theory, we choose a target pixel with the maximum vector length, which corresponds to the brightest pixel in the image, as the initial target pixel vector denoted by .
- Based on the orthogonal subspace projection theory, the ATGP algorithm begins with the initial target pixel vector by applying an orthogonal subspace projector to all pixel vectors in the image and finds the first target pixel vector denoted by with the maximum orthogonal projection in the orthogonal complement space .
- Suppose that we find the target generated at the step by , where is the target pixel vector matrix generated at the step.
- The orthogonal subspace of is given by , where is the pseudoinverse of ; the notation in indicates that the projector maps the observed pixel into the range , the orthogonal complement of ; and is a unit matrix.
- The ATGP stops when equals to the number of the endmembers . The target pixel vector matrix which contains target pixel vectors apart from the initial target pixel vector , is then regarded as the endmember spectra.
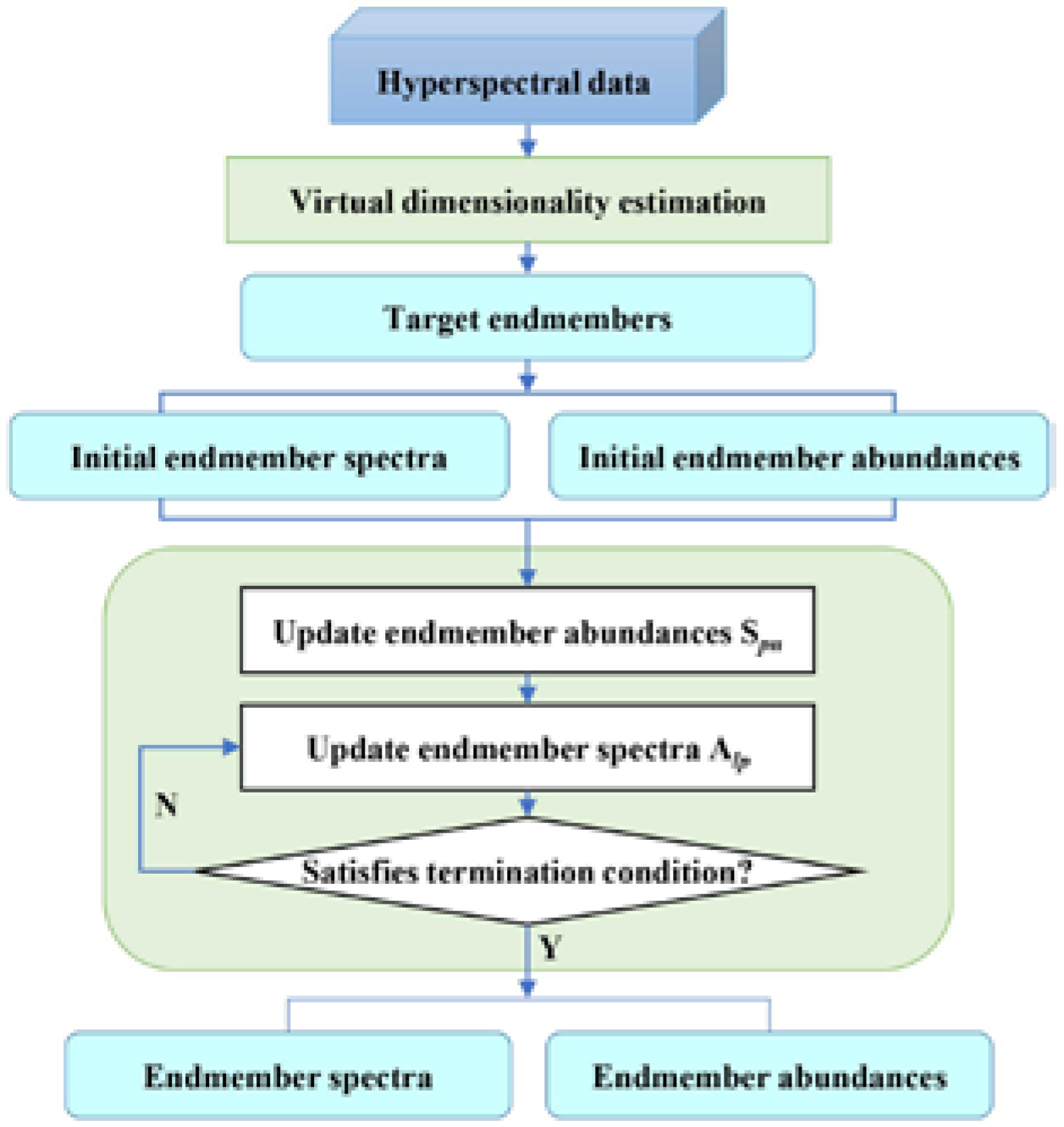
2.4. Proposed Endmember Initialization Scheme for NMF
- Initialization: target endmembers extracted by the ATGP algorithm are used as the initial endmember matrix of NMF. Since the NNLS algorithm has been used for hyperspectral unmixing, especially for the initialization of NMF [33,49], the corresponding abundances of target endmembers derived by NNLS are used as the initial abundance matrix of NMF.
- Objective function and optimization algorithm: The objective functions are constructed based on the Euclidean distance, due to its simplicity, intuition and wide application. To solve the objective functions, the multiplicative update algorithm is selected as the optimization criterion. The update formula of endmember matrix and abundance matrix can be expressed as Equations (4) and (5):where is the endmember abundance value of the mixed pixel, and is the endmember spectrum value of the band. Here, a minimal positive value is used to ensure that the denominator is nonzero [14].
- Update: the rows of the weight coefficient matrix are updated using Equation (4), while the columns of the basic matrix are updated using Equation (5).
- Normalization: according to the ASC in the spectral mixing model, and following the methods suggested in [2,9,14], the weight coefficient matrix is normalized after every iteration using Equation (6) to guarantee that the sum of each column vector in the weight coefficient matrix is always equal to one.
- Final endmember matrix and endmember abundance matrix : matrices and are repeatedly updated until the maximum number of iterations is reached or until the stopping condition is satisfied, i.e., the value of the objective function is equal to zero or the prescribed error threshold .where is the reconstruction of after the iteration.
3. Experimental Results
3.1. Performance Metrics
- Spectral angle distance (SAD):where is the actual spectral vector, is the estimated spectral vector, and is the number of bands. The real endmember spectra can be spectra in the spectral library, observed spectra from the laboratory or field, or spectra extracted from pure pixels in remote sensing imagery.
- Spectral information divergence (SID):where is the actual spectral vector, and is the estimated spectral vector.
- Root mean square error (RMSE):where is the actual abundance of the endmember abundance of the mixed pixel, is the estimated value of and is the number of bands. The RMSE metric can partly reflect how the inversion results reconstruct the original information.
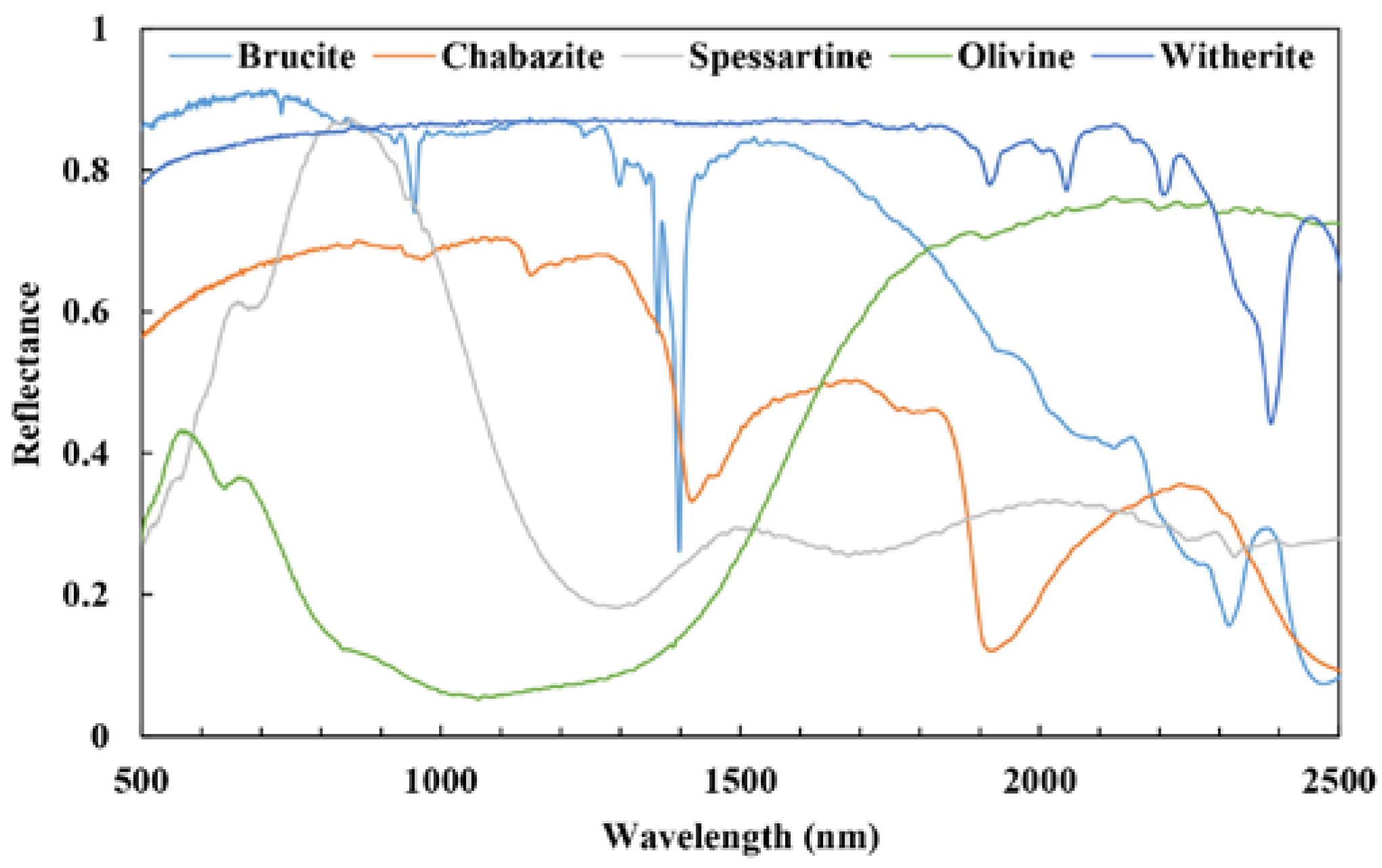
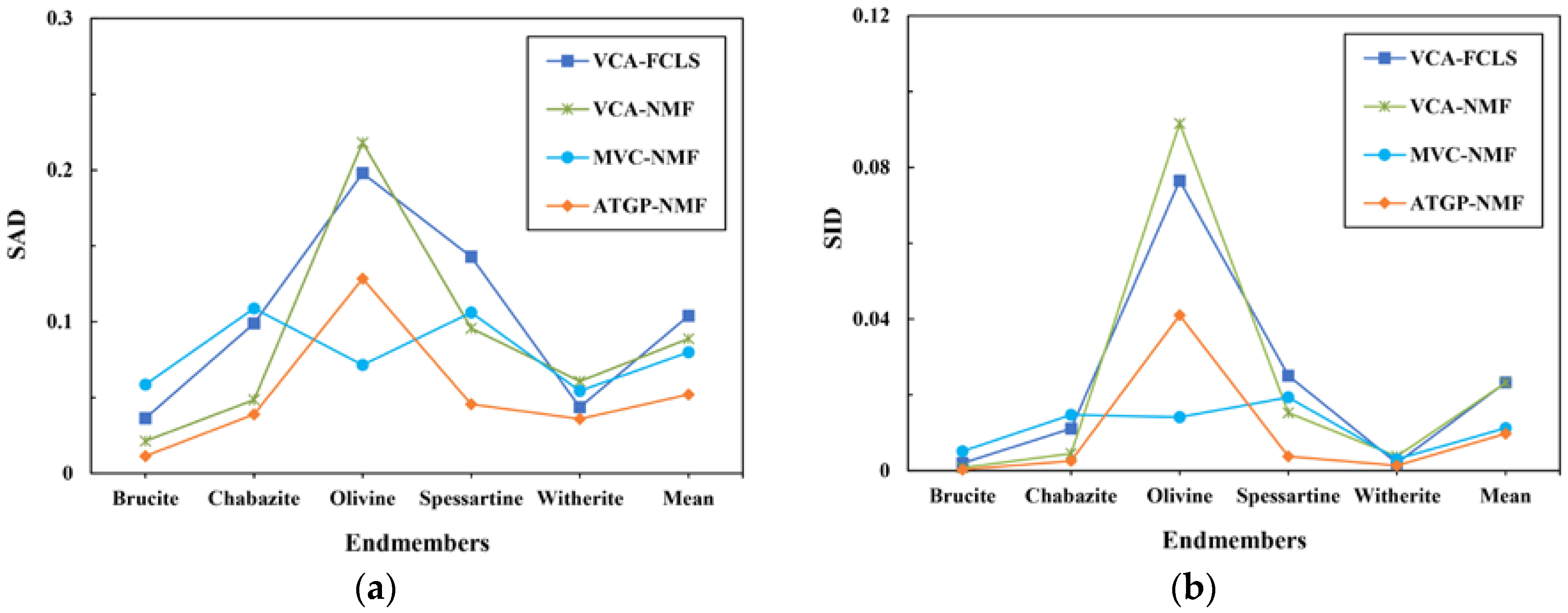
3.2. Spectral Unmixing Using Synthetic Data
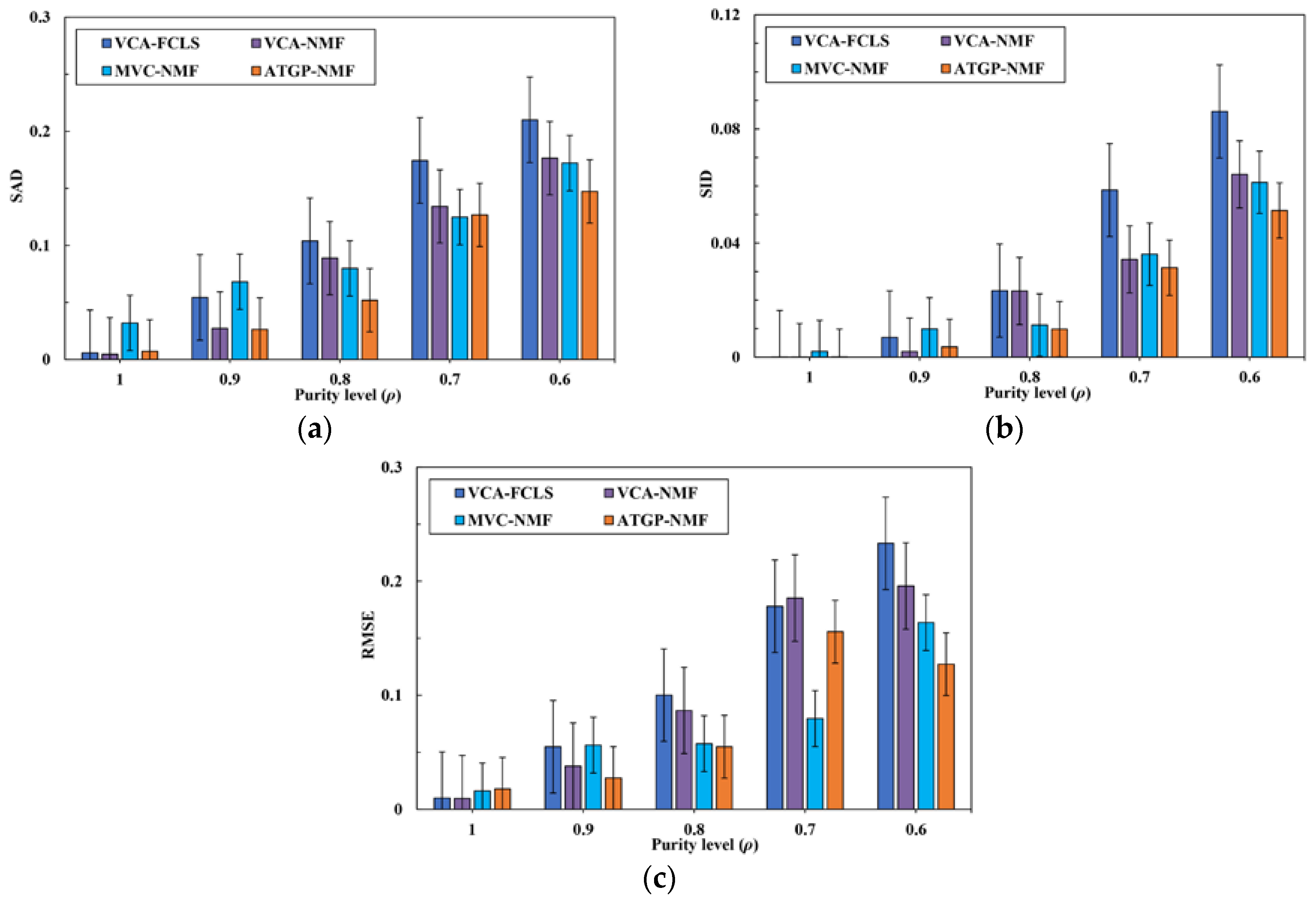
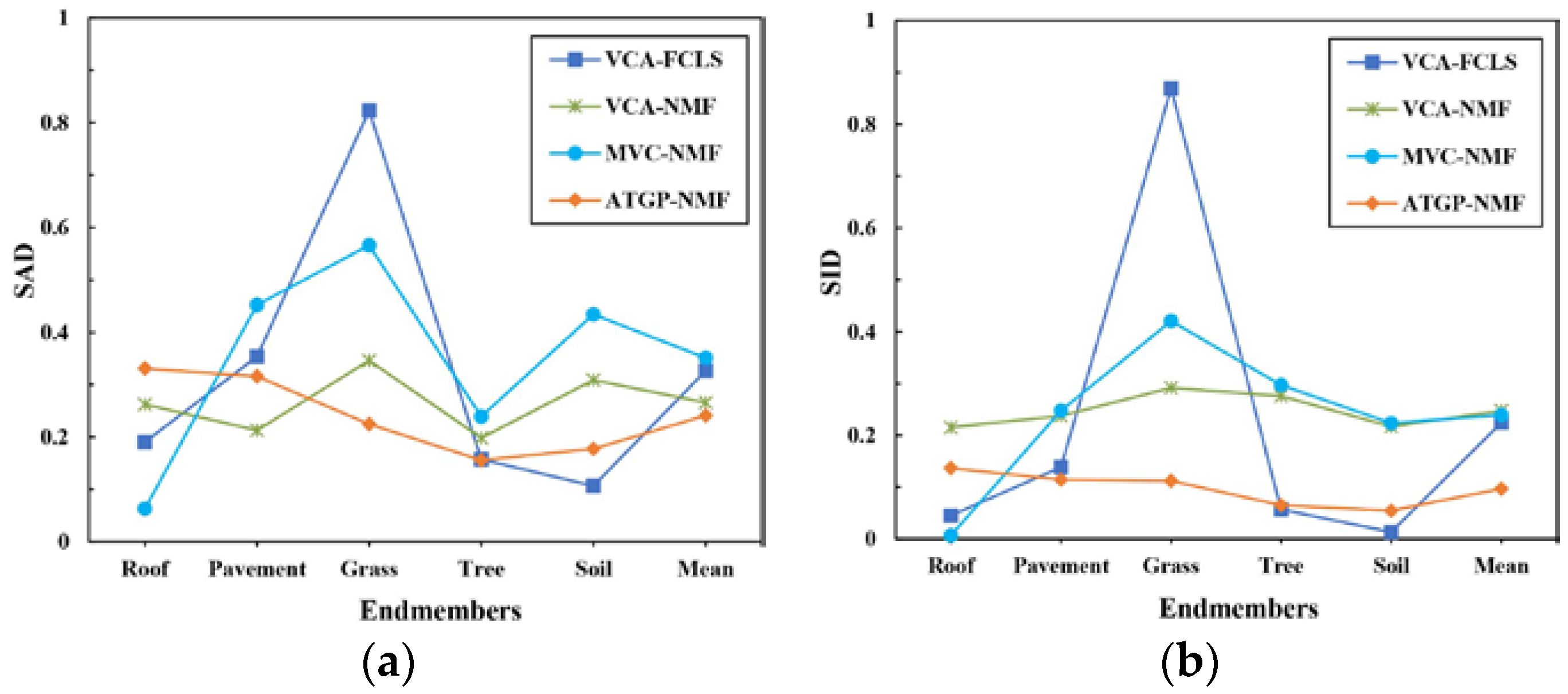
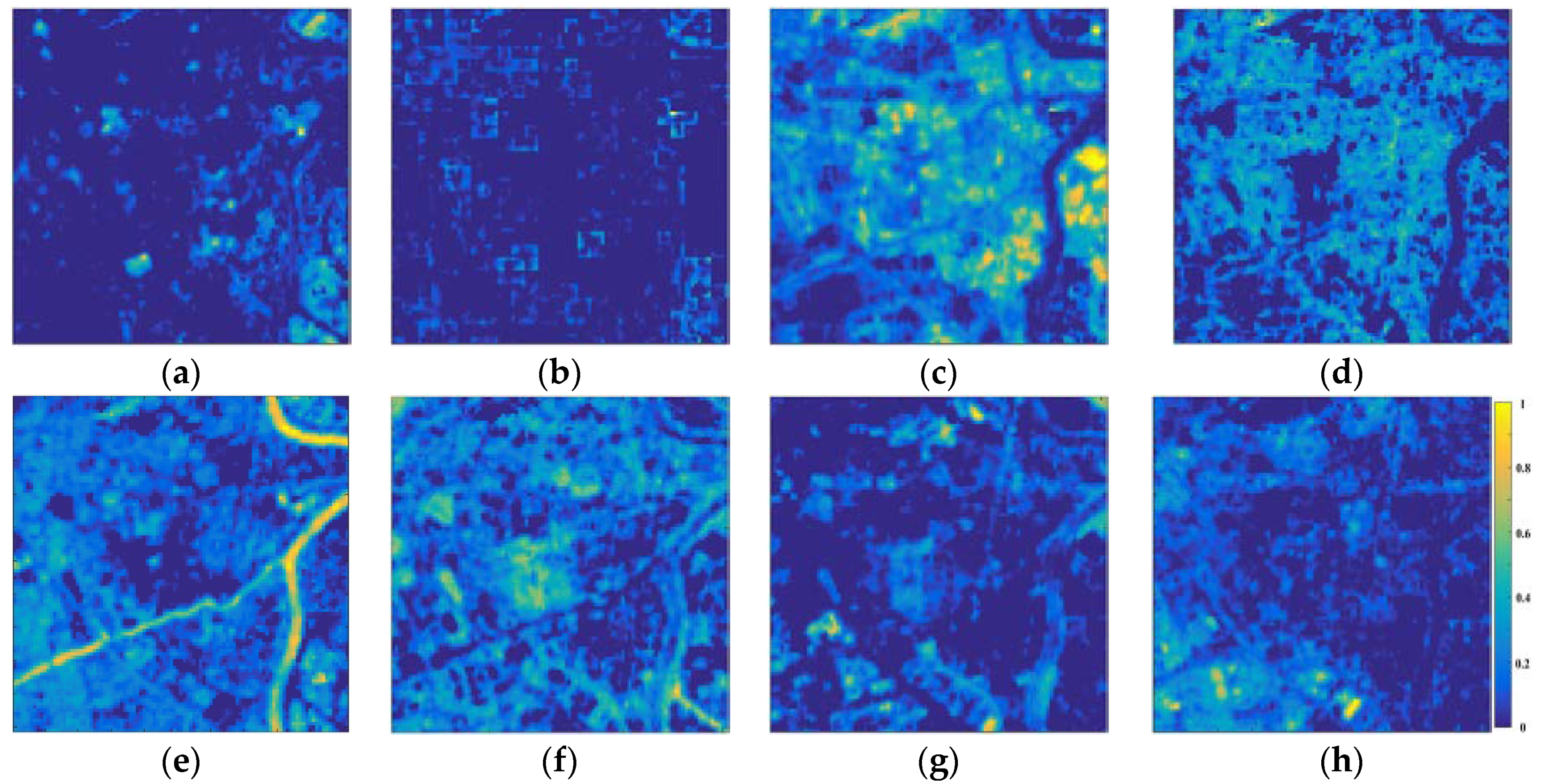
3.3. Spectral Unmixing Using Berlin HyMap Image
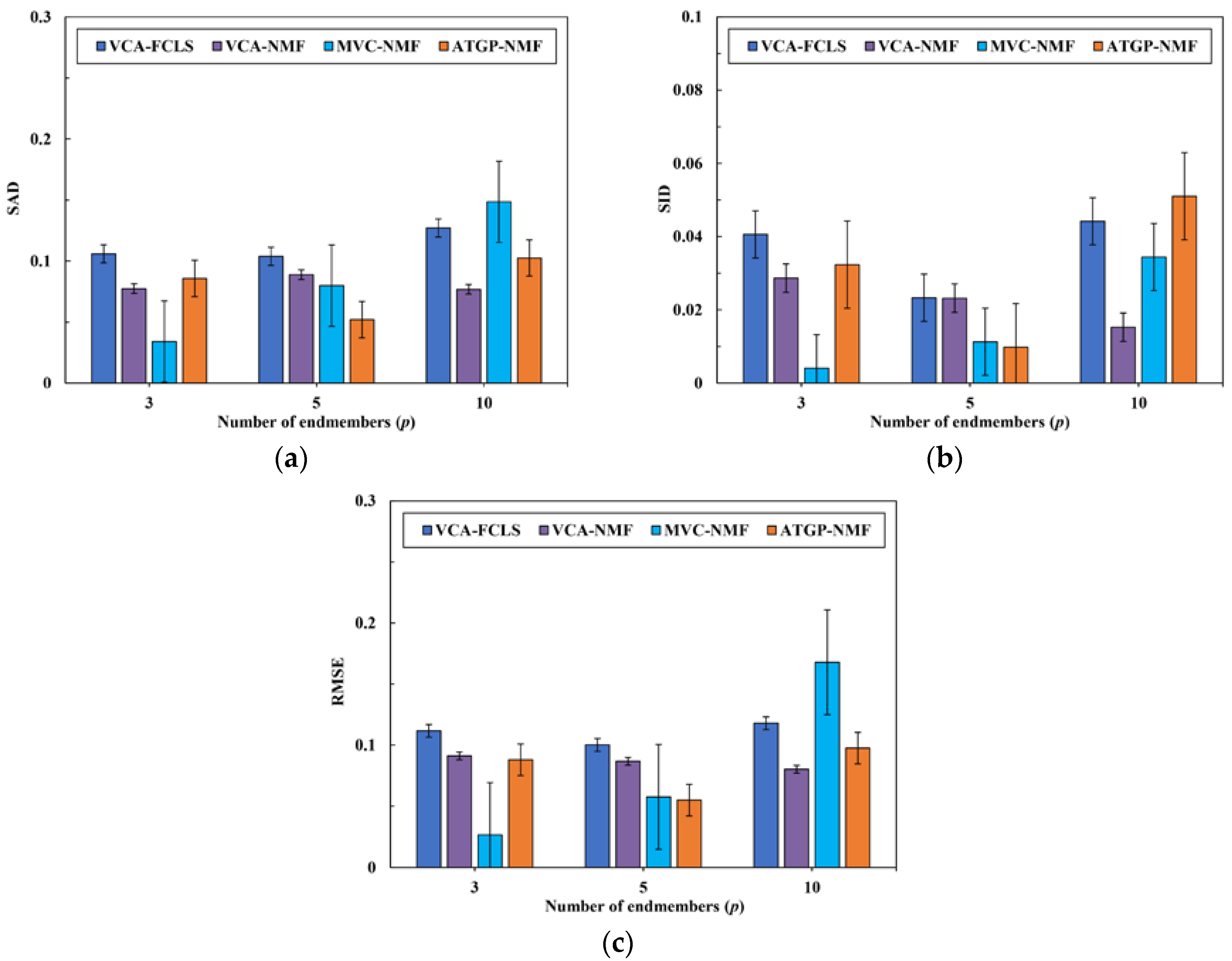
3.4. Spectral Unmixing Using a Hyperion Image
3.5. Computational Efficiency
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Goetz, A.F.H.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging spectrometry for earth remote sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef] [PubMed]
- Heinz, D.C. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 529–545. [Google Scholar] [CrossRef]
- Nascimento, J.M.; Dias, J.M. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Wei, Y.; Jin, C.; Peng, G. A new spectral mixture analysis method based on spectral correlation matching. J. Remote Sens. 2008, 12, 454–461. (In Chinese) [Google Scholar]
- Chen, J.; Jia, X.; Yang, W.; Matsushita, B. Generalization of subpixel analysis for hyperspectral data with flexibility in spectral similarity measures. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2165–2171. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Hu, B.; Strahler, A. Application of priori knowledge in remote sensing inversion. Sci. China (Ser. D) 1998, 28, 67–72. (In Chinese) [Google Scholar]
- Haykin, S.; Chen, Z. The cocktail party problem. Neural Comput. 2005, 17, 1875–1902. [Google Scholar] [CrossRef] [PubMed]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Jia, S.; Qian, Y. Spectral and spatial complexity-based hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3867–3879. [Google Scholar] [CrossRef]
- Georgiev, P.; Theis, F.; Cichocki, A. Sparse component analysis and blind source separation of underdetermined mixtures. IEEE Trans. Neural Netw. 2005, 16, 992–996. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Wang, X.; Zhao, L.; Feng, R.; Zhang, L.; Xu, Y. Blind spectral unmixing based on sparse component analysis for hyperspectral remote sensing imagery. ISPRS-J. Photogramm. Remote Sens. 2016, 119, 49–63. [Google Scholar] [CrossRef]
- Cai, D.; He, X.; Han, J.; Huang, T.S. Graph regularized nonnegative matrix factorization for data representation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1548–1560. [Google Scholar] [CrossRef] [PubMed]
- Pauca, V.P.; Piper, J.; Plemmons, R.J. Nonnegative matrix factorization for spectral data analysis. Linear Algebra Its Appl. 2006, 416, 29–47. [Google Scholar] [CrossRef]
- Pascual-Montano, A.; Carazo, J.M.; Kochi, K.; Lehmann, D.; Pascual-Marqui, R.D. Nonsmooth nonnegative matrix factorization (nsNMF). IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 403–415. [Google Scholar] [CrossRef] [PubMed]
- Miao, L.; Qi, H. Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization. IEEE Trans. Geosci. Remote Sens. 2007, 45, 765–777. [Google Scholar] [CrossRef]
- Li, E.; Zou, Y.; Su, B. Research of the sparseness constraint MVC-NMF algorithm. Hydrogr. Surv. Charting 2011, 31, 43–46. (In Chinese) [Google Scholar]
- Yang, Z.; Zhou, G.; Xie, S.; Ding, S.; Yang, J.; Zhang, J. Blind spectral unmixing based on sparse nonnegative matrix factorization. IEEE Trans. Image Process. 2011, 20, 1112–1125. [Google Scholar] [CrossRef] [PubMed]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Ma, W.K.; Bioucas-Dias, J.M.; Chan, T.H.; Gillis, N.; Gader, P.; Plaza, A.J.; Ambikapathi, A.; Chi, C.Y. A signal processing perspective on hyperspectral unmixing: Insights from remote sensing. IEEE Signal Process. Mag. 2014, 31, 67–81. [Google Scholar] [CrossRef]
- Kizel, F.; Shoshany, M.; Netanyahu, N.S.; Even-Tzur, G.; Benediktsson, J.A. A stepwise analytical projected gradient descent search for hyperspectral unmixing and its code vectorization. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4925–4943. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled nonnegative matrix factorization unmixing for hyperspectral and multispectral data fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Yuan, Y.; Fu, M.; Lu, X. Substance dependence constrained sparse NMF for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2975–2986. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L. Total variation regularized reweighted sparse nonnegative matrix factorization for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3909–3921. [Google Scholar] [CrossRef]
- Tsinos, C.G.; Rontogiannis, A.A.; Berberidis, K. Distributed blind hyperspectral unmixing via joint sparsity and low-rank constrained non-negative matrix factorization. IEEE Trans. Comput. Imaging 2017, 3, 160–174. [Google Scholar] [CrossRef]
- Wang, W.; Qian, Y. Adaptive L1/2 sparsity-constrained NMF with half-thresholding algorithm for hyperspectral unmixing. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 2618–2631. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L. Sparsity-regularized robust non-negative matrix factorization for hyperspectral unmixing. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 4267–4279. [Google Scholar] [CrossRef]
- Salehani, Y.E.; Gazor, S. Smooth and sparse regularization for NMF hyperspectral unmixing. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 3677–3692. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A.; Liu, L. Robust collaborative nonnegative matrix factorization for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6076–6090. [Google Scholar] [CrossRef]
- Wang, R.; Li, H.; Liao, W.; Huang, X. Endmember initialization method for hyperspectral data unmixing. J. Appl. Remote Sens. 2016, 10, 042009. [Google Scholar] [CrossRef]
- Liu, Z.; Tan, V.Y.F. Rank-one NMF-based initialization for NMF and relative error bounds under a geometric assumption. IEEE Trans. Signal Process. 2017, 65, 4717–4731. [Google Scholar] [CrossRef]
- Boutsidis, C.; Gallopoulos, E. Svd based initialization: A head start for nonnegative matrix factorization. Pattern Recognit. 2008, 41, 1350–1362. [Google Scholar] [CrossRef]
- Xue, Y.; Tong, C.S.; Chen, Y.; Chen, W.S. Clustering-based initialization for non-negative matrix factorization. Appl. Math. Comput. 2008, 205, 525–536. [Google Scholar] [CrossRef]
- Tang, A.W.; Shi, Z.; An, Z. Nonnegative matrix factorization for hyperspectral unmixing using prior knowledge of spectral signatures. Opt. Eng. 2012, 51, 087001. [Google Scholar] [CrossRef]
- Chang, C.I.; Li, Y. Recursive band processing of automatic target generation process for finding unsupervised targets in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5081–5094. [Google Scholar] [CrossRef]
- Chang, C.I.; Plaza, A. A fast iterative algorithm for implementation of pixel purity index. IEEE Geosci. Remote Sens. Lett. 2006, 3, 63–67. [Google Scholar] [CrossRef]
- Yao, S.; Zeng, W.; Wang, N.; Chen, L. Validating the performance of one-time decomposition for fMRI analysis using ICA with automatic target generation process. Magn. Reson. Imaging 2013, 31, 970–975. [Google Scholar] [CrossRef] [PubMed]
- Keshava, N. A survey of spectral unmixing algorithms. Lincoln Lab. J. 2003, 14, 55–78. [Google Scholar]
- Xu, X.; Shi, Z. Multi-objective based spectral unmixing for hyperspectral images. ISPRS-J. Photogramm. Remote Sens. 2017, 124, 54–69. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Algorithms for non-negative matrix factorization. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2001; pp. 556–562. [Google Scholar]
- Tao, X. Research of Spectral Unmixing Based on Linear Model for Multi-Channel Remote Sensing Images. Master’s Thesis, Fudan University, Shanghai, China, 2008. (In Chinese). [Google Scholar]
- Plaza, A.; Chang, C.I. Impact of initialization on design of endmember extraction algorithms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3397–3407. [Google Scholar] [CrossRef]
- Ren, H.; Chang, C.I. Automatic spectral target recognition in hyperspectral imagery. IEEE Trans. Aerosp. Electron. Syst. 2006, 39, 1232–1249. [Google Scholar] [CrossRef]
- Harsanyi, J.C.; Farrand, W.H.; Chang, C.I. Determining the number and identity of spectral endmembers: An integrated approach using neyman-pearson eigen-thresholding and iterative constrained rms error minimization. In Proceedings of the 9th Thematic Conference on Geologic Remote Sensing, Pasadena, CA, USA, 8–11 February 1993. [Google Scholar]
- Du, Q.; Raksuntorn, N.; Younan, N.H.; King, R.L. End-member extraction for hyperspectral image analysis. Appl. Opt. 2008, 47, 77–84. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; Xu, X. R-vcanet: A new deep-learning-based hyperspectral image classification method. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 1975–1986. [Google Scholar] [CrossRef]
- Chang, C.I.; Wen, C.H.; Wu, C.C. Relationship exploration among PPI, ATGP and VCA via theoretical analysis. Int. J. Comput. Sci. Eng. 2013, 8, 361–367. [Google Scholar] [CrossRef]
- Chang, C.I.; Chen, S.Y.; Li, H.C.; Chen, H.M.; Wen, C.H. Comparative study and analysis among ATGP, VCA, and SGA for finding endmembers in hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 4280–4306. [Google Scholar] [CrossRef]
- Merentitis, A.; Debes, C.; Heremans, R. Ensemble learning in hyperspectral image classification: Toward selecting a favorable bias-variance tradeoff. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 1089–1102. [Google Scholar] [CrossRef]
- Liu, R.; Du, B.; Zhang, L. Hyperspectral unmixing via double abundance characteristics constraints based NMF. Remote Sens. 2016, 8, 464. [Google Scholar] [CrossRef]
- Mirzal, A. NMF versus ICA for blind source separation. Adv. Data Anal. Classif. 2017, 11, 25–48. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; Xu, X. Hierarchical guidance filtering-based ensemble classification for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4177–4189. [Google Scholar] [CrossRef]
- Plaza, A.; Martinez, P.; Perez, R.; Plaza, J. A quantitative and comparative analysis of endmember extraction algorithms from hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 650–663. [Google Scholar] [CrossRef]
- Clark, R.N.; Swayze, G.A.; King, T.V.V.; Gallagher, A.J.; Calvin, W.M. The US Geological Survey, Digital Spectral Reflectance Library: Version 1: 0.2 to 3.0 Microns; NASA: Washington, DC, USA, 1993. [Google Scholar]
- Harsanyi, J.C.; Chang, C.I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef]
- Chan, T.H.; Chi, C.Y.; Huang, Y.M.; Ma, W.K. A convex analysis-based minimum-volume enclosing simplex algorithm for hyperspectral unmixing. IEEE Trans. Signal Process. 2009, 57, 4418–4432. [Google Scholar] [CrossRef]
- Okujeni, A.; Van Der Linden, S.; Hostert, P. Berlin-Urban-Gradient Dataset 2009-An EnMAP Preparatory Flight Campaign (Datasets). Available online: http://dataservices.gfz-potsdam.de/enmap/showshort.php? id=escidoc:1823890 (accessed on 17 April 2018).
- Okujeni, A.; van der Linden, S.; Hostert, P. Extending the vegetation–impervious–soil model using simulated enmap data and machine learning. Remote Sens. Environ. 2015, 158, 69–80. [Google Scholar] [CrossRef]
- Okujeni, A.; van der Linden, S.; Tits, L.; Somers, B.; Hostert, P. Support vector regression and synthetically mixed training data for quantifying urban land cover. Remote Sens. Environ. 2013, 137, 184–197. [Google Scholar] [CrossRef]
- Degerickx, J.; Okujeni, A.; Iordache, M.D.; Hermy, M.; van der Linden, S.; Somers, B. A novel spectral library pruning technique for spectral unmixing of urban land cover. Remote Sens. 2017, 9, 565. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
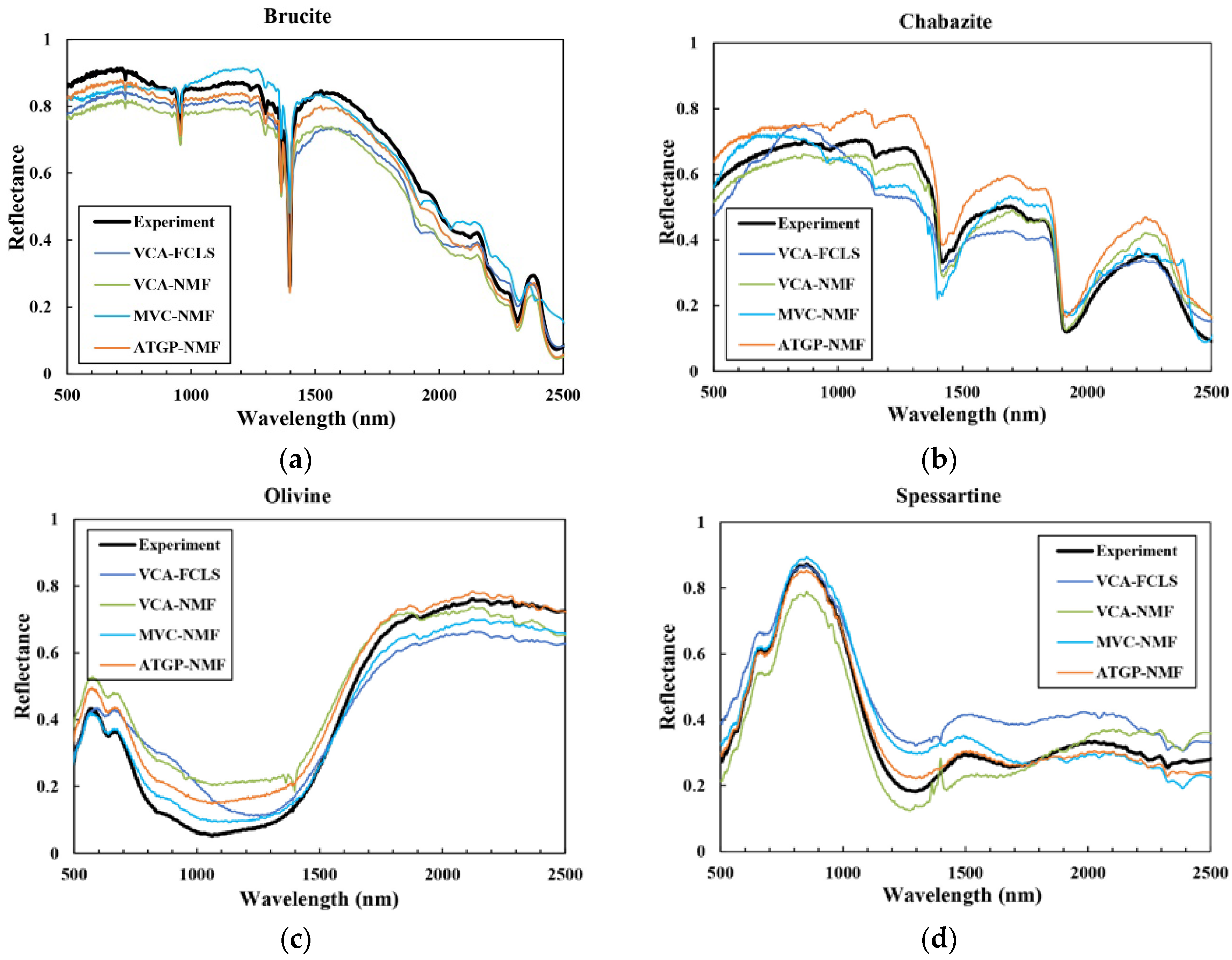
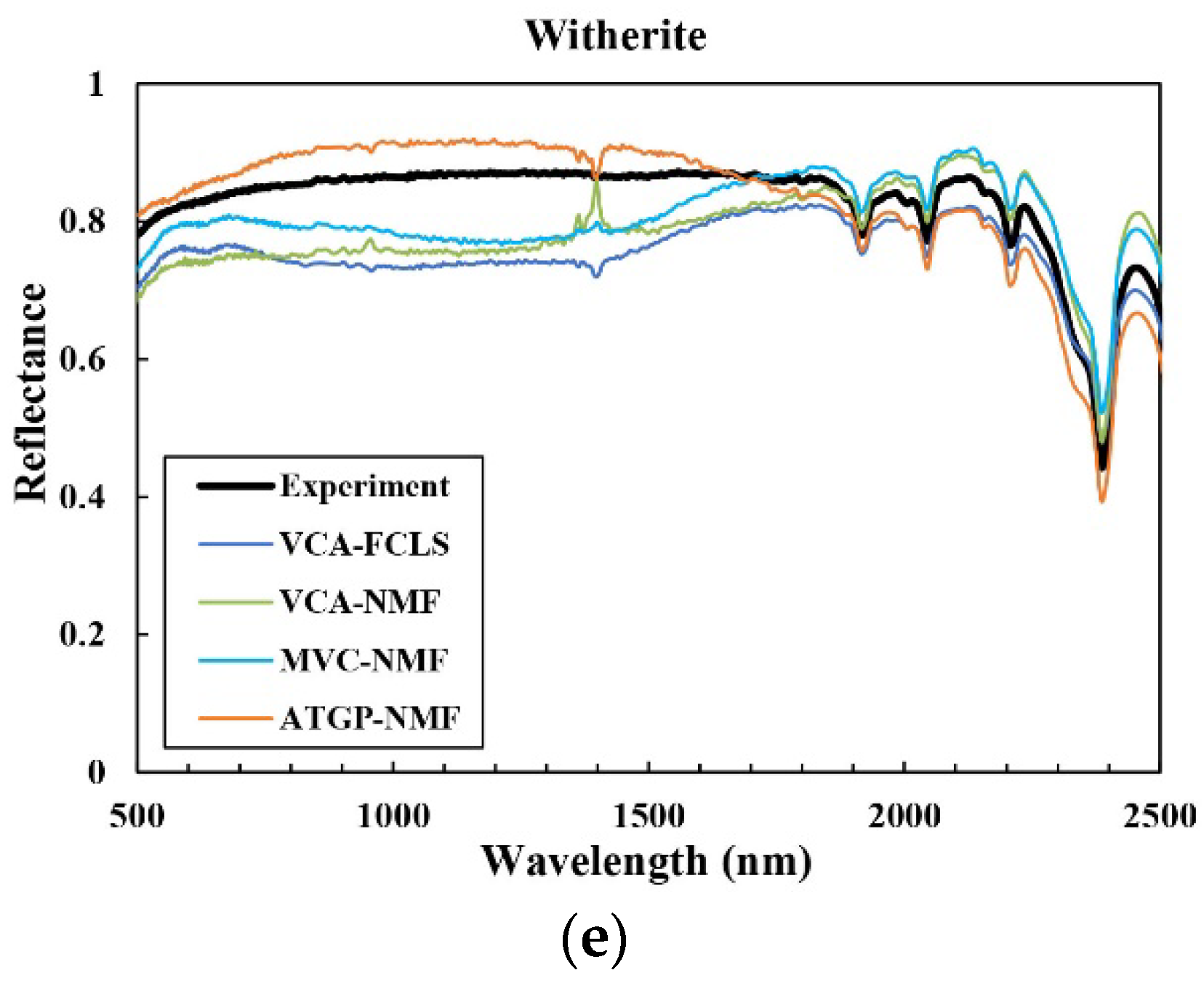







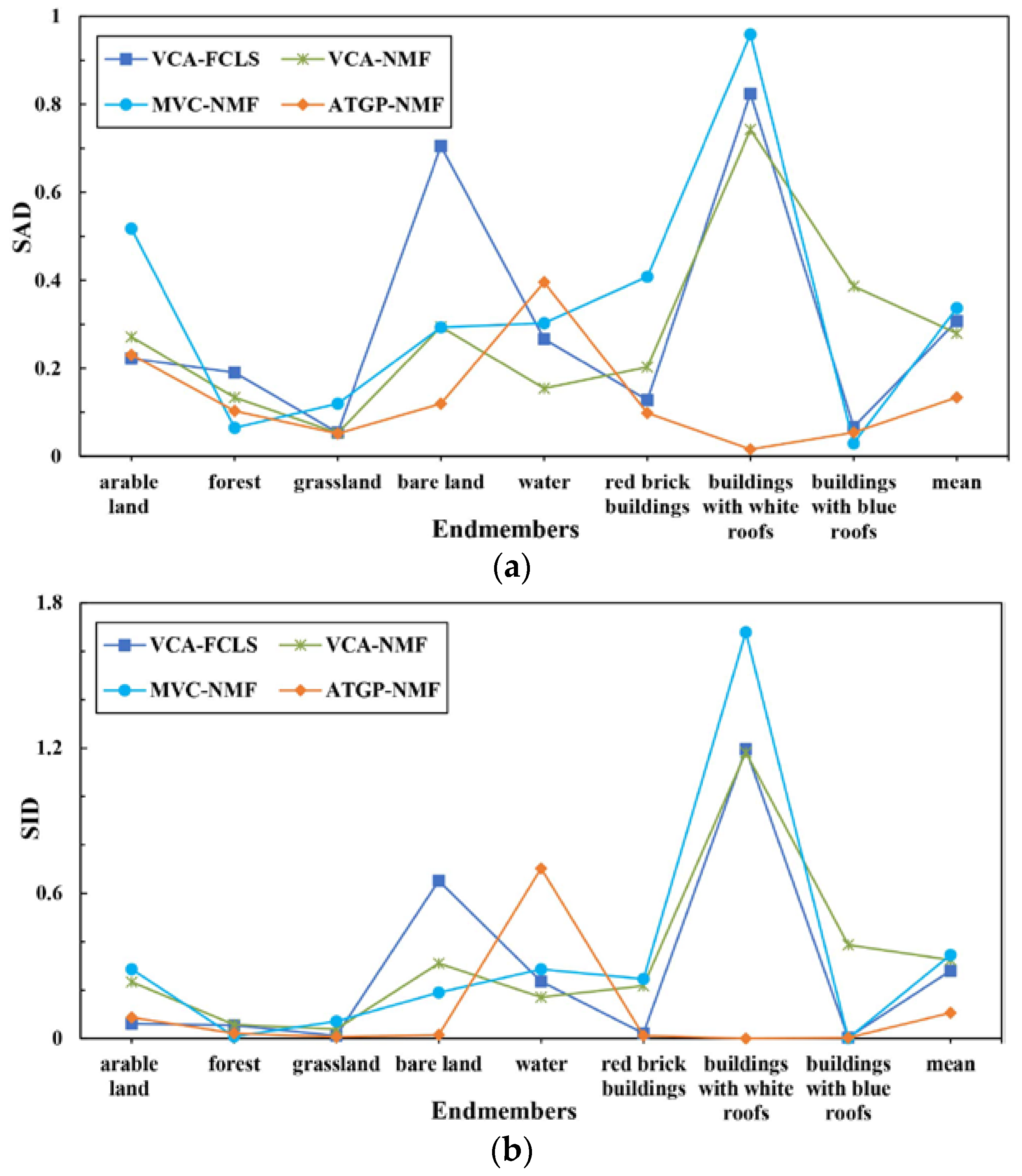
| Method | SAD | SID | RMSE |
|---|---|---|---|
| VCA-FCLS | 0.1039 | 0.0233 | 0.1002 |
| VCA-NMF | 0.0888 | 0.0232 | 0.0867 |
| MVC-NMF | 0.0798 | 0.0113 | 0.0576 |
| ATGP-NMF | 0.0520 | 0.0098 | 0.0549 |
| Method | SAD | SID | RMSE |
|---|---|---|---|
| VCA-FCLS | 0.3260 | 0.2246 | 0.3309 |
| VCA-NMF | 0.2655 | 0.2473 | 0.3249 |
| MVC-NMF | 0.3508 | 0.2389 | 0.3591 |
| ATGP-NMF | 0.2407 | 0.0965 | 0.3011 |
| Method | SAD | SID | RMSE |
|---|---|---|---|
| VCA-FCLS | 0.3072 | 0.2797 | 0.3101 |
| VCA-NMF | 0.2798 | 0.3249 | 0.2866 |
| MVC-NMF | 0.3368 | 0.3459 | 0.2732 |
| ATGP-NMF | 0.1338 | 0.1061 | 0.2659 |
| Method | VCA-FCLS | VCA-NMF | MVC-NMF | ATGP-NMF |
|---|---|---|---|---|
| Synthetic Data | 0.83 | 0.61 | 0.98 | 0.59 |
| Berlin HyMap Image | 2.15 | 1.99 | 65.26 | 1.95 |
| Hyperion Image | 9.37 | 4.37 | 165.66 | 5.28 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, J.; Zhuo, L.; Tao, H. An Endmember Initialization Scheme for Nonnegative Matrix Factorization and Its Application in Hyperspectral Unmixing. ISPRS Int. J. Geo-Inf. 2018, 7, 195. https://doi.org/10.3390/ijgi7050195
Cao J, Zhuo L, Tao H. An Endmember Initialization Scheme for Nonnegative Matrix Factorization and Its Application in Hyperspectral Unmixing. ISPRS International Journal of Geo-Information. 2018; 7(5):195. https://doi.org/10.3390/ijgi7050195
Chicago/Turabian StyleCao, Jingjing, Li Zhuo, and Haiyan Tao. 2018. "An Endmember Initialization Scheme for Nonnegative Matrix Factorization and Its Application in Hyperspectral Unmixing" ISPRS International Journal of Geo-Information 7, no. 5: 195. https://doi.org/10.3390/ijgi7050195
APA StyleCao, J., Zhuo, L., & Tao, H. (2018). An Endmember Initialization Scheme for Nonnegative Matrix Factorization and Its Application in Hyperspectral Unmixing. ISPRS International Journal of Geo-Information, 7(5), 195. https://doi.org/10.3390/ijgi7050195





