Implementation of a Parallel GPU-Based Space-Time Kriging Framework
Abstract
:1. Introduction
2. Methodology and Implementation
2.1. Ordinary Kriging
2.2. Spatiotemporal Kriging Algorithm
- Step 1: Calculate the variograms of the pure time domain and the pure space domain and fit them. At different time points, the space point has a different nugget, sill and range. Calculate the average and here.
- Step 2: Based on the results of Step (1), and are constructed. Substituting and into Equation (8), we get the spatiotemporal variograms, .
- Step 3: Calculate the space–time distance between the point to be measured and the surrounding points (known points, where the sum is × ), i.e., , , …, , , , …, . Obtain the variogram vector (Equation (12)).
- Step 4: Bring the known points and the spatiotemporal variogram into the kriging equations to obtain the weight vector, and then calculate the estimation of an unobserved point.
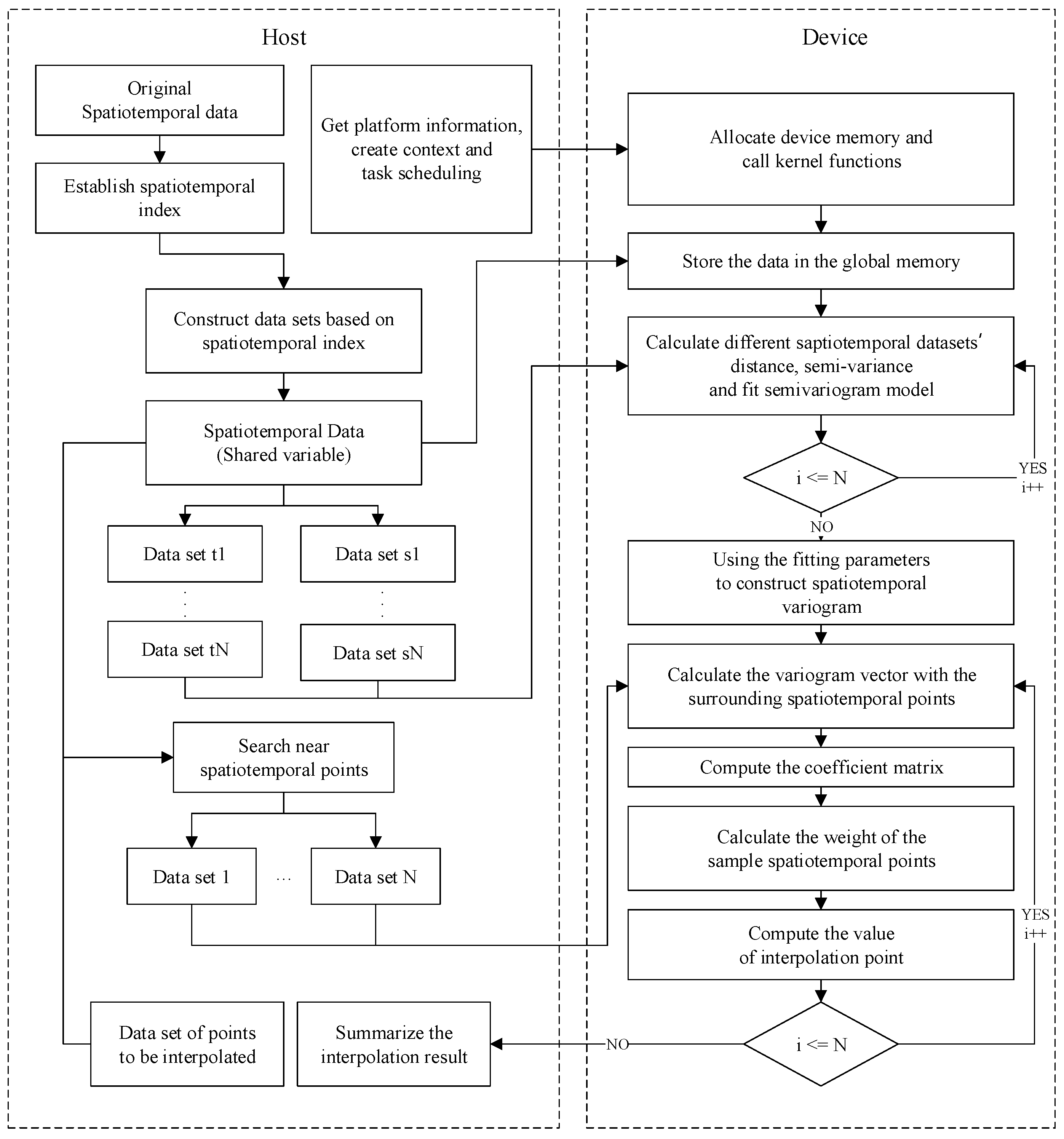
2.3. Parallel Ordinary Spatiotemporal Kriging Algorithm Design and Implementation with OpenCL
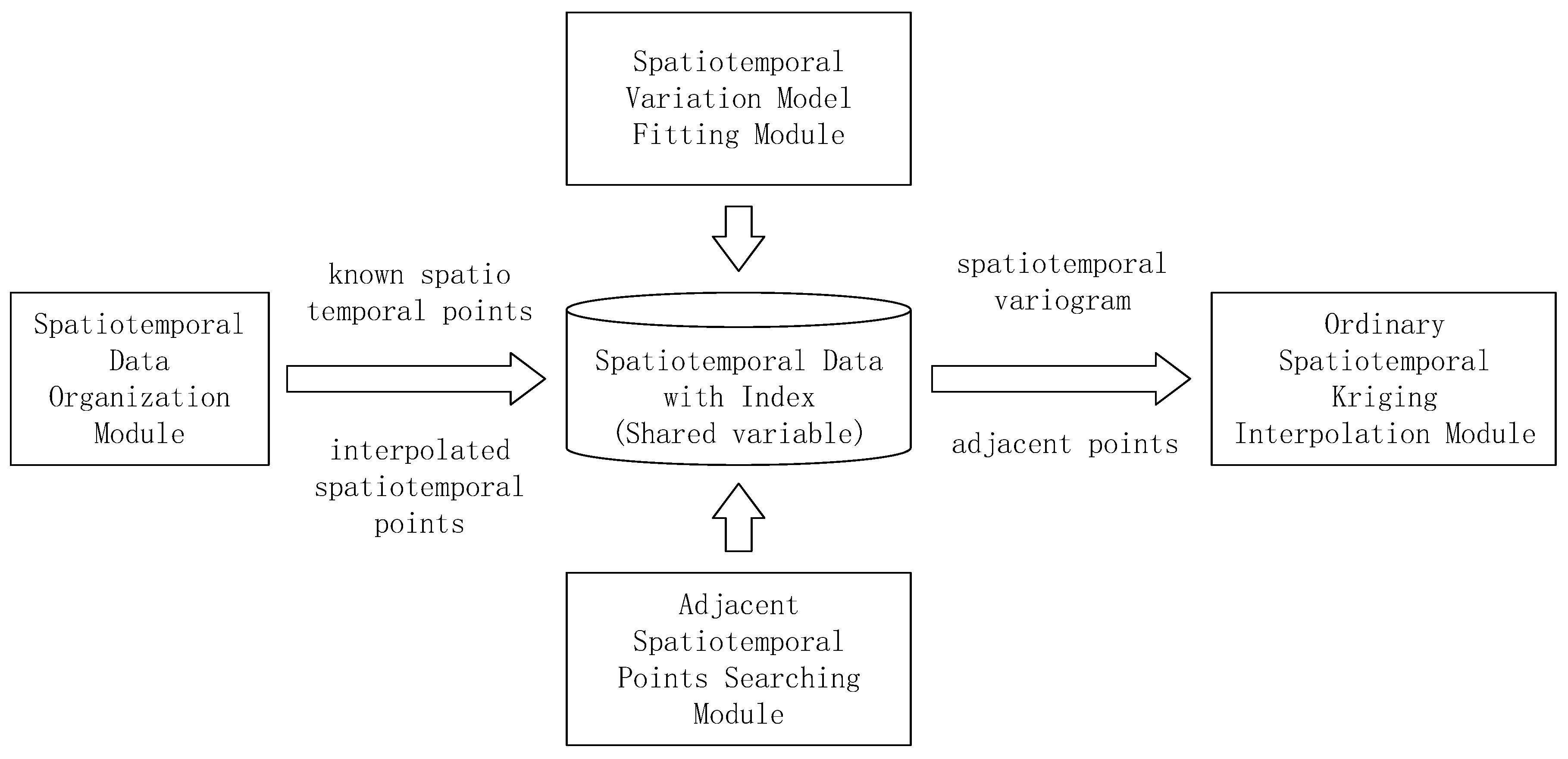
2.3.1. Design and Framework of the Parallel Algorithm
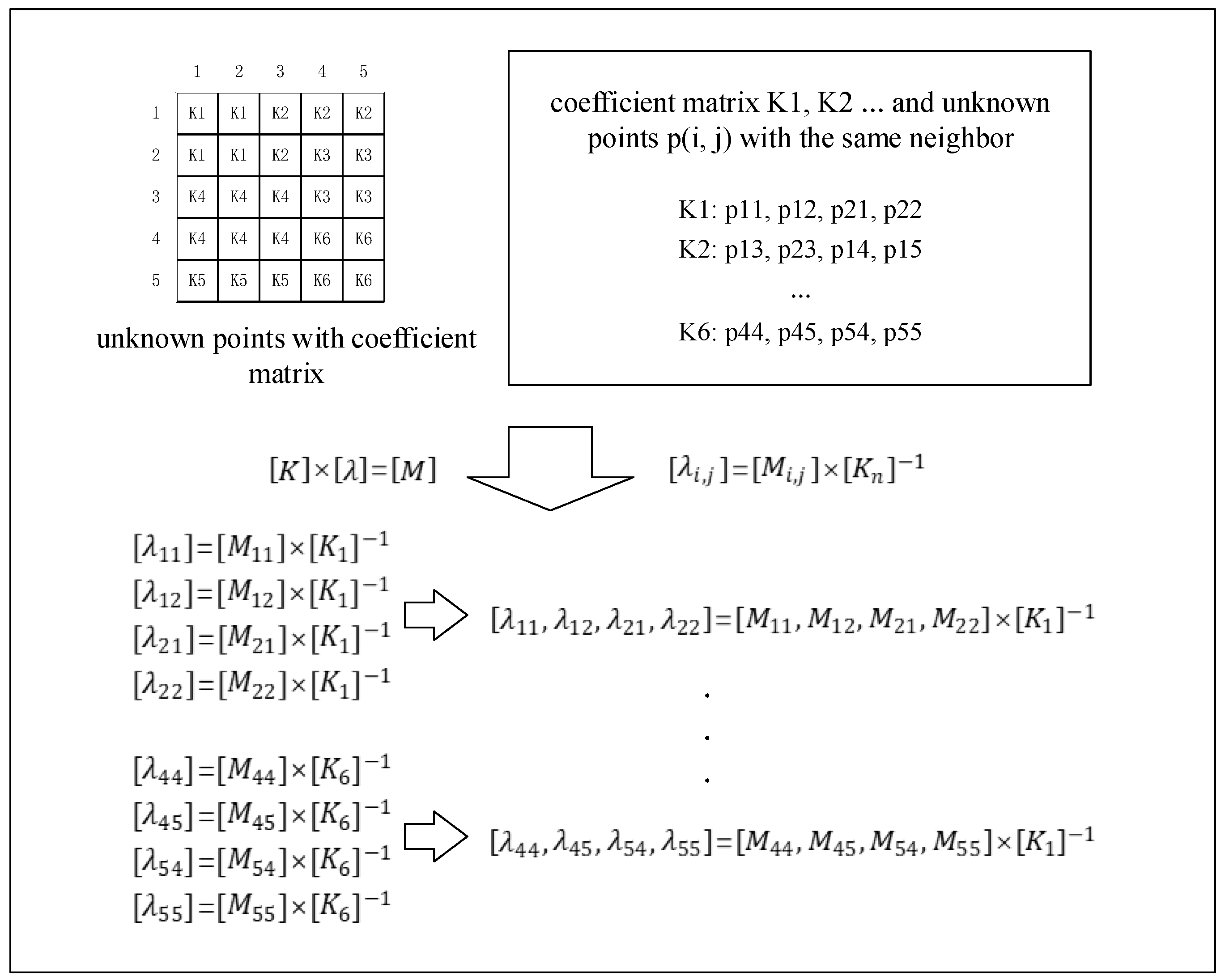
- Step 1: Organize the original data and establish the index to facilitate the query retrieval (Spatiotemporal Data Organization Module, STDOM).
- Step 2: Fit the spatiotemporal variation model of the sample data to obtain the variogram, of the spatiotemporal structure of the representative sample (Spatiotemporal Variation Model Fitting Module, STVMFM).
- Step 3: Proceed with the set of points to be predicted, search for the adjacent spatiotemporal points and set up the data sets (Adjacent Spatiotemporal Points Searching Module).
- Step 4: Use the spatiotemporal variogram, , and the data sets of the neighboring points for the ordinary spatiotemporal kriging interpolation to calculate the estimated values of the unknown points (Ordinary Spatiotemporal Kriging Interpolation Module, OSTKIM), as shown in Figure 1.
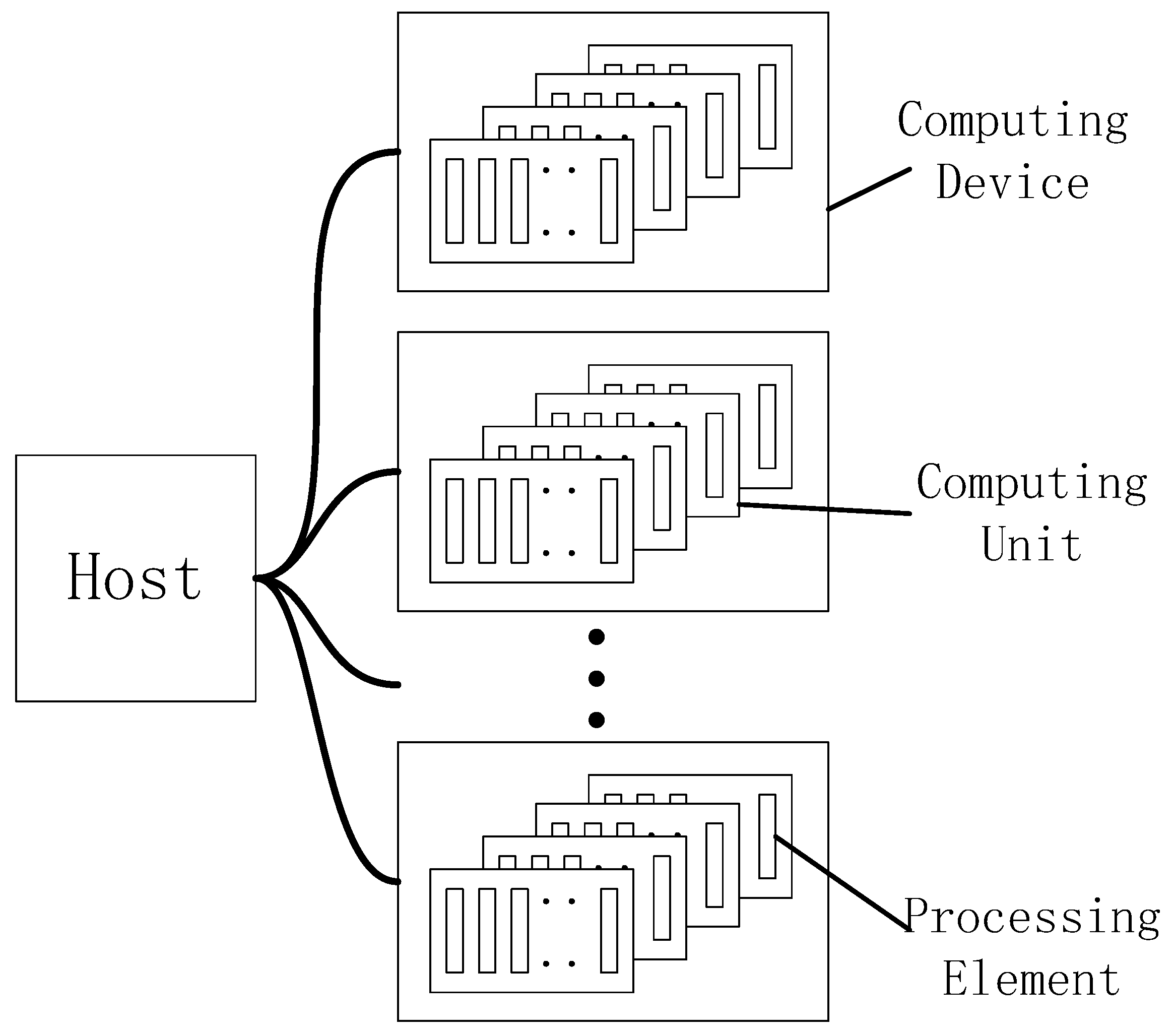
2.3.2. OpenCL-Based Implementation
3. Experiments and Analysis
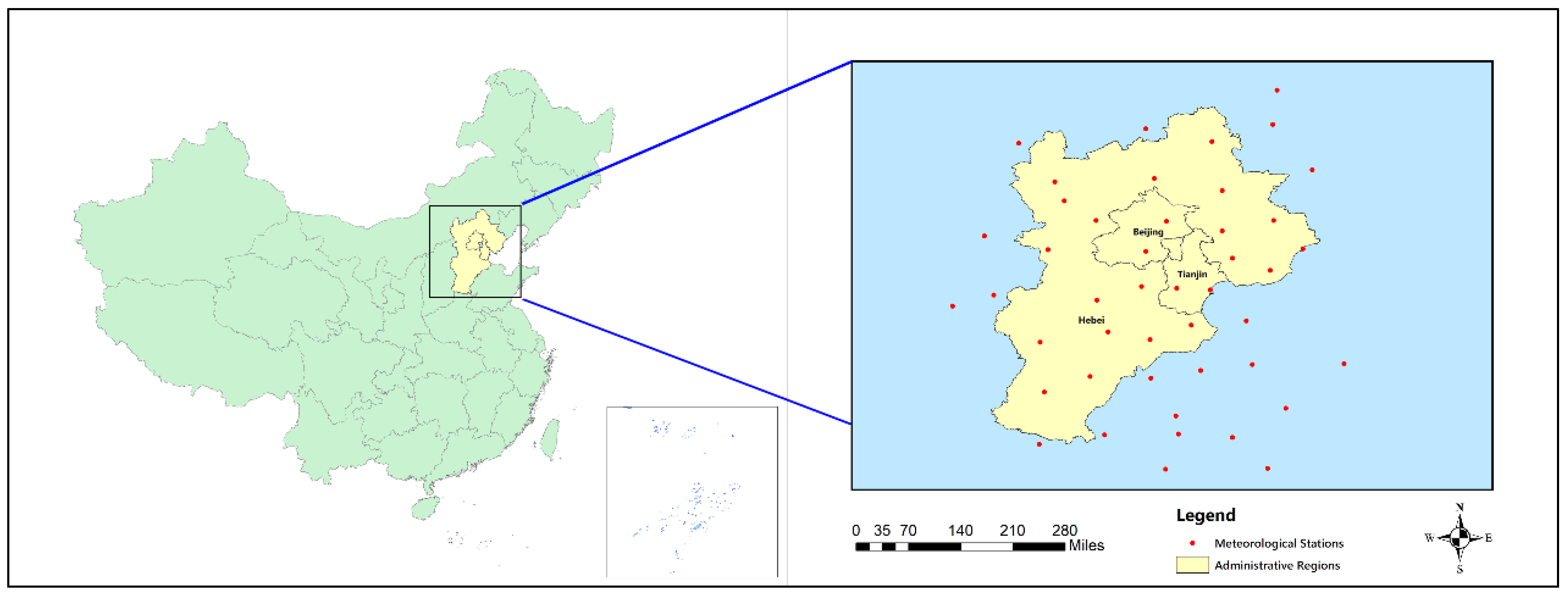
3.1. Computational Environment
3.2. Experimental Methodology Design
- Experiment 1: four observation point dataset sizes of 2000, 3000, 4000 and 5000 points were used to interpolate a regular grid (1000 × 1000) at a specified time, and the influence of the number of sampling points was tested to determine the algorithm’s efficiency.
- Experiment 2: the dataset of observations with 5000 points was used to determine the effect of the number of interpolation points on the efficiency of the algorithm for the interpolation of five types of prediction point datasets including space images of one moment with resolutions of 500 × 500, 800 × 800, 1000 × 1000 and 2000 × 2000.
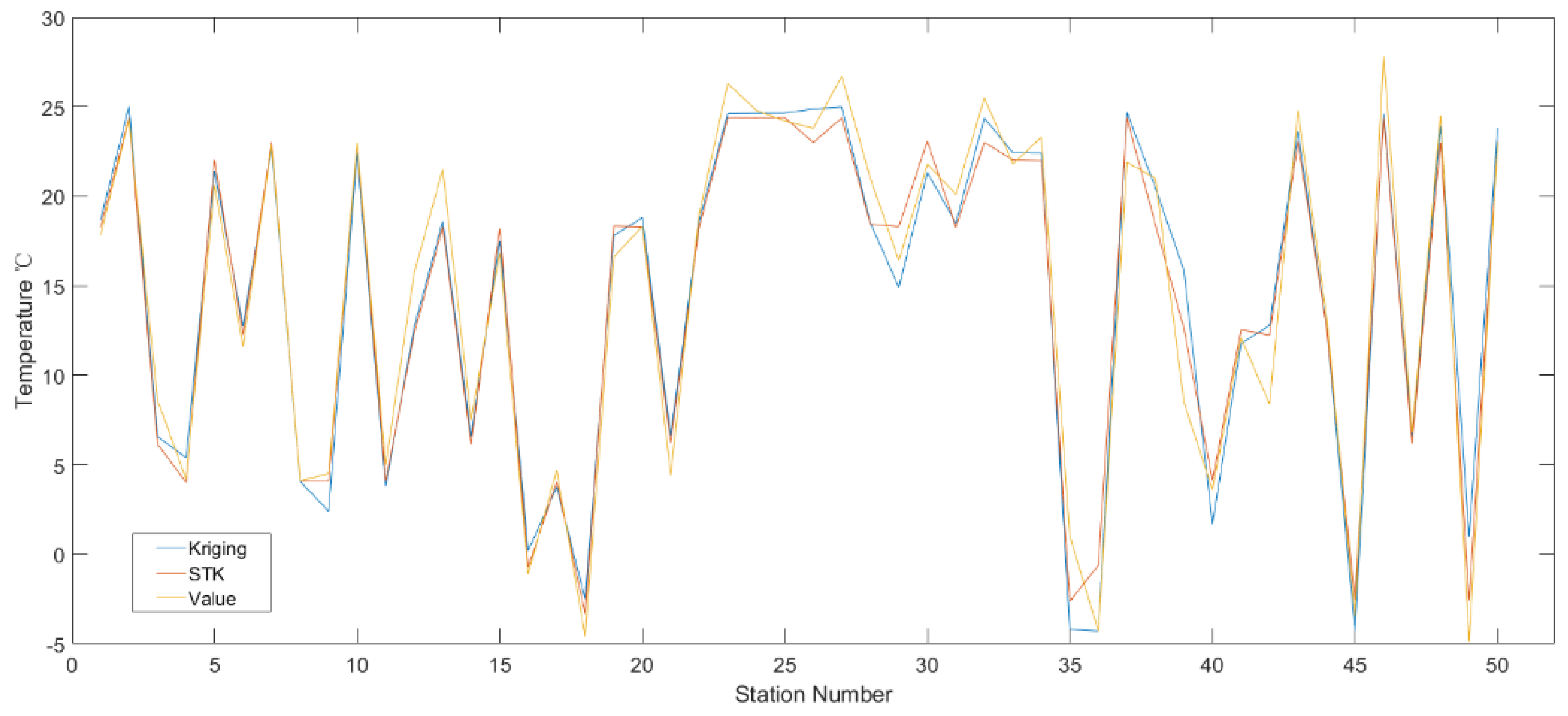
- Experiment 3: the results of the space–time interpolation were verified by cross-validation. The detailed cross-validation process was as follows:
- Step 1: Delete the first observation value, , from the data set.
- Step 2: Use other observations, the variogram model and the kriging method to predict the point value, .
- Step 3: Put into the dataset and repeat Step 1 to Step 4 until the other predicted values, , are obtained.
- Step 4: Through comparison of the original data, , and predicted data, , the error is calculated, and the effect of interpolation can be judged.
3.3. Interpolation Acceleration Effect and Analysis
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| CPU | Central Processing Unit |
| GPU | Graphics Processing Unit |
| GIS | Geographic Information System |
| DE | Digital Earth |
| PC | Personal Computer |
| HPC | High-Performance Computing |
| CUDA | Compute Unified Device Architecture |
| FFT | Fast Fourier Transform |
| STDOM | Spatiotemporal Data Organization Module |
| STVMFM | Spatiotemporal Variation Model Fitting Module |
| ASTPSM | Adjacent Spatiotemporal Points Searching Module |
| OSTKIM | Ordinary Spatiotemporal Kriging Interpolation Module |
| SSTK | Serial Spatiotemporal Kriging |
| PSTK | Parallel Spatiotemporal Kriging |
| RMSE | Root Mean Square Error |
References
- Mohes, M.A.; Shafiqur, R.; Masiur, R.S. Spatial estimation of wind speed. Int. J. Energy Res. 2012, 36, 545–552. [Google Scholar]
- Graeler, B.; Pebesma, E.; Heuvelink, G. Spatio-Temporal Interpolation using gstat. RFID J. 2016, 8, 204–218. [Google Scholar]
- Cressie, N.; Wikle, C.K. Statistics for Spatio-Temporal Data; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Hillier, M.J.; Schetselaar, E.M.; de Kemp, E.A.; Perron, G. Erratum to: Three-Dimensional Modelling of Geological Surfaces Using Generalized Interpolation with Radial Basis Functions. Math. Geosci. 2014, 46, 955–956. [Google Scholar] [CrossRef]
- Das, J.; Umamahesh, N.V. Spatio-Temporal Variation of Water Availability in a River Basin under CORDEX Simulated Future Projections. Water Resour. Manag. 2018, 32, 1399–1419. [Google Scholar] [CrossRef]
- Alamgir, M.; Shahid, S.; Hazarika, M.K.; Nashrrullah, S.; Harun, S.B.; Shamsudin, S. Analysis of Meteorological Drought Pattern During Different Climatic and Cropping Seasons in Bangladesh. JAWRA J. Am. Water Resour. Assoc. 2015, 51, 794–806. [Google Scholar] [CrossRef]
- Ha, H.; Olson, J.R.; Bian, L.; Rogerson, P.A. Analysis of Heavy Metal Sources in Soil Using Kriging Interpolation on Principal Components. Environ. Sci. Technol. 2014, 48, 4999. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Casal, R.; González-Manteiga, W.; Febrero-Bande, M. Flexible spatio-temporal stationary variogram models. Stat. Comput. 2003, 13, 127–136. [Google Scholar] [CrossRef]
- Raja, N.B.; Aydin, O.; Türkoğlu, N.; Çiçek, I. Space-time kriging of precipitation variability in Turkey for the period 1976–2010. Theor. Appl. Climatol. 2017, 129, 293–304. [Google Scholar] [CrossRef]
- Yong, Y.; Christakos, G.; Guo, M.; Xiao, L.; Huang, W. Space-time quantitative source apportionment of soil heavy metal concentration increments. Environ. Pollut. 2017, 223, 560–566. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Wu, J.; Christakos, G. Prediction of soil heavy metal distribution using Spatiotemporal Kriging with trend model. Ecol. Indic. 2015, 56, 125–133. [Google Scholar] [CrossRef]
- Jost, G.; Heuvelink, G.; Papritz, A. Analysing the space–time distribution of soil water storage of a forest ecosystem using spatio-temporal kriging. Geoderma 2005, 128, 258–273. [Google Scholar] [CrossRef]
- Jovein, E.B.; Hosseini, S.M. Predicting saltwater intrusion into aquifers in vicinity of deserts using spatio-temporal kriging. Environ. Monit. Assess. 2017, 189, 81. [Google Scholar] [CrossRef] [PubMed]
- Park, N.W. Time-Series Mapping of PMConcentration Using Multi-Gaussian Space-Time Kriging: A Case Study in the Seoul Metropolitan Area, Korea. Adv. Meteorol. 2016, 2016, 1–10. [Google Scholar]
- Dabass, A.; Talbott, E.O.; Bilonick, R.A.; Rager, J.R.; Venkat, A.; Marsh, G.M.; Duan, C.; Xue, T. Using spatio-temporal modeling for exposure assessment in an investigation of fine particulate air pollution and cardiovascular mortality. Environ. Res. 2016, 151, 564–572. [Google Scholar] [CrossRef] [PubMed]
- Yan, C.; Zhao, G.; Yue, T.; Chen, C.; Liu, J.; Li, H.; Su, N. Speeding up the high-accuracy surface modelling method with GPU. Environ. Earth Sci. 2015, 74, 6511–6523. [Google Scholar] [CrossRef]
- Wang, H.; Guan, X.; Wu, H. A Hybrid Parallel Spatial Interpolation Algorithm for Massive LiDAR Point Clouds on Heterogeneous CPU-GPU Systems. ISPRS Int. J. Geo-Inf. 2017, 6, 363. [Google Scholar] [CrossRef]
- Rizki, P.N.M.; Lee, H.; Lee, M.; Oh, S. High-performance parallel approaches for three-dimensional light detection and ranging point clouds gridding. J. Appl. Remote Sens. 2017, 11, 19. [Google Scholar] [CrossRef]
- Huang, F.; Bu, S.; Tao, J.; Tan, X. OpenCL Implementation of a Parallel Universal Kriging Algorithm for Massive Spatial Data Interpolation on Heterogeneous Systems. ISPRS Int. J. Geo-Inf. 2016, 5, 96. [Google Scholar] [CrossRef]
- Cheng, T.P. Accelerating universal Kriging interpolation algorithm using CUDA-enabled GPU. Comput. Geosci. 2013, 54, 178–183. [Google Scholar] [CrossRef]
- Liu, L.; Wu, C.L.; Wang, Z.B. Parallelization of the Kriging Algorithm in Stochastic Simulation with GPU Accelerators. In Geo-Informatics in Resource Management and Sustainable Ecosystem; Bian, F., Xie, Y., Eds.; Springer: Berlin, Germany, 2016; pp. 197–205. [Google Scholar]
- Wei, H.; Du, Y.; Liang, F.; Zhou, C.; Liu, Z.; Yi, J.; Xu, K.; Wu, D. A k-d tree-based algorithm to parallelize Kriging interpolation of big spatial data. Mapp. Sci. Remote Sens. 2015, 52, 40–57. [Google Scholar] [CrossRef]
- Hu, H.; Xu, J.; Hong, S.; Hu, Z. Using compute unified device architecture-enabled graphic processing unit to accelerate fast Fourier transform-based regression Kriging interpolation on a MODIS land surface temperature image. J. Appl. Remote Sens. 2016, 10, 026036. [Google Scholar] [CrossRef]
- Ma, C. Families of spatio-temporal stationary covariance models. J. Stat. Plan. Inference 2003, 116, 489–501. [Google Scholar] [CrossRef]
- Gneiting, T. Nonseparable, Stationary Covariance Functions for Space-Time Data. Publ. Am. Stat. Assoc. 2002, 97, 590–600. [Google Scholar] [CrossRef]
- De Cesare, L.; Myers, D.E.; Posa, D. Product-sum covariance for space-time modeling: An environmental application. Environmetrics 2015, 12, 11–23. [Google Scholar] [CrossRef]
- Ma, C. Spatio-temporal stationary covariance models. J. Multivar. Anal. 2008, 86, 97–107. [Google Scholar] [CrossRef]
- Cesare, L.D.; Myers, D.E.; Posa, D. Estimating and modeling space-time correlation structures. Stat. Probab. Lett. 2001, 51, 9–14. [Google Scholar] [CrossRef]
- Munshi, A.; Gaster, B.R.; Mattson, T.G.; Fung, G.; Ginsburg, D. OpenCL Programming Guide; Addison-Wesley: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
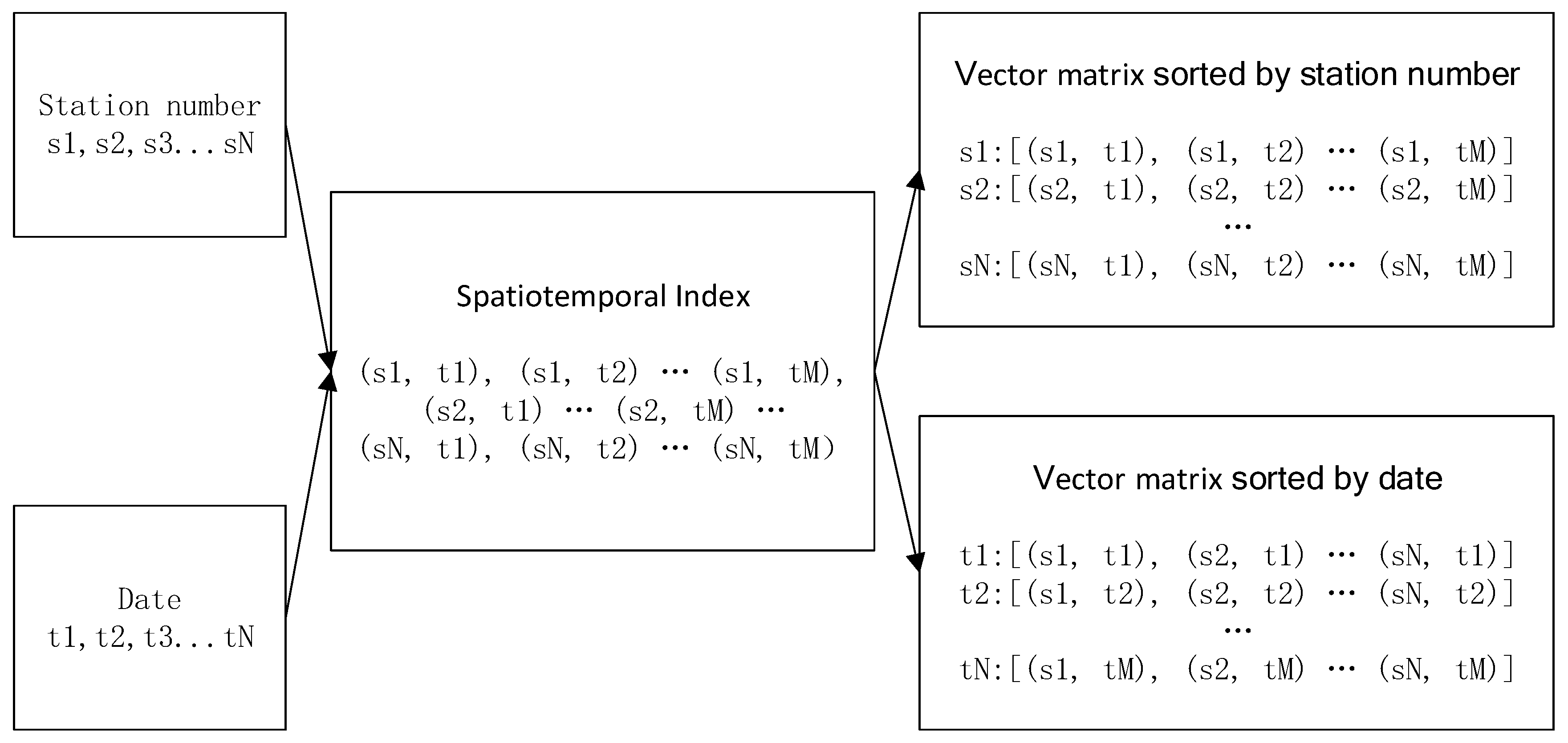
| Station Number () | Date () | Spatiotemporal Index () |
|---|---|---|
| 00001 | 201706 | 00001201706 |
| Platform | Hardware Configuration |
|---|---|
| Intel® Core™ i7-7700 Processor | Cores: 4 |
| Threads: 8 | |
| Processor Base Frequency: 3.60 GHz | |
| Max Turbo Frequency: 4.20 GHz | |
| Cache: 8 MB Smart Cache | |
| Bus Speed: 8 GT/s DMI3 | |
| Nvidia GeForce GTX 1060 | NVIDIA CUDA® Cores: 1280 |
| Base Clock (MHz): 1506 | |
| Boost Clock (MHz): 1708 | |
| Memory Speed: 8 Gbps | |
| Standard Memory Config: 6 GB GDDR5 | |
| Memory Bandwidth (GB/sec): 192 |
| Observation Datasets | Grid Resolution | SSTK/ms | PSTK/ms | Speed Up |
|---|---|---|---|---|
| 2000 | 1000 × 1000 | 25,043 | 8480 | 2.95 |
| 3000 | 1000 × 1000 | 25,654 | 8718 | 2.94 |
| 4000 | 1000 × 1000 | 26,766 | 8847 | 3.02 |
| 5000 | 1000 × 1000 | 27,389 | 8970 | 3.05 |
| Observation Datasets | Grid Resolution | SSTK/ms | PSTK/ms | Speed Up |
|---|---|---|---|---|
| 5000 | 500 × 500 | 8663 | 4009 | 1.41 |
| 5000 | 800 × 800 | 16,780 | 6683 | 2.51 |
| 5000 | 1000 × 1000 | 25,138 | 8970 | 2.80 |
| 5000 | 1500 × 1500 | 56,824 | 18,192 | 3.12 |
| 5000 | 2000 × 2000 | 95,470 | 29,583 | 3.23 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zheng, X.; Wang, Z.; Ai, G.; Huang, Q. Implementation of a Parallel GPU-Based Space-Time Kriging Framework. ISPRS Int. J. Geo-Inf. 2018, 7, 193. https://doi.org/10.3390/ijgi7050193
Zhang Y, Zheng X, Wang Z, Ai G, Huang Q. Implementation of a Parallel GPU-Based Space-Time Kriging Framework. ISPRS International Journal of Geo-Information. 2018; 7(5):193. https://doi.org/10.3390/ijgi7050193
Chicago/Turabian StyleZhang, Yueheng, Xinqi Zheng, Zhenhua Wang, Gang Ai, and Qing Huang. 2018. "Implementation of a Parallel GPU-Based Space-Time Kriging Framework" ISPRS International Journal of Geo-Information 7, no. 5: 193. https://doi.org/10.3390/ijgi7050193
APA StyleZhang, Y., Zheng, X., Wang, Z., Ai, G., & Huang, Q. (2018). Implementation of a Parallel GPU-Based Space-Time Kriging Framework. ISPRS International Journal of Geo-Information, 7(5), 193. https://doi.org/10.3390/ijgi7050193






