1. Introduction
The four global satellite navigation systems, Global Positioning System (GPS), Global Navigation Satellite System (GLONASS), Galileo Satellite Navigation System (Galileo), and Beidou Satellite Navigation System (BDS) have enabled a wide range of applications for positioning, navigation and timing [
1]. BDS started to provide basic service for the Asia-Pacific region in 2012; China has been constantly testing and launching new satellites and BDS will provide a service for global users by 2020 [
2]. The Galileo system currently only achieves part-time global service for insufficient medium earth orbit (MEO) satellites, and its satellite numbers are also expanding quickly [
3]. The Quasi-Zenith Satellite System (QZSS) is being used more frequently by Japan as a non-independent regional satellite system that can provide supplemental positioning and timing information for GPS, BDS, Galileo, and GLONASS [
4].
Although high accuracy demanding users in Asia-Pacific region can typically observe more than eight GPS satellites, it is actually difficult for a single GPS constellation to achieve high-accuracy single-frequency single-epoch (SFSE) positioning—especially when the geometric structure of the constellation-user becomes worse, low-elevation satellites account for a large proportion and high-elevation satellites (>35°) decrease [
5]. Therefore, it is useful to study multisystem positioning to improve availability and reliability. QZSS is not an independent satellite system and is based on GPS, so it can be seen as an enhanced GPS constellation in the range of the Japanese longitude. BDS and QZSS both enhance the coverage of the Asia-Pacific region by adding synchronous orbit satellites to the constellations. Shi et al. (2012) found that BDS could provide high-accuracy location services comparable to GPS in the Asia-Pacific region [
6]. Recently, the number of QZS increased to four in March 2018 and three satellites have been available to users since then. It is necessary to study the enhancement effect of QZSS to GPS and BDS in the Asia-Pacific region.
Much literature has studied the performance of integrated GPS/BDS, and QZSS enhancement in GPS has been discussed since the concept of QZSS was proposed [
7,
8,
9,
10,
11,
12,
13,
14,
15]. A multi-carrier fast partial ambiguity resolution strategy was proposed to sequentially resolve BDS/GPS dual- and triple-frequency ambiguities sequentially to significantly improve the computational efficiency of AR [
7]. The potential of GPS/BDS to serve as the early warning system for tsunamis in the South China Sea region was investigated [
8]. The positioning performance of BDS/GPS is superior to that of GPS/GLONASS or BDS/GLONASS, and can be further improved using BDS/GPS/GLONASS [
9]. The performance of a short baseline ambiguity resolution with different scenarios of the present GPS and future GPS/QZSS system was analyzed when QZSS was still in the argumentation stage [
10]. Meanwhile, the availability, accuracy, and reliability of GPS and GPS/QZSS in the Asia-Pacific and Australian regions were simulated in [
11,
12]. The simulation results showed that QZSS not only improves the availability and accuracy of GPS positioning, but also enhances the reliability of GPS positioning in Japan and its neighboring areas. In [
13], the positioning performance of GPS aided by QZSS was improved by more than 30% for high elevation mask angles and positioning availability, which is more stable than the single GPS. An early assessment of the newly available signal’s quality of the multi-GNSS (GPS + GLONASS + BDS + QZSS) was provided by computing zero-baseline double-differenced carrier phase residuals and it was found that all the available constellations can improve the precision and accuracy in both the horizontal and vertical components [
14]. QZSS is able to decrease the position error and increase the success rate of GPS resolution while offering more available and reliable GPS in Japan and most East Asian regions for a single receiver [
15].
The J01 (QZS numbered 01) was launched in 2010 and the J02 (QZS numbered 02) was fixed in orbit in June 2017. The number of QZS increased to four in March 2018 and three are in normal service. Some literature only analyzed the QZSS positioning performance based on simulation results while other work examined the measured data of only one QZS. These results could not comprehensively reflect the current features of the QZSS constellation and its enhancement effect on GPS. The SFSE double-differenced (DD) baseline resolution is the original and the most classical solution of high accuracy carrier phase positioning, and is also the most essential approach to reflect the reasonableness of the constellation structure and the quality of the measurement data [
16,
17]. Accordingly, the performance of the SFSE carrier phase DD baseline resolution for the integrated GPS/QZSS and BDS/QZSS in the Asia-Pacific region needs more attention.
In this paper, the availability, PDOP, ADOP, success rate, and accuracy of GPS/QZSS and B DS/QZSS were analyzed. The auxiliary and enhancement effects of QZSS were studied and analyzed. This paper is arranged as follows:
Section 1 is the introduction. The basic state of QZSS is introduced in
Section 2. In
Section 3, the SFSE code and carrier phase DD model for the integrated BDS/QZSS and GPS/QZSS are deduced and the corresponding forms of the weighting model are described.
Section 4 presents the promotion of availability and PDOP of BDS and GPS when assisted by QZSS and introduces 3 indicators of ambiguity estimation.
Section 5 analyses the improvement of PDOP, ADOP, actual success rate, and baseline precision of GPS/QZSS and BDS/QZSS with two real-data experiments. Finally, the main conclusions are drawn in
Section 6.
2. Quasi-Zenith Satellite System
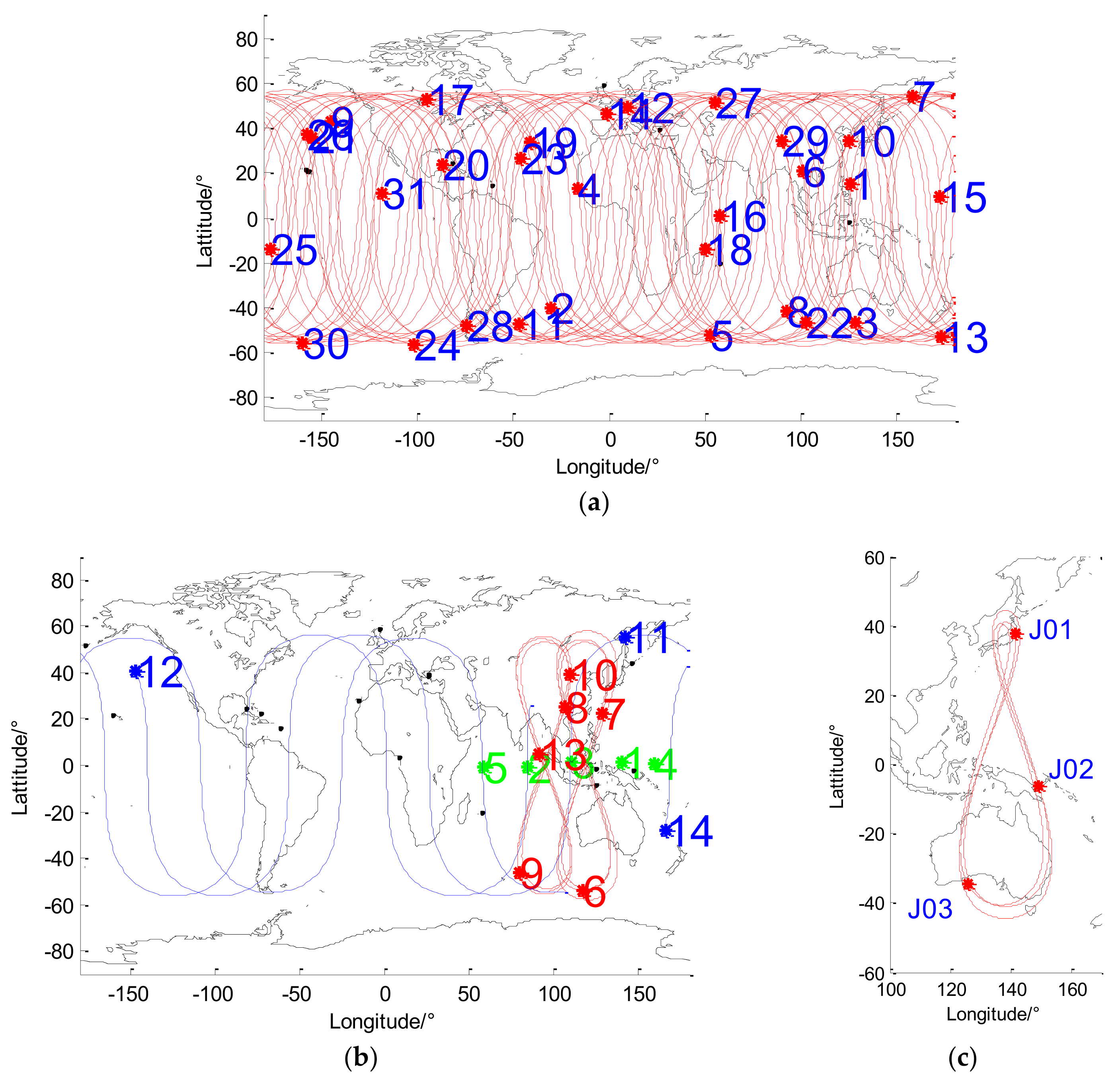
QZSS is a developing regional satellite-based augmentation for GPS, which could be receivable within East Asia and the Oceania region. Currently, the QZSS is composed of three inclined geosynchronous orbit (IGSO) satellites that operate at three orbits of 45° inclination and 140° right ascension of the ascending node (RAAN), and rotate about the Earth in a period of one sidereal day (about 23 h and 56 min). Ground tracks of the GPS satellites, BDS satellites, and QZS on 1 February are computed and are plotted in
Figure 1, and the basic status of the three systems is shown in
Table 1. QZSS has the same L1, L2, and L5 frequency bands as GPS. All QZS operate in the inclined geosynchronous satellite orbit (IGSO) while GPS consists of MEO satellites. The ground tracks of QZS range from 120° E to 155° E and within 45° N/S; the tracks are similar to a variant ‘8′. Due to the unique operating orbits, the elevation of the QZS are above 60° and the coverage rate is up to 100% in Japan. Although the signals from low-elevation GPS satellites could be blocked by city buildings, QZS with a relatively higher elevation can be detected even within downtown. Therefore, when GPS or BDS is implemented with QZSS, the number of available satellites certainly increases, resulting in an improvement in PDOP and positioning accuracy. In addition, there is a good possibility of enhancing the position accuracy for users in the Asia-Pacific region such as Korea, the East China Coast, and Australia, which are also within the QZSS service range.
The GPS constellation is officially designed as 21 working satellites and three orbiting spare satellites but actually contains more than 30 (30–32) GPS satellites working in six 55-degrees-inclination orbital planes; this configuration ensures that more than eight satellites can be received at most time in the most densely populated area of the world. BDS has three signal bands of B1, B2, and B3 and consists of three types of satellites: five geostationary earth orbit (GEO) satellites remain stationary over the equator from 58.75° E to 160° E, six IGSO satellites run in the ‘8′ track, and three MEO satellites are also included. Currently, there are many BDS MEO satellites for the in-orbit test.
4. Positioning Performance of GPS/QZSS and BDS/QZSS in the Asia-Pacific Region
4.1. Availability and PDOP of GPS/QZSS and BDS/QZSS
Availability mainly describes the number of visible satellites above the mask angles and is the most basic performance measure of a navigation system. The theoretical minimum number of satellites to achieve SFSE DD baseline resolution for a single system is 4 and for multisystem is n + 3, where n is the number of systems. PDOP is another indicator revealing the relative position quality of the constellation-user geometric structure. The more scattered the satellite distribution, the larger the geometric volume of the constellation and the higher the position precision [
24]. To evaluate the availability and PDOP of the integrated GPS/QZSS and BDS/QZSS, the GPS, BDS, and QZSS data of a week was collected and calculated. The time interval ranges from 4 February to 2 March 2018, and the sampling frequency is 30 s.
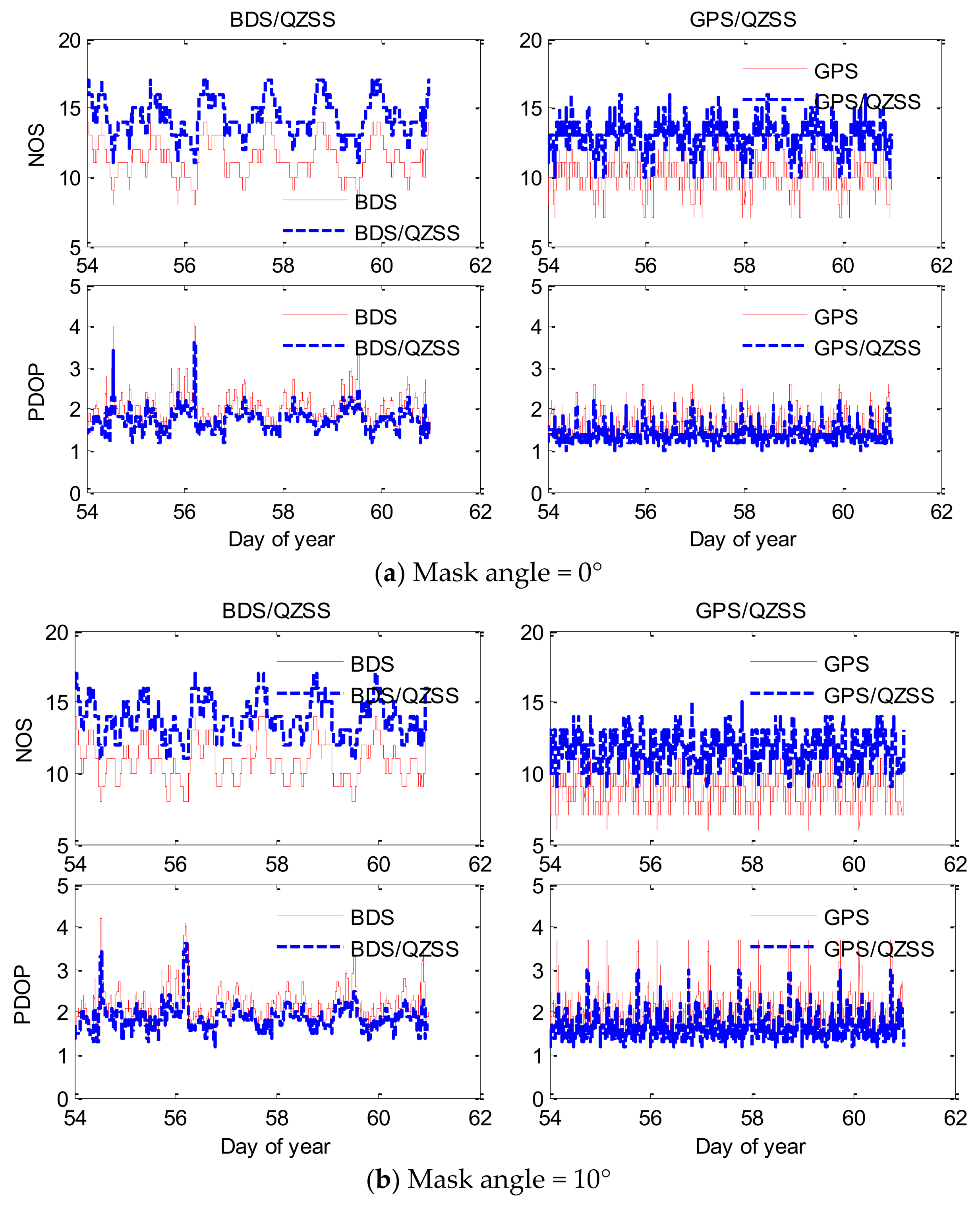
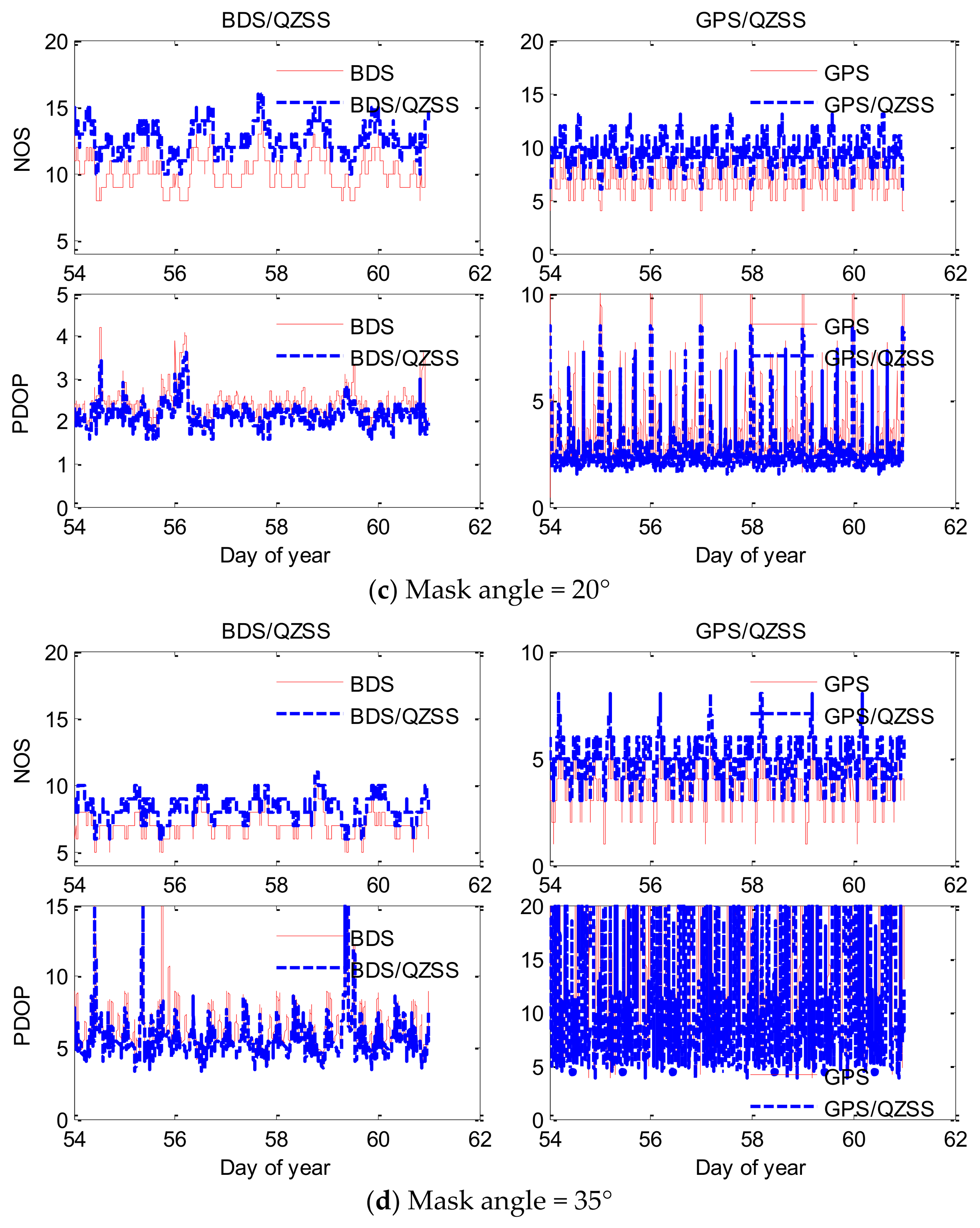
Figure 2 shows the number of visible satellites and the PDOP value under the BDS, GPS, BDS/QZSS, and GPS/QZSS cases with mask angles of 0°, 10°, 20°, and 35° at the HKLT station in Hong Kong, from day of year (DOY) 54 to 60.
Table 2 gives the average number of visible satellites (minimum value) and the mean PDOP displayed in
Figure 2.
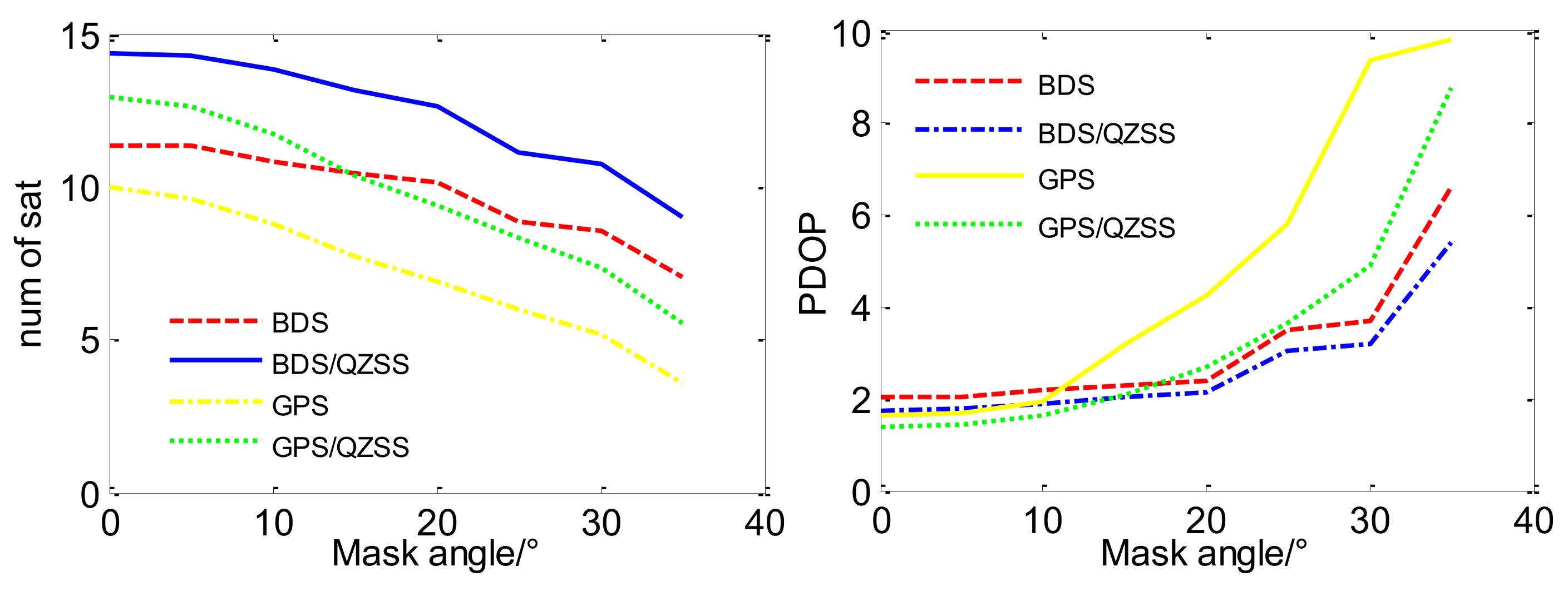
Figure 3 presents availability and PDOP trends with the increasing mask angle from 0° to 35°.
For the single GPS, when the mask angle changes from 0° to 20°, the minimum/mean/maximum number of satellites (NOS) decreases from 7/10/13 to 4/6.9/10 and the corresponding PDOP increases from 2.63/1.62/1.1 to 20.5/4.25/1.65; the differences of the mean NOS and PDOP are 3.1 and 2.63, respectively. When the mask angle increases to 35°, the mean PDOP is 9.39 and the mean NOS is 3.6, which is lower than boundary value of 4. In that case, the single GPS cannot provide constant and accurate position service. For integrated GPS/QZSS, the mean NOS and mean PDOP with mask angles of 0°, 20° and 35° are 13/1.39, 9.4/2.69 and 5.5/4.92, respectively. The improvement in NOS and PDOP are 3/0.23, 2.5/2.44 and 1.9/4.47, respectively. This means that even above elevations of 20° and 35°, there are still 2.5 and 1.9 visible QZS, respectively, which could greatly improve the observation conditions and the positioning accuracy of the single GPS. For the single BDS, when the mask angle is less than 20°, an average of 10.1 BDS satellites can be observed, which is many more satellites than for GPS (6.9). Even when the mask angle is set to 35°, there are still at least five and an average of seven BDS satellites (high-elevation satellites) in the field of vision, which ensures a full-time BDS positioning in Hong Kong. After augmented by QZSS, the improvement in PDOP is approximately 0.27/0.29/0.47 with a mask angle of 0°/20°/35°. QZSS bring about a great improvement in the NOS and PDOP for GPS, which supports the sustainable high accuracy positioning of GPS under difficult conditions.
4.2. ADOP, Success Rate and Baseline Accuracy
The concept of ambiguity dilution of precision (ADOP) was first proposed by Teunissen in 1997 to measure ambiguities by computing the geometric mean of the ambiguity conditional standard deviations [
25]. ADOP was introduced based on the determinant of the ambiguity variance–covariance matrix:
where
is the variance–covariance matrix of the float ambiguities, n is the dimension of the matrix, and
denotes the determinant of the matrix
.
The success rate is the index that indicates whether integer ambiguity resolution can be expected to be successful. Based on the ambiguity estimator theory, the success rate of ambiguity resolution is determined by computing the numerical integration of the probability density function of float ambiguities in the ‘pull-in region’, which is very rigorous in theory [
26]. However, it is difficult to describe the ‘pull-in region’ so the integration process is very complex and the success rate cannot be calculated directly. We can only approximately approach the theoretical success rate through the calculation of the upper and lower success rate bound [
27]. The bootstrapped success rate (Bsrt) is a lower bound of the integer least-squares success rate and is defined based on the variance–covariance matrix of the decorrelated float ambiguities [
28].
where,
is the conditional standard deviations of the estimated ambiguities. We simulated the ADOP and Bsrt of a 10 km baseline at HKLT station in Hong Kong as the base station for a week.
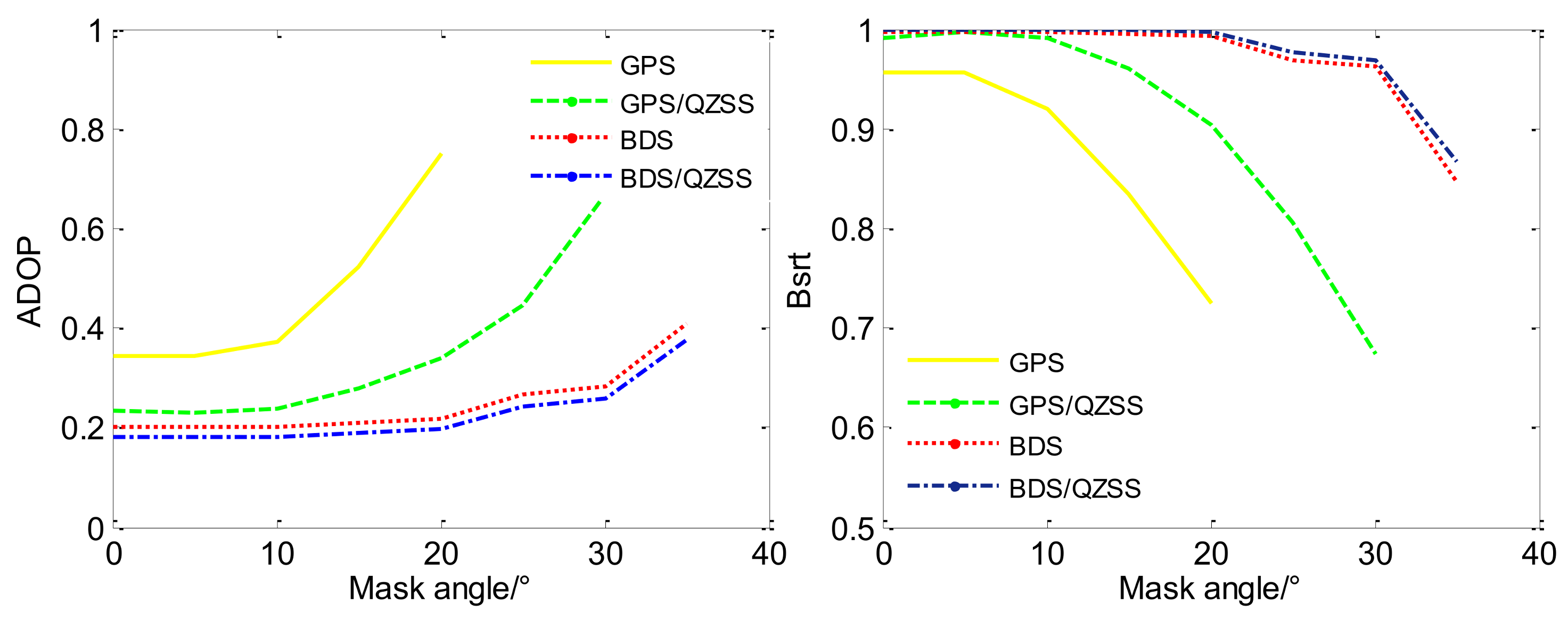
Figure 4 shows the mean ADOP and Bsrt of different systems with different mask angles which are counted in
Table 3. The single GPS ADOP cannot be computed above a 20° mask angle, and GPS/QZSS ADOP cannot be computed above a 30° mask angle because the number of visible satellites is not sufficient. We can clearly draw the following conclusions: (1) The single GPS baseline resolution is limited by the number of satellites, especially when the mask angle is above 20°, and the combination of GPS/QZSS will improve the limitation; (2) GPS/QZSS achieves a great decrease in ADOP and a great increase in Bsrt compared to the single GPS; (3) The ADOP and Bsrt of BDS/QZSS are both better than that of GPS and GPS/QZSS; however, compared with the single BDS, the improvement of BDS/QZSS is relatively slight. In addition, it can be easily found that the Bsrt of a 0° mask angle is slightly lower than that of 5°. The signal from a low-elevation satellite is easily affected by shelter, such as buildings, surface fog, and haze. The noise error of the satellite signal at 0° is relatively larger than that at 5°, which will mitigate the corresponding bootstrapped success rate.
In addition, there are some differences between the bootstrapped success rate and the actual success rate. In some cases, despite the very high bootstrapped success rate of the ambiguity estimation, the actual ambiguity can also be wrong. The main reason may be that ambiguity estimation depends on the precision of the float ambiguities; the estimation could be wrong due to the residual ionosphere, troposphere, or multipath errors in float ambiguities [
29]. This indicates that the Bsrt could become inaccurate when DD residuals become larger with the increase of the baseline length. In the next section, therefore, another indicator called the actual success rate will be used to mainly evaluate the correctness of ambiguity resolution. The actual success rate (Asrt) is defined as [
5]
where,
is the number of correct fixed-ambiguity epochs and
is the number of total epochs. It is decided that the fixed integer ambiguities are correct and successful if the east, north, and up deviations of the baseline calculated by the optimal ambiguities are not more than 4 cm, 4 cm, and 10 cm, respectively.
5. Experiment
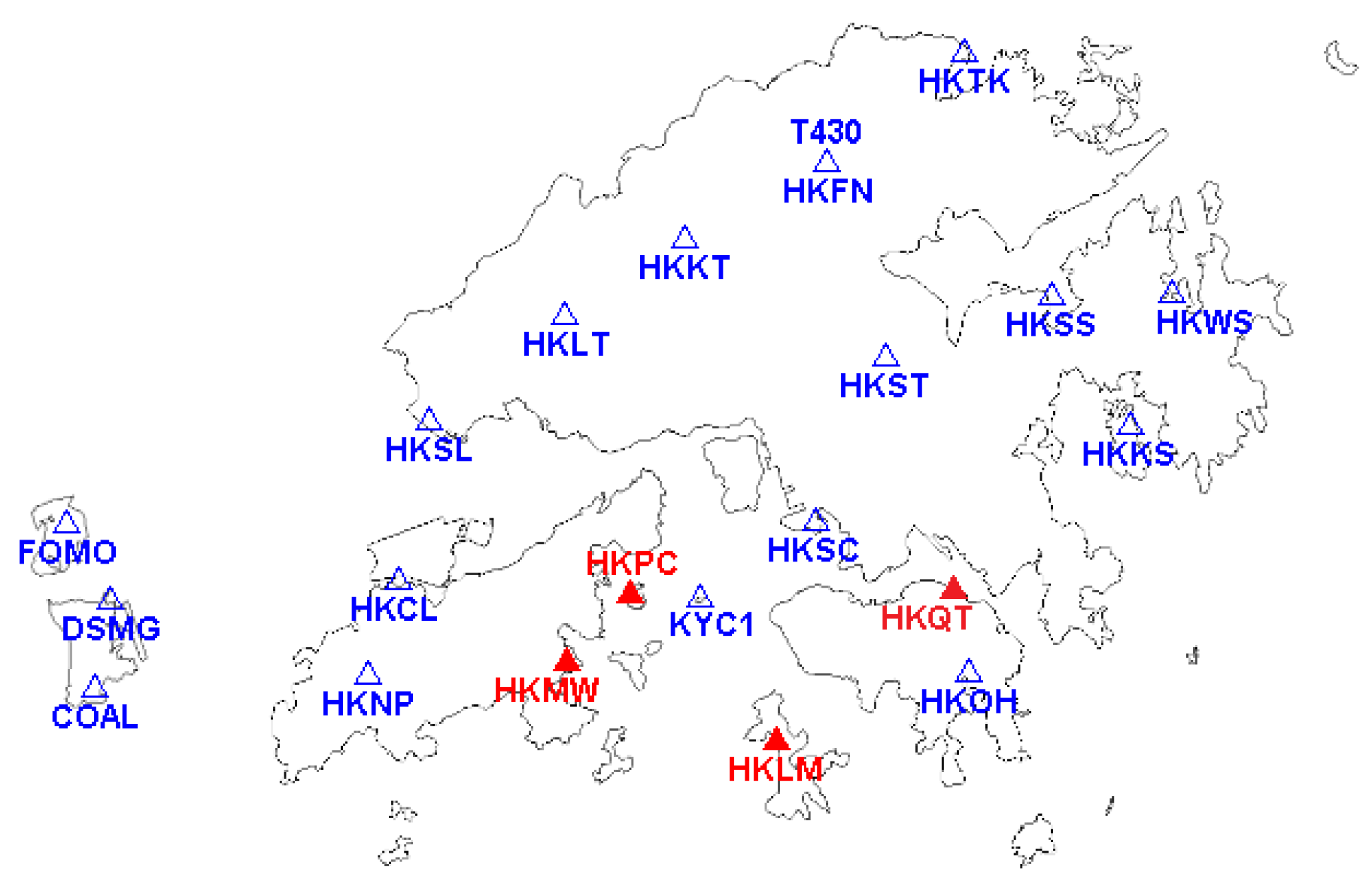
To verify the improvement effect in the SFSE baseline resolution of GPS and BDS augmented by QZSS, two groups of experiments were conducted with a 12.5 km baseline of the HKQT–HKLM stations and a 4.8 km baseline of the HKMW–HKPC stations, respectively. Their distributions and positions in Hong Kong are marked in
Figure 5. To make the two groups with different common satellites, the date from different time periods were used. The time periods of 12.5 km and 4.8 km baseline data ranged from 12:00 to 24:00 on 9 February 2018 and from 8:00 to 20:00 on 28 February 2018, respectively. The sampling frequency is 5 s and the mask angle is set to 5°. The frequencies adopted here are GPS L1, QZSS L1 and BDS B1. The receiver types of the longer baseline are both Trimble NetR9 and those of the shorter baseline are both Leica GR50. Therefore, the ISBs between GPS L1 and QZSS L1 can be ignored here. Stations HKQT and HKLM can track 3 QZS, while stations HKPC and HKMW can only receive carrier signals from J01 and J02 (QZS numbered 01 and 02).
To clearly present the improvement of the GPS and BDS SFSE baseline resolution when augmented by QZSS, we added QZS to DD processing one-by-one immediately following their number (J01, then J02 and finally J03). Since LCM was used in BDS/QZSS, the number of QZS in integrated BDS/QZSS is at least 2. Therefore, we used 8 kinds of processing strategies for the HKQT–HKLM baseline (case 1) as follows: GPS, GPS + 1QZS, GPS + 2QZS, GPS + 3QZS, BDS, BDS + 2QZS, BDS + 3QZS and BDS + GPS + 3QZS. Six kinds of combination forms were used in the HKMW–HKPC baseline including GPS, GPS + 1QZS, GPS + 2QZS, BDS, BDS + 2QZS and BDS + GPS + 2QZS and were analyzed in case 2, where, the combination of BDS/GPS/QZSS was only used in contrast.
Six indicators are used to evaluate the experimental results, NOS, PDOP, ADOP, Brst, Arst, and the baseline precision. The baseline precision is calculated through two steps. First, the mean result of the same data calculated by RTKLIB was used as a reference, which should be correct and reliable since the combination of GPS/BDS/QZSS and frequencies L1/L2 are used. Then the RMS errors of the E, N and U components are computed by
where
denotes the E/N/U sequences of the baseline resolution and
donates the reference value;
represents the RMS errors of the E/N/U component and n is the length of the sequence. Then the precision of the baseline can be computed by
5.1. Case 1: 12.5 km Baseline of HKQT–HKLM Stations in Hong Kong
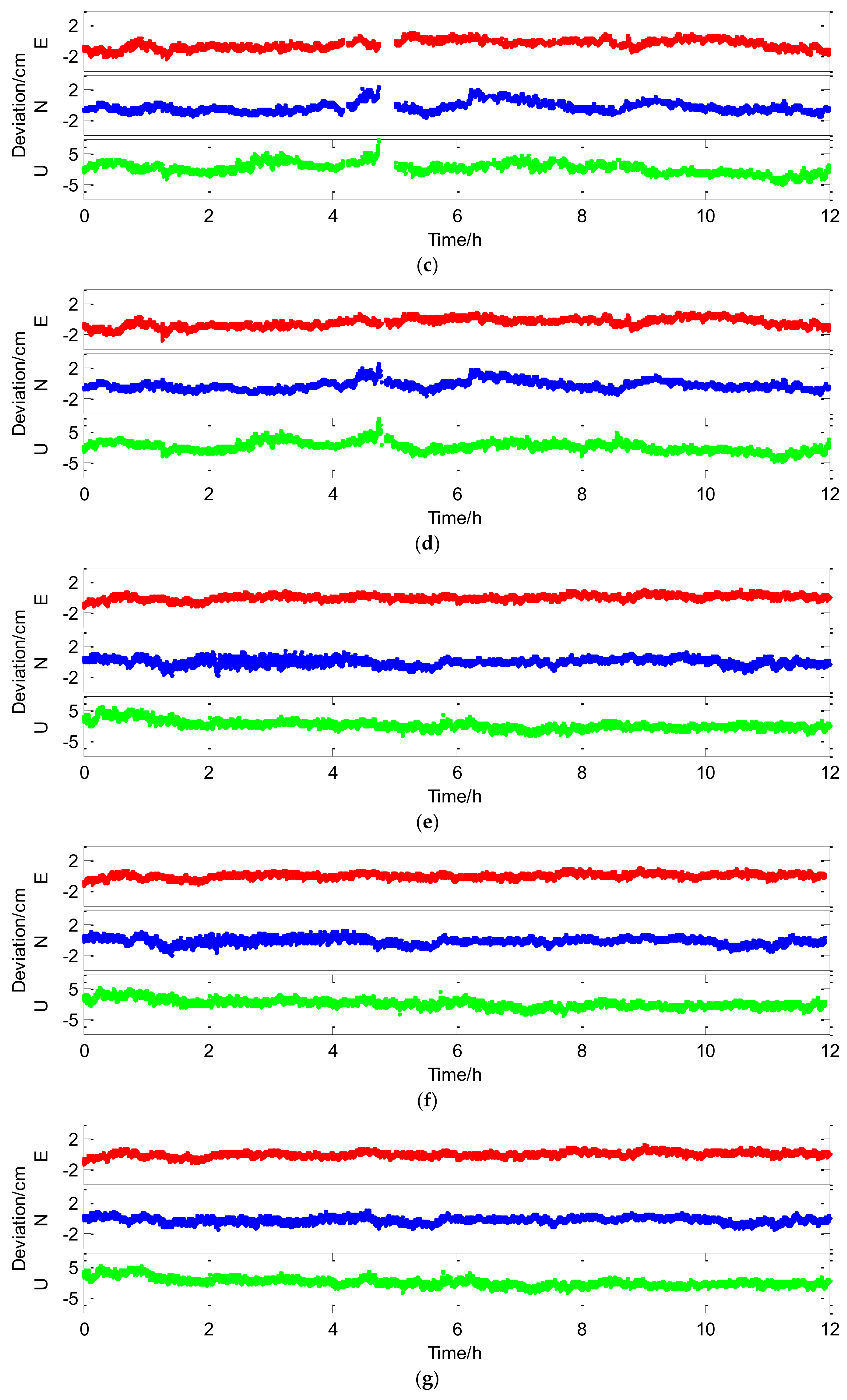
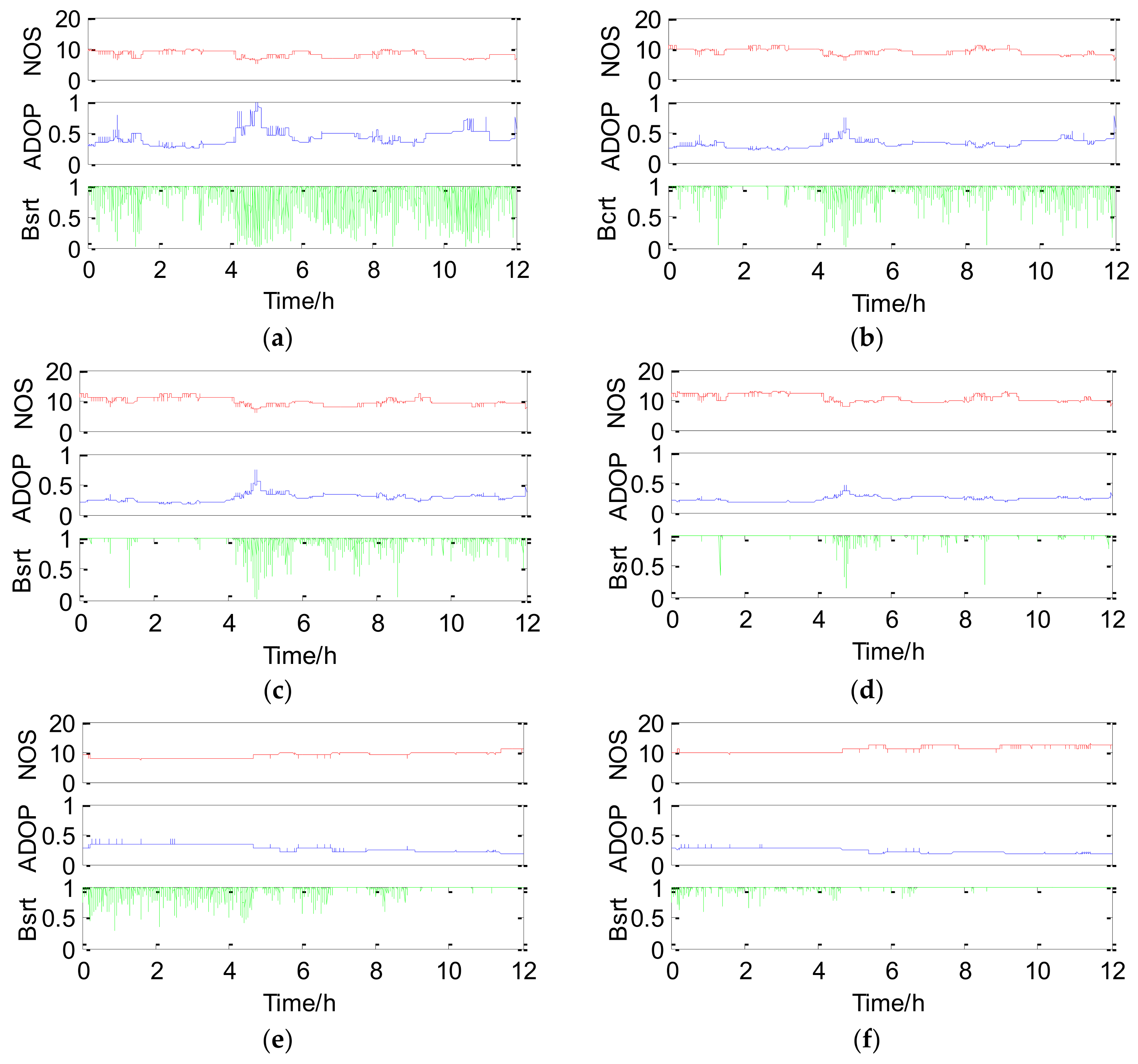
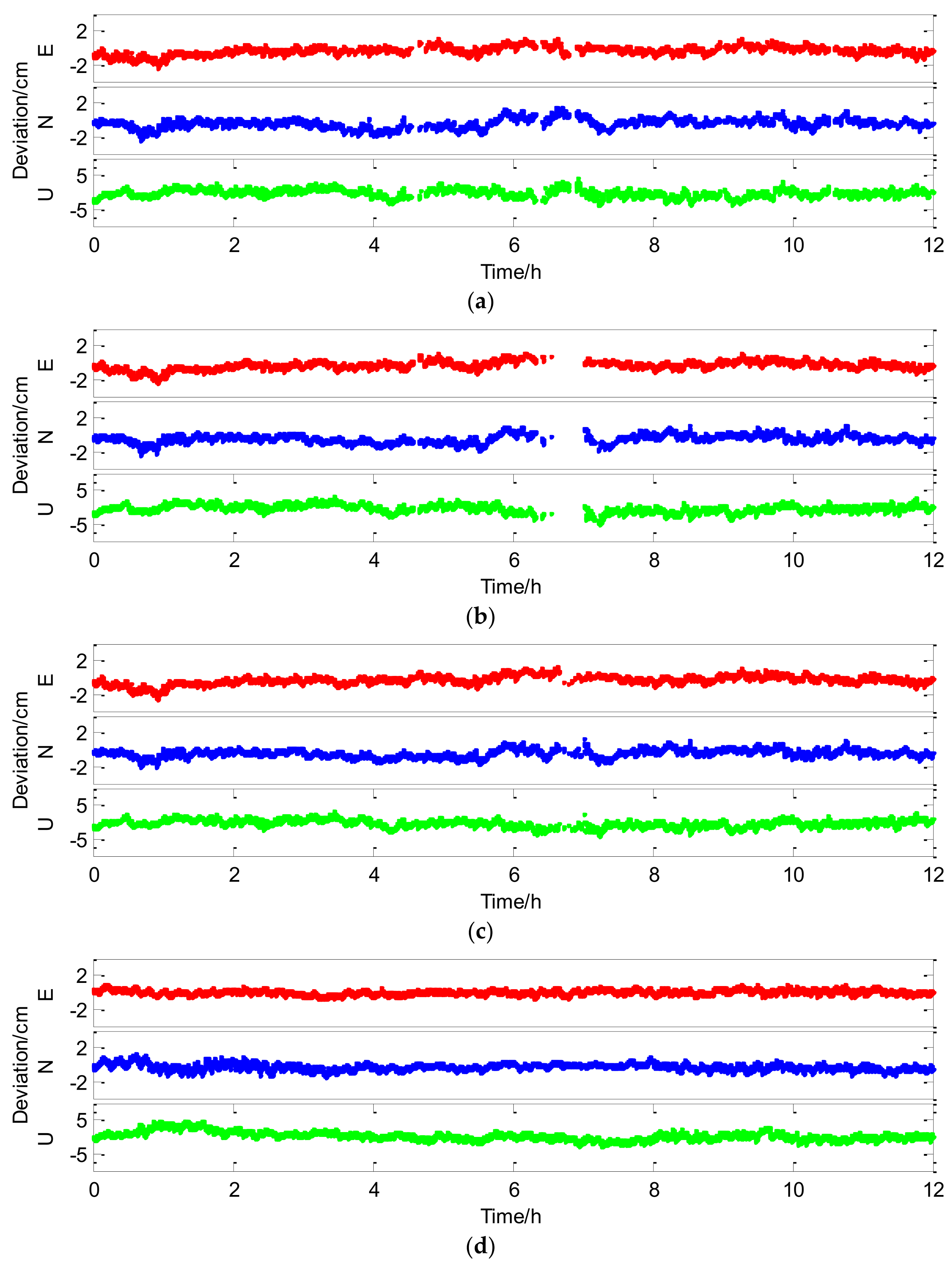
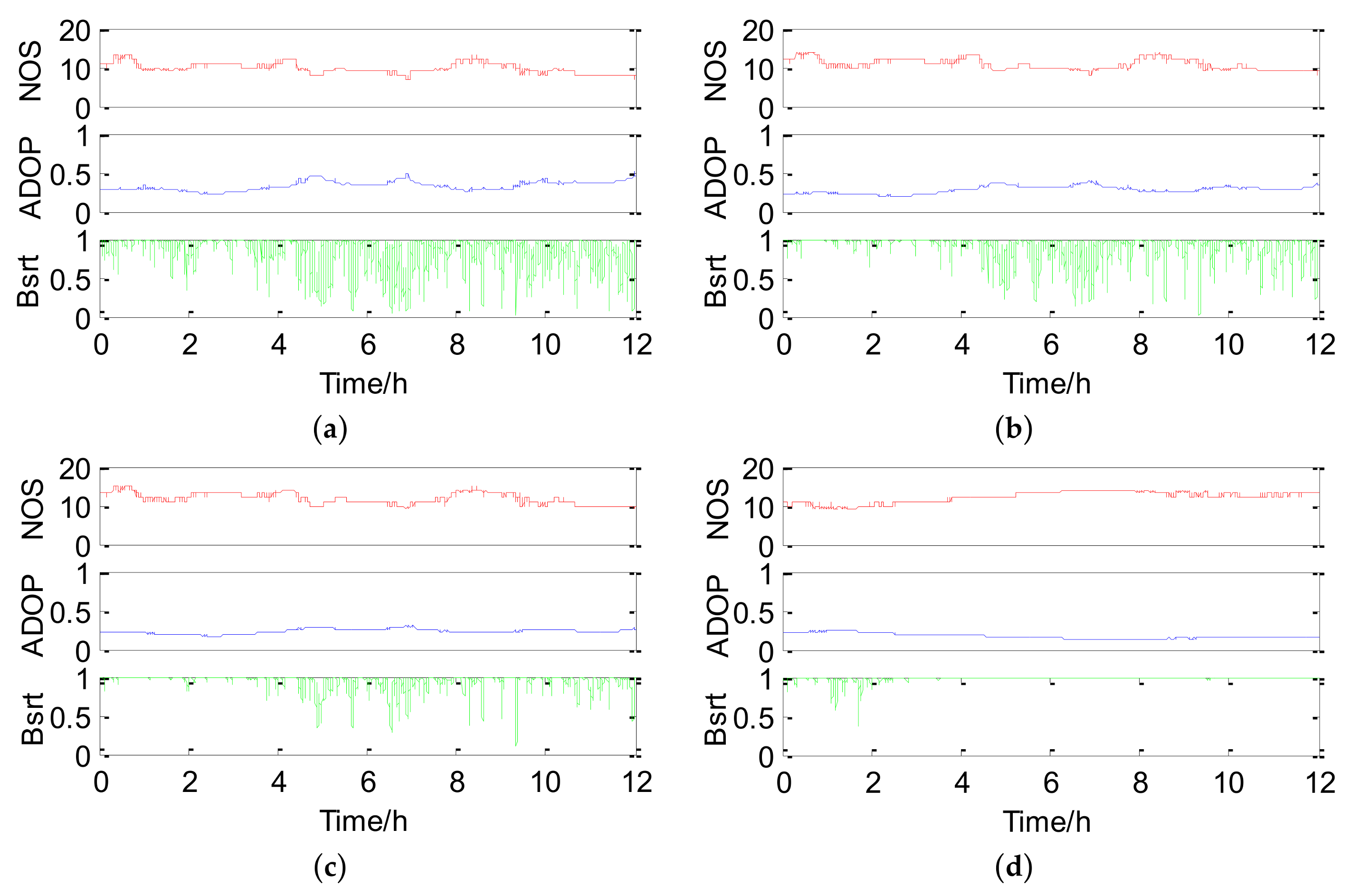
Figure 6 shows position errors of successful epochs (Asrt relevant) with different strategies (GPS, GPS + 1QZS, GPS + 2QZS, GPS + 3QZS, BDS, BDS + 2QZS, BDS + 3QZS, and BDS + GPS + 3QZS) for the 12.5 km baseline and
Figure 7 presents the curves of the corresponding NOS, ADOP, and Bsrt. The baseline deviation of failure epochs is up to several decimeters and is usually not accepted, so only the baseline precision results of successful epochs are counted. The mean NOS, PDOP, ADOP, success rates (both Bsrt and Asrt) and precision of different strategies are presented in
Table 4, which shows that the trend of PDOP and ADOP has a negative correlation with that of the NOS. The mean GPS PDOP and ADOP decrease by 0.26 and 0.18, while the number of QZS increases from 0 to 3. Similarly, the mean PDOP and ADOP of BDS decrease by 0.28 and 0.06, of which the improvement is less than that of GPS. There is an obvious phenomenon shown in
Table 2 and
Table 4, which indicates that BDS has more satellites but poorer PDOP results compared with GPS. This is mainly because GPS satellite positions are more scattered and cause a larger geometric volume of the GPS constellation, which contributes to a better PDOP of GPS. However, BDS has more visible satellites than GPS and most of the BDS satellites are synchronous orbit satellites with higher elevation. Accordingly, BDS and BDS/QZSS perform better in ADOP, success rate, and baseline precision than the GPS and GPS/QZSS.
For the single GPS, it is difficult to obtain a high success rate result for a baseline over 10 km because ionospheric and tropospheric errors cannot be completely eliminated. Meanwhile, the baseline only has 8.1 common satellites. In this condition, the mean Asrt of the single GPS is only 37.40% and many interruptions that represent failure epochs exist, as seen in
Figure 6a. Aided by different numbers of QZS, the mean Asrt is increased to 67.26%, 77.42%, and 94.51%, during which the respective curve interruptions in
Figure 6b–d gradually decrease. Therefore, the QZSS can greatly improve the success rate of GPS baseline resolution. The precision of successful epochs is not changed obviously when aided by only one QZS. With more aided QZS components, the number of successful epochs increases, and the performance of GPS/QZSS is improved palpably. The baseline precision of successful epochs is also improved from 2.16 cm to 1.8 cm. Compared with GPS/QZSS, the success rate promotion with integrated BDS/QZSS is not so obvious. BDS has advantages in NOS and satellite elevation in the Asia-Pacific region; hence Asrt of the single BDS for 12.5 km baseline is up to 96.93%. The Asrt increases to 99.61% when three QZS were added into the BDS baseline solution under the condition that little room is available for improvement of Asrt. This means QZSS can effectively improves BDS’s Asrt and makes it closer to 100%. Furthermore, the BDS baseline precision is also improved by 0.12 cm. Therefore, the QZSS shows comprehensive improvement in the performance of GPS and BDS carrier phase baseline resolution, especially for GPS ambiguity resolution success rate. Finally, for the combination of BDS/GPS/QZSS, the NOS is near 20, the ADOP is only approximately 1.1 and both Bsrt and Asrt reach 100%. As a result, the combination of BDS/GPS/QZSS certainly has the highest accuracy of 1.25 cm.
5.2. Case 2: 4.8 km Baseline of the HKMW–HKPC Stations in Hong Kong
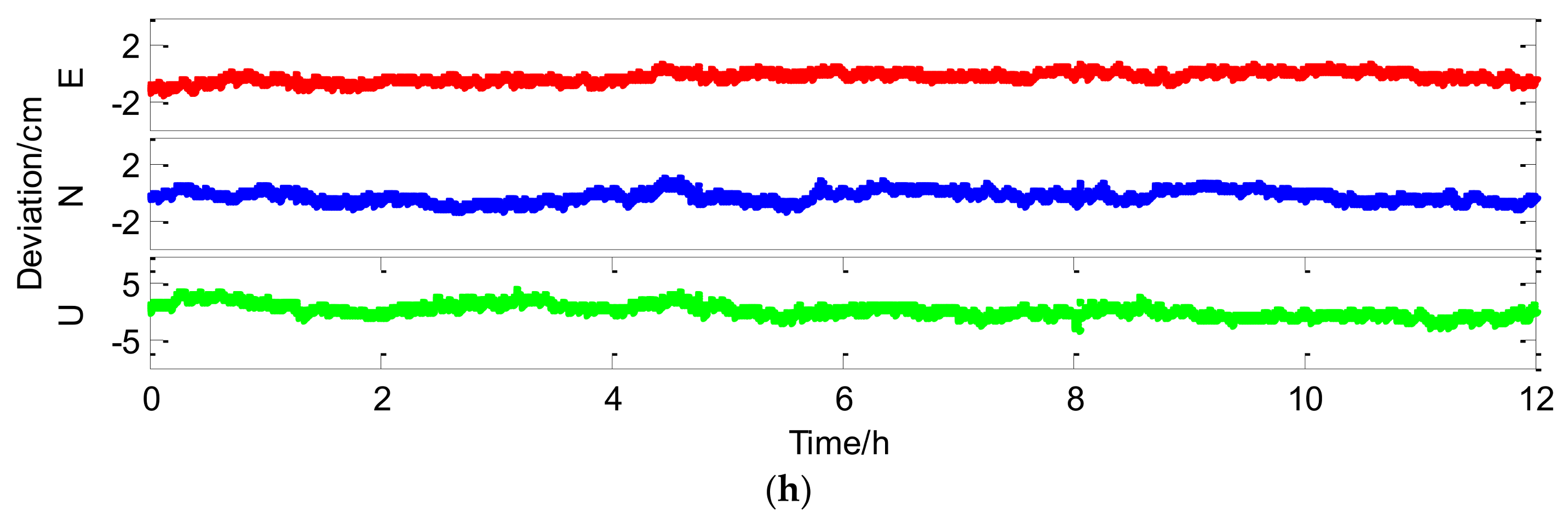
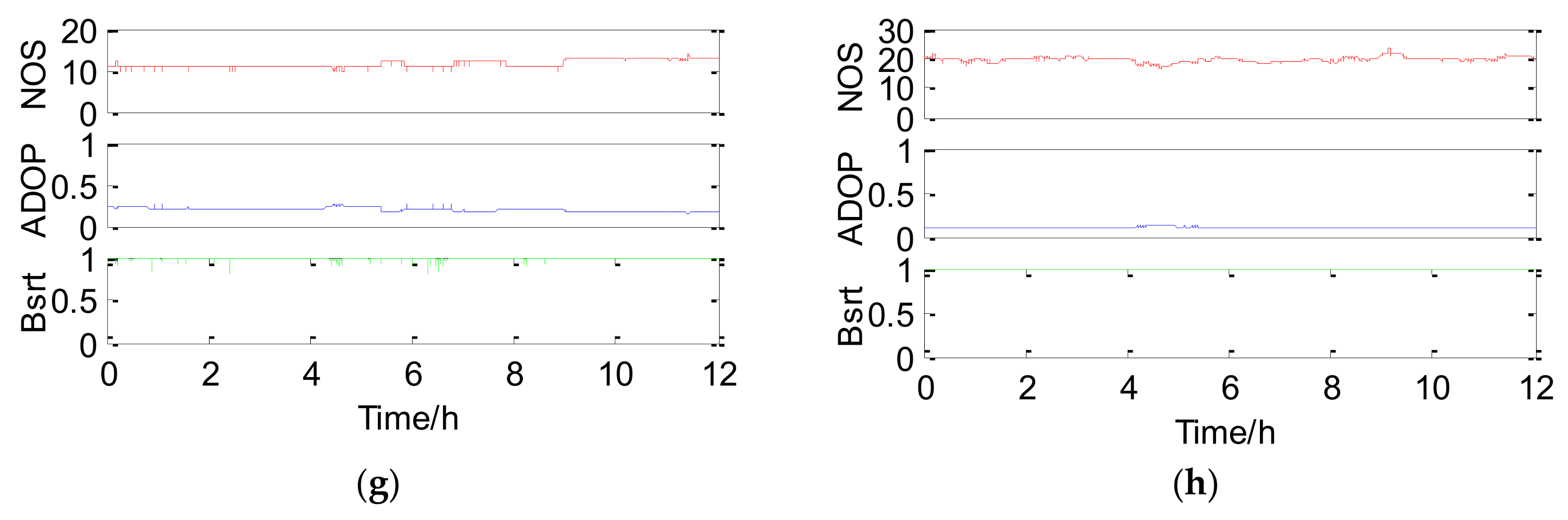
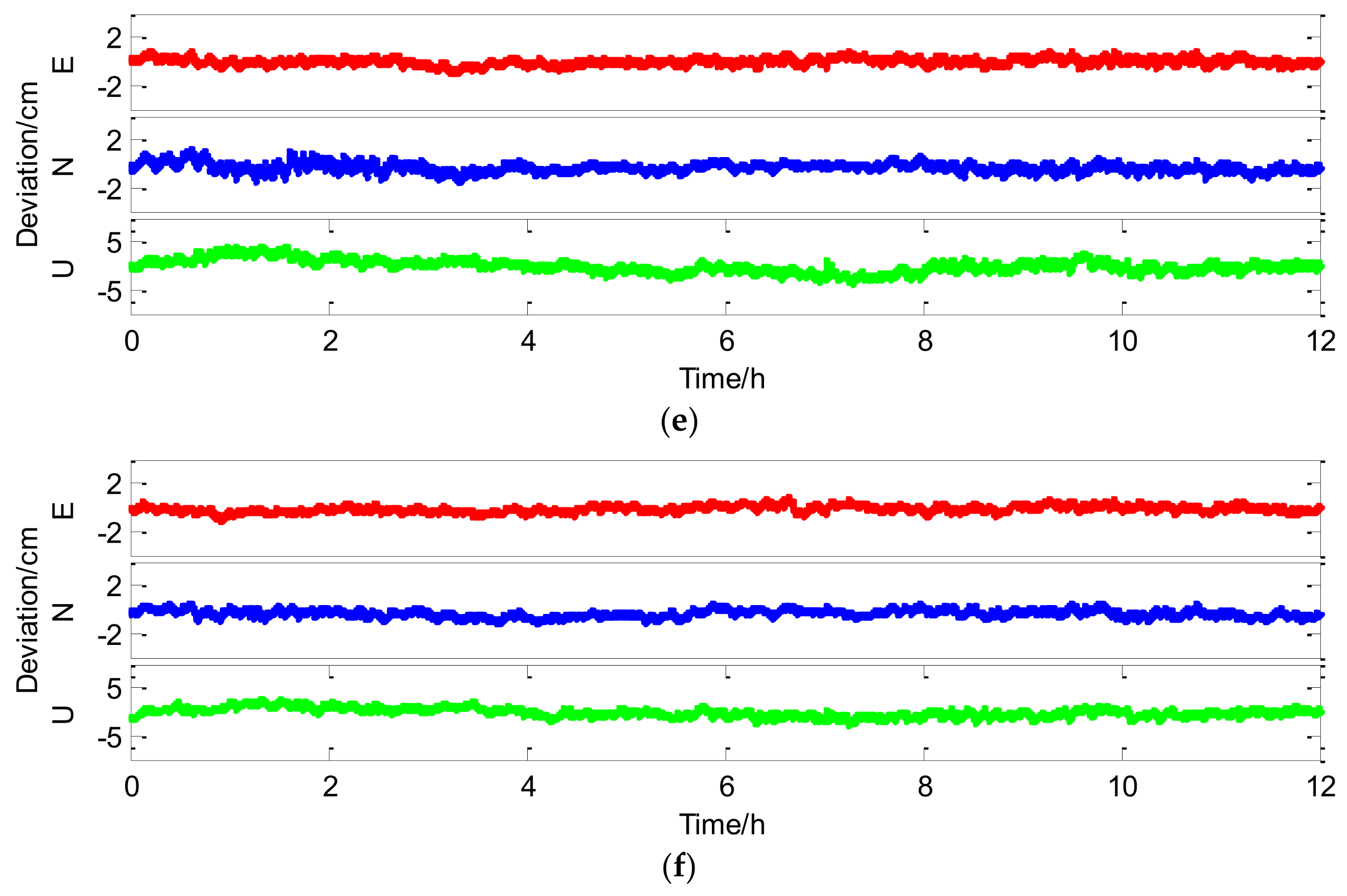
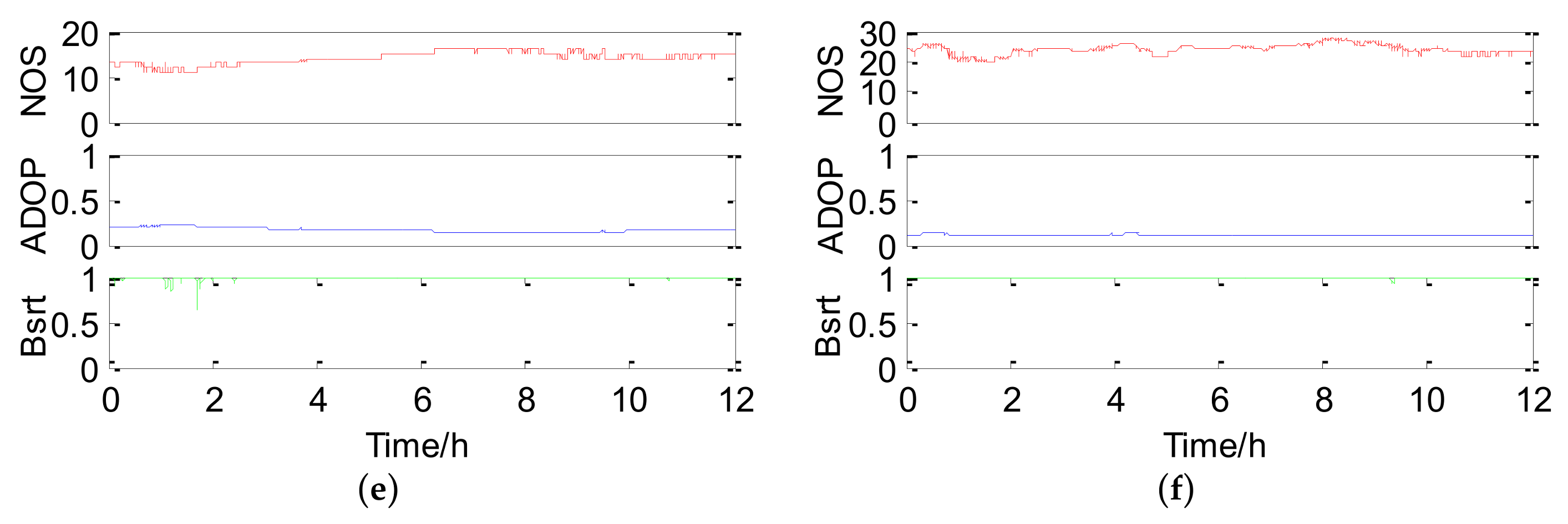
Figure 8 shows position errors of successful epochs with different strategies (GPS, GPS + 1QZS, GPS + 2QZS, BDS, BDS + 2QZS, and BDS + GPS + 2QZS) for the 4.8 km baseline and the curves of the corresponding NOS, ADOP, and Bsrt are presented in
Figure 9. The mean values of NOS, PDOP, ADOP, success rate (both Asrt and Bsrt) and precision of different strategies are listed in
Table 5.
For the single GPS in case 2, the mean NOS is approximately 9.8, which is 1.7 more than that in case 1. Meanwhile, it can be found that the PDOP, ADOP, Bsrt, Asrt, and baseline precision (1.545, 0.326, 83.25%, 75.59%, and 1.33 cm, respectively) are all better compared with case 1. Especially, the Asrt of case 2 is two times that of case 1. This is mainly because there are more GPS satellites in case 2, and the length of the baseline in case 2 is shorter, Therefore, more superfluous measurements and fewer residual errors in DD measurements occurred, making the ambiguity resolution more successful. When the NOS of GPS in case 1 and case 2 both come to approximately 10, their Asrt values are almost equal to each other. When the number of QZS used increases from 0 to 2 the PDOP, ADOP, Bsrt, Asrt, and baseline precision are improved by 0.16, 0.97, 11.77%, 18.99%, and 0.08 cm, respectively. Since case 2 has better GPS resolution conditions (a greater NOS and shorter baseline) and fewer QZS, the improvement effect is smaller compared with case 1. For the single BDS in case 2, the mean NOS in increases to 12.1. The corresponding PDOP, ADOP, Bsrt, Asrt, and baseline precision are 1.973, 0.176, 99.05%, 99.83% and 1.34 cm, respectively. The PDOP and ADOP are respectively improved by 0.186 and 0.013, and Asrt is increased to 99.99% when 2 QZS were added. However, the baseline precision is still 1.34 cm without improvement because the Asrt of the single BDS is very high and little room is available for improvement if only two QZS are added. Undoubtedly, the integrated BDS/GPS/QZSS still has the best performance of the 6 indicators; the Asrt is 100% and baseline precision is improved to 1.03 cm. In case 1, the Bsrt of GPS is not consistent with Asrt, especially when the NOS is small.
Section 4.2 previously mentioned that the Bsrt could become inaccurate when DD residuals became larger with the increase of the baseline length, which leads to low precision of the float ambiguities. However, for the single GPS in case 2, its Bsrt is close to Asrt because more common satellites improved the quality of float ambiguities and increases the success rate of the ambiguity resolution.
Generally, both experiments indicate that not only the availability, PDOP and ADOP are well promoted, but also the success rate and baseline precision are effectively improved when GPS or BDS is augmented by QZSS. When more QZS are used, PDOP and ADOP decrease, the success rate and accuracy become higher and better. In addition, the performance of the single BDS in the two cases both precede that of the single GPS or even GPS/QZSS excluding PDOP because BDS has the advantages of NOS and satellites elevation.
6. Conclusions
In this paper, the current status of QZSS was introduced, and the carrier phase DD models of GPS/QZSS and BDS/QZSS were deduced for baseline resolution. A week of simulation on availability, PDOP, ADOP, and the Bsrt simulation was carried out for GPS/QZSS and BDS/QZSS based in the HKLT station. That QZSS brings about promotion of the NOS and ADOP can make up for the single GPS’s sustainability, reliability, and ambiguity resolution success rate especially under difficult conditions of high mask angles. Two cases of different baseline data were used to present the improvement in GPS and BDS SFSE baseline resolution when using QZSS data. Six indicators were introduced to exhibit the experimental results and two major conclusions were drawn: (1) BDS performs better than GPS in most indicators, excluding PDOP because BDS has more and higher-elevation satellites in the Asia-Pacific region. (2) The systems augmented by QZSS not only achieve a better performance in visibility and PDOP, but also achieve a great improvement in SFSE carrier phase DD ambiguity resolution such as ADOP and success rate. Moreover, the characteristics of ISBs between overlapping (GPS L1 and QZSS L1) and different frequencies (BDS B1 and QZSS L1) will be researched in future work.