Modeling Urban Collaborative Growth Dynamics Using a Multiscale Simulation Model for the Wuhan Urban Agglomeration Area, China
Abstract
:1. Introduction
2. Multiscale Simulation Model of the Urban Agglomeration Growth Dynamic
2.1. Macro-Scale Potential Sub-Model
2.2. Meso-Scale Intercity Sub-Model
2.3. Micro-Scale Cellular Sub-Mode
2.4. Multi-Scale Linking Model
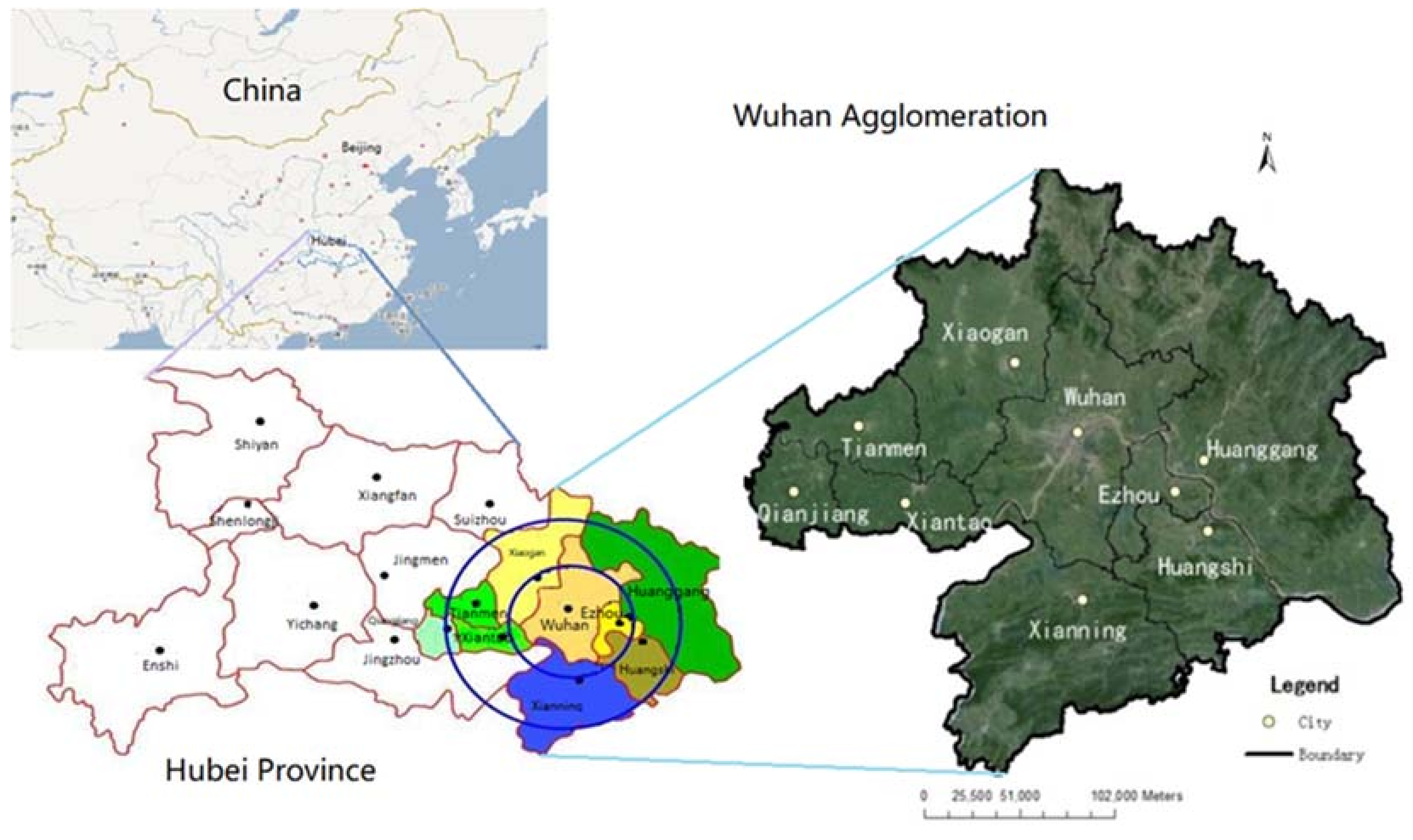
3. Study Area and Data
3.1. Study Area
3.2. Data
4. Results and Analysis
4.1. Result of New Urban Land Demand
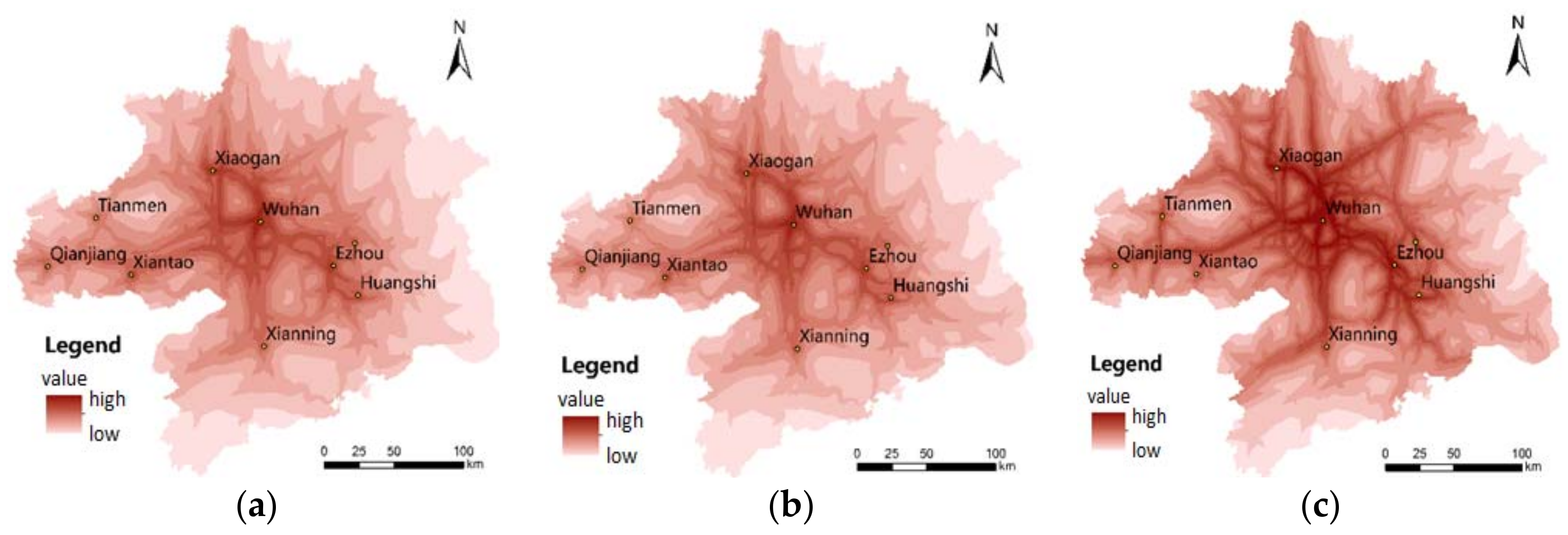
4.2. Result of Interaction
4.3. Simulation Result
4.3.1. Model Calibration
4.3.2. Evaluation the Goodness-of-Fit
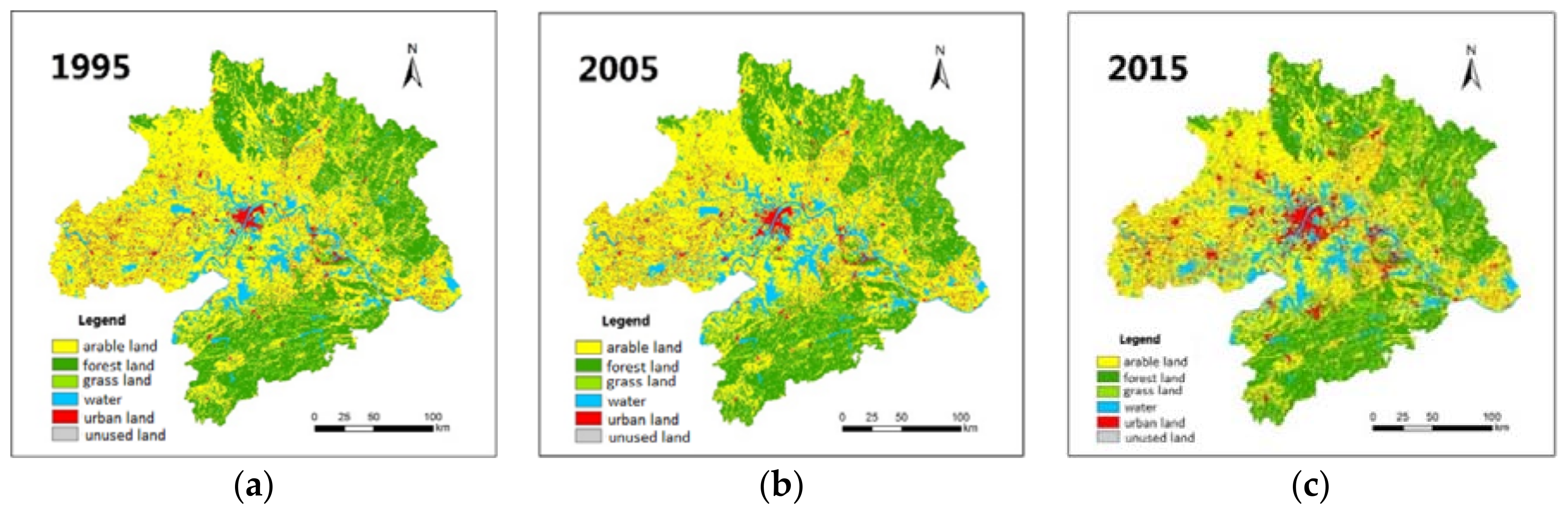
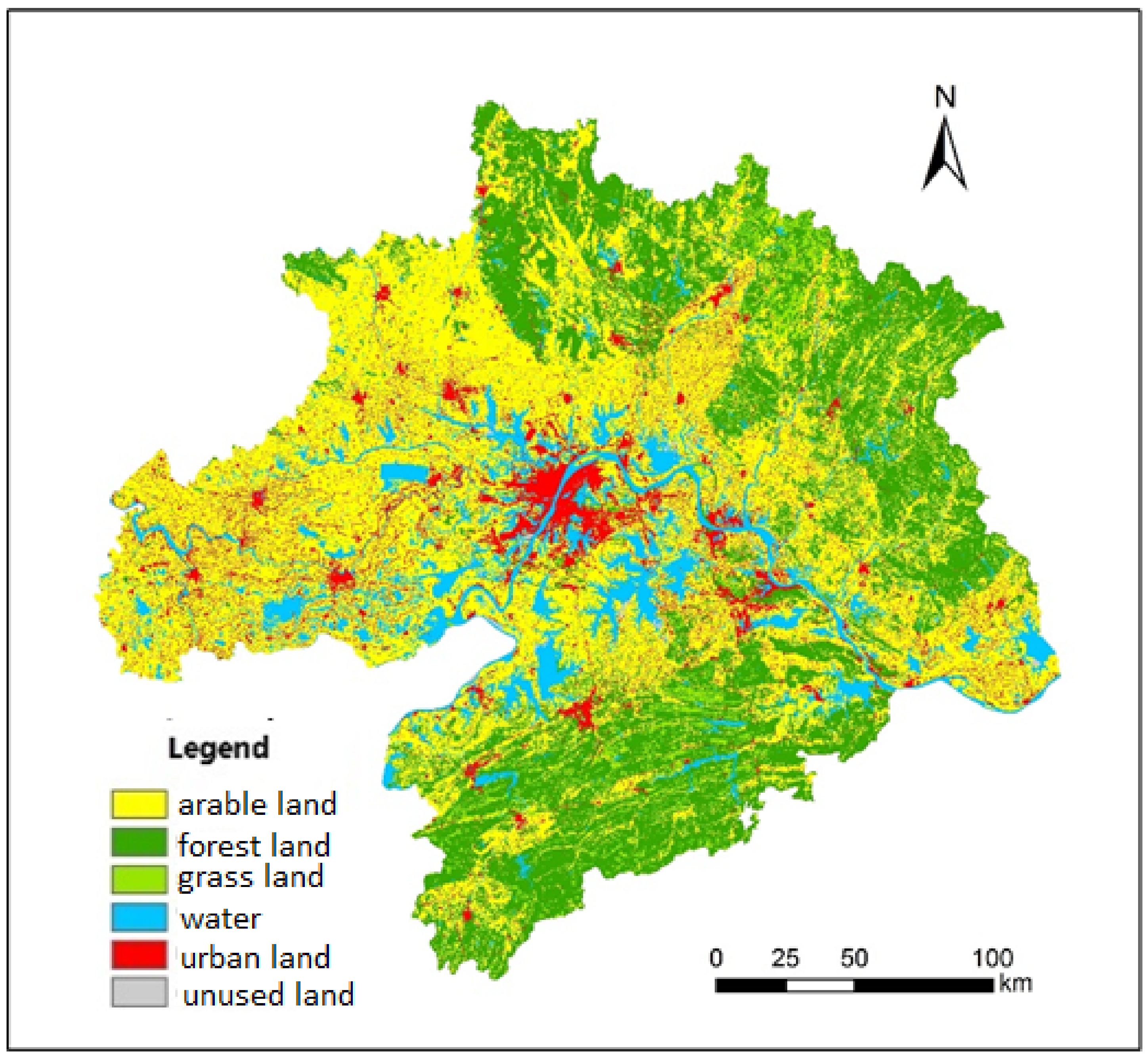
4.3.3. Simulation Results
5. Discussions
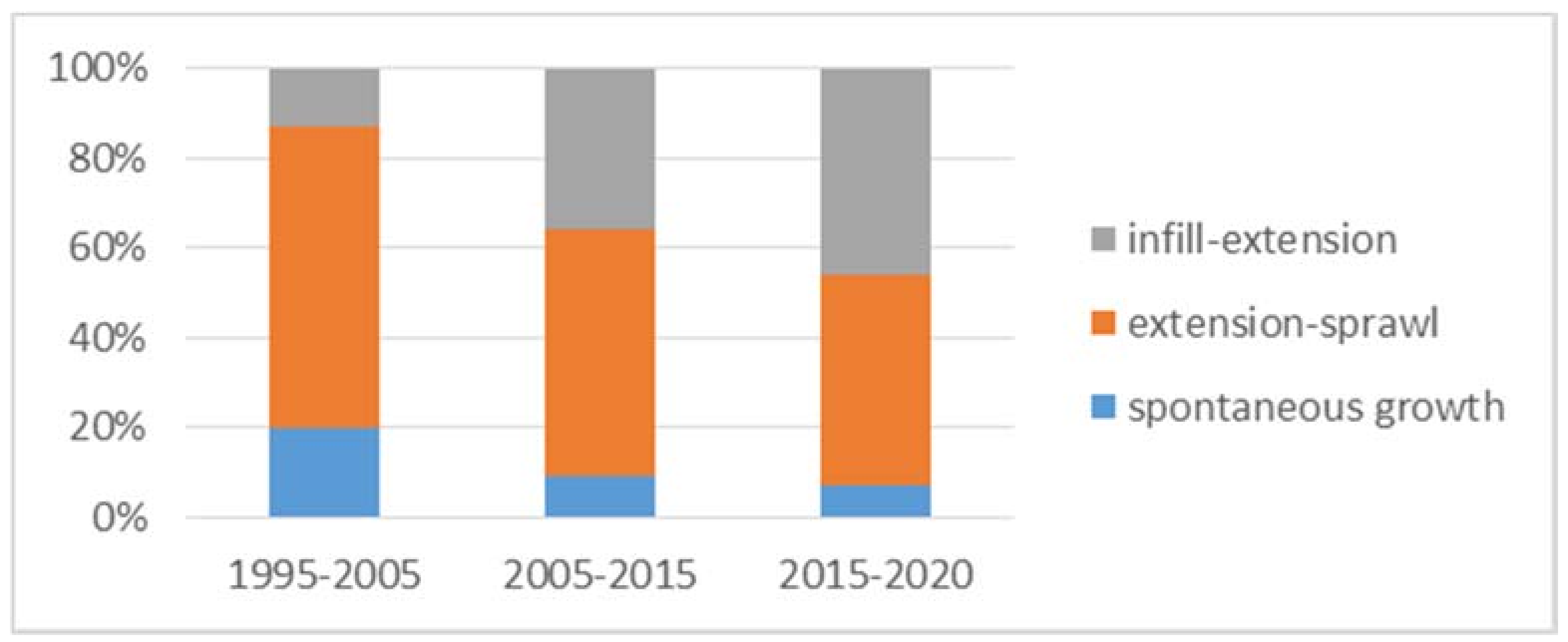
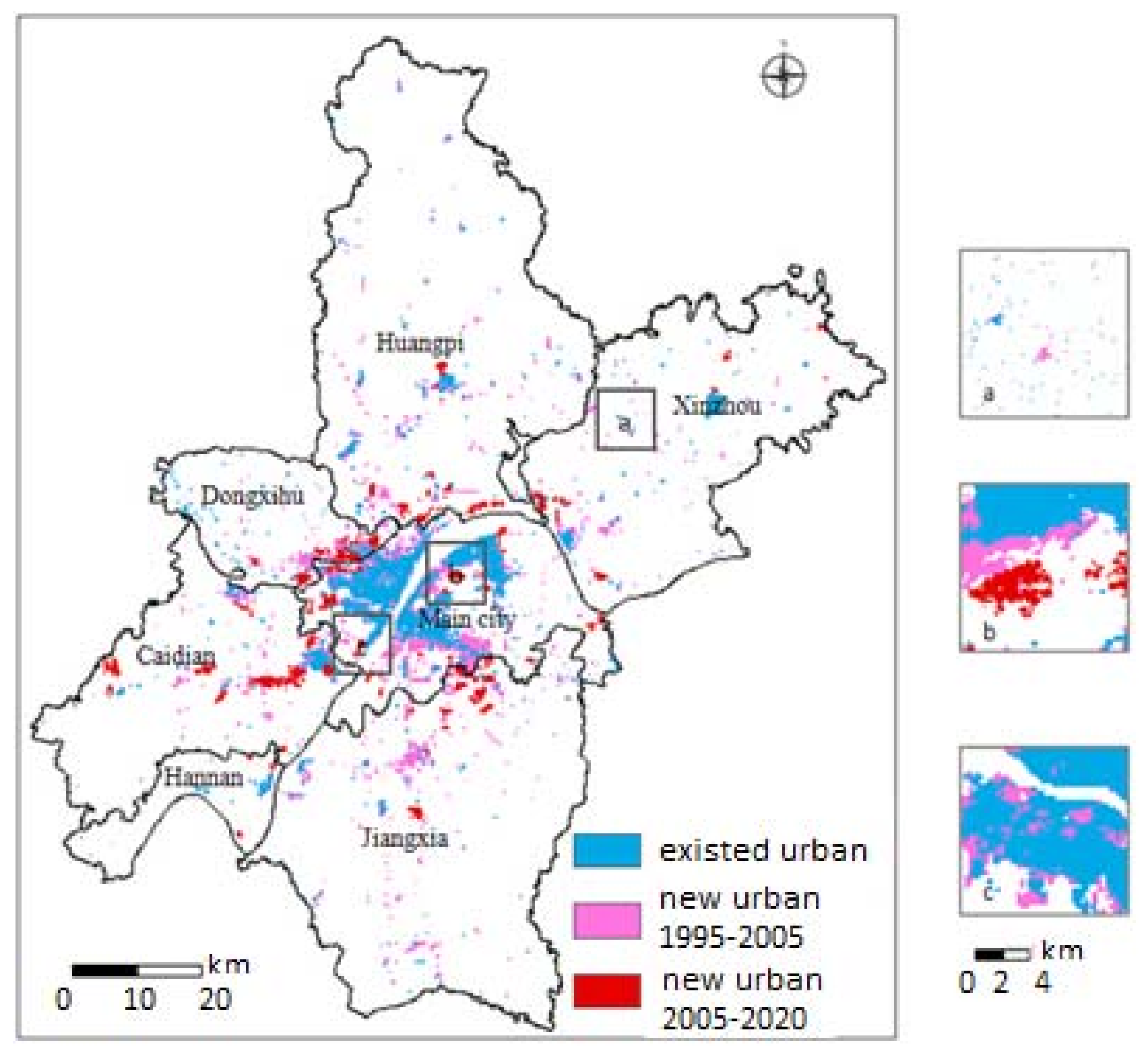
5.1. Urban Spatial Growth Transits from Sprawl to Compact Expansion
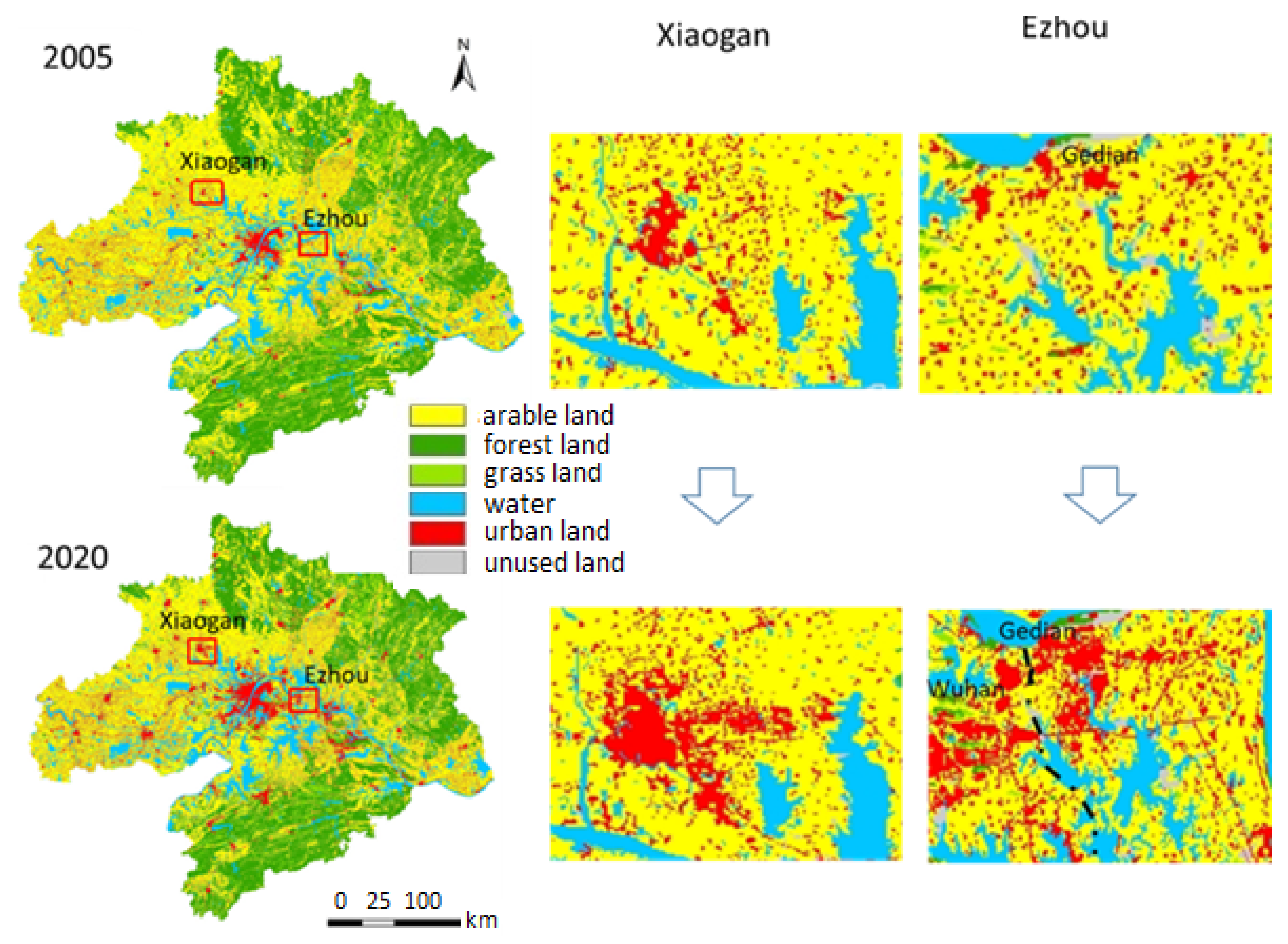
5.2. Intercity Interaction Promotes Urban Collaborative Expansion
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Huang, H.; Wei, Y.D. Intra-metropolitan location of foreign direct investment in Wuhan, China: Institution, urban structure, and accessibility. Appl. Geogr. 2014, 47, 78–88. [Google Scholar] [CrossRef]
- Lu, L.L.; Guo, H.D.; Wang, C.Z.; Pesaresi, M.; Ehrlich, D. Monitoring bidecadal development of urban agglomeration with remote sensing images in the Jing-Jin-Tang area, China. J. Appl. Remote Sens. 2014, 8, 084592. [Google Scholar] [CrossRef]
- UNDP in China. China National Human Development Report 2016. Available online: http://www.cn.undp.org/content/china/en/home/library/human_development/china-human-development-report-2016.html (accessed on 21 August 2018).
- Zhu, Z.; Zheng, B.H. Study on spatial structure of Yangtze River Delta urban agglomeration and its effects on urban and rural regions. J. Urban Plan. Dev. 2012, 138, 78–89. [Google Scholar]
- Xie, Y.C.; Fan, S.Y. Multi-city sustainable regional urban growth simulation-MSRUGS: A case study along the mid-section of Silk Road of China. Stoch. Environ. Res. Risk Assess 2014, 28, 829–841. [Google Scholar] [CrossRef]
- Hosseinali, F.; Alesheikh, A.A.; Nourian, F. Agent-based modeling of urban land-use development, case study: Simulating future scenarios of Qazvin city. Cities 2013, 31, 105–113. [Google Scholar] [CrossRef]
- Liu, X.P.; Ma, L.; Li, X.; Ai, B.; Li, S.Y.; He, Z.J. Simulating urban growth by integrating landscape expansion index (LEI) and cellular automata. Int. J. Geogr. Inf. Sci. 2014, 28, 148–163. [Google Scholar] [CrossRef]
- Clarke, K.C.; Hoppen, S.; Gaydos, J. A self-modifying cellular automatonmodel of historical urbanization in the San Francisco Bay Area. Environ. Plan. B 1997, 24, 247–261. [Google Scholar] [CrossRef]
- De Kok, J.L.; Engelen, G.; White, R.; Wind, H.G. Modeling land-use change in a decision-support system for coastal-zone management. Environ. Model. Assess. 2001, 6, 123–132. [Google Scholar] [CrossRef]
- Fang, S.; Gertner, G.Z.; Sun, Z.; Anderson, A.A. The impact of interactions in spatial simulation of the dynamics of urban sprawl. Landsc. Urban Plan. 2005, 73, 294–306. [Google Scholar] [CrossRef]
- Meentemeyer, R.K.; Tang, W.W.; Dorning, M.A.; Vogler, J.B.; Cunniffe, N.J.; Shoemaker, D.A. FUTURES: Multilevel simulations of emerging urban-rural landscape structure using a stochastic patch-growing algorithm. Ann. Assoc. Am. Geogr. 2013, 103, 785–807. [Google Scholar] [CrossRef]
- Soranno, P.A.; Cheruvelil, K.S.; Bissell, E.G.; Bremigan, M.T.; Downing, J.A.; Fergus, C.E.; Filstrup, C.T.; Henry, E.N.; Lottig, N.R.; Stanley, E.H.; et al. Cross-scale interactions: Quantifying multi-scaled cause–effect relationships in macrosystems. Front. Ecol. Environ. 2014, 12, 65–73. [Google Scholar] [CrossRef]
- Liu, X.J.; Derudder, B.; Wang, M. Polycentric urban development in China: A multi-scale analysis. Environ. Plan. B 2017. [Google Scholar] [CrossRef]
- Jiang, L.; Deng, X.Z.; Seto, K.C. Multi-level modeling of urban expansion and cultivated land conversion for urban hotspot counties in China. Landsc. Urban Plan. 2012, 108, 131–139. [Google Scholar] [CrossRef]
- Overmars, K.P.; Verburg, P.H. Multilevel modelling of land use from field to village level in the Philippines. Agric. Syst. 2006, 89, 435–456. [Google Scholar] [CrossRef]
- Tang, W.; Malanson, G.P.; Entwisle, B. Simulated village locations in Thailand: A multi-scale model including a neural network approach. Landsc. Ecol. 2009, 24, 557–575. [Google Scholar] [CrossRef] [PubMed]
- Chaudhuri, G.; Clarke, K.C. Temporal accuracy in urban growth forecasting: A study using the SLEUTH model. Trans. GIS 2014, 18, 302–320. [Google Scholar] [CrossRef]
- Feng, Y.J.; Liu, Y. A heuristic cellular automata approach for modelling urban land-use change based on simulated annealing. Int. J. Geogr. Inf. Sci. 2013, 27, 449–466. [Google Scholar] [CrossRef]
- Feng, Y.J.; Liu, Y.; Tong, X.H.; Liu, M.L.; Deng, S.S. Modeling dynamic urban growth using cellular automata and particle swarm optimization rules. Landsc. Urban Plan. 2011, 102, 188–196. [Google Scholar] [CrossRef]
- Liu, X.J. Exploring the joint dynamics of intercity internet and corporate networks: A stochastic actor-based modelling approach. Glob. Netw. 2014, 14, 167–187. [Google Scholar] [CrossRef]
- Rimal, B.; Zhang, L.F.; Keshtkar, H.; Barry, N.; Sushila, R.; Zhang, P. Land use/Land cover dynamics and modeling of urban land expansion by the integration of cellular automata and markov chain. ISPRS Int. J. Geo-Inf. 2018, 7, 154. [Google Scholar] [CrossRef]
- Yao, Y.; Li, J.; Zhang, X.; Duan, P.; Li, S.; Xu, Q. Investigation on the expansion of urban construction land use based on the CART-CA model. ISPRS Int. J. Geo-Inf. 2017, 6, 149. [Google Scholar] [CrossRef]
- He, C.Y.; Zhao, Y.Y.; Tian, J.; Shi, P.J. Modeling the urban landscape dynamics in a megalopolitan cluster area by incorporating a gravitational field model with cellular automata. Landsc. Urban Plan. 2013, 113, 78–89. [Google Scholar] [CrossRef]
- Lagarias, A. Urban sprawl simulation linking macro-scale processes to micro-dynamics through cellular automata, an application in Thessaloniki, Greece. Appl. Geogr. 2012, 34, 146–160. [Google Scholar] [CrossRef]
- Li, X. Emergence of bottom-up models as a tool for landscape simulation and planning. Landsc. Urban Plan. 2011, 100, 393–395. [Google Scholar] [CrossRef]
- Zeng, C.; Zhang, M.D.; Cui, J.X.; He, S.W. Monitoring and modeling urban expansion—A spatially explicit and multi-scale perspective. Cities 2015, 43, 92–103. [Google Scholar] [CrossRef]
- Tan, R.H.; Liu, Y.L.; Zhou, K.H.; Tang, W. A game-theory based agent-cellular model for use in urban growth simulation: A case study of the rapidly urbanizing Wuhan area of central China. Comput. Environ. Urban Syst. 2015, 49, 15–29. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, Y.L.; Liu, D.F.; Ma, X.Y. AITSO: A tool for spatial optimization based on artificial immune systems. Comput. Intell. Neurosci. 2015, 2015, 13. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.P.; Hu, G.; Ai, B.; Li, X.; Tian, G.; Chen, Y.M.; Li, S.S. Simulating urban dynamics in China using a gradient cellular automata model based on S-shaped curve evolution characteristics. Int. J. Geogr. Inf. Sci. 2018, 32, 73–101. [Google Scholar] [CrossRef]
- Verburg, P.H.; de Koning, G.H.J.; Kok, K.; Veldkamp, A.; Bouma, J. A spatial explicit allocation procedure for modelling the pattern of land use change based upon actual land use. Ecol. Model. 1999, 116, 45–61. [Google Scholar] [CrossRef]
- Wu, W.J.; Zhang, W.Z.; Jin, F.J.; Deng, Y. Spatio-temporal Analysis of Urban Spatial Interaction in Globalizing China—A Case Study of Beijing-Shanghai Corridor. Chin. Geogr. Sci. 2009, 19, 126–134. [Google Scholar] [CrossRef]
- Xu, C.; Liu, M.S.; Zhang, C.; An, S.Q.; Yu, W.; Chen, J.M. The spatiotemporal dynamics of rapid urban growth in the Nanjing metropolitan region of China. Landsc. Ecol. 2007, 22, 925–937. [Google Scholar] [CrossRef]
- Li, X.; Yeh, A.G. Neural-network-based cellular automata for simulating multiple land use changes using GIS. Int. J. Geogr. Inf. Sci. 2002, 16, 323–343. [Google Scholar] [CrossRef]
- Wu, F.; Webster, C.J. Simulation of natural land use zoning under free-market and incremental development control regimes. Comput. Environ. Urban Syst. 1998, 22, 241–256. [Google Scholar] [CrossRef]
- He, J.H.; Wang, X.J.; Du, C.; Li, C.; Shi, X. Land use simulation and driving forces analysis of Wuhan urban agglomeration. Yangtz River Res. Environ. 2015, 24, 1270–1278. (In Chinese) [Google Scholar]
- He, J.H.; Li, C.; Yu, Y.; Liu, Y.L.; Huang, J.L. Measuring urban spatial interaction in Wuhan urban agglomeration, central China: A spatial explicitly approach. Sustain. Cities Soc. 2017, 32, 569–583. [Google Scholar] [CrossRef]
- Wu, F.L. Calibration of stochastic cellular automata: The application to rural-urban land conversions. Int. J. Geogr. Inf. Sci. 2002, 16, 795–818. [Google Scholar] [CrossRef]

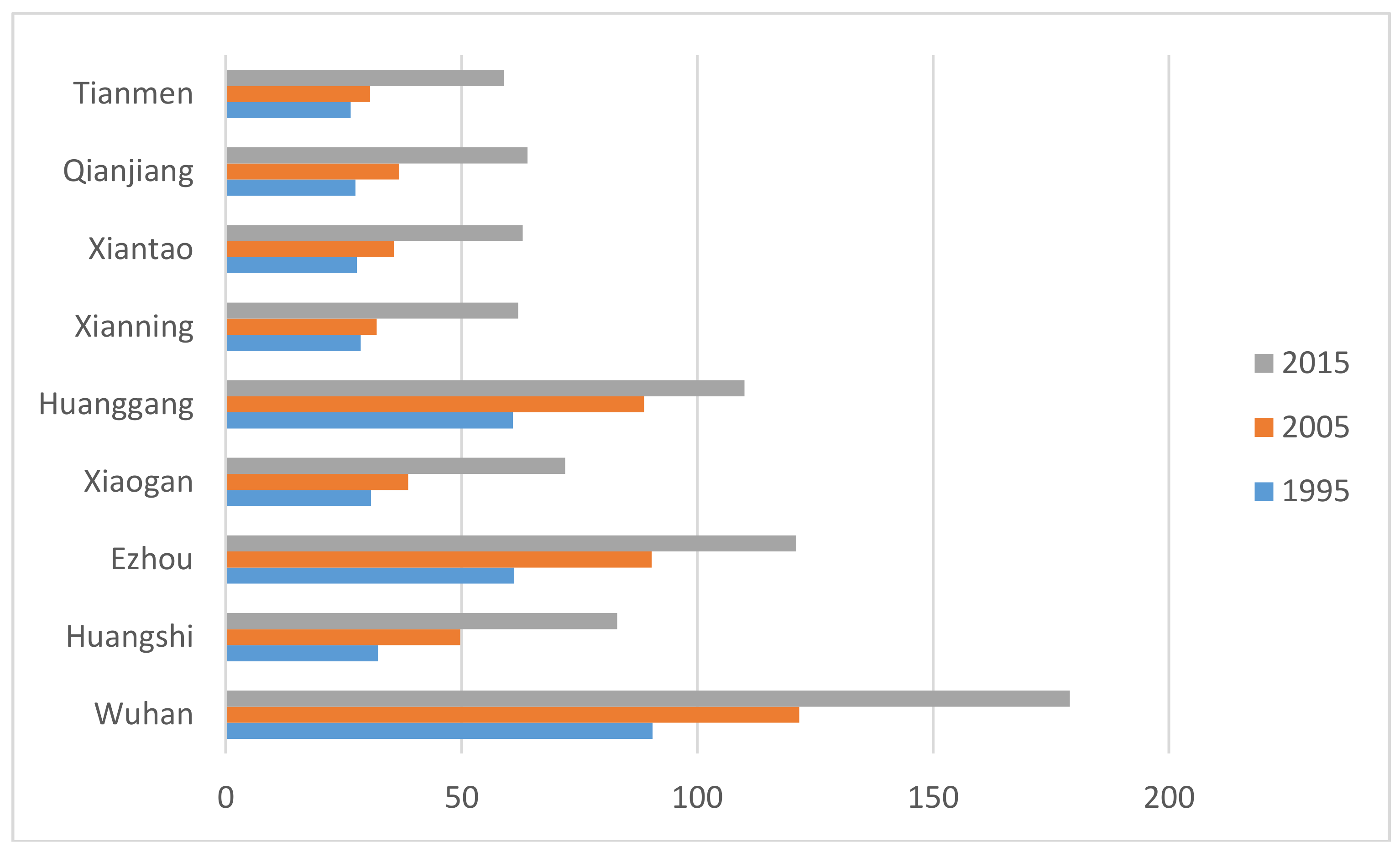
| Wuhan | Huangshi | Huanggang | Xiaogan | Xianning | Tianmen | Ezhou | Qianjiang | Xiantao | |
|---|---|---|---|---|---|---|---|---|---|
| Urban land (Km2) | 602.52 | 64.37 | 172.12 | 131.66 | 99.02 | 49.97 | 59.86 | 56.67 | 62.40 |
| PD | 7.03 | 1.41 | 0.99 | 1.48 | 1.02 | 1.91 | 3.75 | 2.85 | 2.48 |
| Arable Land | Grass Land | Forest Land | Urban Land | Water | Unused Land | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| β | p | β | p | β | p | β | p | β | p | β | p | |
| Soil | 0.041 | 0.0012 | 0.030 | 0.0012 | 0.005 | 0.0013 | 0 | 0 | 0 | 0 | 0.037 | 0.0081 |
| Elevation | −0.006 | 0.0027 | 0.011 | 0.0021 | 0.015 | 0.0024 | −0.052 | 0.0003 | 0.004 | 0.0262 | 0.052 | 0.0052 |
| Slope | −0.039 | 0.0016 | 0.004 | 0.0016 | 0.009 | 0.0061 | −0.171 | 0.0025 | 0.007 | 0.0353 | 0.071 | 0.0102 |
| Hydrology | −0.019 | 0.0038 | −0.012 | 0.0009 | 0 | 0 | 0.006 | 0.0045 | 0.013 | 0.0185 | 0.011 | 0.0317 |
| Geology | 0 | 0 | 0.002 | 0.0023 | 0 | 0 | 0.359 | 0.0087 | 0.002 | 0.0423 | 0.007 | 0.0052 |
| Distance to main center | −0.095 | 0.0016 | −0.019 | 0.0047 | 0.017 | 0.0057 | −0.621 | 0.0139 | 0.006 | 0.0313 | −0.012 | 0.0009 |
| Distance to sub-center | −0.047 | 0.0029 | −0.008 | 0.0050 | 0.022 | 0.0012 | −0.271 | 0.0061 | 0.003 | 0.0227 | −0.014 | 0.0014 |
| Distance to road | −0.052 | 0.0028 | −0.015 | 0.0067 | 0.010 | 0.0006 | −0.421 | 0.0063 | 0.011 | 0.0165 | −0.026 | 0.0007 |
| Distance to railway | 0 | 0 | 0 | 0 | 0.005 | 0.001 | −0.052 | 0.0216 | 0.004 | 0.0292 | 0.012 | 0.0102 |
| Constant | 0.273 | 0.0467 | 0.625 | 0.0132 | −0.385 | 0.0432 | 0.329 | 0.0116 | 0.721 | 0.0312 | 0.532 | 0.0391 |
| Arable | Grass Land | Forest | Constructive | Water | Unused | |
|---|---|---|---|---|---|---|
| Kappa index | 0.81 | 0.89 | 0.86 | 0.82 | 0.91 | 0.79 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; He, J.; Tang, W.; Li, C. Modeling Urban Collaborative Growth Dynamics Using a Multiscale Simulation Model for the Wuhan Urban Agglomeration Area, China. ISPRS Int. J. Geo-Inf. 2018, 7, 176. https://doi.org/10.3390/ijgi7050176
Yu Y, He J, Tang W, Li C. Modeling Urban Collaborative Growth Dynamics Using a Multiscale Simulation Model for the Wuhan Urban Agglomeration Area, China. ISPRS International Journal of Geo-Information. 2018; 7(5):176. https://doi.org/10.3390/ijgi7050176
Chicago/Turabian StyleYu, Yan, Jianhua He, Wenwu Tang, and Chun Li. 2018. "Modeling Urban Collaborative Growth Dynamics Using a Multiscale Simulation Model for the Wuhan Urban Agglomeration Area, China" ISPRS International Journal of Geo-Information 7, no. 5: 176. https://doi.org/10.3390/ijgi7050176
APA StyleYu, Y., He, J., Tang, W., & Li, C. (2018). Modeling Urban Collaborative Growth Dynamics Using a Multiscale Simulation Model for the Wuhan Urban Agglomeration Area, China. ISPRS International Journal of Geo-Information, 7(5), 176. https://doi.org/10.3390/ijgi7050176





