Multi-Temporal Land Cover Classification with Sequential Recurrent Encoders
Abstract
1. Introduction
- (i)
- the adaptation of sequence encoders from the field of sequence-to-sequence learning to Earth observation (EO),
- (ii)
- a visualization of internal gate activations on a sequence of satellite observations and,
- (iii)
- the application of crop classification over two seasons.
2. Related Work
3. Methodology
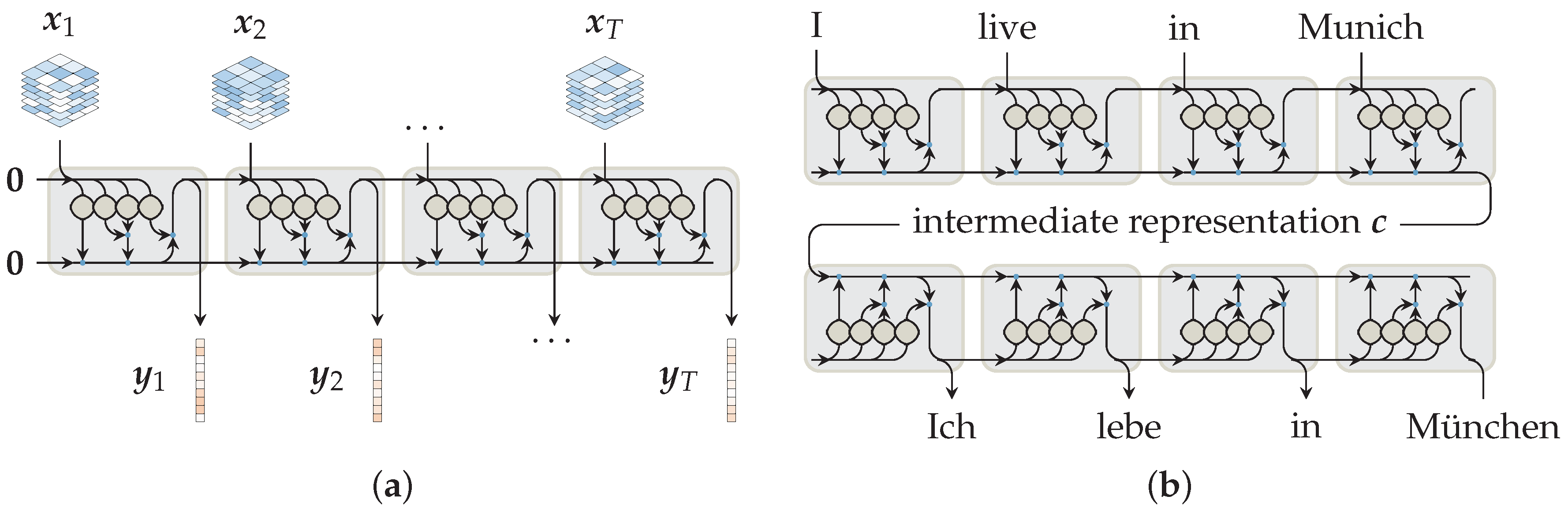
3.1. Network Architectures and Sequential Encoders
3.2. Prior Work
3.3. This Approach
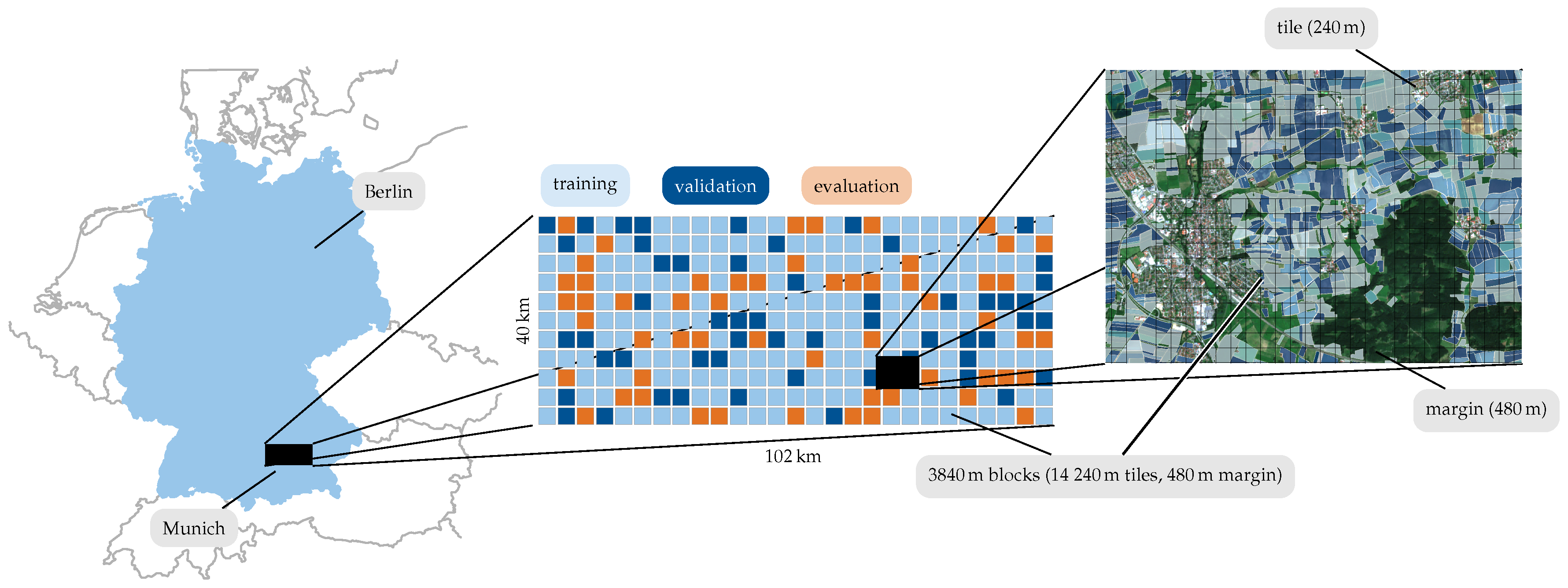
4. Dataset
5. Results
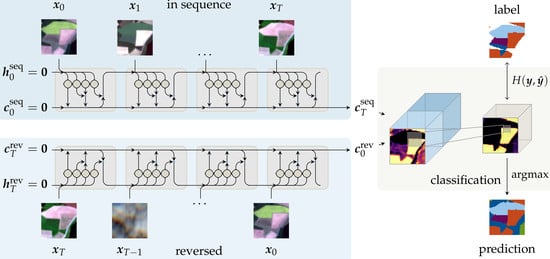
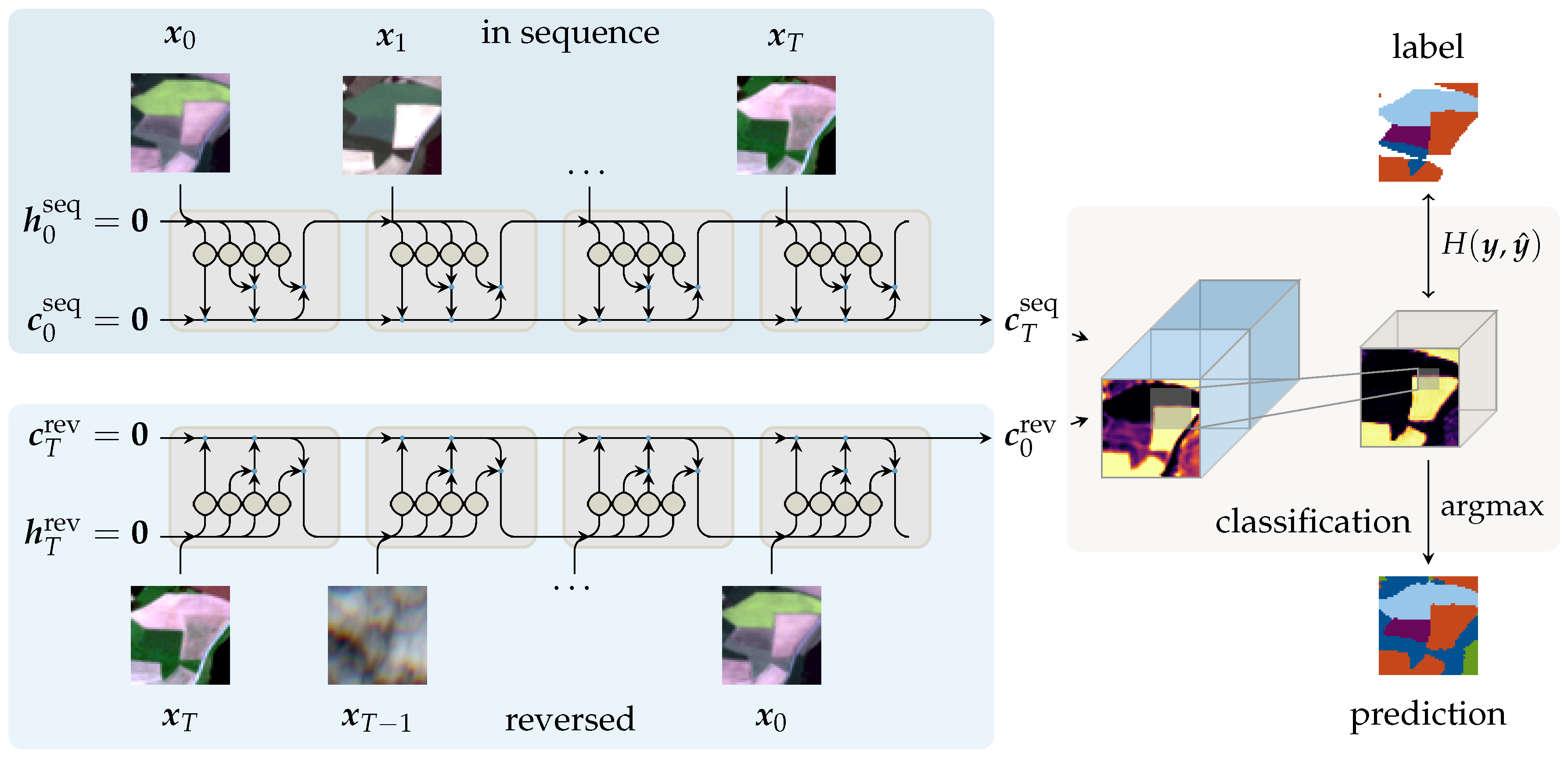
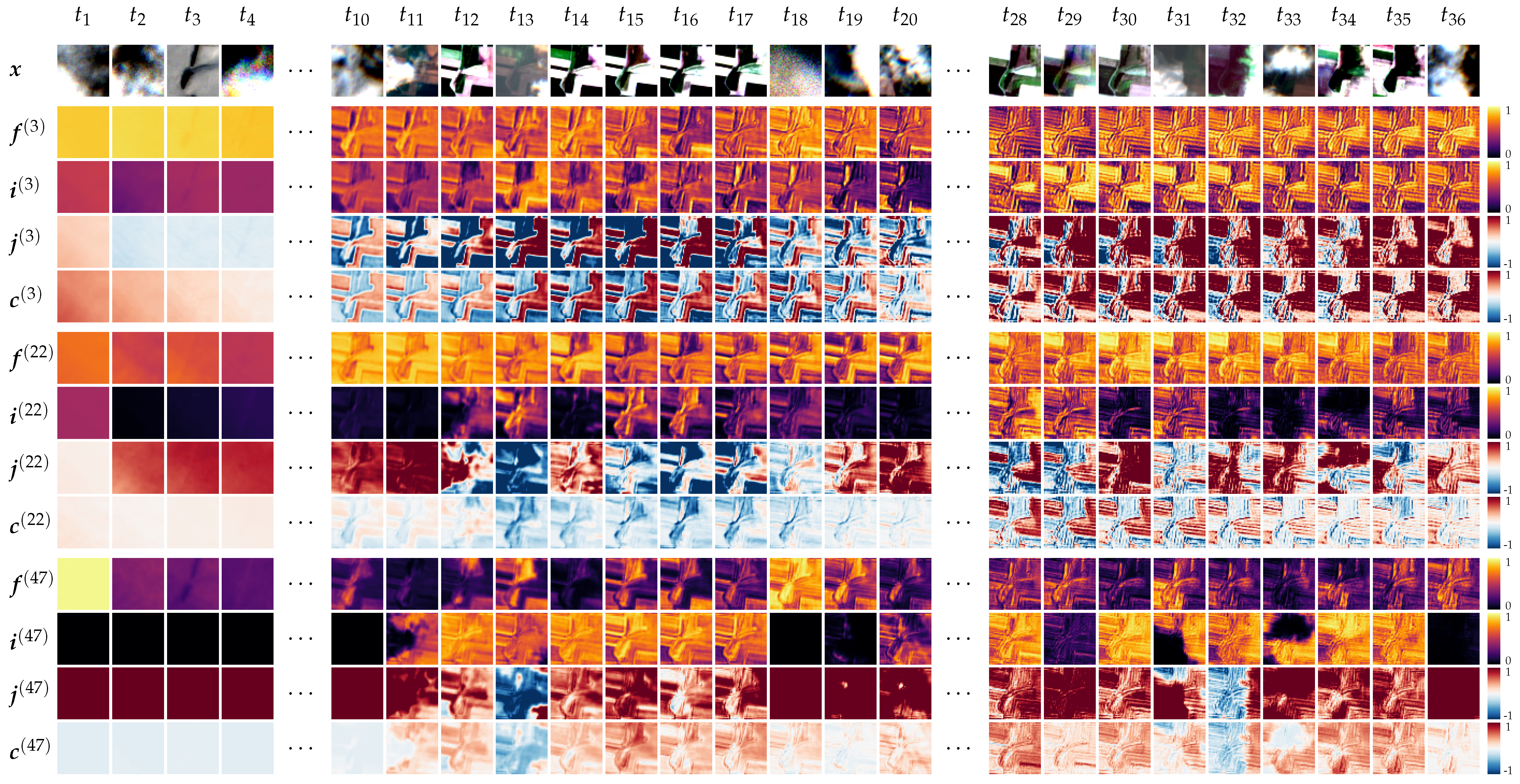
5.1. Internal Network Activations
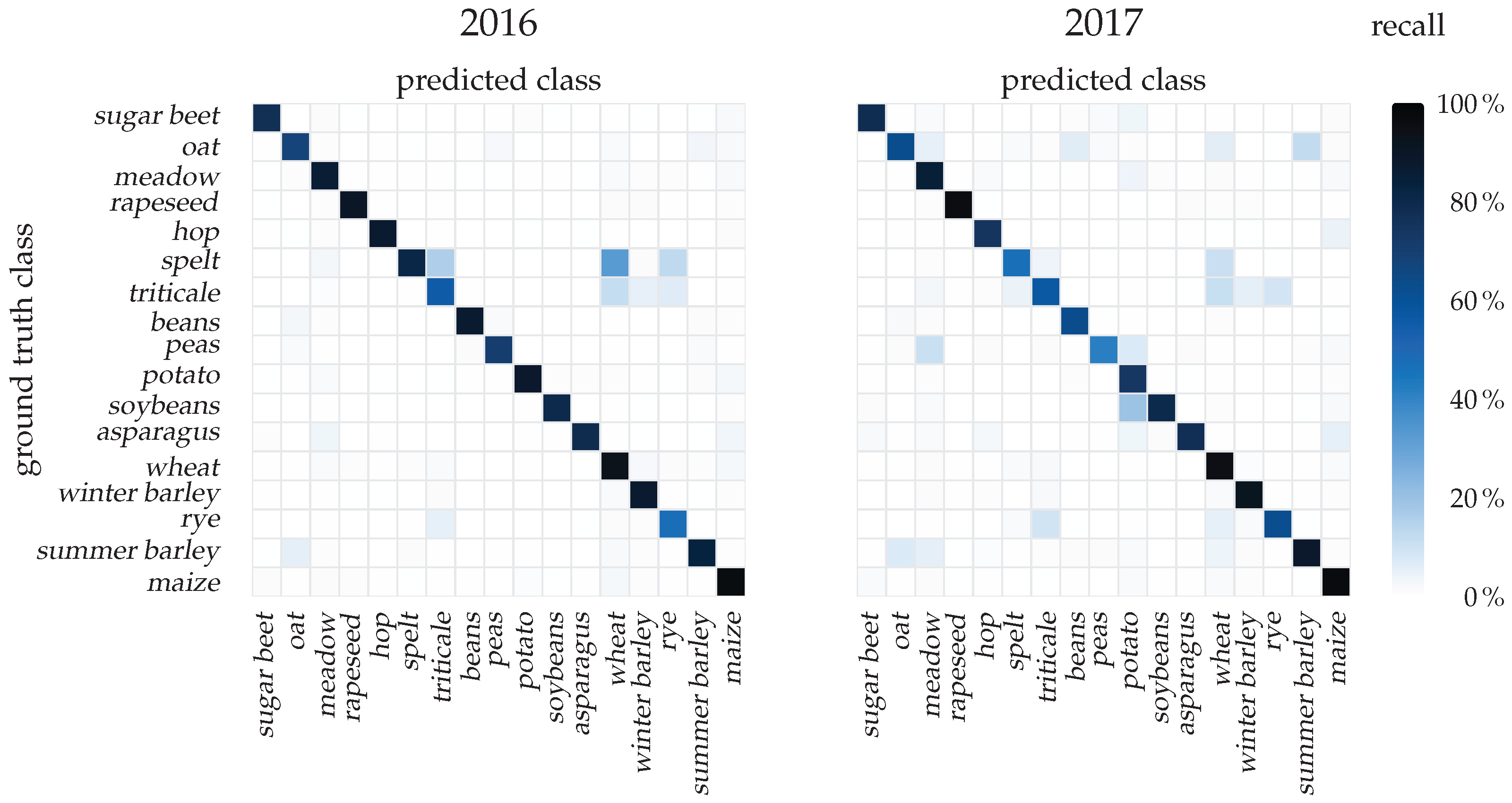
5.2. Quantitative Classification Evaluation
5.3. Qualitative Classification Evaluation
6. Discussion
7. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, L.; Zhang, Q.; Du, B.; Huang, X.; Tang, Y.Y.; Tao, D. Simultaneous Spectral-Spatial Feature Selection and Extraction for Hyperspectral Images. IEEE Trans. Cybern. 2018, 48, 16–28. [Google Scholar] [CrossRef] [PubMed]
- Odenweller, J.B.; Johnson, K.I. Crop identification using Landsat temporal-spectral profiles. Remote Sens. Environ. 1984, 14, 39–54. [Google Scholar] [CrossRef]
- Reed, B.C.; Brown, J.F.; VanderZee, D.; Loveland, T.R.; Merchant, J.W.; Ohlen, D.O. Measuring Phenological Variability from Satellite Imagery. J. Veg. Sci. 1994, 5, 703–714. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. arXiv, 2014; arXiv:1409.0473v7. [Google Scholar]
- Rush, A.; Chopra, S.; Weston, J. A Neural Attention Model for Sentence Summarization. arXiv, 2017; arXiv:1509.00685v2. [Google Scholar]
- Shen, S.; Liu, Z.; Sun, M. Neural Headline Generation with Minimum Risk Training. arXiv, 2016; arXiv:1604.01904v1. [Google Scholar]
- Nallapati, R.; Zhou, B.; dos Santos, C.N.; Gulcehre, C.; Xiang, B. Abstractive Text Summarization Using Sequence-to-Sequence RNNs and Beyond. arXiv, 2016; arXiv:1602.06023v5. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. arXiv, 2014; arXiv:1409.3215v3. [Google Scholar]
- Chorowski, J.; Bahdanau, D.; Serdyuk, D.; Cho, K.; Bengio, Y. Attention-based models for speech recognition. Adv. Neural Inf. Process. Syst. 2015, 1, 557–585. [Google Scholar]
- Foerster, S.; Kaden, K.; Foerster, M.; Itzerott, S. Crop type mapping using spectral-temporal profiles and phenological information. Comput. Electron. Agric. 2012, 89, 30–40. [Google Scholar] [CrossRef]
- Conrad, C.; Fritsch, S.; Zeidler, J.; Rücker, G.; Dech, S. Per-Field Irrigated Crop Classification in Arid Central Asia Using SPOT and ASTER Data. Remote Sens. 2010, 2, 1035–1056. [Google Scholar] [CrossRef]
- Conrad, C.; Dech, S.; Dubovyk, O.; Fritsch, S.; Klein, D.; Löw, F.; Schorcht, G.; Zeidler, J. Derivation of temporal windows for accurate crop discrimination in heterogeneous croplands of Uzbekistan using multitemporal RapidEye images. Comput. Electron. Agric. 2014, 103, 63–74. [Google Scholar] [CrossRef]
- Hao, P.; Zhan, Y.; Wang, L.; Niu, Z.; Shakir, M. Feature Selection of Time Series MODIS Data for Early Crop Classification Using Random Forest: A Case Study in Kansas, USA. Remote Sens. 2015, 7, 5347–5369. [Google Scholar] [CrossRef]
- Peña-Barragán, J.M.; Ngugi, M.K.; Plant, R.E.; Six, J. Object-based crop identification using multiple vegetation indices, textural features and crop phenology. Remote Sens. Environ. 2011, 115, 1301–1316. [Google Scholar] [CrossRef]
- Siachalou, S.; Mallinis, G.; Tsakiri-Strati, M. A hidden markov models approach for crop classification: Linking crop phenology to time series of multi-sensor remote sensing data. Remote Sens. 2015, 7, 3633–3650. [Google Scholar] [CrossRef]
- Hoberg, T.; Rottensteiner, F.; Feitosa, R.Q.; Heipke, C. Conditional random fields for multitemporal and multiscale classification of optical satellite imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 659–673. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep Learning for Remote Sensing Data: A Technical Tutorial on the State of the Art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Hu, F.; Xia, G.S.; Hu, J.; Zhang, L. Transferring Deep Convolutional Neural Networks for the Scene Classification of High-Resolution Remote Sensing Imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Scott, G.J.; England, M.R.; Starms, W.A.; Marcum, R.A.; Davis, C.H. Training Deep Convolutional Neural Networks for Land-Cover Classification of High-Resolution Imagery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 549–553. [Google Scholar] [CrossRef]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep Supervised Learning for Hyperspectral Data Classification through Convolutional Neural Networks. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (GARSS), Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Castelluccio, M.; Poggi, G.; Sansone, C.; Verdoliva, L. Land Use Classification in Remote Sensing Images by Convolutional Neural Networks. arXiv, 2015; arXiv:1508.00092. [Google Scholar]
- Lyu, H.; Lu, H.; Mou, L. Learning a Transferable Change Rule from a Recurrent Neural Network for Land Cover Change Detection. Remote Sens. 2016, 8, 506. [Google Scholar] [CrossRef]
- Jia, X.; Khandelwal, A.; Nayak, G.; Gerber, J.; Carlson, K.; West, P.; Kumar, V. Incremental Dual-memory LSTM in Land Cover Prediction. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 867–876. [Google Scholar]
- Mou, L.; Bruzzone, L.; Zhu, X.X. Learning Spectral-Spatial-Temporal Features via a Recurrent Convolutional Neural Network for Change Detection in Multispectral Imagery. arXiv, 2018; arXiv:1803.02642v1. [Google Scholar]
- Braakmann-Folgmann, A.; Roscher, R.; Wenzel, S.; Uebbing, B.; Kusche, J. Sea Level Anomaly Prediction using Recurrent Neural Networks. arXiv, 2017; arXiv:1710.07099v1. [Google Scholar]
- Sharma, A.; Liu, X.; Yang, X. Land Cover Classification from Multi-temporal, Multi-spectral Remotely Sensed Imagery using Patch-Based Recurrent Neural Networks. arXiv, 2017; arXiv:1708.00813v1. [Google Scholar]
- Rußwurm, M.; Körner, M. Temporal Vegetation Modelling using Long Short-Term Memory Networks for Crop Identification from Medium-Resolution Multi-Spectral Satellite Images. In Proceedings of the IEEE/ISPRS Workshop on Large Scale Computer Vision for Remote Sensing Imagery (EarthVision), Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Graves, A.; Wayne, G.; Danihelka, I. Neural Turing Machines. arXiv, 2014; arXiv:1410.5401v2. [Google Scholar]
- Siegelmann, H.; Sontag, E. On the Computational Power of Neural Nets. J. Comput. Syst. Sci. 1995, 50, 132–150. [Google Scholar] [CrossRef]
- Rafal, J.; Wojciech, Z.; Ilya, S. An Empirical Exploration of Recurrent Network Architectures. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015; Volume 7, pp. 2342–2350. [Google Scholar]
- Hochreiter, S.; Bengio, Y.; Frasconi, P.; Schmidhuber, J. Gradient flow in recurrent nets: The difficulty of learning long-term dependencies. In A Field Guide to Dynamical Recurrent Networks; IEEE Press: New York, NY, USA, 2001; pp. 237–243. [Google Scholar]
- Yoshua, B.; Patrice, S.; Paolo, F. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. arXiv, 2014; arXiv:1406.1078v3. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. Adv. Neural Inf. Process. Syst. 2015, 1, 802–810. [Google Scholar]
- Hahnloser, R.; Sarpeshkar, R.; Mahowald, M.A.; Douglas, R.J.; Seung, H.S. Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. Nature 2000, 405, 947–951. [Google Scholar] [CrossRef] [PubMed]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier Nonlinearities Improve Neural Network Acoustic Models. Proc. Int. Conf. Mach. Learn. 2013, 28, 6. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. arXiv, 2014; arXiv:1412.6980v9. [Google Scholar]
- Cohen, J. A coefficient of agreeement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Karpathy, A.; Johnson, J.; Fei-Fei, L. Visualizing and Understanding Recurrent Networks. arXiv, 2015; arXiv:1506.02078. [Google Scholar]
- Fung, T.; Ledrew, E. The Determination of Optimal Threshold Levels for Change Detection Using Various Accuracy Indices. Photogramm. Eng. Remote Sens. 1988, 54, 1449–1454. [Google Scholar]
- McHugh, M.L. Interrater reliability: the kappa statistic. Biochem. Med. 2012, 22, 276–282. [Google Scholar] [CrossRef]
- Ünsalan, C.; Boyer, K.L. Review on Land Use Classification. In Multispectral Satellite Image Understanding: From Land Classification to Building and Road Detection; Springer: London, UK, 2011; pp. 49–64. [Google Scholar]
- Richter, R. A spatially adaptive fast atmospheric correction algorithm. Int. J. Remote Sens. 1996, 17, 1201–1214. [Google Scholar] [CrossRef]
- Matthew, M.W.; Adler-Golden, S.M.; Berk, A.; Richtsmeier, S.C.; Levine, R.Y.; Bernstein, L.S.; Acharya, P.K.; Anderson, G.P.; Felde, G.W.; Hoke, M.P. Status of Atmospheric Correction using a MODTRAN4-Based Algorithm. In Proceedings of the SPIE Algorithms for Multispectral, Hyperspectral, and Ultra-Spectral Imagery VI, Orlando, FL, USA, 16–20 April 2000; pp. 199–207. [Google Scholar]
- Hagolle, O.; Huc, M.; Villa Pascual, D.; Dedieu, G. A multi-temporal method for cloud detection, applied to FORMOSAT-2, VENuS, LANDSAT and SENTINEL-2 images. Remote Sens. Environ. 2010, 114, 1747–1755. [Google Scholar] [CrossRef]
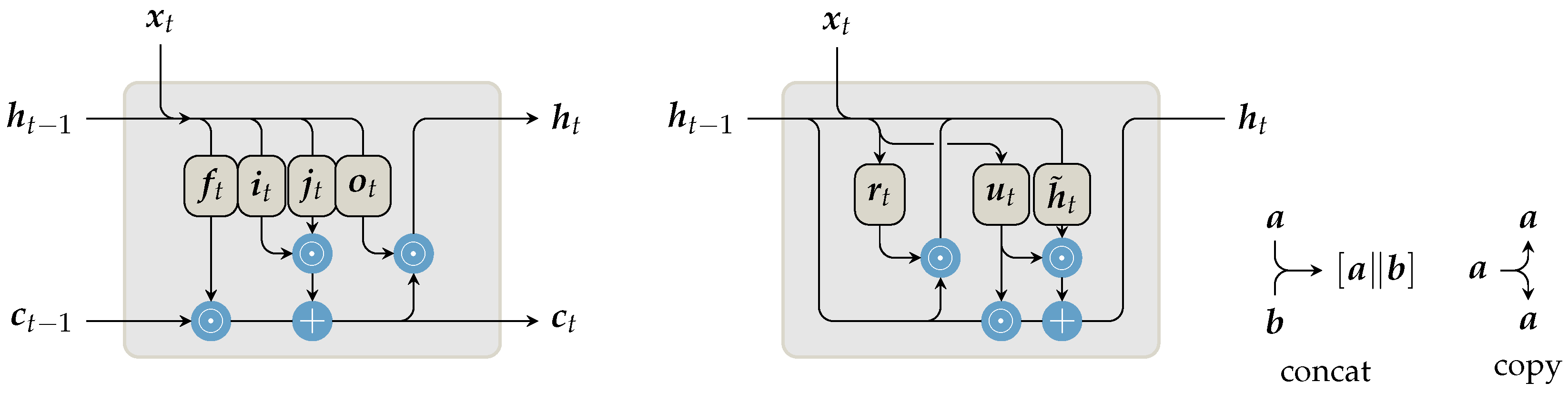
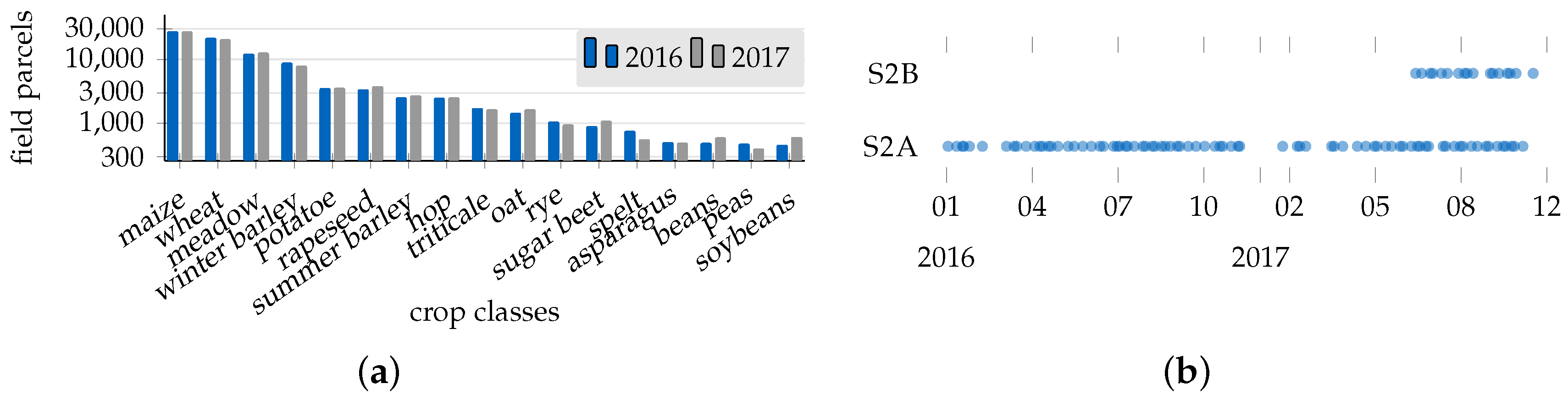

| Gate | Variant | ||
|---|---|---|---|
| RNN | LSTM [34] | GRU [35] | |
| Forget/Reset | |||
| Insert/Update | |||
| Output | |||
| Class | Year | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2016 | 2017 | |||||||||
| Precision (User’s Acc.) | Recall (Prod.Acc.) | -Meas. | Kappa | # of Pixels | Precision (User’s Acc.) | Recall (Prod. Acc.) | -Meas. | Kappa | # of Pixels | |
| sugar beet | 94.6 | 77.6 | 85.3 | 0.772 | 59 k | 89.2 | 78.5 | 83.5 | 0.779 | 94 k |
| oat | 86.1 | 67.8 | 75.8 | 0.675 | 36 k | 63.8 | 62.8 | 63.3 | 0.623 | 38 k |
| meadow | 90.8 | 85.7 | 88.2 | 0.845 | 233 k | 88.1 | 85.0 | 86.5 | 0.837 | 242 k |
| rapeseed | 95.4 | 90.0 | 92.6 | 0.896 | 125 k | 96.2 | 95.9 | 96.1 | 0.957 | 114k |
| hop | 96.4 | 87.5 | 91.7 | 0.873 | 51 k | 92.5 | 74.7 | 82.7 | 0.743 | 53 k |
| spelt | 55.1 | 81.1 | 65.6 | 0.807 | 38 k | 75.3 | 46.7 | 57.6 | 0.463 | 31 k |
| triticale | 69.4 | 55.7 | 61.8 | 0.549 | 65 k | 62.4 | 57.2 | 59.7 | 0.563 | 64 k |
| beans | 92.4 | 87.1 | 89.6 | 0.869 | 27 k | 92.8 | 63.2 | 75.2 | 0.630 | 28 k |
| peas | 93.2 | 70.7 | 80.4 | 0.706 | 9 k | 60.9 | 41.5 | 49.3 | 0.414 | 6 k |
| potato | 90.9 | 88.2 | 89.5 | 0.876 | 126 k | 95.2 | 73.8 | 83.1 | 0.728 | 140 k |
| soybeans | 97.7 | 79.6 | 87.7 | 0.795 | 21 k | 75.9 | 79.9 | 77.8 | 0.798 | 26 k |
| asparagus | 89.2 | 78.8 | 83.7 | 0.787 | 20 k | 81.6 | 77.5 | 79.5 | 0.773 | 19 k |
| wheat | 87.7 | 93.1 | 90.3 | 0.902 | 806 k | 90.1 | 95.0 | 92.5 | 0.930 | 783 k |
| winter barley | 95.2 | 87.3 | 91.0 | 0.861 | 258 k | 92.5 | 92.2 | 92.4 | 0.915 | 255 k |
| rye | 85.6 | 47.0 | 60.7 | 0.466 | 43 k | 76.7 | 61.9 | 68.5 | 0.616 | 30 k |
| summer barley | 87.5 | 83.4 | 85.4 | 0.830 | 73 k | 77.9 | 88.5 | 82.9 | 0.880 | 91 k |
| maize | 91.6 | 96.3 | 93.9 | 0.944 | 919 k | 92.3 | 96.8 | 94.5 | 0.953 | 876 k |
| weight.avg | 89.9 | 89.7 | 89.5 | 89.5 | 89.5 | 89.3 | ||||
| Overall Accuracy | Overall Kappa | Overall Accuracy | Overall Kappa | |||||||
| 89.7 | 0.870 | 89.5 | 0.870 | |||||||
| Approach | Details | |||||
|---|---|---|---|---|---|---|
| Sensor | Preprocessing | Features | Classifier | Accuracy | # of Classes | |
| this work | S2 | none | TOA reflect. | ConvRNN | 90 | 17 |
| Ruwurm and Körner [28], 2017 | S2 | atm. cor.(sen2cor) | BOA reflect. | RNN | 74 | 18 |
| Siachalou et al. [15], 2015 | LS, RE | geometric correction, image registration | TOA reflect. | HMM | 90 | 6 |
| Hao et al. [13], 2015 | MODIS | image reprojection,atm. cor. [45] | statistical phen.features | RF | 89 | 6 |
| Conrad et al. [12], 2014 | SPOT, RE, QB | segmentation, atm. cor. [45] | vegetation indices | OBIA + RF | 86 | 9 |
| Foerster et al. [10], 2012 | LS | phen. normalization,atm. cor. [45] | NDVI statistics | DT | 73 | 11 |
| Pena-Barragán et al. [14], 2011 | ASTER | segmentation,atm. cor. [46] | vegetation indices | OBIA+ DT | 79 | 13 |
| Conrad et al. [11], 2010 | SPOT | segmentation,atm. cor. [45] | vegetation indices | OBIA + DT | 80 | 6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rußwurm, M.; Körner, M. Multi-Temporal Land Cover Classification with Sequential Recurrent Encoders. ISPRS Int. J. Geo-Inf. 2018, 7, 129. https://doi.org/10.3390/ijgi7040129
Rußwurm M, Körner M. Multi-Temporal Land Cover Classification with Sequential Recurrent Encoders. ISPRS International Journal of Geo-Information. 2018; 7(4):129. https://doi.org/10.3390/ijgi7040129
Chicago/Turabian StyleRußwurm, Marc, and Marco Körner. 2018. "Multi-Temporal Land Cover Classification with Sequential Recurrent Encoders" ISPRS International Journal of Geo-Information 7, no. 4: 129. https://doi.org/10.3390/ijgi7040129
APA StyleRußwurm, M., & Körner, M. (2018). Multi-Temporal Land Cover Classification with Sequential Recurrent Encoders. ISPRS International Journal of Geo-Information, 7(4), 129. https://doi.org/10.3390/ijgi7040129