Revealing Recurrent Urban Congestion Evolution Patterns with Taxi Trajectories
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Study Area
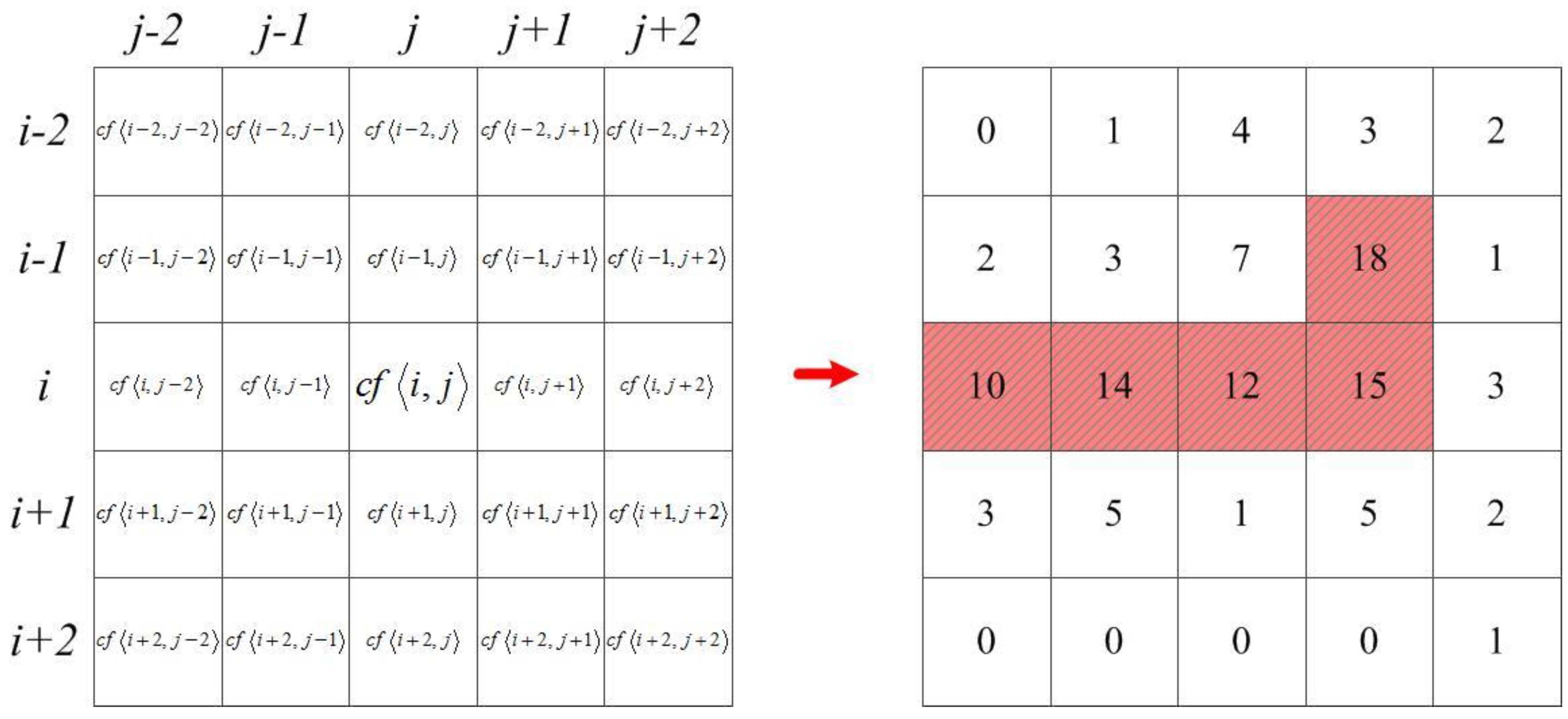
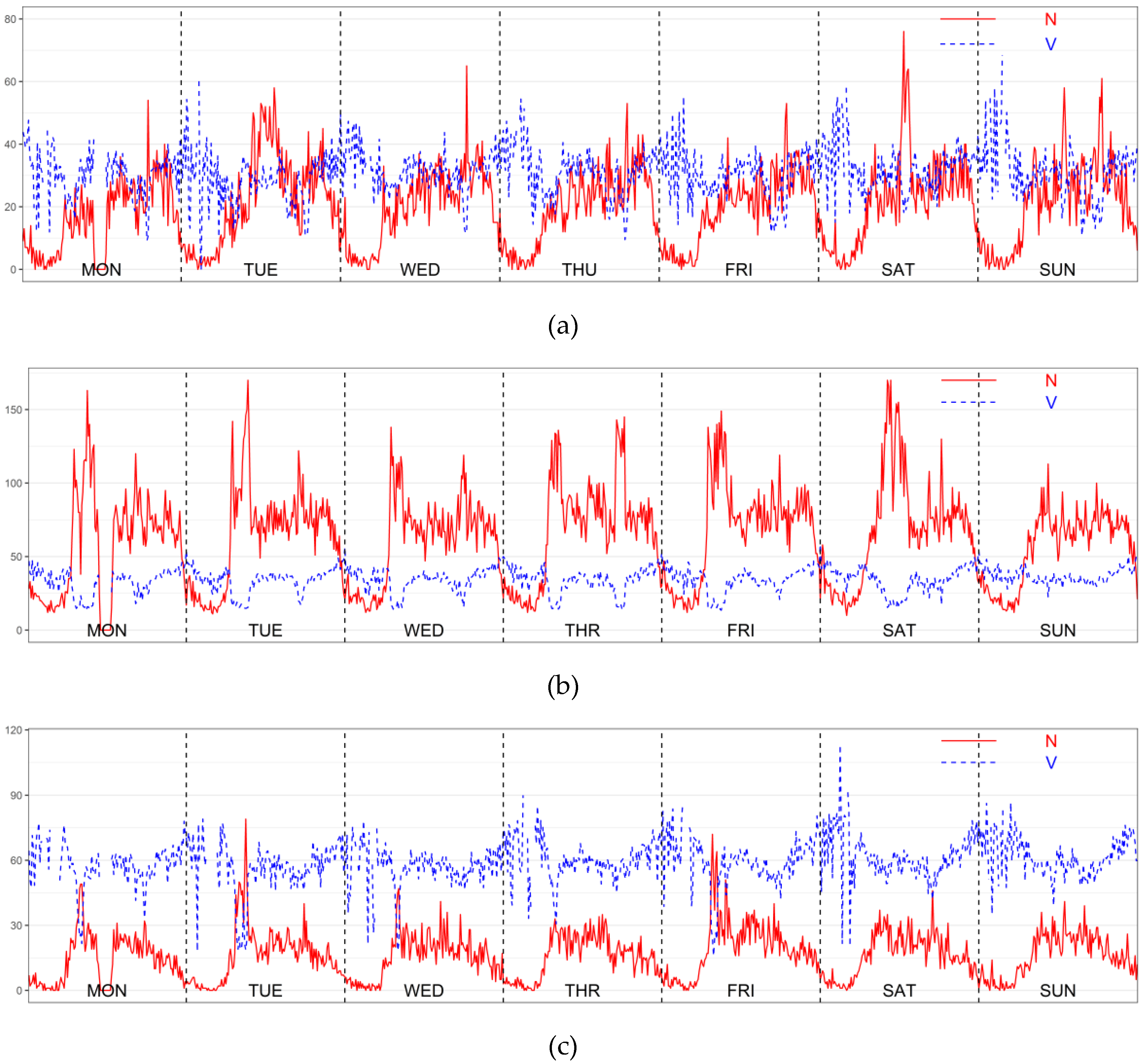
2.3. Detecting Grid Congestion
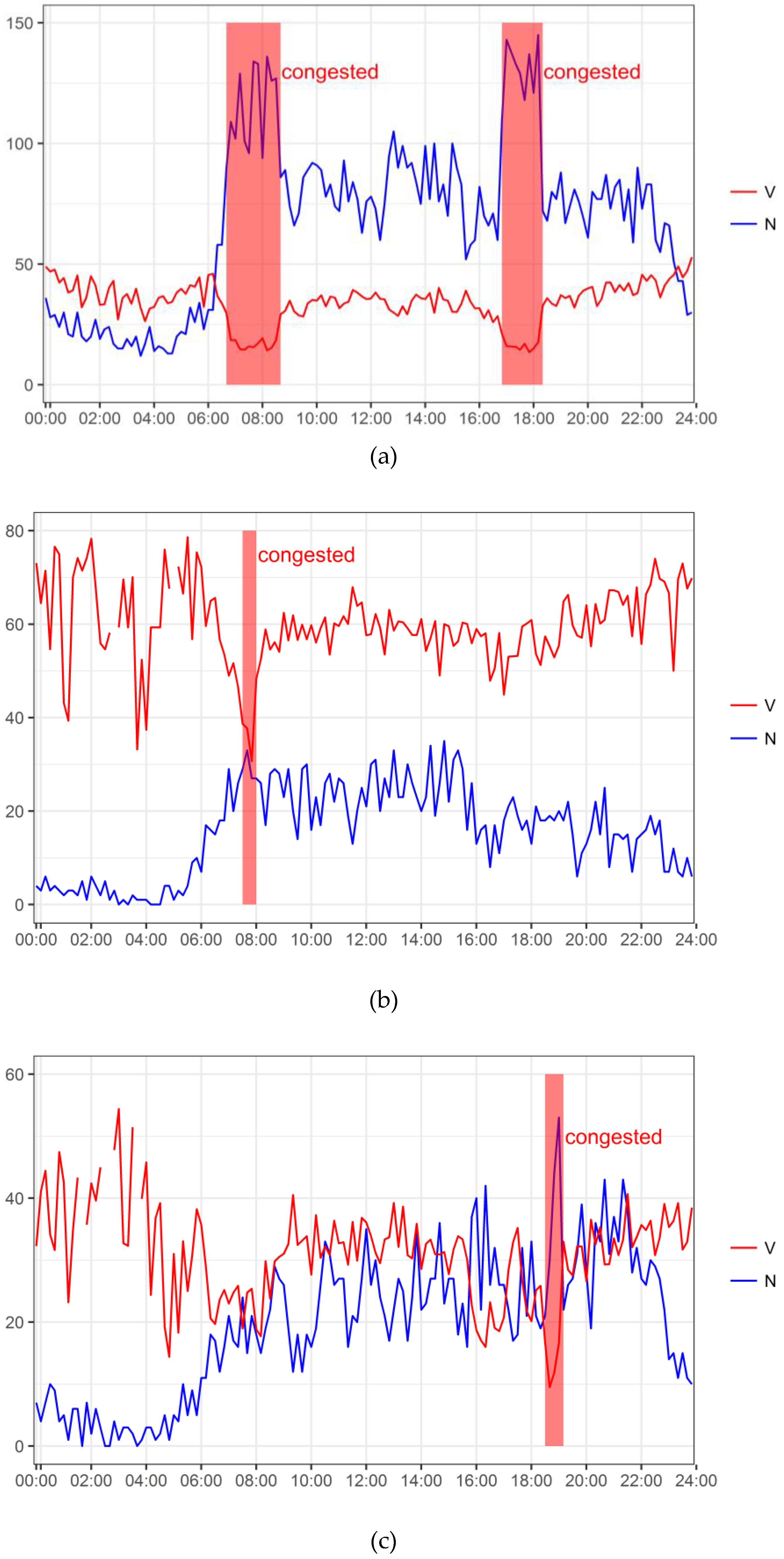
- Type 2: at least one intersection with signal control is included in this kind of grid, such as . Including high-grade road, this kind of grid usually has greater value of and . Due to the signal control, the value of varies minimally, as shown in Figure 4.
- Type 3: at least one intersection with no signal control is included in this kind of grid, such as grid . Including low-grade road, this kind of grid usually obtains a lower value of N. Due to the randomness of the small number of vehicles, V varies considerably, as shown in Figure 4.
- Type 4: no intersection is included in this kind of grid, as per grid . Compared with the other 2 kinds of grids, the variation in and vary considerably, as shown in Figure 4.
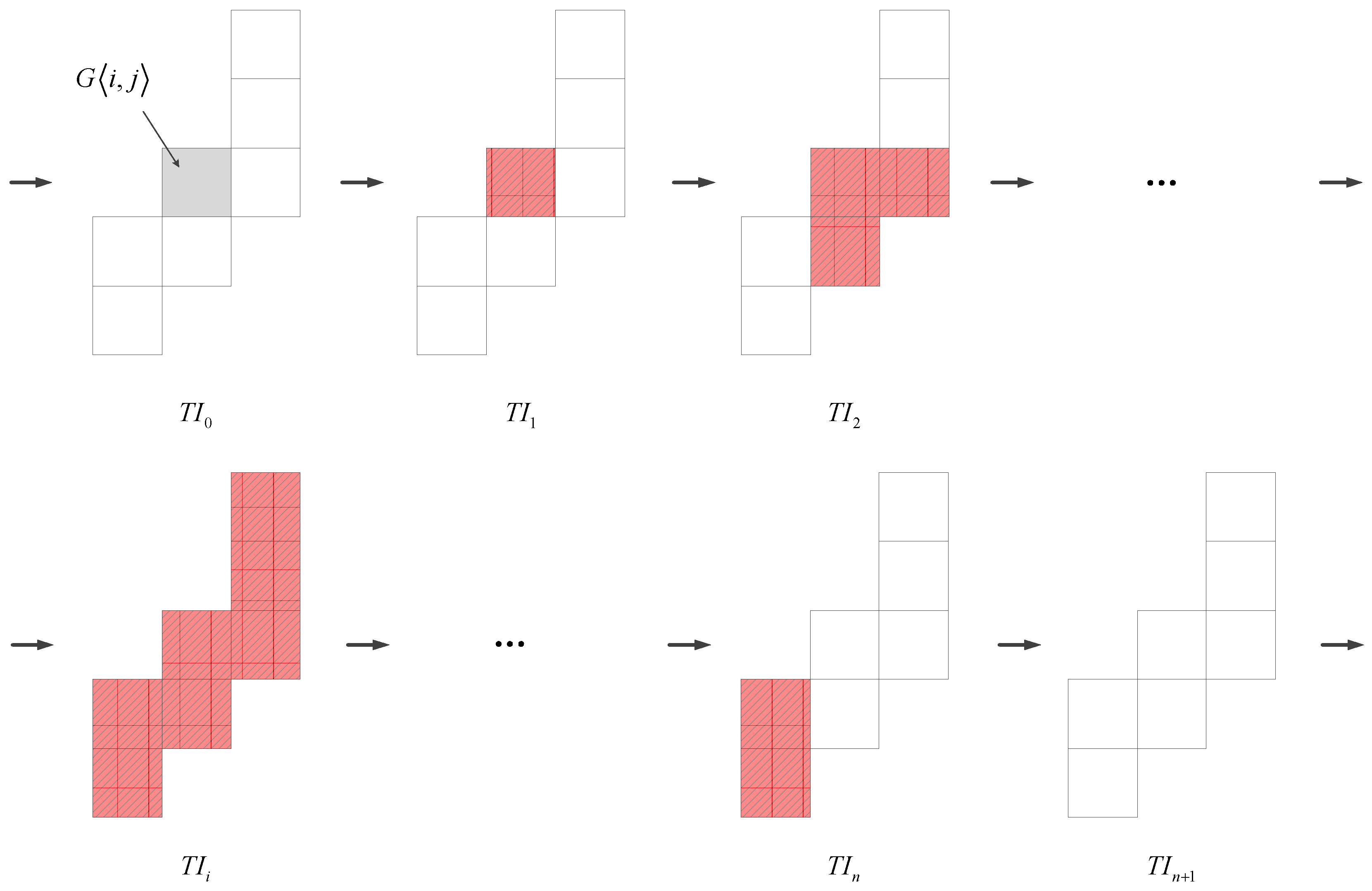
2.4. RC Area Identification
2.5. Measuring the RC Evolution Pattern
- Congestion Start () represents the beginning of a traffic jam in the specific RC area. represents the start time of a jam, which corresponds to a single time interval. The congested grids in represents the start grids of this jam. In Figure 6, at least one grid is congested in , and none of the 7 grids is congested in the 3 previous time intervals (i.e., , and ), meaning this jam started in .
- Congestion End () is the end of a traffic jam in the specific RC area. is the end time of the jam, which corresponds to a single time interval. In Figure 6, at least one grid is congested in , and none of the 7 grids are congested in the 3 latter time intervals, , and , which means this jam ended in .
- Congestion Peak () is the peak with the maximum number of congested grids in a specific RC area. is the peak time of a jam, which corresponds to at least one time interval. In Figure 6, all the 7 grids are congested in , which means this jam reach peak in . Notably, the particular jam reached a peak in several time intervals, thus the congestion peak contains all states from the first peak to the last.
- Congestion Propagation () is the state between and . represents the propagating time of a jam, which corresponds to several time intervals between and . In Figure 6, this state lasts from to .
- Congestion Dissipation () is the states between and . represents the dissipating time for a jam that corresponds to several time intervals between and . In Figure 6, this state lasts from to .
2.5.1. RC Temporal Evolution Pattern
- RC Start time is calculated as:
- RC End time is calculated as:
- RC time is calculated as:
2.5.2. RC Spatial Evolution Pattern
- RC Start Grid is the set of congested grids in of all traffic jams.
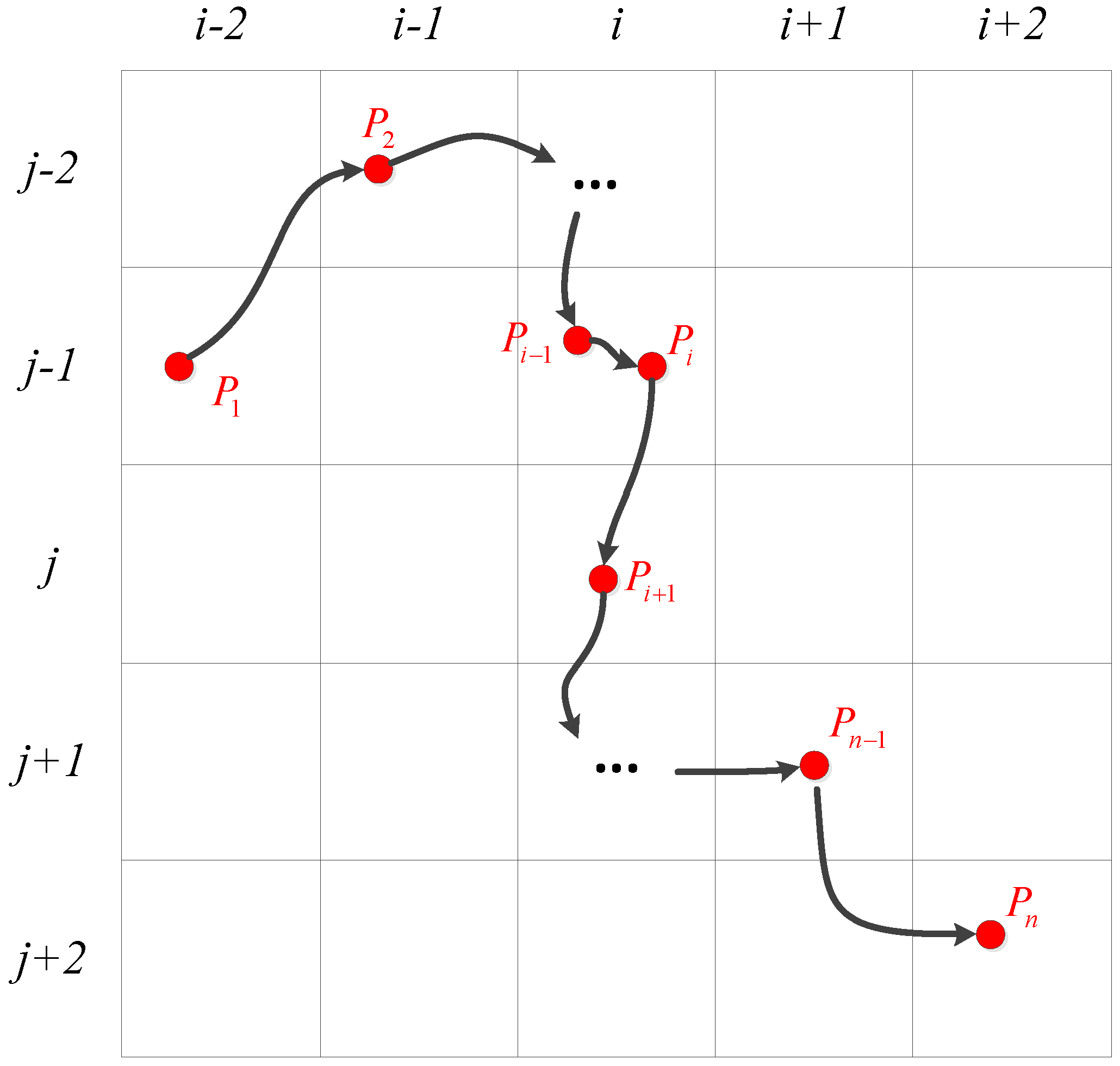
- RC Key Grid is a grid that propagates to the adjacent grids with most frequency. For adjacent grids and , if grid is congested and is not congested in , and then is congested in , it means that traffic jam propagate from to for one time. In Figure 6, the traffic jam propagates from to and in .
3. Experiment and Discussion
3.1. Detecting Grid Congestion
3.2. Measuring the RC Evolution Pattern
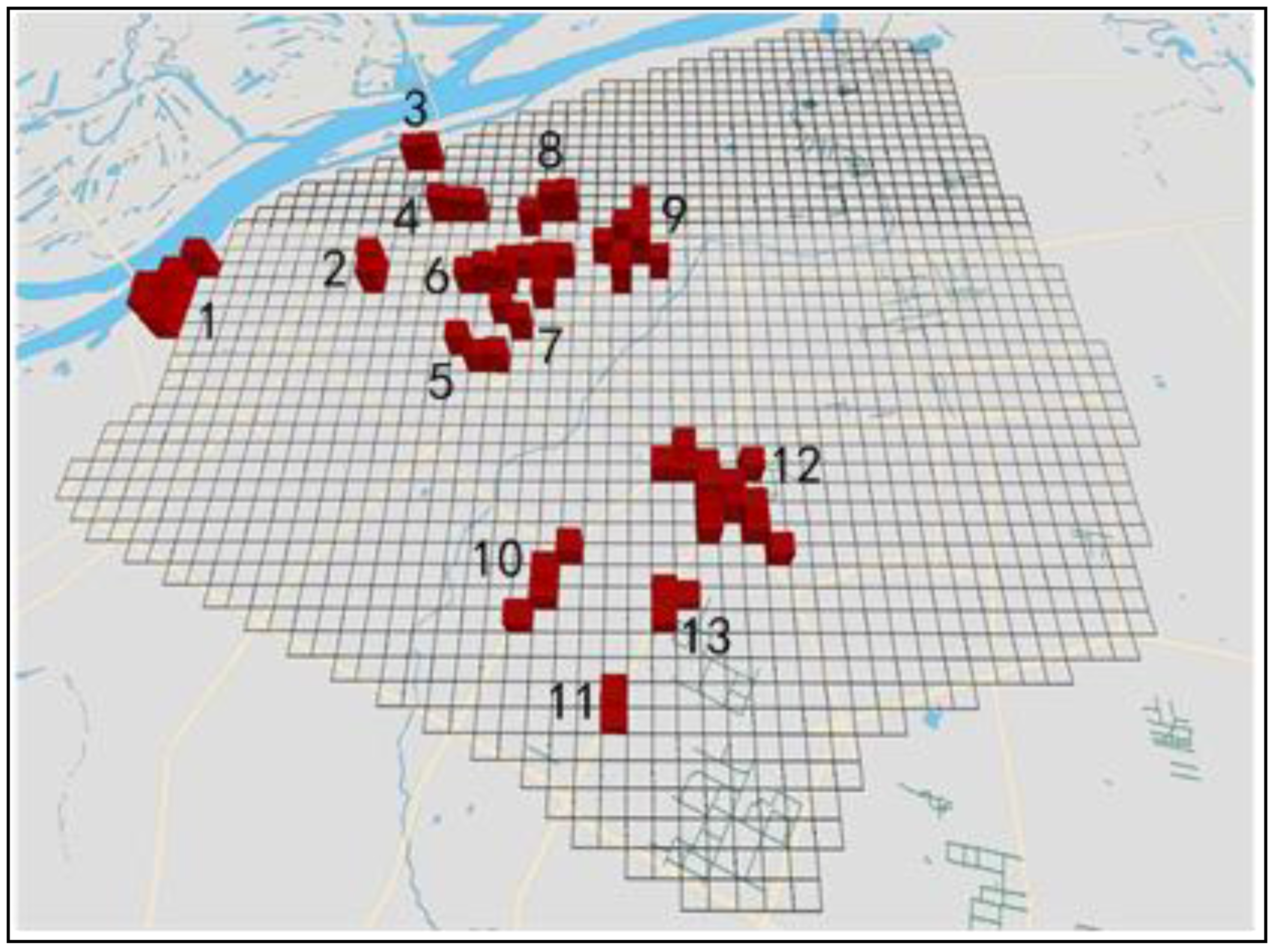
- Some remarkable characteristics of the RC spatial evolution patterns were observed during the winter in Harbin at morning peak hours. Firstly, the RC spatial distribution is extremely uneven. In the second-rind road area of Harbin, the 13 RC areas are concentrated in two main regions, as shown in Figure 10. The first area is a two-kilometer radius circular region, centered on Harbin Train Station. This region is in the northwest part of the urban Harbin area, containing eight RC areas. The second area is also a two-kilometer radius circular region, centered on the Heilongjiang Provincial Government Office Building. This region is in the southern part of the Harbin urban area, containing 4 RC areas. Secondly, the RC areas are very different from each other. The RC range varied considerably. For example, Cluster 12 included 13 grids, with a value almost eight times that of those found in Clusters 2, 3, 7, and 11. The Start Grid (or Key Grid) types are different. For example, the Start Grid in Cluster 12 () is type 2, whereas it is type 3 in Cluster 7 ().
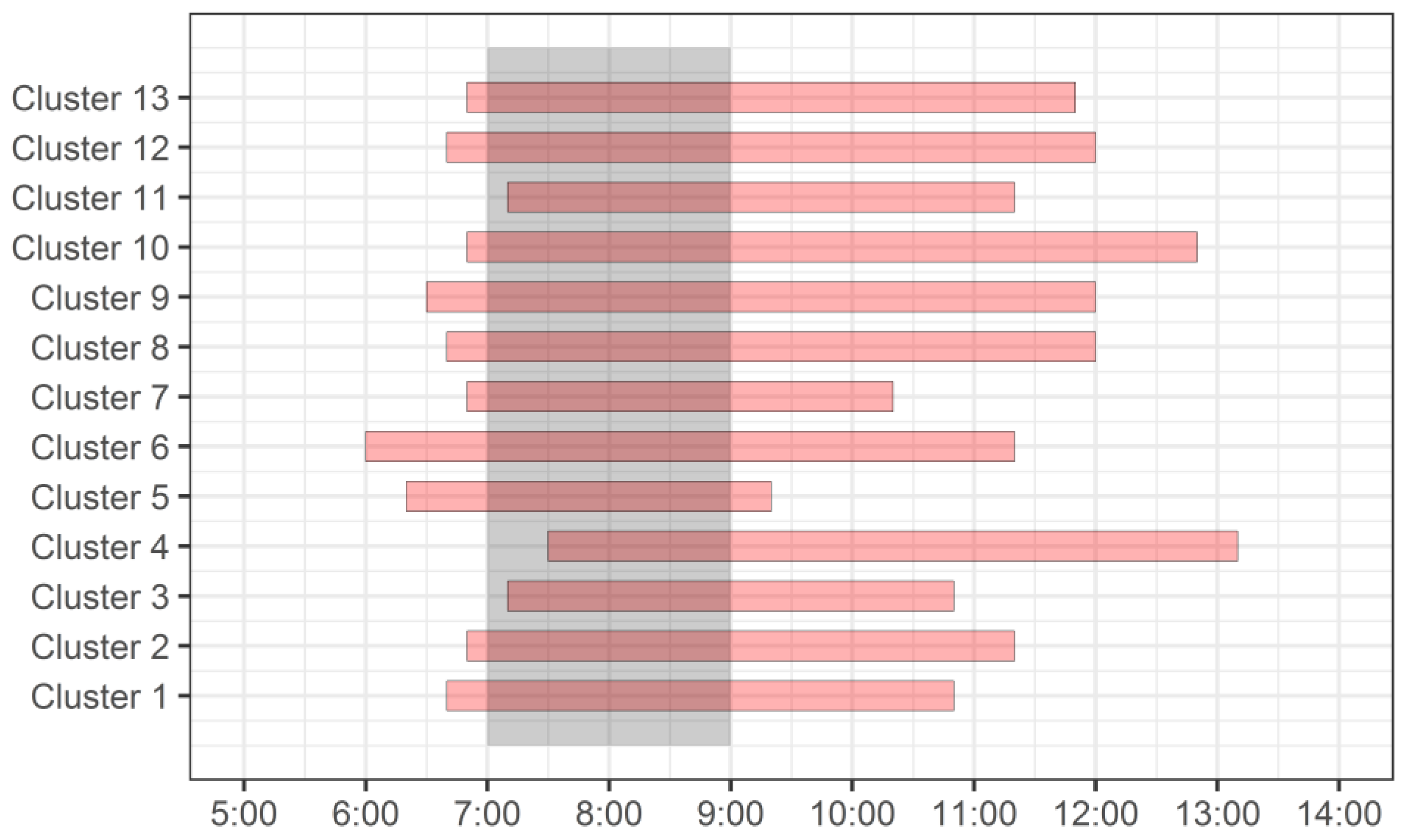
- Some remarkable characteristics of the RC temporal evolution patterns were observed during the winter in Harbin at peak morning hours. The start time of most RC is earlier than morning peak hours. Generally speaking, the urban morning peak hours were from 7:00 to 9:00 a.m., with 77% (N = 10) of the RC appearing earlier than 7:00 a.m. On average, the RC start time was 6:45 a.m. The earliest RC start time was observed in Cluster 6 at 6:00 a.m. additionally, the end times for all RC were later than the morning peak hours. All the RC disappeared after 9:00 a.m., and 92% (N = 12) disappeared after 10:00 a.m. The RC that occurred in Clusters 4 and 10 did not end until afternoon. We also noted that the duration of all RC was longer than the morning peak hours. All the RC lasted for more than two hours. The average congestion time for all RC was 4.7 h.
3.3. Discussion
3.3.1. RC Cause Analysis
3.3.2. RC Alleviating Strategies
4. Conclusions
- (1)
- The main method proposed is based on taxi trajectory data, which has obvious advantages including extensive coverage and lower cost in comparison with the data collected from traditional traffic detectors, such as loops, microwaves, and video detectors.
- (2)
- We created the grid congestion detection method using multivariate trajectory pattern analysis, including the number of taxi trajectories and their average velocity. Then, a rule was used to detect abnormal patterns in the grid. Combined with the lower average velocity information, a specific grid is identified as being congested.
- (3)
- An integrated stepwise method is proposed to measure urban RC evolution patterns at the macroscopic level, including detecting grid congestion, determining RC areas, and measuring the RC evolution patterns. The method provides a new solution for Intelligent Transportation System application.
- (4)
- Based on the proposed methods, a case study was completed in Harbin, China with real GPS data and a digital map, rather than simulation data, to evaluate the stepwise method. A total of 13 RC areas were detected that occur in the Harbin second ring road area in winter during peak morning hours. In addition, some remarkable spatial-temporal evolution pattern characteristics of RC were revealed in this paper.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Moreira-Matias, L.; Alesiani, F. Drift3Flow: Freeway-Incident Prediction Using Real-Time Learning. In Proceedings of the IEEE International Conference on Intelligent Transportation Systems, Las Palmas, Spain, 15–18 September 2015; pp. 566–571. [Google Scholar]
- Chung, Y. Identification of Critical Factors for Non-Recurrent Congestion Induced by Urban Freeway Crashes and Its Mitigating Strategies. Sustainability 2017, 9, 2331. [Google Scholar] [CrossRef]
- Moreira-Matias, L.; Cerqueira, V. CJAMmer—Traffic JAM Cause Prediction using Boosted Trees. In Proceedings of the IEEE International Conference on Intelligent Transportation Systems, Rio de Janeiro, Brazil, 1–4 November 2016; pp. 743–748. [Google Scholar]
- Gurupackiam, S.; Jones, S.L., Jr. Empirical Study of Accepted Gap and Lane Change Duration within Arterial Traffic under Recurrent and Non-Recurrent Congestion. Int. J. Traffic Transp. Eng. 2012, 2, 306–322. [Google Scholar] [CrossRef][Green Version]
- Schimbinschi, F.; Moreira-Matias, L.; Nguyen, V.X.; Bailey, J. Topology-regularized universal vector autoregression for traffic forecasting in large urban areas. Expert Syst. Appl. 2017, 82, 301–316. [Google Scholar] [CrossRef]
- An, S.; Yang, H.; Wang, J.; Cui, N.; Cui, J. Mining urban recurrent congestion evolution patterns from GPS-equipped vehicle mobility data. Inf. Sci. 2016, 373, 515–526. [Google Scholar] [CrossRef]
- Li, R.; Pereira, F.C.; Benakiva, M.E. Competing risks mixture model for traffic incident duration prediction. Accid. Anal. Prev. 2015, 75, 192–201. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.X.; Liu, F.; Janssens, D.; An, S.; Wets, G.; Coolsc, M. Detecting urban road network accessibility problems using taxi GPS data. J. Transp. Geogr. 2016, 51, 147–157. [Google Scholar] [CrossRef]
- Hwang, R.H.; Hsueh, Y.L.; Chen, Y.T. An effective taxi recommender system based on a spatio-temporal factor analysis model. Inf. Sci. 2015, 314, 28–40. [Google Scholar] [CrossRef]
- Woodard, D.; Nogin, G.; Koch, P.; Racz, D.; Goldszmidt, M.; Horvitz, E. Predicting travel time reliability using mobile phone GPS data. Transp. Res. Part C Emerg. Technol. 2017, 75, 30–44. [Google Scholar] [CrossRef]
- Lu, S.F.; Mai, Y.H.; Liu, X.M. The Analysis of Characterization of Urban Traffic Congestion Based on Mixed Speed Distribution of Taxi GPS Data. Appl. Mech. Mater. 2013, 241–244, 2076–2081. [Google Scholar] [CrossRef]
- Cui, J.X.; Liu, F.; Hu, J.; Janssens, D.; Wets, G.; Cools, M. Identifying mismatch between urban travel demand and transport network services using GPS data: A case study in the fast growing Chinese city of Harbin. Neurocomputing 2016, 181, 4–18. [Google Scholar] [CrossRef]
- Daganzo, C.F. The cell transmission model: A dynamic representation of highway traffic consistent with the hydrodynamic theory. Transp. Res. Part B Methodol. 1994, 28, 269–287. [Google Scholar] [CrossRef]
- Chandler, R.E.; Herman, R.; Montroll, E.W. Traffic dynamics: Studies in car following. Oper. Res. 1958, 6, 165–184. [Google Scholar] [CrossRef]
- Zhang, A.; Gao, Z. CTM-based Propagation of Non-recurrent Congestion and Location of Variable Message Sign. In Proceedings of the Fifth International Joint Conference on Computational Sciences and Optimization, Harbin, China, 23–26 June 2012; pp. 462–465. [Google Scholar]
- Chu, C.; Xie, N.; Chen, X.; Wu, Y.; Sun, X. Temporal-Spatial Analysis of Traffic Congestion Based on Modified CTM. Math. Probl. Eng. 2015, 2015, 1–11. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, Z.A.; Yan, Y.S. Incident-based traffic congestion propagation mechanism with improved CTM model. Beijing Gongye Daxue Xuebao 2015, 41, 1061–1066. [Google Scholar]
- Chen, D.; Laval, J.; Zheng, Z.; Ahn, S. A behavioral car-following model that captures traffic oscillations. Transp. Res. Part B Methodol. 2012, 46, 744–761. [Google Scholar] [CrossRef]
- Zhu, F.; Hong, K.L.; Lin, H.Z. Delay and emissions modelling for signalised intersections. Transp. B Transp. Dyn. 2013, 1, 111–135. [Google Scholar] [CrossRef]
- Papathanasopoulou, V.; Antoniou, C. Towards data-driven car-following models. Transp. Res. Part C Emerg. Technol. 2015, 55, 496–509. [Google Scholar] [CrossRef]
- Hofleitner, A.; Herring, R.; Abbeel, P.; Bayen, A. Learning the Dynamics of Arterial Traffic from Probe Data Using a Dynamic Bayesian Network. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1679–1693. [Google Scholar] [CrossRef]
- Castro, P.S.; Zhang, D.; Chen, C.; Li, S.; Pan, G. From taxi GPS traces to social and community dynamics: A survey. ACM Comput. Surv. 2013, 46, 17. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, Y.; Cang, Y. Research of the four seasons division of Harbin. Heilongjian Clim. 2001, 3, 32–33. [Google Scholar]
- The Congestion Ranking of Main Cities in China. Available online: report.amap.com/congestion.do (accessed on 10 January 2016).
- Tang, J.; Liu, F.; Wang, Y.; Wang, H. Uncovering urban human mobility from large scale taxi GPS data. Phys. Stat. Mech. Appl. 2015, 438, 140–153. [Google Scholar] [CrossRef]
- Zheng, K.; Zheng, Y.; Yuan, N.J.; Shang, S.; Zhou, X. Online Discovery of Gathering Patterns over Trajectories. IEEE Trans. Knowl. Data Eng. 2013, 8, 242–253. [Google Scholar] [CrossRef]
- Lehmann, R. 3σ-Rule for Outlier Detection from the Viewpoint of Geodetic Adjustment. J. Surv. Eng. 2014, 139, 157–165. [Google Scholar] [CrossRef]
- Huang, F.; Zhu, Q.; Zhou, J.; Tao, J.; Zhou, X.; Jin, D.; Tan, X.; Wang, L. Research on the Parallelization of the DBSCAN Clustering Algorithm for Spatial Data Mining Based on the Spark Platform. Remote Sens. 2017, 9, 1301. [Google Scholar] [CrossRef]
- Mao, Y.; Zhong, H.; Qi, H.; Ping, P.; Li, X. An Adaptive Trajectory Clustering Method Based on Grid and Density in Mobile Pattern Analysis. Sensors 2017, 17, 2013. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Yan, X.; Wang, Y.; Yang, Z.; Wu, J. Grid Mapping for Spatial Pattern Analyses of Recurrent Urban Traffic Congestion Based on Taxi GPS Sensing Data. Sustainability 2017, 9, 533. [Google Scholar] [CrossRef]

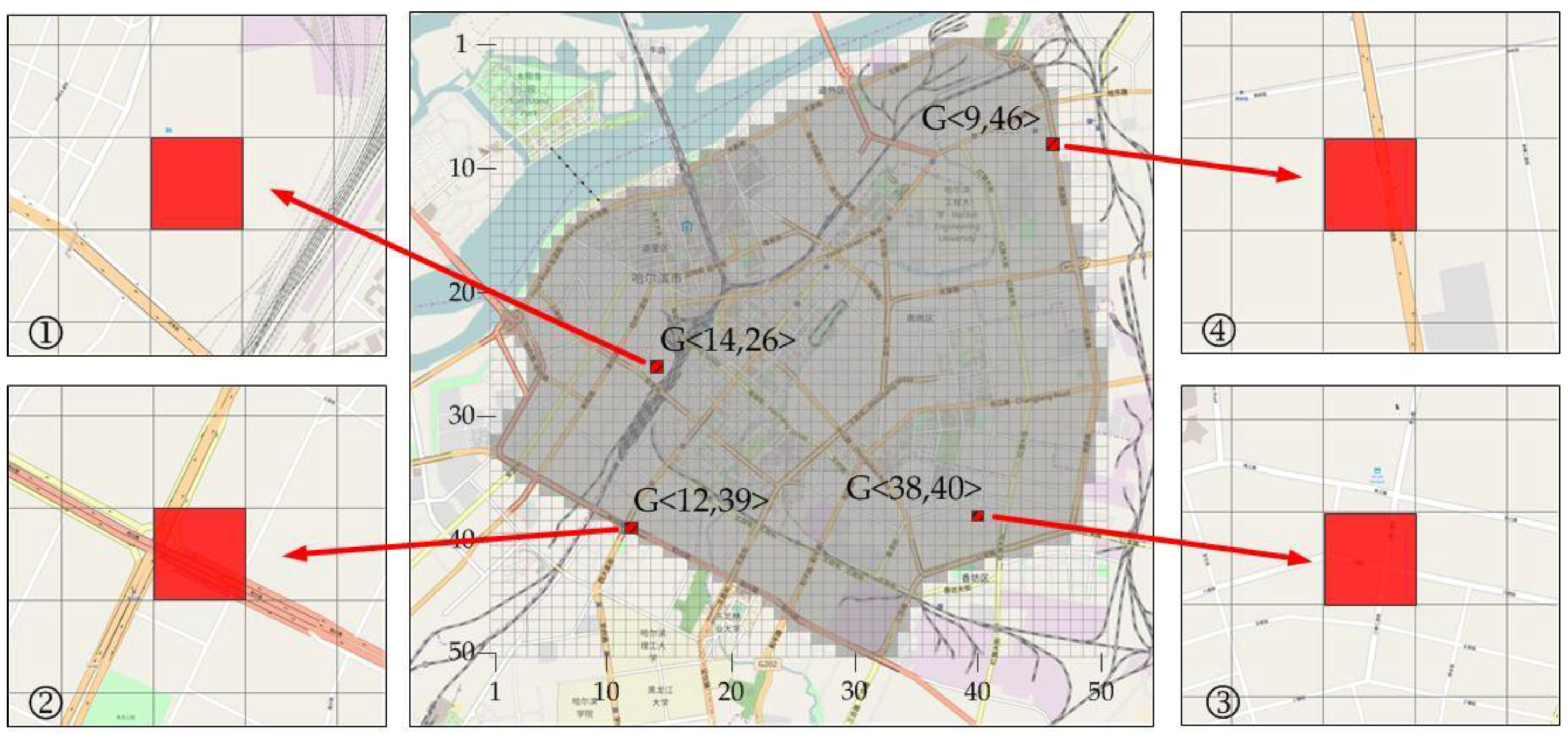



| Taxi ID | Latitude | Longitude | Timestamp | Instantaneous Velocity () |
|---|---|---|---|---|
| 0100322231 | 45.77463 | 126.63945 | 23-02-2015 6:58:51 | 19.6 |
| 0100322231 | 45.77463 | 126.63693 | 23-02-2015 6:59:21 | 22.1 |
| 0100322231 | 45.77461 | 126.63701 | 23-02-2015 6:59:51 | 21.9 |
| 0100322231 | 45.77462 | 126.63711 | 23-02-2015 7:00:21 | 12.5 |
| 0100322231 | 45.77462 | 126.6371 | 23-02-2015 7:00:51 | 0 |
| TI | GS<N,V> | GSavg[ ] | Left of Equation (4) | Right of Equation (4) | Satisfy Equation (4) | Satisfy Equation (6) | Congested |
|---|---|---|---|---|---|---|---|
| … | … | … | … | … | … | … | … |
| 16:10–16:20 | <70,27.6> | <61.8,33.7> | 22.7 | 30.7 | FALSE | TRUE | FALSE |
| 16:20–16:30 | <66,30.9> | <61.8,33.6> | 10 | 15 | FALSE | TRUE | FALSE |
| 16:30–16:40 | <71,25.9> | <61.9,33.6> | 24.9 | 35.7 | FALSE | TRUE | FALSE |
| 16:40–16:50 | <60,28.5> | <61.9,33.5> | 11.5 | 16.1 | FALSE | TRUE | FALSE |
| 16:50–17:00 | <110,21> | <62.4,33.4> | 180.1 | 147.7 | TRUE | TRUE | TRUE |
| 17:00–17:10 | <143,16.1> | <63.1,33.2> | 300.5 | 245 | TRUE | TRUE | TRUE |
| 17:10–17:20 | <138,15.9> | <63.9,33.1> | 278.7 | 228.3 | TRUE | TRUE | TRUE |
| 17:20–17:30 | <133,15.8> | <64.5,32.9> | 241.4 | 211.8 | TRUE | TRUE | TRUE |
| 17:30–17:40 | <129,14.5> | <65.1,32.7> | 237.4 | 199.3 | TRUE | TRUE | TRUE |
| 17:40–17:50 | <118,17.1> | <65.6,32.6> | 211.6 | 163.9 | TRUE | TRUE | TRUE |
| 17:50–18:00 | <137,13.3> | <66.3,32.4> | 255.4 | 219.6 | TRUE | TRUE | TRUE |
| 18:00–18:10 | <121,15.1> | <66.8,32.2> | 202.6 | 170.6 | TRUE | TRUE | TRUE |
| 18:10–18:20 | <145,17.7> | <67.5,32.1> | 344.7 | 236.5 | TRUE | TRUE | TRUE |
| 18:20–18:30 | <72,32.8> | <67.5,32.1> | 29.1 | 13.6 | TURE | FALSE | FALSE |
| 18:30–18:40 | <68,35.9> | <67.5,32.1> | 20.4 | 11.3 | TRUE | FALSE | FALSE |
| 18:40–18:50 | <80,33.7> | <67.6,32.2> | 32.9 | 37.3 | FALSE | FALSE | FALSE |
| … | … | … | … | … | … | … | … |
| TI | GS<N,V> | GSavg[ ] | Left of Equation (4) | Right of Equation (4) | Satisfy Equation (4) | Satisfy Equation (6) | Congested |
|---|---|---|---|---|---|---|---|
| … | … | … | … | … | … | … | … |
| 07:10–07:20 | <29,49> | <5.2,64> | 69.3 | 84.5 | FALSE | TRUE | FALSE |
| 07:20–07:30 | <20,51.7> | <5.5,63.7> | 49.6 | 56.5 | FALSE | TRUE | FALSE |
| 07:30–07:40 | <26,46.6> | <6,63.3> | 65.1 | 78.3 | FALSE | TRUE | FALSE |
| 07:40–07:50 | <29,38.7> | <6.5,62.8> | 118.6 | 99 | TRUE | TRUE | TRUE |
| 07:50–08:00 | <33,37.7> | <7,62.3> | 127.4 | 107.1 | TRUE | TRUE | TRUE |
| 08:00–08:10 | <27,30.7> | <7.5,61.6> | 140.4 | 109.7 | TRUE | TRUE | TRUE |
| 08:10–08:20 | <27,48.3> | <7.9,61.3> | 51.4 | 69.5 | FALSE | TRUE | FALSE |
| 08:20–08:30 | <26,52.5> | <8.2,61.1> | 44.2 | 59.3 | FALSE | TRUE | FALSE |
| … | … | … | … | … | … | … | … |
| TI | GS<N,V> | GSavg[ ] | Left of Equation (4) | Right of Equation (4) | Satisfy Equation (4) | Satisfy Equation (6) | Congested |
|---|---|---|---|---|---|---|---|
| … | … | … | … | … | … | … | … |
| 18:00–18:10 | <21,21.8> | <16.7,31.2> | 25.5 | 31.1 | FALSE | TRUE | FALSE |
| 18:10–18:20 | <33,20.1> | <16.8,31.1> | 37.1 | 58.6 | FALSE | TRUE | FALSE |
| 18:20–18:30 | <21,25.1> | <16.9,31> | 18.1 | 21.6 | FALSE | TRUE | FALSE |
| 18:30–18:40 | <19,25.9> | <16.9,31> | 16.6 | 16.7 | FALSE | TRUE | FALSE |
| 18:40–18:50 | <21,16.7> | <16.9,30.9> | 31.6 | 44.2 | FALSE | TRUE | FALSE |
| 18:50–19:00 | <30,9.5> | <17,30.7> | 132.4 | 74.5 | TRUE | TRUE | TRUE |
| 19:00–19:10 | <44,11.9> | <17.3,30.5> | 174.9 | 97.8 | TRUE | TRUE | TRUE |
| 19:10–19:20 | <53,16.6> | <17.6,30.4> | 205.7 | 114 | TRUE | TRUE | TRUE |
| 19:20–19:30 | <22,33> | <17.6,30.4> | 24.4 | 15.3 | TRUE | FALSE | FALSE |
| 19:30–19:40 | <26,28.4> | <17.7,30.4> | 22 | 25.6 | FALSE | TRUE | FALSE |
| 19:40–19:50 | <27,27.5> | <17.8,30.4> | 26.4 | 29 | FALSE | TRUE | FALSE |
| 19:50–20:00 | <31,32.2> | <17.9,30.4> | 30.6 | 39.8 | FALSE | FALSE | FALSE |
| … | … | … | … | … | … | … | … |
| Cluster ID | Gird Number | RC Start Grid | RC Key Grid | Functional Zone |
|---|---|---|---|---|
| 1 | 7 | G<2,24> G<2,24> | G<3,23> | Urban main road |
| 2 | 2 | G<13,21> | G<13,21> | Residence Zone |
| 3 | 2 | G<14,13> | G<14,13> | Educational Zone |
| 4 | 3 | G<16,17> | G<16,17> | Public Service Zone |
| 5 | 3 | G<19,27> | G<19,27> | Residence Zone |
| 6 | 9 | G<19,22> | G<19,22> | Public Service Zone |
| 7 | 2 | G<20,24> | G<20,24> | Urban main road |
| 8 | 3 | G<23,17> | G<23,17> | Public Service Zone |
| 9 | 9 | G<26,19> | G<27,20> | Mixed Functional Zone |
| 10 | 4 | G<24,38> | G<24,38> | Urban main road |
| 11 | 2 | G<26,43> | G<26,43> | Educational Zone |
| 12 | 13 | G<30,35> | G<30,34> | Urban main road |
| 13 | 3 | G<28,40> | G<28,40> | Residence Zone |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, S.; Yang, H.; Wang, J. Revealing Recurrent Urban Congestion Evolution Patterns with Taxi Trajectories. ISPRS Int. J. Geo-Inf. 2018, 7, 128. https://doi.org/10.3390/ijgi7040128
An S, Yang H, Wang J. Revealing Recurrent Urban Congestion Evolution Patterns with Taxi Trajectories. ISPRS International Journal of Geo-Information. 2018; 7(4):128. https://doi.org/10.3390/ijgi7040128
Chicago/Turabian StyleAn, Shi, Haiqiang Yang, and Jian Wang. 2018. "Revealing Recurrent Urban Congestion Evolution Patterns with Taxi Trajectories" ISPRS International Journal of Geo-Information 7, no. 4: 128. https://doi.org/10.3390/ijgi7040128
APA StyleAn, S., Yang, H., & Wang, J. (2018). Revealing Recurrent Urban Congestion Evolution Patterns with Taxi Trajectories. ISPRS International Journal of Geo-Information, 7(4), 128. https://doi.org/10.3390/ijgi7040128




