Graph-Based Matching of Points-of-Interest from Collaborative Geo-Datasets
Abstract
:1. Introduction
1.1. Steps in the Matching of POIs from Different Datasets
1.2. Previous Works on POI Matching
2. Methods
2.1. POI Similarity Measures
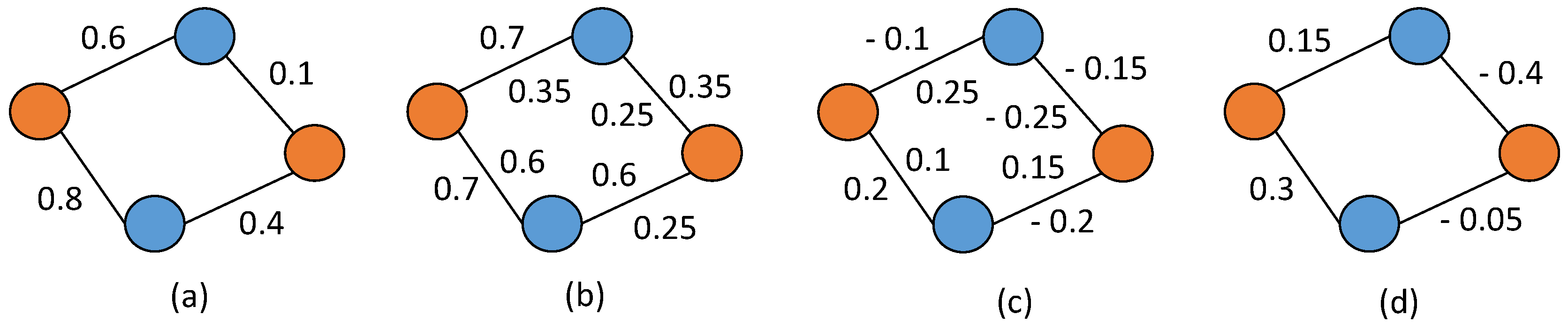
2.2. Aggregation of Similarity Measures
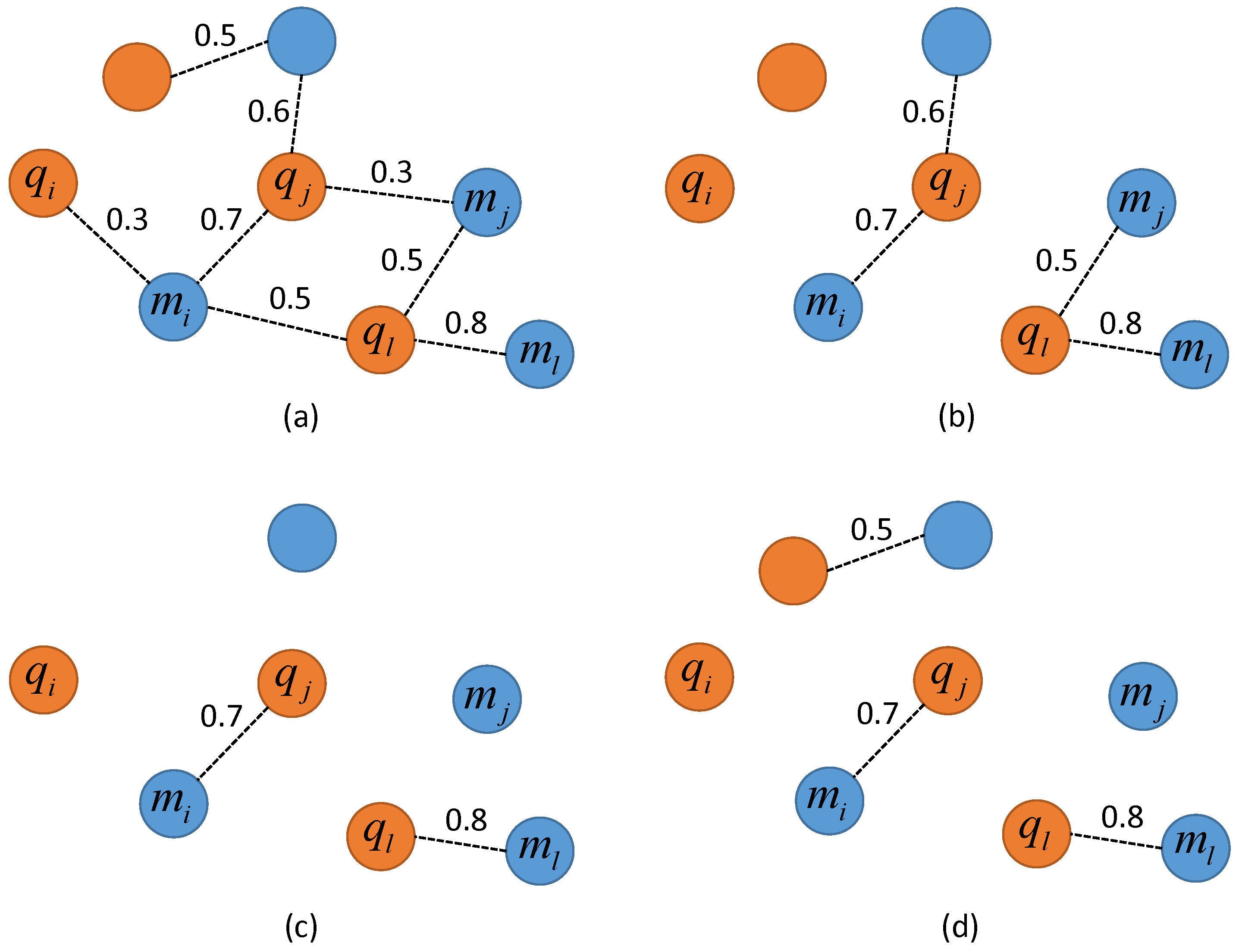
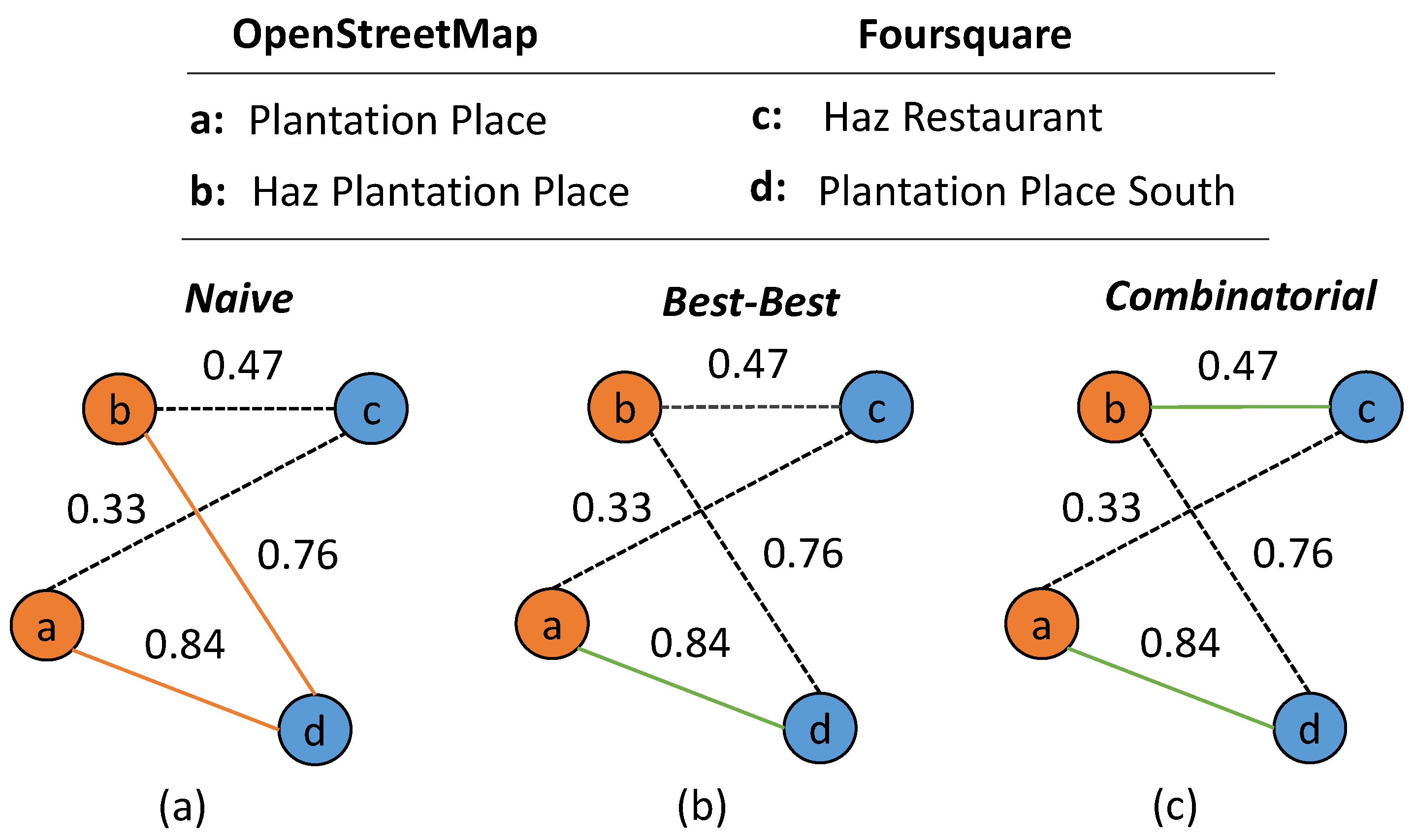
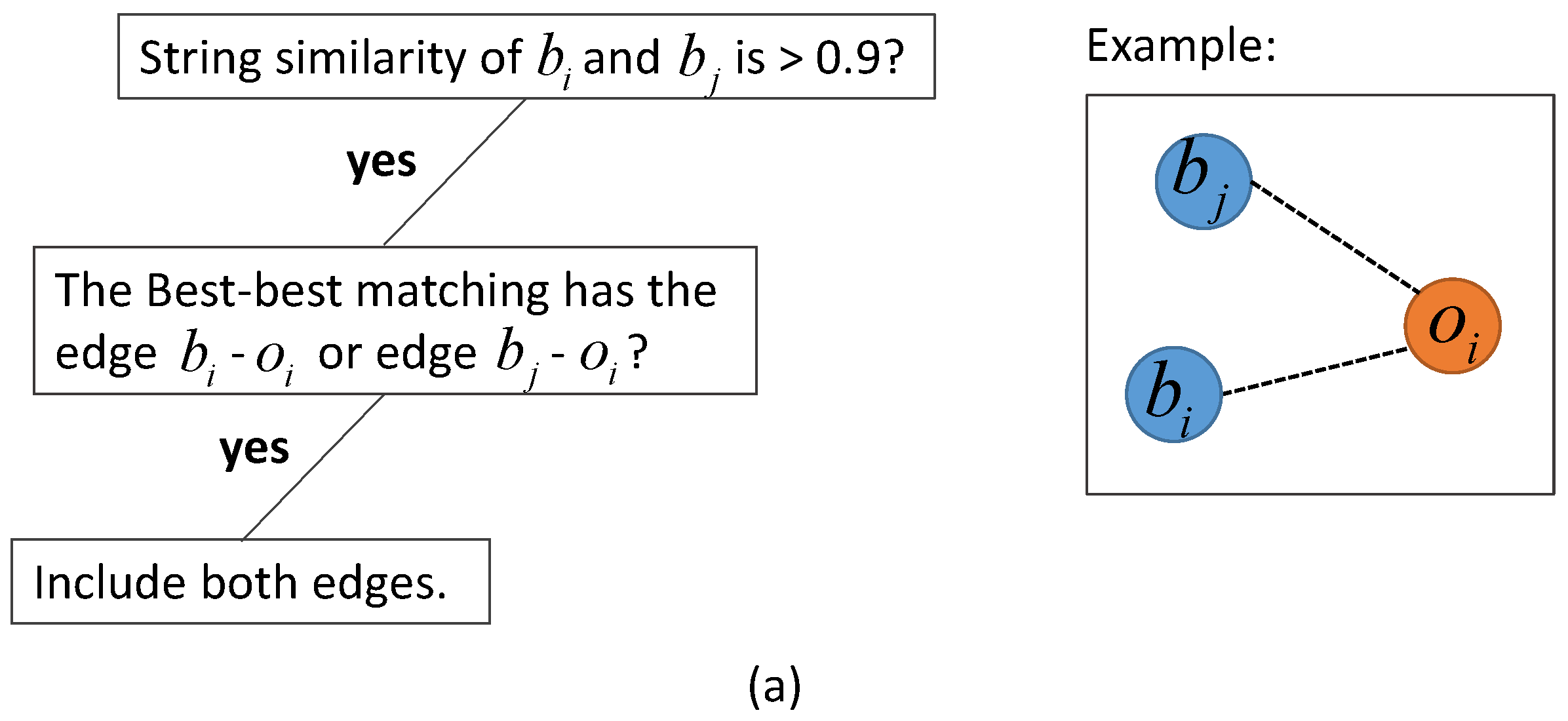
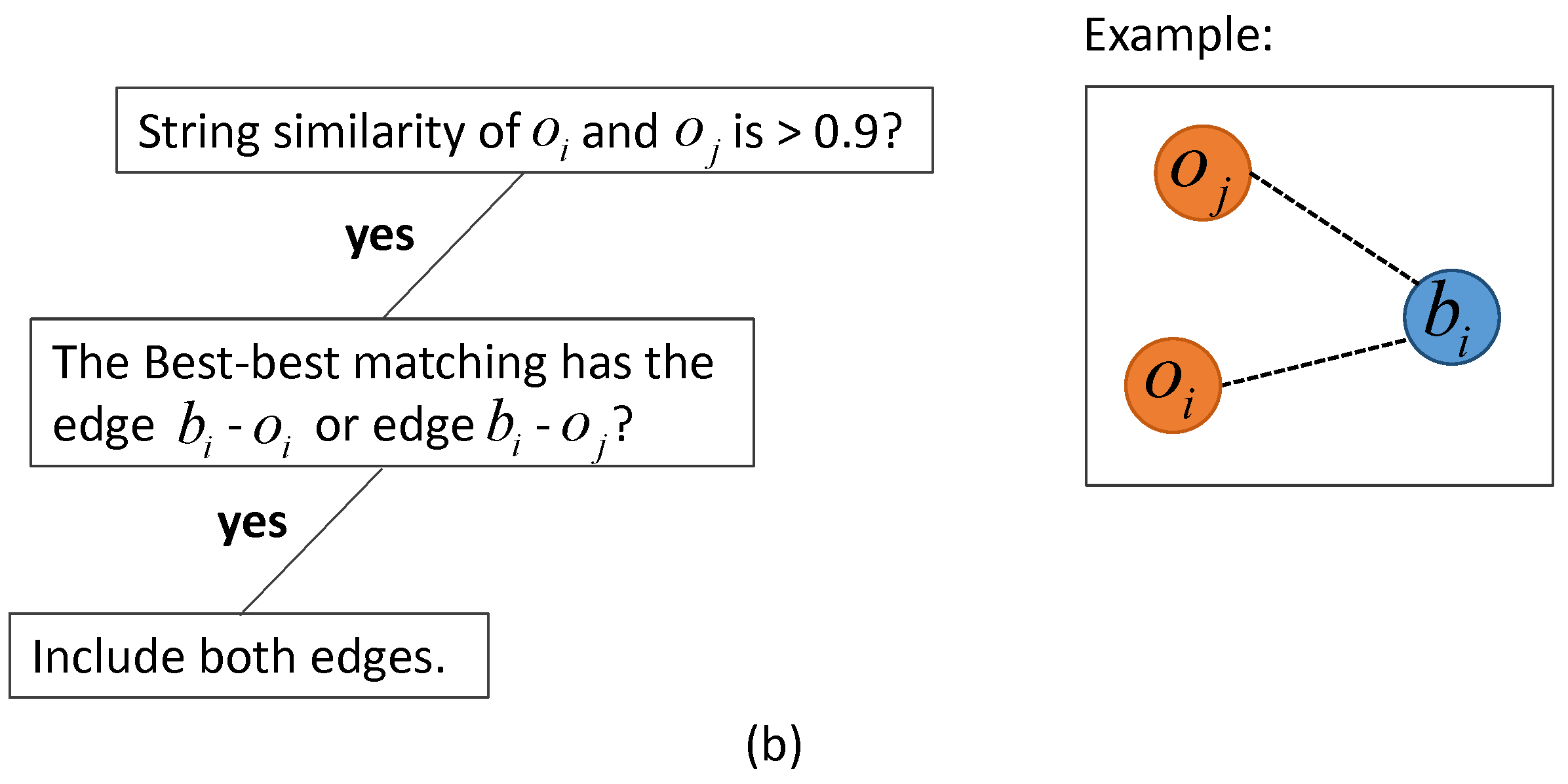
2.3. Graph-Based Matching Strategies
2.4. Considering Multiple Entries from the Same Venue
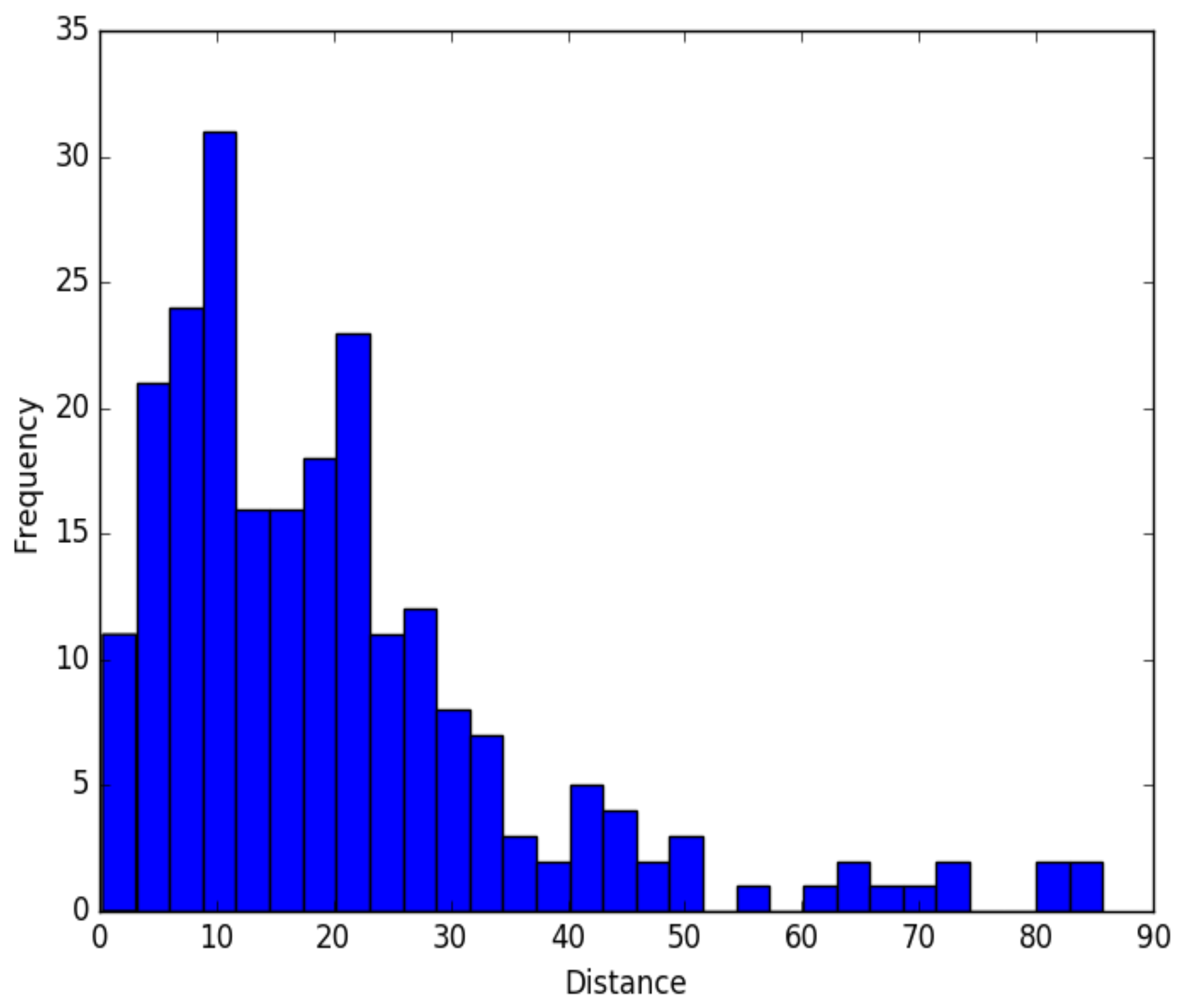
2.5. Experiment Design
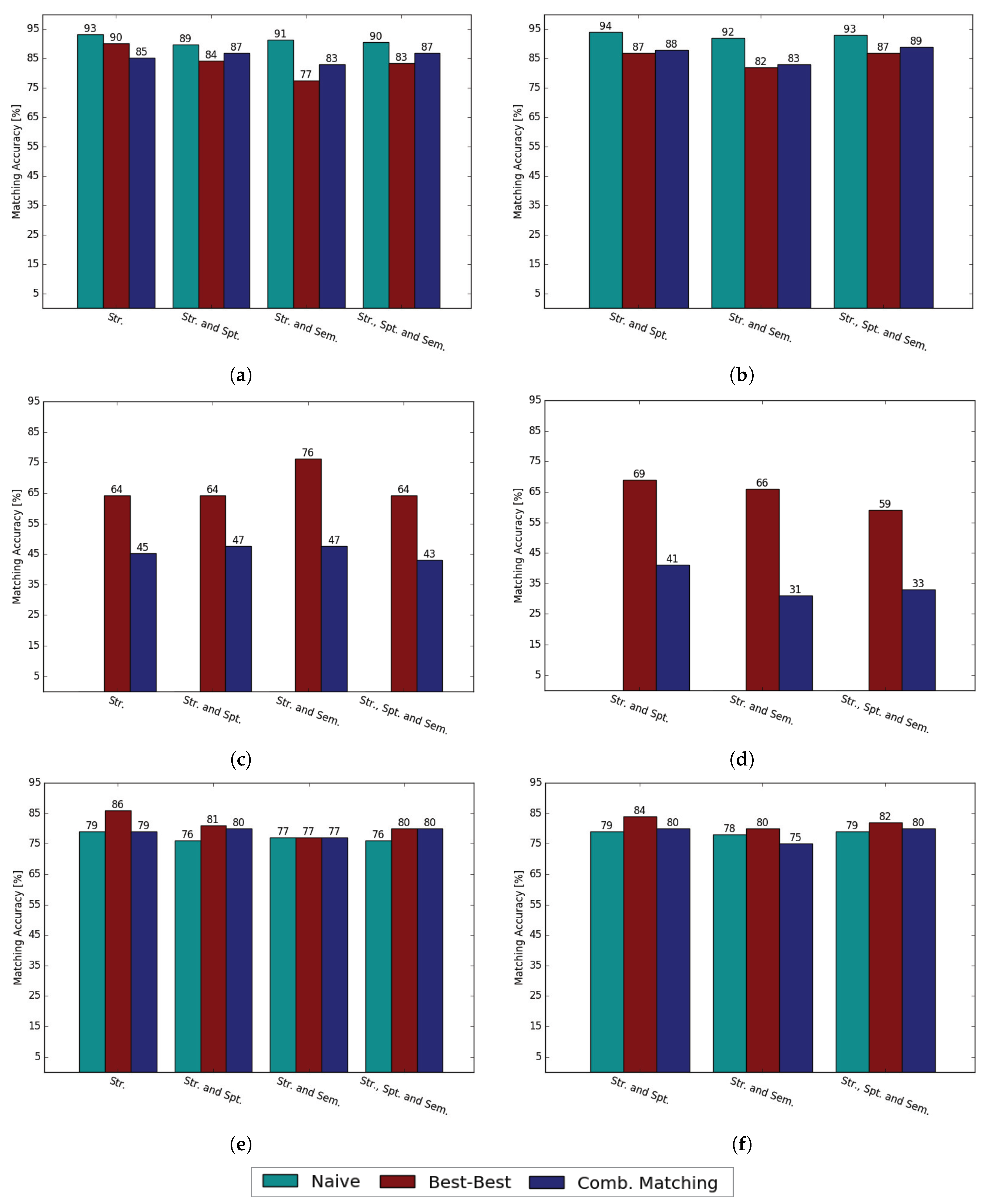
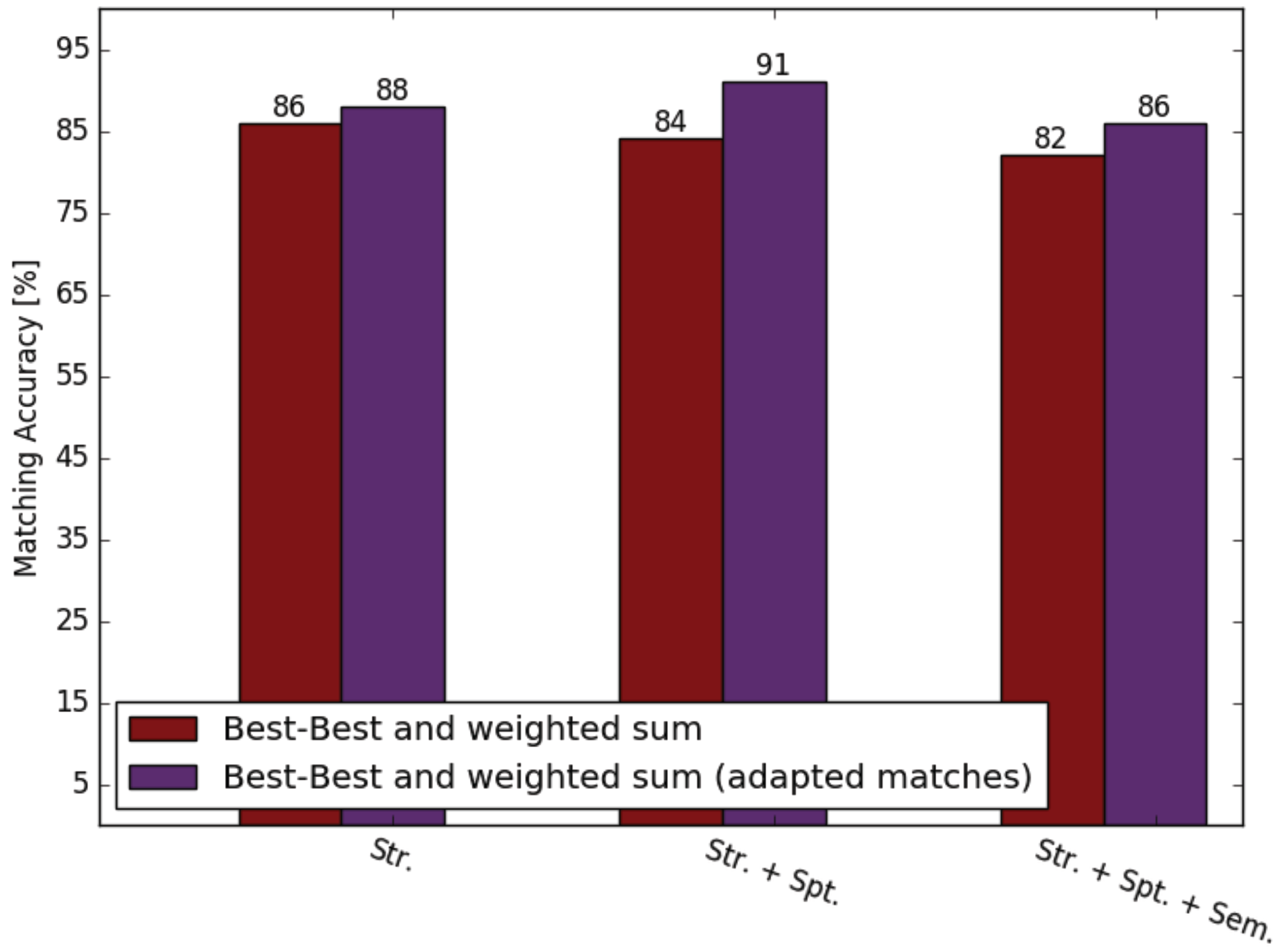
3. Results
4. Summary and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jonietz, D.; Zipf, A. Defining fitness-for-use for crowdsourced points of interest (POI). ISPRS Int. J. Geo-Inf. 2016, 5, 149. [Google Scholar] [CrossRef]
- Touya, G.; Antoniou, V.; Olteanu-Raimond, A.-M.; Van Damme, M.-D. Assessing crowdsourced POI quality: Combining methods based on reference data, history, and spatial relations. ISPRS Int. J. Geo-Inf. 2017, 6, 80. [Google Scholar] [CrossRef]
- Ballatore, A.; Zipf, A. A conceptual quality framework for volunteered geographic information. In Proceedings of the XII Conference on Spatial Information Theory, Santa Fe, NM, USA, 12–16 October 2015. [Google Scholar]
- Senaratne, H.; Mobasheri, A.; Ali, A.L.; Capieri, C.; Haklay, M. A review of volunteered geographic information quality assessment methods. Int. J. Geogr. Inf. Sci. 2016, 31, 139–167. [Google Scholar] [CrossRef]
- Degrossi, L.C.; Albuquerque, J.P.D.; Rocha, R.D.S.; Zipf, A. A framework of quality assessment methods for crowdsourced geographic information: A systematic literature review. In Proceedings of the 14th International Conference on Information Systems for Crisis Response and Management, Albi, France, 21–24 May 2017. [Google Scholar]
- Li, L.; Goodchild, M.F. An optimisation model for linear feature matching in geographical data conflation. Int. J. Image Data Fusion 2011, 2, 309–328. [Google Scholar] [CrossRef]
- Abdolmajidi, E.; Mansourian, A.; Will, J.; Harrie, L. Matching authority and VGI road networks using an extended node-based matching algorithm. Geo-Spat. Inf. Sci. 2015, 18, 65–80. [Google Scholar] [CrossRef]
- Hetch, R.; Kunze, C.; Hahmann, S. Measuring completness of building footprints in OpenStreetMap over space and time. ISPRS Int. J. Geo-Inf. 2013, 2, 1066–1091. [Google Scholar]
- Fan, H.; Zipf, A.; Fu, Q.; Neis, P. Quality assessment for building footprints data on OpenStreetMap. Int. J. Geogr. Inf. Sci. 2014, 28, 700–719. [Google Scholar] [CrossRef]
- Rutta, M.; Scioscia, F.; De Filippis, D.; Ieva, S.; Binetti, M.; Di Sciasco, E. A semantic-enhanced augmented reality tool for OpenStreetMap POI discovery. Transp. Res. Procedia 2014, 3, 479–488. [Google Scholar] [CrossRef]
- Guo, L.; Jiang, H.; Wang, X.; Liu, F. Learning to recommend point-of-interest with the weighted bayseian personalized ranking method in LBSNs. Information 2017, 8, 20. [Google Scholar] [CrossRef]
- Bakillah, M.; Liang, S.; Mobasheri, A.; Arsanjani, J.J.; Zipf, A. Fine-resolution population mapping using OpenStreetMap points-of-interest. Int. J. Geogr. Inf. Sci. 2014, 48, 1940–1963. [Google Scholar] [CrossRef]
- Jiang, S.; Alves, A.; Rodrigues, F.; Ferreira, J.; Pereira, F.C. Mining point-of-interest data from social networks for urban land use classification and disaggregation. Comput. Environ. Urban Syst. 2015, 53, 36–46. [Google Scholar] [CrossRef]
- Kunze, C.; Hecht, R. Semantic enrichment of building data with volunteered geographic information to improve mappings of dwelling units and population. Comput. Environ. Urban Syst. 2015, 53, 4–18. [Google Scholar] [CrossRef]
- Niu, N.; Liu, X.; Jin, H.; Ye, X.; Liu, Y.; Li, X.; Chen, Y.; Li, S. Integrating multi-source big data to infer building functions. Int. J. Geogr. Inf. Sci. 2017, 31, 1871–1890. [Google Scholar] [CrossRef]
- Calegari, G.R.; Carlino, E.; Peroni, D.; Celino, I. Extracting urban land use from linked open geospatial data. ISPRS Int. J. Geo-Inf. 2015, 4, 2109–2130. [Google Scholar] [CrossRef]
- Arsanjani, J.J.; Helbich, M.; Bakillah, M.; Hagenauer, J.; Zipf, A. Toward mapping land-use patterns from volunteered geographic information. Int. J. Geogr. Inf. Sci. 2013, 27, 2264–2278. [Google Scholar] [CrossRef]
- Liu, X.; Long, Y. Automated identification and characterization of parcels with OpenStreetMap and points of interest. Environ. Plan. B Plan. Des. 2016, 42, 341–360. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, Y.; Lu, F. Geometric-based approach for integrating VGI POIs and road networks. Int. J. Geogr. Inf. Sci. 2014, 28, 126–147. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, Y. Pattern-mining approach for conflating crowdsourcing road networks with POIs. Int. J. Geogr. Inf. Sci. 2015, 29, 786–805. [Google Scholar] [CrossRef]
- Pouke, M.; Goncalves, J.; Ferreira, D.; Kostakos, V. Pratical simulation of virtual crowds using points of interests. Comput. Environ. Urban Syst. 2015, 57, 118–129. [Google Scholar] [CrossRef]
- Sun, Y. Investigating “locality” of intra-urban spatial interactions in New York city using Foursquare data. Int. J. Geo-Inf. 2016, 5, 43. [Google Scholar] [CrossRef]
- Fang, Z.; Li, Q.; Zhang, X.; Shaw, S.-L. A GIS data model for landmark-based pedestrian navigation. Int. J. Geogr. Inf. Sci. 2012, 26, 817–838. [Google Scholar] [CrossRef]
- Roussel, A.; Zipf, A. Toward a landmark-based pedestrian navigation service using OSM data. Int. J. Geo-Inf. 2017, 6, 64. [Google Scholar] [CrossRef]
- Delgado, F.; Martínez-Gonzales, M.M.; Finat, J. An evaluation of ontology matching techniques on geospatial ontologies. Int. J. Geogr. Inf. Sci. 2013, 27, 2279–2301. [Google Scholar] [CrossRef]
- Mckenzie, G.; Janowicz, K.; Adams, B. Weighted multi-attribute matching of user-generated points of interest. Cartogr. Geogr. Inf. Sci. 2014, 41, 125–137. [Google Scholar] [CrossRef]
- Li, L.; Xing, X.; Xia, H.; Huang, X. Entropy-weighted instance matching between different sourcing points of interest. Entropy 2016, 18, 45. [Google Scholar] [CrossRef]
- Novack, T.; Peters, R.; Zipf, A. Graph-based strategies for matching points-of-interests from different VGI sources. In Proceedings of the 20th AGILE Conference, Wageningen, The Netherlands, 9–12 May 2017. [Google Scholar]
- Vasardani, M.; Winter, S.; Richter, K.F. Locating place names from place descriptions. Int. J. Geogr. Inf. Sci. 2013, 27, 2509–2532. [Google Scholar] [CrossRef]
- Kim, J.; Vasardani, M.; Winter, S. Similarity matching for integrating spatial information extracted from place descriptions. Int. J. Geogr. Inf. Sci. 2017, 31, 56–80. [Google Scholar] [CrossRef]
- Scheffer, T.; Schirru, R.; Lehmann, P. Matching points of interest from different social networking sites. In KL 2012: Advances in Artificial Intelligence; Glimm, B., Krüger, A., Eds.; Springer: Berlin, Germany, 2012; pp. 245–248. ISBN 978-3-642-33346-0. [Google Scholar]
- Cohen, W.W.; Ravikumar, P.; Fienberg, S.E. A comparison of string distance metrics for name-matching tasks. In Proceedings of the 2003 International Joint Conferences on Artificial Intelligence (IJCAI-03), Acapulco, Mexico, 9–10 August 2003. [Google Scholar]
- Meltzoff, A.N.; Kuhl, P.K.; Movellan, J.; Sejnowski, T.J. Foundations for a new science of learning. Science 2009, 325, 284–288. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Cai, M.; Yuan, H.; Shi, X.; Zhang, W.; Liu, J. Phonotactic language recognition based on Dnn-HMM acoustic model. In Proceedings of the 9th International Symposium on Chinese Spoken Language Processing (ISCSLP), Singapore, 12–14 September 2014; pp. 153–157. [Google Scholar]
- Ballatore, A.; Bertolotto, M.; Wilson, D.C. The semantic similarity ensemble. J. Spat. Inf. Sci. 2016, 7, 27–44. [Google Scholar] [CrossRef]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent Dirichlet Allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Rodrigues, F.; Alves, A.; Polisciuc, E.; Jiang, S.; Ferreira, J.; Pereira, F.C. Estimating disaggregated employment size from points-of-interest and census data: From mining the web to model implementation and visualization. Int. J. Adv. Intell. Syst. 2013, 6, 41–52. [Google Scholar]
- Olteanu-Raimond, A.M.; Mustière, S.; Ruas, A. Knowledge formalization for vector data matching using belief theory. J. Spat. Inf. Sci. 2015, 10, 21–46. [Google Scholar] [CrossRef]
- Foursquare. Available online: https://foursquare.com/about (accessed on 11 January 2018).
- Yelp. Available online: https://www.yelp.com/about (accessed on 11 January 2018).
- Levenshtein, V.I. Binary codes capable of correcting deletions, insertions and reversals. Sov. Phys. Dokl. 1966, 10, 707–710. [Google Scholar]
- Bonzanini, M. Fuzzy String Matching in Python. Available online: https://marcobonzanini.com/2015/02/25/fuzzy-string-matching-in-python/ (accessed on 12 March 2018).
- Miller, G.A. WorldNet: A lexical database for English. Commun. ACM 1995, 38, 39–41. [Google Scholar] [CrossRef]
- Meng, L.; Huang, R.; Gu, J. A review of semantic similarity measures in WordNet. Int. J. Hybrid Inf. Technol. 2013, 6, 1–12. [Google Scholar]
- Sánchez, D.; Batet, M. A semantic similarity method based on information content exploiting multiple ontologies. Expert Syst. Appl. 2013, 40, 1393–1399. [Google Scholar] [CrossRef]
- Al-Bakri, M.; Fairbairn, D. Assessing similarity matching for possible integration of feature classifications of geospatial data from official and informal sources. Int. J. Geogr. Inf. Sci. 1995, 26, 1437–1456. [Google Scholar] [CrossRef]
- Lin, D. An information-theoretic definition of similarity. In Proceedings of the 15th International Conference on Machine Learning, Madison, WI, USA, 24–27 July 1998. [Google Scholar]
- Landes, S.; Leacock, C.; Fellbaum, C. Building semantic concordances. In WordNet: An Electronical Lexical Database; Fellbaum, C., Ed.; The MIT Press: London, UK, 1998; pp. 199–216. [Google Scholar]
- Galil, Z. Efficient algorithms for finding maximal matching in graphs. J. ACM Comput. Surv. 1986, 18, 23–38. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian method for assignment problems. Nav. Res. Logist. Q. 1955, 3, 253–258. [Google Scholar] [CrossRef]
- Zwillinger, D.; Kokosa, S. Standard Probability and Statistics Tables and Formulae; Chapman and Hall: London, UK, 2000; p. 480. [Google Scholar]
| Sample Types | Purpose Is to Evaluate the Models Performance in Detecting … | Amount |
|---|---|---|
| One-to-one | Cases when a POI from OSM should be matched with only one POI from Foursquare and vice-versa. | 195 |
| One-to-none | Cases when a POI from OSM does not have any match in Foursquare and should therefore be left unmatched. | 42 |
| One-to-many | Cases when more than one POI from OSM should be matched to the same Foursquare POI and cases when more than one POI from Foursquare should be matched to the same POI from OSM. | 34 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Novack, T.; Peters, R.; Zipf, A. Graph-Based Matching of Points-of-Interest from Collaborative Geo-Datasets. ISPRS Int. J. Geo-Inf. 2018, 7, 117. https://doi.org/10.3390/ijgi7030117
Novack T, Peters R, Zipf A. Graph-Based Matching of Points-of-Interest from Collaborative Geo-Datasets. ISPRS International Journal of Geo-Information. 2018; 7(3):117. https://doi.org/10.3390/ijgi7030117
Chicago/Turabian StyleNovack, Tessio, Robin Peters, and Alexander Zipf. 2018. "Graph-Based Matching of Points-of-Interest from Collaborative Geo-Datasets" ISPRS International Journal of Geo-Information 7, no. 3: 117. https://doi.org/10.3390/ijgi7030117
APA StyleNovack, T., Peters, R., & Zipf, A. (2018). Graph-Based Matching of Points-of-Interest from Collaborative Geo-Datasets. ISPRS International Journal of Geo-Information, 7(3), 117. https://doi.org/10.3390/ijgi7030117





