Deriving Animal Movement Behaviors Using Movement Parameters Extracted from Location Data
Abstract
1. Introduction
2. Background
3. Methodology
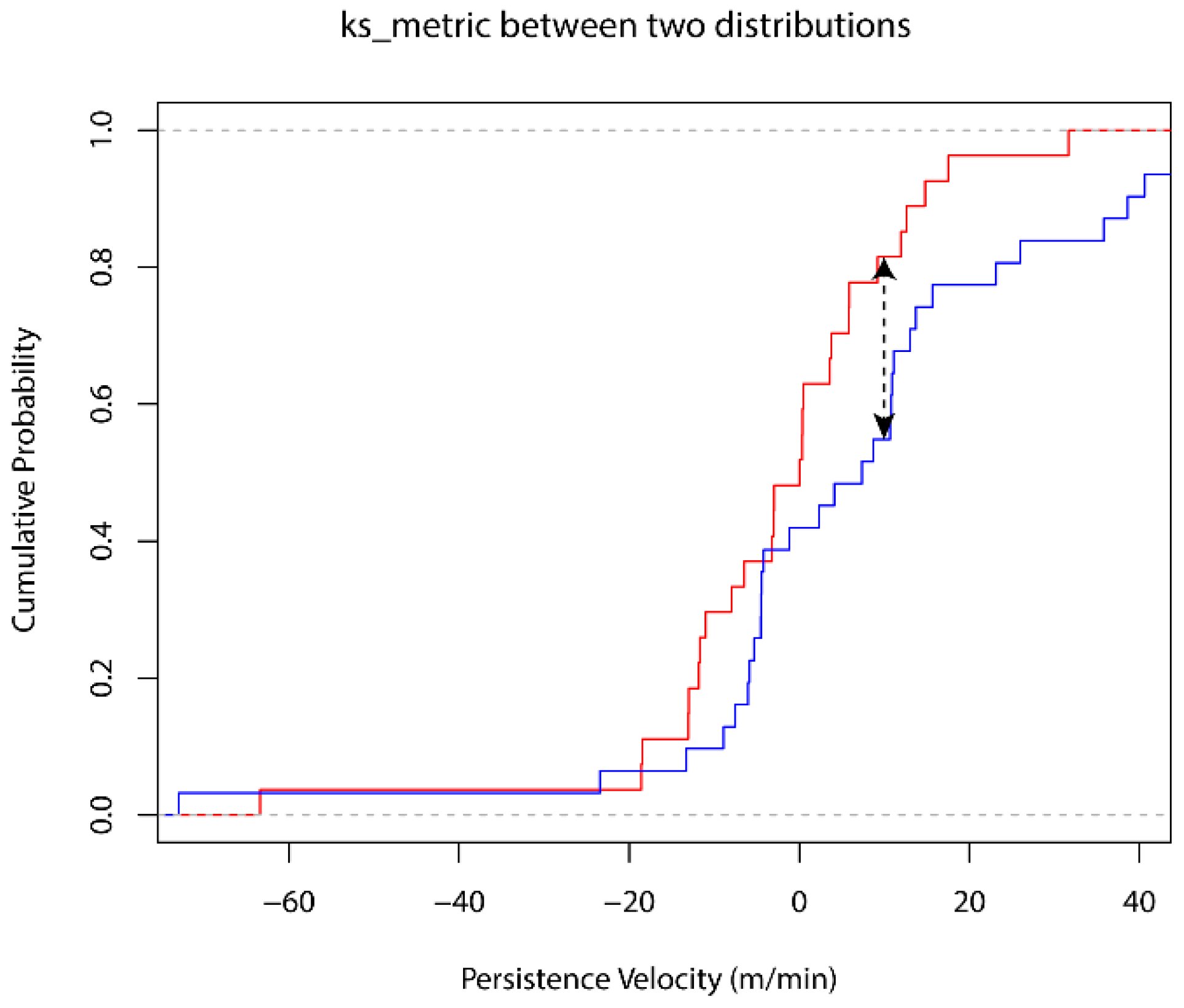
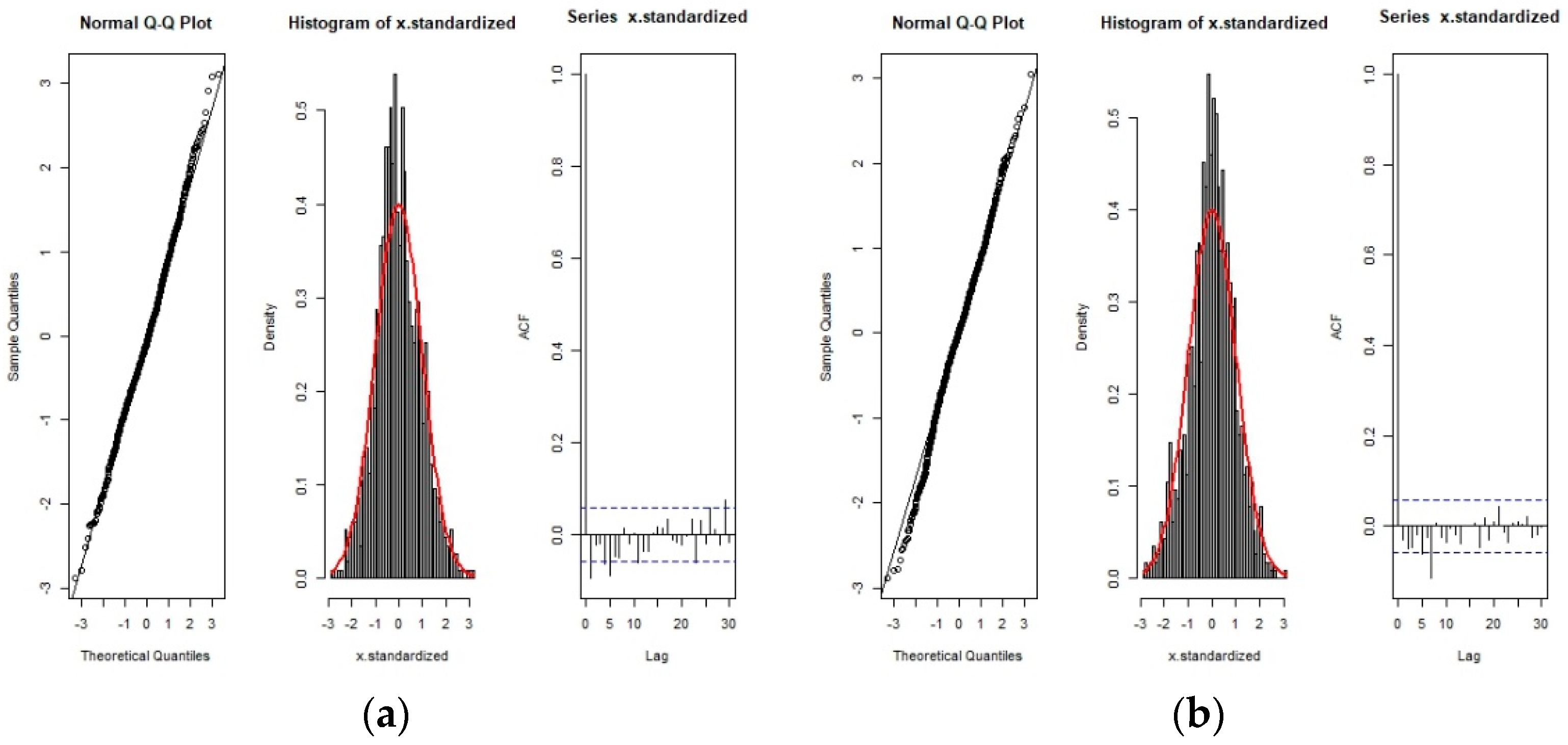
3.1. Behavioral Change Point Analysis (BCPA)
3.1.1. Moving Window Size
3.1.2. Movement Parameters and Movement Behavior
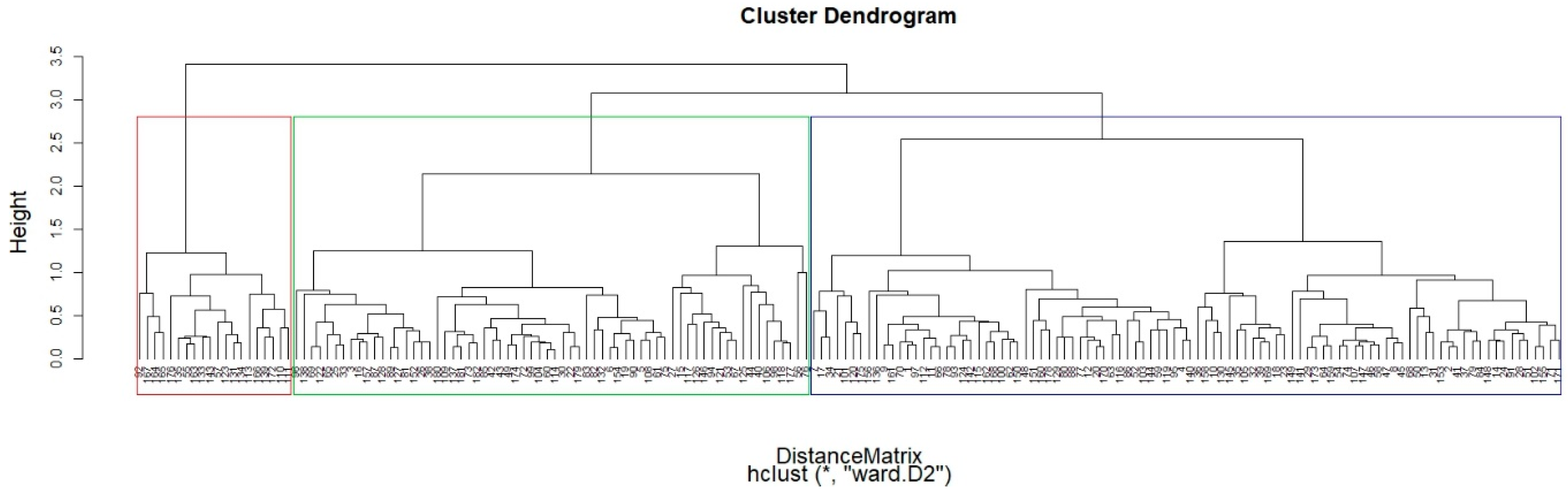
3.2. Hierarchical Clustering
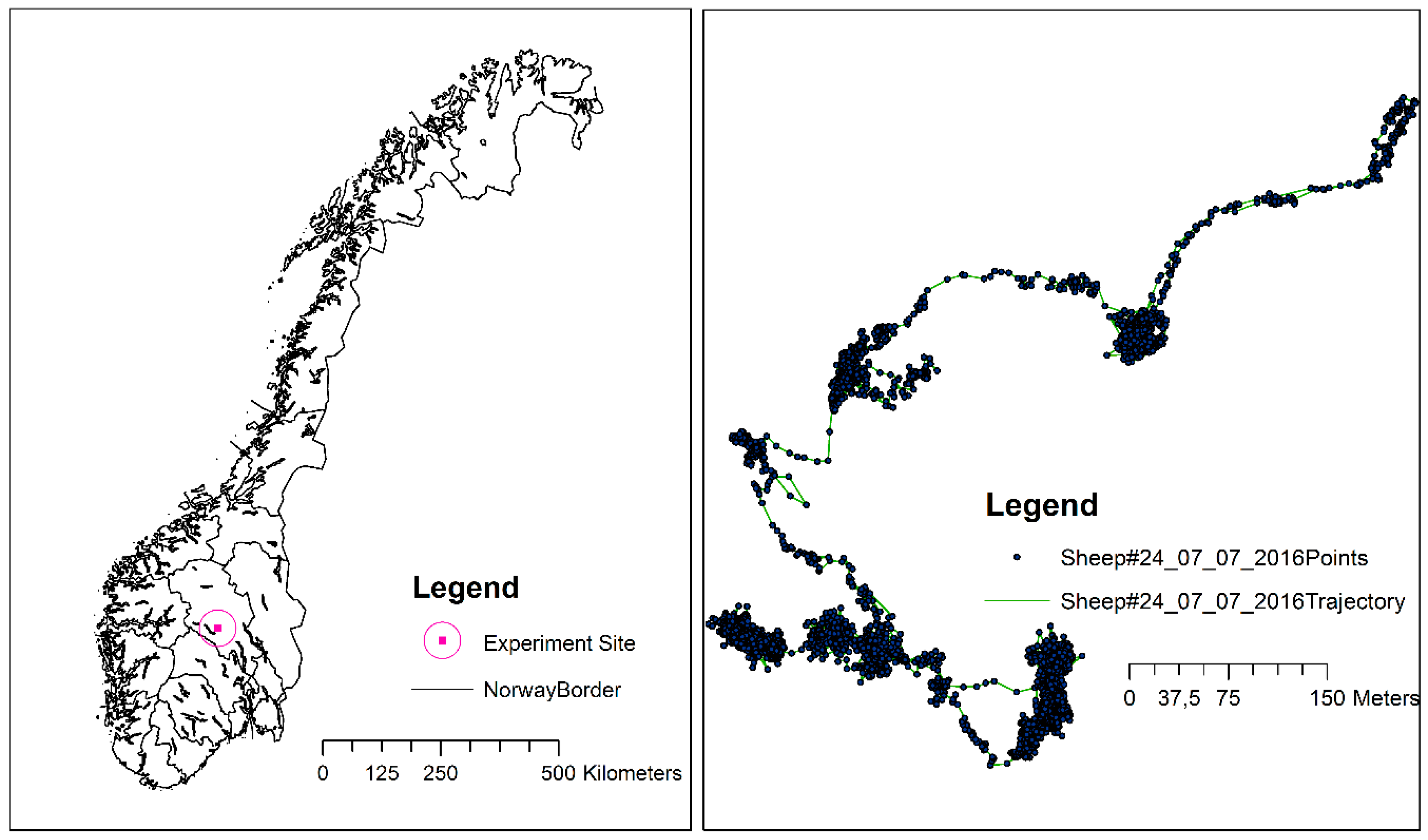
4. Case Study
5. Results
6. Concluding Remarks
Supplementary Materials
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Cooke, S.J.; Hinch, S.G.; Wikelski, M.; Andrews, R.D.; Kuchel, L.J.; Wolcott, T.G.; Butler, P.J. Biotelemetry: A mechanistic approach to ecology. Trends Ecol. Evol. 2004, 19, 334–343. [Google Scholar] [CrossRef] [PubMed]
- Dray, S.; Royer-Carenzi, M.; Calenge, C. The exploratory analysis of autocorrelation in animal-movement studies. Ecol. Res. 2010, 25, 673–681. [Google Scholar] [CrossRef]
- Morales, J.M.; Haydon, D.T.; Frair, J.; Holsinger, K.E.; Fryxell, J.M. Extracting more out of relocation data: Building movement models as mixtures of random walks. Ecology 2004, 85, 2436–2445. [Google Scholar] [CrossRef]
- Edelhoff, H.; Signer, J.; Balkenhol, N. Path segmentation for beginners: An overview of current methods for detecting changes in animal movement patterns. Mov. Ecol. 2016, 4, 21. [Google Scholar] [CrossRef] [PubMed]
- Patterson, T.A.; Thomas, L.; Wilcox, C.; Ovaskainen, O.; Matthiopoulos, J. State-space models of individual animal movement. Trends Ecol. Evol. 2008, 23, 87–94. [Google Scholar] [CrossRef] [PubMed]
- Dodge, S.; Weibel, R.; Lautensch, A.-K. Towards a taxonomy of movement patterns. Inf. Vis. 2008, 7, 240–252. [Google Scholar] [CrossRef]
- Guo, Y.; Poulton, G.; Corke, P.; Bishop-Hurley, G.J.; Wark, T.; Swain, D.L. Using accelerometer, high sample rate GPS and magnetometer data to develop a cattle movement and behaviour model. Ecol. Model. 2009, 220, 2068–2075. [Google Scholar] [CrossRef]
- de Weerd, N.; van Langevelde, F.; van Oeveren, H.; Nolet, B.A.; Kölzsch, A.; Prins, H.H.; de Boer, W.F. Deriving animal behaviour from high-frequency GPS: Tracking cows in open and forested habitat. PLoS ONE 2015, 10, e0129030. [Google Scholar] [CrossRef] [PubMed]
- Gurarie, E.; Andrews, R.D.; Laidre, K.L. A novel method for identifying behavioural changes in animal movement data. Ecol. Lett. 2009, 12, 395–408. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Lee, J.-G.; Kamber, M. An overview of clustering methods in geographic data analysis. In Geographic Data Mining and Knowledge Discovery, 2nd ed.; Miller, H.J., Han, J., Eds.; CRC Press: Boca Raton, FL, USA, 2009; pp. 149–187. [Google Scholar]
- Schick, R.S.; Loarie, S.R.; Colchero, F.; Best, B.D.; Boustany, A.; Conde, D.A.; Halpin, P.N.; Joppa, L.N.; McClellan, C.M.; Clark, J.S. Understanding movement data and movement processes: Current and emerging directions. Ecol. Lett. 2008, 11, 1338–1350. [Google Scholar] [CrossRef] [PubMed]
- Gurarie, E.; Bracis, C.; Delgado, M.; Meckley, T.D.; Kojola, I.; Wagner, C.M. What is the animal doing? Tools for exploring behavioural structure in animal movements. J. Anim. Ecol. 2016, 85, 69–84. [Google Scholar] [CrossRef] [PubMed]
- Demšar, U.; Buchin, K.; Cagnacci, F.; Safi, K.; Speckmann, B.; Van de Weghe, N.; Weiskopf, D.; Weibel, R. Analysis and visualisation of movement: An interdisciplinary review. Mov. Ecol. 2015, 3, 5. [Google Scholar] [CrossRef] [PubMed]
- Postlethwaite, C.M.; Brown, P.; Dennis, T.E. A new multi-scale measure for analysing animal movement data. J. Theor. Biol. 2013, 317, 175–185. [Google Scholar] [CrossRef] [PubMed]
- Schwager, M.; Anderson, D.M.; Butler, Z.; Rus, D. Robust classification of animal tracking data. Comput. Electron. Agric. 2007, 56, 46–59. [Google Scholar] [CrossRef]
- Jonsen, I.D.; Flemming, J.M.; Myers, R.A. Robust state-space modeling of animal movement data. Ecology 2005, 86, 2874–2880. [Google Scholar] [CrossRef]
- Gutenkunst, R.; Newlands, N.; Lutcavage, M.; Edelstein-Keshet, L. Inferring resource distributions from Atlantic bluefin tuna movements: An analysis based on net displacement and length of track. J. Theor. Biol. 2007, 245, 243–257. [Google Scholar] [CrossRef] [PubMed]
- Fauchald, P.; Tveraa, T. Using first-passage time in the analysis of area-restricted search and habitat selection. Ecology 2003, 84, 282–288. [Google Scholar] [CrossRef]
- Tremblay, Y.; Roberts, A.J.; Costa, D.P. Fractal landscape method: An alternative approach to measuring area-restricted searching behavior. J. Exp. Biol. 2007, 210, 935–945. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jonsen, I.D.; Myers, R.A.; Flemming, J.M. Meta-analysis of animal movement using state-space models. Ecology 2003, 84, 3055–3063. [Google Scholar] [CrossRef]
- Zhang, J.; O’Reilly, K.M.; Perry, G.L.W.; Taylor, G.A.; Dennis, T.E. Extending the Functionality of Behavioural Change-Point Analysis with k-Means Clustering: A Case Study with the Little Penguin (Eudyptula minor). PLoS ONE 2015, 10, e0122811. [Google Scholar] [CrossRef] [PubMed]
- Lavielle, M. Detection of multiple changes in a sequence of dependent variables. Stoch. Process. Their Appl. 1999, 83, 79–102. [Google Scholar] [CrossRef]
- Rinzivillo, S.; Pedreschi, D.; Nanni, M.; Giannotti, F.; Andrienko, N.; Andrienko, G. Visually driven analysis of movement data by progressive clustering. Inf. Vis. 2008, 7, 225–239. [Google Scholar] [CrossRef]
- Lee, J.-G.; Han, J.; Whang, K.-Y. Trajectory clustering: A partition-and-group framework. In Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data, Beijing, China, 11–14 June 2007; ACM: New York, NY, USA, 2007; pp. 593–604. [Google Scholar]
- Miller, H.J.; Han, J. Geographic Data Mining and Knowledge Discovery, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Etienne, L.; Devogele, T.; Bouju, A. Spatio-temporal trajectory analysis of mobile objects following the same itinerary. Adv. Geo-Spat. Inf. Sci. 2012, 10, 47–57. [Google Scholar]
- Nanni, M.; Pedreschi, D. Time-focused clustering of trajectories of moving objects. J. Intell. Inf. Syst. 2006, 27, 267–289. [Google Scholar] [CrossRef]
- Dodge, S.; Laube, P.; Weibel, R. Movement similarity assessment using symbolic representation of trajectories. Int. J. Geogr. Inf. Sci. 2012, 26, 1563–1588. [Google Scholar] [CrossRef]
- Yanagisawa, Y.; Akahani, J.-I.; Satoh, T. Shape-Based Similarity Query for Trajectory of Mobile Objects. In Proceedings of the 4th International Conference on Mobile Data Management, Melbourne, Australia, 21–24 January 2003; Chen, M.-S., Chrysanthis, P.K., Sloman, M., Zaslavsky, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 63–77. [Google Scholar]
- Vlachos, M.; Gunopulos, D.; Das, G. Rotation invariant distance measures for trajectories. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004; ACM: New York, NY, USA, 2004; pp. 707–712. [Google Scholar]
- Chen, L.; Özsu, M.T.; Oria, V. Robust and fast similarity search for moving object trajectories. In Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data, Baltimore, Maryland, 14–16 June 2005; ACM: New York, NY, USA, 2005; pp. 491–502. [Google Scholar]
- Vlachos, M.; Gunopoulos, D.; Kollios, G. Discovering Similar Multidimensional Trajectories. In Proceedings of the 18th International Conference on Data Engineering, San Jose, CA, USA, 26 February–1 March 2002; p. 673. [Google Scholar]
- Alt, H.; Guibas, L.J. Discrete geometric shapes: Matching, interpolation, and approximation. Handb. Comput. Geom. 1999, 1, 121–153. [Google Scholar]
- Alt, H.; Godau, M. Computing the Fréchet distance between two polygonal curves. Int. J. Comput. Geom. Appl. 1995, 5, 75–91. [Google Scholar] [CrossRef]
- Andrienko, G.; Andrienko, N.; Wrobel, S. Visual analytics tools for analysis of movement data. ACM SIGKDD Explor. Newsl. 2007, 9, 38–46. [Google Scholar] [CrossRef]
- Pelekis, N.; Andrienko, G.; Andrienko, N.; Kopanakis, I.; Marketos, G.; Theodoridis, Y. Visually exploring movement data via similarity-based analysis. J. Intell. Inf. Syst. 2012, 38, 343–391. [Google Scholar] [CrossRef]
- Thiebault, A.; Tremblay, Y. Splitting animal trajectories into fine-scale behaviorally consistent movement units: Breaking points relate to external stimuli in a foraging seabird. Behav. Ecol. Sociobiol. 2013, 67, 1013–1026. [Google Scholar] [CrossRef]
- Cagnacci, F.; Boitani, L.; Powell, R.A.; Boyce, M.S. Animal ecology meets GPS-based radiotelemetry: A perfect storm of opportunities and challenges. R. Soc. 2010. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Gurarie, E. Behavioral Change Point Analysis in R: The bcpa package (R package version 1.1). Available online: https://pdfs.semanticscholar.org/dc3e/3c9baac39d228f1dd2de4b35431395c76fd3.pdf (accessed on 22 February 2018).
- Calenge, C.; Dray, S.; Royer-Carenzi, M. The concept of animals’ trajectories from a data analysis perspective. Ecol. Inf. 2009, 4, 34–41. [Google Scholar] [CrossRef]
- Benhamou, S. How to reliably estimate the tortuosity of an animal’s path: Straightness, sinuosity, or fractal dimension? J. Theor. Biol. 2004, 229, 209–220. [Google Scholar] [CrossRef] [PubMed]
- Laube, P.; Purves, R.S. How fast is a cow? Cross-scale analysis of movement data. Trans. GIS 2011, 15, 401–418. [Google Scholar] [CrossRef]
- Murtagh, F. A survey of recent advances in hierarchical clustering algorithms. Comput. J. 1983, 26, 354–359. [Google Scholar] [CrossRef]
- Berkhin, P. A survey of clustering data mining techniques. Group. Multidimens. Data 2006, 25, 71. [Google Scholar]
- Van Moorter, B.; Visscher, D.R.; Jerde, C.L.; Frair, J.L.; Merrill, E.H. Identifying movement states from location data using cluster analysis. J. Wildl. Manag. 2010, 74, 588–594. [Google Scholar] [CrossRef]
- Garriga, J.; Palmer, J.R.; Oltra, A.; Bartumeus, F. Expectation-maximization binary clustering for behavioural annotation. PLoS ONE 2016, 11, e0151984. [Google Scholar] [CrossRef] [PubMed]
- Braun, E.; Geurten, B.; Egelhaaf, M. Identifying prototypical components in behaviour using clustering algorithms. PLoS ONE 2010, 5, e9361. [Google Scholar] [CrossRef] [PubMed]
- Hurford, A. GPS measurement error gives rise to spurious 180 turning angles and strong directional biases in animal movement data. PLoS ONE 2009, 4, e5632. [Google Scholar] [CrossRef] [PubMed]
- Pewsey, A.; Neuhäuser, M.; Ruxton, G.D. Circular Statistics in R; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Jammalamadaka, S.R.; Sengupta, A. Topics in Circular Statistics; World Scientific: Singapore, 2001. [Google Scholar]
- Rachev, S.T.; Klebanov, L.B.; Stoyanov, S.V.; Fabozzi, F.J. Probability distances and probability metrics: Definitions. In The Methods of Distances in the Theory of Probability and Statistics; Springer: Cham, Switzerland, 2013; pp. 11–31. [Google Scholar]
- Rokach, L. A survey of clustering algorithms. In Data Mining and Knowledge Discovery Handbook; Maimon, O., Rokach, L., Eds.; Springer: New York, NY, USA, 2010; pp. 269–298. [Google Scholar]
- Calenge, C. The package “adehabitat” for the R software: A tool for the analysis of space and habitat use by animals. Ecol. Model. 2006, 197, 516–519. [Google Scholar] [CrossRef]
- Kareiva, P.; Shigesada, N. Analyzing insect movement as a correlated random walk. Oecologia 1983, 56, 234–238. [Google Scholar] [CrossRef] [PubMed]
- Deza, M.M.; Deza, E. Encyclopedia of distances. In Encyclopedia of Distances; Springer: Cham, Switzerland, 2009; pp. 1–583. [Google Scholar]
- Gibbs, A.L.; Su, F.E. On choosing and bounding probability metrics. Int. Stat. Rev. 2002, 70, 419–435. [Google Scholar] [CrossRef]
- Murtagh, F.; Legendre, P. Ward’s hierarchical agglomerative clustering method: Which algorithms implement ward’s criterion? J. Classif. 2014, 31, 274–295. [Google Scholar] [CrossRef]
- Bridges, C.C., Jr. Hierarchical cluster analysis. Psychol. Rep. 1966, 18, 851–854. [Google Scholar] [CrossRef]
- Xu, R.; Wunsch, D. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef] [PubMed]
- Köhn, H.-F.; Hubert, L.J. Hierarchical Cluster Analysis. In Wiley StatsRef: Statistics Reference Online; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Vijaya, P.; Murty, M.N.; Subramanian, D. Leaders—Subleaders: An efficient hierarchical clustering algorithm for large data sets. Pattern Recognit. Lett. 2004, 25, 505–513. [Google Scholar] [CrossRef]

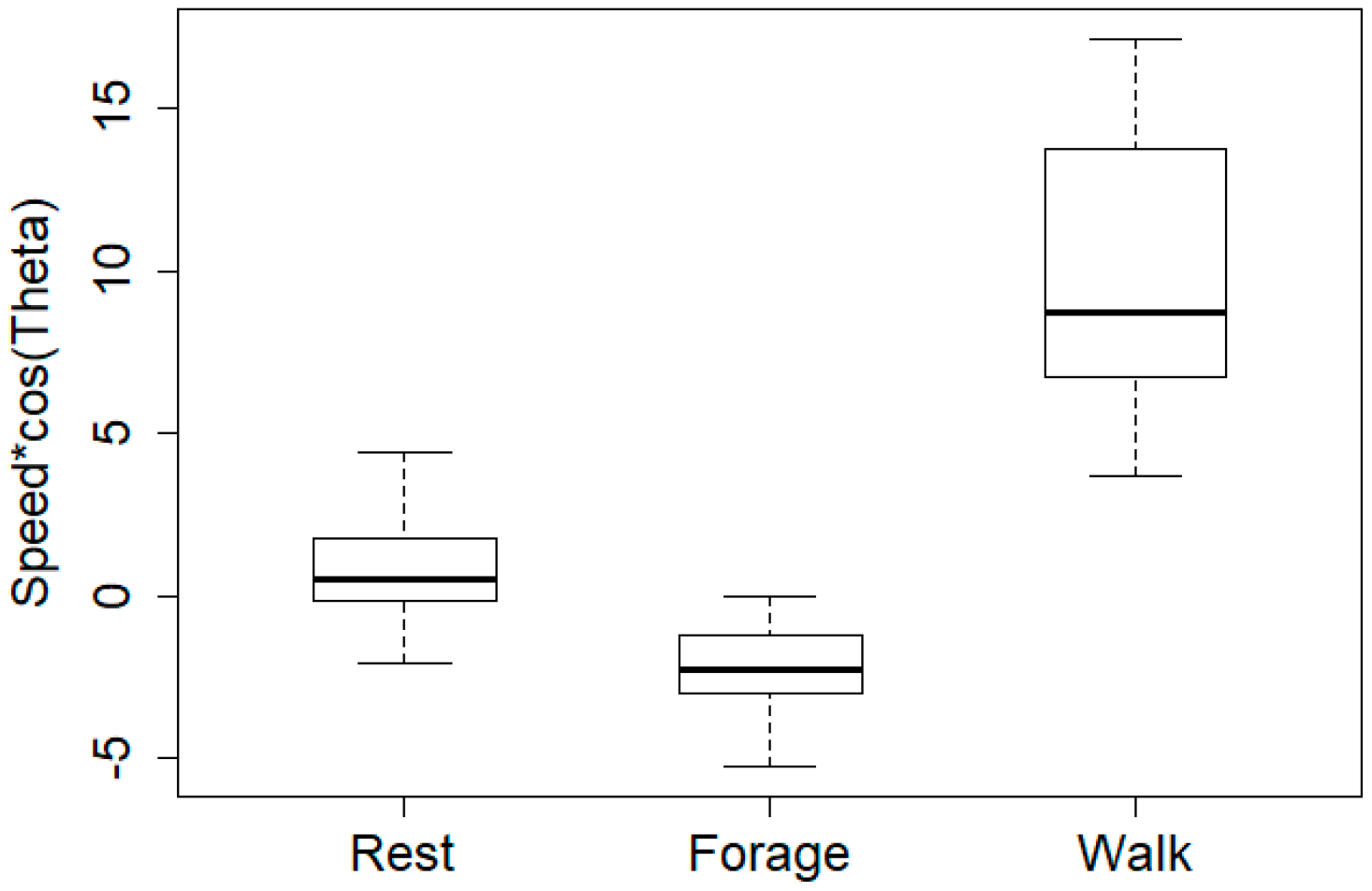
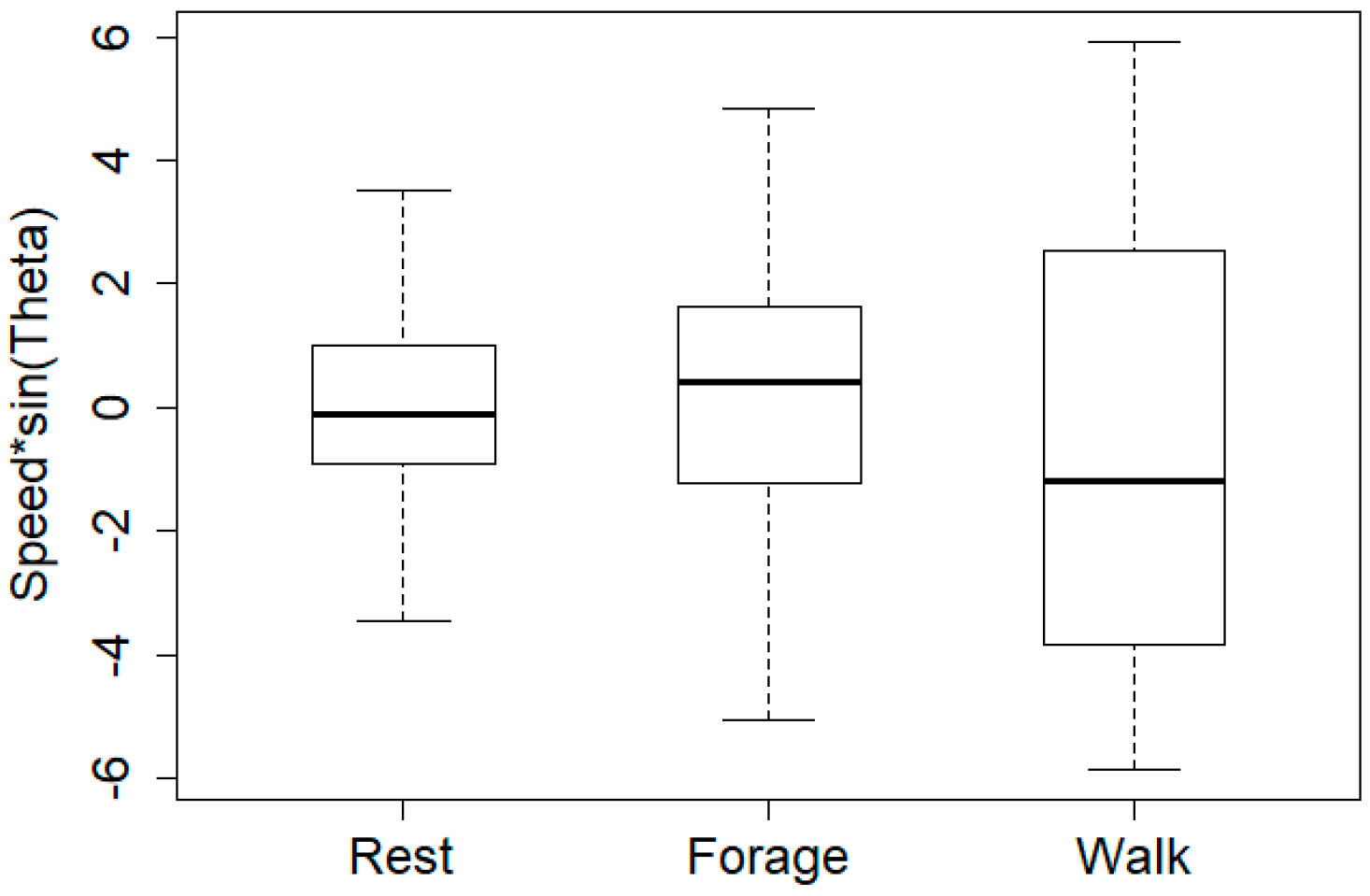
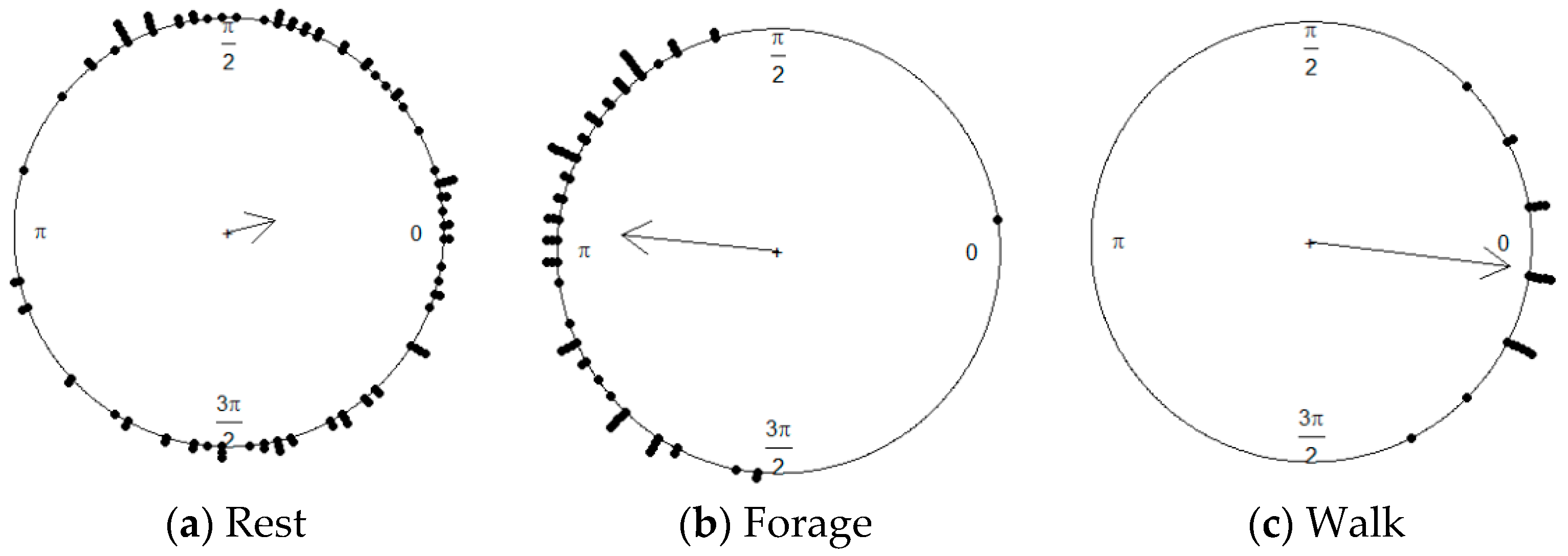
| Predicted | Forage | Rest | Walk | |
|---|---|---|---|---|
| Real | ||||
| Forage | 184 (min) | 73 (min) | 15 (min) | |
| Rest | 26 (min) | 160 (min) | 0 | |
| Walk | 0 | 0 | 35 (min) | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teimouri, M.; Indahl, U.G.; Sickel, H.; Tveite, H. Deriving Animal Movement Behaviors Using Movement Parameters Extracted from Location Data. ISPRS Int. J. Geo-Inf. 2018, 7, 78. https://doi.org/10.3390/ijgi7020078
Teimouri M, Indahl UG, Sickel H, Tveite H. Deriving Animal Movement Behaviors Using Movement Parameters Extracted from Location Data. ISPRS International Journal of Geo-Information. 2018; 7(2):78. https://doi.org/10.3390/ijgi7020078
Chicago/Turabian StyleTeimouri, Maryam, Ulf Geir Indahl, Hanne Sickel, and Håvard Tveite. 2018. "Deriving Animal Movement Behaviors Using Movement Parameters Extracted from Location Data" ISPRS International Journal of Geo-Information 7, no. 2: 78. https://doi.org/10.3390/ijgi7020078
APA StyleTeimouri, M., Indahl, U. G., Sickel, H., & Tveite, H. (2018). Deriving Animal Movement Behaviors Using Movement Parameters Extracted from Location Data. ISPRS International Journal of Geo-Information, 7(2), 78. https://doi.org/10.3390/ijgi7020078





