Assessment of Displacements of Linestrings Based on Homologous Vertexes
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
- Lines are prepared with the aim of helping the evaluation of geospatial matching methods for vector data and consequently can be used to assess displacements.
- The dataset was built up from mapping data at scale 1:25,000 produced by official mapping agencies.
- The dataset offers five different morphology classes of linestrings, from very smooth to very sinuous lines (CL1 to CL5) (see [31] for details). Accordingly, we actually consider five categories of lines (each one corresponding to a sub-dataset).
- The lines of these five categories (sub-datasets) were modified applying systematic perturbations (translations, rotations, and scaling), random perturbations, and combinations of these types.
- The values of these perturbations were known, so we were able to use them to see if our method can properly estimate them.
2.2. Method
- 1.
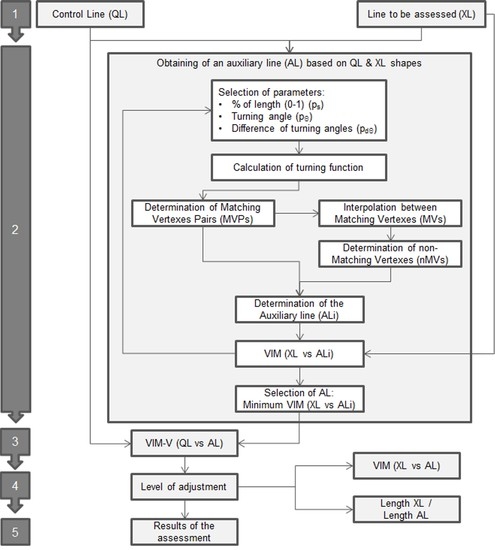
- First, the process starts with two lines: the line to be assessed (XL) and the line to assess (QL), which are obtained from a more accurate source.
- 2.
- Obtaining of an auxiliary line (AL) based on QL & XL shapes: In this stage we develop an iterative optimization procedure in order to obtain an auxiliary line (AL) which has the best adjustment to the shape of XL and is defined by the same number of vertexes of QL (following its geometrical behavior). To obtain this, we develop a procedure that is based on the comparison of the turning functions [4] of XL and QL in order to determine a set of Matching Vertexes Pairs (MVPs) that are considered as homologous in both lines (Figure 5). The turning function is adapted to linestrings considering a part of the function between two well-defined points of each line (start and end points). The turning function is obtained by scaling the length (s) of the line in the range 0 to 1 and determining the turning angles (Θ) of the segment at each vertex. This aspect is very interesting when comparing turning functions in avoiding the scale discrepancies between both lines. Obviously, the lines usually included in spatial databases present different behaviors and singularities, so we establish three parameters in order to control the process and to determine the set of MVPs between QL and XL. These parameters are:
- ps = neighborhood threshold. A maximum normalized distance [0, 1] allowable between homologous vertices of both lines. This parameter ensures that both homologous vertices are close together.
- pΘ = angle threshold. The minimum angle change in the turning function in order to pay attention to a line vertex. This parameter ensures that each vertex of each line has some relevance in the shape of the line.
- pdΘ = difference angle threshold. The maximum angle change that is allowed between two homologous vertices. This parameter ensures that both homologous vertices are representing more or less the same angular change in both lines.
- 3.
- Apply the VIM-V: Once we have two lines that are composed of the same number of vertexes and those vertexes are considered as homologous, the VIM-V method is applied from QL to AL, obtaining a mean displacement vector for the line.
- 4.
- Level of adjustment: The quality of the mean displacement vector obtained is directly related to the adjustment of the AL to XL. There are two metrics that can be used to analyze this level of adjustment: The mean displacement value of AL with respect to XL (previously obtained using VIM); and, the ratio between the lengths of the XL and the AL. In this context, we can use these metrics in order to filter those results that will be considered in the assessment.
- 5.
- Results of the assessment: The displacement vectors of a set of lines that have met the requirements imposed in the previous stage are used in the final assessment.
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Goodchild, M.F. Citizens as sensors: The world of volunteered geography. GeoJournal 2007, 69, 211–221. [Google Scholar] [CrossRef]
- MacEachren, A.M. Compactness of geographic shape: Comparison and evaluation of measures. Geogr. Ann. Ser. B Hum. Geogr. 1985, 67, 53–67. [Google Scholar] [CrossRef]
- Wentz, E.A. Shape analysis in GIS. In Proceedings of the Auto-Carto 13, Seattle, WA, USA, 7–10 April 1997. [Google Scholar]
- Arkin, E.M.; Chew, L.P.; Huttenlocher, D.P.; Kedem, K.; Mitchell, J.S.B. An efficiently computable metric for comparing polygonal shapes. IEEE Trans. Pattern Anal. 1991, 13, 209–216. [Google Scholar] [CrossRef]
- Perkal, J. On epsilon length. Bull. Acad. Pol. Sci. 1956, 4, 399–403. [Google Scholar]
- Chrisman, N.R. A theory of cartographic error and its measurement in digital bases. In Proceedings of the Fifth International Symposium on Computer-Assisted Cartography, Crystal City, VI, USA, 22–28 August 1982; Foreman, J., Ed.; pp. 159–168. [Google Scholar]
- Blakemore, M. Generalisation and error in spatial data bases. Cartographica 1984, 21, 131–139. [Google Scholar] [CrossRef]
- Caspary, W.; Scheuring, R. Positional accuracy in spatial databases. Comput. Environ. Urban Syst. 1993, 17, 103–110. [Google Scholar] [CrossRef]
- Shi, W.; Liu, W. A stochastic process-based model for the positional error of line segments in GIS. Int. J. Geogr. Inf. Sci. 2000, 14, 51–66. [Google Scholar] [CrossRef]
- Heuvelink, G.; Brown, J.D.; Van Loon, E.E. A Probabilistic Framework for Representing and Simulating Uncertain Environmental Variables. Int. J. Geogr. Inf. Sci. 2007, 21, 497–513. [Google Scholar] [CrossRef]
- Wu, H.S.; Liu, Z.L. Simulation and Model Validation of Positional Uncertainty of Line Feature on Manual Digitizing a Map. In The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; Chen, J., Jiang, J., Kainz, W., Eds.; The International Society of Photogrammetry and Remote Sensing (ISPRS): Beijing, China, 2008; Volume XXXVII, Part B2; pp. 843–848. [Google Scholar]
- Gil de la Vega, P.; Ariza-López, F.J.; Mozas-Calvache, A.T. Models for positional accuracy assessment of linear features: 2D and 3D cases. Surv. Rev. 2016, 48, 347–360. [Google Scholar] [CrossRef]
- McMaster, R.B. A statistical analysis of mathematical measures for linear simplification. Am. Cartogr. 1986, 13, 103–116. [Google Scholar] [CrossRef]
- Jasinski, M.J. The Comparison of Complexity Measuresfor Cartographic Lines. Technical Report 90-1; National Center for Geographic Information and Analysis: Buffalo, NY, USA, 1990. [Google Scholar]
- Lawford, G.J. Examination of the Positional Accuracy of Linear Features. J. Spat. Sci. 2010, 55, 219–235. [Google Scholar] [CrossRef]
- Abbas, I.; Grussenmeyer, P.; Hottier, P. Contrôle de la planimétrie d’une base de données vectorielles: Une nouvelle méthode basée sur la distance de Haussdorff: La méthode du contrôle linéaire. Bull. SFPT 1995, 137, 6–11. [Google Scholar]
- Mozas, A.T.; Ariza, F.J. Methodology for positional quality control in cartography using linear features. Cartogr. J. 2010, 47, 371–378. [Google Scholar] [CrossRef]
- Mozas-Calvache, A.T.; Ariza-López, F.J. New method for positional quality control in cartography based on lines. A comparative study of methodologies. Int. J. Geogr. Inf. Sci. 2011, 25, 1681–1695. [Google Scholar] [CrossRef]
- Mozas-Calvache, A.; Ariza-López, F.J. Adapting 2D positional control methodologies based on linear elements to 3D. Surv. Rev. 2015, 47, 195–201. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Hunter, G.J. A simple positional accuracy measure for linear features. Int. J. Geogr. Inf. Sci. 1997, 11, 299–306. [Google Scholar] [CrossRef]
- Tveite, H.; Langaas, S. An accuracy assessment method for geographical line data sets based on buffering. Int. J. Geogr. Inf. Sci. 1999, 13, 27–47. [Google Scholar] [CrossRef]
- Asakura, K.; Takeuchi, M.; Watanabe, T. A Map Matching Algorithm for Sharing Map Information among Refugees in Disaster Areas. In Intelligent Interactive Multimedia: Systems and Services; Watanabe, T., Watada, J., Takahashi, N., Howlett, R., Jain, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 22–31. [Google Scholar] [CrossRef]
- Xi, L.; Liu, Q.; Li, M.; Liu, Z. Map matching algorithm and its application. In Proceedings of the International Conference on Intelligent Systems and Knowledge Engineering, Chengdu, China, 15–16 October 2007; Atlantis Press: Paris, France, 2007; pp. 1–7. [Google Scholar] [CrossRef]
- Quddus, M.A.; Ochieng, W.Y.; Noland, R.B. Current map-matching algorithms for transport applications: State-of-the art and future research directions. Transp. Res. C-Emererg. 2007, 15, 312–328. [Google Scholar] [CrossRef]
- Kieler, B.; Huang, W.; Haunert, J.H.; Jiang, J. Matching River Datasets of Different Scales. In Advances in GIScience; Sester, M., Bernard, L., Paelke, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 135–154. [Google Scholar] [CrossRef]
- Reinoso, J.F. A priori horizontal displacement (HD) estimation of hydrological features when versioned DEMs are used. J. Hydrol. 2010, 384, 130–141. [Google Scholar] [CrossRef]
- Xavier, E.; Ariza-López, F.J.; Ureña-Cámara, M.A. A Survey of Measures and Methods for Matching Geospatial Vector Datasets. ACM Comput. Surv. 2016, 49, 1–34. [Google Scholar] [CrossRef]
- Mozas-Calvache, A.T.; Ariza-López, F.J. Detection of systematic displacements in spatial databases using linear elements. Cartogr. Geogr. Inf. Sci. 2014, 41, 309–322. [Google Scholar] [CrossRef]
- Xavier, E.; Ariza-López, F.J.; Ureña-Cámara, M.A. MatchingLand, geospatial data testbed for the assessment of matching methods. Sci. Data 2017, 4, 170180. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2010; ISBN 978-0470053041. [Google Scholar]
- Ariza-López, F.J.; García-Balboa, J.L. Generalization-oriented road line segmentation by means of an artificial neural network applied over a moving window. Pattern Recognit. 2008, 41, 1593–1609. [Google Scholar] [CrossRef]







| Class | Number of Lines | Total Length (m) | Minimum Length (m) | Maximum Length (m) | Number of Vertexes (n) | Mean Segment (m) |
|---|---|---|---|---|---|---|
| CL1 | 496 | 183,736.15 | 4.48 | 3614.79 | 6555 | 30.33 |
| CL2 | 496 | 186,386.59 | 4.48 | 3636.38 | 13,813 | 13.99 |
| CL3 | 496 | 190,659.09 | 4.48 | 3754.90 | 11,718 | 16.99 |
| CL4 | 496 | 193,552.72 | 4.48 | 3614.79 | 9765 | 20.88 |
| CL5 | 496 | 194,166.64 | 4.48 | 3614.79 | 9209 | 22.28 |
| Perturbed Sets (XL) 1 | Random (m) | Translation (m) | Rotation (rad) | Scaling |
|---|---|---|---|---|
| ra1_t0_r0_s0 | 5 | - | - | - |
| ra2_t0_r0_s0 | 12.5 | - | - | - |
| ra3_t0_r0_s0 | 25 | - | - | - |
| ra0_t0_r0_s1 | - | - | - | 1.00052 |
| ra0_t0_r0_s2 | - | - | - | 0.999478 |
| ra0_t0_r1_s0 | - | - | 0.000521513 | - |
| ra0_t0_r1_s1 | - | - | 0.000521513 | 1.00052 |
| ra0_t0_r1_s2 | - | - | 0.000521513 | 0.999478 |
| ra0_t0_r2_s0 | - | - | 0.000521513 | - |
| ra0_t0_r2_s1 | - | - | 0.000521513 | 1.00052 |
| ra0_t0_r2_s2 | - | - | 0.000521513 | 0.999478 |
| ra0_t2_r0_s0 | - | 5 | - | - |
| ra0_t2_r0_s1 | - | 5 | - | 1.00052 |
| ra0_t2_r0_s2 | - | 5 | - | 0.999478 |
| ra0_t2_r1_s0 | - | 5 | 0.000521513 | - |
| ra0_t2_r1_s1 | - | 5 | 0.000521513 | 1.00052 |
| ra0_t2_r1_s2 | - | 5 | 0.000521513 | 0.999478 |
| ra0_t2_r2_s0 | - | 5 | 0.000521513 | - |
| ra0_t2_r2_s1 | - | 5 | 0.000521513 | 1.00052 |
| ra0_t2_r2_s2 | - | 5 | 0.000521513 | 0.999478 |
| ra0_t10_r0_s0 | - | 12.5 | - | - |
| ra0_t10_r0_s1 | - | 12.5 | - | 1.00052 |
| ra0_t10_r0_s2 | - | 12.5 | - | 0.999478 |
| ra0_t10_r1_s0 | - | 12.5 | 0.000521513 | - |
| ra0_t10_r1_s1 | - | 12.5 | 0.000521513 | 1.00052 |
| ra0_t10_r1_s2 | - | 12.5 | 0.000521513 | 0.999478 |
| ra0_t10_r2_s0 | - | 12.5 | 0.000521513 | - |
| ra0_t10_r2_s1 | - | 12.5 | 0.000521513 | 1.00052 |
| ra0_t10_r2_s2 | - | 12.5 | 0.000521513 | 0.999478 |
| Perturbed SETS (XL) 1 | Random (m) | Translation (m) | Rotation (rad) | Scaling |
|---|---|---|---|---|
| ra1_t0_r1_s0 | 5 | - | 0.000521513 | - |
| ra1_t0_r0_s1 | 5 | - | - | 1.00052 |
| ra1_t2_r0_s0 | 5 | 5 | - | - |
| ra1_t2_r1_s0 | 5 | 5 | 0.000521513 | - |
| ra1_t2_r0_s1 | 5 | 5 | - | 1.00052 |
| ra1_t2_r1_s1 | 5 | 5 | 0.000521513 | 1.00052 |
| ra1_t10_r0_s0 | 5 | 12.5 | - | - |
| ra1_t10_r1_s0 | 5 | 12.5 | 0.000521513 | - |
| ra1_t10_r0_s1 | 5 | 12.5 | - | 1.00052 |
| ra1_t10_r1_s1 | 5 | 12.5 | 0.000521513 | 1.00052 |
| ra2_t0_r1_s0 | 12.5 | - | 0.000521513 | - |
| ra2_t0_r0_s1 | 12.5 | - | - | 1.00052 |
| ra2_t2_r0_s0 | 12.5 | 5 | - | - |
| ra2_t2_r1_s0 | 12.5 | 5 | 0.000521513 | - |
| ra2_t2_r0_s1 | 12.5 | 5 | - | 1.00052 |
| ra2_t2_r1_s1 | 12.5 | 5 | 0.000521513 | 1.00052 |
| ra2_t10_r0_s0 | 12.5 | 12.5 | - | - |
| ra2_t10_r1_s0 | 12.5 | 12.5 | 0.000521513 | - |
| ra2_t10_r0_s1 | 12.5 | 12.5 | - | 1.00052 |
| ra2_t10_r1_s1 | 12.5 | 12.5 | 0.000521513 | 1.00052 |
| ra3_t0_r1_s0 | 25 | - | 0.000521513 | - |
| ra3_t0_r0_s1 | 25 | - | - | 1.00052 |
| ra3_t2_r0_s0 | 25 | 5 | - | - |
| ra3_t2_r1_s0 | 25 | 5 | 0.000521513 | - |
| ra3_t2_r0_s1 | 25 | 5 | - | 1.00052 |
| ra3_t2_r1_s1 | 25 | 5 | 0.000521513 | 1.00052 |
| ra3_t10_r0_s0 | 25 | 12.5 | - | - |
| ra3_t10_r1_s0 | 25 | 12.5 | 0.000521513 | - |
| ra3_t10_r0_s1 | 25 | 12.5 | - | 1.00052 |
| Parameter | Minimum | Maximum | Step | Cases |
|---|---|---|---|---|
| ps | 10% of the mean segment | 50% of the mean segment | 10% of the mean segment | 5 |
| pΘ | 0.0157 rad | 0.3142 rad | 0.0785 rad | 5 |
| pdΘ | 0.1571 rad | 0.4712 rad | 0.1571 rad | 4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mozas-Calvache, A.T.; Ariza-López, F.J. Assessment of Displacements of Linestrings Based on Homologous Vertexes. ISPRS Int. J. Geo-Inf. 2018, 7, 473. https://doi.org/10.3390/ijgi7120473
Mozas-Calvache AT, Ariza-López FJ. Assessment of Displacements of Linestrings Based on Homologous Vertexes. ISPRS International Journal of Geo-Information. 2018; 7(12):473. https://doi.org/10.3390/ijgi7120473
Chicago/Turabian StyleMozas-Calvache, Antonio Tomás, and Francisco Javier Ariza-López. 2018. "Assessment of Displacements of Linestrings Based on Homologous Vertexes" ISPRS International Journal of Geo-Information 7, no. 12: 473. https://doi.org/10.3390/ijgi7120473
APA StyleMozas-Calvache, A. T., & Ariza-López, F. J. (2018). Assessment of Displacements of Linestrings Based on Homologous Vertexes. ISPRS International Journal of Geo-Information, 7(12), 473. https://doi.org/10.3390/ijgi7120473