Abstract
Urban land cover classification and mapping is an important and ongoing research field in monitoring and managing urban sprawl and terrestrial ecosystems. The changes in land cover largely affect the terrestrial ecosystem, thus information on land cover is important for understanding the ecological environment. Quantification of land cover in urban areas is challenging due to their diversified activities and large spatial and temporal variations. To improve urban land cover classification and mapping, this study presents three new spectral indices and an automated approach to classifying four major urban land types: impervious, bare land, vegetation, and water. A modified normalized difference bare-land index (MNDBI) is proposed to enhance the separation of impervious and bare land. A tasseled cap water and vegetation index (TCWVI) is proposed to enhance the detection of vegetation and water areas. A shadow index (ShDI) is proposed to further improve water detection by separating water from shadows. An approach for optimizing the thresholds of the new indices is also developed. Finally, the optimized thresholds are used to classify land covers using a decision tree algorithm. Using Landsat-8 Operational Land Imager (OLI) data from two study sites (Hong Kong and Dhaka City, Bangladesh) with different urban characteristics, the proposed approach is systematically evaluated. Spectral separability analysis of the new indices is performed and compared with other common indices. The urban land cover classifications achieved by the proposed approach are compared with those of the classic support vector machine (SVM) algorithm. The proposed approach achieves an overall classification accuracy of 94–96%, which is superior to the accuracy of the SVM algorithm.
1. Introduction
Land cover analysis is a fundamental procedure in the study of the geographic environment [1,2]. Urban sprawl largely affects land covers and the terrestrial ecosystems [3,4]. The changes in land cover result in changes in ecosystems [5]. Information on land cover is essential for monitoring and managing the ecosystem, and is also important for regional and local level planning and for managing urban sprawl [6,7]. Traditional land cover surveys are labor intensive and time-consuming [8]. It is highly desirable to develop reliable and more automated methods for land cover mapping. Satellite imagery provides efficient data for monitoring land cover changes at local and global scales [2,6]. However, in urban areas, land cover mapping is challenging due to the large spatial and temporal variations caused by the diversified activities in these areas [9].
Over the past decades, remote sensing has been widely used to map urban land covers. The land cover maps derived from image classification is important for monitoring multi-temporal changes and analyzing socio-ecological issues [10]. Various image classification approaches [11,12,13,14,15,16] have been developed to classify urban land covers. The classification approaches have been commonly grouped as parametric and non-parametric classifiers. Image classification based on either pixels or objects have also been widely used in the past [17]. Although various land cover classification approaches are available [12,13,14,15,16], the selection of the best classifier is difficult because each of the methods has its own strengths and limitations. Use of spectral indices has proved to be an effective alternative means of mapping land covers. Because spectral indices demonstrate the relative abundance of features of interest [18]. Moreover, the spectral index values primarily characterize a particular land cover.
Various spectral indices have been developed and used to detect different land cover types [6,19]. For example, the normalized difference vegetation index (NDVI), developed by Rouse et al. [20], extracts vegetation and biomass information. The soil-adjusted vegetation index (SAVI) proposed by Huete [21] separates vegetation and water in urban areas. The normalized difference water index (NDWI) developed by McFeeters [22] delineates open water features in remote sensing images. The modified normalized difference water index (MNDWI) [23] enhances accurate water detection. The normalized difference built-up index (NDBI), developed by Zha et al. [24] is widely used to map built-up urban areas. The built-up index (BUI) [25] and the indexed-based built-up index (IBI) [26] delineate urban built-up features. The tasseled cap (TC) indices have been used to enhance the information on biophysical coastal zones, water, soil, and vegetation [27].
In addition to the individual indices, different combinations of indices or modified indices have been developed and used to map land covers [6,28,29,30]. Although there are various methods for mapping land cover types, the existing approaches face limitations to classify urban land covers. First, separating impervious and bare land is still a challenge [6,31]. Second, although several indices can detect vegetation and water, no single index can detect them both. Third, the existing water indices do not accurately separate water from shadows. In urban areas, detecting surface water is a challenge because of the existence of dark building shadows [32]. However, no previous studies have considered shadows when detecting urban water in relatively low-resolution images. In this study, we propose three novel indices: the modified normalized difference bare-land index (MNDBI), tasseled cap water and vegetation index (TCWVI), and shadow index (ShDI). Together, they address the above-mentioned limitations of existing methods. Approaches for optimizing the thresholds of the proposed indices are also developed. Based on the new indices, an automatic approach for urban land cover classification is implemented.
In the next section, the paper continues with a brief literature review on land cover classification. Section 3 describes the study areas and data sources, and presents the principles of the formulation of the three novel spectral indices in detail. An approach of threshold optimization for the spectral indices is elaborated in this section. Section 4 details the experimental validation and results. Section 5 discusses the findings, and finally, concluding remarks are presented in Section 6.
2. Literature Review
Various image classification approaches; e.g., parametric and non-parametric classification methods have been used to map land covers [11,12,18,33,34,35,36,37,38,39]. Among these works, the traditional parametric maximum likelihood classifier (MLC) has been widely used. This approach has proved to be an optimal classifier for normally distributed training data [11]. Non-parametric algorithms, e.g., support vector machines (SVMs), neural networks (NNs), decision tree (DT) and random forest (RF), have been developed to enhance the classification accuracy. SVM employs optimization algorithms to generate boundaries and provides good classification results with limited spectral-mixed training data. However, the selection of required parameters of the SVM algorithm significantly influence the classification accuracy [40,41], thus requires an optimum parameter search [13]. NN classifier involves a repeated feedforward and back-propagation process and performs well for land cover classification. However, the training phase requires many input parameters that are difficult to set, and the efficiency is low during the training phase [42]. DT is a non-parametric classifier that does not require any a priori statistical assumptions regarding the distribution of data. However, the performance of this classifier is affected by the decision threshold [43,44]; therefore, it is important to assign appropriate thresholds. RF is an ensemble classifier that breaks down the classification process into a series of trees [11]. The land cover classification methods can also be based on either pixels or objects [17]. Pixel-based methods are favorable to moderate and low-resolution images, but they may fail to accurately differentiate adjacent classes that have a high spectral similarity [45]. In contrast, object-oriented classification uses a minimum unit of information and minimizes the salt-and-pepper effect [15], and this technique has been proved to be suitable for high-resolution images [17,46].
Spectral index has also been widely used as an effective alternative means of mapping land covers. Over the last decades, various spectral index based automatic and semi-automatic classification methods have been exploited for mapping land covers [6,33,47]. For example, Li et al. [6] applied a combination of the NDVI, vegetation and water masking index (VWMI), bright impervious surface binary (BISB), and normalized difference bare land index (NDBLI) to classify urban land covers using Landsat-8 Operational Land Imager (OLI) images. In this approach, the spectral indices were used to select training data, and then a machine learning classifier support vector machine (SVM) was applied to detect land covers. He et al. [33] applied a semiautomatic segmentation approach to map urban built-up areas by enhancing the normalized difference built-up index. Chen et al. [47] developed an integrated automated approach to map land covers using iterated training samples and markov random fields (MRFs) model. They applied iterations to refine the unchanged area as training samples and the MRF model to reduce salt-and-pepper effects. Different combinations of indices have also been used to map land covers. For example, Doustfatemeh and Baleghi [1] used Landsat 7 Enhanced Thematic Mapper Plus (ETM+) to extract urban areas. In the first step, they used Otsu optimal thresholding [48] to extract features using the NDVI, NDWI, and SVI, and then extracted urban points (UPs) using a symmetric gradient calculation based on structural features. When the results were combined, 90–95% overall accuracy was achieved at three study sites. Patel and Mukherjee [28] extracted impervious features by inputting the SAVI, MNDWI, NDBI, BUI, and IBI indices into a backpropagation neural network. However, this approach detected only impervious features; all of the other land cover types were grouped into a single class. Bhatt et al. [29] used the NDVI, MNDWI, and modified SAVI indices and applied object-oriented classification to Landsat-5 (TM) and Landsat-8 (OLI) images. It is notable that the object-based classification is appropriate for high-resolution imagery; this approach achieved an overall accuracy of 90.1%. Eslami and Mohammadzadeh [30] introduced two novel vegetation indices, subdividing vegetation index (SVI) and minus/subdividing vegetation index (MSVI), to extract vegetation. Then, they extracted 24 textural features using the gray level co-occurrence matrix (GLCM) and applied the maximum noise fraction (MNF) to map urban land cover using hyperspectral thermal infrared data.
The existing land cover classification approaches have their merits but they also face limitations as described previously, especially in the complex urban environment. Precise land cover mapping in a heterogeneous urban environment is still a challenge and it is an ongoing subject of research. This study proposes three novel spectral indices, MNDBI, TCWVI, and ShDI, and a threshold optimization approach to enhance urban land cover mapping. This paper highlights the following contributions:
1. The proposed MNDBI is effective to separate impervious and bare land by using the spectral bands blue and shortwave infrared 2 (SWIR2).
2. The proposed TCWVI can facilitate simultaneous detection of vegetation and water using the tasseled cap brightness index (TCBI) and the tasseled cap greenness index (TCGI).
3. The proposed ShDI uses the spectral bands near infrared (NIR), SWIR2, blue and red for delineating shadows in low-resolution images in order to improve the accuracy of water extraction in urban areas.
4. The proposed threshold optimization approach for the spectral indices is able to maximize spectral separability between adjacent land covers for enhanced land cover classification.
3. Urban Land Cover Classification Based on Novel Spectral Indices
In this study, we automatically map four major urban land covers, i.e., water, vegetation, bare land, and impervious areas, using three new spectral indices and optimized thresholds for the indices. These are the fundamental components of an urban ecosystem [6,49]. The information on these land covers is essential to monitor and manage the urban environment, water resources, microclimate, and urban sprawl. An understanding of the spatial and temporal changes of water is important for protecting ecosystems, and planning and managing watersheds. The size of the impervious area is widely used as an indicator of urbanization [50], which is used to monitor urban sprawl. Bare land is recognized as an indicator of activities associated with expanding urban areas [51]. The proportions of water, vegetation, and human activities can be used to assess the ecosystems and urban microclimate [52]. Thus, this study focuses on the four types of land covers as shown in Figure 1.
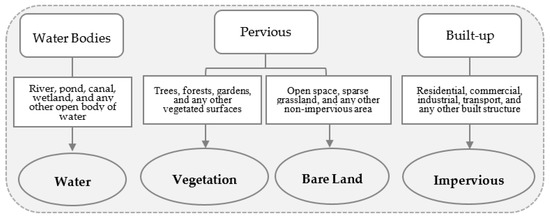
Figure 1.
Composition of land cover classes.
3.1. Study Areas and Datasets
Two study areas (Hong Kong and Dhaka City, Bangladesh) with different geographic characteristics are selected to test the transferability of the proposed indices and to evaluate their robustness in urban land cover classification. The first study site, Hong Kong, has an area of 1095 km2 and is situated between latitudes 22°09′ to 23°37′ and longitudes 113°52′ to 114°30′. It is surrounded by the South China Sea to the east, west, and south, and shares a border to the north with the Guangdong province of China. It is a mountainous area that contains skyscrapers and several country parks. Due to its rugged terrain, a significant portion of the area is undeveloped; therefore, the urban population is squeezed into less than 25% of the area (the built-up area is approximately 260 km2) [53]. For this study, an area of 285 km2 is selected as the study site (see Figure 2a).
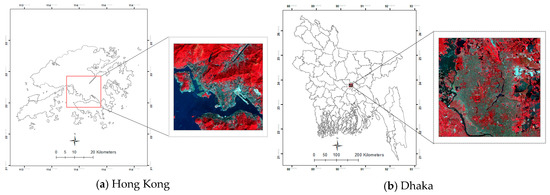
Figure 2.
Location of the study sites.
The second study site, Dhaka, the capital city of Bangladesh, is located at 23°43′ north and 90°24′ east. The entire city is 1464 km2. For this study, an area of 285 km2, shown in Figure 2b, is selected. The study area is almost flat and its surface elevation ranges between 1 and 14 m. It is surrounded by three major rivers, the Buriganga, Turag, and Balu, which flow to the south, west, and east, respectively. Dhaka is one of the most densely populated megacities in the world; with a population of nearly 18.23 million. As a major economic hub, the area is experiencing enormous urbanization pressure. This extensive industrialization and urbanization are changing the land cover and degrading the city’s natural ecosystem.
In the current decade, other high-resolution satellite data are available for mapping urban land covers. However, this study uses Landsat data because it offers a cross-calibrated earth observation data of more than four decades [54]. Moreover, these data are publicly available and users are no longer restricted by processing limitations [55]. Landsat data is favored for longitudinal analysis and importantly favorable to cities where other satellite data are not available.
This study uses Landsat-8 Operational Land Imager (OLI) level 1 data to classify land cover. The 2013 Landsat imagery for Hong Kong and the 2016 data for Dhaka are obtained from the official website (https://earthexplorer.usgs.gov/) of the US Geological Survey. Landsat Path 122, Row 44 covers the entire area of Hong Kong, and Path 137, Row 44 covers the whole study area of Dhaka. The Map Projection of the collected images is the Universal Transverse Mercator (UTM) within Zone 49N (Hong Kong) and Zone 46N (Dhaka) Datum World Geodetic System (WGS) 84. The spatial resolution of all of the Landsat-8 images is 30 m/pixel. In this study, ZY-3 multispectral images (5.8 m/pixel) of Hong Kong collected in 2013 and SPOT-6 multispectral images (6 m/pixel) of Dhaka collected in 2016 are used for validation. The attributes of the satellite datasets are shown in Table 1. We have tried to collect and use similar dated images to avoid seasonal variation. Because the solar angle and the seasonal variation influence the spectral reflectance of land covers including water and shadow. However, the datasets have some variations, because the temporal resolution of the satellite data (Landsat, SPOT, and ZY) are different. Moreover, similar dated cloud-free Landsat images are rarely available. The datasets also have some variation in the solar angle, because the view angle, revisit cycle, and the equator crossing time of the satellites are distinct. Considering these limitations, a careful assessment is done throughout the study.

Table 1.
Description of the satellite data.
3.2. Image Processing
In the proposed framework, image processing is carried out before the spectral indices are generated. The collected raw images store digital number (DN) values. To some extent, atmospheric effects change the image properties. Thus, it is desirable to convert DN values to surface reflectance values, a process that requires radiometric and atmospheric correction. The atmospheric effects and solar incidence angle change the spectral properties of the images; thus, image processing is required to eliminate these effects [27]. Several atmospheric correction models, such as 6s, ATCOR, FLAASH (FLS), dark subtraction (DS), empirical line method (ELM), and gain and bias (GB), are available. The selection of the appropriate atmospheric correction model is necessary to obtain the desired results. In this study, three atmospheric correction models (FLAASH, DS, and GB) are applied to assess the effect of atmospheric correction on band reflectance, index values and on the degree of mean difference between adjacent land covers. The GB model is selected for this study because an analysis of the three methods showed that the GB model gives a consistent performance at both study sites and maximizes the degree of spectral reflectance between adjacent land covers.
3.3. Formulation of Novel Spectral Indices
Spectral indices are used to demonstrate the relative abundance of features of interest, which are distinguished by differences in the surface reflectance values of two or more particular bands [18]. To address the previously discussed challenges in urban land cover mapping, this study develops the three novel spectral indices: MNDBI, TCWVI and ShDI. The following section describes the rationale and principles of the formulation of the novel spectral indices.
3.3.1. Modified Normalized Difference Bare-land Index (MNDBI)
The size of the impervious area is an important indicator of urbanization [50] but its separation from bare land is a challenge [6,31]. Many indices e.g., NDBI, NDBLI, and BUc [6,24,33] have been developed to enhance the detection of impervious and bare land. For example, Zha et al. [24] used the spectral bands near-infrared (NIR) and shortwave infrared 1 (SWIR1) to develop NDBI, but it does not accurately distinguish built-up areas from bare lands. Li et al. [6] developed the NDBLI using the spectral bands green and coastal aerosol. However, the NDBLI was favorable to extract bare land from only dark impervious surfaces. In contrary, He et al. [33] developed the built-up continuous (BUc) index using the continuous image of NDBIc and NDVIc. These indices are to some extent able to separate built-up areas from bare land; however, their complete separation is still a challenge, as the reflectance values of impervious areas are very similar to those of bare land. To enhance their separation, the spectral reflectance between adjacent land covers must be maximized. Thus, this study proposes the MNDBI using the spectral bands blue and SWIR2. The following describes the principle of the formulation of the proposed MNDBI.
Figure 3 is a false color image of Hong Kong that illustrates the clear distinctions between the four common land covers (impervious, bare land, vegetation, and water). In this process, with the help of a high-resolution ZY3 image, a total 200 representative pixels of the individual land cover types are selected manually from the false-color image, and their average band reflectance is computed, as shown in Figure 4a. The band reflectance profile indicates that shortwave infrared (SWIR) band 1 has the highest reflectance for bare land, but that the reflectance for vegetation and impervious areas is almost the same. The SWIR band 2 shows clear distinctions between all land cover types; bare land has the highest reflectance and has a significant mean difference from impervious areas. In contrast, in the blue band, impervious areas have the highest reflectance. Thus, combining the SWIR band 2 and blue band, as in Equation (1), results in positive values for bare land only, and negative values for all of the other land cover types, as shown in Figure 4b. Moreover, it maximizes the reflectance between impervious and bare land.
where and are the reflectance values of the shortwave infrared 2 (wavelength: 2.107–2.294 μm) and blue (wavelength: 0.452–0.512 μm) bands.
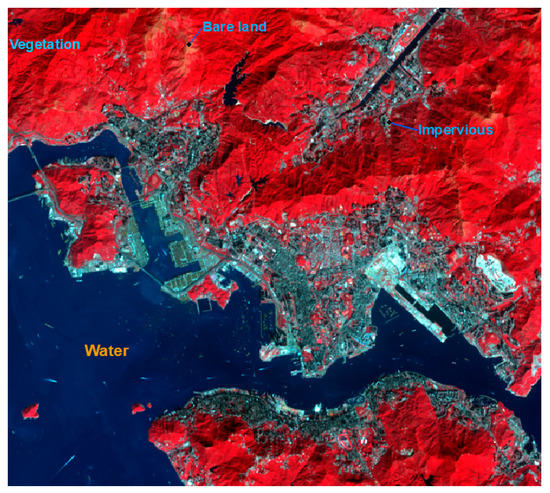
Figure 3.
False color image of Hong Kong. Typical land covers: water (dark blue), vegetation (red), bare land (yellow), and impervious (bluish ash).
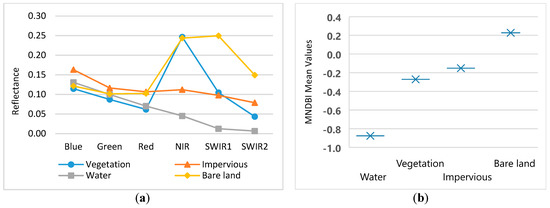
Figure 4.
Reflectance of the typical land cover types in the Hong Kong study area: (a) band reflectance and (b) proposed modified normalized difference bare-land index (MNDBI).
3.3.2. Tasseled Cap Water and Vegetation Index (TCWVI)
This study develops the TCWVI to facilitate simultaneous detection of vegetation and water. The NDWI and MNDWI are widely used for water extraction and the NDVI for vegetation extraction [6,56]. McFeeters [22] developed the NDWI using the spectral bands NIR and green with the aim to detect water. Xu [23] developed the MNDWI using the spectral bands green and SWIR to enhance water detection. In contrary, Rouse et al. [20] developed the NDVI using the spectral bands NIR and red to facilitate vegetation detection. Although, several indices are available to detect vegetation and water none of them can simultaneously detect and separate water and vegetation. The tasseled cap brightness index (TCBI) is responsive to physical properties and the tasseled cap greenness index (TCGI) is responsive to healthy green vegetation [57]. This study proposes the TCWVI using the TCBI and TCGI to enhance the relative abundance of natural features in order to facilitate simultaneous detection of vegetation and water. The following describes the principle of the formulation of the proposed TCWVI.
The representative pixels selected in the previous section are used to compute the appropriate index values (Figure 5a). The spectral reflectance illustrates that TCGI has the highest index values for vegetation, but water and impervious areas have almost the same spectral reflectance. In contrast, TCBI has the lowest values for water, whereas vegetation and impervious areas have almost the same reflectance. Thus, combining these indices, as in Equation (2), yields the highest positive values for water and the lowest values for vegetation (Figure 5b). These high and low index values facilitate the simultaneous detection of water and vegetation. Moreover, the proposed TCWVI generates a significant high index value for water that maximizes its separability from other land cover types, thus minimizes misclassification in the detection of water.
where TCBI and TCGI are the tasseled cap brightness index and tasseled cap greenness index, respectively.
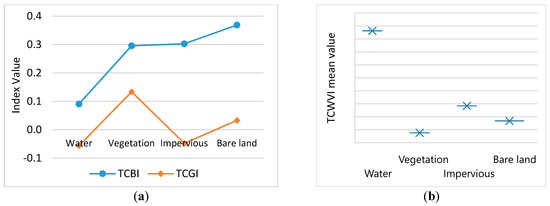
Figure 5.
Reflectance of the typical land cover types in the Hong Kong study area: (a) index values and (b) proposed tasseled cap water and vegetation index (TCWVI).
3.3.3. Shadow Index (ShDI)
Shadows are in general less significant in land cover mapping that uses low-resolution imagery. However, in metropolitan cities such as Hong Kong, skyscrapers throw shadows that create problems in the analysis of low-resolution images, as shown in Figure 6a. Shadowed areas have reflectance that is similar to water, and it can be difficult to distinguish them in land cover mapping. Many shadow detection techniques [58,59] are available for high-resolution images (HRI), however, none are available for low-resolution images (LRI). For example, He et al. [59] detected shadows using object-based classification. In contrary, Li et al. [58] used vectorization algorithms based on object shape features to remove shadow and other noises from water. However, none of these methods is favorable to LRI. Therefore, to improve the accuracy of water extraction in urban areas, we develop an index for delineating shadows in low-resolution images. The proposed index uses the spectral bands NIR, SWIR2, blue, and red. The following describes the principle of the formulation of the proposed ShDI.

Figure 6.
Building shadows in Hong Kong: (a) 30 m Landsat-8 and (b) 5.8 m ZY-3.
The false-color images shown in Figure 6a generally distinguish water from shadow. Representative pixels of water and shadow are selected and their average band reflectance is computed, as shown in Figure 7a. A close examination of Figure 7a demonstrates that the band reflectance differences between water and shadow are slight (ranging from 0.01 to 0.03); therefore, the standardized differentiation between the two bands is not large enough to distinguish water and shadow. The band reflectance profile demonstrates that the blue band and the SWIR band 2 have respectively the highest and lowest reflectance of water. In contrast, the shadow areas have a high reflectance for the blue band but it is low compared to the reflectance of water. The results also demonstrate that the NIR band has the highest reflectance difference (0.03) between water and shadow. Moreover, the red band shows a sharp increase in the reflectance of water. Thus, combining the NIR, SWIR2, blue, and red bands, as in Equation (3), maximizes the index reflectance between water and shadow, as shown in Figure 7b.
where , , , and are the reflectance values of the near infrared (wavelength: 0.851–0.879 μm), SWIR2 (wavelength: 2.107–2.294 μm), blue (wavelength: 0.452–0.512 μm), and red (wavelength: 0.636–0.673 μm) bands.
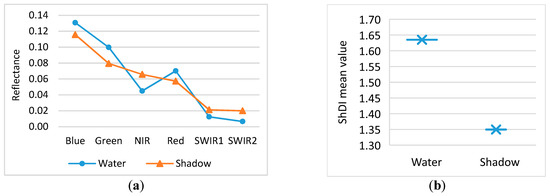
Figure 7.
Reflectance of surface water and shadow in the Hong Kong study area: (a) band reflectance and (b) proposed shadow index (ShDI).
3.4. Spectral Separability Analysis and Threshold Optimization
An important step in urban land cover mapping is optimizing the threshold for a particular land cover type when applying the spectral indices. This study uses ground spectral reflectance to optimize the thresholds and then conducts spectral separability analysis. In the first stage, to evaluate spectral separability, 1200 ground sample points, 300 for each land cover type, are collected from the high-resolution ZY-3 images for Hong Kong and the SPOT 6 images for Dhaka. To account for potential variability in the surface reflectance, the ground sample points are randomly selected from the entire study area, and then the spectral values are extracted. In the next stage, the graphical and statistical analyses are used to compute the degree of spectral mean difference and the thresholds between adjacent land cover types. For example, Figure 8 illustrates the distribution of observed MNDBI values in Dhaka. Table 2 shows the statistics of different land cover types identified by the proposed indices.
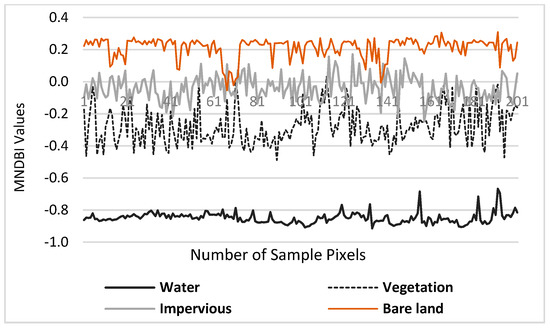
Figure 8.
Ground reflectance of different land cover types identified by the MNDBI in the Dhaka dataset.

Table 2.
Statistics of different land cover types identified by the proposed indices.
After the separability analysis, the threshold is optimized to segment the land cover areas. The image segmentation method used is thresholding. The most common thresholding methods are based on histograms, clustering, entropy, and spatial, local, and object attributes [60]. Otsu optimal multilevel thresholding, which uses histograms of grey-level images, is a well-known approach to image thresholding [48]. However, none of these methods is designed for threshold optimization using ground reflectance data. Therefore, this study uses a novel approach to threshold optimization based on the ground spectral reflectance between adjacent land covers, as Equation (4). The proposed threshold optimization approach is developed considering the typical statistics; i.e., maximum, minimum, and mean ground reflectance of each land covers. In addition, to minimize the influence of any extreme values the mean of less than mean and mean of greater than mean values of adjacent land covers are considered, and then the standard deviation is enumerated. Thus, the proposed approach highly optimizes the spectral reflectance difference between adjacent land covers.
where To is the optimized threshold between adjacent land covers, . indicate the observed minimum and maximum mean values of adjacent land covers and . is the standard deviation of mean threshold (Equation 5), mean of less than mean and mean of greater than mean values.
where is the mean threshold, n is the total number of ground samples, and is the spectral reflectance of ith observed points for a particular land cover.
3.5. Land Cover Classification Using the Novel Spectral Indices
In the proposed framework, the performances of the indices are evaluated, and the threshold is optimized before the land cover is segmented. Then, using an optimized threshold (OT) a decision tree algorithm is implemented to detect land covers. Figure 9 illustrates the workflow of the urban land cover classification procedure using the new spectral indices. The TCWVI index results in vegetation and bare land as adjacent land covers. Thus, in the first stage, the TCWVI is used as the starting node to segregate vegetation and bare land from other land cover types. Second, the optimized threshold of the MNDBI is used to segregate bare land from vegetation. Third, impervious and shaded areas are segregated from water using the ShDI. Fourth, the optimized threshold of the TCWVI is used to enhance water detection. Fifth, impervious and shaded areas are segregated using the ShDI. Notably, the ShDI enhances the separation of shadow from water, however, the complete separation between impervious and shaded areas are not possible using the optimized threshold of the ShDI. Shadows consist of both impervious and vegetative lands thus, after careful examination, finally, NDVI is used to improve the segregation of shaded areas as impervious and vegetation. In the final stage, the threshold of the MNDBI is used to enhance further separation of impervious areas. Finally, the detected land covers types are combined into four classes, as shown in Figure 1. Table 3 summarizes the thresholds of the developed indices for both study sites. The investigation confirms that thresholds of the spectral indices are variable to study sites thus careful consideration should be given when applying this approach of classification to other cities of the world.
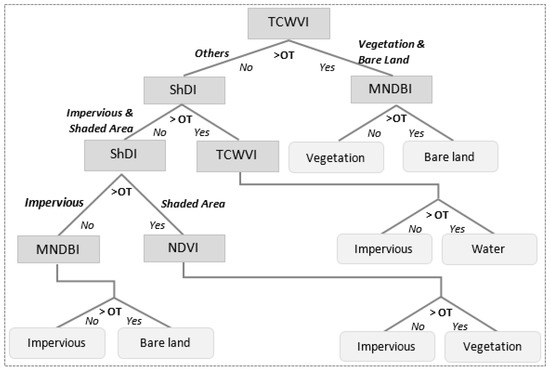
Figure 9.
Workflow for the proposed land cover classification procedure.

Table 3.
Optimized thresholds of the land cover classes.
4. Experimental Validation
This section describes the evaluation of the proposed indices, threshold optimization, and the final classification results. In the first stage, the performances of the proposed indices are evaluated. To evaluate the performance of the MNDBI, two other indices, the NDBI and NDBLI, are used in a comparative analysis. Next, impervious and bare lands are segregated using optimized thresholds for the MNDBI, NDBI, and NDBLI. As a further test, a sensitivity analysis is carried out. The performance of the TCWVI is compared to the performance of the MNDWI and NDVI. First, the accuracy of the TCWVI’s detection of water is assessed by comparing it with the MNDWI. Second, a comparative analysis of the TCWVI and NDVI is performed to assess the accuracy of the TCWVI in detecting vegetation. Finally, quantitative accuracy assessment measures are used to evaluate the indices sensitivity. The performance of the ShDI is also evaluated by comparing the results of the two study sites.
In the second stage, the threshold optimization procedure is evaluated. First, mean and optimized thresholds are used to detect land covers; then sensitivity analysis is performed for both study sites. The most frequently used accuracy assessment measures, overall accuracy (OA) and kappa coefficient, are computed to assess the sensitivity of the threshold optimization. In the final stage, the results of the automated classification are evaluated. A comparative analysis is performed using the SVM algorithm because a number of studies used this robust classifier for comparison with other land cover classification methods [36,37,38,39]. In this study, the SVM algorithm is implemented using the radial basis function (RBF) kernel. The optimized parameters C, P and γ are set to 312, 0 and 0.5, respectively, for the Hong Kong dataset, and to 100, 0 and 0.5, respectively, for the Dhaka dataset. For evaluation, the accuracy assessment measures are computed. Several studies [6,12,18] have conducted accuracy assessments using random sample pixels. In contrast, Goodchild et al. [61] suggested using a minimum of 50 random point samples for each class to assess accuracy. However, it is important to select an appropriate number of samples to accurately assess post classification [12]. To determine the number of required samples, the Multinominal Distribution Equation (6) offered by Congalton [62] is used.
where n is the number of required pixels, B = (α/k)*100, α is the confidence interval, k is the number of classes, is the ratio of area of the ith class, and is the desired precision.
In the Hong Kong dataset, a minimum of 53 reference pixels are required to accurately assess bare land and a maximum of 615 are required to assess vegetation. For the Dhaka dataset, a minimum of 114 pixels is required for bare land and a maximum of 618 for vegetation. In this study, we use more than the minimum requirement. To improve the accuracy of our assessment, 4000 ground truth data are collected from high-resolution images of Hong Kong and 4100 from images of Dhaka. In this study, land covers are classified using images with a resolution of 30 m/pixel, afterward, ground truth data is collected from high-resolution images (6 m/pixel) for validation purpose. A classified pixel of 30 m is equivalent to a patch of 25 pixels on the high-resolution image. Thus, careful consideration is given so that the selected ground truth data adequately form a patch of 25 pixels of the high-resolution image.
4.1. Performance Evaluation of the Proposed Indices
The following section presents the performance of the proposed indices in addressing the previously mentioned limitations of urban land cover classification. In this study, to test the transferability and robustness a similar evaluation approach is implemented in both study sites. However, to be concise, the results of the Hong Kong study site are provided in detail. In contrast, the evaluation results of the Dhaka study site are summarized in brief.
4.1.1. Evaluation of the MNDBI
Figure 10 shows the delineated MNDBI maps for the Hong Kong and Dhaka datasets. The highest values indicate bare land and the lowest values indicate water. The intermediate values indicate impervious areas and vegetation.
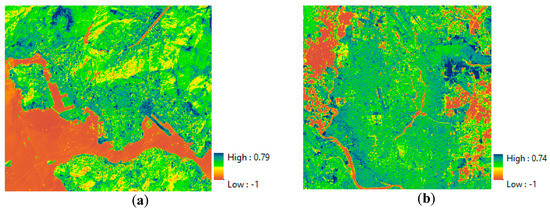
Figure 10.
MNDBI-based maps of two study sites: (a) Hong Kong and (b) Dhaka.
Figure 11 presents the evaluation results of the MNDBI for the Hong Kong dataset. As illustrated in Figure 11a, the impervious and bare land are integrated and the spectral mean difference is not significant; thus, the NDBI is not good enough to separate impervious and bare land. However, the NDBI clearly separates natural features such as vegetation and water from other types of land cover. Figure 11c indicates that, to some extent, the NDBLI can separate bare land from impervious areas but complete separation is still a challenge. As large numbers of areas of impervious and bare land have similar reflectance values, there is a high degree of misclassification of these types, as shown in Figure 11d. However, Figure 11e illustrates that the MNDBI has the highest positive values for bare land and the spectral mean difference between bare land and adjacent impervious areas are significant. Thus, the MNDBI is better at separating impervious and bare land, as shown in Figure 11f.
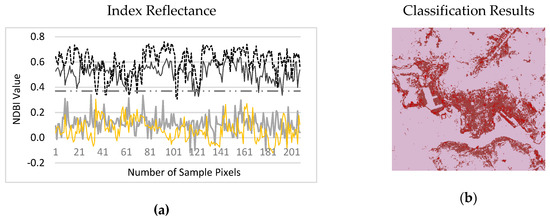
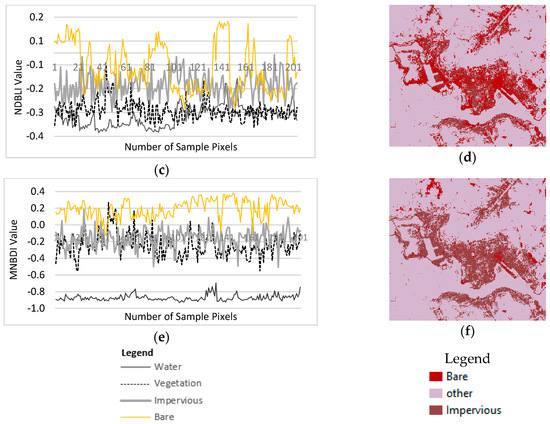
Figure 11.
Impervious and bare land separation in Hong Kong using (a,b) normalized difference bare-land index (NDBI), (c,d) normalized difference bare land index (NDBLI), (e,f) MNDBI.
As a further comparison, the Dhaka dataset is used to evaluate the performance of the MNDBI. The accuracy of the results is summarized in Table 4. The sensitivity analysis results indicate that the MNDBI has a better performance than the other indices. Specifically, the highest accuracy is observed for the MNDBI and the lowest for the NDBLI. The investigation confirms that the results are consistent and similar to those for the Hong Kong dataset. In summary, the proposed MNDBI is better than the other indices in separating impervious and bare land.

Table 4.
Sensitivity of indices in the detection of impervious and bare land.
4.1.2. Evaluation of the TCWVI
Figure 12 shows the delineated TCWVI maps based on the Hong Kong and Dhaka datasets. These maps show a clear separation between water and vegetation, with the highest values indicating water and the lowest vegetation. The intermediate values indicate areas of impervious and bare land.
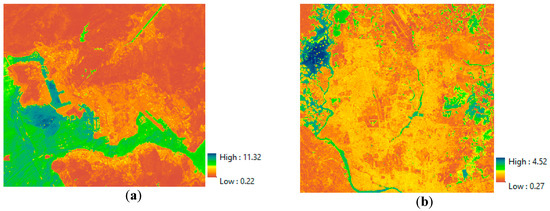
Figure 12.
TCWVI-based maps of the two study sites: (a) Hong Kong and (b) Dhaka.
The results of the evaluation of the TCWVI for the Hong Kong dataset are presented in Figure 13. As illustrated in Figure 13a, in the MNDWI map water has the lowest negative values and bare land has the highest positive values. There is also a significant mean difference between water and adjacent land cover types. The separability analysis shows that the MNDWI is a good indicator of water, but a salt and pepper effect is observed when thresholds are used to extract water, as shown in Figure 13b. As illustrated in Figure 13c, the scatter plot of the NDVI results indicates that vegetation has the highest positive values, bare land has the second highest values, and these two are adjacent land cover types. Water has the lowest values. The extracted vegetation using the optimized threshold of the NDVI is shown in Figure 13d. The spectral separability of the TCWVI produces results that are opposite those of the NDVI. In this case, the highest values are observed for water, with a significant mean difference between water and adjacent land cover types, and the lowest values are observed for vegetation, as shown in Figure 13e. In the proposed framework, vegetation and water are extracted together using the TCWVI, as shown in Figure 13f. The comparative analysis demonstrates a good agreement between the NDVI and TCWVI for detecting vegetation, and a good agreement between the MNDWI and TCWVI for detecting water.
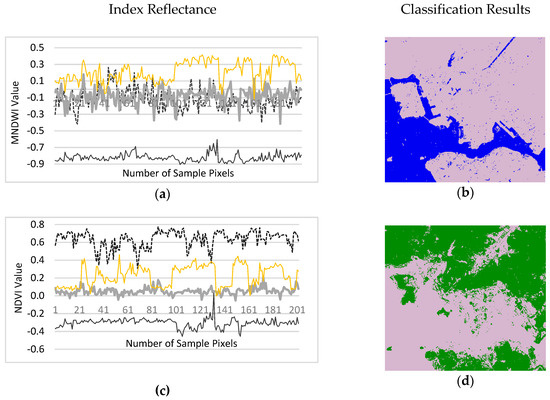
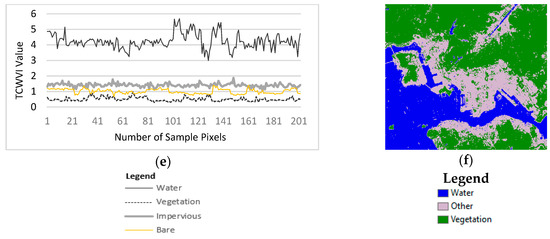
Figure 13.
Water and vegetation detection in Hong Kong using (a,b) MNDWI, (c,d) NDVI, and (e,f) TCWVI.
As a further comparison, the Dhaka dataset is used to evaluate the performance of the TCWVI. The results of the sensitivity analysis, shown in Table 5, indicate an acceptable performance of the TCWVI for both study sites. In summary, the results demonstrate that the proposed TCWVI can simultaneously detect water and vegetation with a satisfactory degree of accuracy. Moreover, the TCWVI improves the detection of water, as it minimizes the salt and pepper effect. The results also demonstrate that the TCWVI reduces dependency on two indices and enhances the extraction of vegetation and water using a single index.

Table 5.
Sensitivity of indices in the detection of vegetation and water.
4.1.3. Evaluation of the ShDI
Figure 14 shows the delineated ShDI maps for the Hong Kong and Dhaka datasets. In the Hong Kong dataset, the highest values indicate water, the second highest shadow, and the lowest vegetation (Figure 14a). In the Dhaka dataset, the highest values indicate water, the second highest impervious land, and the lowest vegetation (Figure 14b).
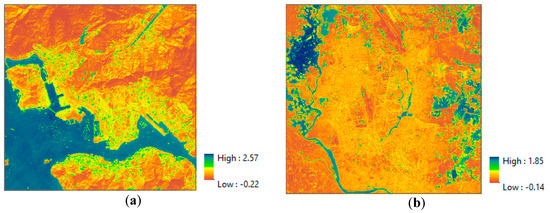
Figure 14.
ShDI-based maps of the two study sites: (a) Hong Kong and (b) Dhaka.
Figure 15 presents the results of the evaluation of the ShDI. Landsat-8 false-color images of Hong Kong indicate the existence of shadows, as shown in Figure 6a. Therefore, although water is extracted, as shown in Figure 13b, the salt-and-pepper effect is observed. As illustrated in Figure 15a, for the ShDI, water has the highest reflectance values, the second highest is shadow, and vegetation has the lowest values. The classification results illustrated in Figure 15b show that the ShDI can separate water from shadows. A similar pattern is observed at the second study site, but as shadow is not detected in Dhaka, water has the highest values and vegetation has the lowest values.
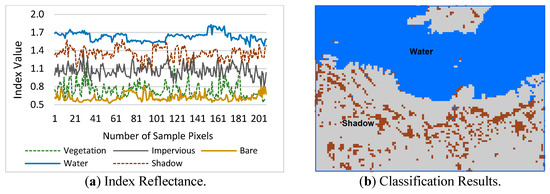
Figure 15.
Water and shadow detection using the ShDI in Hong Kong.
4.2. Sensitivity of Threshold Optimization
Table 6 shows the impact of the mean and optimized threshold values for the TCWVI on the detection of water and vegetation. The water detection results demonstrate that the optimized threshold provides higher accuracy than the mean threshold. The result also indicates that the optimized threshold improves the detection of vegetation. Similar findings are observed in the separation of impervious and bare land. In this section, we have illustrated the sensitivity of the TCWVI. A similar approach to assess the sensitivity of other indices demonstrates that the optimized threshold produces the most consistent performance and the highest accuracy in detecting land covers of both study sites.

Table 6.
Impact of the parameter threshold of the TCWVI on detection of water and vegetation.
4.3. Results of the Land Cover Classification and Comparative Analysis
In this section, the results of the proposed method for classifying urban land cover based on three new indices are compared to the results of a popular classifier, the SVM algorithm. The proposed method is automated and uses the optimized thresholds of the new indices. In contrast, the SVM algorithm is implemented after optimization the parameters C, P and γ. Figure 16 presents a visual comparison of the classifications obtained by the proposed approach and the SVM algorithm for the Hong Kong dataset. The results of the SVM algorithm have an over-detection of water and bare land, reducing the accuracy of the detection of these land cover types compared to the proposed approach. As illustrated in Table 7, the classified data of the SVM algorithm substantially deviate from the user and producer accuracy for all land cover types. In contrast, the proposed approach has a better overall performance with slight deviations. Its overall accuracy, 96.1% with a kappa coefficient of 0.95, also demonstrates that the proposed approach performs better than the SVM algorithm. The assessment indicates that the approach is most accurate for classifying water and least accurate for classifying bare land. Although the accuracy in classifying bare land is relatively low compared to other land covers, the proposed approach improves the separation of impervious and bare land. Overall, the approach has an accuracy of 94% in the detection of impervious areas.
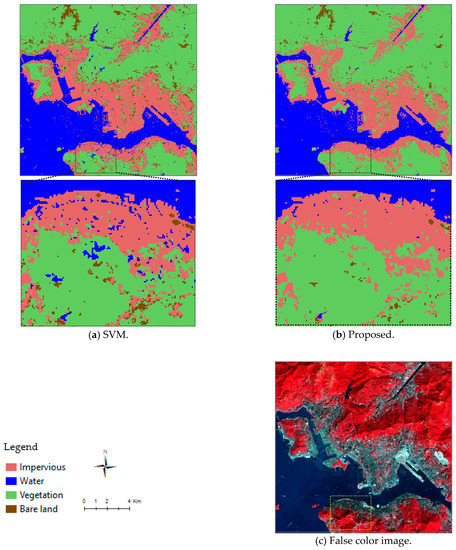
Figure 16.
Classification of land cover in Hong Kong.

Table 7.
Accuracy of results for the Hong Kong dataset.
A comparison of the results of the proposed approach and the SVM algorithm for the Dhaka dataset is presented in Figure 17. The results are very similar to those for Hong Kong. The accuracy assessment for the Dhaka dataset, shown in Table 8, indicates that the proposed approach has a better performance than the SVM algorithm. The overall classification accuracy, 94.1% with a kappa coefficient of 0.92, is higher than the classification accuracy of the SVM algorithm. In the Dhaka example, the best performance is in the classification of water and the worst in the classification of bare land. Impervious areas are detected with an accuracy of nearly 94%. Overall, our proposed approach can detect land covers with a level of accuracy that is better than that of the SVM algorithm. However, the proposed approach is slightly more accurate for Hong Kong than for Dhaka.
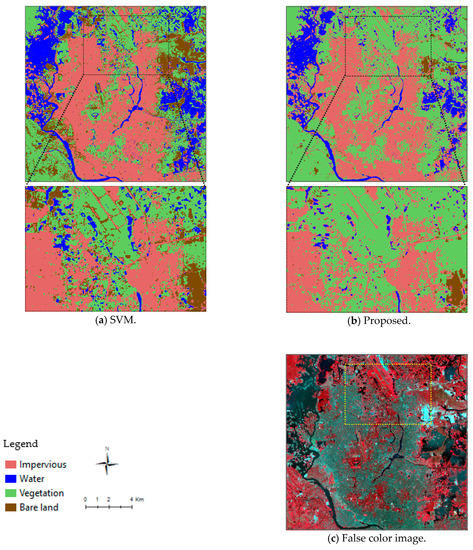
Figure 17.
Classification of land cover in Dhaka.

Table 8.
Accuracy of results for the Dhaka dataset.
5. Discussion
Various factors, e.g., atmospheric transmission, cloud, wind, image acquisition time, and vegetation types, can affect spectral band reflectance. Moreover, the characteristics of the physical properties and the variation in atmospheric correction altogether can affect the threshold values of the indices. Thus, careful consideration should be given to choosing spectral thresholds to detect land cover types in different cities. For example, the bare land in Dhaka is sand and soil, the geology of Hong Kong is dominated by rocks. As the physical properties of bare land in these two study sites are dissimilar, the range of band reflectance and index values using the proposed MNDBI varies between the two study sites. Moreover, as the vegetative covers are also variable, the band reflectance and threshold of the TCWVI and NDVI also vary between the two study sites. Similarly, the thresholds for other land cover types are variable, thus it is important to identify the local spectral values to each land cover type prior to applying this approach of classification. The proposed approach is a pixel-based solution; thus, its performance with high-resolution images must be assessed. In this study, we have used only Landsat-8 OLI images. A future study is required to fully evaluate the applicability of this approach to other higher resolution dataset; e.g., the Sentinel 2 data.
The results indicate high accuracy in Hong Kong compared to the Dhaka case study. In terms of development, Hong Kong is compact and has a less fragmented pattern of land cover, whereas Dhaka is very dense, but characterized by fragmented urban sprawl. The extent of fragmentation is reflected in the complicated and diverse pattern of land cover types in Dhaka. Dhaka also encompasses several small bodies of water, such as ponds and canals, which are surrounded by vegetation that reduces visibility. The use of low-resolution image is impotent to properly detect narrow water bodies and results in misclassification. An example of such misclassification is illustrated in Figure 18. It is noticeable that a narrow strip of water body is classified as vegetation 18c. In this illustration, the existence of water is verified using the Google Earth image and the high-resolution SPOT-6 image. The verifications confirm that the strip covers a body of water having an average width of 10 m (Google Earth) and 6 m (SPOT 6), respectively. However, the resolution of Landsat data is 30 m/pixel. Thus, such narrow water bodies are not properly detected in the low-resolution Landsat images. These underlying factors contribute to the relatively lower accuracy in the detection of water and vegetation, and the overall lower accuracy in the Dhaka case study compared to the Hong Kong case study.

Figure 18.
Effect of image resolution to the detection of small bodies of water.
Statistical accuracy assessment is important to the thematic maps derived from remote sensing data, thus the Kappa coefficient is often used. This study uses similar accuracy assessment measures. However, the Kappa coefficient does not deal with the pairwise comparison, and agreement and disagreement between categories [63]. Moreover, the Kappa index compares accuracy to a baseline of randomness. However, randomness is not a reasonable alternative for mapping [64]. The use of the Bradley–Terry (BT) model determines the agreement within a category and disagreement in relation to another category [63]. In addition, the quantity disagreement and allocation disagreement of two simple measures are useful compared to Kappa indices [64]. In this study, we have estimated only the kappa coefficient, however, other accuracy assessment measures will be considered in our future works to facilitate a pairwise comparison, and agreement and disagreement between categories.
6. Conclusions
The main purpose of this study is to improve automatic land cover mapping in urban areas. To achieve this task, we propose three novel indices and a new approach to threshold optimization. As band reflectance and index values vary over different physical properties and land covers, spectral separability analysis is needed to effectively determine the optimized threshold for separating land cover types. The evaluation of the proposed indices and the process of threshold optimization indicates that they perform satisfactorily at both study sites. Specifically, we achieve better results separating impervious and bare land with the MNDBI than with other indices. The MNDBI also has the lowest negative values for water, and the mean difference with other land covers are significant at both study sites. Thus, future studies could evaluate the ability of the MNDBI to detect water. The TCWVI can simultaneously detect vegetation and water with acceptable accuracy. Moreover, the shadow index developed in this study improves water detection by maximizing the reflectance between water and shadow. The experimental analysis demonstrates that the proposed approach performs better than the SVM algorithm. The new approach is a reliable automatic classification method that provides between 94% and 96% accuracy.
Although this method enhances land cover classification and improves the separation between impervious and bare land, complete separation is still a challenge. In addition, thresholds are optimized using training data, thus further study is required to develop an automatic approach of threshold optimization and make the proposed approach more functional in the near future. The overall results indicate that the proposed method is promising and reliable to enhance land cover classification in urban areas. The proposed land cover classification approach is of significance to facilitate the monitoring of terrestrial ecosystems, water resources, and urban sprawl.
Author Contributions
M.I.F. conceived and designed the experiment and B.W. provided constructive suggestions and guidelines to improve the quality of the paper.
Funding
The work described in this paper was supported by the funding from the Hong Kong Ph.D. Fellowship.
Acknowledgments
The authors thank the US Geological Survey (USGS) for making the Landsat datasets publicly available.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Doustfatemeh, I.; Baleghi, Y. Comprehensive urban area extraction from multispectral medium spatial resolution remote-sensing imagery based on a novel structural feature. Int. J. Remote Sens. 2016, 37, 4225–4242. [Google Scholar] [CrossRef]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Zhou, Y.; Xing, B.; Ju, W. Assessing the impact of urban sprawl on net primary productivity of terrestrial ecosystems using a process-based model—A case study in Nanjing, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2318–2331. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, L.; Liu, J.; Liu, Y.; Li, C. The impact of land cover change on ecosystem service values in urban agglomerations along the coast of the Bohai Rim, China. Sustainability 2015, 7, 10365–10387. [Google Scholar] [CrossRef]
- Shuster, W.D.; Bonta, J.; Thurston, H.; Warnemuende, E.; Smith, D.R. Impacts of impervious surface on watershed hydrology: A review. Urban Water J. 2005, 2, 263–275. [Google Scholar] [CrossRef]
- Li, E.; Du, P.; Samat, A.; Xia, J.; Che, M. An automatic approach for urban land-cover classification from Landsat-8 OLI data. Int. J. Remote Sens. 2015, 36, 5983–6007. [Google Scholar] [CrossRef]
- Chen, X.-L.; Zhao, H.-M.; Li, P.-X.; Yin, Z.-Y. Remote sensing image-based analysis of the relationship between urban heat island and land use/cover changes. Remote Sens. Environ. 2006, 104, 133–146. [Google Scholar] [CrossRef]
- Idol, T.; Haack, B.; Mahabir, R. Radar and optical remote sensing data evaluation and fusion; a case study for Washington, DC, USA. Int. J. Image Data Fusion 2015, 6, 138–154. [Google Scholar] [CrossRef]
- Dujardin, J.; Batelaan, O.; Canters, F.; Boel, S.; Anibas, C.; Bronders, J. Improving surface–subsurface water budgeting using high resolution satellite imagery applied on a brownfield. Sci. Total. Environ. 2011, 409, 800–809. [Google Scholar] [CrossRef] [PubMed]
- Paneque-Gálvez, J.; Mas, J.-F.; Moré, G.; Cristóbal, J.; Orta-Martínez, M.; Luz, A.C.; Guèze, M.; Macía, M.J.; Reyes-García, V. Enhanced land use/cover classification of heterogeneous tropical landscapes using support vector machines and textural homogeneity. Int. J. Appl. Earth Obs. Geoinform. 2013, 23, 372–383. [Google Scholar] [CrossRef]
- He, J.; Harris, J.R.; Sawada, M.; Behnia, P. A comparison of classification algorithms using Landsat-7 and Landsat-8 data for mapping lithology in Canada’s Arctic. Int. J. Remote Sens. 2015, 36, 2252–2276. [Google Scholar] [CrossRef]
- Akar, Ö.; Güngör, O. Integrating multiple texture methods and NDVI to the random forest classification algorithm to detect tea and hazelnut plantation areas in northeast turkey. Int. J. Remote Sens. 2015, 36, 442–464. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Colkesen, I. A kernel functions analysis for support vector machines for land cover classification. Int. J. Appl. Earth Obs. Geoinform. 2009, 11, 352–359. [Google Scholar] [CrossRef]
- Zhai, L.; Sun, J.; Sang, H.; Yang, G.; Jia, Y. Large area land cover classification with Landsat ETM+ images based on decision tree. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Melbourne, Australia, 25 August–1 September 2012. [Google Scholar]
- Li, G.; Wan, Y. A new combination classification of pixel- and object-based methods. Int. J. Remote Sens. 2015, 36, 5842–5868. [Google Scholar] [CrossRef]
- Srimani, P.K.; Prasad, S.N. Decision tree classification model for land use and land cover mapping- a case study. Int. J. Curr. Res. 2012, 4, 177–181. [Google Scholar]
- Darius, P.; Justin, M. Developments in Landsat land cover classification methods: A review. Remote Sens. 2017, 9, 967. [Google Scholar] [CrossRef]
- Hamedianfar, A.; Shafri, H.Z.M.; Mansor, S.; Ahmad, N. Improving detailed rule-based feature extraction of urban areas from Worldview-2 image and LIDAR data. Int. J. Remote Sens. 2014, 35, 1876–1899. [Google Scholar] [CrossRef]
- Szabó, S.; Gácsi, Z.; Balázs, B. Specific features of NDVI, NDWI and MNDWI as reflected in land cover categories. Landsc. Environ. Ser. 2016, 10, 194–202. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. In Proceedings of the Third ERTS Symposium; NASA SP-351; NASA: Washington, DC, USA, 1973; pp. 309–317. [Google Scholar]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the normalized difference water index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. A study on information extraction of water body with the modified normalized difference water index (MNDWI). J. Remote Sens. 2005, 9, 589–595. [Google Scholar]
- Zha, Y.; Gao, J.; Ni, S. Use of normalized difference built-up index in automatically mapping urban areas from TM imagery. Int. J. Remote Sens. 2003, 24, 583–594. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S.; Chi, K. Development of an urban classification method using a built-up index. In Proceedings of the Sixth WSEAS International Conference on Remote Sensing, Iwate Prefectural University, Iwate, Japan, 6–8 October 2010. [Google Scholar]
- Xu, H. A new index for delineating built-up land features in satellite imagery. Int. J. Remote Sens. 2008, 29, 4269–4276. [Google Scholar] [CrossRef]
- Amine, R.; Hadria, F. Integration of NDVI indices from the tasseled cap transformation for change detection in satellite images. Int. J. Computer Sci. Issues 2012, 9, 172–177. [Google Scholar]
- Patel, N.; Mukherjee, R. Extraction of impervious features from spectral indices using artificial neural network. Arab. J. Geosci. 2015, 8, 3729–3741. [Google Scholar] [CrossRef]
- Bhatt, A.; Ghosh, S.K.; Kumar, A. Spectral indices based object oriented classification for change detection using satellite data. Int. J. Syst. Assur. Eng. Manag. 2016, 9, 33–42. [Google Scholar] [CrossRef]
- Eslami, M.; Mohammadzadeh, A. A novel method for urban land cover mapping based on new vegetation indices and texture-spectral information from fused visible and hyperspectral thermal infrared airborne data. Eur. J. Remote Sens. 2017, 50, 320–331. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, H.; Lin, H. Improving the impervious surface estimation with combined use of optical and SAR remote sensing images. Remote Sens. Environ. 2014, 141, 155–167. [Google Scholar] [CrossRef]
- Yao, F.; Wang, C.; Dong, D.; Luo, J.; Shen, Z.; Yang, K. High-resolution mapping of urban surface water using ZY-3 multi-spectral imagery. Remote Sens. 2015, 7, 12336–12355. [Google Scholar] [CrossRef]
- He, C.; Shi, P.; Xie, D.; Zhao, Y. Improving the normalized difference built-up index to map urban built-up areas using a semiautomatic segmentation approach. Remote Sens. Lett. 2010, 1, 213–221. [Google Scholar] [CrossRef]
- Ghimire, B.; Rogan, J.; Galiano, V.; Panday, P.; Neeti, N. An evaluation of bagging, boosting, and random forests for land-cover classification in Cape Cod, Massachusetts, USA. GISci. Remote Sens. 2012, 49, 623–643. [Google Scholar] [CrossRef]
- Rahman, M.; Paul, A.; Doreen, S.B. Mapping complex urban land cover from spaceborne imagery: The influence of spatial resolution, spectral band set and classification approach. Remote Sens. 2016, 8, 88. [Google Scholar]
- Abe, B.T.; Olugbara, O.O.; Marwala, T. Experimental comparison of support vector machines with random forests for hyperspectral image land cover classification. J. Earth Syst. Sci. 2014, 123, 779–790. [Google Scholar] [CrossRef]
- Deilmai, B.R.; Ahmad, B.B.; Zabihi, H. Comparison of two classification methods (MLC and SVM) to extract land use and land cover in Johor Malaysia. In Proceedings of the 7th IGRSM International Remote Sensing & GIS Conference and Exhibition, Malaysia, 21–22 April 2014. [Google Scholar]
- Phan, T.; Kappas, M. Comparison of random forest, k-nearest neighbor, and support vector machine classifiers for land cover classification using Sentinel-2 imagery. Sensors 2018, 18, 18. [Google Scholar]
- Wu, Q.; Zhong, R.; Zhao, W.; Fu, H.; Song, K. A comparison of pixel-based decision tree and object-based support vector machine methods for land-cover classification based on aerial images and airborne lidar data. Int. J. Remote Sens. 2017, 38, 7176–7195. [Google Scholar] [CrossRef]
- Foody, G.M.; Mathur, A. The use of small training sets containing mixed pixels for accurate hard image classification: Training on mixed spectral responses for classification by a SVM. Remote Sens. Environ. 2006, 103, 179–189. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Arora, M.K.; Tiwari, K.C.; Mohanty, B. Effect of neural network variables on image classification. Asian Pacific Remote Sens. GIS J. 2000, 13, 1–11. [Google Scholar]
- Pal, M.; Mather, P.M. An assessment of the effectiveness of decision tree methods for land cover classification. Remote Sens. Environ. 2003, 86, 554–565. [Google Scholar] [CrossRef]
- Otukei, J.R.; Blaschke, T. Land cover change assessment using decision trees, support vector machines and maximum likelihood classification algorithms. Int. J. Appl. Earth Obs. Geoinform. 2010, 12, S27–S31. [Google Scholar] [CrossRef]
- Akbari, D.; Homayouni, S.; Safari, A.; Mehrshad, N. Mapping urban land cover based on spatial-spectral classification of hyperspectral remote-sensing data. Int. J. Remote Sens. 2016, 37, 440–454. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, L.; Huang, X. Object-oriented change detection based on the Kolmogorov–Smirnov test using high-resolution multispectral imagery. Int. J. Remote Sens. 2011, 32, 5719–5740. [Google Scholar] [CrossRef]
- Chen, X.; Chen, J.; Shi, Y.; Yamaguchi, Y. An automated approach for updating land cover maps based on integrated change detection and classification methods. ISPRS J. Photogramm. Remote Sens. 2012, 71, 86–95. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Transact. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Ridd, M.K. Exploring a V-I-S (vegetation-impervious surface-soil) model for urban ecosystem analysis through remote sensing: Comparative anatomy for cities. Int. J. Remote Sens. 1995, 16, 2165–2185. [Google Scholar] [CrossRef]
- Ebrahimian, A.; Wilson, B.N.; Gulliver, J.S. Improved methods to estimate the effective impervious area in urban catchments using rainfall-runoff data. J. Hydrol. 2016, 536, 109–118. [Google Scholar] [CrossRef]
- Li, H.; Wang, C.; Cheng, Z.; Su, A.; Xiong, C.; Wang, J.; Liu, J. Mapping urban bare land automatically from Landsat imagery with a simple index. Remote Sens. 2017, 9, 249. [Google Scholar] [CrossRef]
- Robitu, M.; Musy, M.; Inard, C.; Groleau, D. Modeling the influence of vegetation and water pond on urban microclimate. Sol. Energy 2006, 80, 435–447. [Google Scholar] [CrossRef]
- Abbas, S. Remote Sensing of Forest Succession in Hong Kong’s Country Parks; Department of Land Surveying and Geo-Informatics, The Hong Kong Polytechnic University: Hong Kong, 2017. [Google Scholar]
- Markham, B.L.; Helder, D.L. Forty-year calibrated record of earth-reflected radiance from landsat: A review. Remote Sens. Environ. 2012, 122, 30–40. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Loveland, T.R.; Woodcock, C.E.; Belward, A.S.; Cohen, W.B.; Fosnight, E.A.; Shaw, J.; Masek, J.G.; Roy, D.P. The global Landsat archive: Status, consolidation, and direction. Remote Sens. Environ. 2016, 185, 271–283. [Google Scholar] [CrossRef]
- Mozumder, C.; Tripathi, N.; Tipdecho, T. Ecosystem evaluation (1989–2012) of Ramsar wetland Deepor Beel using satellite-derived indices. Environ. Monit. Assess. 2014, 186, 7909–7927. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Liu, G.; Huang, C.; Xie, C. Comparison of tasselled cap transformations based on the selective bands of Landsat 8 OLI TOA reflectance images. Int. J. Remote Sens. 2015, 36, 417–441. [Google Scholar] [CrossRef]
- Li, B.; Zhang, H.; Xu, F. Water extraction in high resolution remote sensing image based on hierarchical spectrum and shape features. IOP Conf. Ser.: Earth Environ. Sci. 2014, 17, 012123. [Google Scholar] [CrossRef]
- He, Y.; Zhang, X.; Hua, L. Object-based distinction between building shadow and water in high-resolution imagery using fuzzy-rule classification and artificial bee colony optimization. J. Sens. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Sezgin, M.; Sankur, B. Survey over image thresholding techniques and quantitative performance evaluation. J. Electron. Imaging 2004, 13, 146–168. [Google Scholar]
- Goodchild, M.F.; Biging, G.S.; Congalton, R.G.; Langley, P.G.; Chrisman, N.R.; Davis, F.W. Final Report of the Accuracy Assessment Task Force; California Assembly Bill AB1580; University of California, National Center for Geographic Information and Analysis (NCGIA): Santa Barbara, CA, USA, 1994. [Google Scholar]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 2nd ed.; CRC Press, Taylor & Francis Group: New York, NY, USA, 2009; pp. 1–179. [Google Scholar]
- Stein, A.; Aryal, J.; Gort, G. Use of the bradley-terry model to quantify association in remotely sensed images. IEEE Transact. Geosci. Remote Sens. 2005, 43, 852–856. [Google Scholar] [CrossRef]
- Pontius, R.G.; Millones, M. Death to kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).