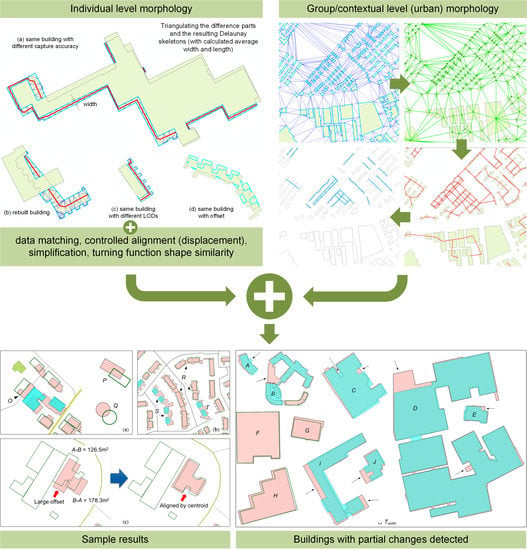
Change Detection for Building Footprints with Different Levels of Detail Using Combined Shape and Pattern Analysis
Abstract
1. Introduction
1.1. Related Concepts and Issues in Change Detection
1.1.1. Nature of Changes
- (1)
- Data acquisition: Positional discrepancies could be the result of varying accuracy, resolution, and so on in data capture. Some objects might be deliberately omitted during data acquisition for certain purposes.
- (2)
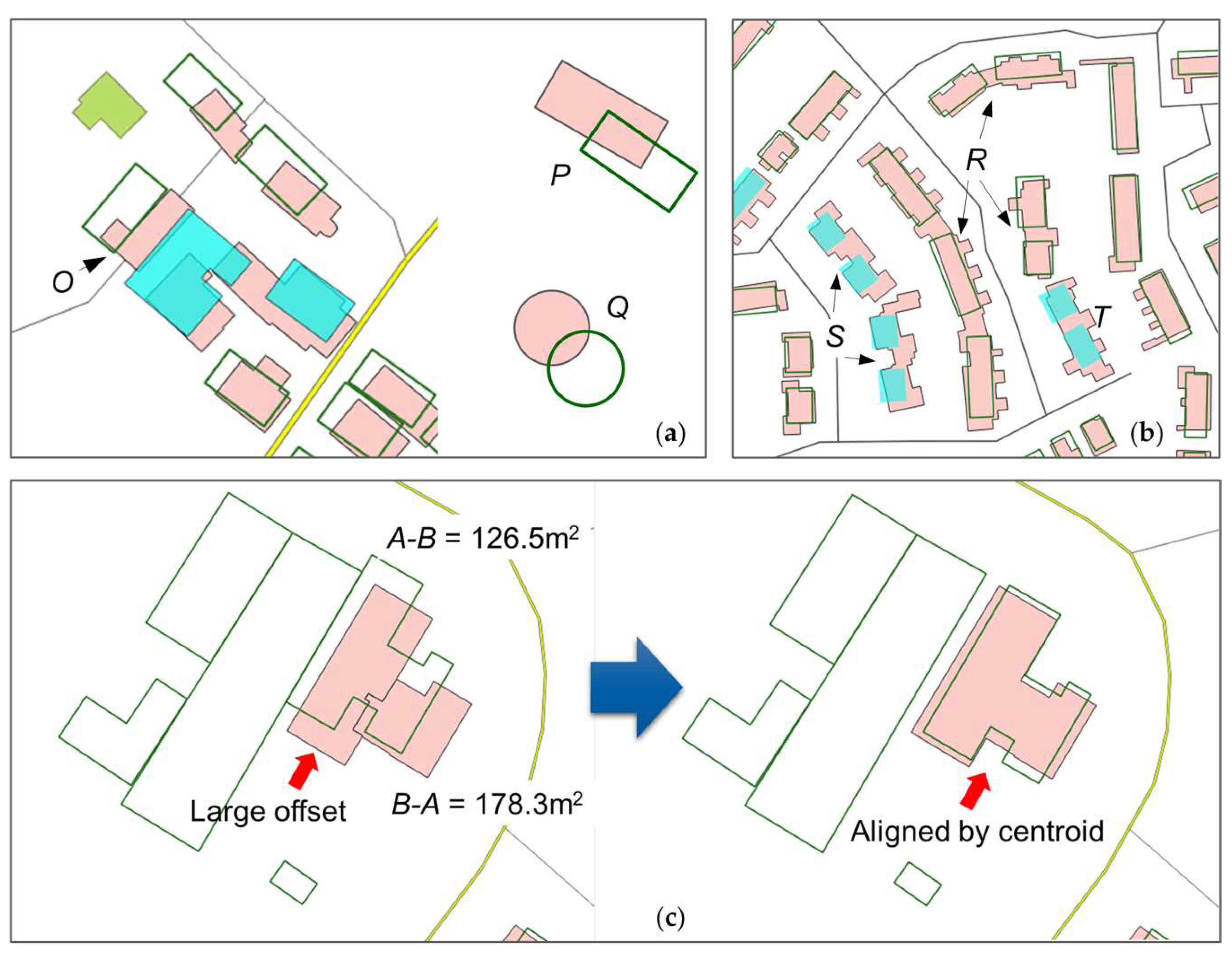
- Data specifications: By comparison with high-resolution images, we found that OSM buildings with greater details were outlined by including the main building and annexes such as fences, courtyards, and garages, whereas in topographic datasets, mainly building roofs were recorded (Figure 1).
- (3)
- Generalization (or LOD): Objects can be simplified, displaced, aggregated, or typified during generalization, which creates apparent discrepancies between data representations.
- (4)
- Physical and nominal changes: The discrepancies due to real world changes to the construction itself (e.g., new construction, removal, and partial rebuilt) or to its semantics (e.g., land-use type, name, etc.)
1.1.2. Previous Work and Issues in Change Detection
2. Methodology
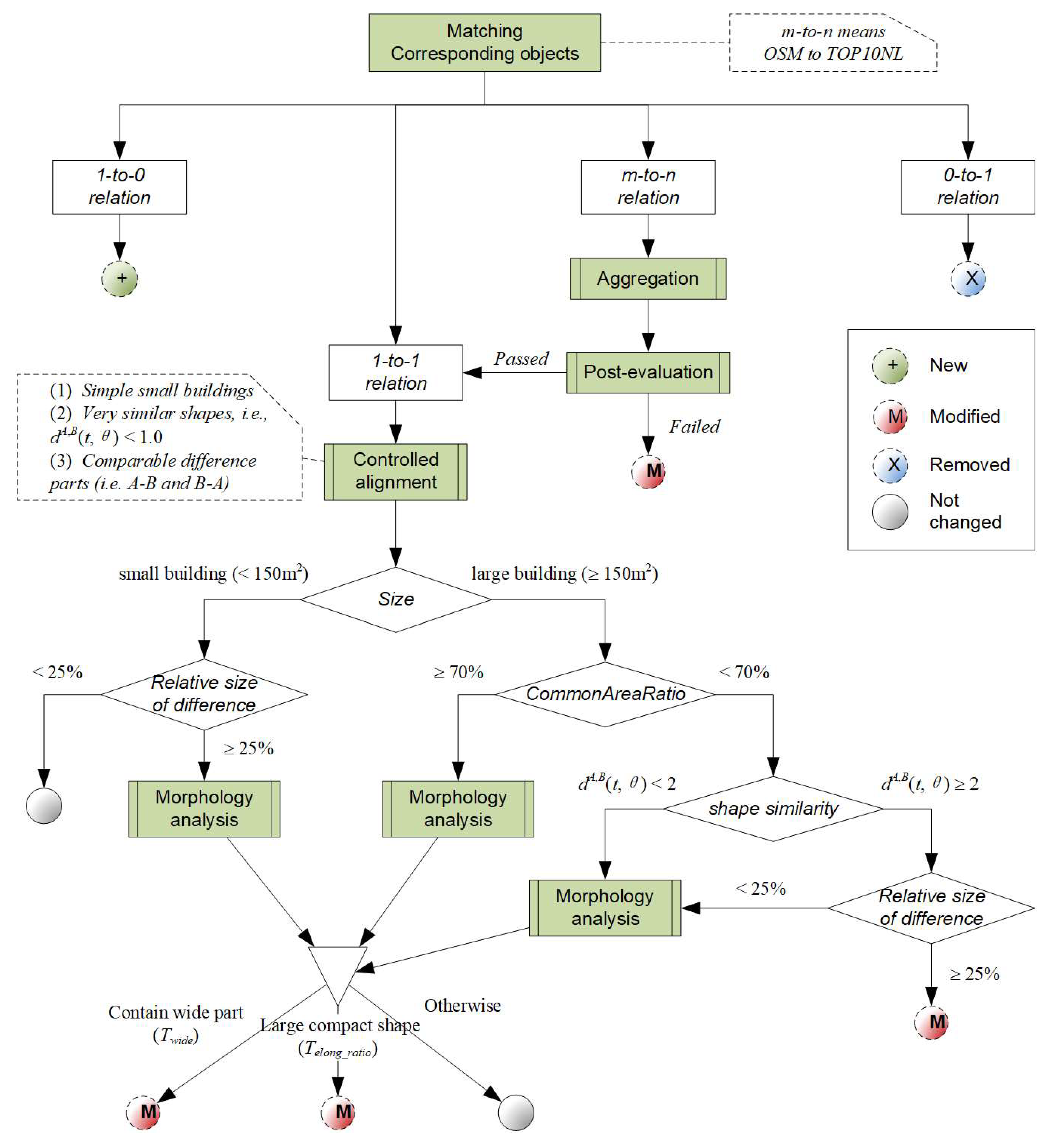
2.1. Overall Process
- Identifying corresponding objects between two datasets (Section 2.2). We aim to identify objects (or a group of objects) in the two datasets that correspond to each other, which is a prerequisite for the subsequent analysis.
- Rule-based change detection (Section 2.3). During this stage, change detection is carried out at the individual level (i.e., building footprints) using different rules and analysis proposed in this paper.
- Refining results with patterns and contextual information (Section 2.4). In this stage, we show how inconsistent results in change detection can be corrected using the building pattern constraint.
2.2. Object Matching
2.3. Rules for Change Detection
- (1)
- Absolute and relative size of the differences.
- (2)
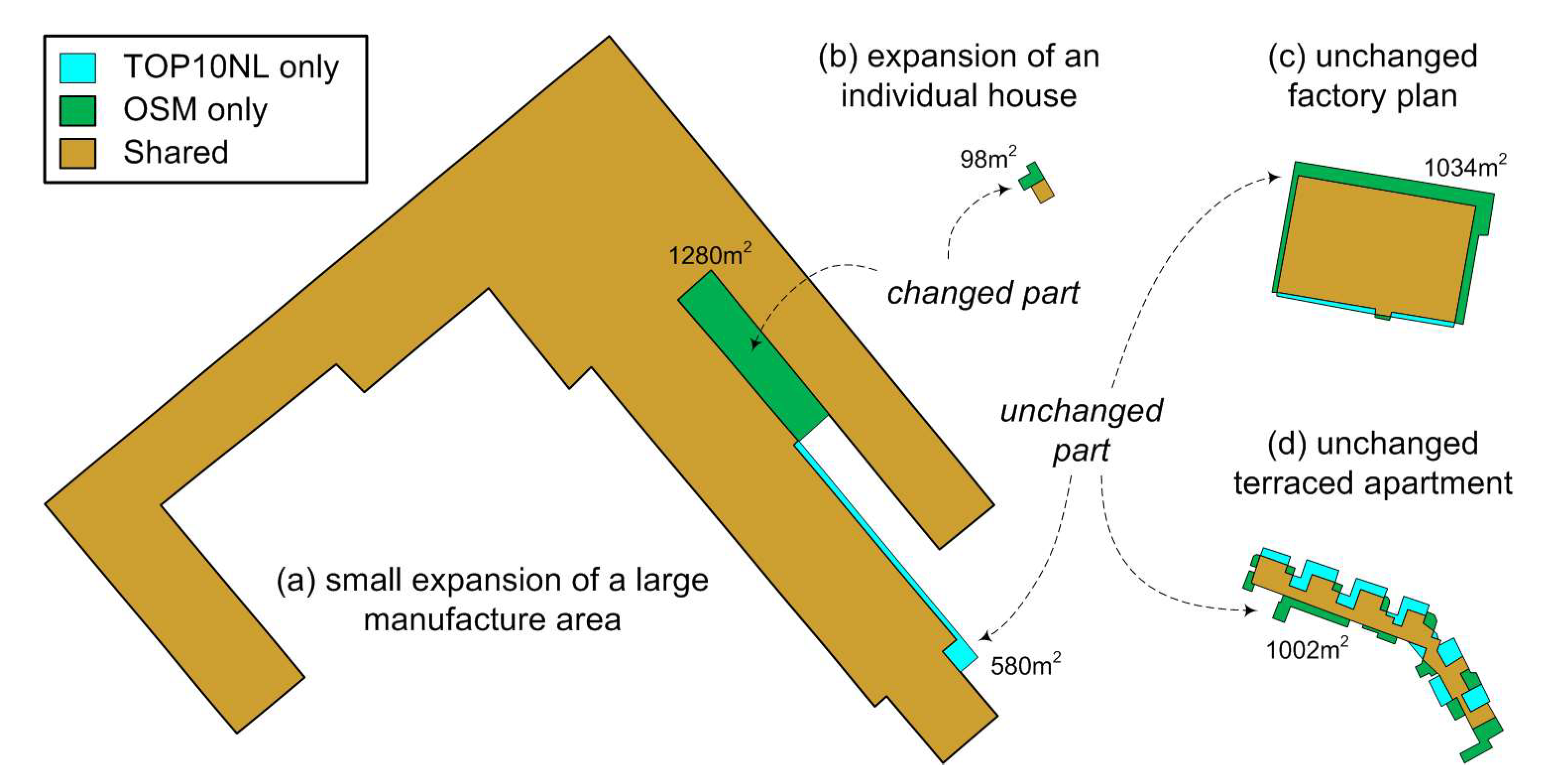
- Set-based similarity: For any two overlapping polygons A and B, three basic sets can be distinguished: A-B, B-A, and A∩B (Figure 1). At the implementation level, A and B result in three non-overlapping polygons, some of which may contain multiple parts (Figure 1b). Basic geometric measures and advanced morphological analysis are performed on these parts.
- (3)
- Shape-based analysis [25] for measuring building similarity and characterizing the overall shape and difference parts.
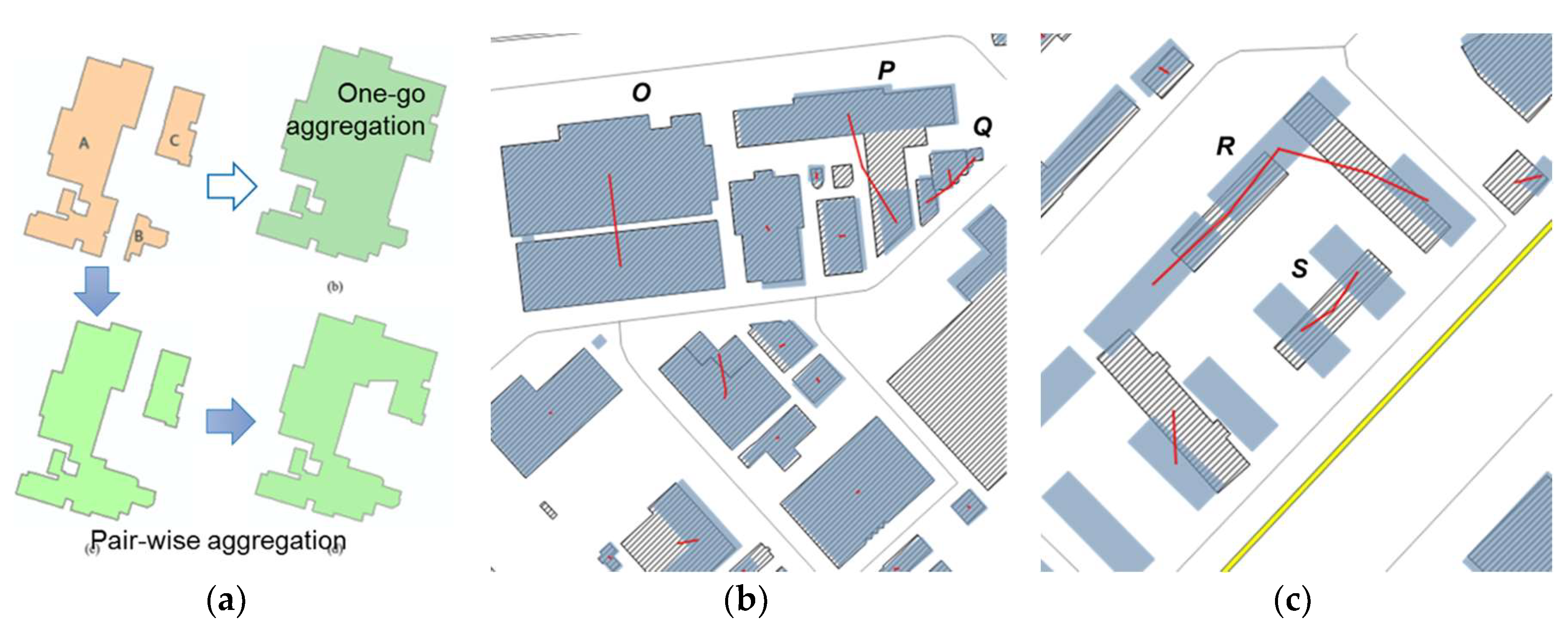
2.3.1. Aggregation with Minimum Cost for the Many-to-Many Correspondence
2.3.2. Controlled Alignment of Corresponding Objects
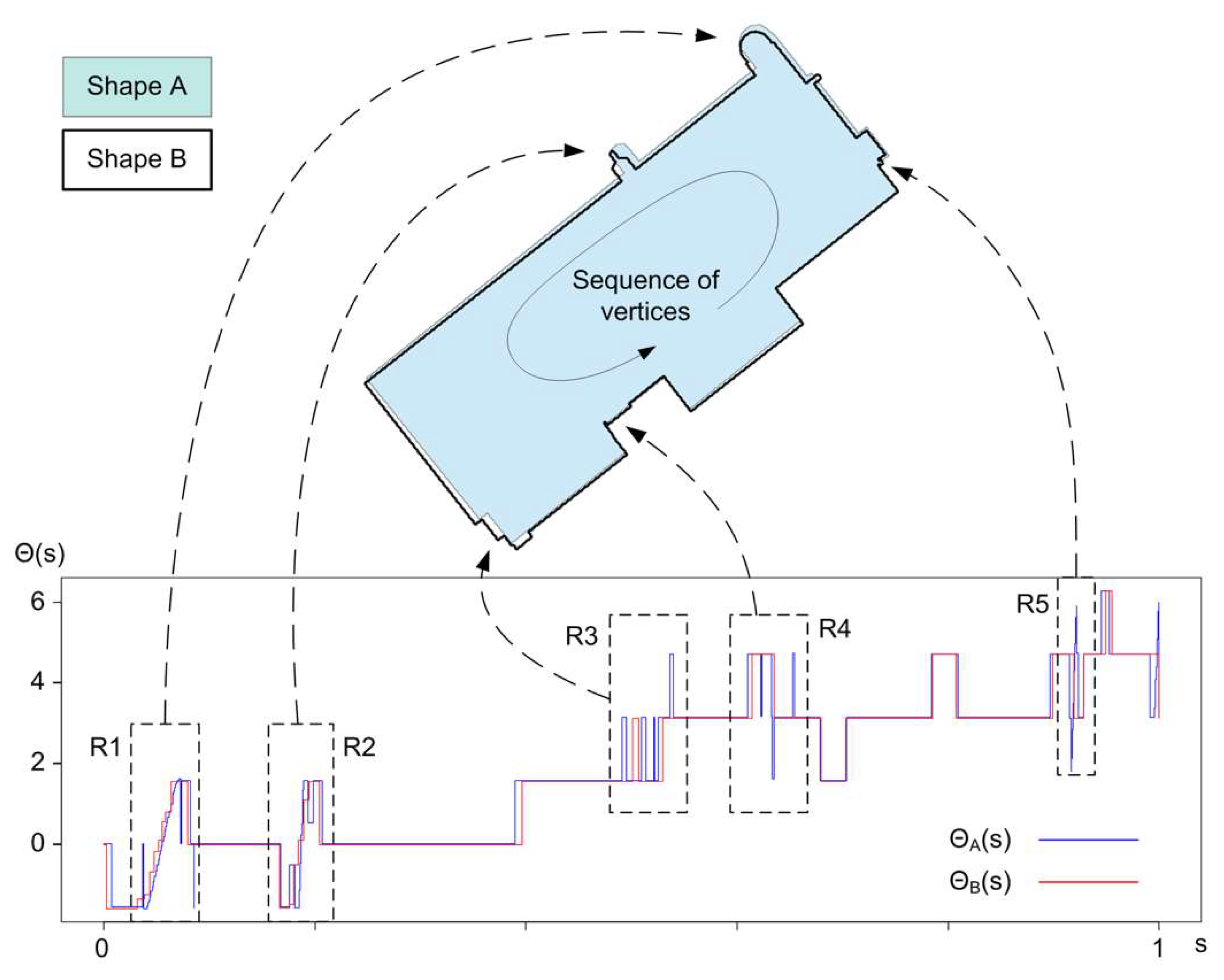
2.3.3. Global Shape Similarity Using Turning Function
2.3.4. Morphological Analysis of Difference Parts
- For small buildings, absolute and relative size of the difference should be considered.
- For large buildings, absolute size of the difference is used as a first criterion, and if the size of the difference exceeds Tsize_diff_abs,
- First check if the part can be segmented into multiple smaller pieces (Figure 7d). If any of them exceeds Tsize_diff_abs, proceed with the analysis in sub-step b; if none of them is large enough, the building is regarded as unchanged;
- For any significant part (or segmented piece), quantify their shape by examining if it is long and narrow, thin belt-shaped (not changed), or in a more compact form (changed).
2.3.5. Rules and Parameters
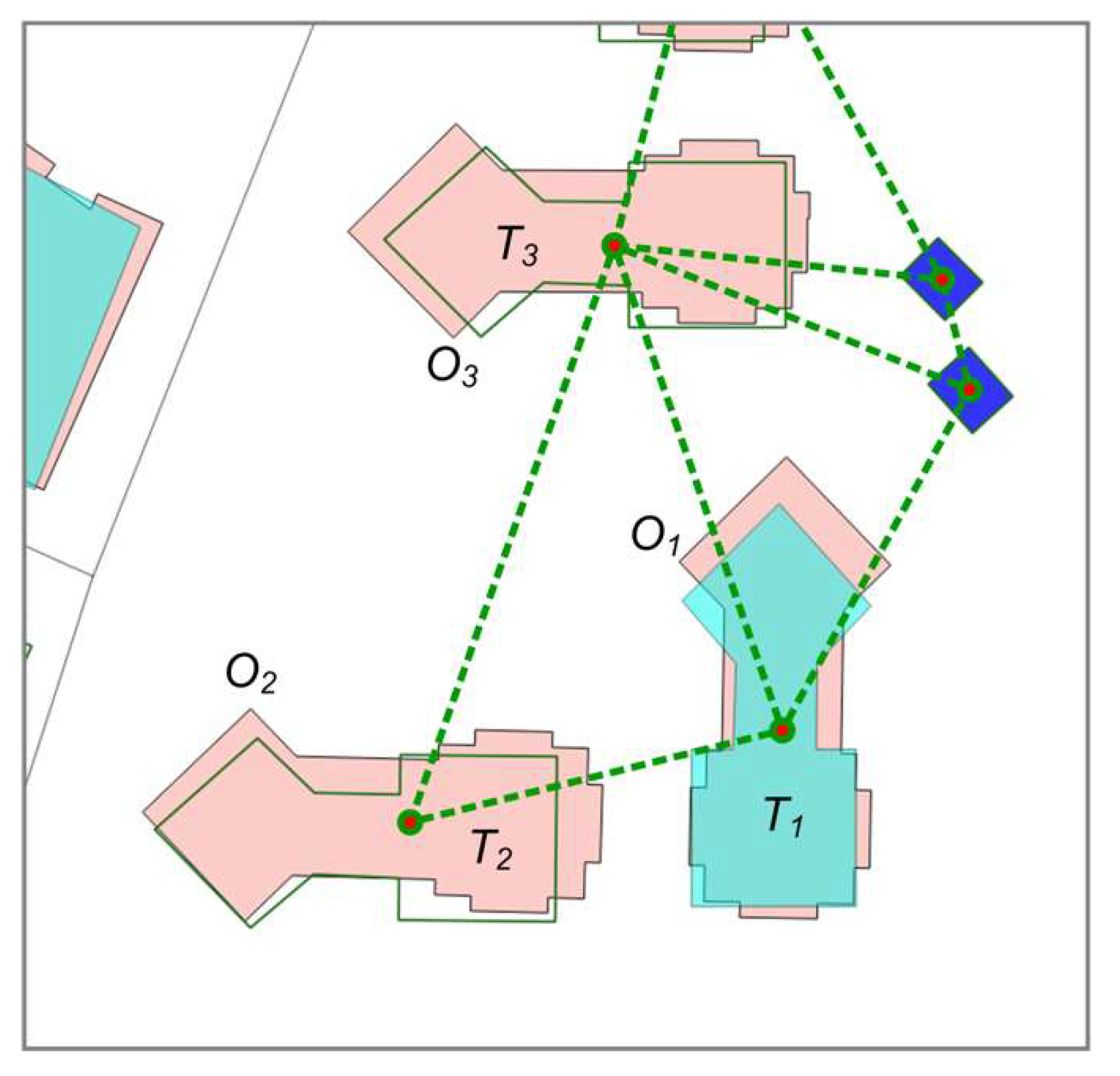
2.4. Correcting Detected Changes with Pattern and Contextual Information
- Compute Delaunay triangulation (DT) on the data area.
- Derive the proximity graph of building footprints, ProxG〈V, E〉, where V is the set of buildings and E is the set of building pairs connected by at least a triangle.
- Prune any edge in ProxG if its two connecting buildings are very different in size, shape, and orientation.
- Trace alignments in the pruned ProxG following the criteria in Zhang et al. [35] and characterized by their homogeneity value (i.e., significance).
3. Experiment Design and Results
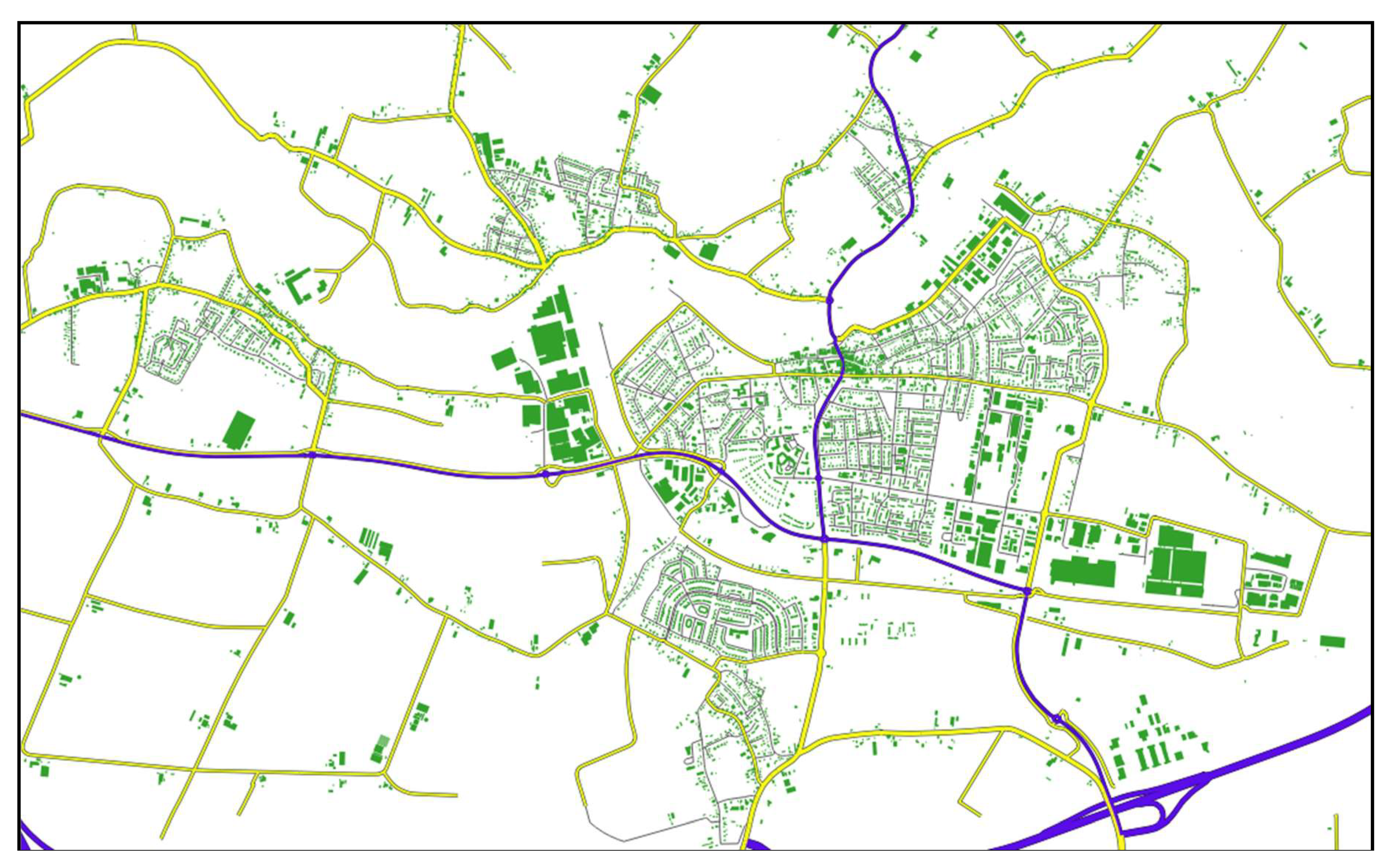
3.1. Data Description and Evaluation Methods
3.2. Detected Changes
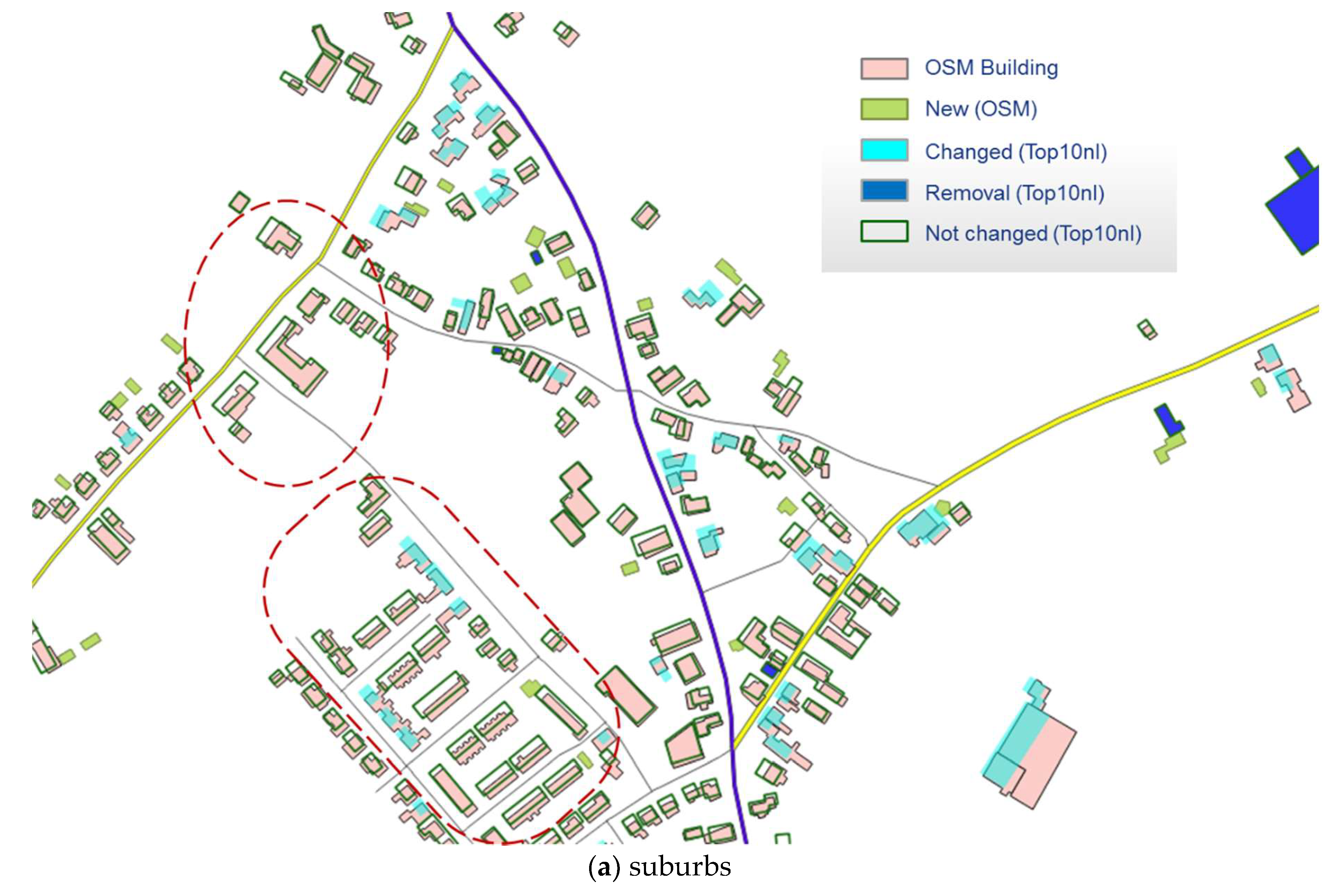
3.2.1. General Results
3.2.2. Effectiveness of the Chosen Rules and Parameters
3.2.3. Corrections Guided by Building Patterns
4. Discussion
4.1. Uncertainty and User Parameters
4.2. Effect of Scales on Change Detection
4.3. Potential Use of Contextual Information
4.4. Fit into Machine Learning?
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haklay, M. How good is volunteered geographical information? A comparative study of OpenStreetMap and ordnance survey datasets. Environ. Plan. B Plan. Des. 2010, 37, 682–703. [Google Scholar] [CrossRef]
- Neis, P.; Zipf, A. Analyzing the contributor activity of a volunteered geographic information project—The case of OpenStreetMap. ISPRS Int. J. Geo-Inf. 2012, 1, 146–165. [Google Scholar] [CrossRef]
- Stoter, J.E.; van Smaalen, J.; Bakker, N.; Hardy, P. Specifying map requirements for automated generalisation of topographic data. Cartogr. J. 2009, 46, 214–227. [Google Scholar] [CrossRef]
- Zielstra, D.; Zipf, A. A Comparative Study of Proprietary Geodata and Volunteered Geographic Information for Germany. In Proceedings of the 13th AGILE International Conference on Geographic Information Science, Guimarães, Portugal, 10–14 May 2010. [Google Scholar]
- Fan, H.; Zipf, A.; Fu, Q.; Neis, P. Quality assessment for building footprints data on OpenStreetMap. Int. J. Geogr. Inf. Sci. 2014, 28, 700–719. [Google Scholar] [CrossRef]
- Touya, G.; Brando-Escobar, C. Detecting level-of-detail inconsistencies in volunteered geographic information data sets. Cartogr. Int. J. Geogr. Inmation Geovis. 2013, 48, 134–143. [Google Scholar] [CrossRef]
- Olteanu-Raimond, A.-M.; Hart, G.; Foody, G.M.; Touya, G.; Kellenberger, T.; Demetriou, D. The scale of VGI in map production: A perspective on European national mapping agencies. Trans. GIS 2016, 21, 74–90. [Google Scholar] [CrossRef]
- Matikainen, L.; Hyyppä, J.; Ahokas, E.; Markelin, L.; Kaartinen, H. Automatic detection of buildings and changes in buildings for updating of maps. Remote Sens. 2010, 2, 1217–1248. [Google Scholar] [CrossRef]
- Tian, J.; Cui, S.; Reinartz, P. Building change detection based on satellite stereo imagery and digital surface models. IEEE Trans. Geosci. Remote. Sens. 2014, 52, 406–417. [Google Scholar] [CrossRef]
- Bouziani, M.; Goïta, K.; He, D.-C. Automatic change detection of buildings in urban environment from very high spatial resolution images using existing geodatabase and prior knowledge. ISPRS J. Photogramm. Remote Sens. 2010, 65, 143–153. [Google Scholar] [CrossRef]
- Ye, S.; Chen, D.; Yu, J. A targeted change-detection procedure by combining change vector analysis and post-classification approach. ISPRS J. Photogramm. Remote Sens. 2016, 114, 115–124. [Google Scholar] [CrossRef]
- Wijngaarden, F.; Putten, J.; Oosterom, P.; Uitermark, H. Map Integration—Update Propagation in a Multi-source Environment. In Proceedings of the 5th ACM International Workshop on Advances in Geographic Information Systems, Las Vegas, NV, USA, 10–14 November 1997; pp. 71–76. [Google Scholar]
- Mas, J.F. Change estimates by map comparison: A method to reduce erroneous changes due to positional error. Trans. GIS 2005, 9, 619–629. [Google Scholar] [CrossRef]
- Kuo, C.; Hong, J. Interoperable cross-domain semantic and geospatial framework for automatic change detection. Comput. Geosci. 2016, 86, 109–119. [Google Scholar] [CrossRef]
- Qi, H.; Li, Z.; Chen, J. Automated change detection for updating settlements at smaller-scale maps from updated larger-scale maps. J. Spat. Sci. 2010, 55, 133–146. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, T.; Huang, J.; Xin, Q. Propagating updates of residential areas in multi-representation databases using constrained Delaunay triangulations. ISPRS Int. J. Geo-Inf. 2016, 5, 80. [Google Scholar] [CrossRef]
- Yang, M.; Ai, T.; Yan, X.; Chen, Y.; Zhang, X. A map-algebra-based method for automatic change detection and spatial data updating across multiple scales. Trans. GIS 2018, 22, 435–454. [Google Scholar] [CrossRef]
- Brychtová, A.; Çöltekin, A.; Paszto, V. Do the visual complexity algorithms match the generalization process in geographical displays? In Proceedings of the XXIII ISPRS Congress, Commission II, Prague, Czech Republic, 12–19 July 2016; pp. 375–378. [Google Scholar]
- Zhang, X.; Yin, W.; Yang, M.; Ai, T.; Stoter, J. Updating authoritative spatial data from timely sources: A multiple representation approach. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 42–56. [Google Scholar] [CrossRef]
- Xie, X.; Wong, K.; Aghajan, H.; Veelaert, P.; Philips, W. Road network inference through multiple track alignment. Transp. Res. Part C 2016, 72, 93–108. [Google Scholar] [CrossRef]
- Liu, C.; Xiong, L.; Hu, X.; Shan, J. A progressive buffering method for road map update using OpenStreetMap data. ISPRS Int. J. Geo-Inf. 2015, 4, 1246–1264. [Google Scholar] [CrossRef]
- Touya, G.; Reimer, A. Inferring the scale of OpenStreetMap features. In OpenStreetMap in GIScience: Experiences, Research, Applications; Jokar Arsanjani, J., Zipf, A., Mooney, P., Helbich, M., Eds.; Springer: Berlin, Germany, 2014; pp. 81–99. [Google Scholar]
- Zhang, X.; Ai, T.; Stoter, J.; Zhao, X. Data matching of building polygons at multiple map scales improved by contextual information and relaxation. ISPRS J. Photogramm. Remote Sens. 2014, 92, 147–163. [Google Scholar] [CrossRef]
- Rutzinger, M.; Rottensteiner, F.; Pfeifer, N. A comparison of evaluation techniques for building extraction from airborne laser scanning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 2, 11–20. [Google Scholar] [CrossRef]
- Pászto, V.; Brychtová, A.; Marek, L. On shape metrics in cartographic generalization: A case study of the building footprint geometry. In Modern Trends in Cartography; Brus, J., Vondrakova, A., Vozenilek, V., Eds.; Springer: Berlin, Heidelberg, 2014; pp. 397–407. [Google Scholar]
- Arkin, E.M.; Chew, L.P.; Huttenlocher, D.P.; Kedem, K.; Mitchell, J.S. An efficiently computable metric for comparing polygonal shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 209–216. [Google Scholar] [CrossRef]
- Yan, X.; Ai, T.; Zhang, X. Template matching and simplification method for building features based on shape cognition. ISPRS Int. J. Geo-Inf. 2017, 6, 250. [Google Scholar] [CrossRef]
- Jones, C.B.; Bundy, G.L.; Ware, J.M. Map generalization with a triangulated data structure. Cartogr. Geogr. Inf. Sci. 1995, 22, 317–331. [Google Scholar] [CrossRef]
- Ai, T.; Guo, R.; Liu, Y. A binary tree representation of curve hierarchical structure based on Gestalt principles. In Proceedings of the 9th international symposium on Spatial Data Handling, Beijing, China, 10–12 August 2000; pp. 2a30–2a43. [Google Scholar]
- Haunert, J.-H.; Sester, M. Area collapse and road centerlines based on straight skeletons. Geoinformatica 2007, 12, 169–191. [Google Scholar] [CrossRef]
- Zhang, X.; Ai, T.; Stoter, J. The evaluation of spatial distribution density in map generalization. In Proceedings of the XXI ISPRS Congress, Beijing, China, 3–11 July 2008; Volume XXXVII, Part B2. pp. 181–187. [Google Scholar]
- Ai, T.; Ke, S.; Yang, M.; Li, J. Envelope generation and simplification of polylines using Delaunay triangulation. Int. J. Geogr. Inf. Sci. 2016, 31, 297–319. [Google Scholar] [CrossRef]
- Ai, T.; Zhang, X.; Zhou, Q.; Yang, M. A vector field model to handle the displacement of multiple conflicts in building generalization. Int. J. Geogr. Inf. Sci. 2015, 29, 1310–1331. [Google Scholar] [CrossRef]
- Anders, K.H. Grid typification. In Progress in Spatial Data Handling; Riedl, A., Kainz, W., Elmes, G.A., Eds.; Springer: Berlin, Heidelberg, 2006; pp. 633–642. [Google Scholar]
- Zhang, X.; Ai, T.; Stoter, J.; Kraak, M.-J.; Molenaar, M. Building pattern recognition in topographic data: Examples on collinear and curvilinear alignments. Geoinformatica 2011, 17, 1–33. [Google Scholar] [CrossRef]
- Zhang, X.; Stoter, J.; Ai, T.; Kraak, M.-J.; Molenaar, M. Automated evaluation of building alignments in generalized maps. Int. J. Geogr. Inf. Sci. 2013, 27, 1550–1571. [Google Scholar] [CrossRef]






| Method | precision | recall | accuracy | k |
|---|---|---|---|---|
| Basic 1 | 0.55 | 0.76 | 0.77 | 0.47 |
| Advanced 2 | 0.82 | 0.87 | 0.90 | 0.77 |
| Advanced + Pattern 3 | 0.87 | 0.87 | 0.92 | 0.81 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Chen, Z.; Zhang, X.; Ai, T. Change Detection for Building Footprints with Different Levels of Detail Using Combined Shape and Pattern Analysis. ISPRS Int. J. Geo-Inf. 2018, 7, 406. https://doi.org/10.3390/ijgi7100406
Zhou X, Chen Z, Zhang X, Ai T. Change Detection for Building Footprints with Different Levels of Detail Using Combined Shape and Pattern Analysis. ISPRS International Journal of Geo-Information. 2018; 7(10):406. https://doi.org/10.3390/ijgi7100406
Chicago/Turabian StyleZhou, Xiaodong, Zhe Chen, Xiang Zhang, and Tinghua Ai. 2018. "Change Detection for Building Footprints with Different Levels of Detail Using Combined Shape and Pattern Analysis" ISPRS International Journal of Geo-Information 7, no. 10: 406. https://doi.org/10.3390/ijgi7100406
APA StyleZhou, X., Chen, Z., Zhang, X., & Ai, T. (2018). Change Detection for Building Footprints with Different Levels of Detail Using Combined Shape and Pattern Analysis. ISPRS International Journal of Geo-Information, 7(10), 406. https://doi.org/10.3390/ijgi7100406