Duality and Dimensionality Reduction Discrete Line Generation Algorithm for a Triangular Grid
Abstract
1. Introduction
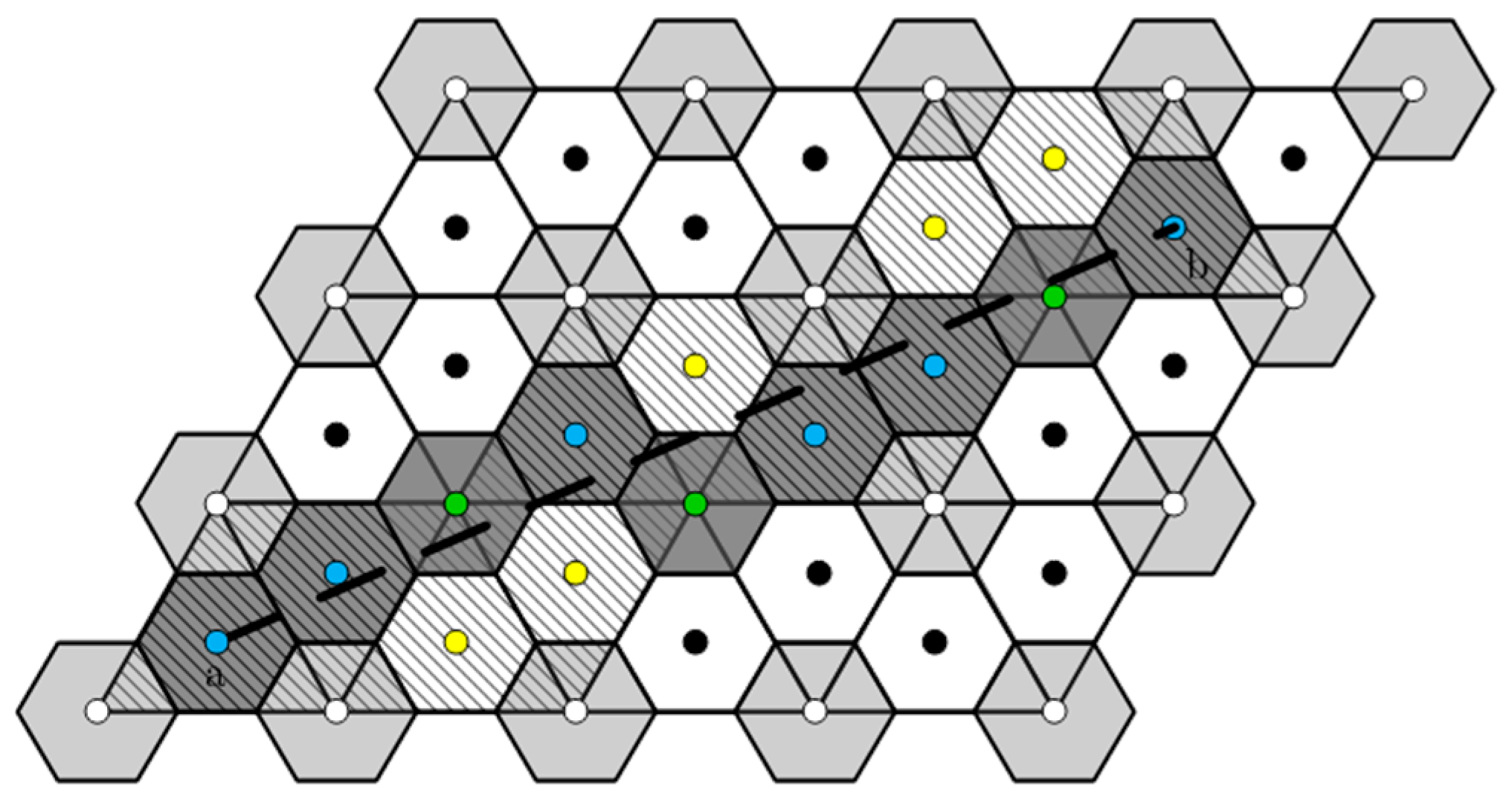
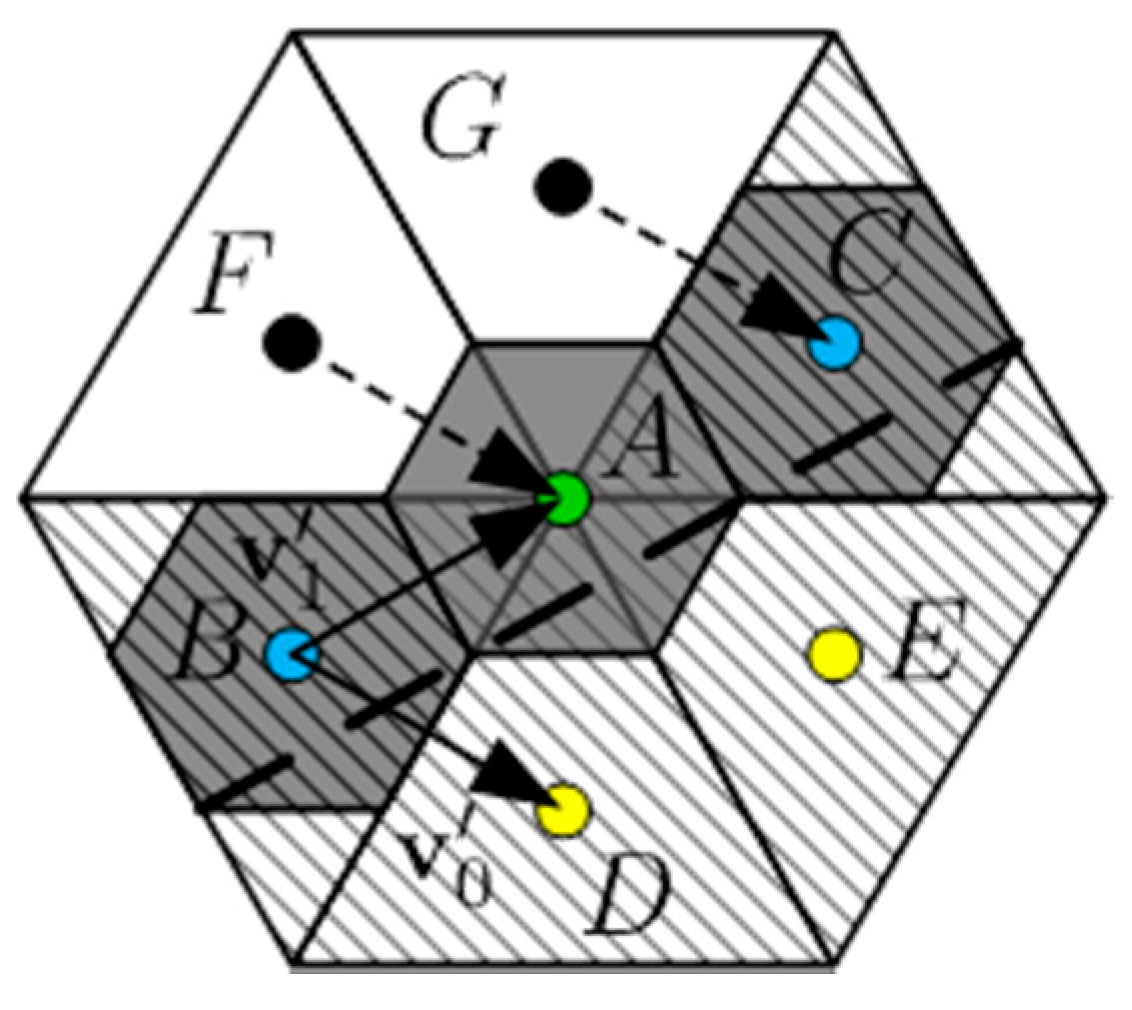
2. Definition of Duality and Weak Duality
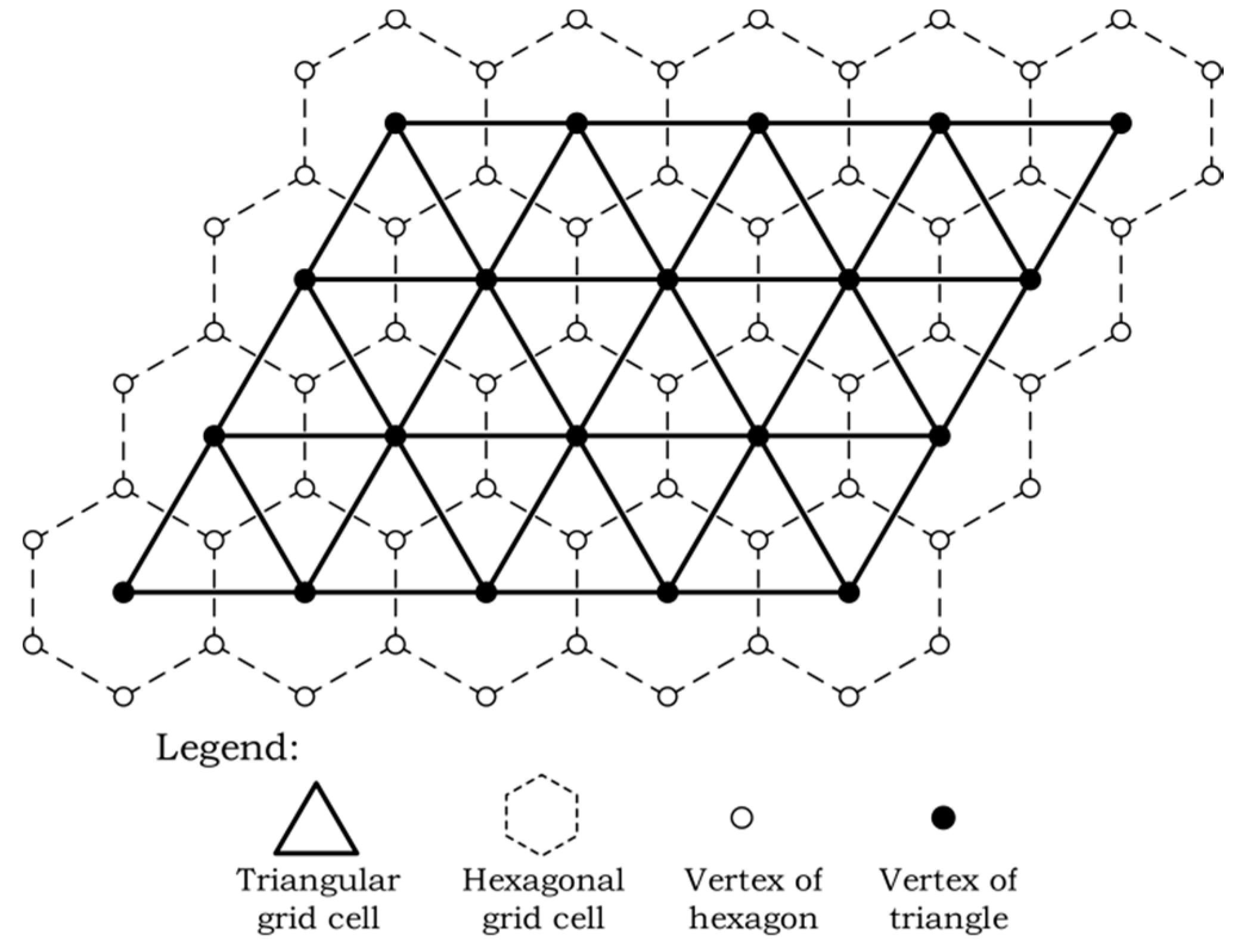
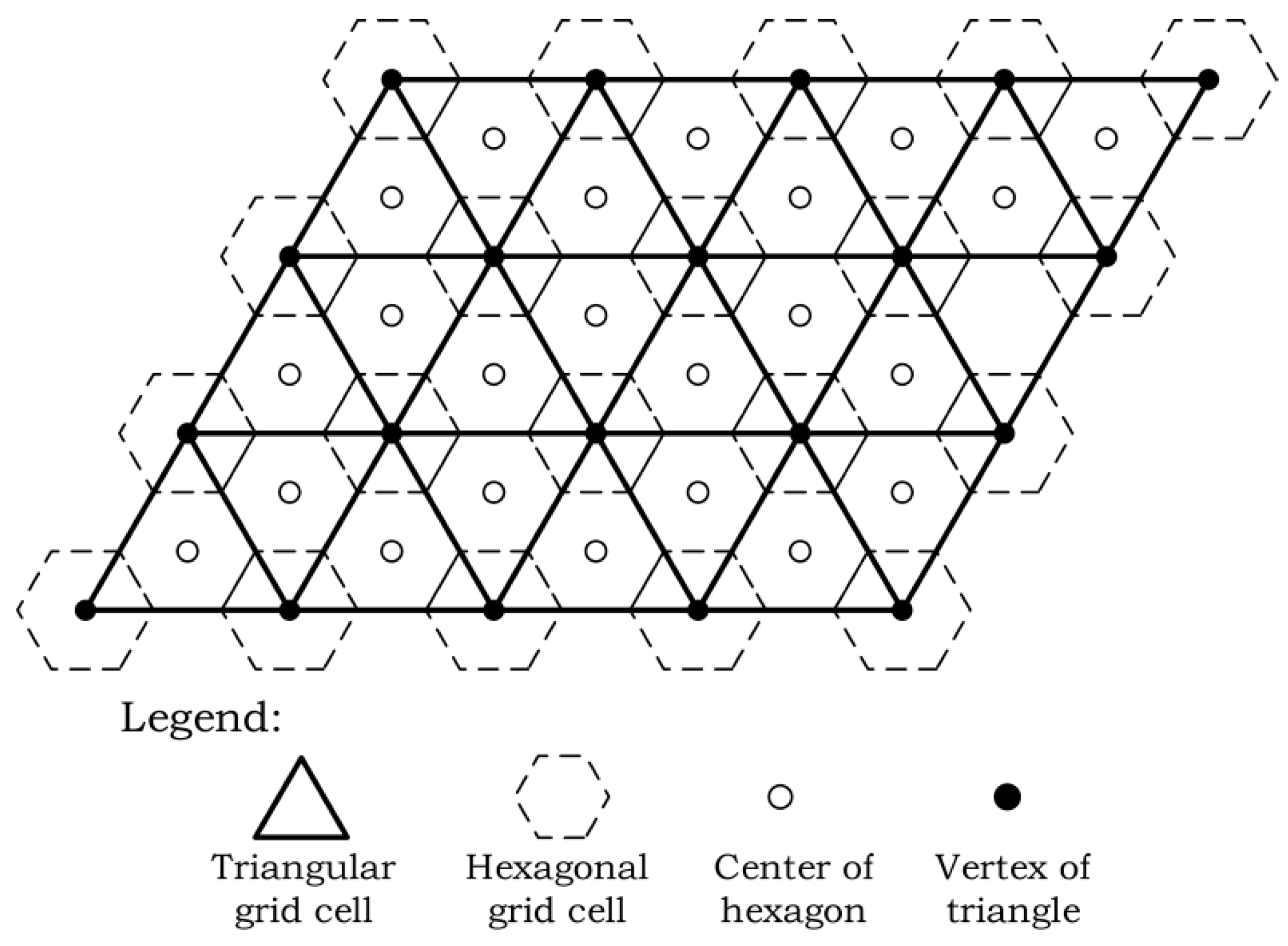
3. Discrete Line Model of a Triangular Grid
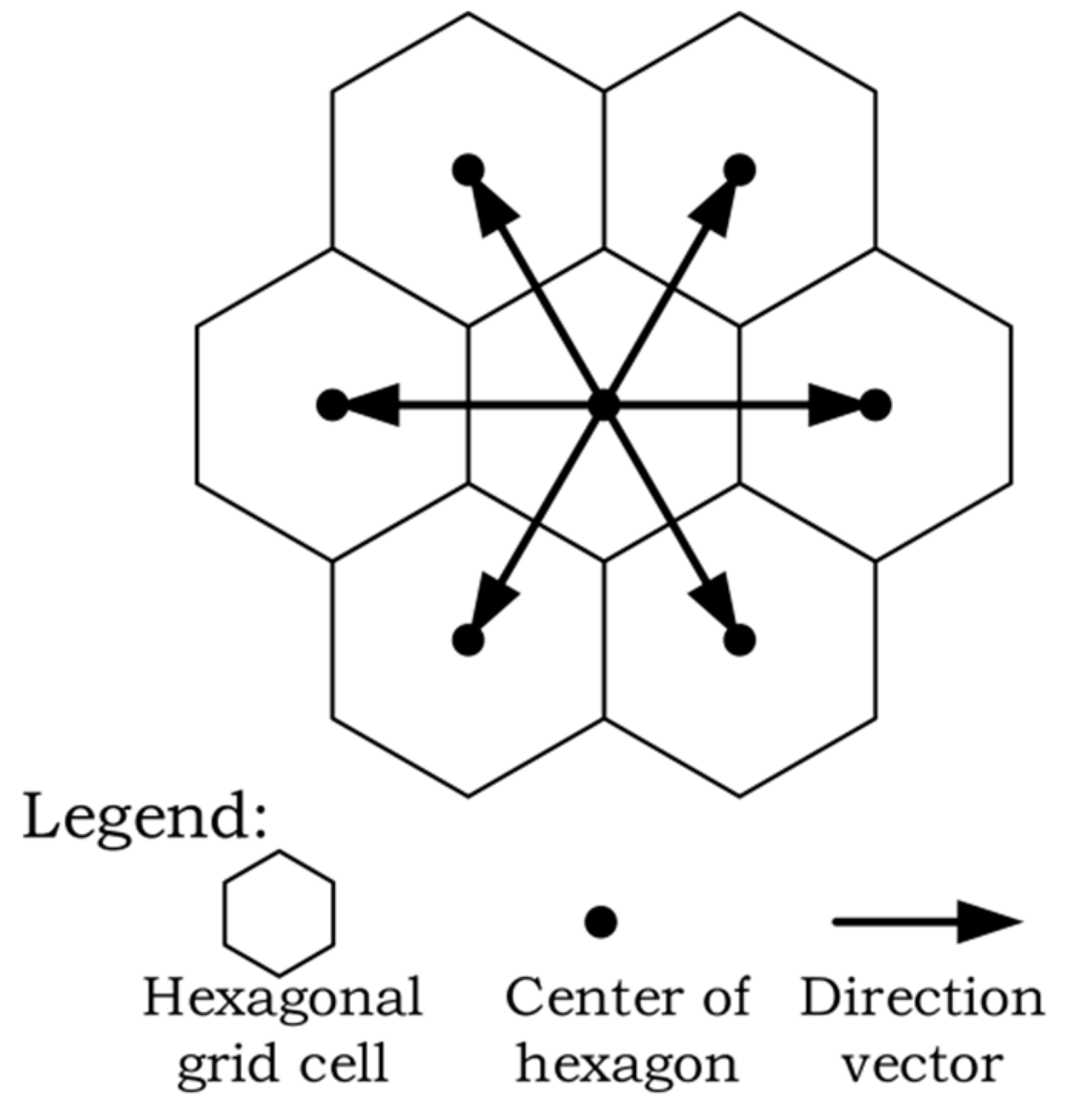
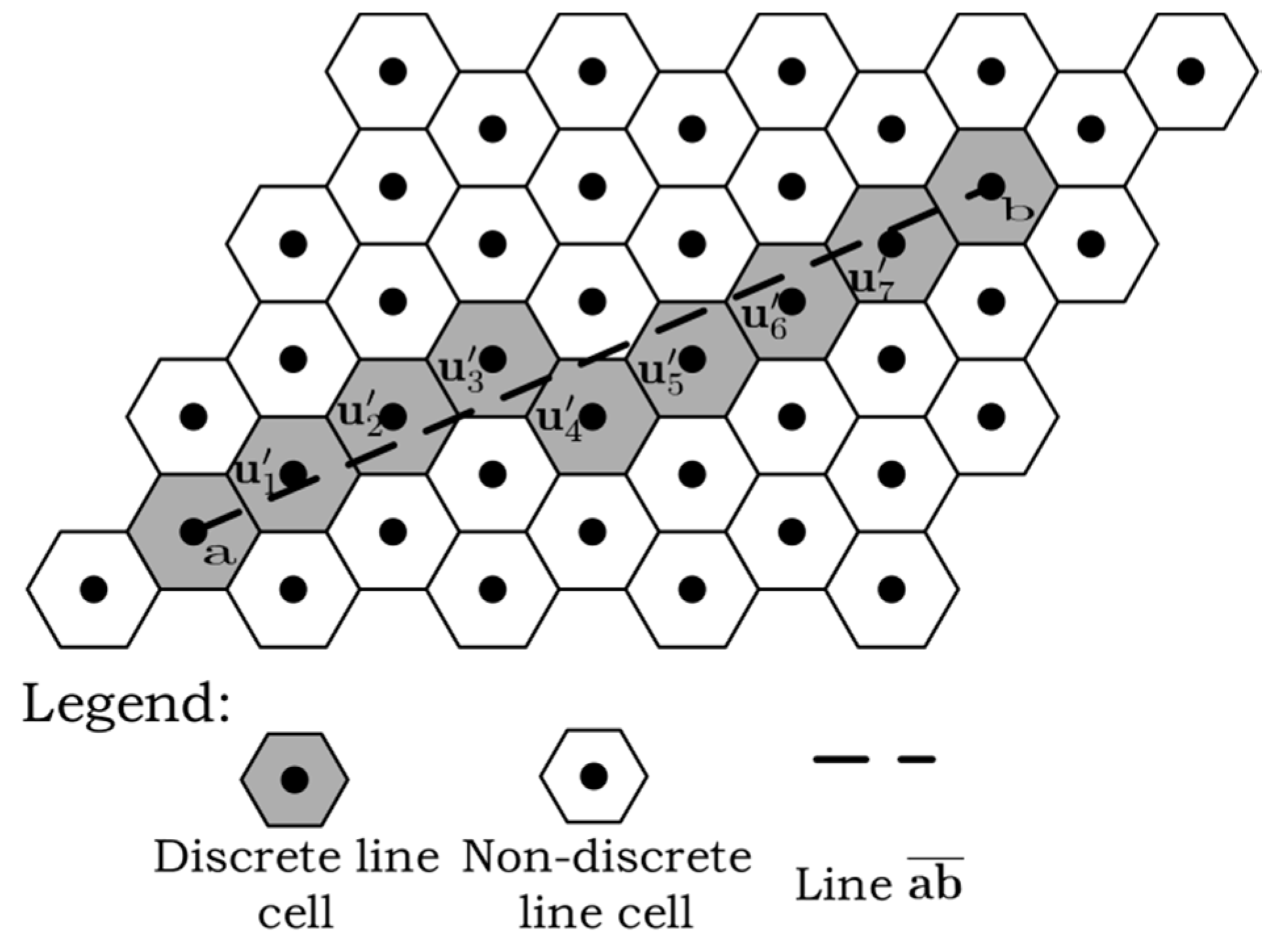
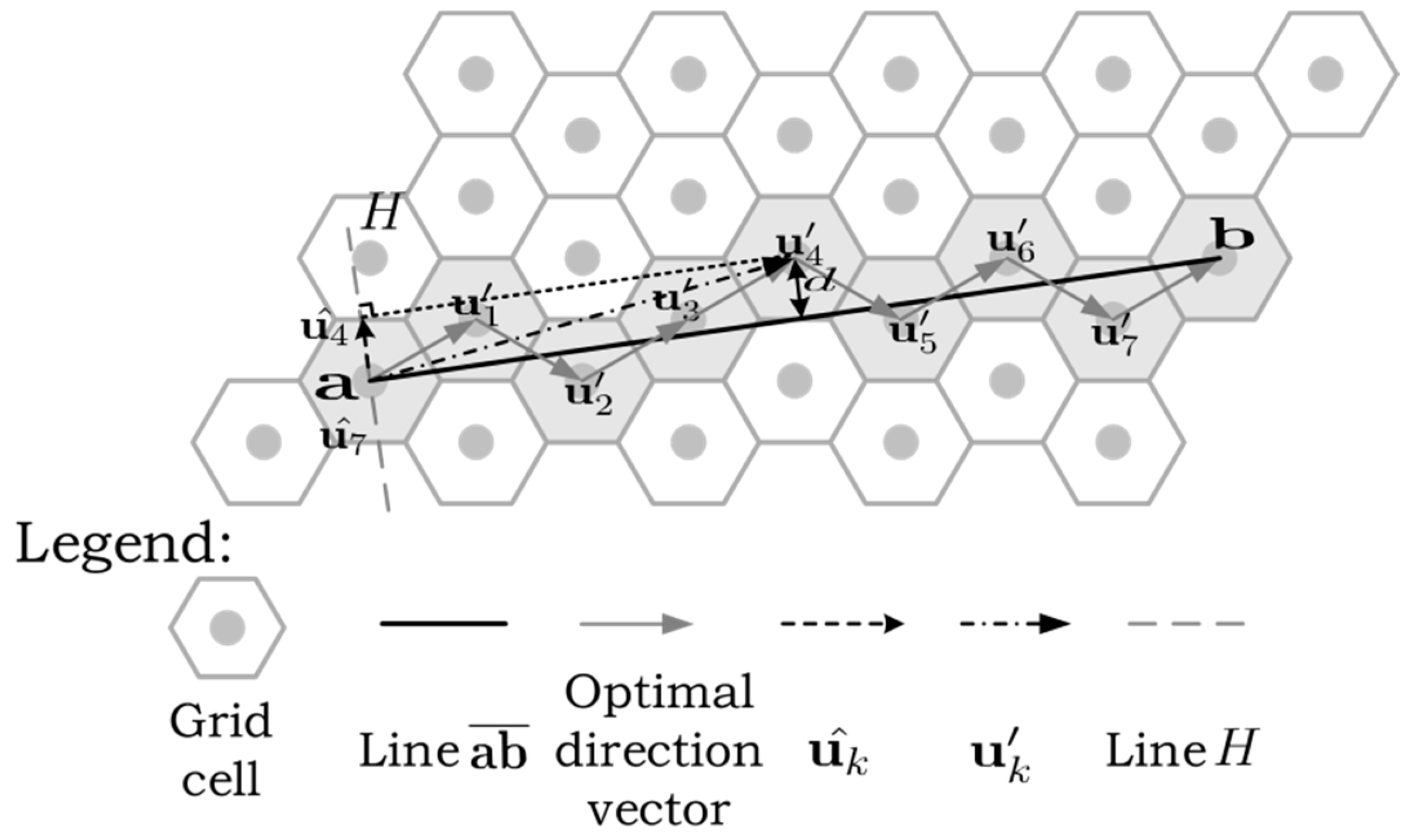
3.1. Discrete Line Model of a Hexagonal Grid
- There should be a minimum number of discrete line cells;
- Of all discrete lines that satisfy (1), the selected discrete line should minimize , where is the vertical distance from to .
3.2. Discrete Line Model of a Weak Duality Triangular Grid
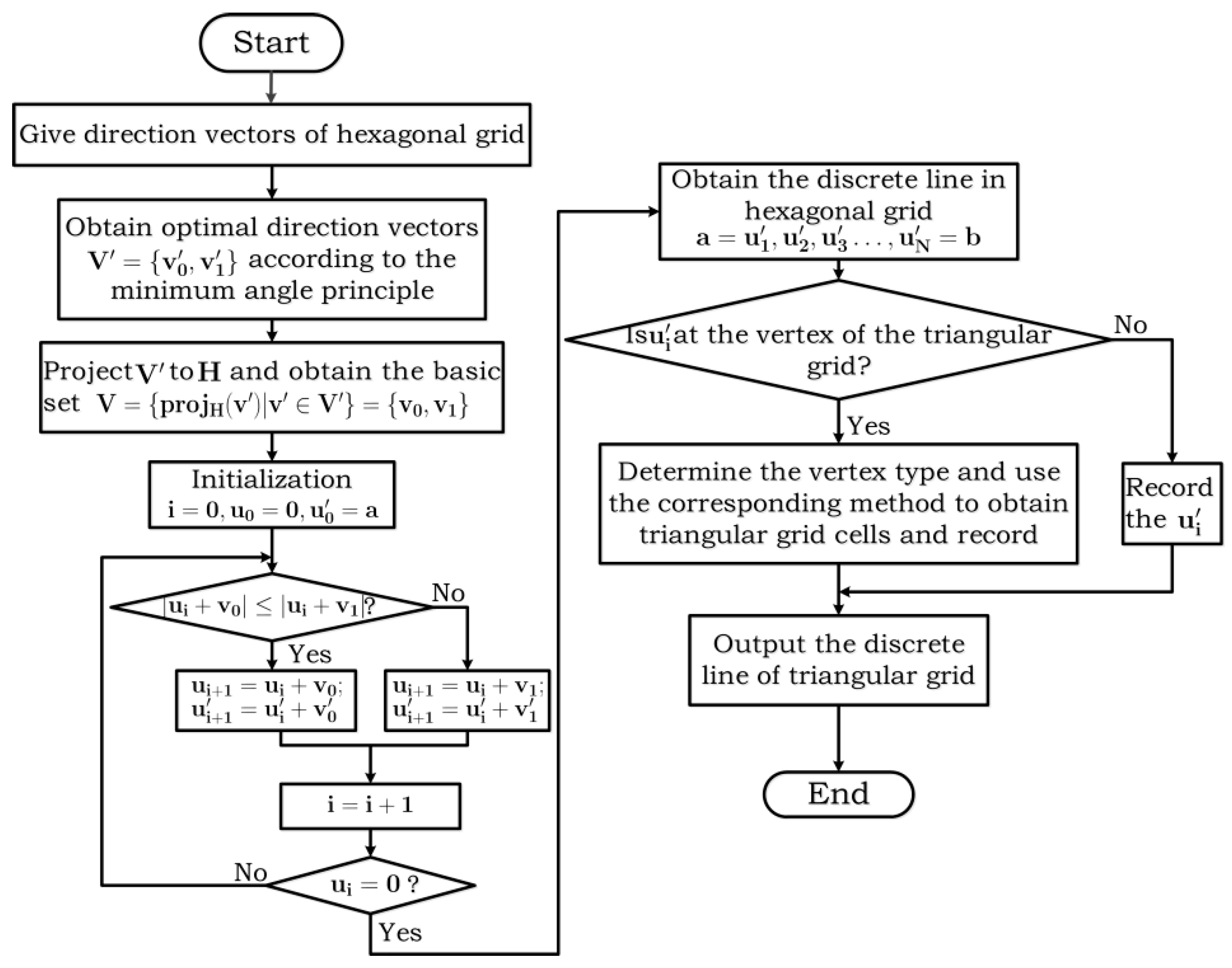
4. Dimensionality Reduction Algorithm of the Discrete Line Model
4.1. One-Dimensional Equivalent Form of the Hexagonal Grid Discrete Line Model
4.2. Algorithm for Solving the Discrete Line of a Triangular Grid
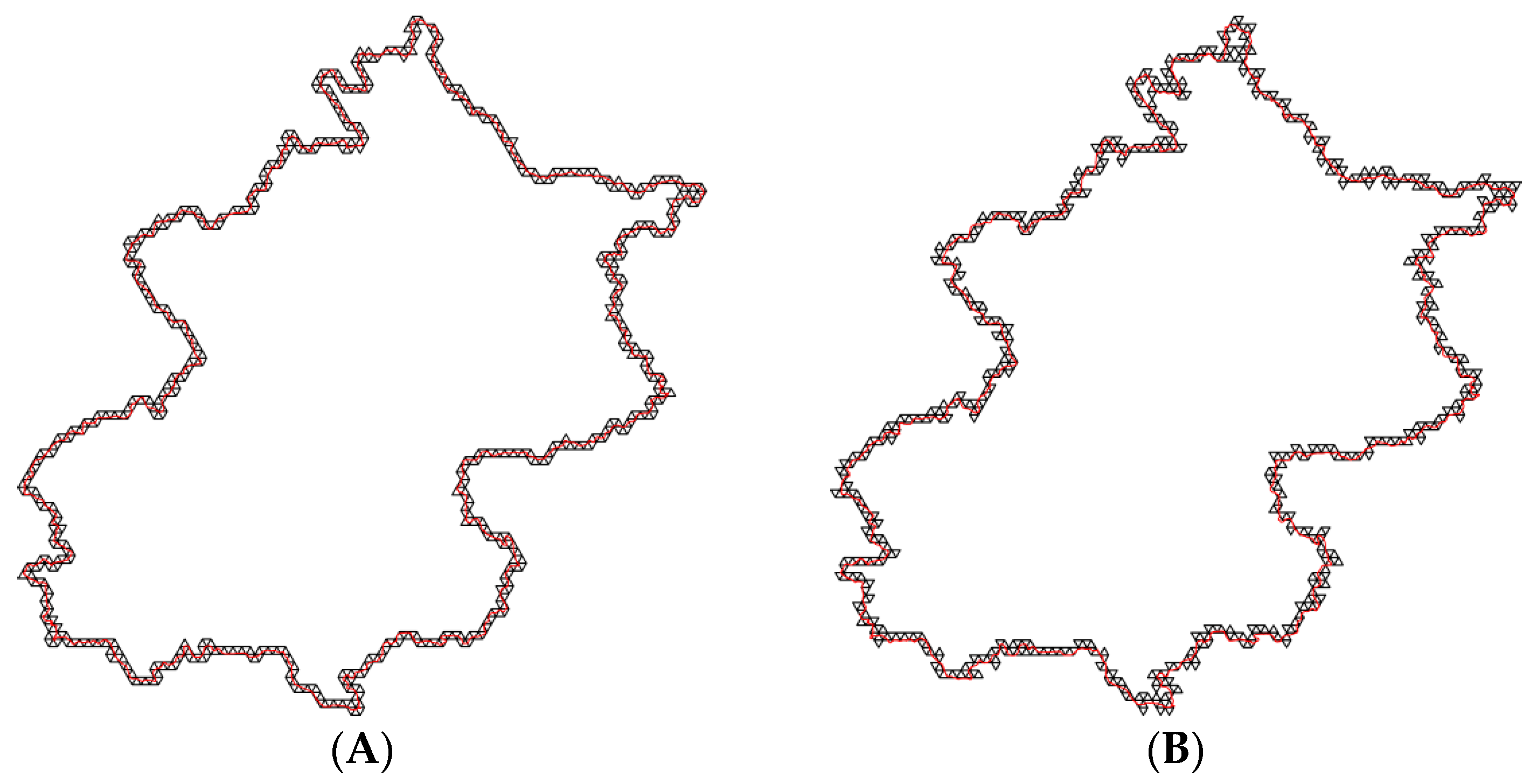
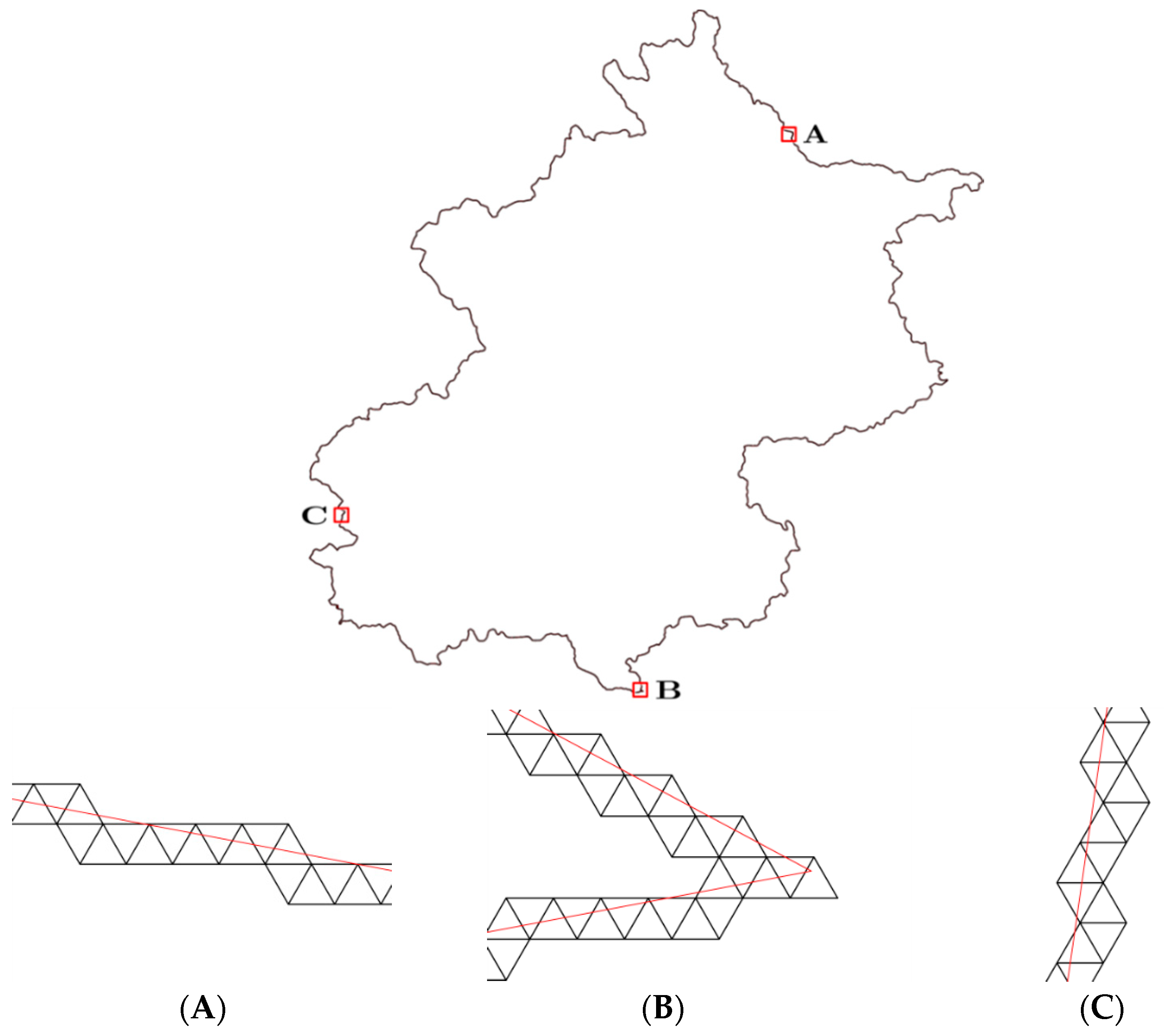
5. Experiments and Analysis
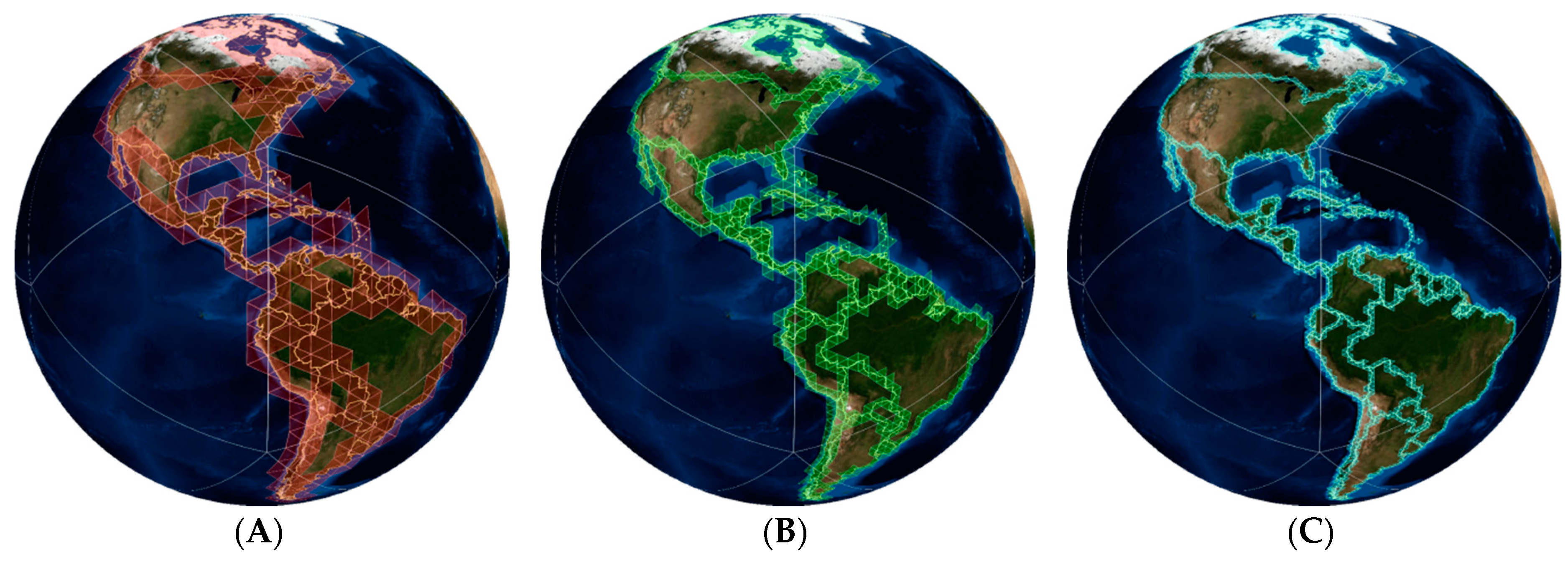
6. Application of Our Algorithm in DGGS
7. Conclusions and Future Directions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, X.; Bai, J.; Wang, Z. An Adaptive Visualized Model of the Global Terrain Based on QTM. Acta Geod. Cartogr. Sin. 2007, 36, 316–320. [Google Scholar]
- Zhang, H.; Wen, Y.; Liu, A. The Basis of Geographic Information System Algorithm; Science Press: Beijing, China, 2006. [Google Scholar]
- Liu, R.; Li, Y. Study of Auto-vectorization Based on Scan-thinning Algorithm. Acta Geod. Cartogr. Sin. 2012, 41, 309–314. [Google Scholar]
- Mccrea, P.G.; Baker, P.W. On Digital Differential Analyzer (DDA) Circle Generation for Computer Graphics. IEEE Comput. Soc. 1975, 100, 1109–1110. [Google Scholar] [CrossRef]
- Reid-Green, K.S. Three Early Algorithms. IEEE Ann. Hist. Comput. 2002, 24, 10–13. [Google Scholar] [CrossRef]
- Bresenham, J.E. Algorithm for Computer Control of a Digital Plotter. IBM Syst. J. 1965, 4, 25–30. [Google Scholar] [CrossRef]
- Wu, X.; Rokne, J.G. Double-step Incremental Generation of Lines and Circles. Comput. Vis. Graph. Image Process. 1987, 37, 331–344. [Google Scholar] [CrossRef]
- Jia, Y.; Zhang, H.; Jing, Y.; Liu, J. A Six-step Algorithm for Line Drawing. J. Shandong Univ. 2007, 37, 61–64. [Google Scholar]
- Huang, B.; Zhang, L. Self-adaptive Step Straight-line Algorithms. J. Tsinghua Univ. 2006, 46, 1719–1722. [Google Scholar]
- Vince, A. Discrete Lines and Wandering Paths. Siam J. Discret. Math. 2007, 21, 647–661. [Google Scholar] [CrossRef]
- Fekete, G.; Treinish, L.A. Sphere Quadtrees: A New Data Structure to Support the Visualization of Spherically Distributed Data. In Proceedings of SPIE—The International Society for Optical Engineerin; SPIE Digital Library: Bellingham, WA, USA; Washington, DC, USA, 1990; Volume 1259. [Google Scholar] [CrossRef]
- Dutton, G. A Hierarchical Coordinate System for Geoprocessing and Cartograph; Springer: Berlin, Germany, 1999; Volume 79. [Google Scholar]
- Bartholdi, J.; Goldsman, P. Continuous Indexing of Hierarchical Subdivision of the Global. Int. J. Geogr. Inf. Sci. 2001, 15, 489–522. [Google Scholar] [CrossRef]
- Dutton, G. Digital Map Generalization Using a Hierarchical Coordinate System. In Proceedings of the Automated Cartography 13, Seattle, WA, USA, 7–10 April 1997. [Google Scholar]
- Shreiner, D.; Woo, M.; Neider, J.; Davis, T. OpenGL Programming Guide: The Official Guide to Learning OpenGL, 5th ed.; Version 2; Xu, B., Translator; China Machine Press: Beijing, China, 2006; pp. 324–341. [Google Scholar]
- Freeman, H. Algorithm for Generating a Digital Straight Line on a Triangular Grid. IEEE Comput. Soc. 1979, 28, 150–152. [Google Scholar] [CrossRef]
- Nagy, B.N. Shortest Paths in Triangular Grids with Neighbourhood Sequences. J. Comput. Inf. Technol. 2003, 11, 55–60. [Google Scholar] [CrossRef]
- Sarkar, A.; Biswas, A.; Mondal, S.; Dutt, M. Finding Shortest Triangular Path in a Digital Object. In Discrete Geometry for Computer Imagery; Springer: Cham, Switzerland, 2016; pp. 206–218. [Google Scholar]
- Dutt, M.; Andres, E.; Skapin, G.L. Characterization and Generation of Straight Line Segments on Triangular Cell Grid. Pattern Recognit. Lett. 2018, 103, 68–74. [Google Scholar] [CrossRef]
- Maurin, K. Duality (polarity) in Mathematics, Physics and Philosophy. Rep. Math. Phys. 1988, 25, 357–388. [Google Scholar] [CrossRef]
- Mahdavi-Amiri, A.; Harrison, E.; Samavati, F. Hierarchical grid conversion. Comput. Aided Des. 2016, 79, 12–26. [Google Scholar] [CrossRef]
- Zhou, C.; Ou, Y.; Ma, T. Progresses of Geographical Grid Systems Researches. Prog. Geogr. 2009, 28, 657–662. [Google Scholar]
- Alderson, T.; Mahdavi-Amiri, A.; Samavati, F. Offsetting spherical curves in vector and raster form. Vis. Comput. 2018, 8, 973–984. [Google Scholar] [CrossRef]

| Side Length of Grid Cell (m) | Proposed Algorithm (m) | Freeman Algorithm (m) |
|---|---|---|
| 3000 | 522.829 | 1102.95 |
| 1500 | 277.862 | 584.722 |
| 750 | 162.739 | 287.156 |
| 375 | 94.7479 | 143.333 |
| 188 | 49.917 | 68.807 |
| 94 | 25.473 | 33.800 |
| 47 | 12.828 | 17.096 |
| 23 | 6.292 | 8.253 |
| 12 | 3.295 | 4.339 |
| 6 | 1.650 | 2.152 |
| 3 | 0.823 | 1.075 |
| Province (Points) | Proposed Algorithm (ms) | Full-Path Algorithm (ms) | Time Ratio |
|---|---|---|---|
| Inner Mongolia (52,486) | 2086.43 | 28,999.20 | 13.90 |
| Heilongjiang (27,521) | 1079.67 | 16,511.36 | 15.29 |
| Xinjiang (37,855) | 1306.59 | 13,895.09 | 10.63 |
| Tibet (39,184) | 1065.33 | 10,135.34 | 9.51 |
| Liaoning (35,732) | 676.80 | 4804.96 | 7.10 |
| Guangdong (28,887) | 689.23 | 5684.01 | 8.25 |
| Jilin (21,588) | 656.53 | 5563.50 | 8.47 |
| Henan (21,567) | 491.06 | 3982.95 | 8.11 |
| Jiangxi (13,621) | 393.64 | 3339.67 | 8.48 |
| Hubei (19,335) | 519.29 | 4543.93 | 8.75 |
| Hainan (6065) | 203.55 | 1640.03 | 8.06 |
| Tianjin (4206) | 141.69 | 1065.81 | 7.52 |
| Beijing (3661) | 144.36 | 1175.63 | 8.14 |
| Ningxia (9704) | 298.29 | 2423.04 | 8.12 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, L.; Ma, Q.; Ben, J.; Wang, R.; Li, J. Duality and Dimensionality Reduction Discrete Line Generation Algorithm for a Triangular Grid. ISPRS Int. J. Geo-Inf. 2018, 7, 391. https://doi.org/10.3390/ijgi7100391
Du L, Ma Q, Ben J, Wang R, Li J. Duality and Dimensionality Reduction Discrete Line Generation Algorithm for a Triangular Grid. ISPRS International Journal of Geo-Information. 2018; 7(10):391. https://doi.org/10.3390/ijgi7100391
Chicago/Turabian StyleDu, Lingyu, Qiuhe Ma, Jin Ben, Rui Wang, and Jiahao Li. 2018. "Duality and Dimensionality Reduction Discrete Line Generation Algorithm for a Triangular Grid" ISPRS International Journal of Geo-Information 7, no. 10: 391. https://doi.org/10.3390/ijgi7100391
APA StyleDu, L., Ma, Q., Ben, J., Wang, R., & Li, J. (2018). Duality and Dimensionality Reduction Discrete Line Generation Algorithm for a Triangular Grid. ISPRS International Journal of Geo-Information, 7(10), 391. https://doi.org/10.3390/ijgi7100391




