1. Introduction
Soil moisture constitutes approximately 0.89% of the total quantity of water within the global hydrological cycle, but it is an important element of the hydrosphere, biosphere, and atmospheric water cycle [
1,
2]. Soil moisture significantly influences the partition of precipitation into infiltration, runoff, and evapotranspiration and benefits the analysis of the global water cycle and climatic variation [
3,
4,
5]. When soil moisture is maintained at optimum levels, it supports risk reduction for crop science and minimizes nutrient leaching [
6]. Thus, the acquisition and regulation of soil moisture datasets are important.
There are two primary ways to acquire spatiotemporal soil moisture data. With the improvements in sensor technologies and retrieval algorithms, spaceborne microwave remote sensing (RS) has become a powerful tool to retrieve soil moisture data at a large scale (e.g., regional and global levels) [
7] and several satellite-based soil moisture products have been released [
8,
9,
10]. Soil moisture products that are derived from the same satellite tend to be characterized by diverse resolutions to accommodate the diverse needs of different users, such as the Advanced Microwave Scanning Radiometer E (AMSR-E) for the Earth Observing System with spatial resolutions ranging from 5.4 to 56 km [
8,
11], the Advanced Scatterometer (ASCAT) with spatial resolutions ranging from 25 to 50 km [
8,
10,
12], and the Soil Moisture Active Passive (SMAP) with spatial resolutions ranging from 10 km to 50 km [
9,
13]. And, with downscaling methods, some RS soil moisture products with high spatial resolution are also available for research at the field level. For example, soil moisture ocean salinity (SMOS) imagery has been downscaled to resolutions of 10 km, 4 km, or 1 km using moderate resolution imaging spectroradiometer (MODIS) data [
14,
15]. In addition, with the development of wireless communication techniques, the wireless sensor network (WSN) has been increasingly used to obtain in situ soil moisture observations (ISMO) in some projects [
16,
17,
18,
19]. ISMO with high temporal resolutions could provide accurate and credible estimations at observation sites, but the spatial extent would be limited; however, this limitation could be compensated for by using spaceborne microwave RS data. Hence, one significant issue of combining satellite-based soil moisture products with ground-based observations is the disparity in observation scales between the two types of data [
20].
An upscaling method and a data assimilation strategy are necessary to convert multipoint WSN soil moisture observations to a pixel format covering the satellite footprint to eliminate this mismatch. There are four commonly used upscaling methods for in situ observations. The first and the most commonly used approach is the simple averaging of in situ data [
21,
22]. The second is to introduce a kriging algorithm while considering spatial autocorrelation [
23]. The third approach is using distributed land surface modeling to simulate the spatial pattern of soil moisture [
24], and the fourth approach is using the apparent-thermal-inertia-based method to derive the soil moisture from fine-resolution satellite thermal signals [
19,
22]. However, these four methods focus on the upscaling and validation of ISMO to the footprint of just one RS soil moisture product [
20,
22]. This leads to an obvious question that we want to answer: whether the upscaled results at different resolutions obtained by the same upscaling method are statistically comparable and spatially stable. If the answer is yes, that method will contribute to the data fusion of ISMO with multiresolution RS data as well. In addition, soil moisture is characterized by spatial–temporal heterogeneity, and this heterogeneity will change with the different soil texture, vegetation, topography, and meteorological conditions at different scales, adding uncertainty to the upscaling and validation processes [
20,
25,
26]. How to quantitatively evaluate the scale effects in kriging from the perspective of spatial heterogeneity is another important question that we want to answer in this paper. Some researchers have realized the question and have done some simple descriptions in their works [
27,
28].
In this paper, we studied the two questions mentioned above to analyze statistical and spatial comparability and uncertainties in the upscaling processes of in situ soil moisture to multitarget scales and to explain the sources of uncertainties. We used block kriging (BK), a common geostatistical method used for soil moisture data [
20,
22,
29], to upscale in situ soil moisture data, while ordinary kriging (OK) and simple averaging (SA) were used as contrasting methodologies. In addition, we utilized comparison analysis against RS data, statistical analysis, spatial trend surface analysis, and semivariogram analysis to describe and quantitatively evaluate the uncertainties in the upscaling processes. The remainder of this paper is organized as follows.
Section 2 describes the data and the study area.
Section 3 introduces the BK, OK, and SA upscaling methods for the soil moisture data at a variety of spatial scales and quantitatively evaluates the uncertainties occurring during the upscaling processes. The results are presented and discussed in
Section 4 and
Section 5, respectively. Key conclusions are drawn in the last section.
2. Data and Data Preprocessing
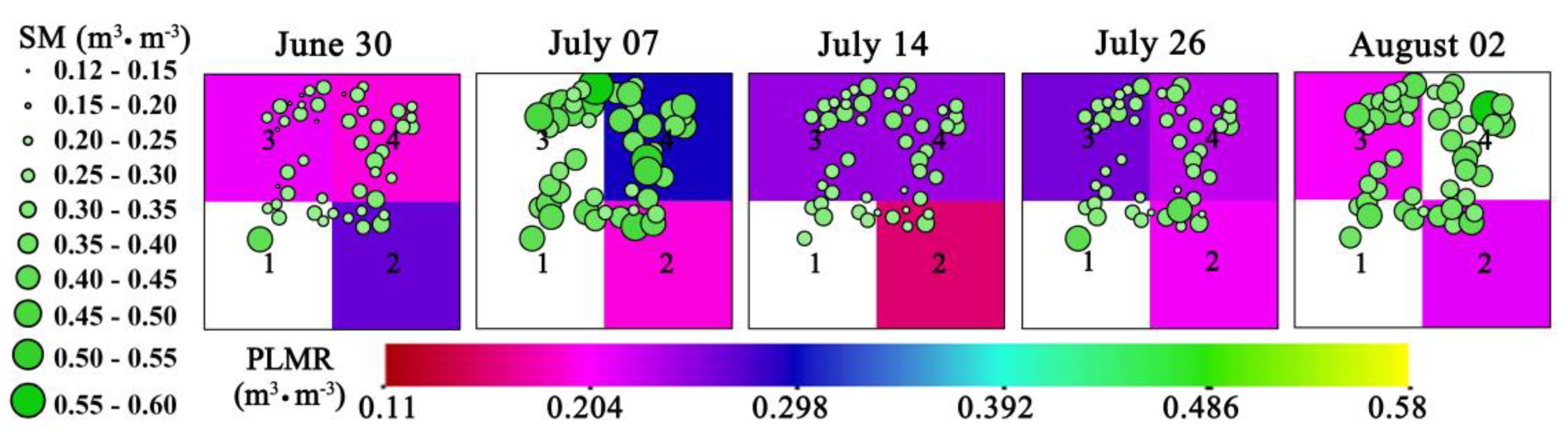
Datasets from the Heihe Watershed Allied Telemetry Experimental Research (HiWATER) project [
17,
30] were used in this study. The RS soil moisture data were extracted from a dataset of retrieved soil moisture products (5 cm depth) using airborne polarimetric L-band (1.4 GHz) multibeam radiometer (PLMR) brightness temperatures with 700 m spatial resolution on 30 June, 7 July, 14 July, 26 July, and 2 August 2012. The in situ soil moisture data were acquired from SoilNET observation data (4 cm depth) on 30 June, 7 July, 14 July, 26 July, and 2 August 2012 (synchronous with the PLMR data) [
31,
32,
33].
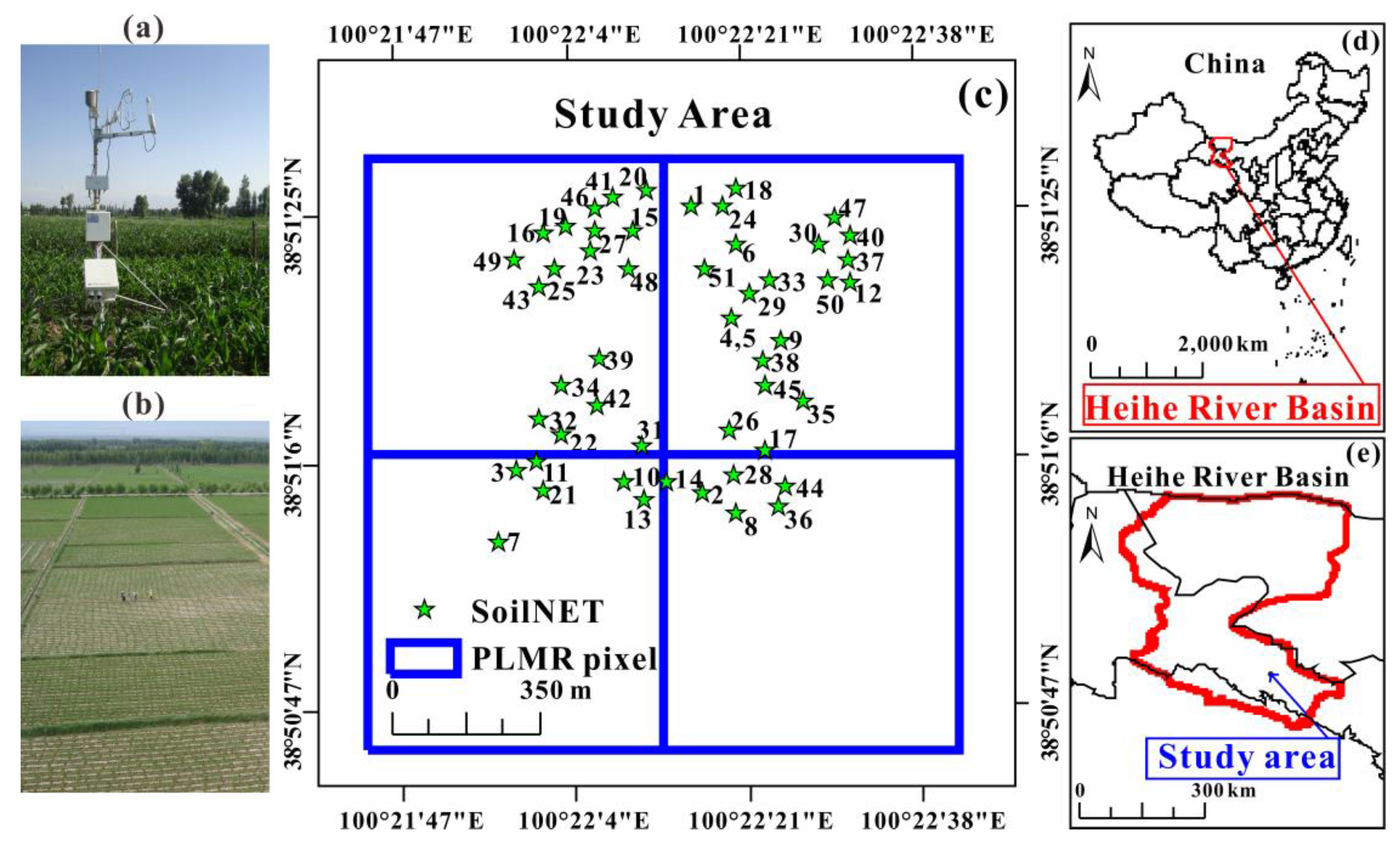
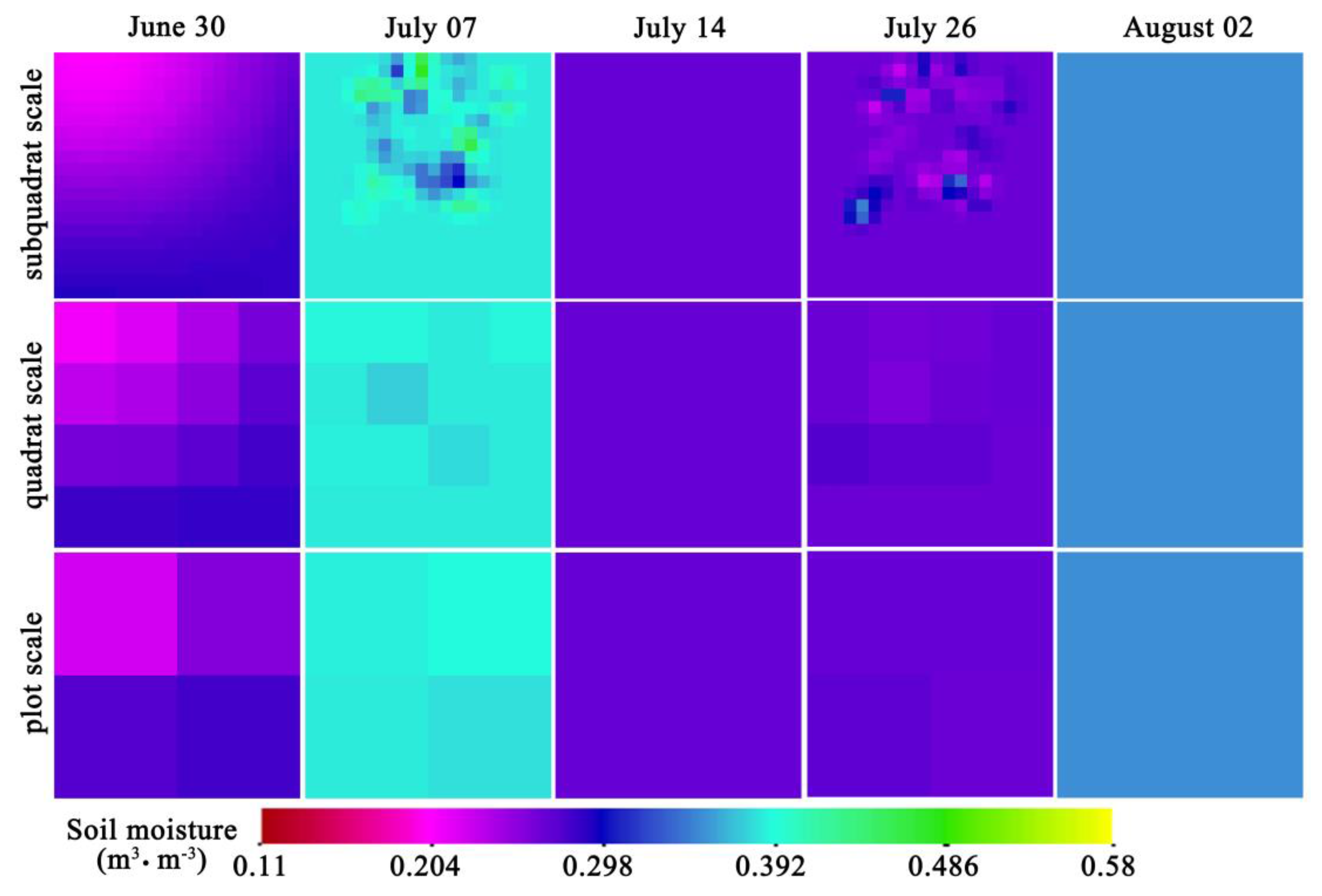
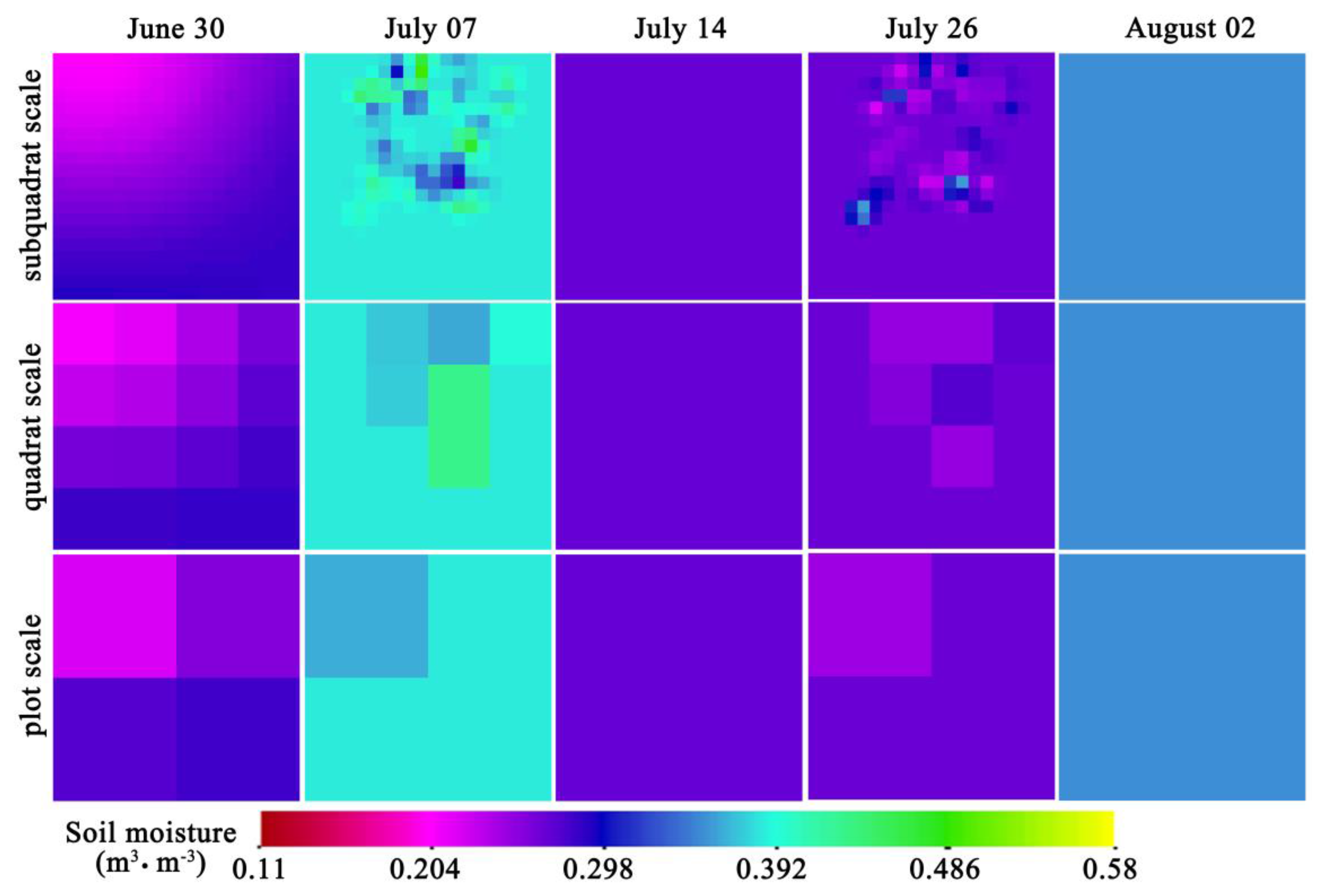
SoilNET is one of three WSN nodes (WaterNET, SoilNET, and BNUNET) adopted in the Ecological and Hydrological WSN (EHWSN) that uses optimal geostatistical sampling methods [
32]. The EHWSN is located in both the Yingke and Daman irrigation districts of the Zhangye Artificial Oasis, where the irrigation system infrastructures are complete. The districts are in a typical semiarid and arid agricultural region and the main crop types are corn, wheat, vegetables, and fruits. In the districts, agricultural irrigation is essential for crop growth. Because of unscheduled agriculture irrigation, soil moisture has strong heterogeneity with complicated spatial processes [
33]. Specifically, 51 SoilNET nodes designed by the Jülich Research Center [
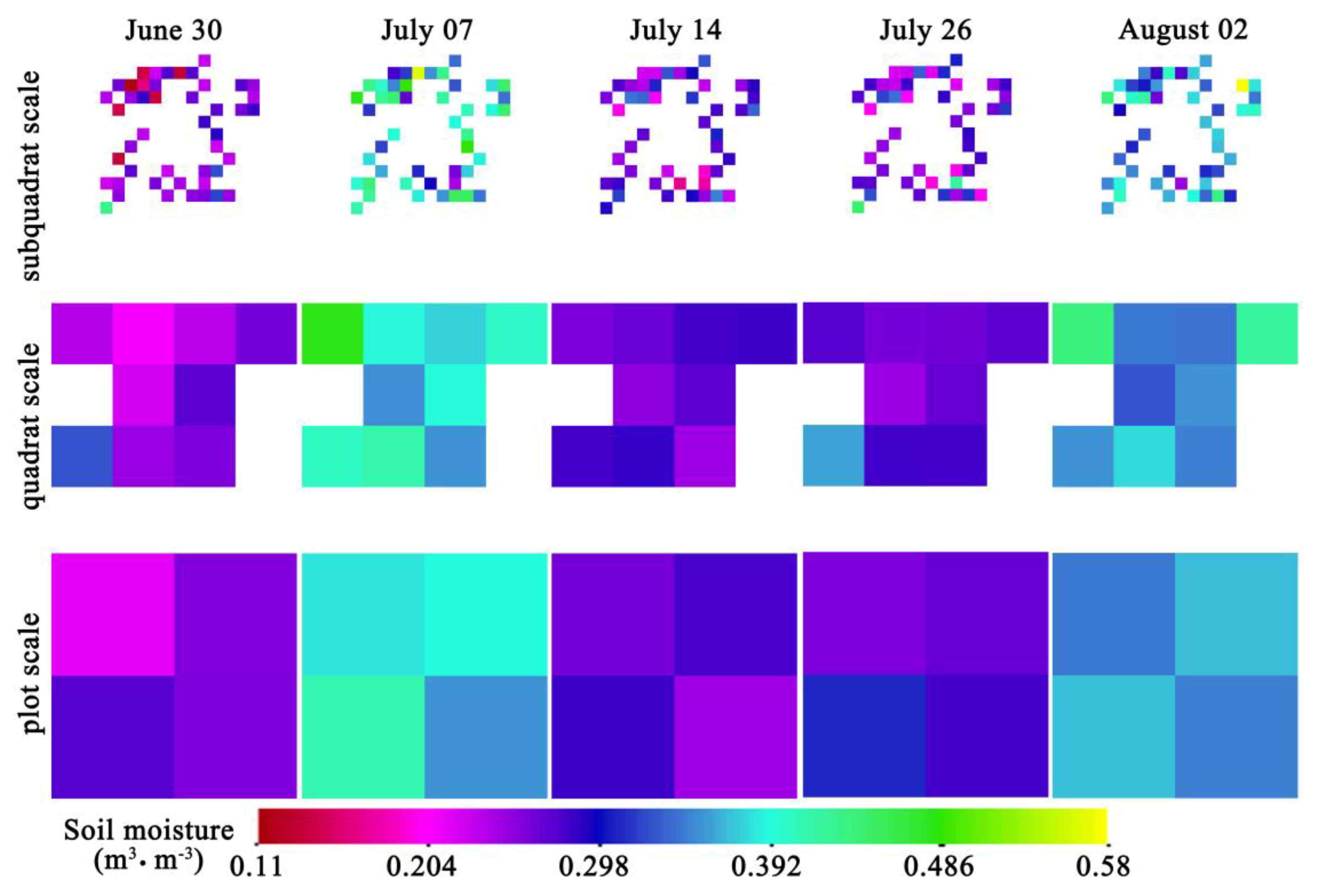
16] were used to capture the small-scale soil moisture variations, and the observations were covered by four (2 × 2) PLMR pixels. These four PLMR pixels represented the final study area in this study (
Figure 1).
Because the RS soil moisture products were retrieved primarily by PLMR brightness temperature data, the PLMR flight time was selected as the reference time in this paper [
34]. PLMR measured both V and H polarizations using a single receiver with polarization switching at incidence angles of ±7°, ±21.5°, and ±38.5° [
17]. Therefore, there were several flight times in each PLMR pixel, and the temporal resolution of the in situ soil moisture data was 10 min. Therefore, all SoilNET data corresponding to all PLMR flight times in each PLMR pixel were averaged to guarantee data synchronicity and minimize errors.
Before the ISMO data were upscaled, a histogram and a Normal QQ plot were created using the exploratory data analysis tool in the Geostatistical Analyst toolbox of ESRI ArcGIS
® 10.4 software, and the outliers and data distributions were analyzed and processed to support the reliability and stability of the geostatistical methods [
23,
29,
35]. The normal distribution was examined according to the kurtosis and skewness (both ideally close to 0) of the data on each date, supported by the Shapiro–Wilk test [
35,
36]. After careful scrutiny, nodes NO. 4, NO. 29, NO. 42, and NO. 47 were broken on multiple dates and were deleted as outliers on all dates [
37,
38] (
Figure 2). Moreover, the SoilNET data on 26 July and on 2 August were not normally distributed. Thus, the logarithmic normalized transformations were conducted on those in situ observations of 26 July and of 2 August before using the kriging method, and back-transformations were conducted on the kriged results of 26 July and of 2 August.
5. Discussion
According to the results mentioned above, it is relatively obvious that the statistical and spatial characteristics of the pixel estimations with BK and OK differed across the scale series. The scale issue and spatial heterogeneity introduce uncertainties into the upscaling of soil moisture data to different target scales, and these uncertainties are inevitable. It is reasonable to discuss why scale matters in this prediction and how to notice and handle the uncertainties. Scale, as mentioned in previous studies, consists of the observational scale (or measurement scale), or the unit of measurement or sampling [
42,
60]; operational scale, or the operational extent of a certain process [
42]; and the phenomenon scale, or the size of a geographic structure [
61]. Many studies have shown that conclusions derived at one scale can be identified on that scale but may not be applicable to another scale [
62,
63,
64]. Hence, the mismatch among the observational scale, operational scale, and phenomenon scale could introduce uncertainties; this is the essence of the scale issue.
The mismatch between the observational scales of satellite RS and in situ sensor measurements for soil moisture stems from the differences in the fractal dimensions [
60,
65]. The ISMO data are zero-dimensional data, and the RS data are two-dimensional data. Therefore, an upscaling method for ISMO to RS footprints can remedy the differences caused by different observational scales. Observational scales are believed to consist of three different scales: support (resolution or grain in landscape ecology), spacing (lag), and extent [
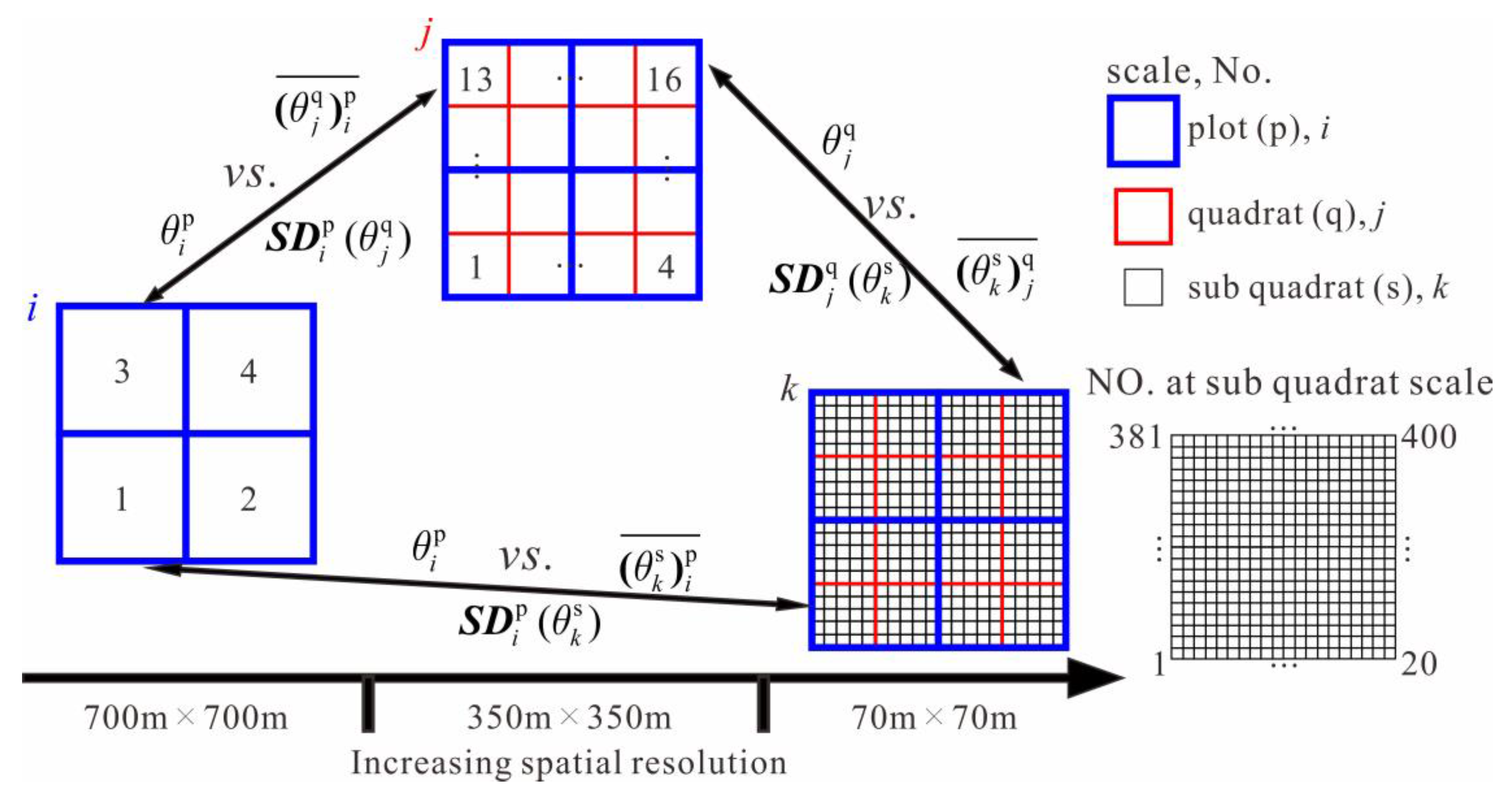
60]. In reality, soil moisture products are characterized by diverse resolutions, and the various resolutions mean that there are multiple support scales and target scales in the upscaling processes for ISMO. Thus, a spatial scale series (subquadrat, quadrat, and plot) was established as the target scale for the ISMO upscaling processes and the USME at the scale series based on BK, OK, and SA were obtained. The scale series shows an even hierarchy nesting relation (another expression for multiscale [
50,
66,
67]), and the hierarchical idea provides a method to represent or quantify the multiresolution characteristics of RS data and a basis for analyzing multiscale issues that arise in the ISMO upscaling process. However, the actual RS soil moisture products with diverse resolution may not show such a nested relation, and it should be noted in future research.
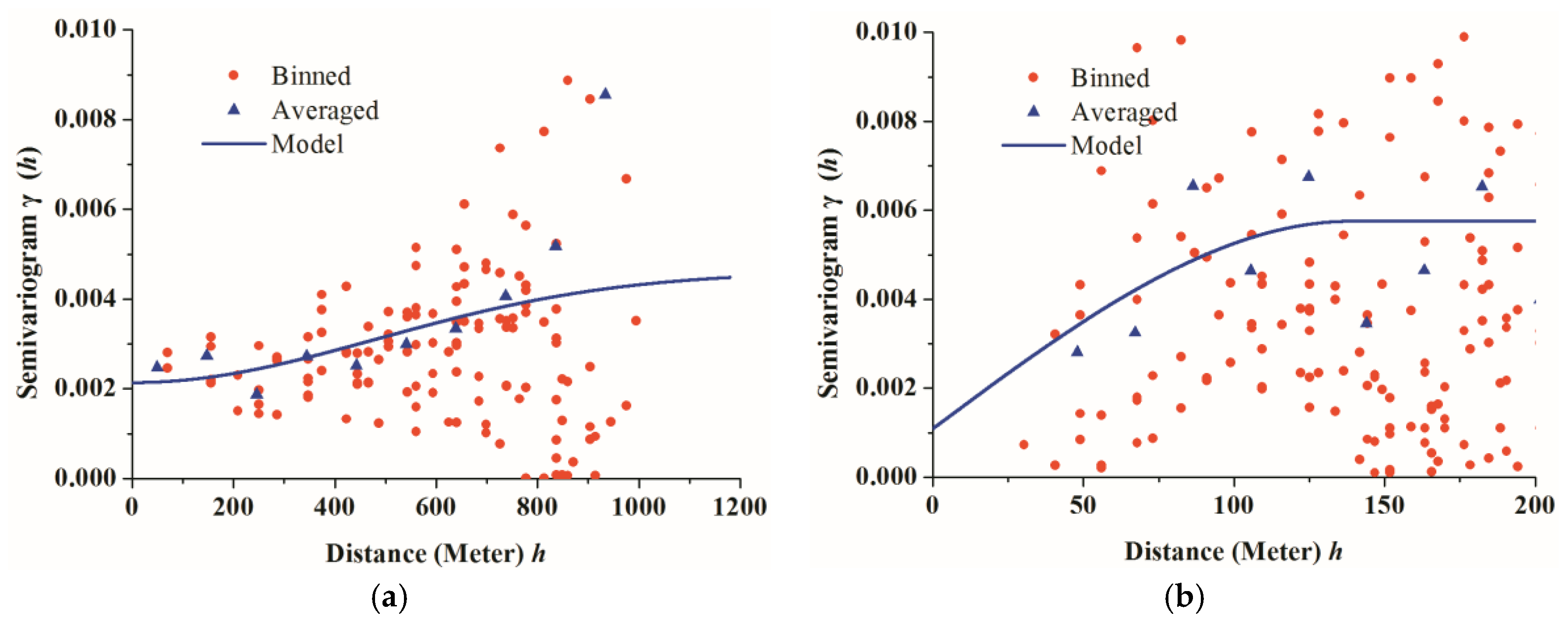
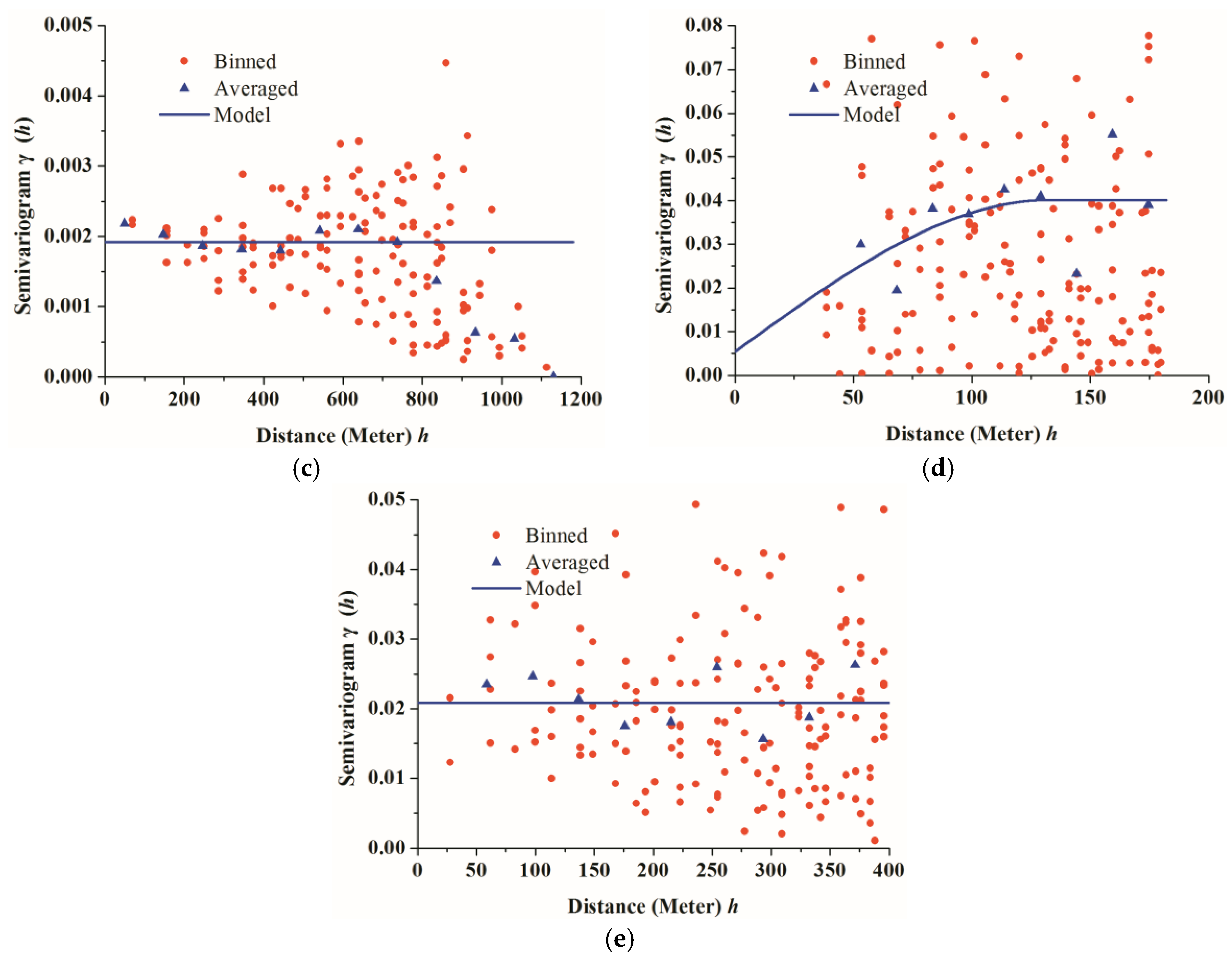
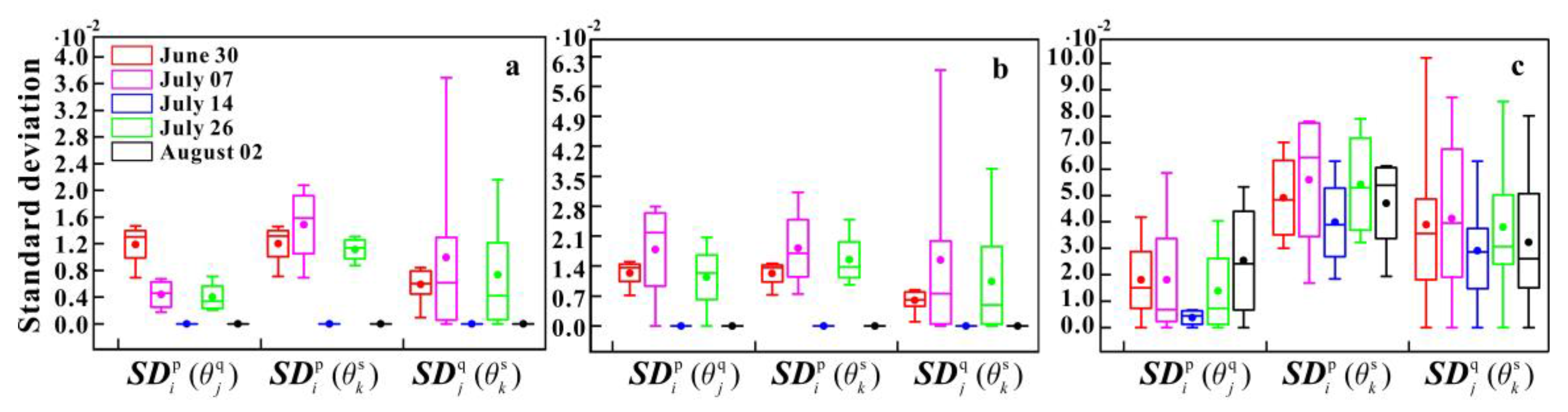
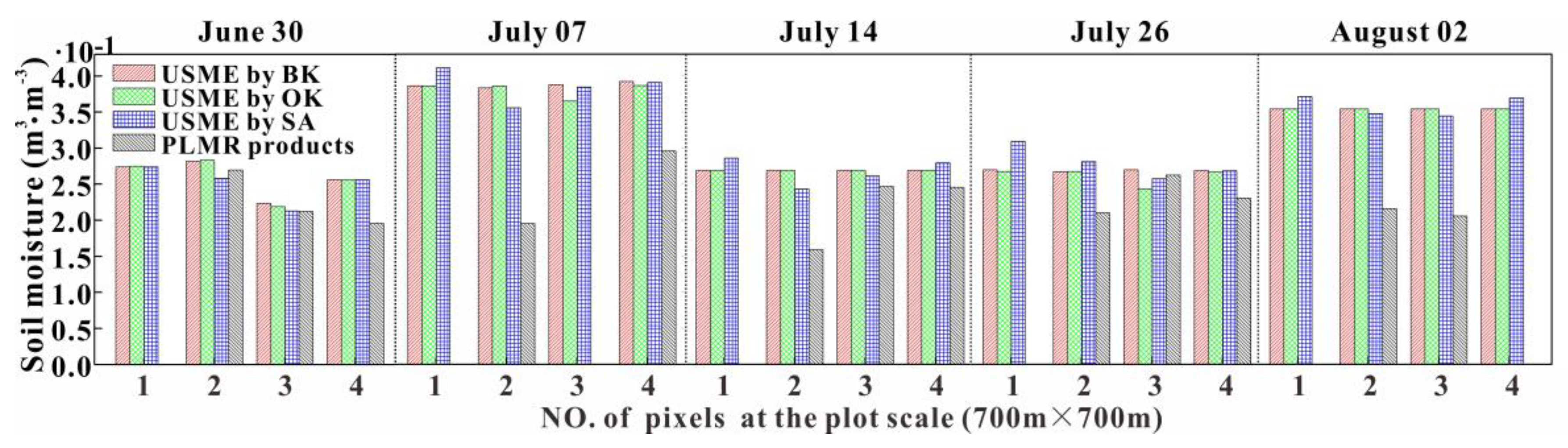
Statistical index analysis (average value and standard deviation), spatial trend surface analysis, and comparison analysis against RS data were conducted to reveal the scale effects in the hierarchical geographical data structures. These scale effects were explained from the perspective of spatial heterogeneity revealed by semivariogram analysis on the original in situ point data. According to the results, when the target scale is shorter than the range of the semivariogram (phenomenon scale) of ISMO, or when the original in situ soil moisture data are spatially homogeneous within the RS observational scale, BK, OK, and SA could be selected as the upscaling methods because the differences between the RS data and the estimations upscaled by those methods are relatively slight, and the kriging methods are not worse than the SA method.
RS soil moisture data contains large uncertainties, and several studies have been conducted to validate satellite-based soil moisture products by upscaling in situ measurements using a modified method [
20,
22,
27]. In some works, the comparisons of upscaled data against RS data differ in the different spatial heterogeneity of in situ data, and the reliability of the validation is sensitive to the spatial variation of the input observation data [
18,
27,
28]. This also adds reliability to the conjectures in our paper. Thus, employing a modified kriging method to verify the accuracy of satellite-based soil moisture products may not be universally applicable. This applicability would be influenced by the spatial structures of the ISMO and the parameters of the kriging model, both of which contain large uncertainties. If we obtain multiresolution RS data in future research, this conclusion would be enhanced and perfected.
According to our results, when the target scale is shorter than the range of the semivariogram of ISMO, the USME upscaled by BK presents the following clear characteristics compared with those by OK and SA: the actual upscaled estimation of each LS pixel is relatively close to the arithmetic average of those of the SS pixels within each LS pixel; the multiscale estimations maintain consistent scale effects and similar global trend surfaces throughout the upscaling process (
Table 7). Thus, from the standpoint of upscaling ISMO to multiscale pixel estimations covering the RS footprint with only one upscaling method, the USME by BK at the scale series are more statistically comparable and more spatially stable, and are more appropriate for upscaling ISMO. When the target scale is larger than the range of the selected semivariogram of ISMO, the statistical comparability and the spatial stability of the USME by BK are lost and the variability of the USME by BK and OK continually declines with decreasing spatial resolutions. Moreover, when original in situ soil moisture data has no spatial autocorrelation (range equal to 0), the spatial process can be modelled as a pure nugget effect, the weights in Equation (2) all become 1/
n, and the estimation procedure becomes an average of all ISMO [
23]. Hence, the USME by kriging are constant values at each scale. In the latter two conditions, a kriging method with the selected semivariogram model should not be used to upscale ISMO, but the SA method based on the sample points within each pixel is more suitable.
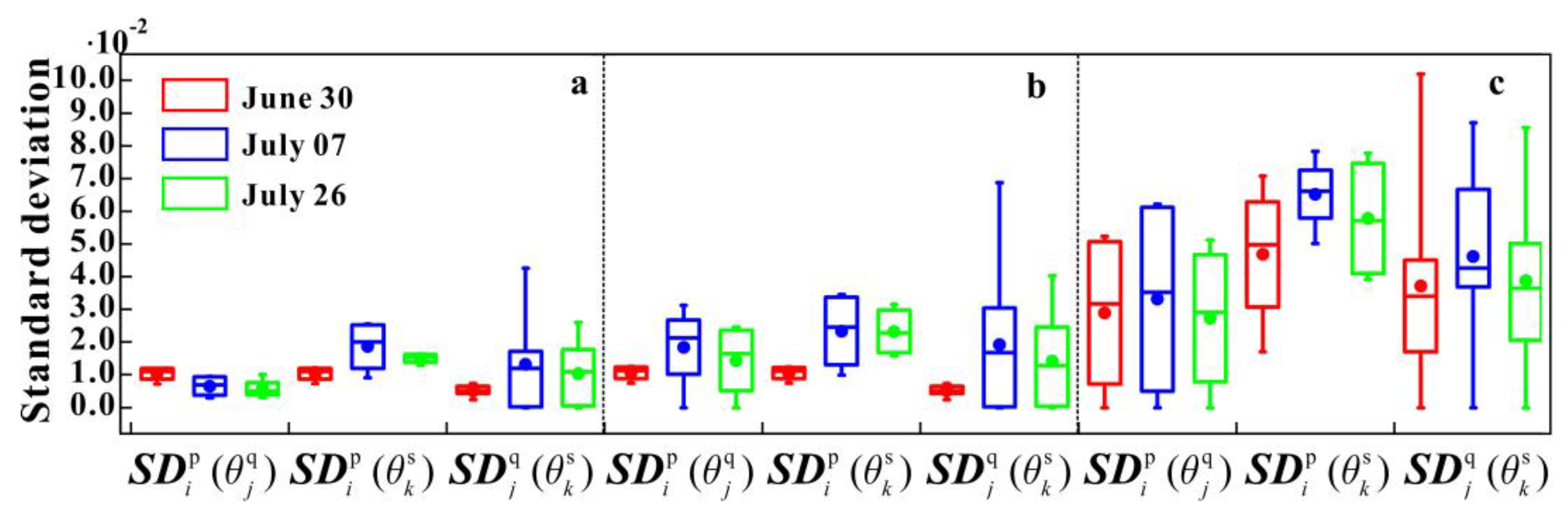
Moreover, many previous studies have applied variogram modeling and the characteristic length (or range) to evaluate the spatial variability at different observational scales and its impact (change in support) [
43,
68,
69]. However, in our research, to validate the conjectures shown in
Table 7, the SoilNET and WaterNET soil moisture data from the HiWATER project [
17] within the study area were merged, and these merged data on 30 June (range: 1325.13 m), 7 July (range: 121.1 m), and 26 July (range: 128.7 m) were utilized to repeat the methods mentioned above. The results of the
and
for the merged data on 30 June, 7 July, and 26 July are shown in
Table 8 and the results of
are shown in
Figure 11. The linear trend surface analyses for those data on 30 June are shown in
Table 9. As shown in these charts, the USME for these data with kriging on 30 June, 7 July, and 26 July demonstrate these conjectures.
Previous studies have calculated soil moisture variance or standard deviation (STD) at different scales and noted that soil moisture variability decreased with increasing support but increased with extent scale [
3,
40,
53,
69]. However, averaged values and STD are insufficient for multiscale modeling of USME. Some landscape ecologists and geographers have built multiscale models on hierarchical data. These researchers believe that the value of a spatial unit (e.g., a pixel) at the lowest level can be determined by the overall mean, the effect of the lowest level, the effect of the median level, and the effect of the highest level [
66,
67]. These models may be beneficial for formulizing multiscale relations and should be studied. Hence, in this paper, a modified STD was calculated based on hierarchical nesting pixels to benefit the analysis of the scale effects.
The kriging method proved to be suitable for the field level through the cross-validation in this study. However, predicting the data over a larger area using sparse samples in an incomparable small region still needs to be studied. The foregoing analysis methods were applied to the kriging upscaling method and simple averaging upscaling method, and not to the other two common upscaling methods [
22]. Whether scale dependence or scale effects exist in multiscale estimations using those surplus two methods and whether they are caused by the spatial structure of the soil moisture data are ongoing topics of research. Moreover, we notice that the choice of theoretical semivariogram model is important for a semivariogram analysis, and, in our research, different spatial processes of soil moisture occurred on different acquisition dates [
33]. We cannot stick to a unique theoretical semivariogram model. A different theoretical semivariogram brings about a different empirical semivariogram with different parameters [
35,
46,
58]. The statistical ways or empirical ways for choosing an applicable theoretical semivariogram are not always practical. The simple ways by cross-validation and sensitivity analysis are only helpful in selecting a relatively more applicable model, but cannot determine a unique ideal model. Hence, spatial heterogeneity of the same dataset differs with different selected semivariogram models, which is critical in the kriging method. This is the main reason for uncertainties, including scale effects, in upscaling IMSO to pixel estimations with kriging. Besides this, we did not analyze the relation between any of the parameters of the semivariogram other than the range and their scale effects in the multiscale ISMO upscaling processes, both of which need to be further discussed.