Analyzing and Predicting Micro-Location Patterns of Software Firms
Abstract
:1. Introduction
- RQ1
- Are the effects of location factors, as reported by previous studies using aggregated spatial units, robust at the microgeographic level?
- RQ2
- How does a firm location prediction model perform at the microgeographic level and to what degree does it provide valuable new insights into the firm allocation process? What are the distinct requirements to the data and the statistical model?
2. Data
2.1. OpenStreetMap Data
2.2. Official Geodata
2.3. The Mannheim Enterprise Panel
3. Methods
3.1. Exploratory Spatial Data Analysis
3.2. Count Data Regression Models
4. Results
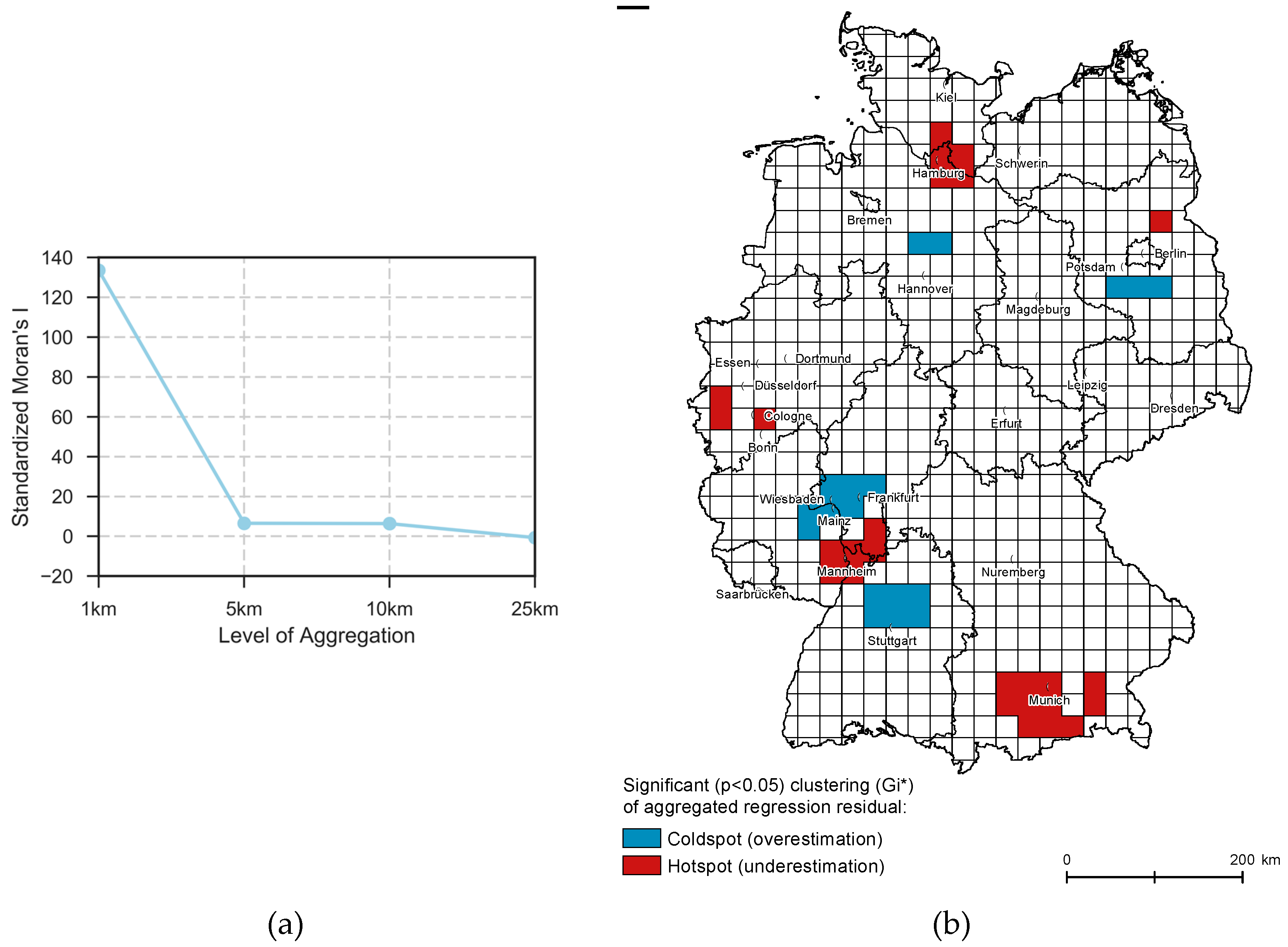
4.1. Exploratory Spatial Data Analysis Results
4.2. Regression Analysis Results
4.2.1. Interpretation of Regression Coefficients
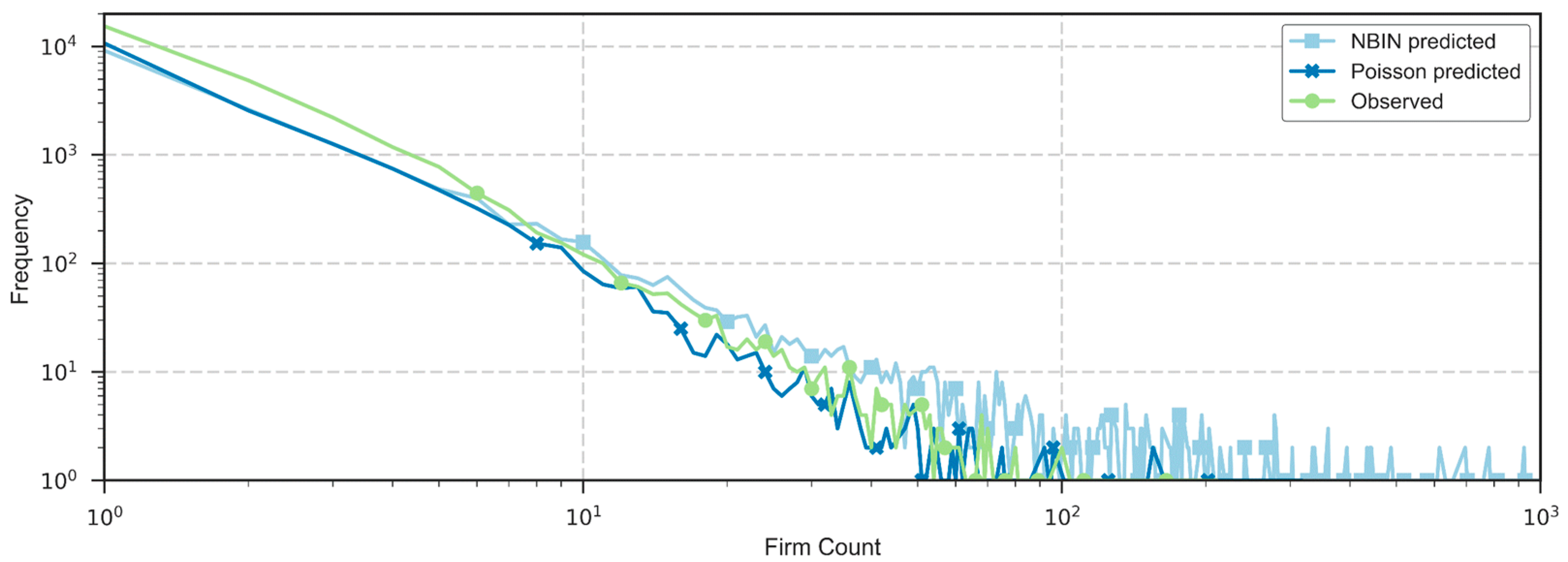
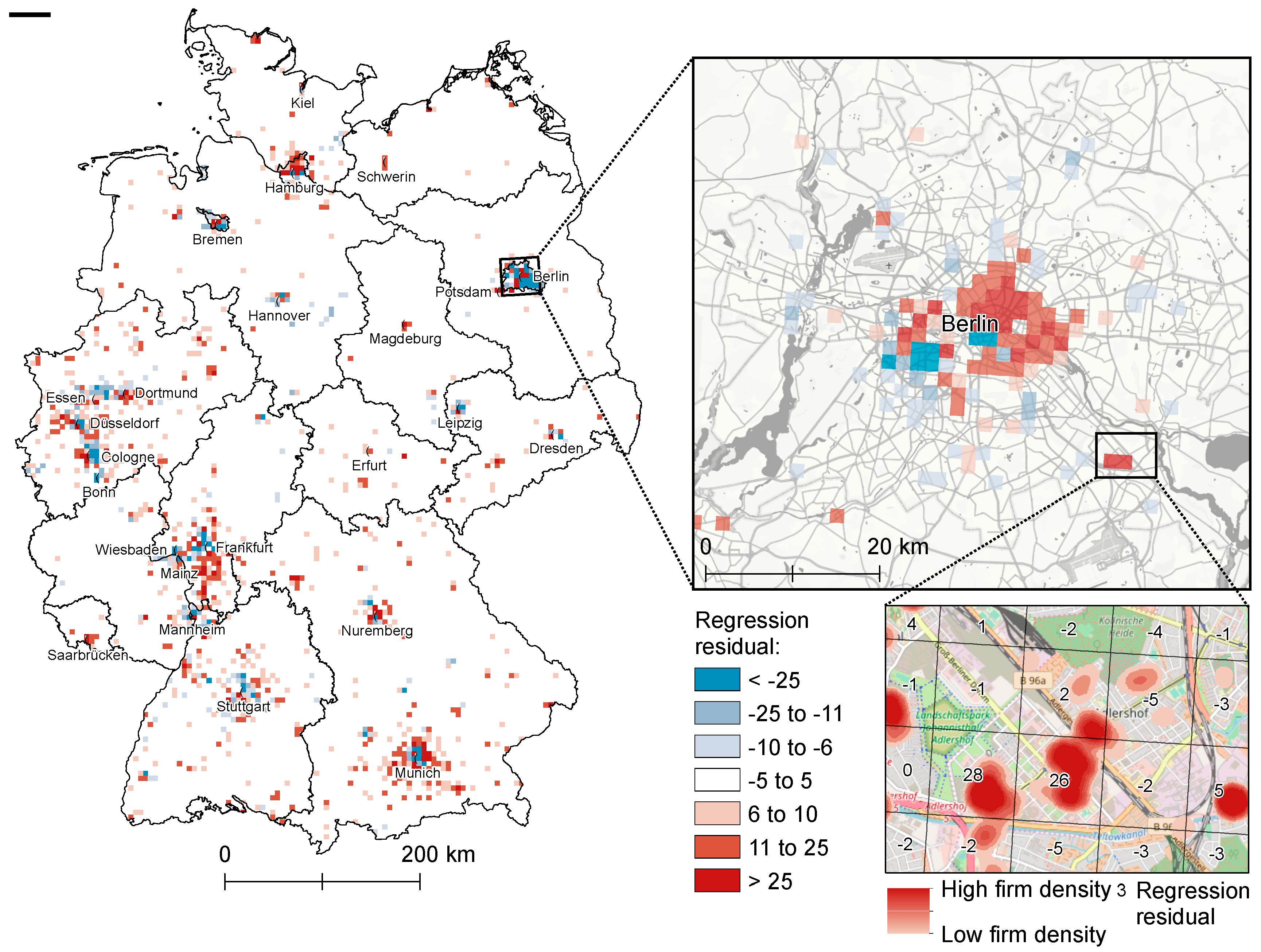
4.2.2. Model Fit and Spatial Residual Analysis
5. Discussion
5.1. Discussion of Regression Coefficients
5.1.1. Agglomeration Location Factors
5.1.2. Infrastructure Location Factors
5.1.3. Socio-Economic Location Factors
5.1.4. Quality of Life and Amenities Location Factors
5.1.5. Other Location Factors
5.2. Discussion of Model Adequacy
6. Conclusions
6.1. RS1: Scale-Robust Location Factors
6.2. RS2: Microgeographic Location Prediction
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Strotmann, H. Entrepreneurial survival. Small Bus. Econ. 2007, 28, 87–104. [Google Scholar] [CrossRef]
- Capello, R. Classical contributions to location theory. In Handbook of Regional Science; Fischer, M.M., Nijkamp, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 507–526. [Google Scholar]
- Clark, W.A.V.; Avery, K.L. The effects of data aggregation in statistical analysis. Geogr. Anal. 1976, 8, 428–438. [Google Scholar] [CrossRef]
- Manley, D. Scale, aggregation, and the modifiable areal unit problem. In Handbook of Regional Science; Fischer, M.M., Nijkamp, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1157–1171. [Google Scholar]
- Flowerdew, R. How serious is the modifiable areal unit problem for analysis of English census data? Popul. Trends 2011, 145, 106–118. [Google Scholar] [CrossRef] [PubMed]
- Bluemke, M.; Resch, B.; Lechner, C.; Westerholt, R.; Kolb, J.-P. Integrating geographic information into survey research: Current applications, challenges and future avenues. Surv. Res. Methods 2017, 11, 307–327. [Google Scholar]
- Arauzo-Carod, J.M.; Manjón-Antolín, M. (Optimal) spatial aggregation in the determinants of industrial location. Small Bus. Econ. 2012, 39, 645–658. [Google Scholar] [CrossRef]
- Lee, Y. Geographic redistribution of US manufacturing and the role of state development policy. J. Urban Econ. 2008, 64, 436–450. [Google Scholar] [CrossRef]
- Garrett, T.A. Aggregated versus disaggregated data in regression analysis: Implications for inference. Econ. Lett. 2003, 81, 61–65. [Google Scholar] [CrossRef]
- Cherry, T.L.; List, J.A. Aggregation bias in the economic model of crime. Econ. Lett. 2002, 75, 81–86. [Google Scholar] [CrossRef]
- Amrhein, C.G. Searching for the elusive aggregation effect: Evidence from statistical simulations. Environ. Plan. A 1995, 27, 105–119. [Google Scholar] [CrossRef]
- Arauzo-Carod, J.-M. Industrial location at a local level: Some comments about the territorial level of the analysis. Tijdschr. Voor Econ. Soc. Geogr. 2008, 99, 193–208. [Google Scholar] [CrossRef]
- Manjon-Antolin, M.; Arauzo-Carod, J.M. Locations and relocations: Modelling, determinants, and interrelations. Ann. Reg. Sci. 2006, 47, 131–146. [Google Scholar] [CrossRef]
- Briant, A.; Combes, P.P.; Lafourcade, M. Dots to boxes: Do the size and shape of spatial units jeopardize economic geography estimations? J. Urban Econ. 2010, 67, 287–302. [Google Scholar] [CrossRef]
- Arauzo-Carod, J.-M.; Liviano-Solis, D.; Manjon-Antolin, M. Empirical studies in industrial location: An assessment of their methods and results. J. Reg. Sci. 2010, 50, 685–711. [Google Scholar] [CrossRef]
- Goodchild, M.F. Citizens as sensors: The world of volunteered geography. GeoJournal 2007, 69, 211–221. [Google Scholar] [CrossRef]
- Elwood, S.; Goodchild, M.F.; Sui, D.Z. Researching volunteered geographic information: Spatial data, geographic research, and new social practice. Ann. Assoc. Am. Geogr. 2012, 102, 571–590. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Longley, P.A. The practice of geographic information science. In Handbook of Regional Science; Fischer, M.M., Nijkamp, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1107–1122. [Google Scholar]
- Sui, D.; Goodchild, M. The convergence of GIS and social media: Challenges for GIScience. Int. J. Geogr. Inf. Sci. 2011, 25, 1737–1748. [Google Scholar] [CrossRef]
- OpenStreetMap Foundation OpenStreetMap. Available online: http://www.openstreetmap.org (accessed on 1 November 2016).
- Ahlfeldt, G.M. Urbanity; SERC Discussion Paper, 136; London School of Economics and Political Science: London, UK, 2013. [Google Scholar]
- Möller, K. Culturally Clustered or in the Cloud? Location of Internet Start-Ups in Berlin; London School of Economics: London, UK, 2014; Volume 157. [Google Scholar]
- Ahlfeldt, G.M.; Richter, F.J. Urban Renewal after the Berlin Wall; SERC Discussion Paper, 151; London School of Economics and Political Science: London, UK, 2013. [Google Scholar]
- Grasland, C.; Madelin, M. The Modifiable Areas Unit Problem; ESPON: Luxembourg, 2006. [Google Scholar]
- Wooldridge, J.M. Econometric Analysis of Cross Section and Panel Data; The MIT Press: Cambridge, MA, USA; London, UK, 2002. [Google Scholar]
- Cameron, C.; Trivedi, P. Microeconomics Using Stata, Revised ed.; Stata Press: College Station, TX, USA, 2009. [Google Scholar]
- Pereira, R.H.M.; Nadalin, V.; Monasterio, L.; Albuquerque, P.H.M. Urban centrality: A simple index. Geogr. Anal. 2013, 45, 77–89. [Google Scholar] [CrossRef]
- Flanagin, A.J.; Metzger, M.J. The credibility of volunteered geographic information. GeoJournal 2008, 72, 137–148. [Google Scholar] [CrossRef]
- Haklay, M. How good is volunteered geographical information? A comparative study of OpenStreetMap and ordnance survey datasets. Environ. Plan. B Plan. Des. 2010, 37, 682–703. [Google Scholar] [CrossRef]
- Girres, J.F.; Touya, G. Quality assessment of the French OpenStreetMap dataset. Trans. GIS 2010, 14, 435–459. [Google Scholar] [CrossRef]
- Neis, P.; Zielstra, D.; Zipf, A. The street network evolution of crowdsourced maps: OpenStreetMap in Germany 2007–2011. Future Internet 2011, 4, 1–21. [Google Scholar] [CrossRef]
- Hecht, R.; Kunze, C.; Hahmann, S. Measuring completeness of building footprints in OpenStreetMap over space and time. ISPRS Int. J. Geo-Inf. 2013, 2, 1066–1091. [Google Scholar] [CrossRef]
- Arsanjani, J.J.; Mooney, P.; Zipf, A.; Schauss, A. Quality assessment of the contributed land use information from OpenStreetMap versus authoritative datasets. In OpenStreetMap in GIScience: Experiences, Research, and Applications; Arsanjani, J.J., Zipf, A., Mooney, P., Helbich, M., Eds.; Springer: Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2015; p. 324. [Google Scholar]
- Arsanjani, J.J.; Vaz, E. An assessment of a collaborative mapping approach for exploring land use patterns for several European metropolises. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 329–337. [Google Scholar] [CrossRef]
- Dorn, H.; Törnros, T.; Zipf, A. Geo-Information comparison with land use data in Southern Germany. Int. J. Geo-Inf. 2015, 4, 1657–1671. [Google Scholar] [CrossRef]
- Gallego, F.J. A population density grid of the European Union. Popul. Environ. 2010, 31, 460–473. [Google Scholar] [CrossRef]
- Bersch, J.; Gottschalk, S.; Müller, B.; Niefert, M. The Mannheim Enterprise Panel (MUP) and Firm Statistics for Germany; ZEW Discussion Paper, 14-104; Centre for European Economic Research: Mannheim, Germany, 2014. [Google Scholar]
- Zandbergen, P.A. A comparison of address point, parcel and street geocoding techniques. Comput. Environ. Urban Syst. 2008, 32, 214–232. [Google Scholar] [CrossRef]
- Miller, H.J.; Han, J. Geographic Data Mining and Knowledge Discovery, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Cheng, T.; Haworth, J.; Anbaroglu, B.; Tanaksaranond, G.; Wang, J. Spatiotemporal data mining. In Handbook of Regional Science; Fischer, M.M., Nijkamp, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1173–1193. [Google Scholar]
- Andrienko, N.; Andrienko, G. Exploratory Analysis of Spatial and Temporal Data: A Systematic Approach; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Andrienko, G.; Andrienko, N.; Bak, P.; Keim, D.; Wrobel, S. Visual Analytics; Springer: Heidelberg/Berlin, Germany, 2013. [Google Scholar]
- Maciejewski, R. Geovisualization. In Handbook of Regional Science; Fischer, M.M., Nijkamp, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1137–1155. [Google Scholar]
- Illian, J.; Penttinen, A.; Stoyan, H.; Stoyan, D. Statistical Analysis and Modelling of Spatial Point Patterns; Senn, S., Scott, M., Barnett, V., Eds.; John Wiley & Sons: Chichester, UK, 2008. [Google Scholar]
- Selvin, S. Statistical Analysis of Epidemiologic Data, 2nd ed.; Oxford University Press: New York, NY, USA; Oxford, UK, 1996. [Google Scholar]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Getis, A. Spatial weights matrices. Geogr. Anal. 2009, 41, 404–410. [Google Scholar] [CrossRef]
- Greene, W.H. Econometric Analysis, 7th ed.; Pearson: Harlow, UK, 2014. [Google Scholar]
- Coxe, S.; West, S.G.; Aiken, L.S. The analysis of count data: A gentle introduction to poisson regression and its alternatives. J. Pers. Assess. 2009, 91, 121–136. [Google Scholar] [CrossRef] [PubMed]
- Lambert, D.M.; McNamara, K.T.; Garrett, M.I. An application of spatial poisson models to manufacturing investment location analysis. J. Agric. Appl. Econ. 2006, 38, 105–121. [Google Scholar] [CrossRef]
- Liviano, D.; Arauzo-Carod, J.M. Industrial location and interpretation of zero counts. Ann. Reg. Sci. 2013, 50, 515–534. [Google Scholar] [CrossRef]
- Gehrke, B.; Frietsch, R.; Neuhäusler, P.; Rammer, C. Neuabgrenzung Forschungsintensiver Industrien und Güter; EFI: Berlin, Germany, 2013. [Google Scholar]
- Florida, R.; King, K. Rise of the Urban Startup Neighborhood; Martin Prosperity Institute Working Paper; Martin Prosperity Institute: Toronto, ON, Canada, 2016. [Google Scholar]
- Florida, R.; Adler, P.; Mellander, C. The city as innovation machine. Reg. Stud. 2017, 51, 86–96. [Google Scholar] [CrossRef]
- Projekt Adlershof Adlershof Science City. Available online: https://www.adlershof.de/en/sectors-of-technology/it-media/info/ (accessed on 1 October 2017).
- Weber, A. Über den Standort der Theorien: Reine Theorie des Standortes, 2nd ed.; J.C.B. Mohr: Tübingen, Germany, 1922. [Google Scholar]
- Marshall, A. Principles of Economics, 8th ed.; Macmillan Co.: London, UK, 1890. [Google Scholar]
- Hoover, E.M. Location Theory and the Shoe Leather Industries; Harvard University Press: Cambridge, MA, USA, 1937. [Google Scholar]
- Carlino, G.A.; Chatterjee, S.; Hunt, R.M. Urban density and the rate of invention. J. Urban Econ. 2007, 61, 389–419. [Google Scholar] [CrossRef]
- Hansen, E.R. Industrial location choice in São Paulo, Brazil: A nested logit model. Reg. Sci. Urban Econ. 1987, 17, 89–108. [Google Scholar] [CrossRef]
- Friedman, J.; Gerlowski, D.A.; Silberman, J. What attracts foreign multinational coproations? Evidence from branch plant location in the United States. J. Reg. Sci. 1992, 32, 403–418. [Google Scholar] [CrossRef]
- Smith, D.F.J.; Florida, R. Agglomeration and industrial location: An econometric analysis of Japanese-Affiliated manufacturing establishments in automotive-related industries. J. Urban Econ. 1994, 36, 23–41. [Google Scholar] [CrossRef]
- Ahlfeldt, G.; Pietrostefani, E. The Economic Effects of Density: A Synthesis; SERC Discussion Paper, 210; London School of Economics and Political Science: London, UK, 2017. [Google Scholar]
- Rosenthal, S.S.; Strange, W.C. Evidence on the nature and sources of agglomeration economies. In Handbook of Regional and Urban Economics; Henderson, J.V., Thisse, J.-F., Eds.; Elsevier B.V.: Amsterdam, The Netherlands, 2004; Volume 4, pp. 2120–2167. [Google Scholar]
- Eicher, T.S.; Strobel, T. Information Technology and Productivity Growth; Edward Elgar Publishing Ltd.: Cheltenham/Northampton, UK, 2009. [Google Scholar]
- Jang, S.; Kim, J.; von Zedtwitz, M. The importance of spatial agglomeration in product innovation: A microgeography perspective. J. Bus. Res. 2017, 78, 143–154. [Google Scholar] [CrossRef]
- List, J.A. US county-level determinants of inbound FDI: Evidence from a two-step modified count data model. Int. J. Ind. Organ. 2001, 19, 953–973. [Google Scholar] [CrossRef]
- Coughlin, C.C.; Segev, E. Location determinants of new foreign-owned manufacturing plants. J. Reg. Sci. 2000, 40, 323–351. [Google Scholar] [CrossRef]
- Arauzo-Carod, J.-M. Determinants of industrial location: An application for Catalan municipalitie. Pap. Reg. Sci. 2005, 84, 105–120. [Google Scholar] [CrossRef]
- Peter, R. Kapazitäten und Flächenbedarf Öffentlicher Verkehrssysteme in Schweizerischen Agglomerationen; Term Paper; ETH Zürich: Zürich, Switzerland, 2005. [Google Scholar]
- Coughlin, C.C.; Terza, J.V.; Arromdee, V. State characteristics and the location of foreign direct investment within the United States. Rev. Econ. Stat. 1991, 73, 675–683. [Google Scholar] [CrossRef]
- Audretsch, D.B.; Lehmann, E.E. Does the knowledge spillover theory of entrepreneurship hold for regions? Res. Policy 2005, 34, 1191–1202. [Google Scholar] [CrossRef]
- Rammer, C.; Kinne, J.; Blind, K. Microgeography of Innovation in the City: Location Patterns of Innovative Firms in Berlin; ZEW Discussion Paper; ZEW: Mannheim, Germany, 2016. [Google Scholar]
- Basile, R. Acquisition versus greenfield investment: The location of foreign manufacturers in Italy. Reg. Sci. Urban Econ. 2004, 34, 3–25. [Google Scholar]
- Barbosa, N.; Guimaraes, P.; Woodward, D. Foreign firm entry in an open economy: The case of Portugal. Appl. Econ. 2004, 36, 465–472. [Google Scholar] [CrossRef]
- Goodchild, M.F. Scale in GIS: An overview. Geomorphology 2011, 130, 5–9. [Google Scholar] [CrossRef]
- Cohendet, P.; Grandadam, D.; Simon, L. The anatomy of the creative city. Ind. Innov. 2010, 17, 91–111. [Google Scholar] [CrossRef]
- Gottlieb, P.D. Residential amenities, firm location and economic development. Urban Stud. 1995, 32, 1413–1436. [Google Scholar] [CrossRef]
- Glaeser, E.L.; Kerr, W.R.; Ponzetto, G.A.M. Clusters of Entrepreneurship; NBER Working Paper; NBER: Cambridge, MA, USA, 2009. [Google Scholar]
- Ahlfeldt, G.M. Blessing or curse? Appreciation, amenities and resistance to urban renewal. Reg. Sci. Urban Econ. 2011, 41, 32–45. [Google Scholar] [CrossRef]
- Eurostat. Quality of Life: Facts and Views; Mercy, J.-L., Litwinska, A., Dupré, D., Clarke, S., Ivan, G., Stewart, C., Eds.; Eurostat: Luxembourg, Luxembourg, 2015. [Google Scholar]
- Månssona, K.; Shukur, G. A poisson ridge regression estimator. Econ. Model. 2011, 28, 1475–1481. [Google Scholar] [CrossRef]
- Westerholt, R.; Resch, B.; Zipf, A. A local scale-sensitive indicator of spatial autocorrelation for assessing high- and low-value clusters in multiscale datasets. Int. J. Geogr. Inf. Sci. 2015, 1–20. [Google Scholar] [CrossRef]
- LeSage, J.; Pace, R.K. Introduction to Spatial Econometrics; Balakrishnan, N., Schucany, W.R., Eds.; Chapmann & Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Anselin, L. Spatial Econometrics: Methods and Models; Springer: Heidelberg/Berlin, Germany, 1988. [Google Scholar]
- Sagl, G.; Loidl, M.; Beinat, E. A visual analytics approach for extracting spatio-temporal urban mobility information from mobile network traffic. ISPRS Int. J. Geo-Inf. 2012, 1, 256–271. [Google Scholar] [CrossRef] [Green Version]
- Miller, H.J.; Goodchild, M.F. Data-driven geography. GeoJournal 2015, 80, 449–461. [Google Scholar] [CrossRef]
- Berlin-Brandenburg Bureau of Statistics Statistik Berlin-Brandenburg. Available online: https://www.statistik-berlin-brandenburg.de/ (accessed on 1 October 2017).
- Carlino, G.A.; Carr, J.; Hunt, R.M.; Smith, T.E. The agglomeration of R&D labs. J. Urban Econ. 2017, 101, 14–26. [Google Scholar]
- Scholl, T.; Brenner, T. Detecting spatial clustering using a firm-level cluster index. Reg. Stud. 2014, 3404, 1–15. [Google Scholar] [CrossRef]
- Kukuliač, P.; Hor, J.R.I. W Function: A new distance-based measure of spatial distribution of economic activities. Geogr. Anal. 2016, 49, 1–16. [Google Scholar] [CrossRef]
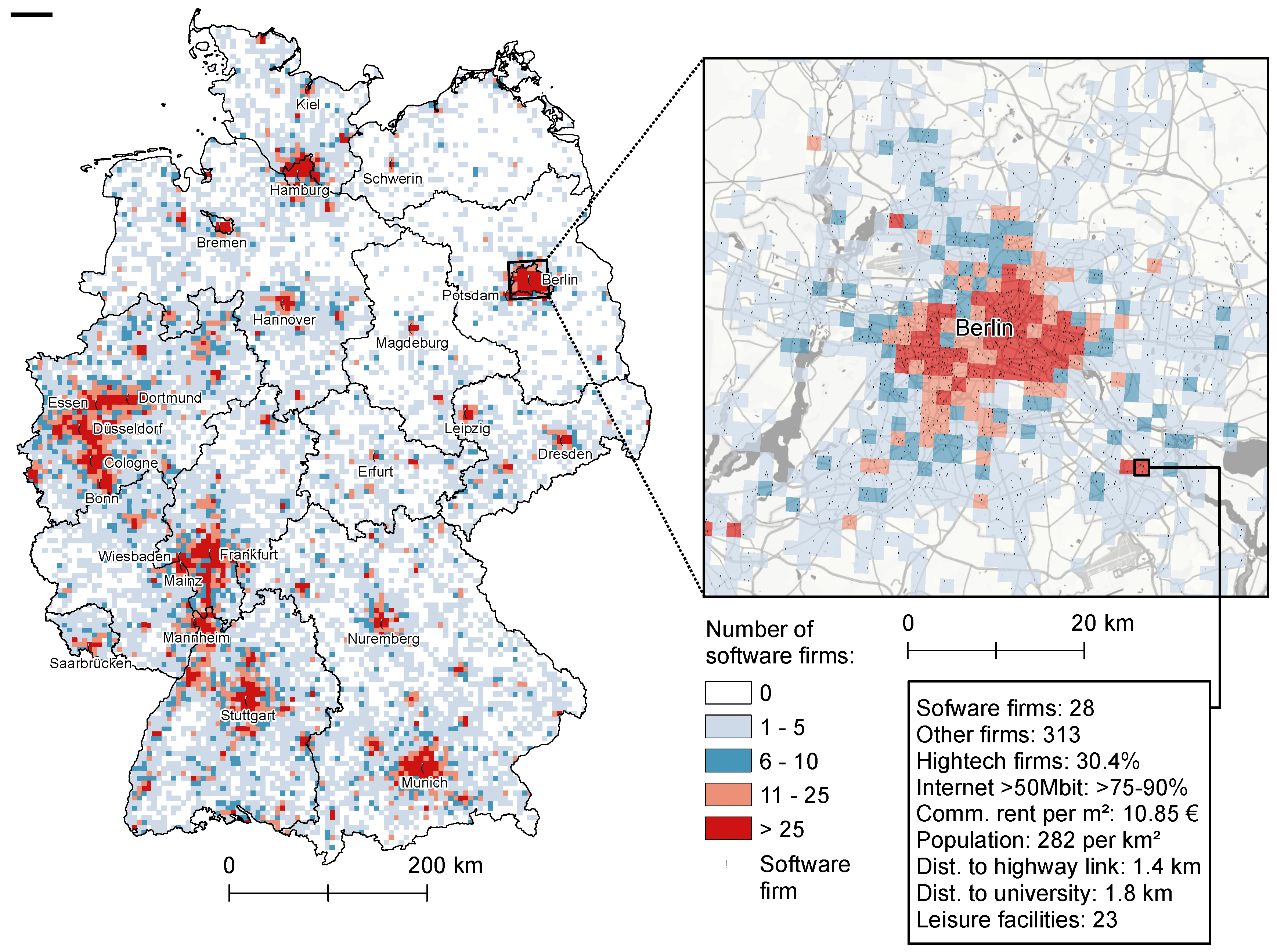
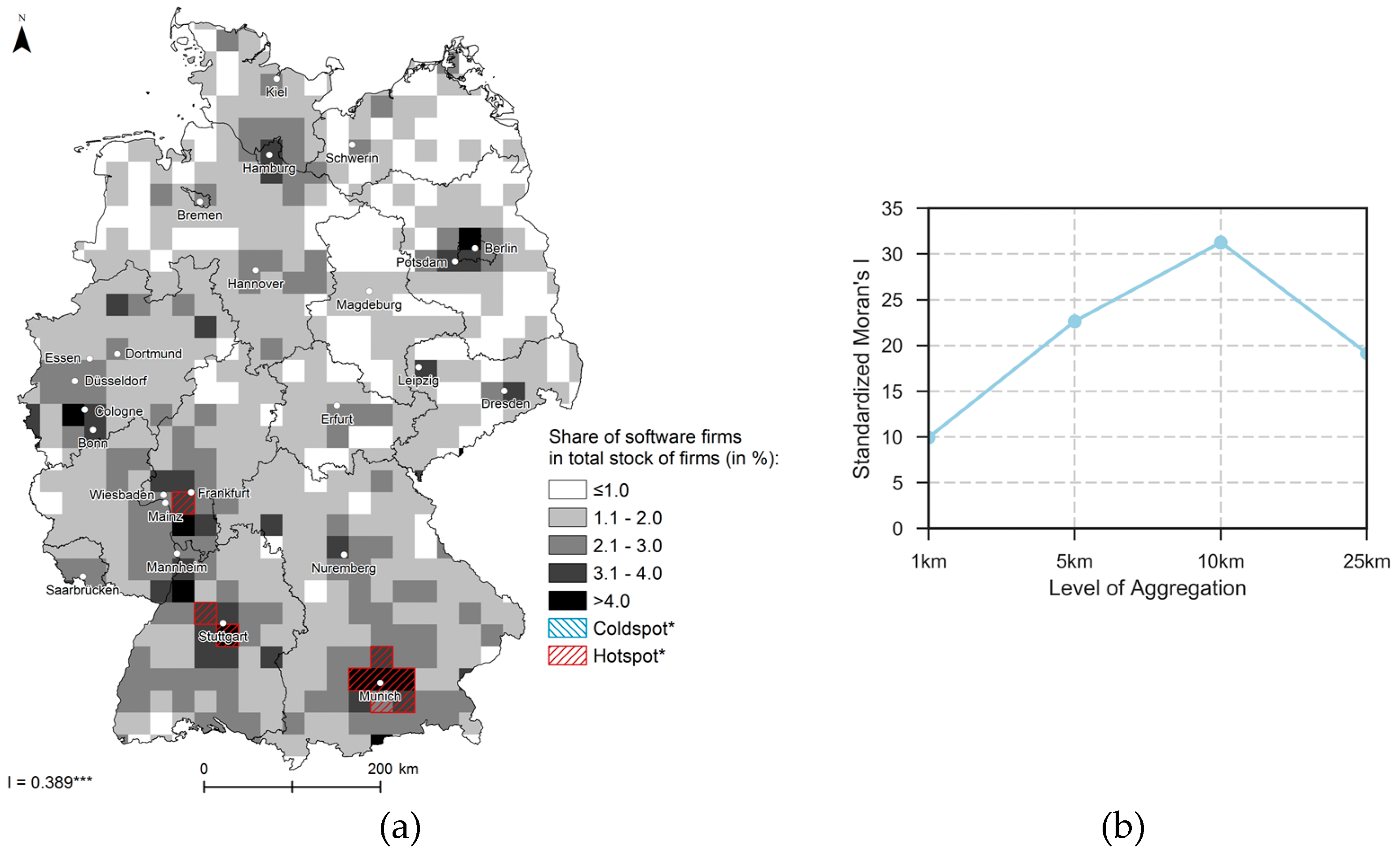

| Scale | Obs. | SD | Min. | Max. | VMR | Histogram | ||
|---|---|---|---|---|---|---|---|---|
| 1 km | 361,453 | 0.19 | 0 | 1.64 | 0 | 211 | 14.12 | 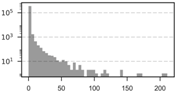 |
| 5 km | 14,951 | 4.58 | 1 | 25.98 | 0 | 1604 | 147.39 | 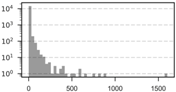 |
| 10 km | 3860 | 17.74 | 4 | 87.07 | 0 | 3265 | 427.35 | 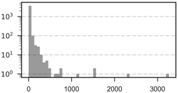 |
| 25 km | 671 | 102.06 | 27 | 301.74 | 0 | 4105 | 892.11 | 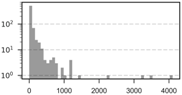 |
| Location Factor | Description | IRR |
|---|---|---|
| Agglomeration Location Factors | ||
| Firm density | Number of local firms (in 10) | 1.028 *** (0.003) |
| Firm density² | Squared number of local firms (in 10) | 0.999 *** (0.000) |
| High-tech firms | Proportion of high-tech firms in local stock of firms (in %) | 1.021 *** (0.000) |
| Major firms | Distance to next major firm in km | 0.998 *** (0.000) |
| Commercial rent | Difference local rent to mean rent in neighborhood (in Euro) | 1.127 *** (0.12) |
| Population | Population per cell (in 100) | 1.081 *** (0.003) |
| Population² | Squared population per cell (in 100) | 0.999 *** (0.000) |
| Population centrality | Urban Centrality Index (in 0.1 UCI) high value ≙ monocentricity | 1.079 *** (0.192) |
| Infrastructure Location Factors | ||
| Broadband Internet | Availability of ≥50 mb Internet (categories) high value ≙ low availability of Internet | 0.764 *** (0.009) |
| Motorway | Distance to nearest motorway access (in km) | 0.977 *** (0.001) |
| Railway | Distance to nearest main-line railway station (in km) | 0.998 *** (0.000) |
| Airport | Distance to nearest main airport (in km) | 0.998 *** (0.000) |
| Public transport | Weighted count of public transport stops | 1.000 (0.001) |
| Socio-economic Location Factors | ||
| Wages | Median income of full time employee (in 100 Euro) | 1.005 (0.003) |
| Universities | Distance to nearest university (in km) | 0.980 *** (0.000) |
| Research institutes | Number of research institutes | 1.004 (0.036) |
| Educated workforce | Proportion of graduate employees in % | 1.063 ***(0.006) |
| Students | Proportion of students in local population in % | 0.986 *** (0.003) |
| Business tax | Business tax factor (in 100) high values ≙ high taxes | 0.925 ** (0.023) |
| Quality of Life and Amenities Location Factor | ||
| Life expectancy | Mean life expectancy of population | 1.092 *** (0.012) |
| Crime | Violent and street crime incidents per 1000 inhabitants | 1.021 (0.015) |
| Recreation | Number of recreational, community, and sports facilities | 1.056 *** (0.008) |
| Culture | Number of cultural facilities | 1.015 0.017 |
| Leisure | Number of gastronomy, nightlife, and general leisure facilities | 1.002 (0.002) |
| Other | ||
| Terrain | Difference in elevation to mean neighborhood elevation (in 100m) high values ≙ hillside location | 0.919 *** (0.004) |
| Geocoding control variable | Geocoding match rate (in %) high value ≙ high completeness | 1.018 *** (0.002) |
| GoF Measure | Poisson | Negative Binomial |
|---|---|---|
| Pseudo-R² | 0.58 | 0.33 |
| RMSE | 1.36 | 483,735 |
| AIC | 211,603 | 179,705 |
| BIC | 211,892 | 180,004 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kinne, J.; Resch, B. Analyzing and Predicting Micro-Location Patterns of Software Firms. ISPRS Int. J. Geo-Inf. 2018, 7, 1. https://doi.org/10.3390/ijgi7010001
Kinne J, Resch B. Analyzing and Predicting Micro-Location Patterns of Software Firms. ISPRS International Journal of Geo-Information. 2018; 7(1):1. https://doi.org/10.3390/ijgi7010001
Chicago/Turabian StyleKinne, Jan, and Bernd Resch. 2018. "Analyzing and Predicting Micro-Location Patterns of Software Firms" ISPRS International Journal of Geo-Information 7, no. 1: 1. https://doi.org/10.3390/ijgi7010001
APA StyleKinne, J., & Resch, B. (2018). Analyzing and Predicting Micro-Location Patterns of Software Firms. ISPRS International Journal of Geo-Information, 7(1), 1. https://doi.org/10.3390/ijgi7010001






