Spatial-Spectral Graph Regularized Kernel Sparse Representation for Hyperspectral Image Classification
Abstract
:1. Introduction
2. KSRC
3. Proposed Approach
3.1. Proposed Model
3.2. Optimization Algorithm
- Input: A training dictionary and a hyperspectral data matrix .
- Choose , and compute the weight matrix according to (11).
- Select the parameter for the RBF kernel and compute the matrices and .
- Set ; choose , , , , , , , .
- Repeat
- Compute , , , , using (18).
- .
- Until some stopping criterion is satisfied.
- Output: The estimated label of using (6), .
3.3. Analysis and Comparison
- The graph-based spatially-smooth constraint is proposed by measuring the spatial relationship between every two spatially-adjacent pixels. If using this term, the test pixels should be arranged in the form of images.
- The spatial location constraint is exploited by integrating the location information of anchor samples, which are assumed to be taken from the test area and labeled by experts.
4. Experimental Results
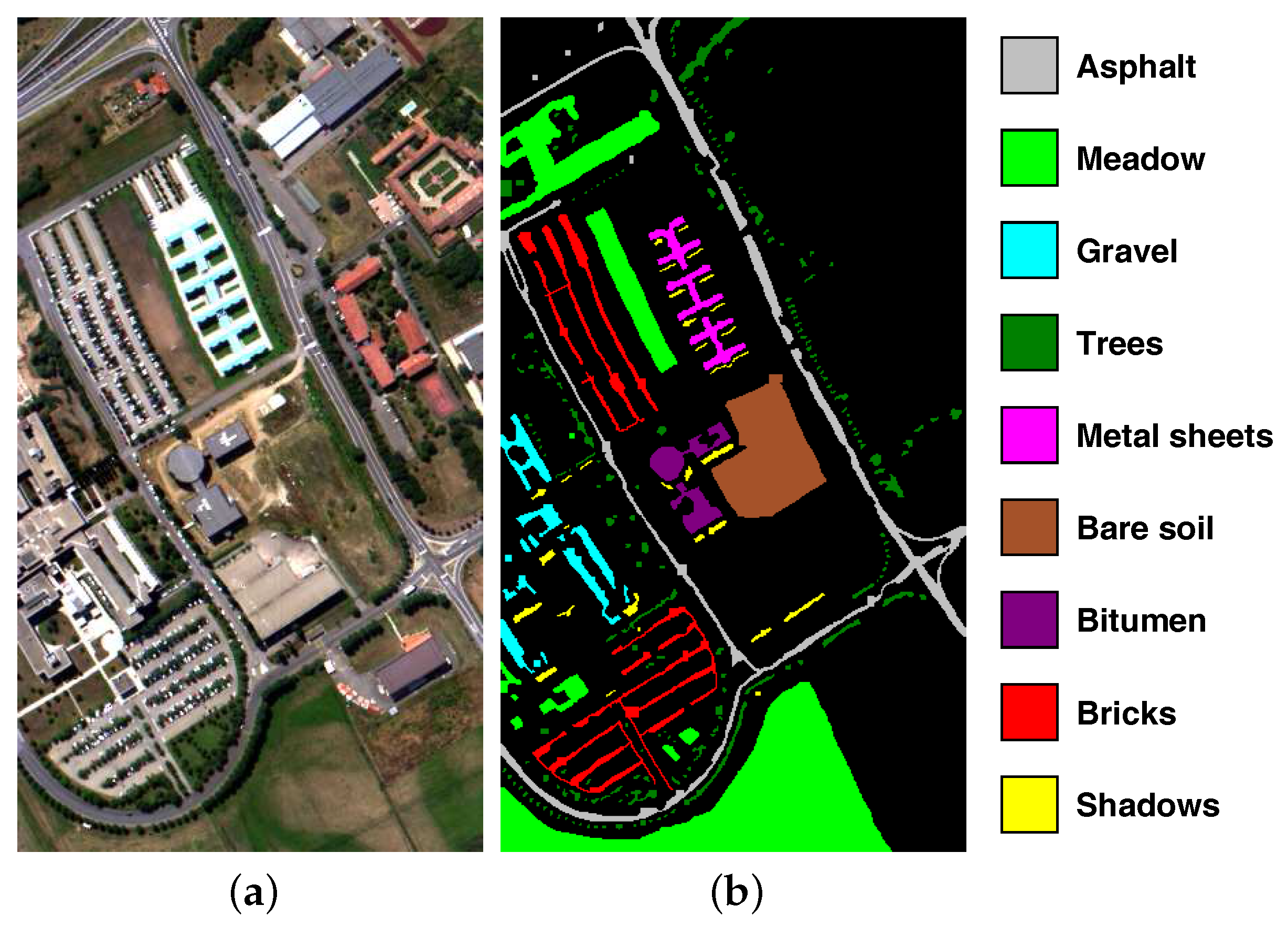
4.1. Datasets
4.2. Model Development and Experimental Setup
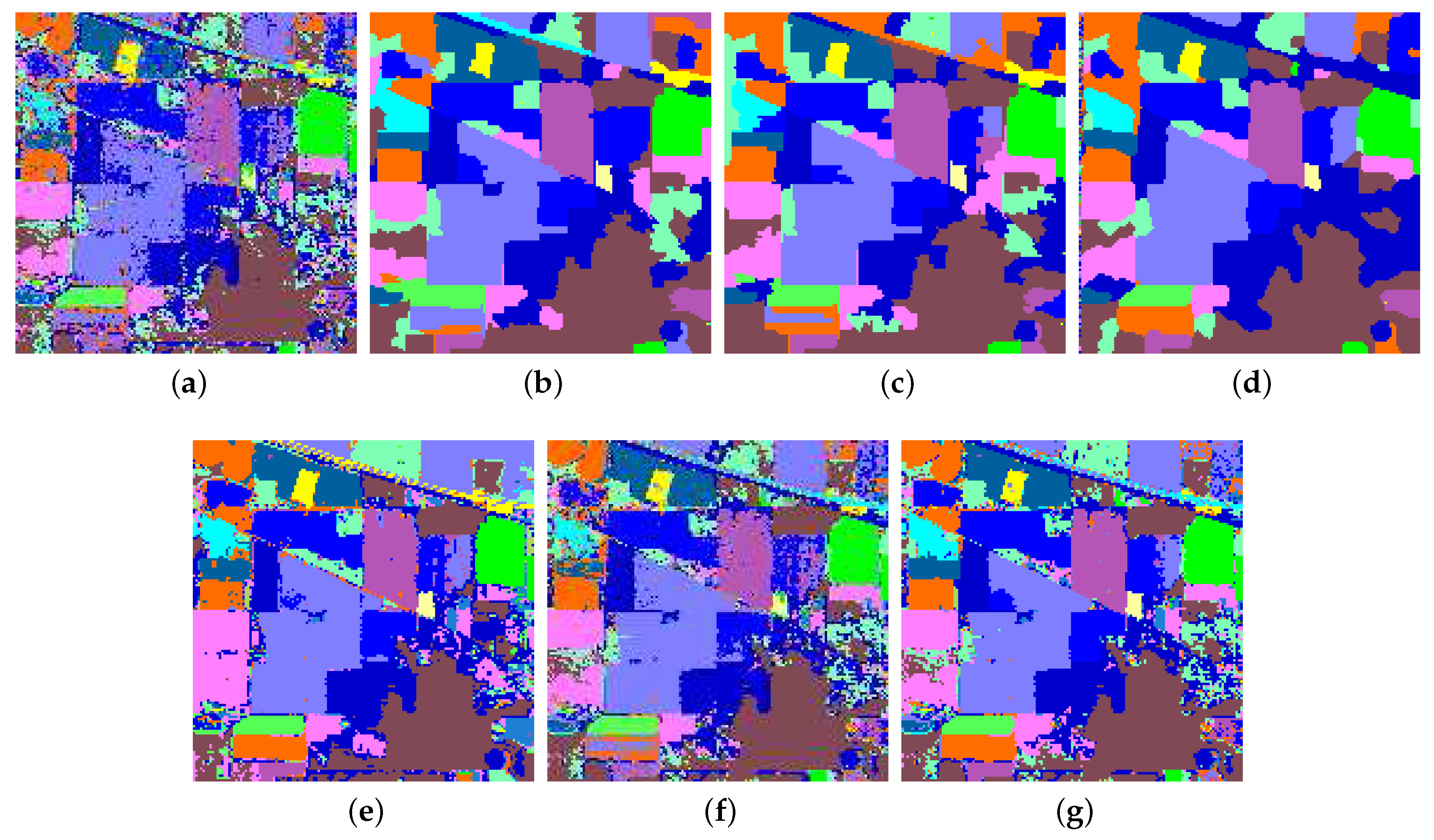
4.3. Numerical and Visual Comparisons
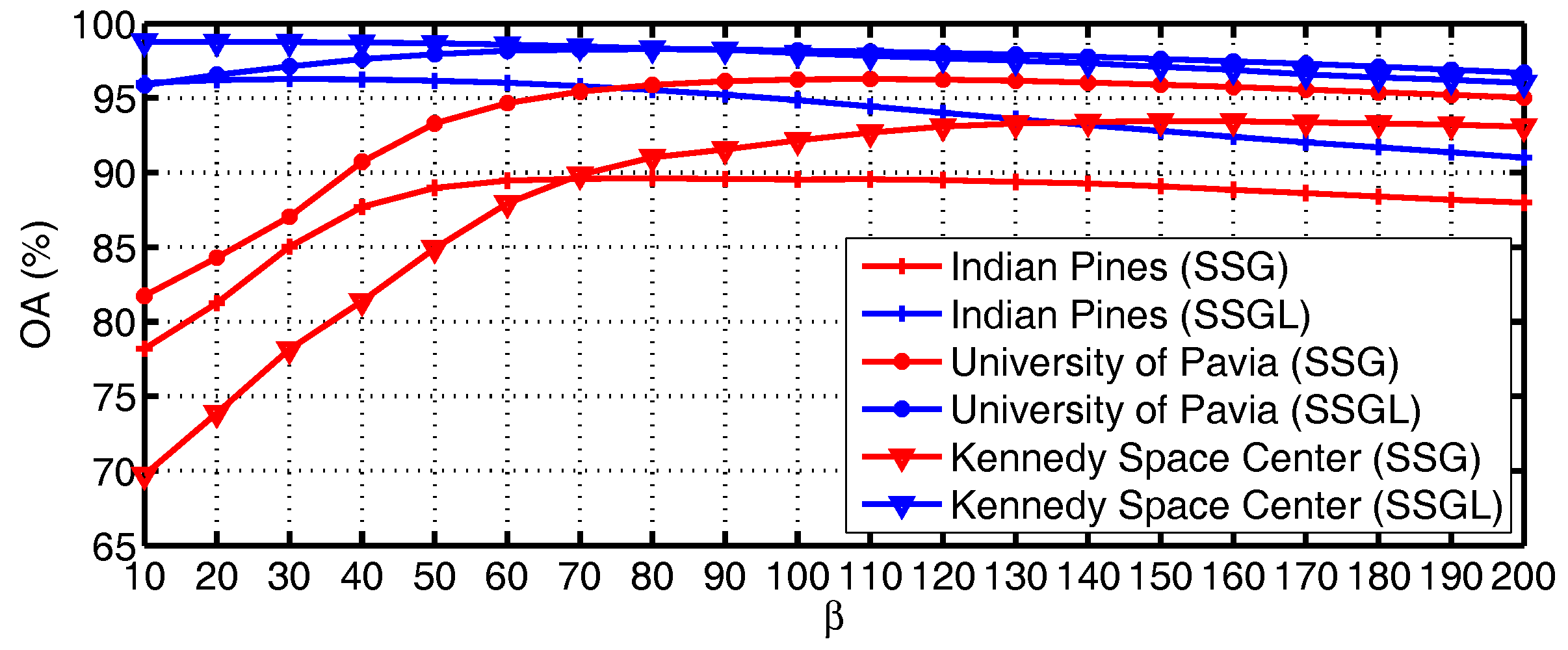
4.4. Analysis of Parameters
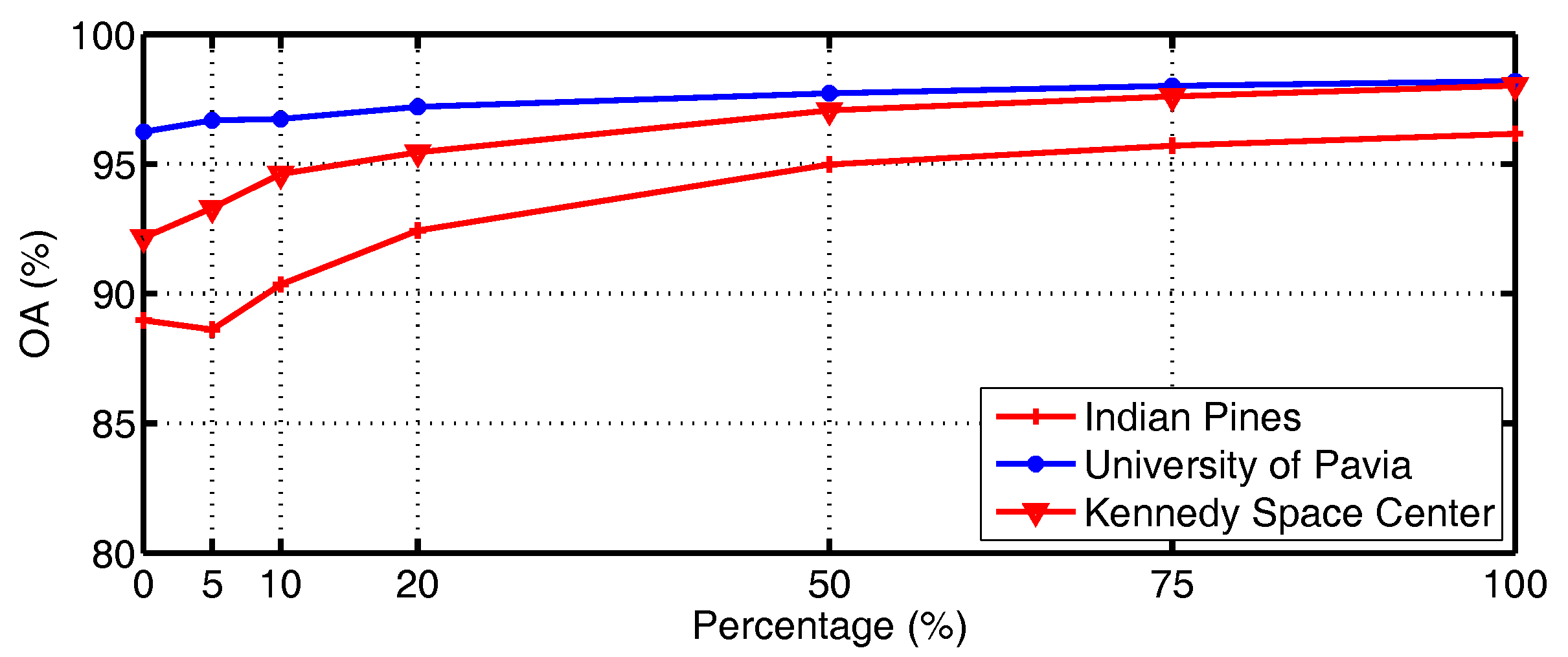
4.5. Influence of Anchor Samples
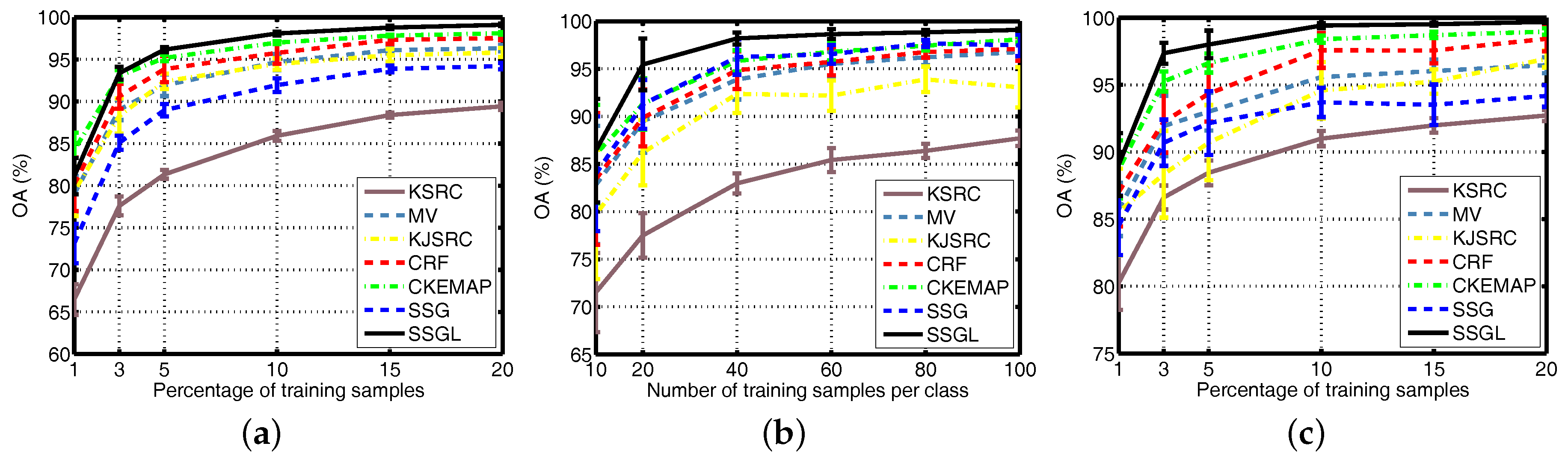
4.6. Different Numbers of Training Samples
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SVM | support vector machines |
| SRC | sparse representation classification |
| KSRC | kernel sparse representation classification |
| SSGL | spatial-spectral graph regularization with location information |
| RBF | Gaussian radial basis function |
| ADMM | alternating direction method of multipliers |
| AVIRIS | Airborne Visible/Infrared Imaging Spectrometer |
| ROSIS | Reflective Optics System Imaging Spectrometer |
| MV | majority voting |
| KJSRC | kernel joint sparse representation classification |
| CRF | condition random fields |
| CKEMAP | composite kernel with extended multi-attribute profile features |
| EMAP | extended multi-attribute profile |
| ERS | entropy rate superpixel |
| SSG | spatial-spectral graph regularization |
| OA | overall accuracy |
| AA | average accuracy |
| KA | kappa coefficient of agreement |
References
- Manolakis, D.; Shaw, G. Detection algorithms for hyperspectral imaging applications. IEEE Signal Process. Mag. 2005, 19, 29–43. [Google Scholar] [CrossRef]
- Datt, B.; Mcvicar, T.R.; Van Niel, T.G.; Jupp, D.L.B. Preprocessing EO-1 Hyperion hyperspectral data to support the application of agricultural indexes. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1246–1259. [Google Scholar] [CrossRef]
- Horig, B.; Kuhn, F.; Oschutz, F.; Lehmann, F. HyMap hyperspectral remote sensing to detect hydrocarbons. Int. J. Remote Sens. 2001, 22, 1413–1422. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Gamba, P.; Bioucas-Dias, J.M.; Zhang, L.; Benediktsson, J.A.; Plaza, A. Multiple feature learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1592–1606. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Gomez-Chova, L.; Munoz-Mari, J.; Vila-Frances, J.; Calpe-Maravilla, J. Composite kernels for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2006, 3, 93–97. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015. [Google Scholar]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Wan, L.; Liu, N.; Huo, H.; Fang, T. Selective convolutional neural networks and cascade classifiers for remote sensing image classification. Remote Sens. Lett. 2017, 8, 917–926. [Google Scholar] [CrossRef]
- Wang, J.; Luo, C.; Huang, H.; Zhao, H.; Wang, S. Transferring Pre-Trained Deep CNNs for Remote Scene Classification with General Features Learned from Linear PCA Network. Remote Sens. 2017, 9, 225. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral Image Classification via Kernel Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 217–231. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Z.; Wei, Z.; Xiao, L.; Sun, L. Spatial-spectral kernel sparse representation for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2462–2471. [Google Scholar] [CrossRef]
- Yuan, H.; Tang, Y.Y.; Lu, Y.; Yang, L.; Luo, H. Hyperspectral Image Classification Based on Regularized Sparse Representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2174–2182. [Google Scholar] [CrossRef]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 31, 210–227. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Tsang, I.W.H.; Chia, L.T. Kernel Sparse Representation for Image Classification and Face Recognition. In Proceedings of the 11th European Conference on Computer Vision: Part IV, Heraklion, Greece, 5–11 September 2010; pp. 1–14. [Google Scholar]
- Goldstein, T.; Osher, S. The split Bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Y. Alternating direction algorithms for l1-problems in compressive sensing. SIAM J. Sci. Comput. 2011, 33, 250–278. [Google Scholar] [CrossRef]
- Combettes, P.L.; Wajs, V.R. Signal Recovery by Proximal Forward-Backward Splitting. Multiscale Model. Simul. 2005, 4, 1168–1200. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Chanussot, J.; Benediktsson, J.A. Segmentation and classification of hyperspectral images using watershed transformation. Pattern Recogition 2010, 43, 2367–2379. [Google Scholar] [CrossRef]
- Liu, J.; Shi, X.; Wu, Z.; Xiao, L.; Xiao, Z.; Yuan, Y. Hyperspectral image classification via region-based composite kernels. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2015. [Google Scholar]
- Liu, M.Y.; Tuzel, O.; Ramalingam, S.; Chellappa, R. Entropy rate superpixel segmentation. In Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011. [Google Scholar]
- Feng, J.; Cao, Z.; Pi, Y. Polarimetric Contextual Classification of PolSAR Images Using Sparse Representation and Superpixels. Remote Sens. 2014, 6, 7158–7181. [Google Scholar] [CrossRef]
- Roscher, R.; Waske, B. Superpixel-based classification of hyperspectral data using sparse representation and conditional random fields. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014. [Google Scholar]
- Mura, M.D.; Benediktsson, J.A.; Waske, B.; Bruzzone, L. Extended profiles with morphological attribute filters for the analysis of hyperspectral data. Inte. J. Remote Sens. 2010, 31, 5975–5991. [Google Scholar] [CrossRef]
- Mura, M.D.; Benediktsson, J.A.; Waske, B.; Bruzzone, L. Morphological Attribute Profiles for the Analysis of Very High Resolution Images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3747–3762. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Kang, X.; Benediktsson, J.A. Spectral–Spatial Classification of Hyperspectral Images with a Superpixel-Based Discriminative Sparse Model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4186–4201. [Google Scholar] [CrossRef]
- Li, J.; Marpu, P.R.; Plaza, A.; Bioucas-Dias, J.M.; Benediktsson, J.A. Generalized Composite Kernel Framework for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4816–4829. [Google Scholar] [CrossRef]





| Deep Learning Methods | SSGL | |
|---|---|---|
| No. of parameters | Several parameters needed to be trained. | Four model parameters: , , and . One algorithm parameter . |
| No. of training samples | Abundant training samples needed. | Moderate (or even limited) training samples needed. |
| Computational cost | Expensive | Moderate |
| Flexibility | Robust to the spectral distortion. | Restricted to the test area. |
| Accuracy | High | Moderate |
| Class | Set | ||
|---|---|---|---|
| No. | Name | Train | Test |
| C01 | Alfalfa | 3 | 51 |
| C02 | Corn-no till | 72 | 1362 |
| C03 | Corn-min till | 42 | 792 |
| C04 | Corn | 12 | 222 |
| C05 | Grass/pasture | 25 | 472 |
| C06 | Grass/trees | 38 | 709 |
| C07 | Grass/pasture-mowed | 2 | 24 |
| C08 | Hay-windrowed | 25 | 464 |
| C09 | Oats | 2 | 18 |
| C10 | Soybeans-no till | 49 | 919 |
| C11 | Soybeans-min till | 124 | 2344 |
| C12 | Soybean-clean till | 31 | 583 |
| C13 | Wheat | 11 | 201 |
| C14 | Woods | 65 | 1229 |
| C15 | Bldg-grass-tree drives | 19 | 361 |
| C16 | Stone-steel towers | 5 | 90 |
| Total | 525 | 9841 | |
| Class | Set | ||
|---|---|---|---|
| No. | Name | Train | Test |
| C1 | Asphalt | 40 | 6812 |
| C2 | Meadow | 40 | 18,646 |
| C3 | Gravel | 40 | 2167 |
| C4 | Trees | 40 | 3396 |
| C5 | Metal sheets | 40 | 1338 |
| C6 | Bare soil | 40 | 5064 |
| C7 | Bitumen | 40 | 1316 |
| C8 | Bricks | 40 | 3838 |
| C9 | Shadows | 40 | 986 |
| Total | 360 | 43,563 | |
| Class | Set | ||
|---|---|---|---|
| No. | Name | Train | Test |
| C01 | Scrub | 39 | 722 |
| C02 | Willow swamp | 13 | 230 |
| C03 | Cabbage palm hammock | 13 | 243 |
| C04 | Cabbage palm/oak hammock | 13 | 239 |
| C05 | Slash pine | 9 | 152 |
| C06 | Oak/broadleaf hammock | 12 | 217 |
| C07 | Hardwood swamp | 6 | 99 |
| C08 | Graminoid marsh | 22 | 409 |
| C09 | Spartina marsh | 26 | 494 |
| C10 | Cattail marsh | 21 | 383 |
| C11 | Salt marsh | 21 | 398 |
| C12 | Mud flats | 26 | 477 |
| C13 | Water | 47 | 880 |
| Total | 268 | 4943 | |
| Class Type | KSRC | MV | KJSRC | CRF | CKEMAP | SSG | SSGL |
|---|---|---|---|---|---|---|---|
| C01 | 56.67 | 72.35 | 81.57 | 80.78 | 89.61 | 68.43 | 91.18 |
| C02 | 78.33 | 85.27 | 87.22 | 88.84 | 91.24 | 79.90 | 95.01 |
| C03 | 64.31 | 82.15 | 92.29 | 89.31 | 96.74 | 76.98 | 96.48 |
| C04 | 52.07 | 90.86 | 87.88 | 91.98 | 84.91 | 69.37 | 85.68 |
| C05 | 89.03 | 90.97 | 90.97 | 88.88 | 92.65 | 90.15 | 93.09 |
| C06 | 96.46 | 96.11 | 96.33 | 99.31 | 98.70 | 98.58 | 98.77 |
| C07 | 74.58 | 19.17 | 19.17 | 56.25 | 96.67 | 88.33 | 97.08 |
| C08 | 98.75 | 99.78 | 99.57 | 99.66 | 99.70 | 99.44 | 99.48 |
| C09 | 57.78 | 30.00 | 40.00 | 20.00 | 97.78 | 51.67 | 93.33 |
| C10 | 72.87 | 86.74 | 85.91 | 86.59 | 90.48 | 84.41 | 92.76 |
| C11 | 82.43 | 97.42 | 93.95 | 97.11 | 96.92 | 93.78 | 97.42 |
| C12 | 76.74 | 97.75 | 95.61 | 97.99 | 91.36 | 90.03 | 96.72 |
| C13 | 98.76 | 100 | 99.00 | 99.60 | 99.50 | 99.45 | 99.55 |
| C14 | 95.30 | 99.78 | 97.99 | 98.53 | 99.06 | 98.49 | 99.29 |
| C15 | 53.80 | 69.56 | 86.26 | 90.61 | 95.51 | 73.16 | 90.42 |
| C16 | 88.56 | 91.89 | 96.78 | 96.33 | 93.78 | 87.89 | 88.67 |
| OA(%) | 81.33 | 91.92 | 92.39 | 93.83 | 95.17 | 88.97 | 96.16 |
| AA(%) | 77.28 | 81.86 | 84.41 | 86.36 | 94.66 | 84.38 | 94.68 |
| KA(%) | 78.66 | 90.75 | 91.34 | 92.96 | 94.50 | 87.39 | 95.62 |
| Time(s) | 17.03 | 17.33 | 17.31 | 18.48 | 23.48 | 34.69 | 36.16 |
| Class Type | KSRC | MV | KJSRC | CRF | CKEMAP | SSG | SSGL |
|---|---|---|---|---|---|---|---|
| C1 | 73.25 | 91.69 | 92.01 | 91.92 | 97.30 | 93.30 | 97.49 |
| C2 | 83.24 | 93.23 | 95.25 | 94.77 | 94.94 | 97.01 | 98.48 |
| C3 | 78.68 | 93.01 | 90.90 | 91.54 | 91.86 | 90.58 | 97.70 |
| C4 | 91.65 | 86.39 | 89.32 | 91.58 | 95.58 | 94.44 | 94.90 |
| C5 | 99.42 | 99.17 | 99.49 | 99.89 | 99.57 | 99.37 | 99.36 |
| C6 | 84.77 | 98.20 | 99.26 | 99.53 | 96.85 | 98.70 | 98.90 |
| C7 | 92.65 | 99.70 | 95.30 | 99.06 | 98.40 | 99.70 | 99.86 |
| C8 | 77.99 | 98.00 | 70.73 | 94.72 | 95.52 | 96.11 | 99.00 |
| C9 | 99.27 | 95.86 | 89.62 | 99.73 | 99.60 | 99.50 | 99.51 |
| OA(%) | 82.96 | 93.88 | 92.38 | 94.86 | 95.83 | 96.24 | 98.19 |
| AA(%) | 86.77 | 95.03 | 91.32 | 95.86 | 96.62 | 96.52 | 98.36 |
| KA(%) | 78.21 | 92.04 | 90.05 | 93.32 | 94.56 | 95.09 | 97.63 |
| Time(s) | 98.80 | 100.61 | 137.69 | 107.55 | 322.54 | 224.29 | 210.24 |
| Class Type | KSRC | MV | KJSRC | CRF | CKEMAP | SSG | SSGL |
|---|---|---|---|---|---|---|---|
| C01 | 95.69 | 100 | 100 | 100 | 99.03 | 99.18 | 99.04 |
| C02 | 85.09 | 79.43 | 80.61 | 88.30 | 88.39 | 90.22 | 95.35 |
| C03 | 90.62 | 97.94 | 97.94 | 98.31 | 97.08 | 98.02 | 98.27 |
| C04 | 46.78 | 63.05 | 50.92 | 56.90 | 86.86 | 45.48 | 88.49 |
| C05 | 61.64 | 82.76 | 82.63 | 82.30 | 87.63 | 80.13 | 92.57 |
| C06 | 45.58 | 73.04 | 69.45 | 60.05 | 89.08 | 35.02 | 99.12 |
| C07 | 83.54 | 92.83 | 100 | 98.99 | 89.29 | 99.09 | 100 |
| C08 | 89.29 | 99.12 | 99.29 | 98.78 | 98.07 | 98.26 | 99.05 |
| C09 | 96.01 | 98.42 | 98.42 | 98.42 | 98.54 | 98.34 | 98.34 |
| C10 | 95.30 | 87.08 | 87.57 | 100 | 99.19 | 99.63 | 99.71 |
| C11 | 94.30 | 86.83 | 90.65 | 98.94 | 97.74 | 96.71 | 97.14 |
| C12 | 88.05 | 100 | 78.07 | 97.17 | 97.04 | 95.30 | 97.63 |
| C13 | 99.84 | 100 | 100 | 100 | 100 | 100 | 100 |
| OA(%) | 88.45 | 93.01 | 90.70 | 94.35 | 96.63 | 92.15 | 98.01 |
| AA(%) | 82.44 | 89.27 | 87.35 | 90.63 | 94.46 | 87.34 | 97.29 |
| KA(%) | 87.12 | 92.19 | 89.60 | 93.69 | 96.25 | 91.22 | 97.78 |
| Time(s) | 111.68 | 116.40 | 576.78 | 153.00 | 626.01 | 192.24 | 198.11 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Xiao, Z.; Chen, Y.; Yang, J. Spatial-Spectral Graph Regularized Kernel Sparse Representation for Hyperspectral Image Classification. ISPRS Int. J. Geo-Inf. 2017, 6, 258. https://doi.org/10.3390/ijgi6080258
Liu J, Xiao Z, Chen Y, Yang J. Spatial-Spectral Graph Regularized Kernel Sparse Representation for Hyperspectral Image Classification. ISPRS International Journal of Geo-Information. 2017; 6(8):258. https://doi.org/10.3390/ijgi6080258
Chicago/Turabian StyleLiu, Jianjun, Zhiyong Xiao, Yufeng Chen, and Jinlong Yang. 2017. "Spatial-Spectral Graph Regularized Kernel Sparse Representation for Hyperspectral Image Classification" ISPRS International Journal of Geo-Information 6, no. 8: 258. https://doi.org/10.3390/ijgi6080258
APA StyleLiu, J., Xiao, Z., Chen, Y., & Yang, J. (2017). Spatial-Spectral Graph Regularized Kernel Sparse Representation for Hyperspectral Image Classification. ISPRS International Journal of Geo-Information, 6(8), 258. https://doi.org/10.3390/ijgi6080258






