Template Matching and Simplification Method for Building Features Based on Shape Cognition
Abstract
1. Introduction
2. Related Work
2.1. General Building Simplification
2.2. Shape Recognition in Building Simplification
3. Methodology
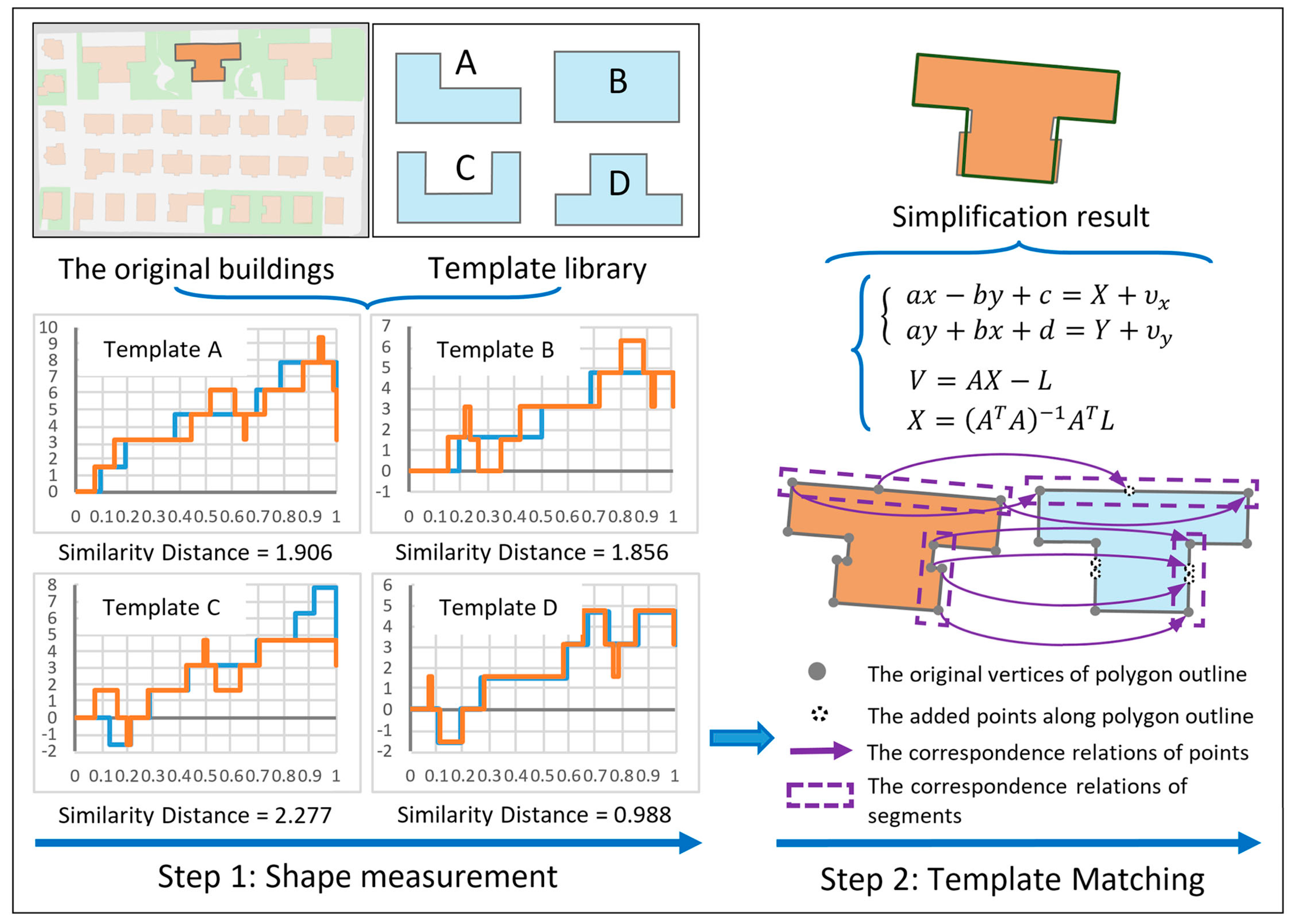
3.1. The Creation of Templates
- Simple Shape: Simple shape uses some basic geometrics to represent buildings abstractly. Typically, buildings have a rectangular geometric form and could even be represented by the minimum bounding rectangle after generalization. Thus, we could employ a rectangle as a template where orthogonality and parallelism could also be imposed.
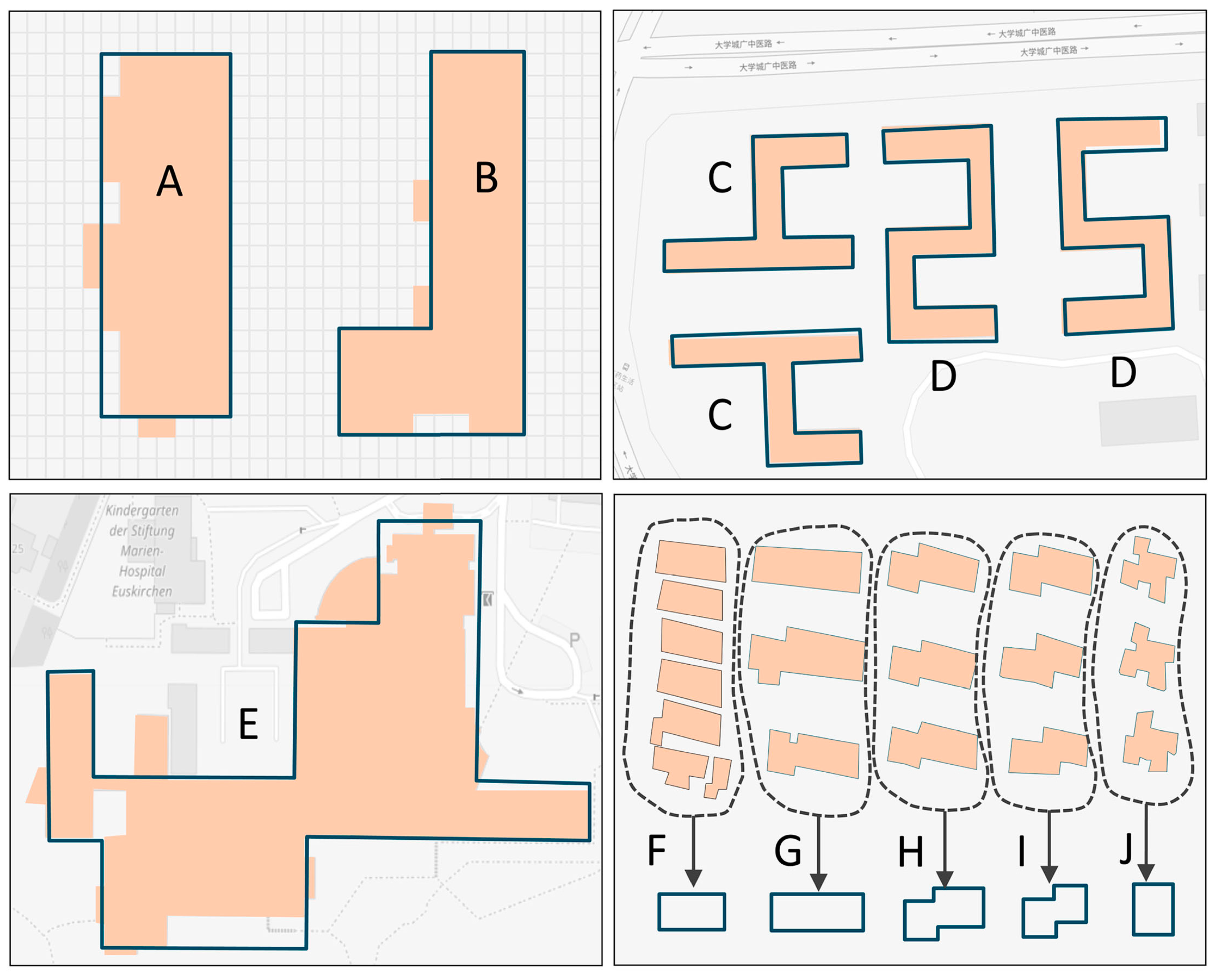
- Symbolic Shape: A symbolic shape template tries to depict the recognized objects through some imaginable and familiar things to make them easier to understand and be communicated. It is an effective way to enrich the template library by introducing some alphabetic letters, e.g., “E” “T” “Z” “U”, or a familiar animal.
- Composite Shape: Some complex structures can hardly be represented by a simple or symbolic template and, thus, the composite shape template should be employed. Such a template has a higher level of abstraction and symbolism and can infuse some more complicated characteristics by arranging different components [43], for example, contextual and humanistic characteristics.
- Automatic Extracted Shape: Manually creating templates may be tedious and time-consuming; thus, some automated method can be introduced to template generation, such as information extraction and shape classification. Similar objects can be extracted from the training samples as templates and used to match buildings within regions with similar environmental patterns.
3.2. Building Simplification Using the Template Matching Method
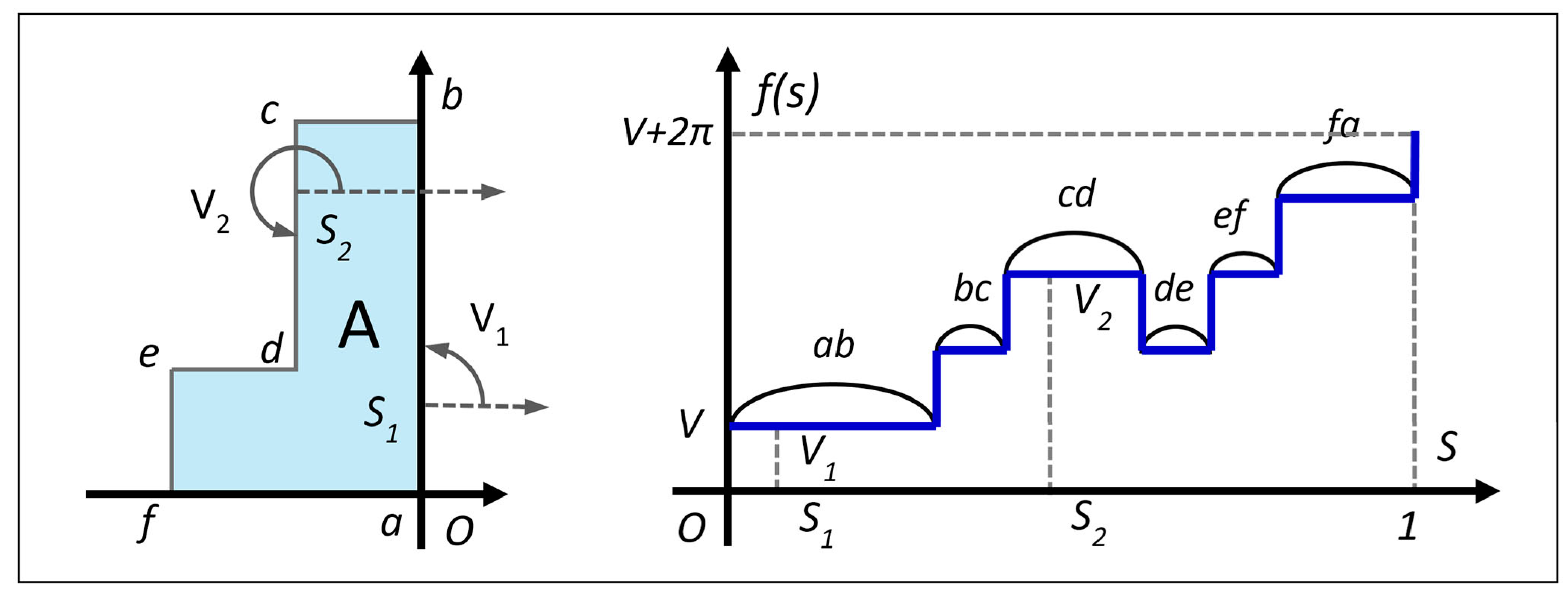
3.2.1. Shape Measurement Based on the Turning Function
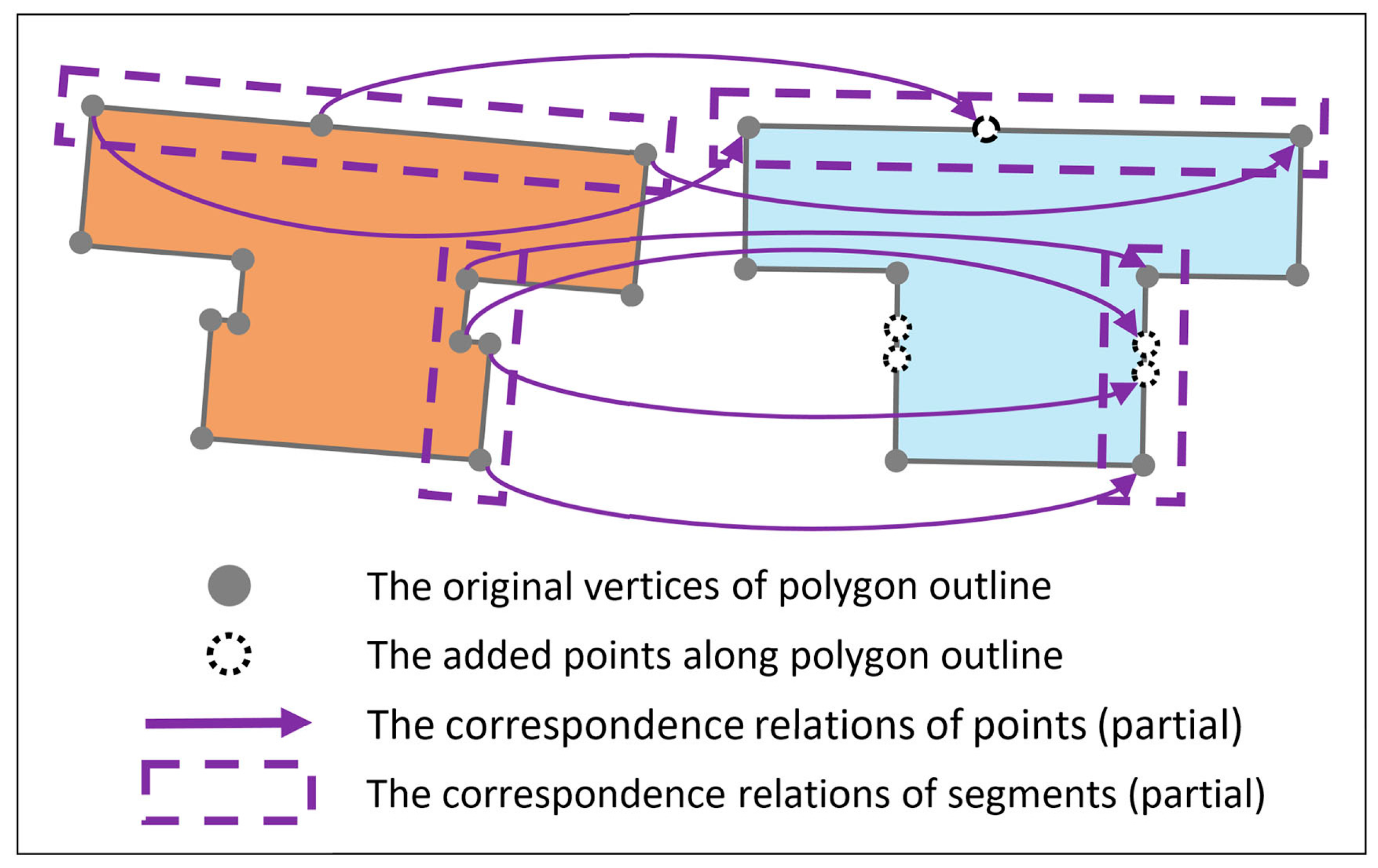
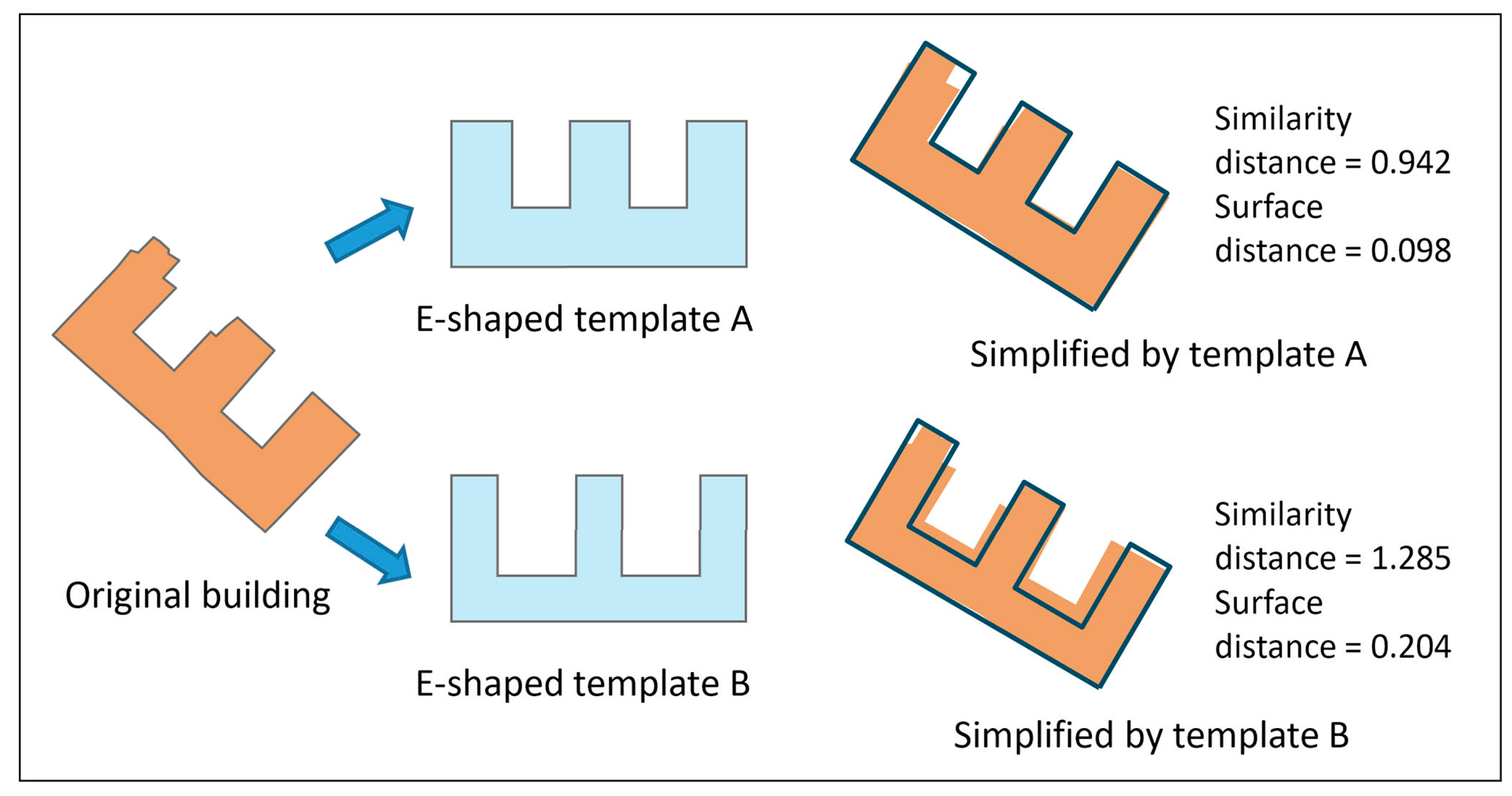
3.2.2. Template Matching Based on Least-Squares Adjustment
4. Experiments and Discussion
4.1. Quality Assessment of Simplification
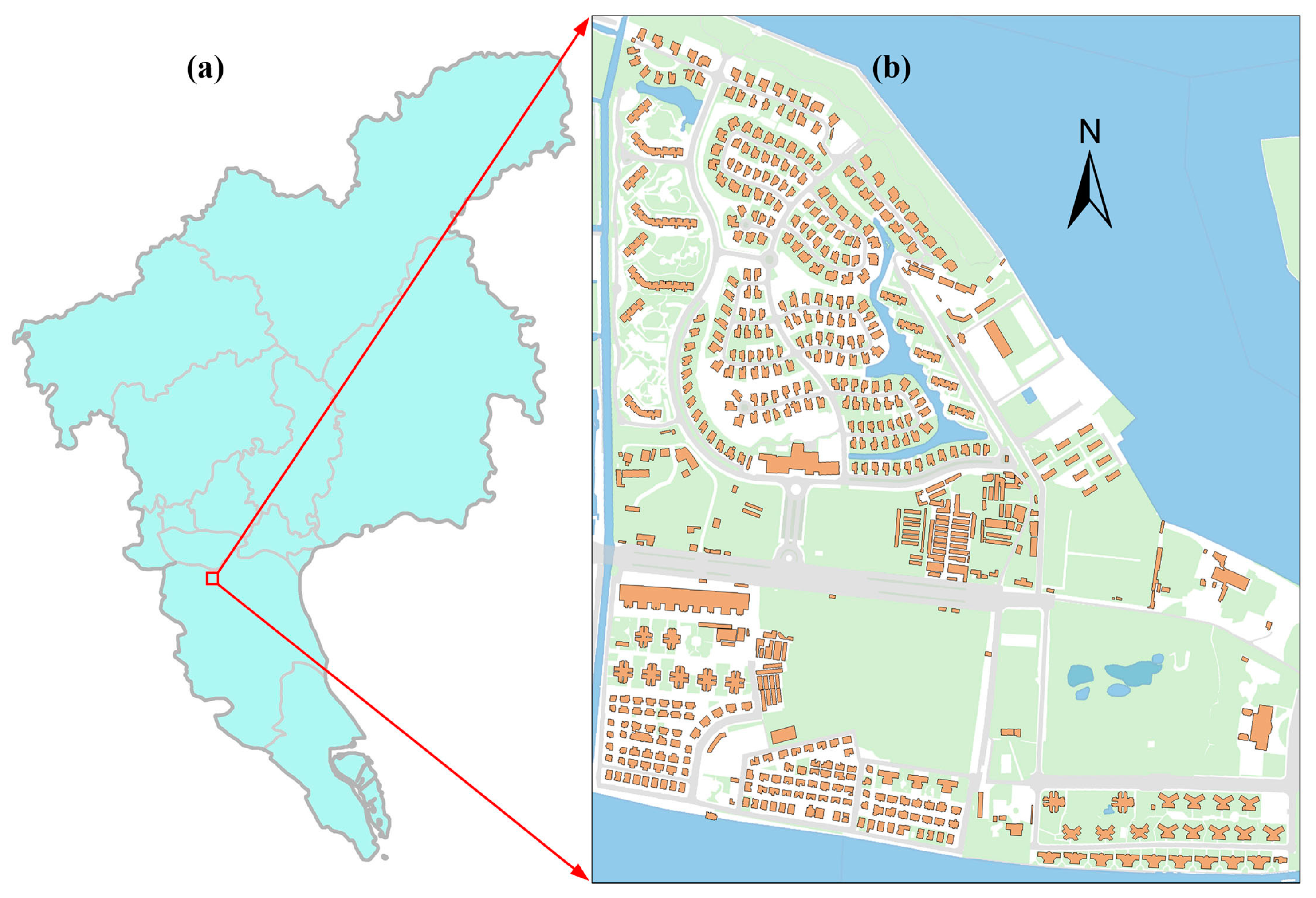
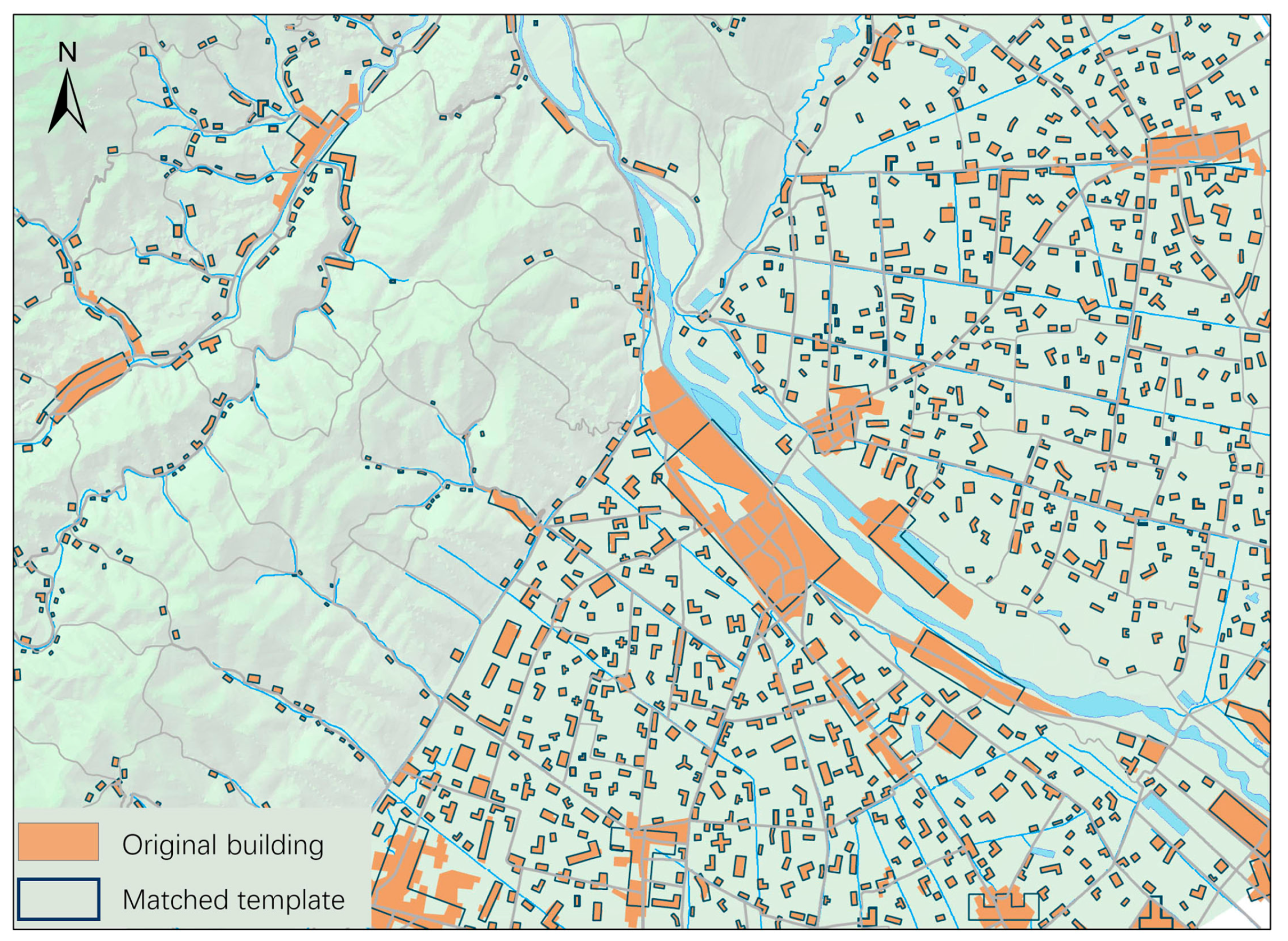
4.1.1. Experimental Datasets and Templates
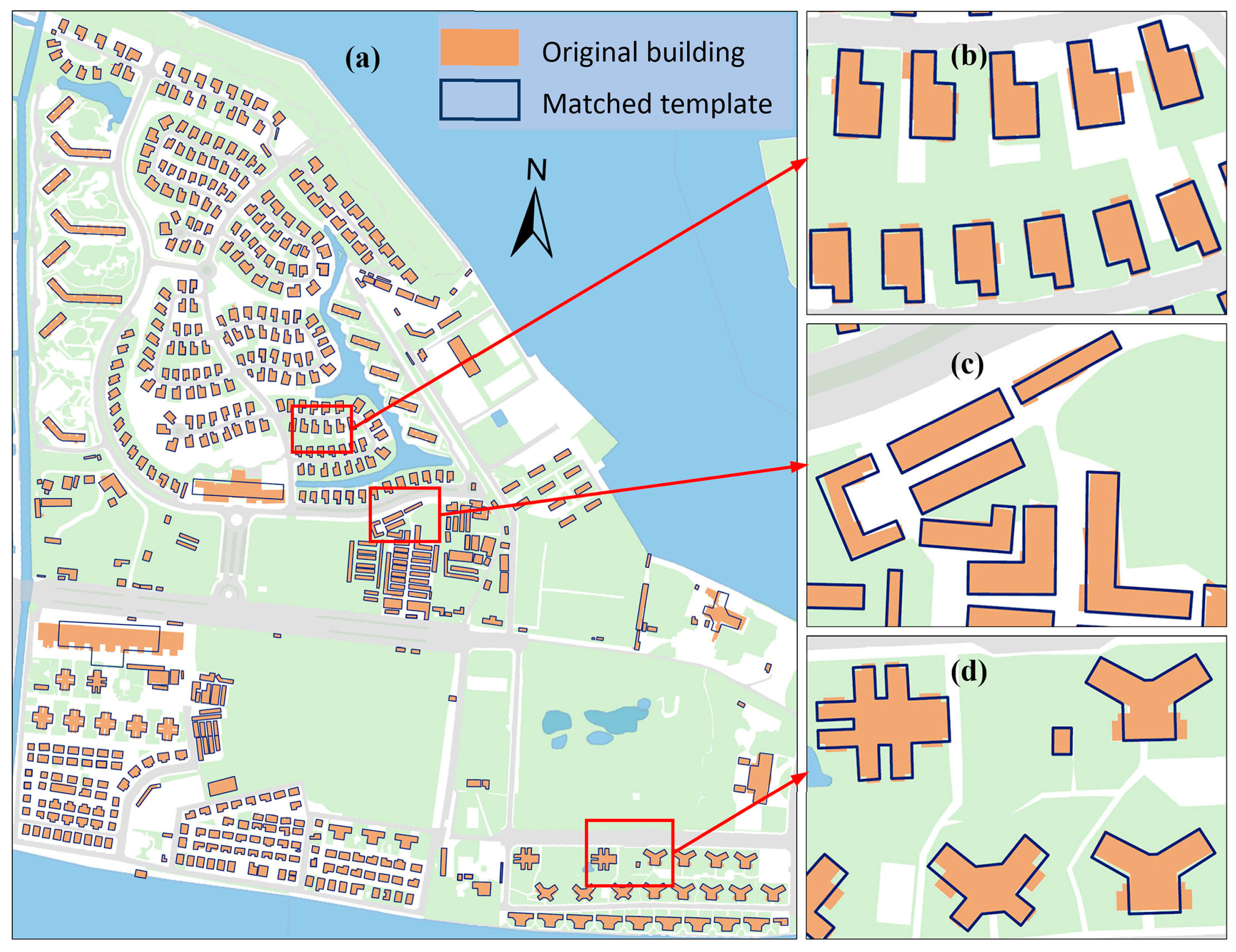
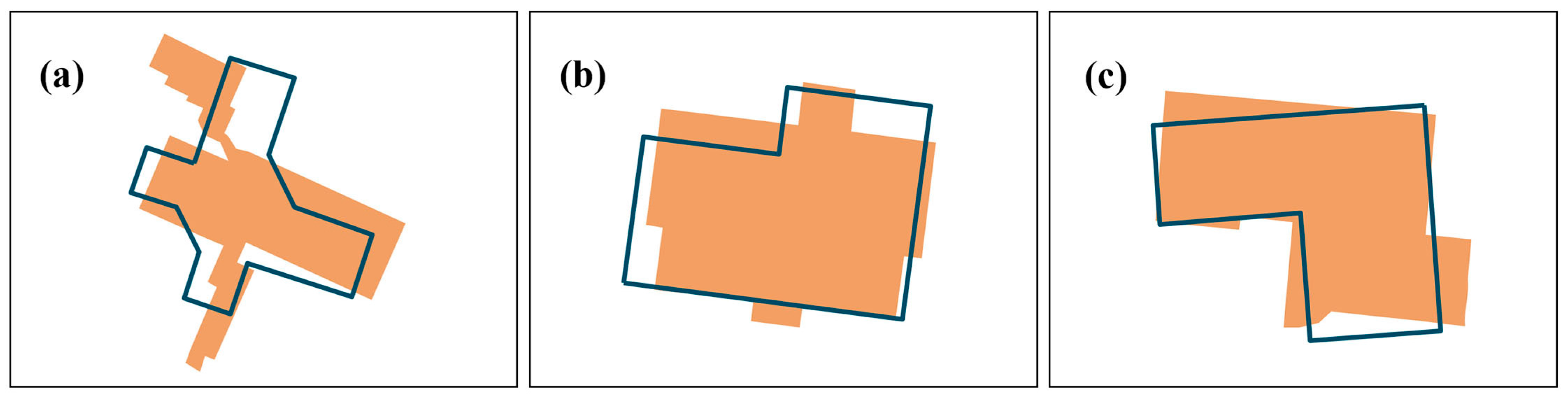
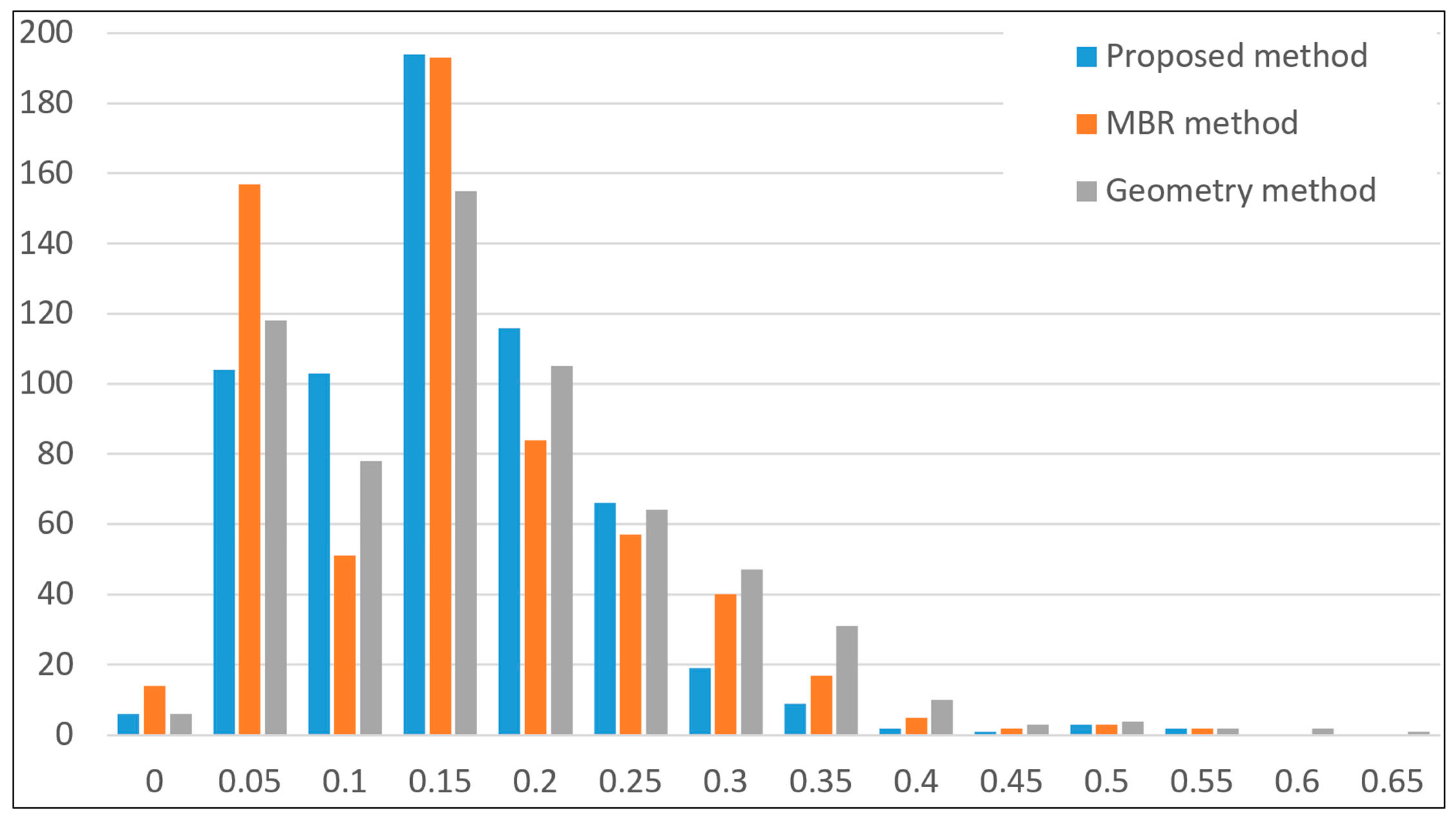
4.1.2. Qualitative and Statistical Evaluation
4.2. Discussion of the Scaling of Template Matching
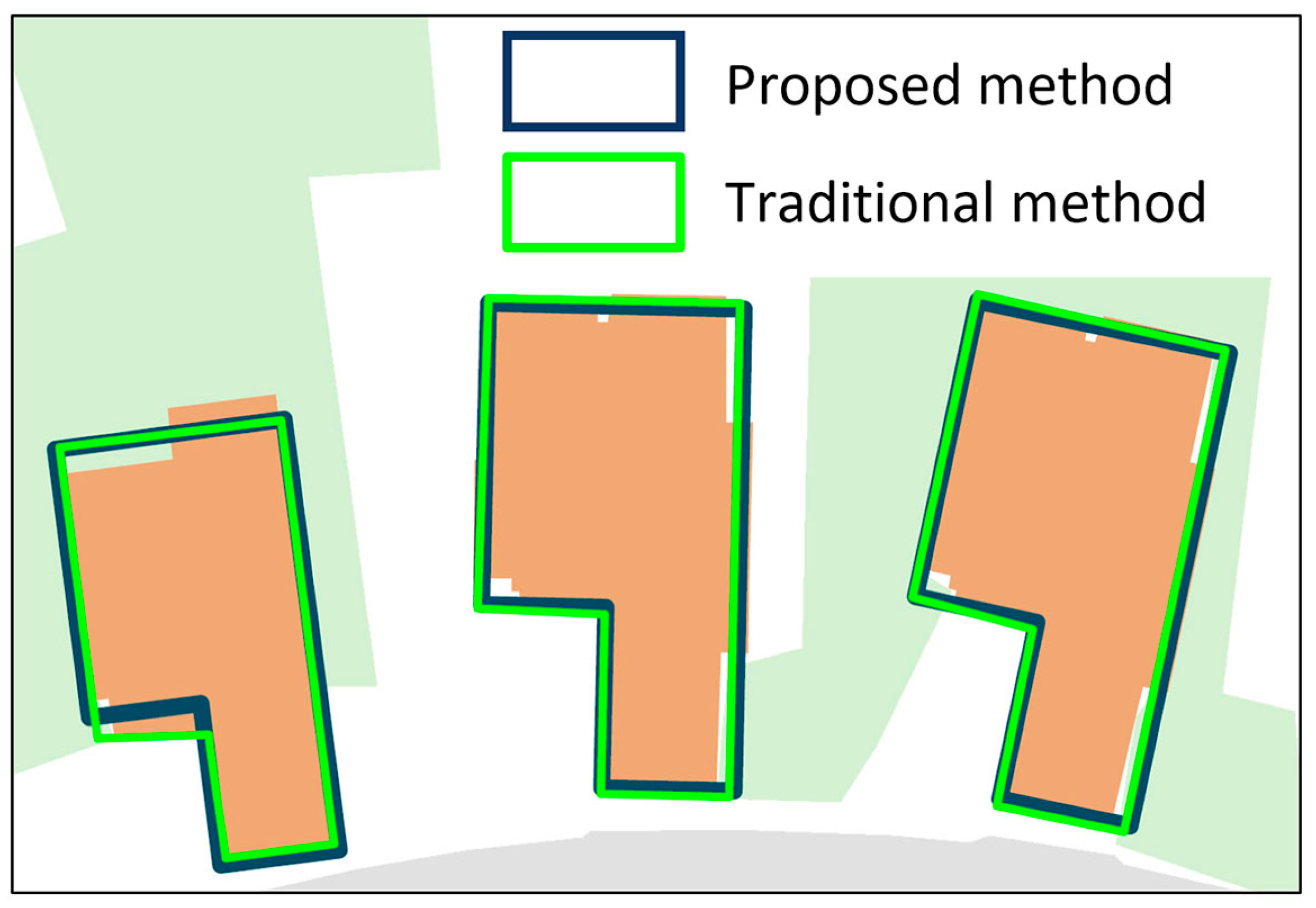
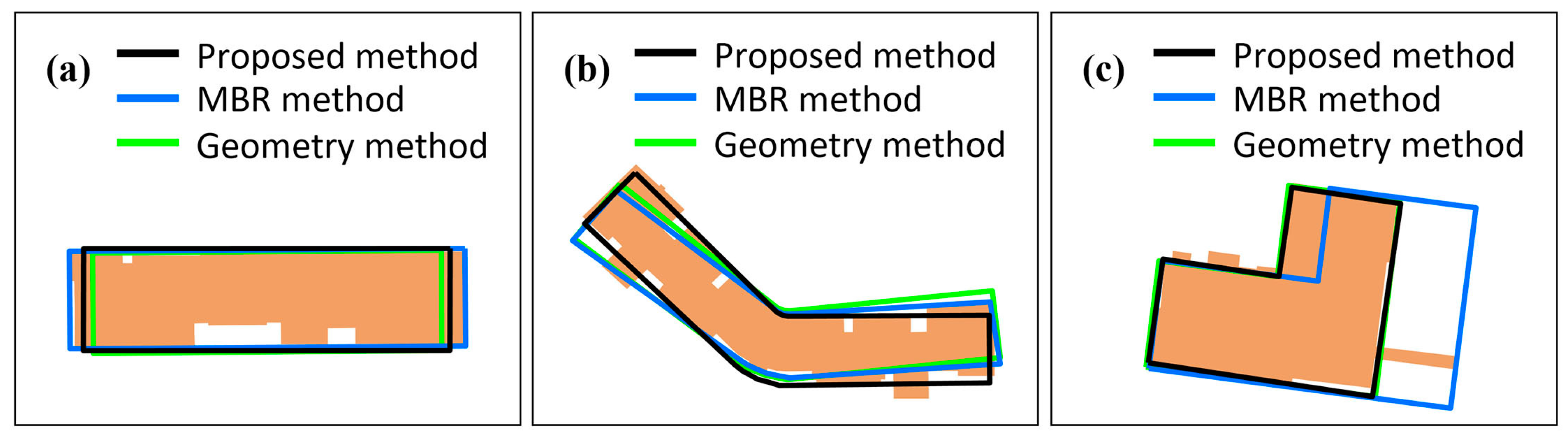
4.3. Comparison with Existing Methods
5. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ai, T.; Cheng, X.; Liu, P.; Yang, M. A shape analysis and template matching of building features by the Fourier transform method. Comput. Environ. Urban Syst. 2013, 41, 219–233. [Google Scholar] [CrossRef]
- Ai, T.; Ke, S.; Yang, M.; Li, J. Envelop generation and simplification of polylines using Delaunay triangulation. Int. J. Geogr. Inf. Sci. 2017, 31, 297–319. [Google Scholar] [CrossRef]
- Lokhat, I.; Touya, G. Enhancing building footprints with squaring operations. J. Spat. Inf. Sci. 2016, 13, 1–28. [Google Scholar]
- Mackaness, W.; Burghardt, D.; Duchêne, C. Map generalisation: Fundamental to the modelling and understanding of geographic space. In Abstracting Geographic Information in a Data Rich World; Burghardt, D., Duchêne, C., Machaness, W., Eds.; Springer: Cham, Switzerland, 2014; pp. 1–15. [Google Scholar]
- Ai, T.; Guo, R. Polygon cluster pattern mining based on Gestalt principles. Acta Geod. Cartogr. Sin. 2007, 36, 302–308. [Google Scholar]
- Steiniger, S.; Taillandier, P.; Weibel, R. Utilising urban context recognition and machine learning to improve the generalisation of buildings. Int. J. Geogr. Inf. Sci. 2010, 24, 253–282. [Google Scholar] [CrossRef]
- Du, S.; Shu, M.; Feng, C. Representation and discovery of building patterns: A three-level relational approach. Int. J. Geogr. Inf. Sci. 2016, 30, 1161–1186. [Google Scholar] [CrossRef]
- Ai, T.; Zhang, X.; Zhou, Q.; Yang, M. A vector field model to handle the displacement of multiple conflicts in building generalization. Int. J. Geogr. Inf. Sci. 2015, 29, 1310–1331. [Google Scholar] [CrossRef]
- Yu, W.; Ai, T.; Liu, P.; Cheng, X. The analysis and measurement of building patterns using texton co-occurrence matrices. Int. J. Geogr. Inf. Sci. 2017, 31, 1–22. [Google Scholar] [CrossRef]
- Gaffuri, J.; Trévisan, J. Role of urban patterns for building generalisation: An application of AGENT. In Proceedings of the 8th ICA Workshop on Generalisation and Multiple representation, Leicester, UK, 20–21 August 2004. [Google Scholar]
- Gong, X.; Wu, F. A typification method for linear pattern in urban building generalization. Geocarto Int. 2016, 1–19. [Google Scholar] [CrossRef]
- Zhang, X.; Ai, T.; Stoter, J.; Kraal, M.; Molenaar, M. Building pattern recognition in topographic data: Examples on collinear and curvilinear alignments. Geoinformatica 2013, 17, 1–33. [Google Scholar] [CrossRef]
- Yang, W. Identify building patterns. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing, Beijing, China, 3–11 July 2008. [Google Scholar]
- Li, Z.; Yan, H.; Ai, T.; Chen, J. Automated building generalization based on urban morphology and Gestalt theory. Int. J. Geogr. Inf. Sci. 2004, 18, 513–534. [Google Scholar] [CrossRef]
- Buchin, K.; Meulemans, W.; Renssen, A.; Speckmann, B. Area-preserving simplification and schematization of polygonal subdivisions. ACM Trans. Spat. Algorithms Syst. 2016, 2, 1–35. [Google Scholar] [CrossRef]
- Chen, W.; Long, Y.; Shen, J.; Li, W. Structure recognition and progressive simplification of the concaves of building polygon based on constrained D-TIN. Geomat. Inf. Sci. Wuhan Univ. 2011, 36, 584–587. [Google Scholar]
- Xu, W.; Long, Y.; Zhou, T.; Chen, L. Simplification of building polygon based on adjacent four-point method. Acta Geod. Cartogr. Sin. 2013, 42, 929–936. [Google Scholar]
- Damen, J.; van Kreveld, M.; Spaan, B. High quality building generalization by extending the morphological operators. In Proceedings of the 12th ICA Workshop on Generalisation and Multiple Representation, Montpellier, France, 20–21 June 2008. [Google Scholar]
- Meijers, M. Building simplification using offset curves obtained from the straight skeleton. In Proceedings of the 19th ICA workshop on Generalisation and Multiple Representation, Helsinki, Finland, 14 June 2016. [Google Scholar]
- Guo, R.; Ai, T. Simplification and aggregation of building polygon in automatic map generalization. J. Wuhan Technol. Univ. Surv. Map. 1999, 25, 25–30. [Google Scholar]
- Kada, M. Aggregation of 3D buildings using a hybrid data approach. Cartogr. Geogr. Inf. Sci. 2011, 38, 153–160. [Google Scholar] [CrossRef]
- Wang, H.; Wu, F.; Zhang, L.; Deng, H. The application of mathematical morphology and pattern recognition to building polygon simplification. Acta Geod. Cartogr. Sin. 2005, 34, 269–276. [Google Scholar]
- Sester, M. Optimization approaches for generalization and data abstraction. Int. J. Geogr. Inf. Sci. 2005, 19, 871–897. [Google Scholar] [CrossRef]
- Sester, M. Generalization based on least squares adjustment. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing, Amsterdam, The Netherlands, 16–23 July 2000. [Google Scholar]
- Bayer, T. Automated building simplification using a recursive approach. In Cartography in Central and Eastern Europe; Gartner, G., Ortag, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 121–146. [Google Scholar]
- Liu, P.; Ai, T.; Deng, J. Simplification and rectangularity of building-polygon based on least squares adjustment. J. China Univ. Min. Technol. 2008, 37, 699–704. [Google Scholar]
- Haunert, J.H.; Wolff, A. Optimal and topologically safe simplification of building footprints. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 3–5 November 2010. [Google Scholar]
- Cheng, B.; Liu, Q.; Li, X.; Wang, Y. Building simplification using backpropagation neural networks: A combination of cartographers’ expertise and raster-based local perception. GISci. Remote Sens. 2013, 50, 527–542. [Google Scholar]
- MacEachren, A. Compactness of geographic shape: Comparison and evaluation of measures. Geogr. Ann. Ser. B-Hum. Geogr. 1985, 67, 53–67. [Google Scholar] [CrossRef]
- Wentz, E.A. Shape analysis in GIS. In Proceedings of the Auto-Carto, Seattle, WA, USA, 7–10 April 1997. [Google Scholar]
- Belongie, S.; Malik, J.; Puzicha, J. Shape matching and object recognition using shape contexts. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 509–522. [Google Scholar] [CrossRef]
- Persoon, E.; Fu, K.S. Shape discrimination using Fourier descriptors. IEEE Trans. Syst. Man Cybern. 1977, 7, 170–179. [Google Scholar] [CrossRef]
- Arkin, E.M.; Chew, L.P.; Huttenlocher, D.P.; Kedem, K.; Mitchell, J.S. An efficiently computable metric for comparing polygonal shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 209–216. [Google Scholar] [CrossRef]
- Rainsford, D.; Mackaness, W. Template matching in support of generalisation of rural buildings. In Advances in Spatial Data Handling, Proceedings of the 10th International Symposium on Spatial Data Handling, Ottawa, ON, Canada, 9–12 July 2002; Richardson, D.E., van Oosterom, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 137–151. [Google Scholar]
- Sabo, M.N.; Bédard, Y.; Bernier, E. Methodology for developing a database of geometric patterns to better support on-the-fly map generalization. In Proceedings of the 22th International Cartographic Conference, A Coruna, Spain, 9–16 July 2005. [Google Scholar]
- Sabo, M.N.; Bédard, Y.; Moulin, B.; Bernier, E. Toward self-generalizing objects and on-the-fly map generalization. Cartogr. Int. J. Geogr. Inf. Geovis. 2008, 43, 155–173. [Google Scholar] [CrossRef]
- Liu, P.; Ai, T.; Hu, J.; Cheng, X. Building-polygon simplification based on shape matching of prototype template. Geomat. Inf. Sci. Wuhan Univ. 2010, 35, 1369–1372. [Google Scholar]
- Li, H.; Wang, Y.; Yu, Z. Template match of buildings and results analysis. In Proceedings of the 18th IEEE International Conference on Geoinformatics, Beijing, China, 18–20 June 2010. [Google Scholar]
- Yan, X.; Ai, T.; Yang, M. A simplification of residential feature by the shape cognition and template matching method. Acta Geod. Cartogr. Sin. 2016, 45, 874–882. [Google Scholar]
- Mackaness, W.; Edwards, G. The importance of modeling pattern and structure in automated map generalization. In Proceedings of the Joint ISPRS/ICA Workshop on Multi-Scale Representations of Spatial Data, Ottawa, ON, Canada, 7–8 July 2002. [Google Scholar]
- Haunert, J.H. A symmetry detector for map generalization and urban-space analysis. ISPRS J. Photogramm. Remote Sens. 2012, 74, 66–77. [Google Scholar] [CrossRef]
- Weibel, R.; Dutton, G. Constraint-based automated map generalization. In Proceedings of the 8th International Symposium on Spatial Data Handling, Vancouver, BC, Canada, 12–15 July 1998. [Google Scholar]
- Biederman, I. Recognition-by-components: A theory of human image understanding. Psychol. Rev. 1987, 94, 115. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Zipf, A.; Fu, Q.; Neis, P. Quality assessment for building footprints data on OpenStreetMap. Int. J. Geogr. Inf. Sci. 2014, 28, 700–719. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Collins, J. Global Positioning System Theory and Practice, 5th ed.; Springer: Vienna, Austria, 2001; pp. 229–251. [Google Scholar]
- Nöllenburg, M.; Merrick, D.; Wolff, A.; Benkert, M. Morphing polylines: A step towards continuous generalization. Comput. Environ. Urban Syst. 2008, 32, 248–260. [Google Scholar] [CrossRef]
- Vauglin, F.; Bel Hadj Ali, A. Geometric matching of polygonal surfaces in GISs. In Proceedings of the ASPRS Annual Meeting, Tampa, FL, USA, 30 March–3 April 1998. [Google Scholar]
- Duchêne, C.; Bard, S.; Barillot, X.; Ruas, A.; Trévisan, J.; Holzapfel, F. Quantitative and qualitative description of building orientation. In Proceedings of the 7th ICA Workshop on Progress in Automated Map Generalisation, Paris, France, 28–30 April 2003. [Google Scholar]
| Categories | Template | |||
|---|---|---|---|---|
| Simple template | Square-shaped | Rectangle-shaped | General-shaped | General-shaped |
 |  |  |  | |
| Symbolic template | U-shaped | Y-shaped | T-shaped | L-shaped |
 |  |  |  | |
| Composite shape |  |  |  |  |
| I-Shaped Template | T-Shaped Template | |
|---|---|---|
 |  | |
| Building to be simplified | Similarity Dis = 2.167 Surface Dis = Null | Similarity Dis = 2.083 Surface Dis = 0.500 |
 |  |  |
| Mean | Median | Standard Deviation | Maximum | Minimum | |
|---|---|---|---|---|---|
| Proposed method | 0.126 | 0.126 | 0.075 | 0.520 | 0.0 |
| MBR method | 0.123 | 0.122 | 0.093 | 0.522 | 0.0 |
| Geometry method | 0.144 | 0.131 | 0.097 | 0.610 | 0.0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Ai, T.; Zhang, X. Template Matching and Simplification Method for Building Features Based on Shape Cognition. ISPRS Int. J. Geo-Inf. 2017, 6, 250. https://doi.org/10.3390/ijgi6080250
Yan X, Ai T, Zhang X. Template Matching and Simplification Method for Building Features Based on Shape Cognition. ISPRS International Journal of Geo-Information. 2017; 6(8):250. https://doi.org/10.3390/ijgi6080250
Chicago/Turabian StyleYan, Xiongfeng, Tinghua Ai, and Xiang Zhang. 2017. "Template Matching and Simplification Method for Building Features Based on Shape Cognition" ISPRS International Journal of Geo-Information 6, no. 8: 250. https://doi.org/10.3390/ijgi6080250
APA StyleYan, X., Ai, T., & Zhang, X. (2017). Template Matching and Simplification Method for Building Features Based on Shape Cognition. ISPRS International Journal of Geo-Information, 6(8), 250. https://doi.org/10.3390/ijgi6080250






