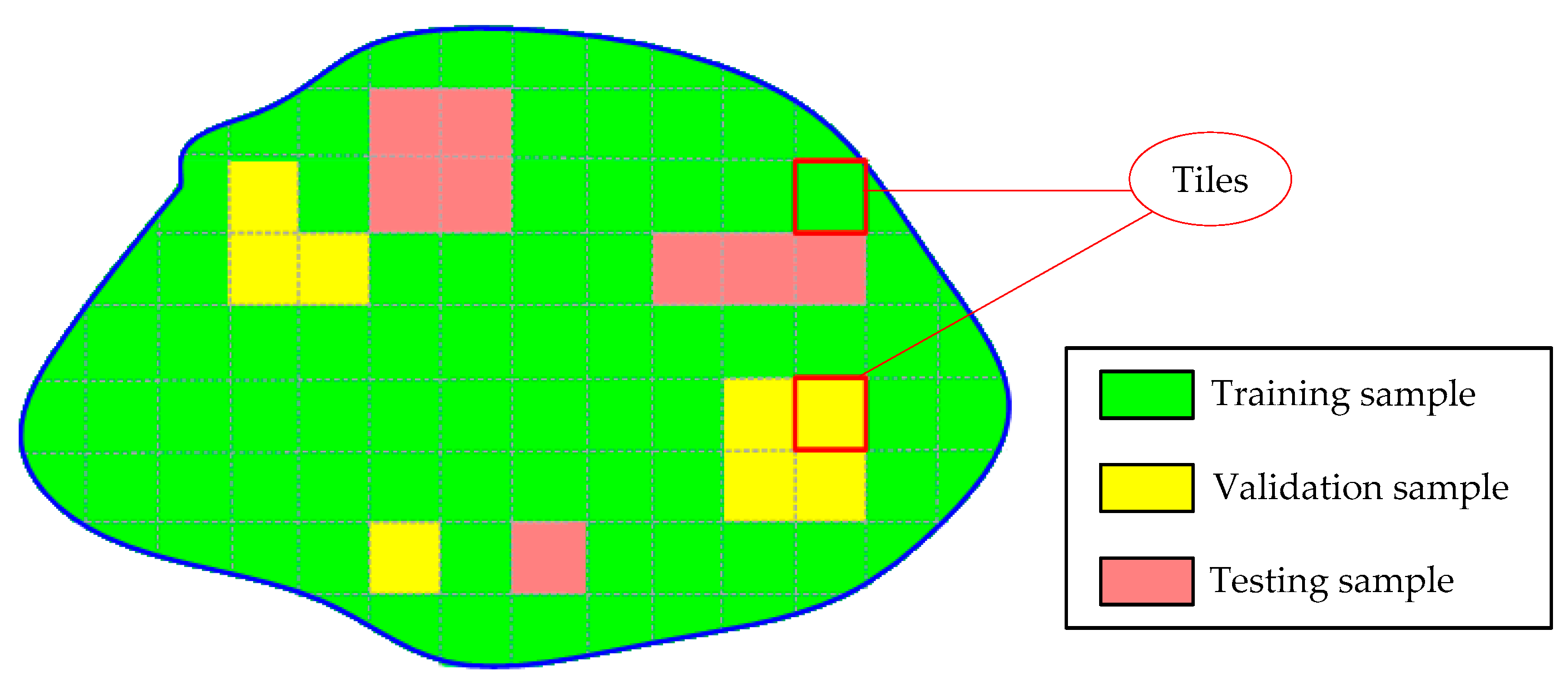
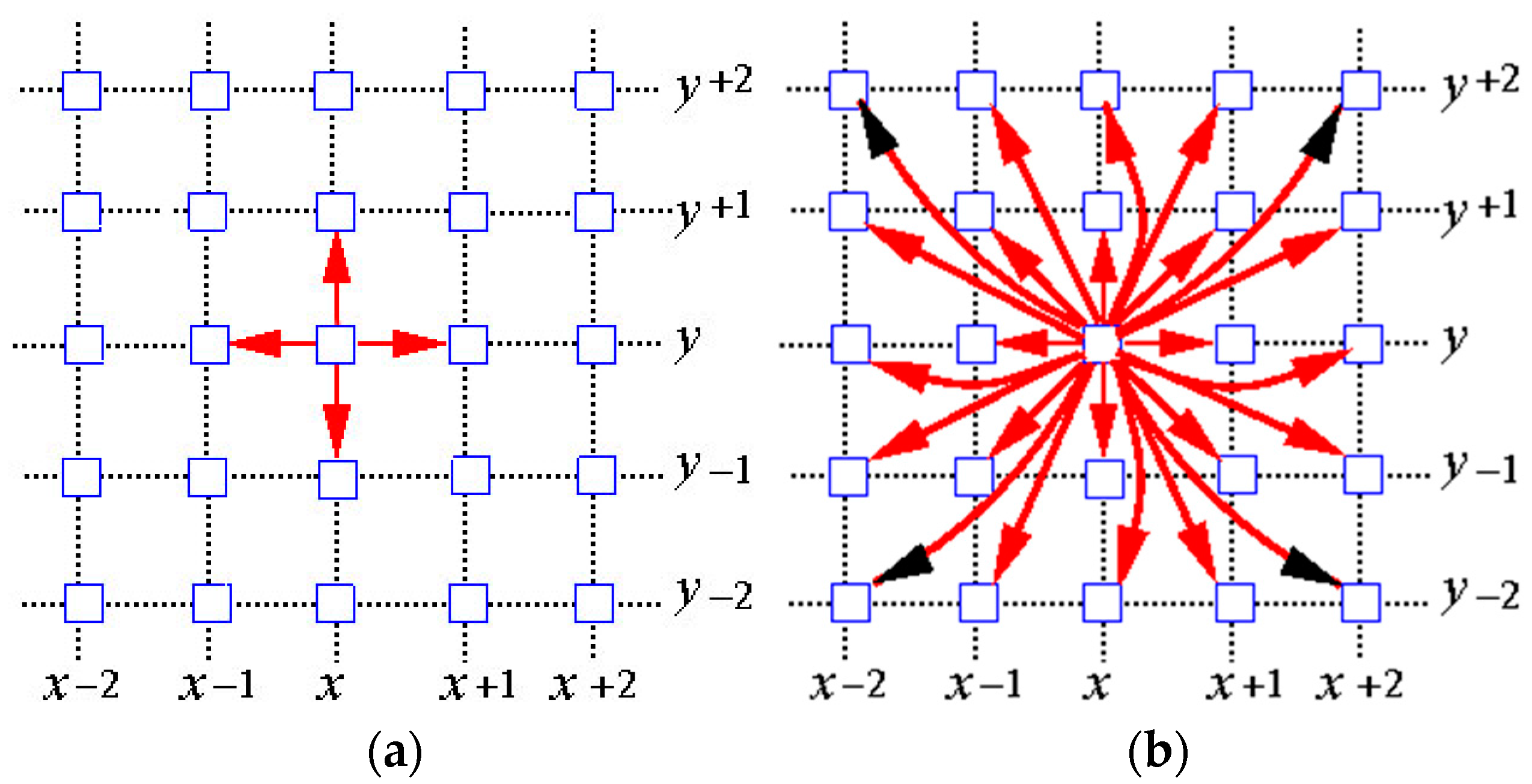
1. Introduction
As one of the most challenging and important problems in the remote sensing community, high-resolution remote sensing data classification is very useful for many applications such as geographical database construction, digital map updating, 3D building reconstruction, land cover mapping and change detection. The objective of this kind of classification task is to assign an object class to each spatial position recorded by the given data. Although many different algorithms have been proposed in the past, many of the problems related to the classification task have not been solved [
1]. Based on different criteria, the existing classification methods can be categorized into several groups. A brief review of these existing methods is provided in the following.
According to the types of data sources employed, the existing methods can be categorized into image-based classification, 3D point cloud-based classification and data fusion-based classification. Image-based classification only makes use of the available multispectral or hyperspectral image as the sole data source in the classification, as done in previous studies [
2,
3]. Three dimensional points acquired by light detection and ranging (LIDAR) and dense image matching techniques [
4,
5] are other effective data sources for classification. For example, Vosselman [
6] used high-density point clouds of urban scenes to identify buildings, vegetation, vehicles, the ground, and water. Zhang et al. [
7] used the geometry, radiometry, topology and echo characteristics of airborne LIDAR point cloud to perform an object-based classification. To exploit the complementary characteristics of multisource data, data fusion based methods are also popular and have been proven to be more reliable than the single-source data methods used by many researchers [
8]. For example, both images and 3D geometry data have been used in several previous studies [
9,
10,
11,
12].
In terms of the basic element employed in the classification process, the existing methods can be categorized as object-based and pixel/point-based. Object-based methods typically use a cascade of bottom-up data segmentation and regional classification, which makes the system commit to potential errors from the front-end segmentation system [
13]. For instance, Gerke [
14] first segmented an image into small super-pixels and then extracted the features of each super-pixel to input to an AdaBoost classifier. Zhang et al. [
7] first grouped points into segments using a surface growing algorithm then classified the segments using a support vector machine (SVM) classifier. Pixel/point-based methods leave out the segmentation process and directly classify each pixel or point. However, due to the lack of contextual information, the classified results usually seem noisy. As a remedial measure, a conditional random field (CRF) is usually used to smooth the classification result. For example, both Marmanis et al. [
15] and Paisitkriangkrai et al. [
1] used deep convolutional neural networks (CNN) to classify each pixel, then used a CRF to refine the results, whereas Niemeyer et al. [
16] first classified each 3D point using a random forest (RF) classifier then smoothed them using a CRF.
Based on the classifiers used, the existing methods can be divided into two types: unsupervised and supervised. For the unsupervised methods, expert knowledge of each class is usually summarized and used to classify the data into different categories. For instance, a rule-based hierarchical classification scheme that utilizes spectral, geometry and topology knowledge of different classes was used by both Rau et al. [
9] and Speldekamp et al. [
17] to classify different data. For the supervised methods, samples with labeled ground truth data are first used to train a statistical classifier (e.g., AdaBoost, SVM and RF), then the samples without labels are classified by this learned classifier. Previously, samples from small areas have been used to train the classifier, and the features of these samples have all been designed manually [
7,
16,
18]. More recently, with the progress of sensor technology, an increasing amount of high quality remote sensing data are available for research. At the same time, progress in graphic processing unit (GPU) and parallel computing technology has significantly increased the computing capability, such that learning a more complicated classifier with a larger amount of training data has becomes accessible to more researchers. Specifically, one of the most successful practices in this direction was the launch of deep CNN (convolutional neural networks) [
19,
20,
21,
22] in the computer vision community, which has become the dominant method for visual recognition and semantic classification [
13,
23,
24,
25,
26]. Furthermore, one of the most distinct characteristics of CNN is its ability to automatically learn the most suitable features, which has made the manual feature extraction process that is used in the traditional supervised-based classification methods unnecessary. Although there exists great differences between the data used in the computer vision community and the data used in the remote sensing community, some researchers [
1,
27] have found that the CNN models trained by the computer vision community generalize the remote sensing data and some of the features learned by the models were more discriminative than the hand-crafted features.
To promote the scientific progress of remote sensing data classification, the international society for photogrammetry and remote sensing (ISPRS) launched a semantic labeling benchmark [
28] in 2014. Using the datasets provided by the benchmark, different classification methods can be evaluated and compared conveniently. We have observed an interesting phenomenon from these evaluated classification methods. On the one hand, the performances of the CNN-based methods are generally better than the non-CNN-based methods. On the other hand, the non-CNN-based methods generally use fewer training samples than the CNN-based methods. As a result, we want to explore whether the notable gap between the non-CNN and CNN-based methods can be reduced by training a traditional supervised classifier with a larger training dataset.
It is widely known that for CNN-based methods, more benefits are gained when more training data are available. However, too many training samples may lead to disaster for some traditional supervised classifiers. For example, SVMs trained by a large-scale dataset often suffer from large memory storage requirements and extensive time consumption, since an SVM solves a complex dual quadratic optimization problem [
29]. In addition, the existence of too many support vectors makes the solving process extremely slow [
30]. Although the RF and AdaBoost classifiers can theoretically handle a large-scale dataset, the large memory storage and computational load still hamper their applications to big training datasets. To tackle this problem and take full advantage of the information in the large-scale dataset, an RF-based ensemble learning strategy is proposed by combining several RF classifiers together in the present study. Ensemble learning or a multiple classifier system (MCS) is well established in remote sensing and has shown great potential to improve the accuracy and reliability of remote sensing data classification over the last two decades [
31,
32,
33]. For example, Waske et al. [
34] fused two SVM classifiers to classify both optical imagery and synthetic aperture radar data, and each data source was treated separately and classified by an independent SVM. Experiments have shown that their fusion method outperforms many approaches and significantly improves the results of a single SVM that was trained on the whole multisource dataset. Ceamanos et al. [
35] designed a classifier ensemble to classify hyperspectral data. Spectral bands of the hyperspectral image were first divided into several subgroups according to their similarities. Then, each group was used to train an individual SVM classifier. Finally, an additional SVM classifier was used to combine these classifiers together. The results also demonstrated the effectiveness of their model fusion scheme. Recently, several fusion methods have investigated the dependence among detectors or classifiers. For example, Vergara et al. [
36] derived the optimum fusion rule of N non-independent detectors in terms of the individual probabilities of detection and false alarms and defined the dependence factors. This could be a future line of research in the remote sensing community. In the present study, remote sensing data (both multispectral images and 3D geometry data) are first divided into tiles. Then, some of them are selected and labeled by a human operator. After that, each selected and labeled tile is used to train an individual RF model. Finally, a Bayesian weighted average method [
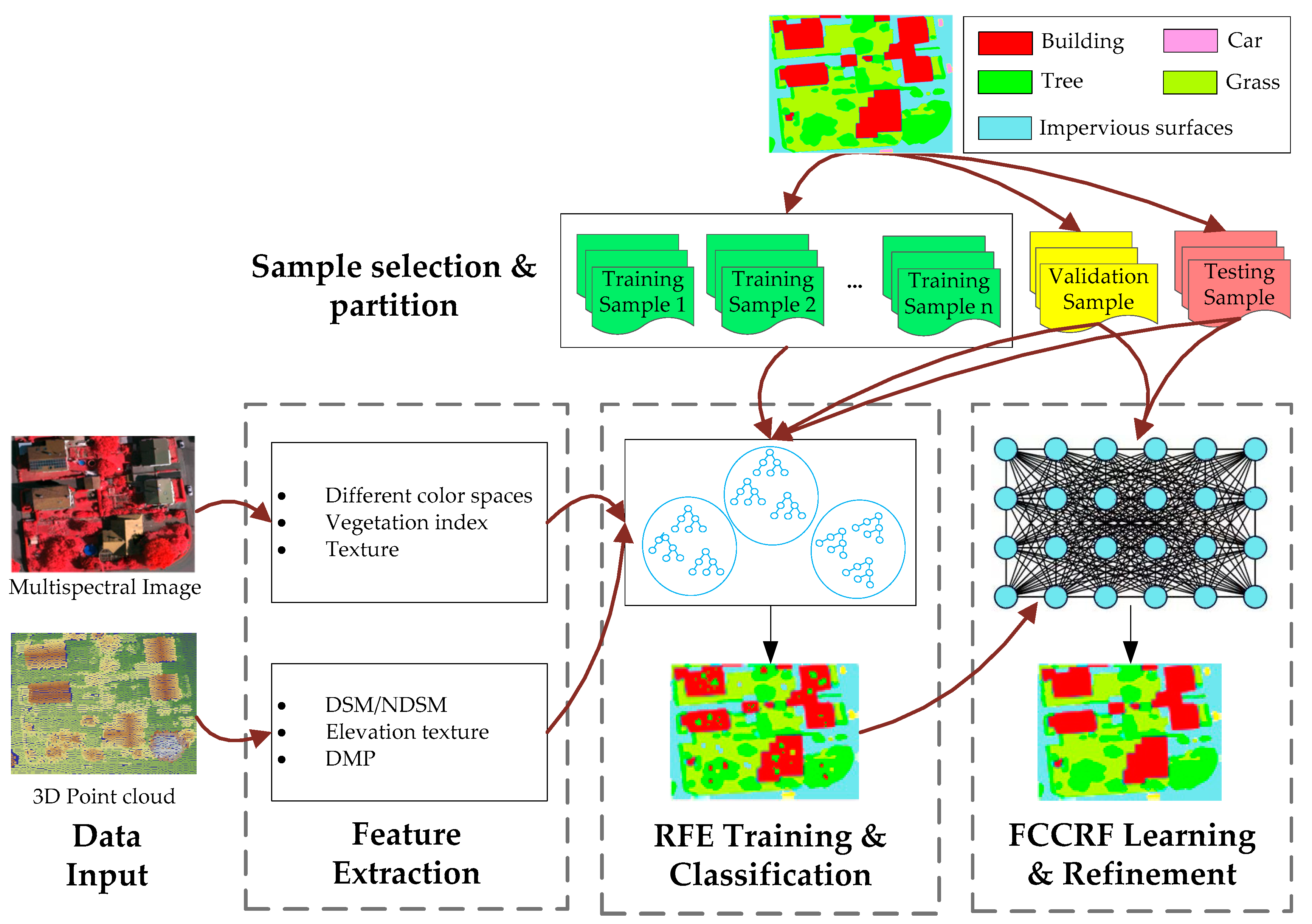
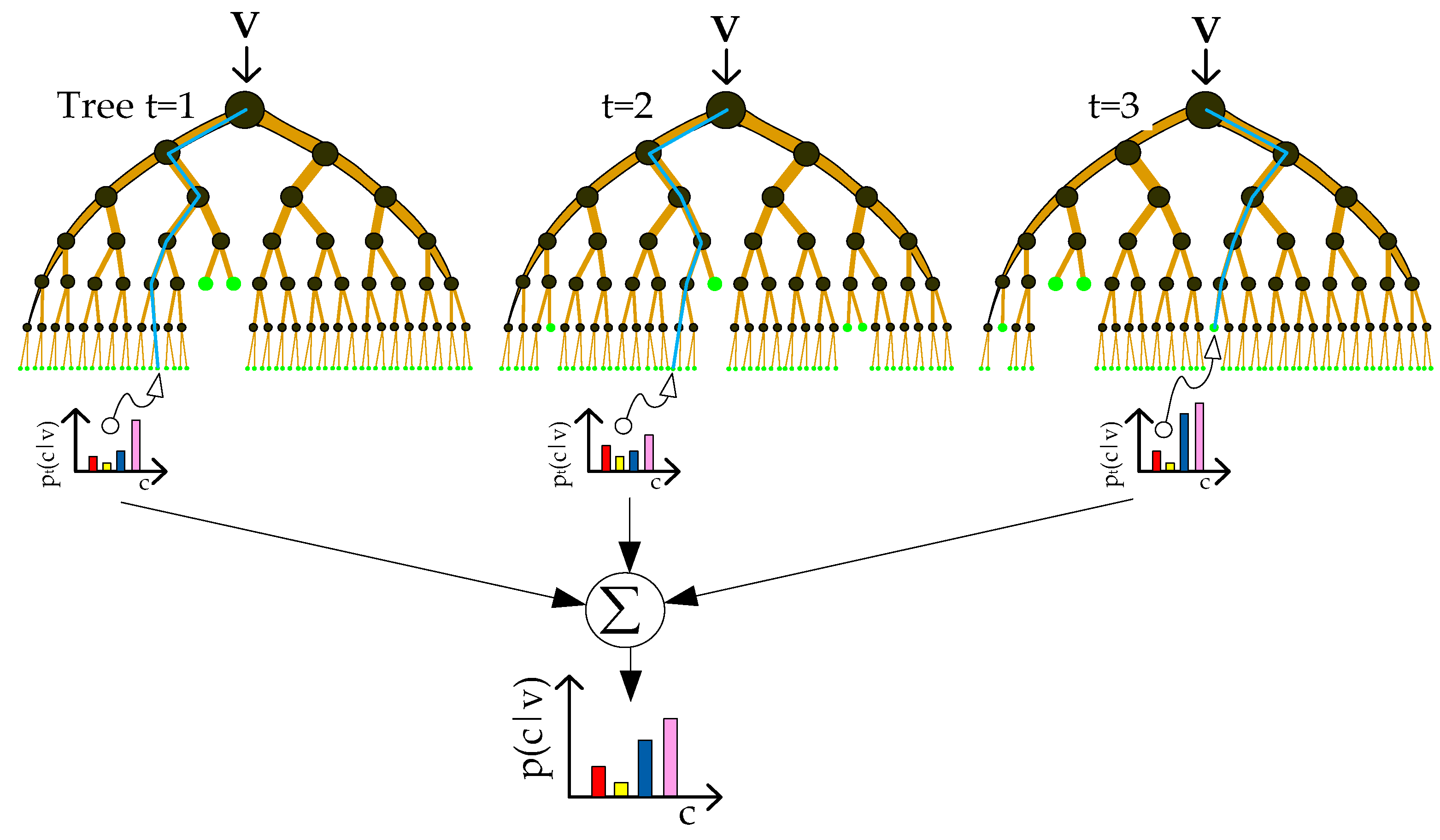
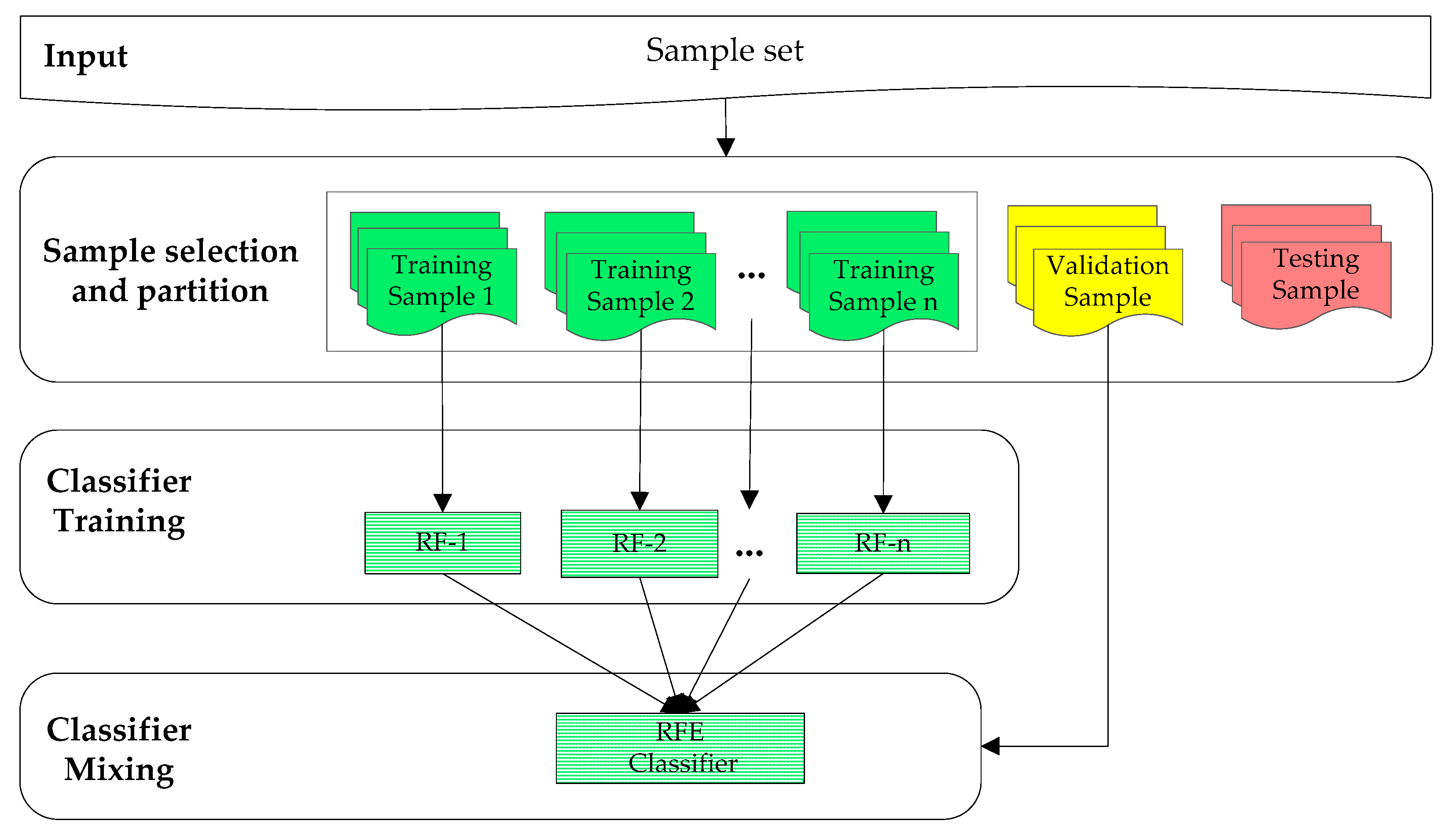
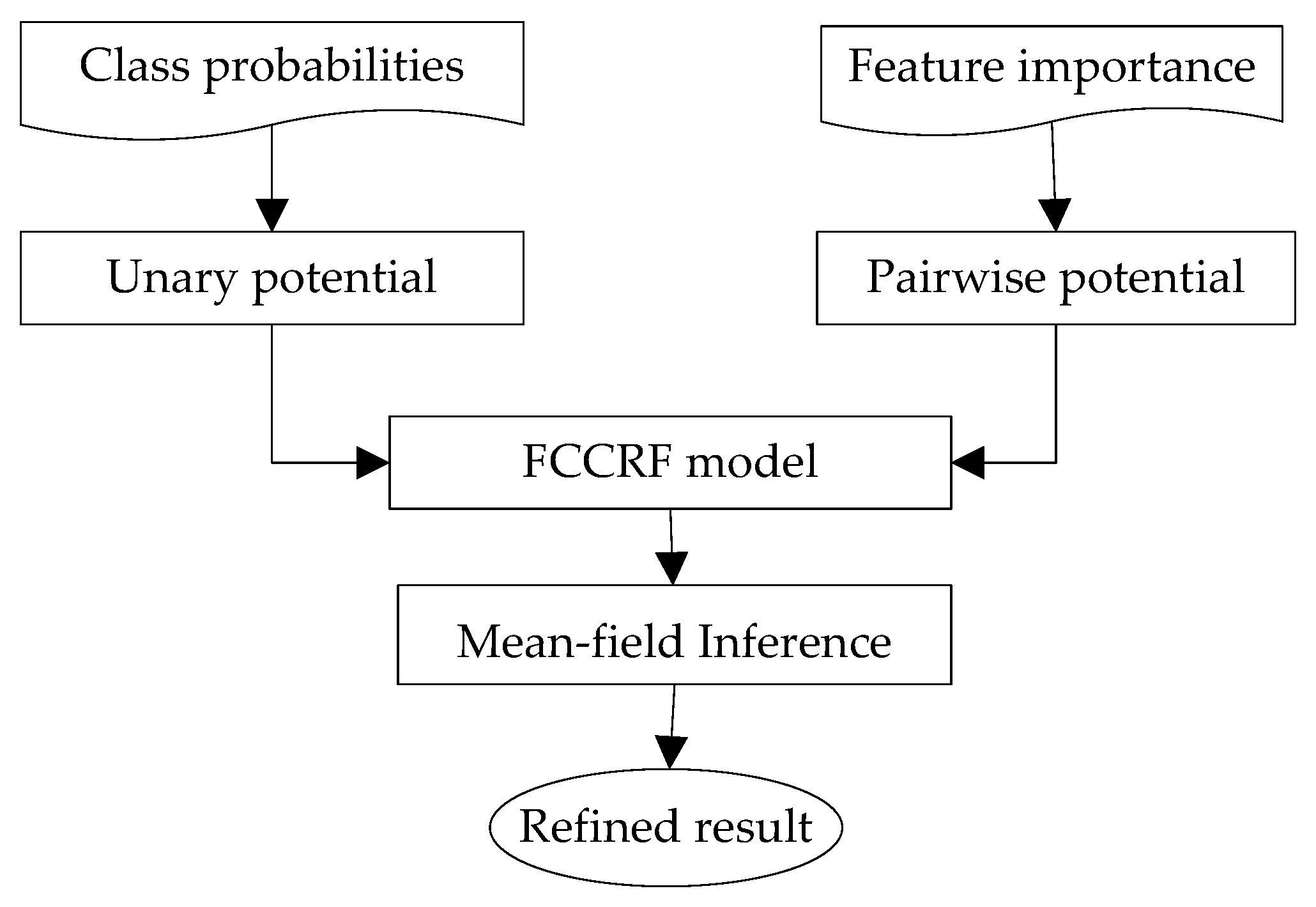
31] is employed to combine these individual RF models into a global classifier. In addition, to take full advantage of the contextual information in the data, an effective fully connected conditional random field (FCCRF) model is constructed and optimized to refine the classified results.
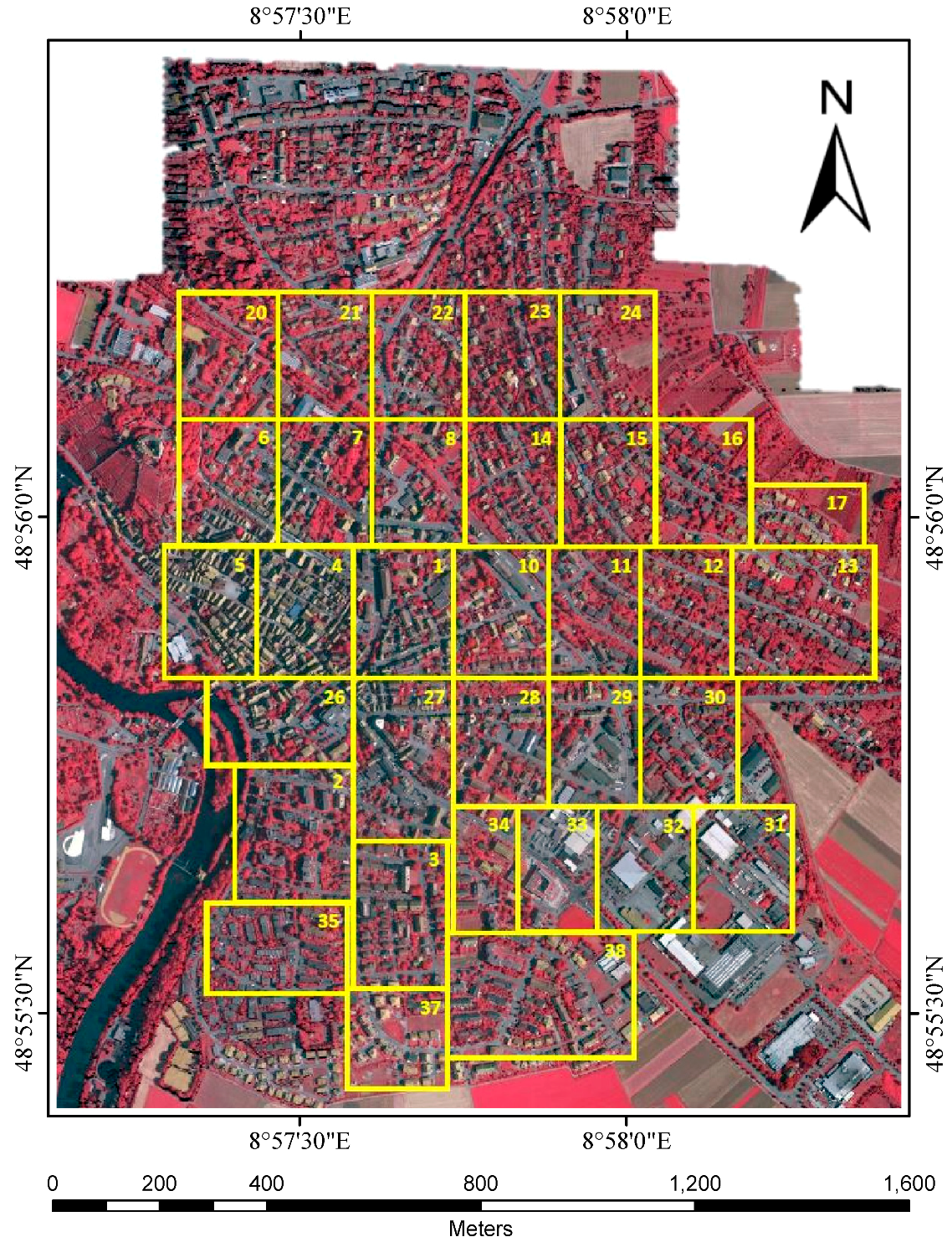
In general, the present study describes a pixel-based, supervised and data fusion-based method. The main contributions of the current study are three-fold. First, a new RF ensemble learning strategy is introduced to explore the information in the large-scale training dataset. Second, through utilizing the contextual information, an improved FCCRF graph model is designed to refine the classification result. Third, an efficient pipeline is designed and parallelized to classify the multisource remote sensing data. By testing the method on the ISPRS Semantic Labeling Contest, we achieved the highest overall accuracy among the non-CNN-based methods, which provides a state-of-the-art method and reduces the gap between the non-CNN and CNN-based methods.
The rest of this paper is organized as follows. In
Section 2, details of the presented high-resolution remote sensing data classification method are elaborated. Then, experimental evaluation and analysis are reported in
Section 3, and followed by some concluding remarks and future work in
Section 4.
4. Conclusions
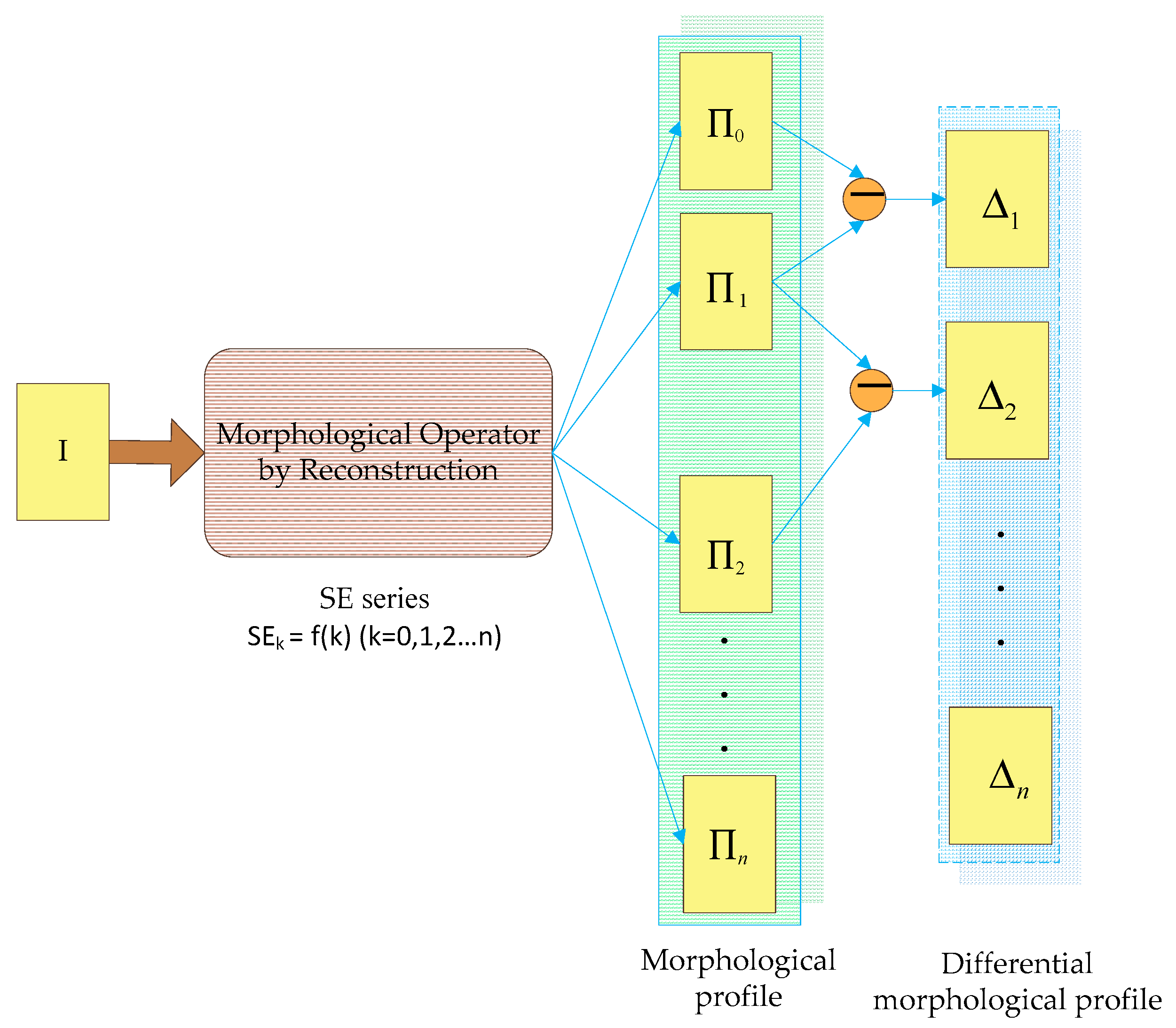
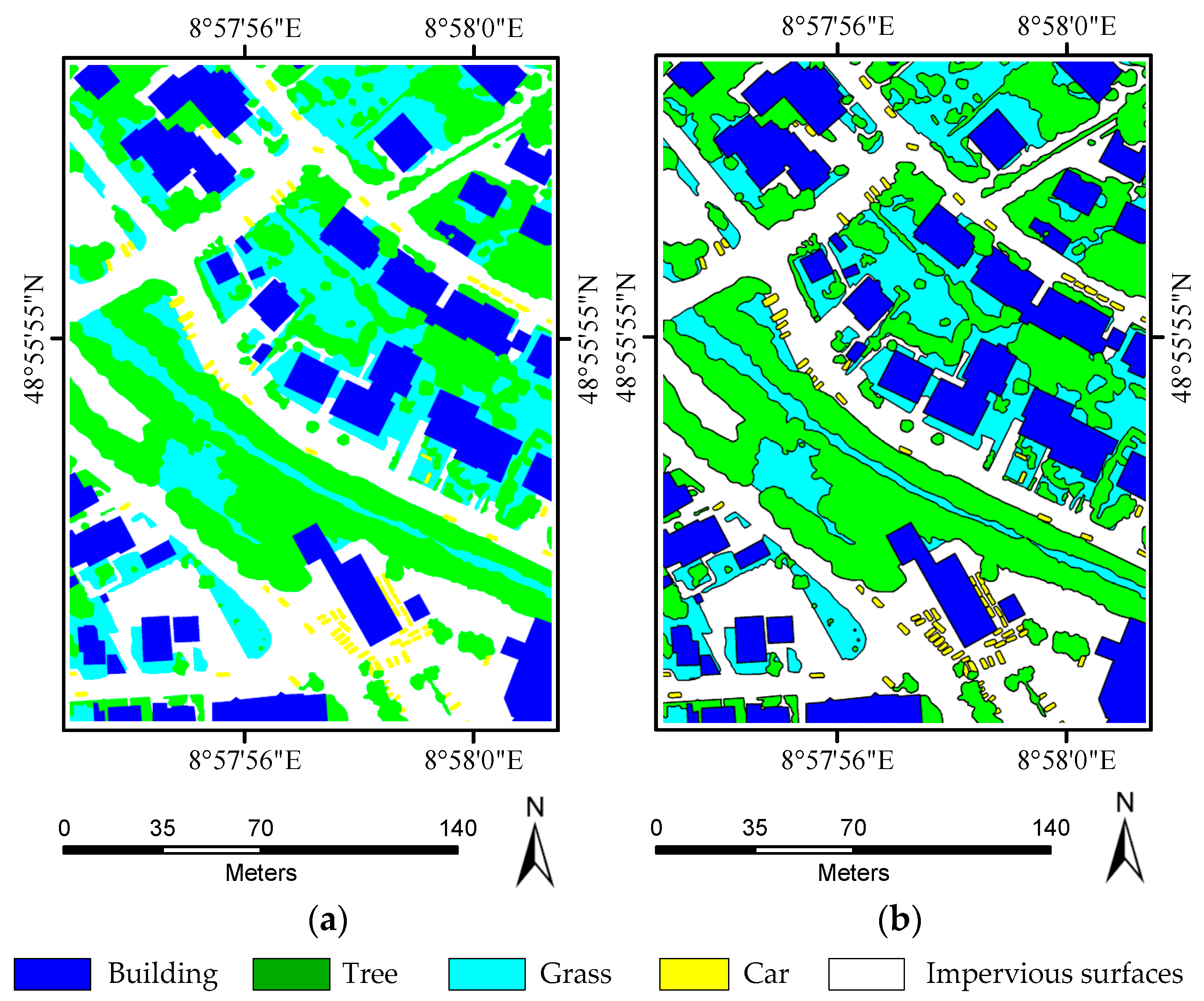
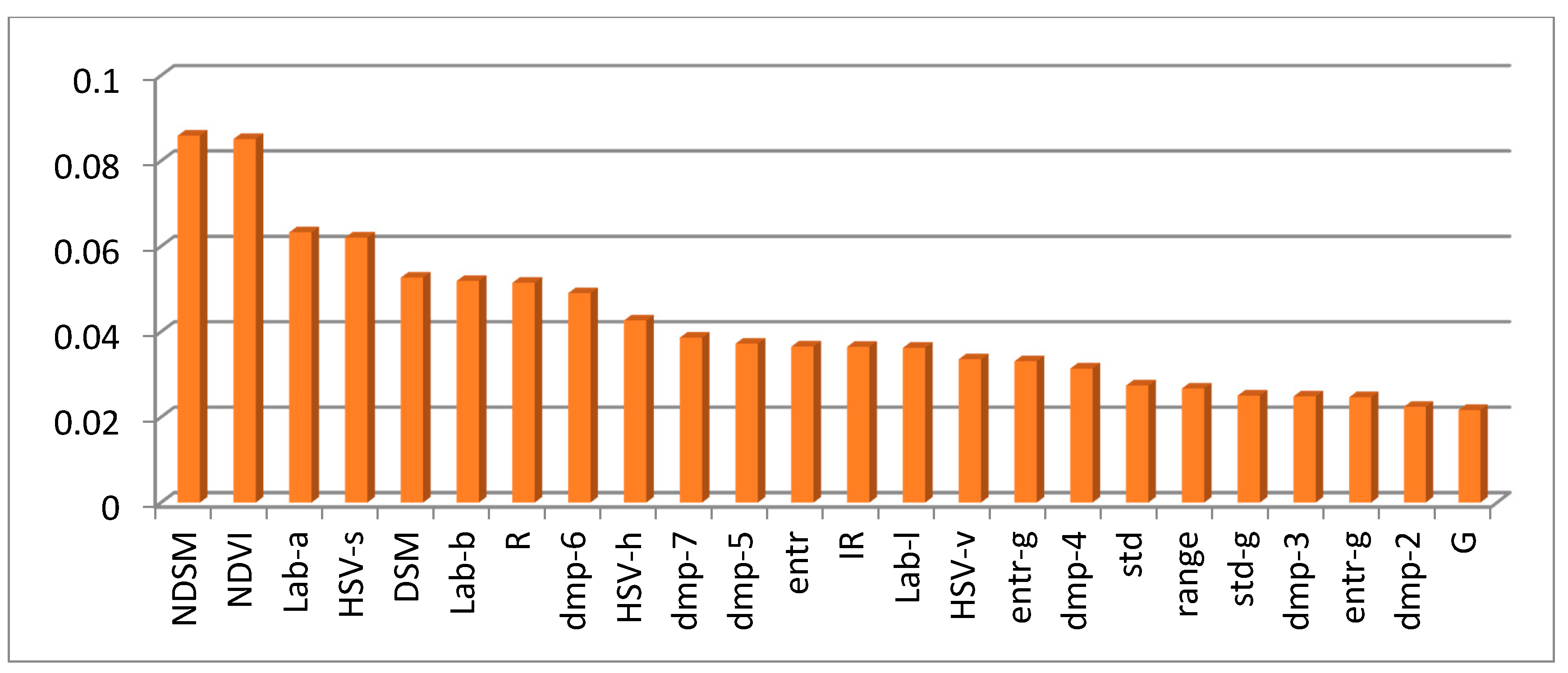
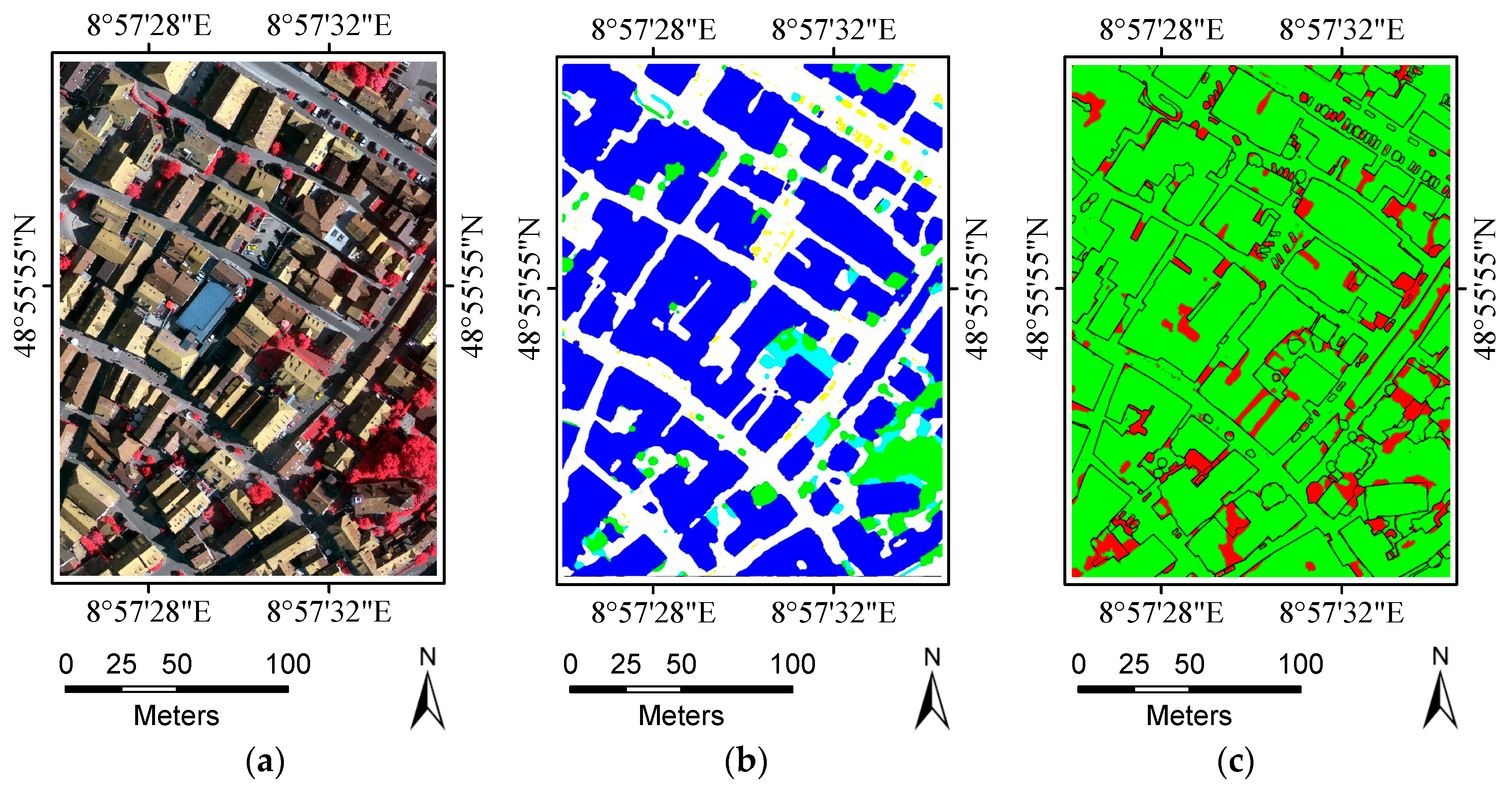
The current study combines methods from RF and probabilistic graphical models to classify high-resolution remote sensing data. Using high-resolution multispectral images and 3D geometry data, the method proceeds in three main stages: feature extraction, classification and refinement. A total of 13 features (color, vegetation index and texture) from the multispectral image and 11 features (height, elevation texture and DMP) from the 3D geometry data are first extracted to form the feature space. Then, the random forest is selected as the basic classifier for semantic classification. Inspired by the big training data and ensemble learning strategy adopted in the machine learning and remote sensing communities, a tile-based scheme is used to train multiple RFs separately. The multiple RFs are then combined to jointly predict the category probabilities of each sample. Finally, the probabilities and the feature importance indicators are used to construct an FCCRF graph model, and a mean-field-based statistical inference is carried out to refine the above classification results.
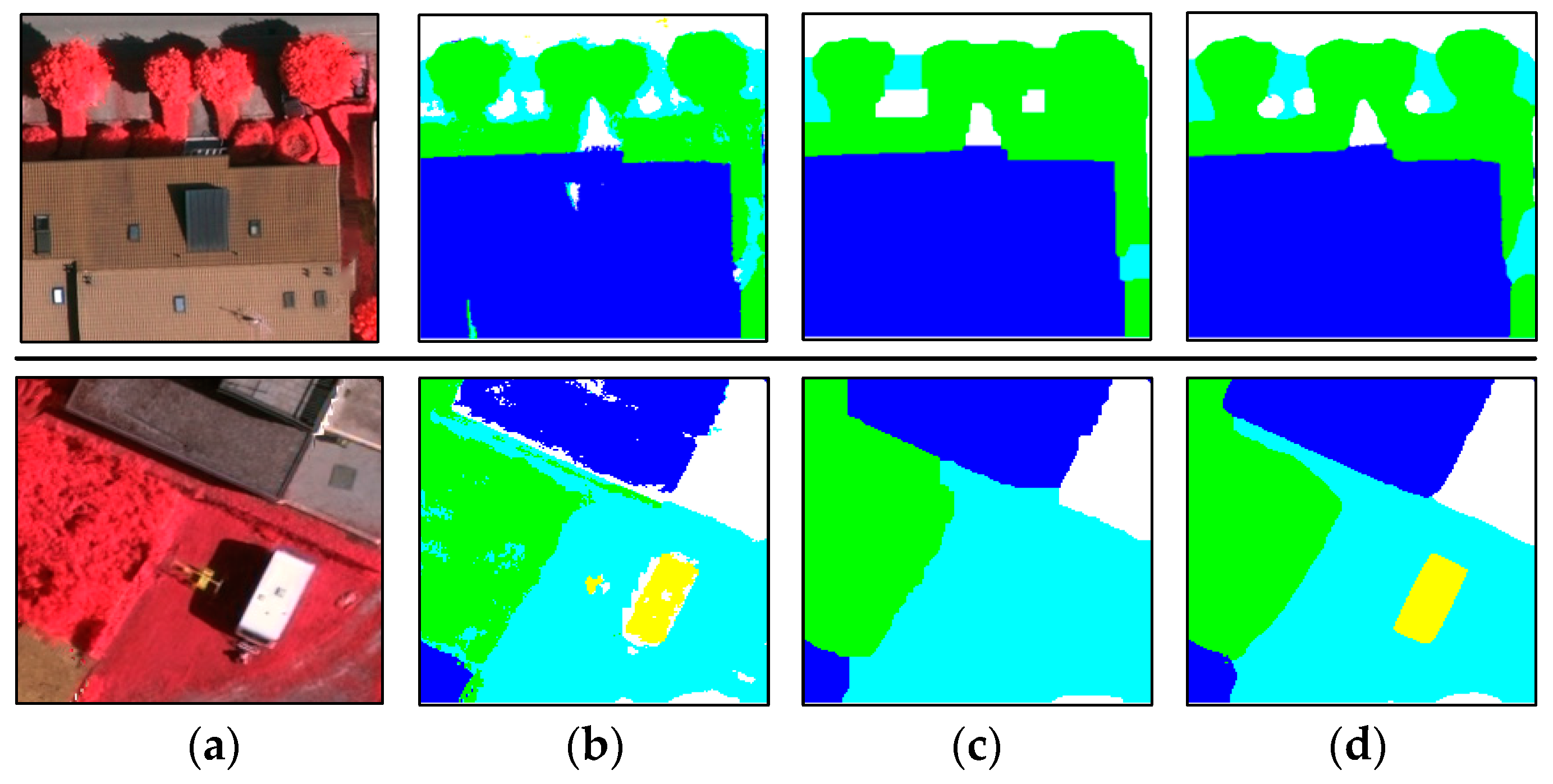
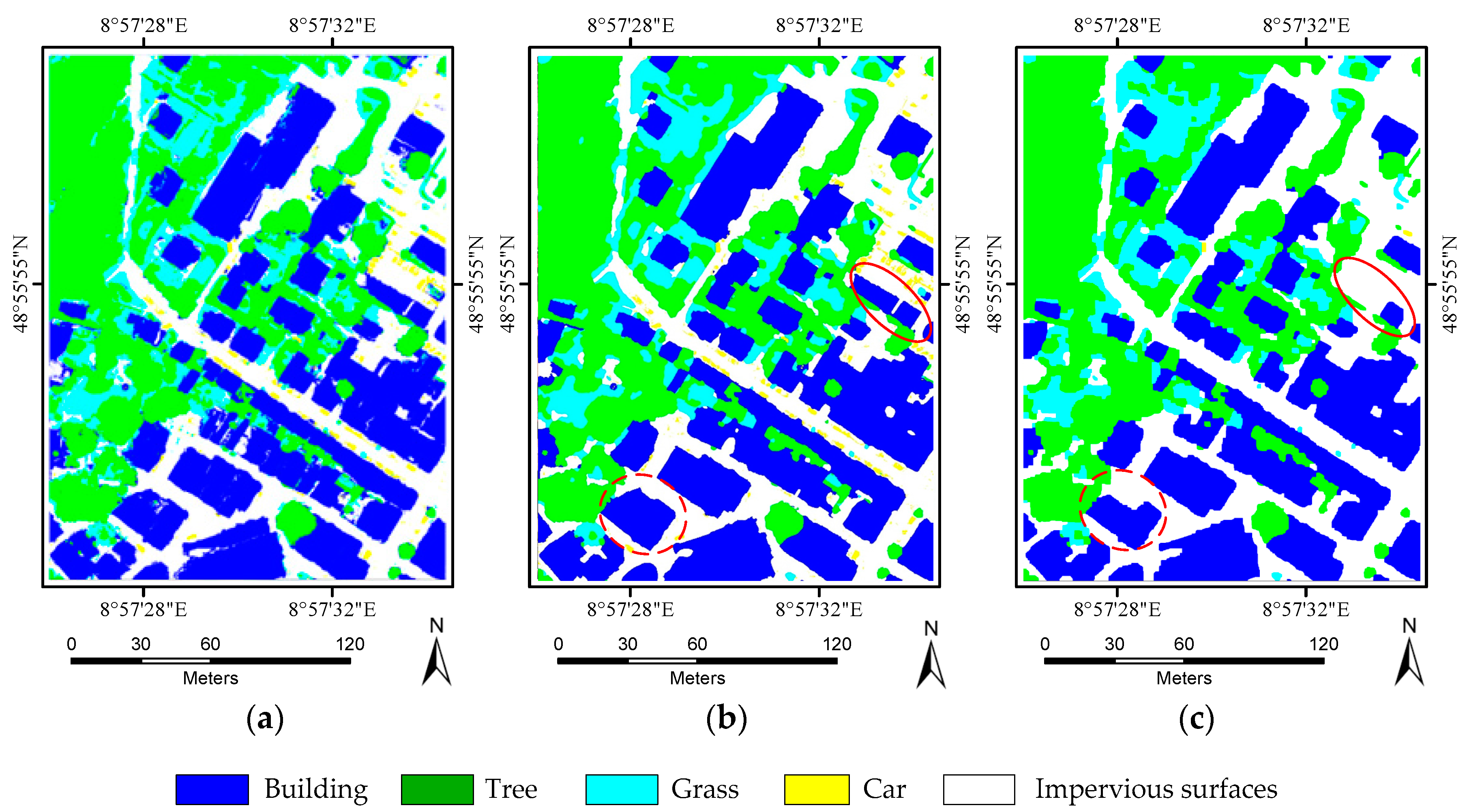
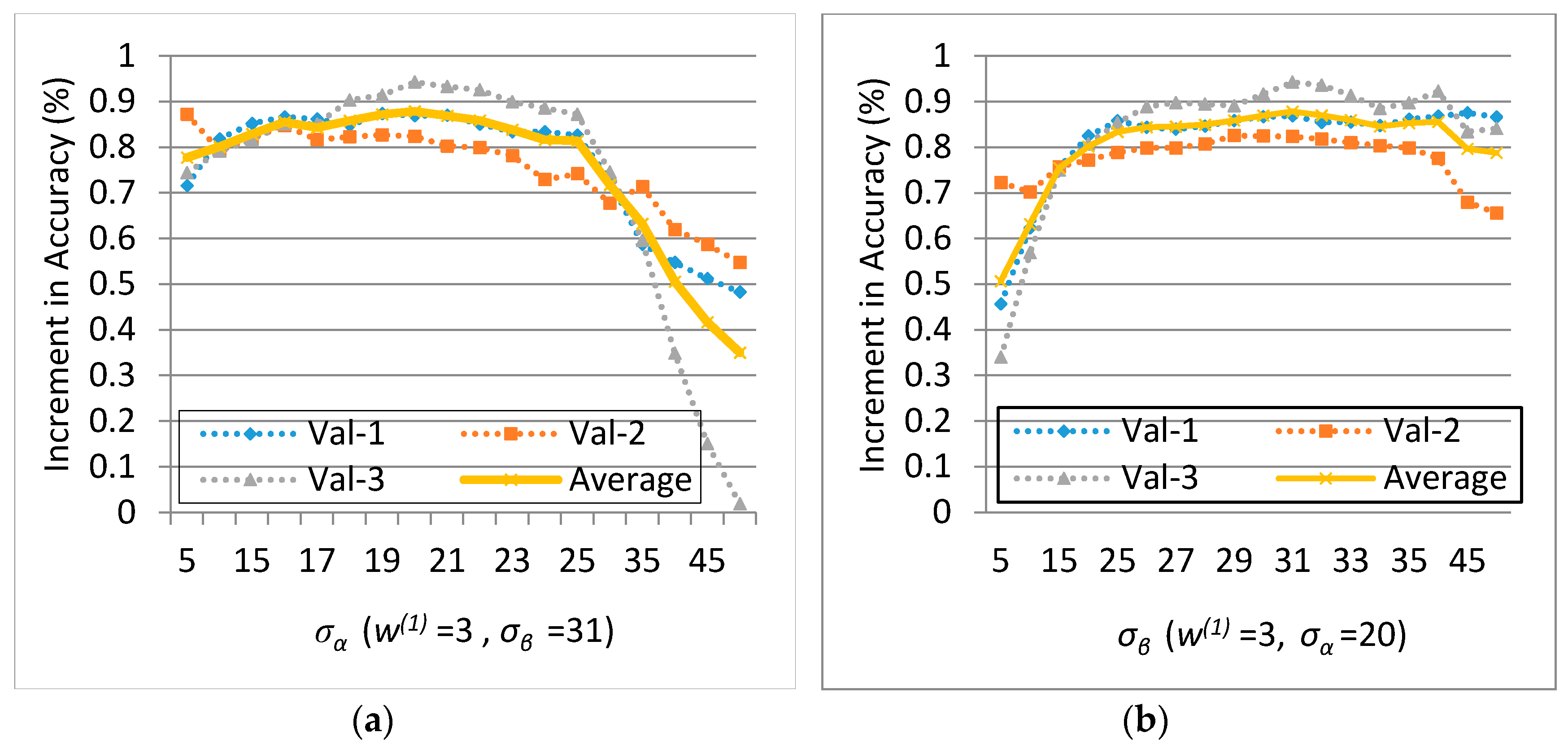
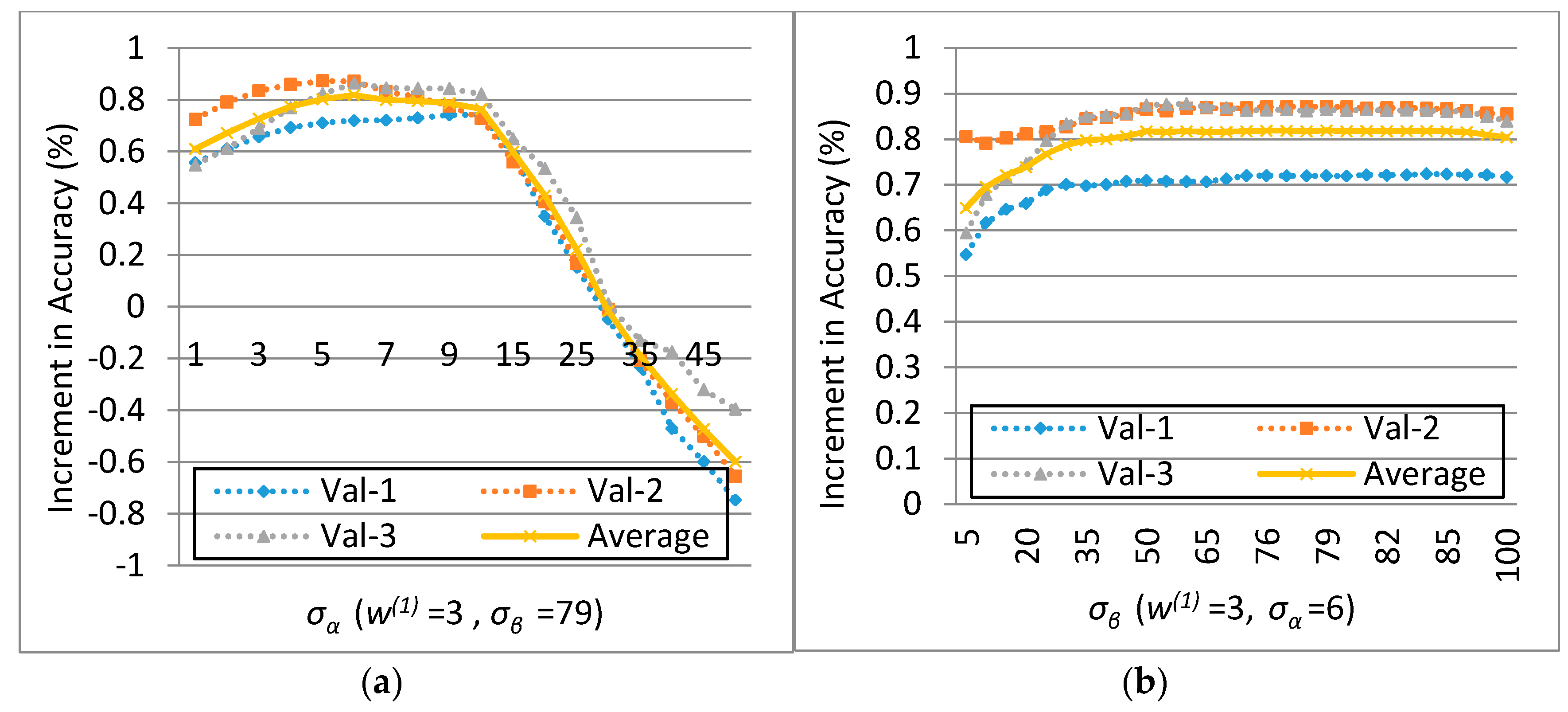
Experiments on the ISPRS Semantic Labeling Contest data show that features from both the multispectral image and the 3D geometry data are important and indispensable for the accurate semantic classification. Moreover, multispectral image-derived features play a greater role than the 3D geometry features. When comparing the classification accuracy of the single RF classifier and the fused RF ensemble, we found that both the generalization capability and the discriminability were enhanced significantly. Consistent with the conclusions drawn by others, the smoothness effect of the CRF is also evident in the presented work. Moreover, by introducing the 3 most important features to the pairwise potential of CRF, the classification accuracy is improved by approximately 1% in the presented experiments.
Note that in addition to urban land cover mapping, the current study can also be extended and used for other activities, such as vegetation mapping, water body mapping, and change detection.
Among the non-CNN-based methods, we achieve the highest overall accuracy, 86.9%. When compared to the CNN-based approaches, the gap between the current method and the best CNN method in the contest is still notable. However, we found that the presented method indeed outperformed several CNN-based methods. Furthermore, CNN can be conveniently integrated into the present RFE framework, as a feature extraction submodule to further boost the classification performance of the presented method. Hopefully, the integrated method could outperform the current best CNN method, which will be one of our future directions.