Continuous Scale Transformations of Linear Features Using Simulated Annealing-Based Morphing
Abstract
1. Introduction
2. Methodology
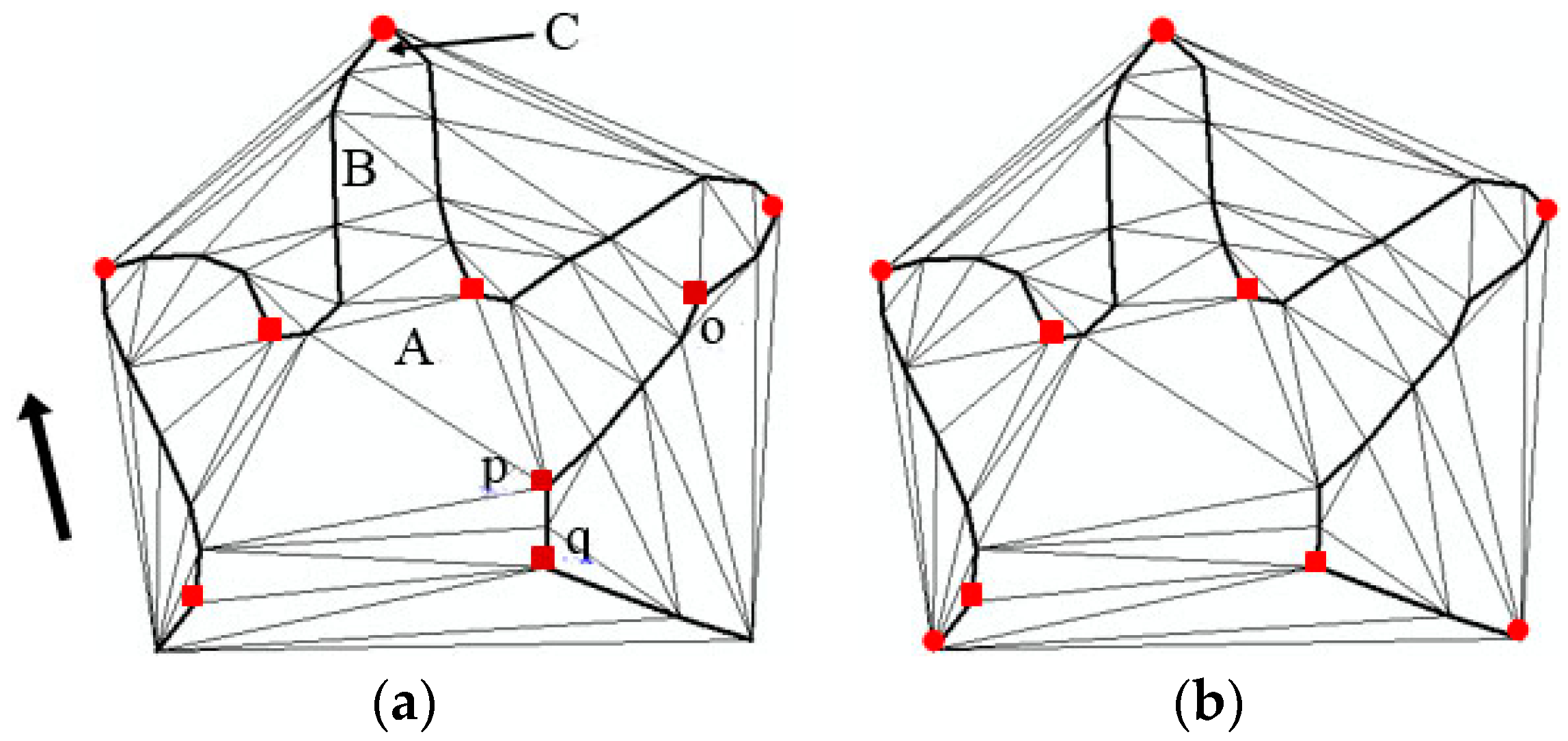
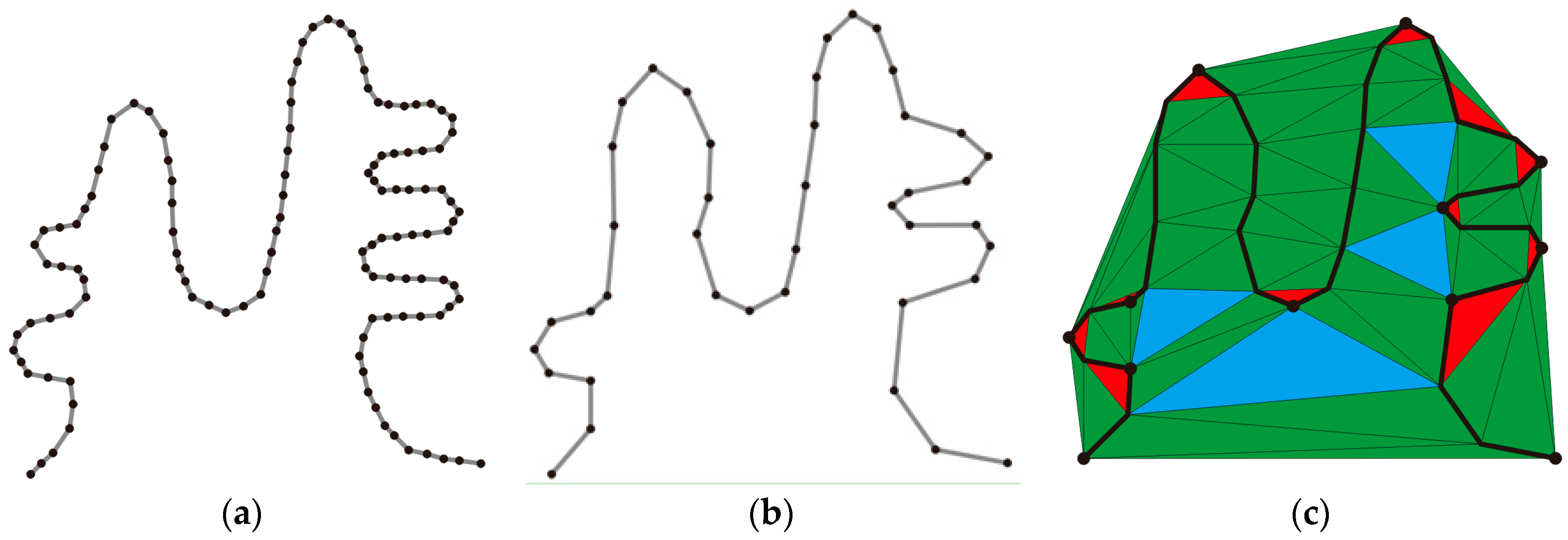
2.1. Characteristic Point Extraction
| Algorithm 1 Characteristic Point Extraction |
| Input: points on β . Output: characteristic points of β. For polyline β at small scale do 1 Construction of CDT 2 Classification of triangles 3 Extraction of characteristic points 4 Elimination of pseudo-characteristic points 5 Supplement with start and end points End |
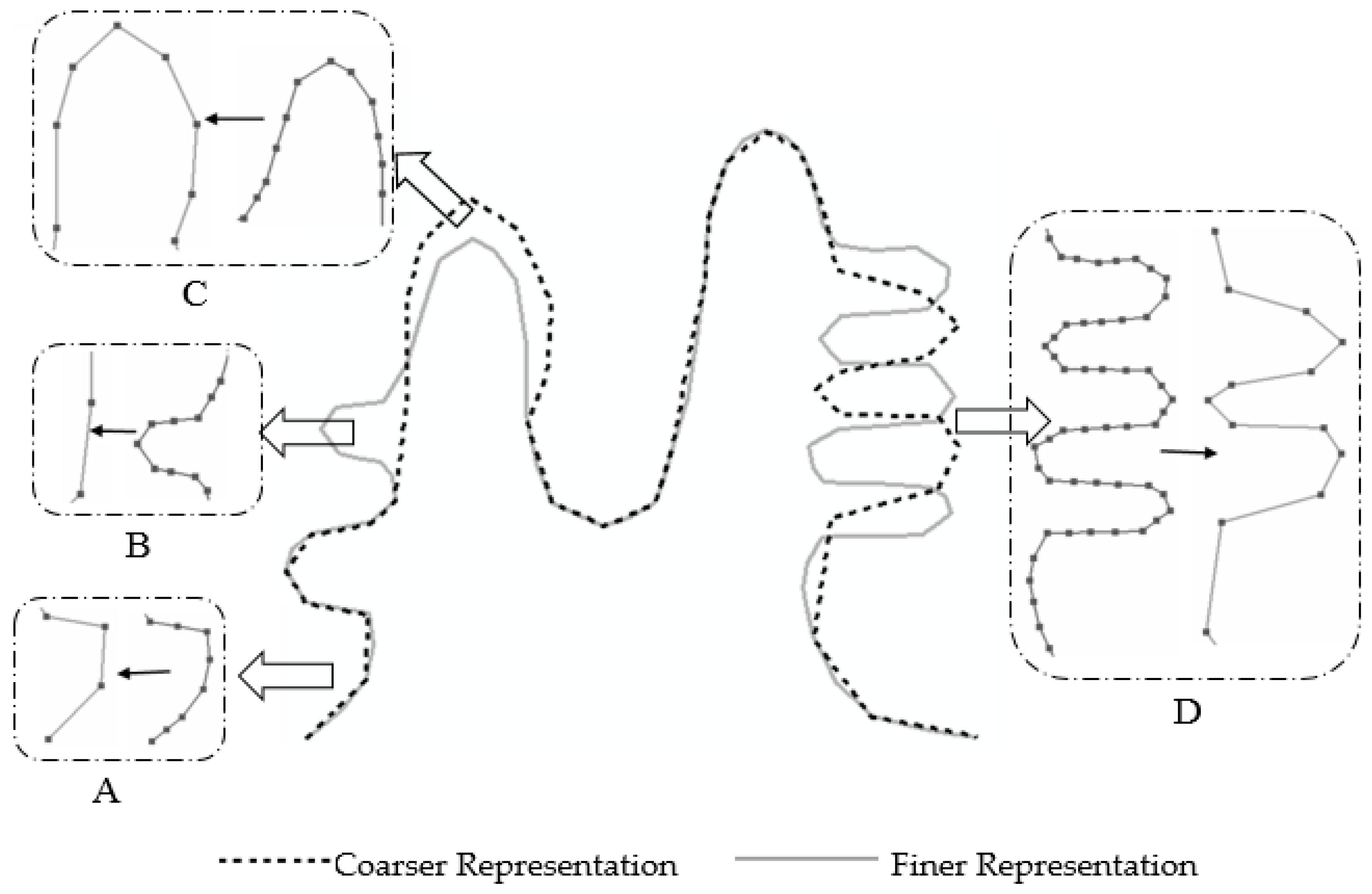
2.2. Characteristic Point Correspondence Using the Simulated Annealing Algorithm
2.2.1. Objective Function
| Algorithm 2 Correspondence of Characteristic Points by SA |
| Input: Initial matching state , initial temperature T0, annealing speed w. Output: Optimum correspondence for and . |
| Evaluate initial matching state |
| If (initial state = solution) then |
| Final state initial state |
| Else |
| Current state initial state |
| Initialize T0 according to annealing schedule |
| Do |
| Select candidate corresponding point that has not yet been applied to the current state |
| Apply candidate corresponding point to produce a new state |
| Evaluate new state |
| Compute |
| If (new state is better than current state) then |
| Current state new state |
| Else |
| P |
| Generate random number R between 0 and 1 |
| If (R<P) then |
| Current state new state |
| Endif |
| Endif |
| Revise T according to annealing schedule |
| Until (current state = solution ) or (no new candidate corresponding points left to apply) |
| Final state current state |
| Endif |
2.2.2. Search Space
2.2.3. Acceptance Probabilities
2.2.4. Annealing Schedule
2.3. Path Interpolation
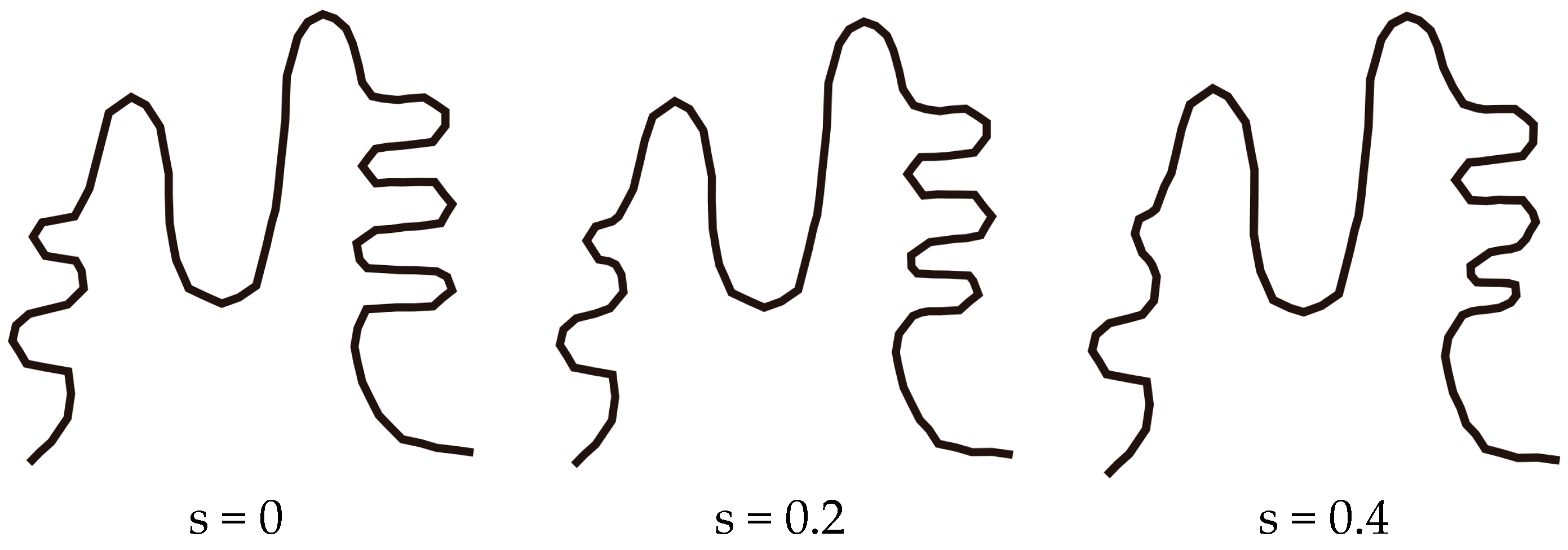
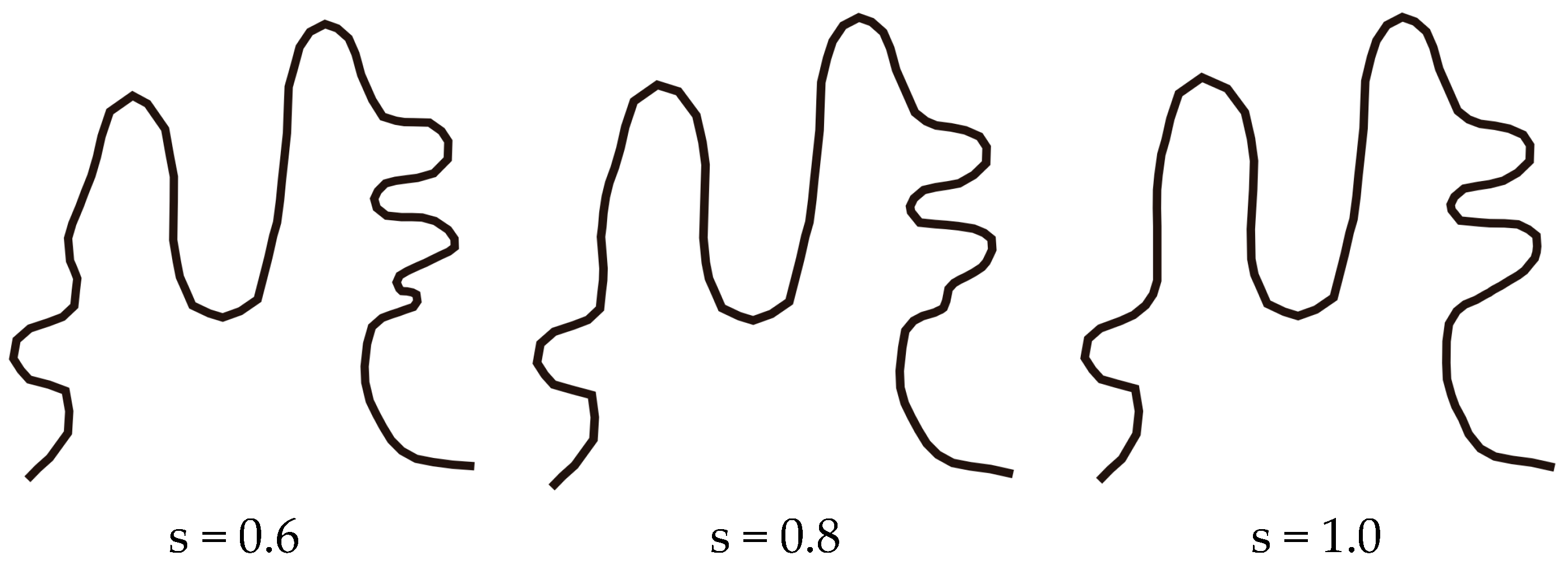
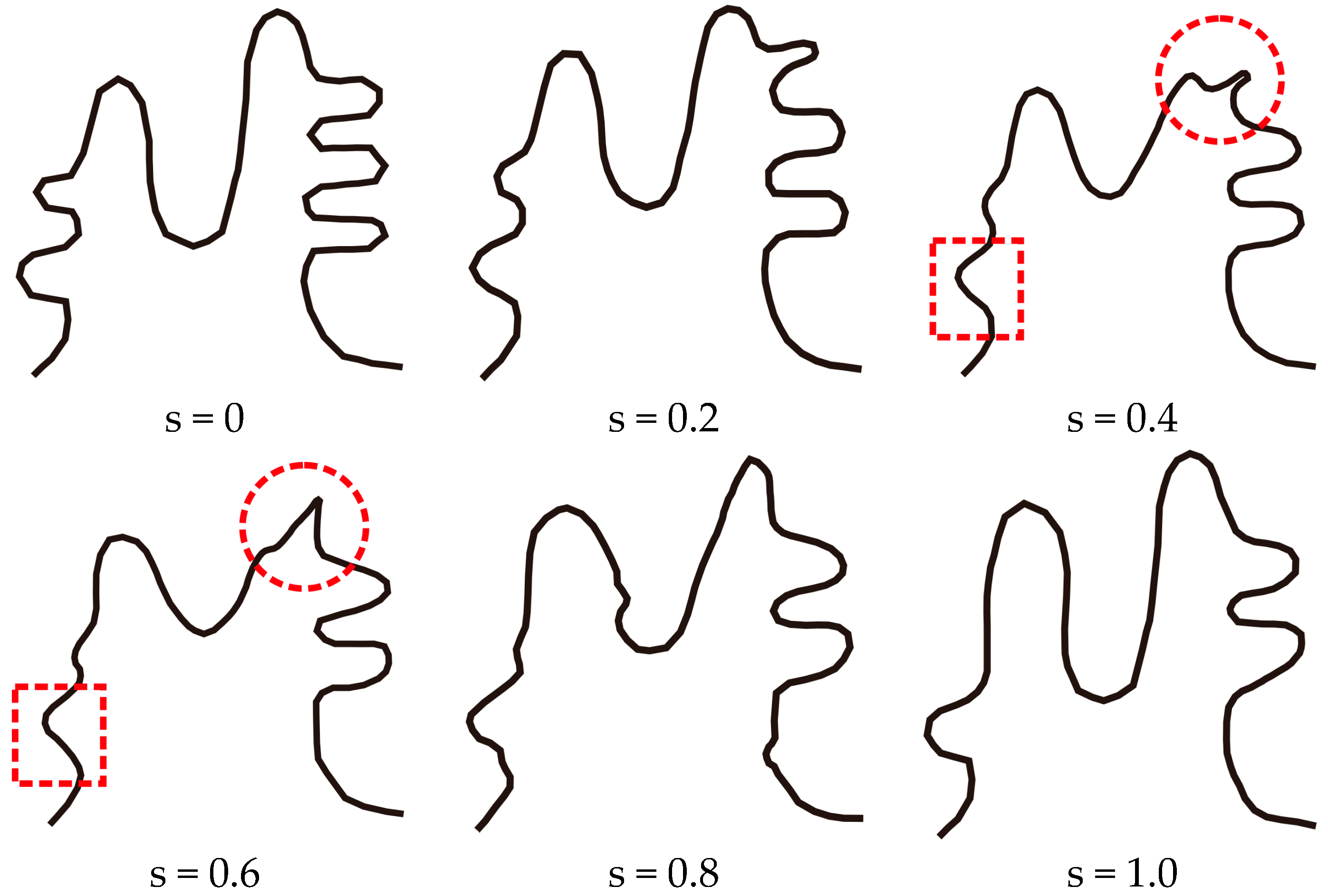
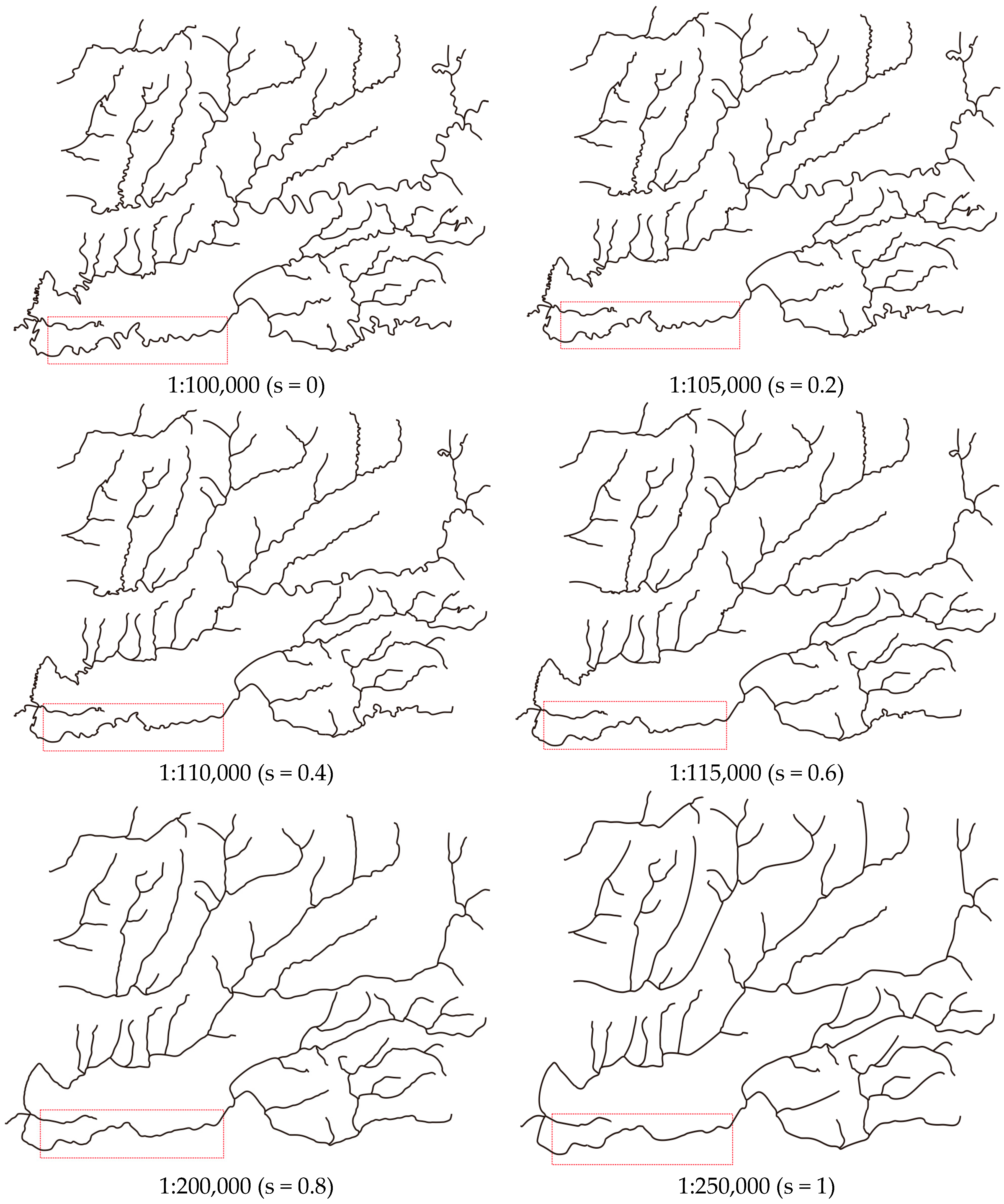
3. Case Study
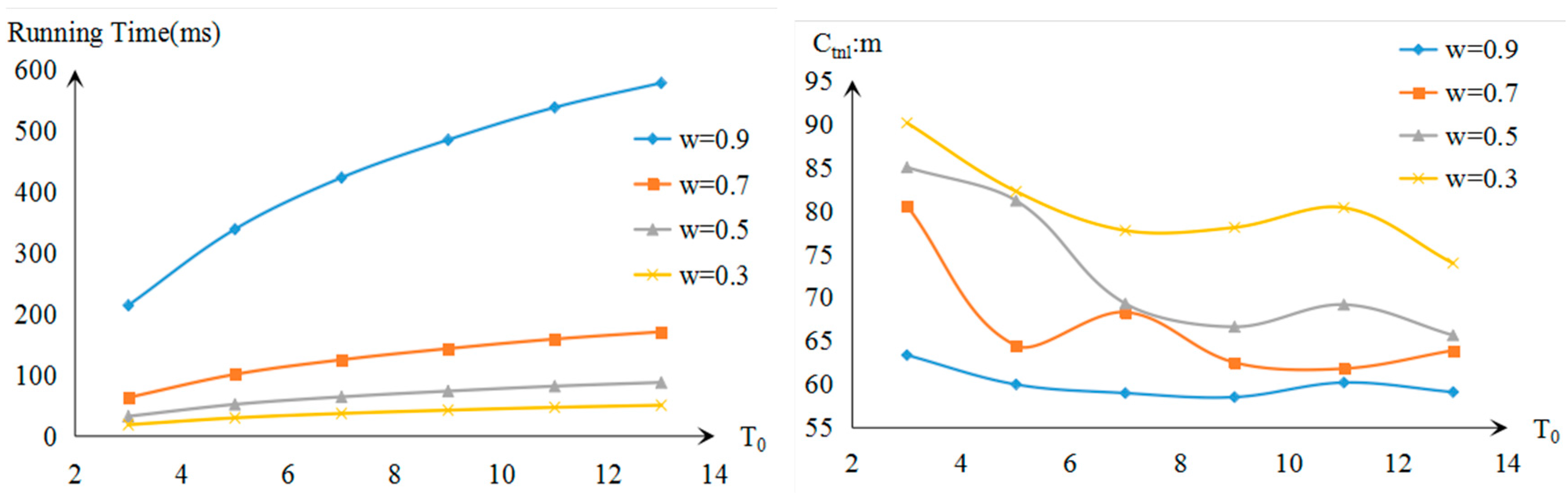
3.1. Simulation Experiments and Analysis
3.2. The Application of SABM for Continuous Scale Transformation
4. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bereuter, P.; Weibel, R. Real-time generalization of point data in mobile and web mapping using quadtrees. Cartogr. Geogr. Inf. Sci. 2013, 40, 271–281. [Google Scholar] [CrossRef]
- Meng, L.; Murphy, C.; Ding, L.; Yang, J. A Review of Research Works on VGI Understanding and Image Map Design. Kartographische Nachrichten. Available online: https://www.researchgate.net/publication/316277984_A_Review_of_Research_Works_on_VGI_Understanding_and_Image_Map_Design (accessed on 7 August 2017).
- Ai, T.H. The drainage network extraction from contour lines for contour line generalization. ISPRS J. Photogramm. Remote Sens. 2007, 62, 93–103. [Google Scholar] [CrossRef]
- Ai, T.H.; Li, J. A DEM generalization by minor valley branch detection and grid filling. ISPRS J. Photogramm. Remote Sens. 2010, 65, 198–207. [Google Scholar] [CrossRef]
- Jones, C.B.; Ware, J.M. Map generalization in the web age. Int. J. Geogr. Inf. Sci. 2005, 19, 859–870. [Google Scholar] [CrossRef]
- Danciger, J.; Devadoss, S.L.; Mugno, J.; Sheehy, D.; Ward, R. Shape deformation in continuous map generalization. Geoinformatica 2009, 13, 203–221. [Google Scholar] [CrossRef]
- Sester, M.; Brenner, C. Continuous generalization for visualization on small mobile devices. In Development of the Spatial Data Handling; Fisher, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 355–368. [Google Scholar]
- Van Oosterom, P. Variable-scale Topological Data Structures Suitable for Progressive Data Transfer: The GAP-face Tree and GAP-edge Forest. Cartogr. Geogr. Inf. Sci. 2005, 32, 331–346. [Google Scholar] [CrossRef]
- Liu, P.C.; Li, X.G.; Liu, W.B.; Ai, T.H. Fourier based multi-scale representation and progressive transmission of cartographic curves on the internet. Cartogr. Geogr. Inf. Sci. 2016, 43, 454–468. [Google Scholar] [CrossRef]
- Ai, T.; Li, Z.; Liu, Y. Progressive Transmission of Vector Data Based on Changes Accumulation Model; SDH: Leicester, UK; Springer: Berlin, Germany, 2003; pp. 85–96. [Google Scholar]
- Van Kreveld, M. Smooth generalization for continuous zooming. In Proceedings of the 20th International Cartographic Conference (ICC’01), Beijing, China, 6–10 August 2001; pp. 2180–2185. [Google Scholar]
- Cecconi, A.; Galanda, M. Adaptive zooming in Web cartography. Comput. Graph. Forum 2002, 21, 787–799. [Google Scholar] [CrossRef]
- Nöellenburg, M.; Merrick, D.; Wolff, A.; Benkert, M. Morphing polylines: A step towards continuous generalization. Comput. Environ. Urban Syst. 2008, 32, 248–260. [Google Scholar] [CrossRef]
- Deng, M.; Peng, D. Morphing Linear Features Based on Their Entire Structures. Trans. GIS. 2015, 19, 653–677. [Google Scholar] [CrossRef]
- Whited, B.; Rossignac, J. B-morphs between b-compatible curves in the plane. In Proceedings of the ACM/SIAM Joint Conference on Geometric and Physical Modeling, San Francisco, CA, USA, 5–8 October 2009; pp. 187–198. [Google Scholar]
- Li, J.Z.; Li, X.G.; Xie, T. Morphing of Building Footprints Using a Turning Angle Function. ISPRS Int. J. Geo-Inf. 2017, 6, 173. [Google Scholar] [CrossRef]
- Yang, W.; Feng, J. 2D shape morphing via automatic feature matching and hierarchical interpolation. Comput. Graph. 2009, 33, 414–423. [Google Scholar] [CrossRef]
- Gomes, J.; Darsa, L.; Costa, B.; Velho, L. Warping and Morphing of Graphical Objects; Morgan Kaufman: San Francisco, CA, USA, 1999. [Google Scholar]
- Sederberg, T.; Greenwood, E. A physically based approach to 2D shape blending. ACM Comput. Graph. 1992, 26, 25–34. [Google Scholar] [CrossRef]
- Efrat, A.; Har-Peled, S.; Guibas, L.J.; Murali, T.M. Morphing between polylines. In Proceedings of the 12th ACM-SIAM Symposium on Discrete Algorithms, Washington, DC, USA, 7–9 January 2001; pp. 680–689. [Google Scholar]
- Van, O.R.; Veltkamp, R.C. Parametric search made practical. Comput. Geom. 2004, 28, 75–88. [Google Scholar]
- Sederberg, T.; Gao, P.; Wang, G.; Mu, H. 2-D shape blending: An intrinsic solution to the vertex path problem. Comput. Graph. 1993, 27, 15–18. [Google Scholar]
- Alexa, M.; Cohen-Or, D.; Levin, D. As-rigid-as-possible shape interpolation. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’00), New Orleans, LA, USA, 23–28 July 2000; pp. 157–164. [Google Scholar]
- Surazhsky, V.; Gotsman, C. Intrinsic morphing of compatible triangulations. Int. J. Shape Model. 2003, 9, 191–201. [Google Scholar] [CrossRef]
- Ware, J.M.; Jones, C.B.; Thomas, N. Automated map generalization with multiple operators: A simulated annealing approach. Int. J. Geogr. Inf. Sci. 2003, 17, 743–769. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelattjr, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]

| TS | CP | TS | CP | TS | CP | TS | CP |
|---|---|---|---|---|---|---|---|
| w = 0.9 | w = 0.7 | w = 0.5 | w = 0.3 | |||||
|---|---|---|---|---|---|---|---|---|
| Running Time | Running Time | Running Time | Running Time | |||||
| 13 | 578.3 | 59.105 | 170.8 | 63.896 | 87.9 | 65.65 | 50.6 | 73.94 |
| 11 | 538.1 | 60.202 | 158.9 | 61.807 | 81.8 | 69.17 | 47.1 | 80.326 |
| 9 | 485.2 | 58.527 | 143.3 | 62.512 | 73.7 | 66.62 | 42.5 | 78.05 |
| 7 | 423.2 | 58.99 | 125.0 | 68.3 | 64.3 | 69.29 | 37.1 | 77.7 |
| 5 | 338.7 | 59.98 | 101.1 | 64.446 | 52.0 | 81.13 | 29.9 | 82.2 |
| 3 | 214.1 | 63.36 | 63.2 | 80.53 | 32.5 | 84.97 | 18.7 | 90.09 |
| Num1 | Num2 | T1 | T2 | Ctnl (s = 0.2) | Ctnl (s = 0.4) | Ctnl (s = 0.6) | Ctnl (s = 0.8) | |
|---|---|---|---|---|---|---|---|---|
| Contours | 17 | 982 | 13.18 | 24.51 | 468 | 355 | 279 | 144 |
| Rivers | 57 | 212 | 2.71 | 5.7 | 399 | 307 | 226 | 136 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Ai, T.; Liu, P.; Yang, M. Continuous Scale Transformations of Linear Features Using Simulated Annealing-Based Morphing. ISPRS Int. J. Geo-Inf. 2017, 6, 242. https://doi.org/10.3390/ijgi6080242
Li J, Ai T, Liu P, Yang M. Continuous Scale Transformations of Linear Features Using Simulated Annealing-Based Morphing. ISPRS International Journal of Geo-Information. 2017; 6(8):242. https://doi.org/10.3390/ijgi6080242
Chicago/Turabian StyleLi, Jingzhong, Tinghua Ai, Pengcheng Liu, and Min Yang. 2017. "Continuous Scale Transformations of Linear Features Using Simulated Annealing-Based Morphing" ISPRS International Journal of Geo-Information 6, no. 8: 242. https://doi.org/10.3390/ijgi6080242
APA StyleLi, J., Ai, T., Liu, P., & Yang, M. (2017). Continuous Scale Transformations of Linear Features Using Simulated Annealing-Based Morphing. ISPRS International Journal of Geo-Information, 6(8), 242. https://doi.org/10.3390/ijgi6080242





