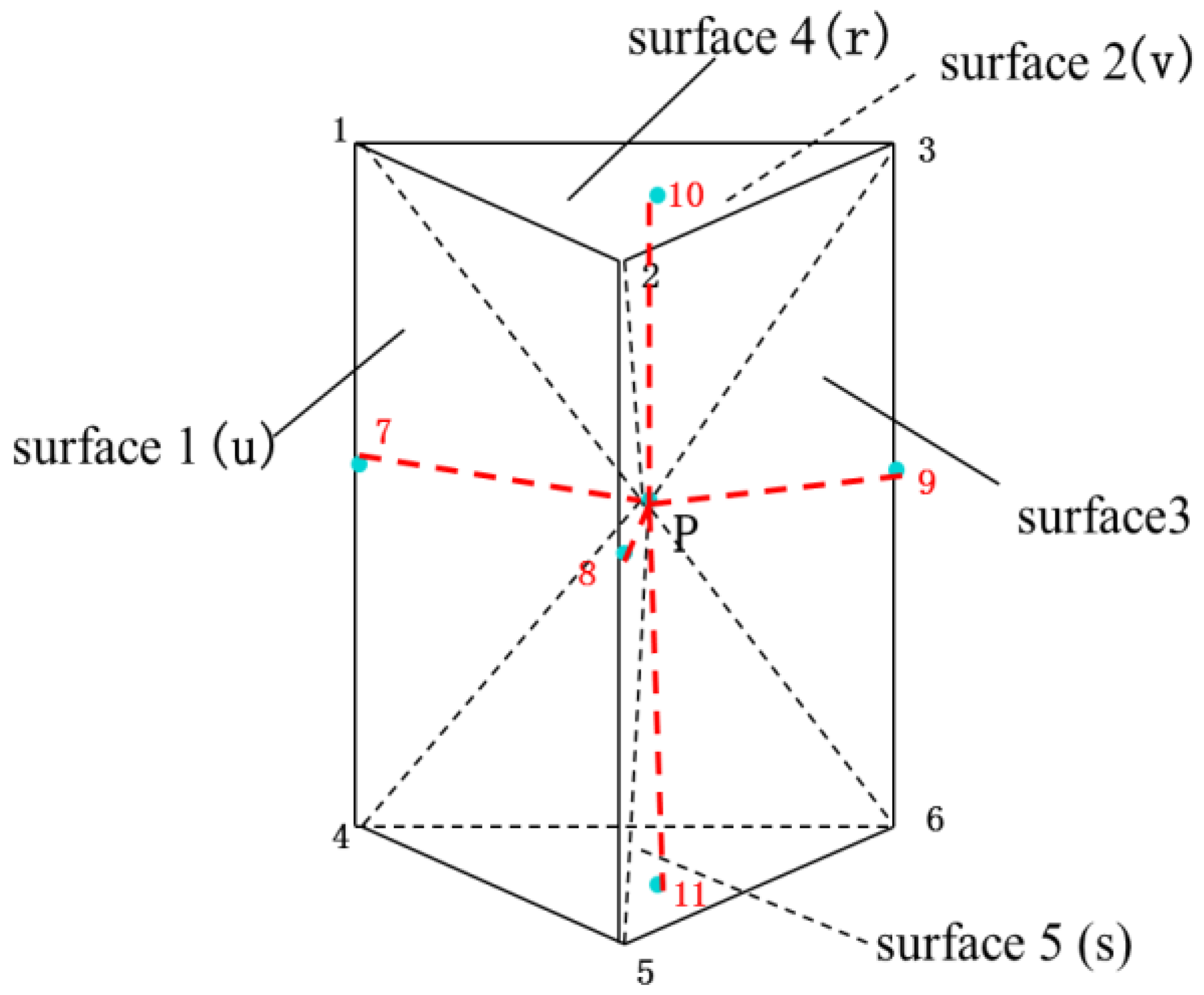
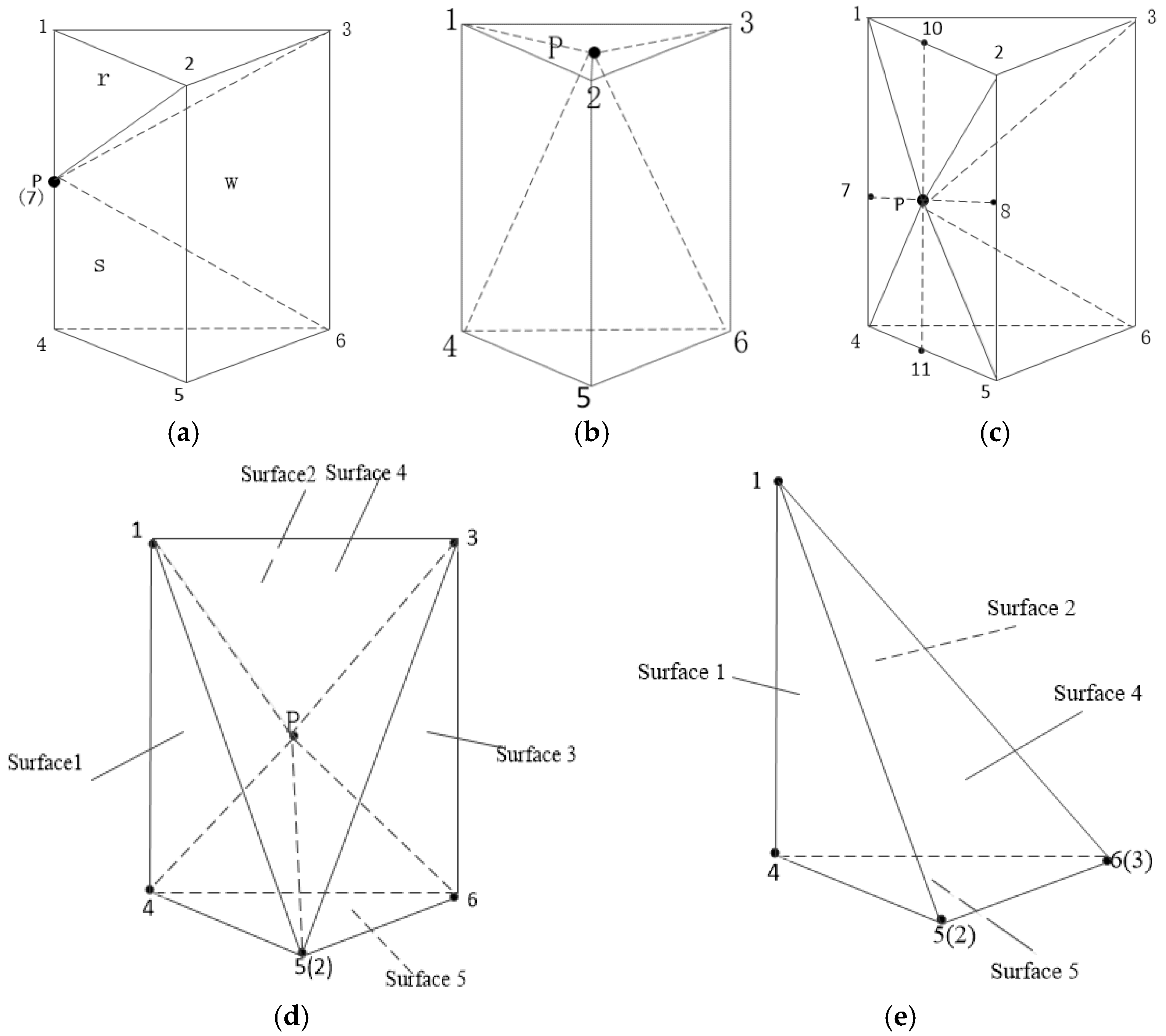
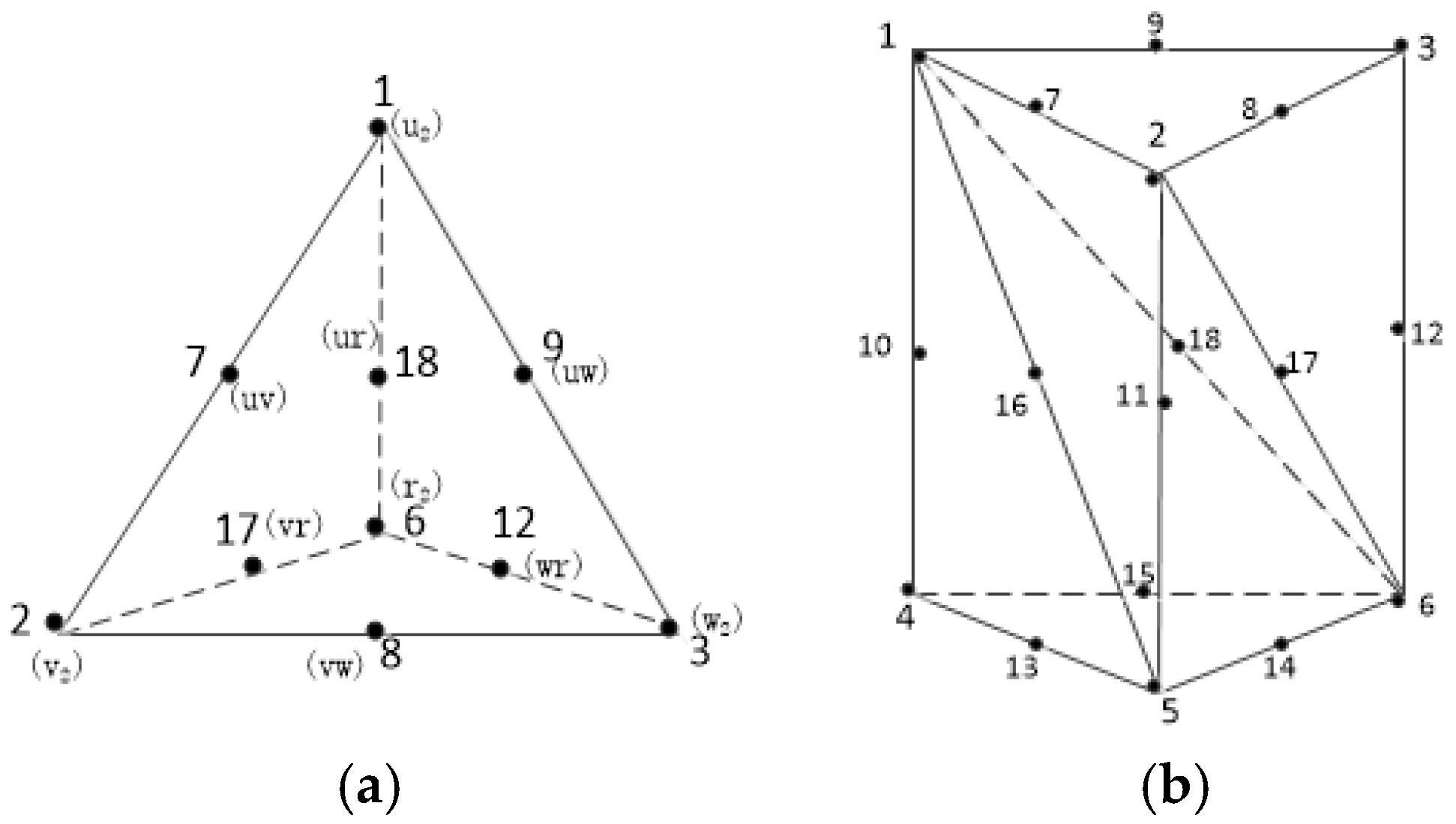
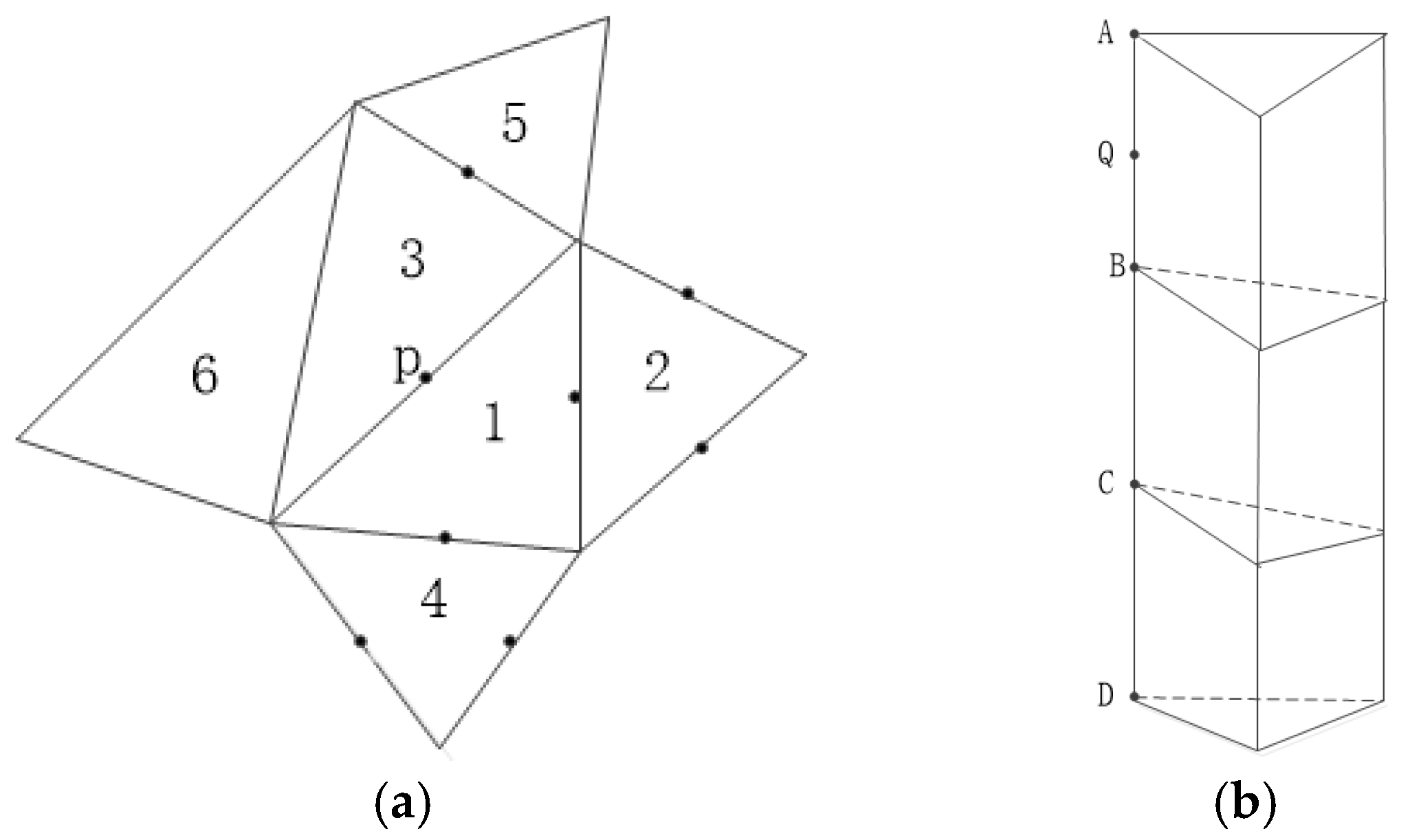
1. Introduction
Three-dimensional (3D) geological modeling (3DGM) is an area of interest and technological development, involving geology, geo-statistics, and computer science. Three-dimensional geometric shapes and the internal property distributions of geological bodies can be built with 3DGM techniques using the available geological modeling data and appropriate modeling methods. A geographic information system (GIS) platform is not only required to express the boundaries of geological bodies, but also the internal heterogeneous properties, such as the rock property fields (mechanical strength, porosity, etc.), the distribution of gas in coal beds and surrounding rocks, crustal stresses, temperature fields, grade changes in ore, and so on. A 3D property field is an abstract mathematical definition of the spatial distribution of geological properties. However, the existing GIS platforms can only describe the vector structures [
1,
2,
3] of a geological model, and cannot achieve a heterogeneous expression of a 3D property field. Furthermore, due to the relatively high cost of underground sampling, sparsely distributed sampling points are often used to infer the distribution of the properties of a study area. As a result, 3D spatial interpolation in most geological models is undertaken using sparsely distributed sampling points.
Stratification is one manifestation of heterogeneity and is a critical element in geology. Materials with a layered structure always show large differences in property change rates between the horizontal and vertical directions. The change rate in the horizontal direction is relatively uniform and slow, while it is rapid in the vertical direction [
4]. The mathematical expression of these heterogeneous properties benefits from the accurate calculation and analysis of geological property fields, such as organic matter measurements from bore samples. Improved methods for visualization and 3D modeling support advances in many practical applications, such as mining and oil and gas exploration.
Much research has been done on the interpolation of the property fields of geological bodies; Li has proposed a “volume function model” [
5,
6]. The volume function model complements traditional vector boundary and volume element models, splitting a geological body into adjacent and non-intersecting elements (such as tetrahedrons, triangular prisms or hexahedrons). A volume function can be built to mathematically express continuous change, the distribution and the inter-relationship of heterogeneous property fields. This interpolation method is faster and has a greater accuracy than IDW and kriging interpolation, as the heterogeneity of a geological body can be expressed by the volume function of the non-overlapping volume elements. Three-dimensional spatial interpolation using a fitted volume function ensures
,
or
continuity in the same layer rather than between different strata [
5]. Interpolated property values using volume function satisfy positional continuity, first derivative continuity, or second derivative continuity, and are similar to curve and surface interpolation
,
and
continuity. Previous research has been done on the volume function and related fields. Zhou and Chen [
7,
8] used a tetrahedral region high-order volume function to fit values of a property to an entire stratum. Alfeld [
9] proposed first-order smoothing (
) based on the Clough–Tocher tetrahedral interpolation method; Barnhill and Little [
10] proposed a tetrahedral interpolation formula based on the Barnhill, Birkhof, and Gordon (BBG) transfinite interpolation method; Soh [
11] successfully applied quadrilateral area coordinates to the thin plate element; Li [
12] studied the interpolation discretization of two types of hexahedral volume coordinates based on mechanical 3D finite element calculation theory; Wang [
13] used a piecewise spline polynomial that satisfied the continual condition in the finite element method. Bhattacharjee [
14] proposed semantic kriging to blend the semantics of spatial features with an ordinary kriging method for prediction of an attribute. Experimentation was carried out with land surface temperature data of four major metropolitan cities in India. Anderson demonstrated that kriging produces a better estimation of a continuous surface of air temperature than IDW and spline [
15]. A radial basis function in a neural network improved spatial interpolation performance more than traditional methods for soil properties in Kunming [
16]. Karydas evaluated prediction maps created with interpolation for five common topsoil properties; namely, organic matter, total CaCO
3, and electric conductivity [
17]. However, all these methods have a common drawback in that the directivity of their heterogeneous attributes cannot be effectively expressed.
To handle the directivity of heterogeneous property changes, an appropriate body element needs to be selected as the base component unit for a geological body. A tetrahedron is suitable for complex strata modeling and can represent the heterogeneous property changes of a local area. However, it has several drawbacks for geological modeling. A geological model contains a large amount of data, and using a tetrahedron is time-consuming. Furthermore, a tetrahedron element cannot express the directivity of a geological body [
5]. A hexahedron is also not appropriate, as its regular formation is not suitable for complex geological strata [
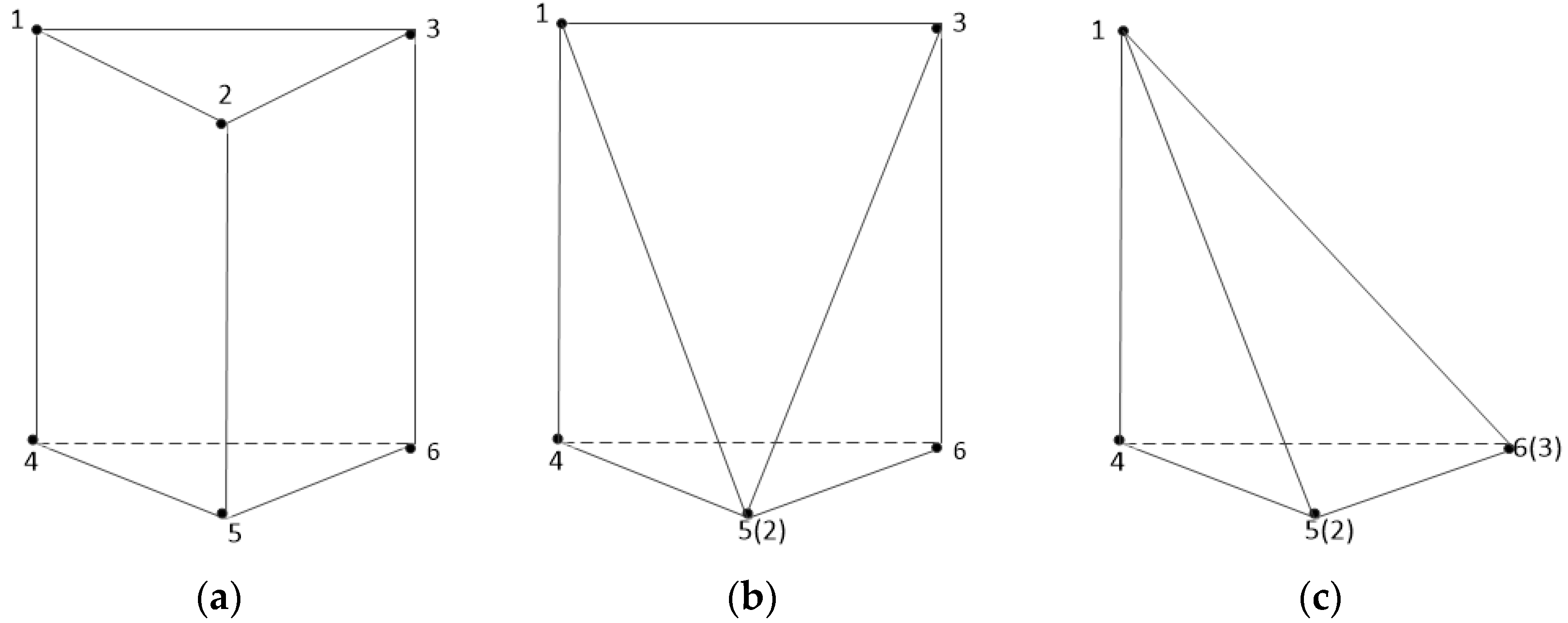
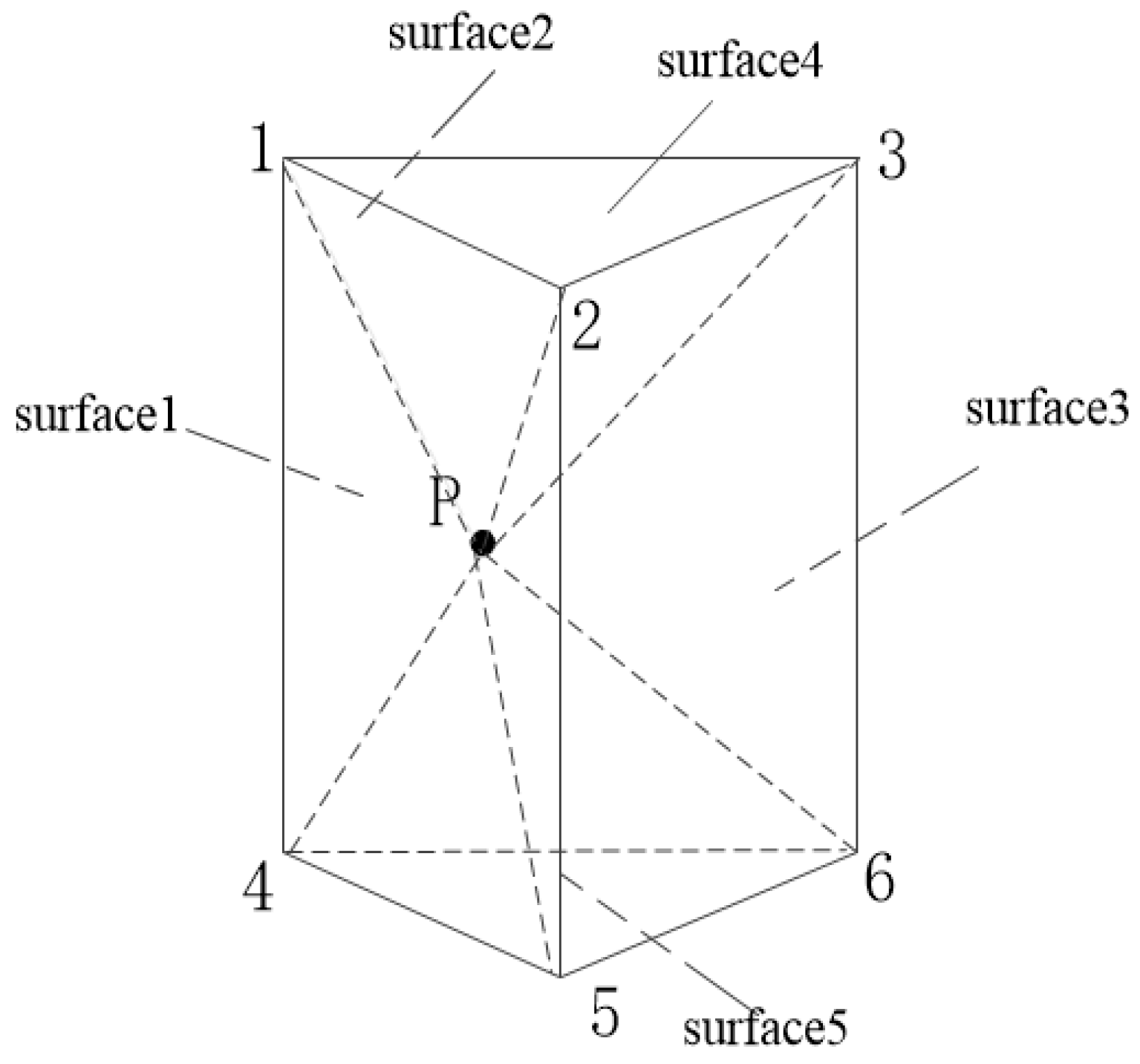
12]. In this study, we selected the triangular prism as the body element for the modeling. A triangular prism can be decomposed into the basic tetrahedron elements and can fit the features of borehole data and the trends found in geological strata. It can also effectively describe regional and directional changes in the properties of a geological body.
This paper explores different triangular prism interpolation algorithms. Unlike conventional geostatistical methods, these methods are based on volume element interpolation. A new triangular prism linear interpolation method is proposed to express the properties of a layered stratum that achieves a complete
continuity in a single triangular prism. A triangular prism quadric interpolation algorithm is designed for a smooth transition between adjacent triangular prisms, expressing the continuity of the whole model, reaching approximate
continuity. We deduce the triangular prism linear interpolation formula based on the existing methods for tetrahedron and hexahedron volume coordinates [
5,
12]. The triangular prism quadric interpolation is designed by modifying the existing B-net method for tetrahedron domains [
7,
18,
19]. In our research, the triangular prism element is used to express the 3D geometric shapes of geological bodies and structural mechanics, building on these past studies [
20,
21]. The related tetrahedron and hexahedron interpolation methods have been extensively researched [
7,
8,
12]. Triangular prism interpolation, however, is a new solution for interpolating and predicting geological property fields based on sparse sample data.
The remainder of this paper is organized as follows.
Section 2 summarizes several related geostatistical interpolation methods.
Section 3 introduces the experimental data and algorithms.
Section 4 describes the geostatistical model for 3D interpolation.
Section 5 presents the results. In
Section 6, the results are discussed, and we end with some concluding remarks.
2. Related Work
Interpolation issues are a focus of much work in the geostatistical field. Royse [
22] argues that three-dimension modeling is developing in two directions: digital three-dimension interpolation and cognitive interpretation. Three-dimensional data interpolation is a heterogeneous expression of 3D properties. Scholars from different fields have done similar research on the 3D modeling of heterogeneous data fields; the main methods are the distance power inverse ratio, kriging interpolation, finite element and spline interpolation.
(1) Distance Power Inverse Ratio Interpolation
The distance power inverse ratio method was proposed by meteorologists and geologists. It is simple, and has a wide applicability. The closer the space points are, the stronger the similarity, and the farther the distance, the weaker the similarity. This indicates that the unknown point is similar to the values of the nearest
known points. The property value
of the interpolation point is defined as the weighted average value of the known point property
, which treats the distance as inverse between the interpolation point and the known points, as shown in Equation (1).
where
is the weight of known points;
is the Euclidean distance from
to
;
is the power exponent. The accuracy is acceptable when the sample points are adequate. In terms of its application, engineering practice shows that this interpolation is an effective method for simple-structure stratiform deposits; however, this method has some problems stemming from “outliers”, “decluttering” and “anisotropy” [
23].
(2) Kriging Interpolation
Kriging is also called the spatial autocovariance best interpolation method, developed by the French geographical mathematician Georges Matheron and South African mining engineer D.G. Krige, and is a mature, unbiased, optimal interpolation method widely used in geo-statistics for the calculation of ore reserves, hydrology, meteorology, topography, and soil mapping. This geostatistical method provides an optimization strategy for spatial interpolation; in the interpolation process, the variables are determined dynamically according to set optimization criteria. Matheron and Krige focused on the determination of the weight coefficients, so that the interpolation function is in the best state: the best linear unbiased estimate for the variable values at the given point. Kriging is based on the known points to estimate the unknown points with a minimum prediction error. In addition, the corresponding minimum estimation variance can be obtained. The Kriging method however, is complex and requires a great deal of computation time. The kriging interpolation effect depends on the selection of variation functions in the theoretical model. However, a variogram appropriate for a geological model is not known in advance, thus the human factor in the kriging method is strong, as a user determines if the variogram function is reasonable or not. Some scholars [
24,
25,
26] have extended the kriging method, but the kriging method is still a low-pass filter and cannot reconstruct local, high-frequency, or weak signals reflected by an original signal.
(3) Finite Element Interpolation
Geostatistical methods interpolate subsurface property fields by modeling voxels [
27], expressing a continuous geological field using discrete adjacent volume elements such as tetrahedrons, triangular prisms, or hexahedrons. A volume element is only a property value, and is very small; thus, if expressed reasonably and effectively, it can represent the heterogeneous properties in the real body. However, with the gradual division of the volume element, the storage space becomes huge, and the amount of data will expand three-fold, while the computation speed is greatly reduced. However, the approximation function of a volume element is expressed by the node of each element, and its interpolation function in an unknown field effectively and efficiently expresses internal features of the data. Li, Cen [
12,
28] and others studied the interpolation methods for two kinds of hexahedral volume coordinates from the point of view of mechanical three-dimensional finite element calculation. The tetrahedron unstructured model is suitable for complex structural models and finite element simulations based on irregular discrete points [
29]. In geology, a triangular prism can be decomposed into the basic tetrahedron elements to fit the features of borehole data and the trends of the strata. It can also effectively describe the regional and directional changes of the properties of a geological body.
(4) Spline Interpolation
In the numerical analysis, Spline interpolation is a form of interpolation where the interpolant is a special type of a piecewise polynomial called a spline. Spline interpolation is often preferred over polynomial interpolation because the interpolation error can be reduced even when using low degree polynomials for the spline [
13]. Spline interpolation avoids the problem of Runge’s phenomenon, as oscillation can occur between points when interpolating using high degree polynomials. The main advantages of spline interpolation are its stability and calculation simplicity. Sets of linear equations used to solve to construct splines are very well-conditioned; therefore, the polynomial coefficients are calculated precisely.
In the existing body of work, however, little attention has been paid to methods that describe the regional and directional changes of the properties of a geological body. To fill this gap, we propose two interpolation methods based on a triangular prism volume element, as a triangular prism structure best represents directivity, to express geological property fields.
4. Geostatistical Model of 3D Interpolation
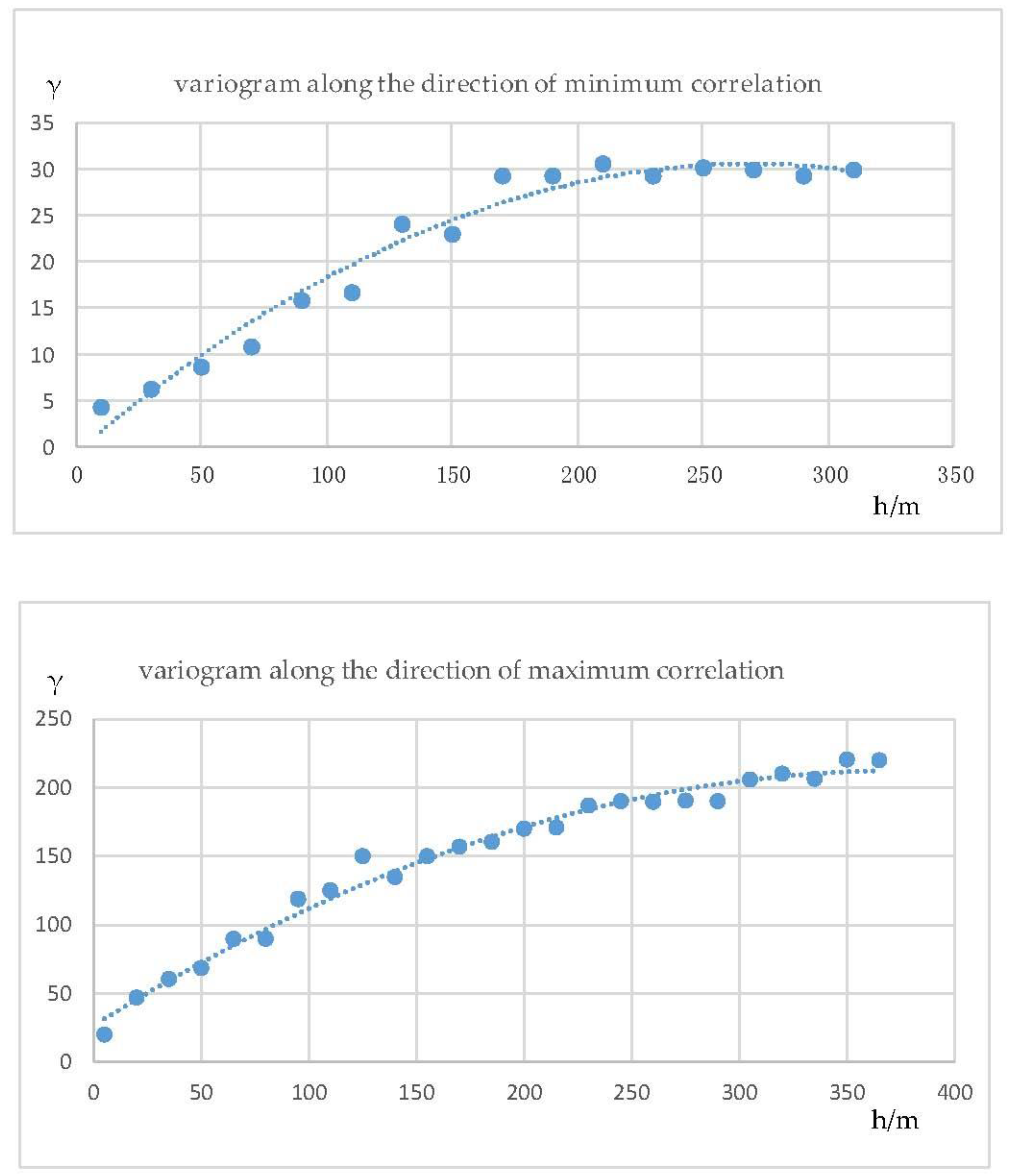
Anisotropy is common phenomenon in geoscience applications [
4]; therefore, it is necessary to design a specific model that accounts for spatial correlations in three dimensions. The variogram is a basic visualization tool to represent spatial correlations in geostatistics. In terms of a regionalized variable, a variogram reflects the spatial variation characteristics of properties, especially the structural characteristics. We can explore geological phenomena by fitting the variogram model. The variogram guarantees an effective spatial prediction in interpolation methods, most notably in kriging [
35].
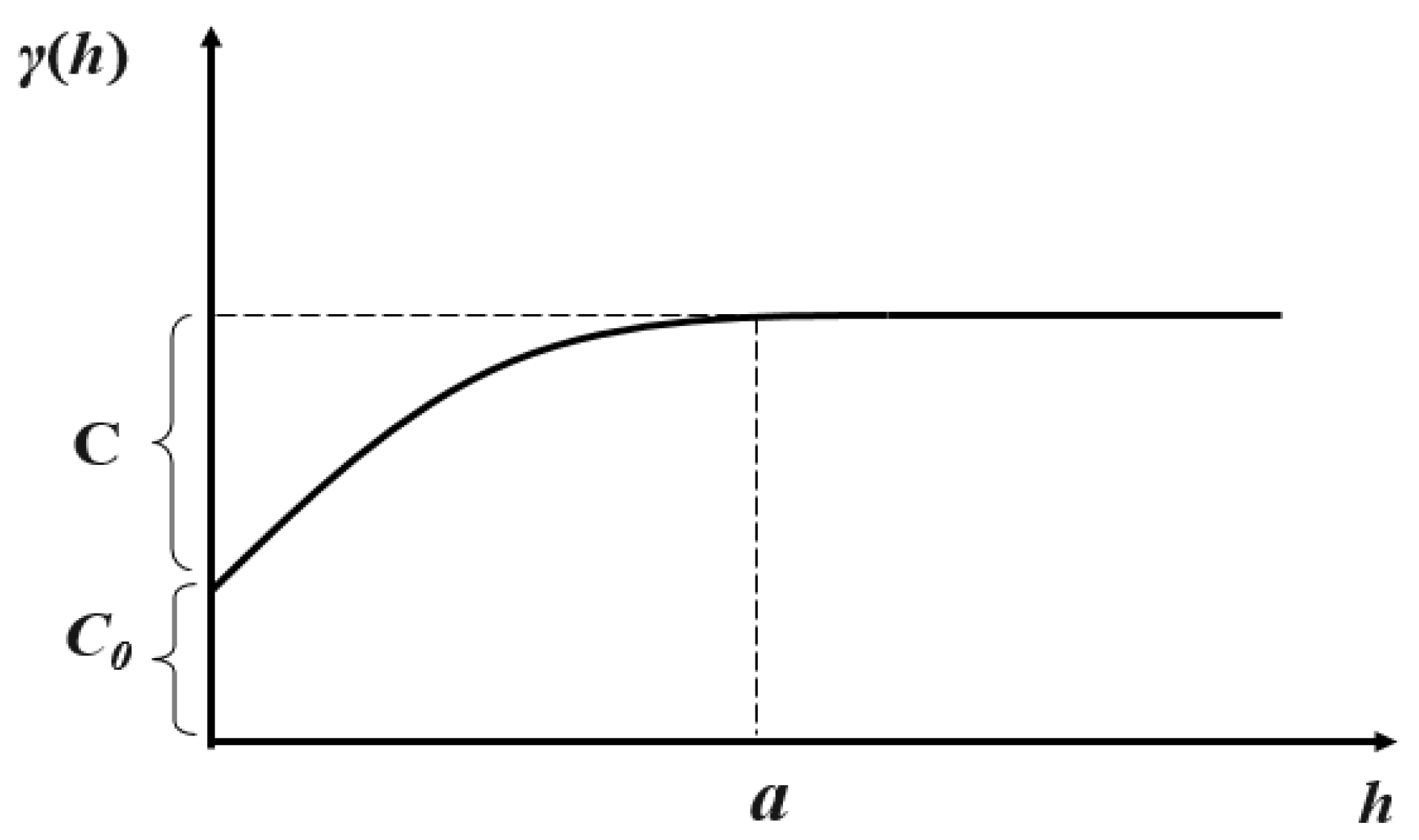
The variogram is estimated according to the coordinates and properties of a set of sampling points in geological space, as shown in Equation (23).
where
is the number of pairs of sample data from a distance of
.
and
are the property values located in
and
. A variogram is a variation map which plots change in
together with the changes in
, as shown in
Figure 8.
where
is the still,
is nugget,
is the arch height, and
is the range.
When interpolating 3D spatial properties, we use the eighth-sphere method to search all the near neighbors of the interpolation point with an appropriate search radius [
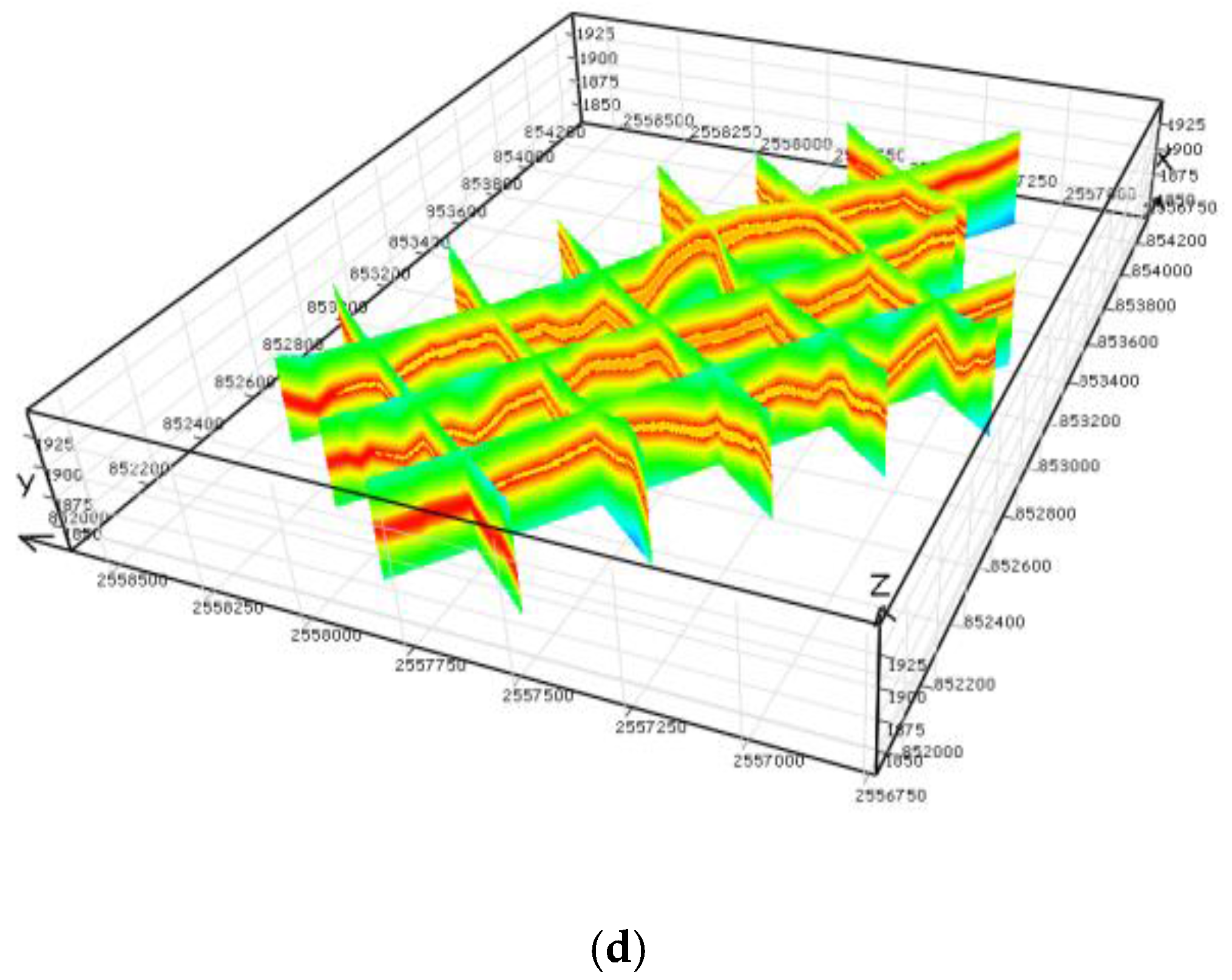
35]. Given the heterogeneity and geometrical anisotropy of 3D geological property fields, the direction of the variable range will be an ellipsoid, as an ellipsoid generalizes the direction and size of the autocorrelation structure of the data represented by the variogram. In our experimental data, organic matter displays a uniform and slow change in the horizontal direction, while rapid change occurs in the vertical direction. We infer that the horizontal direction is the minimum correlation and the vertical direction is maximum correlation. Variograms of organic matter are shown in
Figure 9. We find that the range of the vertical direction (the direction of the maximum) is shorter than the horizontal direction (the direction of the minimum). This indicates that organic matter changes faster with stronger anisotropy and heterogeneity in the vertical direction. In addition, the still is larger, indicating that the magnitude of the change in organic matter is greater and anisotropy stronger in the vertical direction than in the horizontal direction. Our experimental results are consistent with the statistical theory [
36]. In kriging interpolation, we use the fitting variogram model to obtain weights for the sampling points and interpolation point properties.
6. Conclusions
Most current 3DGM techniques focus on geometric and visualized models to explore geological data. A geometric model however, can only satisfy basic requirements. Obtaining an accurate and precise model of property fields in a geological body permits more advanced exploration for greater insights into a phenomenon of interest. Most of the interpolation methods generate large errors, as they apply general 3D statistical interpolation methods, such as kriging and IDW, and ignore the property characteristics in a geological model.
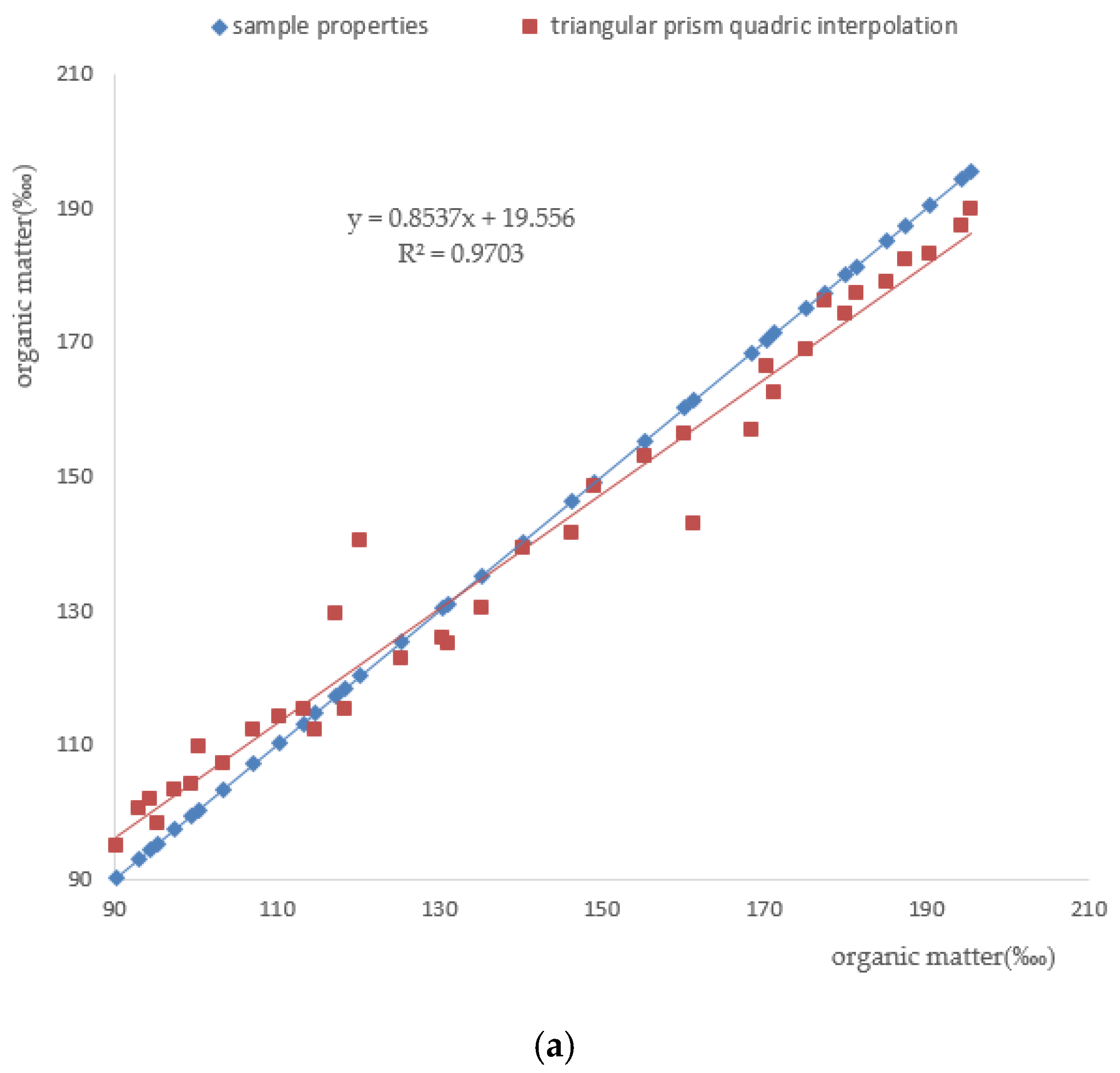
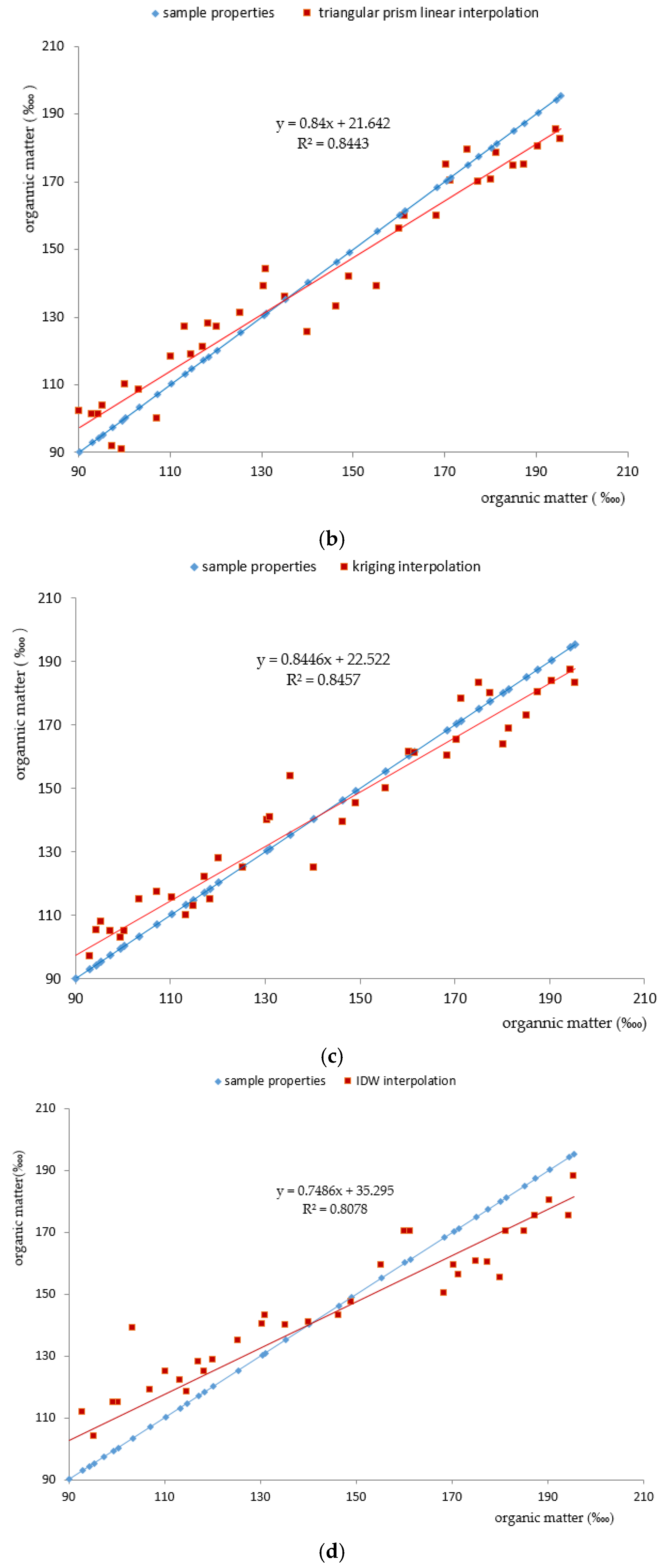
This paper compensates for the shortcomings of the traditional interpolation methods algorithmically, and proposes a function that expresses the heterogeneous distribution of properties in geological bodies: a spatial interpolation function based on the GTP. With this idea, we can build both a vector model and a geometric model. In addition, we can also express the internal change in the properties of a geological body. The experimental profile results, statistical errors, and cross-validation are used to analyze the accuracy of interpolation methods.
The experiments undertaken in this study show that the triangular prism quadric interpolation algorithm is more than comparable to kriging and IDW [
26,
37,
38], and is actually superior. The spline elements of the 15 nodes on the triangular prism show a high accuracy and stability and are insensitive to mesh distortion. In terms of its application, it reflects both overall trends and local change in a property field, achieving smoothness when reaching an adjacent body. In addition, the triangular prism quadric interpolation algorithm also has directivity, expressing properties along both the horizontal and vertical layers. Some other interpolation algorithms, such as the 13-node pyramid element and the 21-node hexahedral element, have been successfully applied in elasticity mechanics [
21]. The linear triangular prism interpolation algorithm does not perform as well as the interpolation algorithm tested; however, it is easy to use, has a high efficiency, and expresses local changes in properties. Kriging is a traditional low-pass filter interpolation algorithm [
26], and expresses a property better than the linear triangular prism overall; however, this approach cannot reflect local information found in the original data. IDW interpolation has a “cluster” effect with no directivity; therefore, it gives the least satisfying results.
While we argue that the triangular prism interpolation algorithm is an effective and efficient method for expressing the heterogeneity of a property field, its accuracy and reliability have nevertheless not yet been fully established when considering restricted conditions such as folds, faults, and so on. Furthermore, in this paper, we achieve complete and continuity in a single triangular prism, but the splicing method for the adjacent triangular prisms yields only an approximate continuity. These issues will be addressed in our future research.