A Hierarchical Approach for Measuring the Consistency of Water Areas between Multiple Representations of Tile Maps with Different Scales
Abstract
:1. Introduction
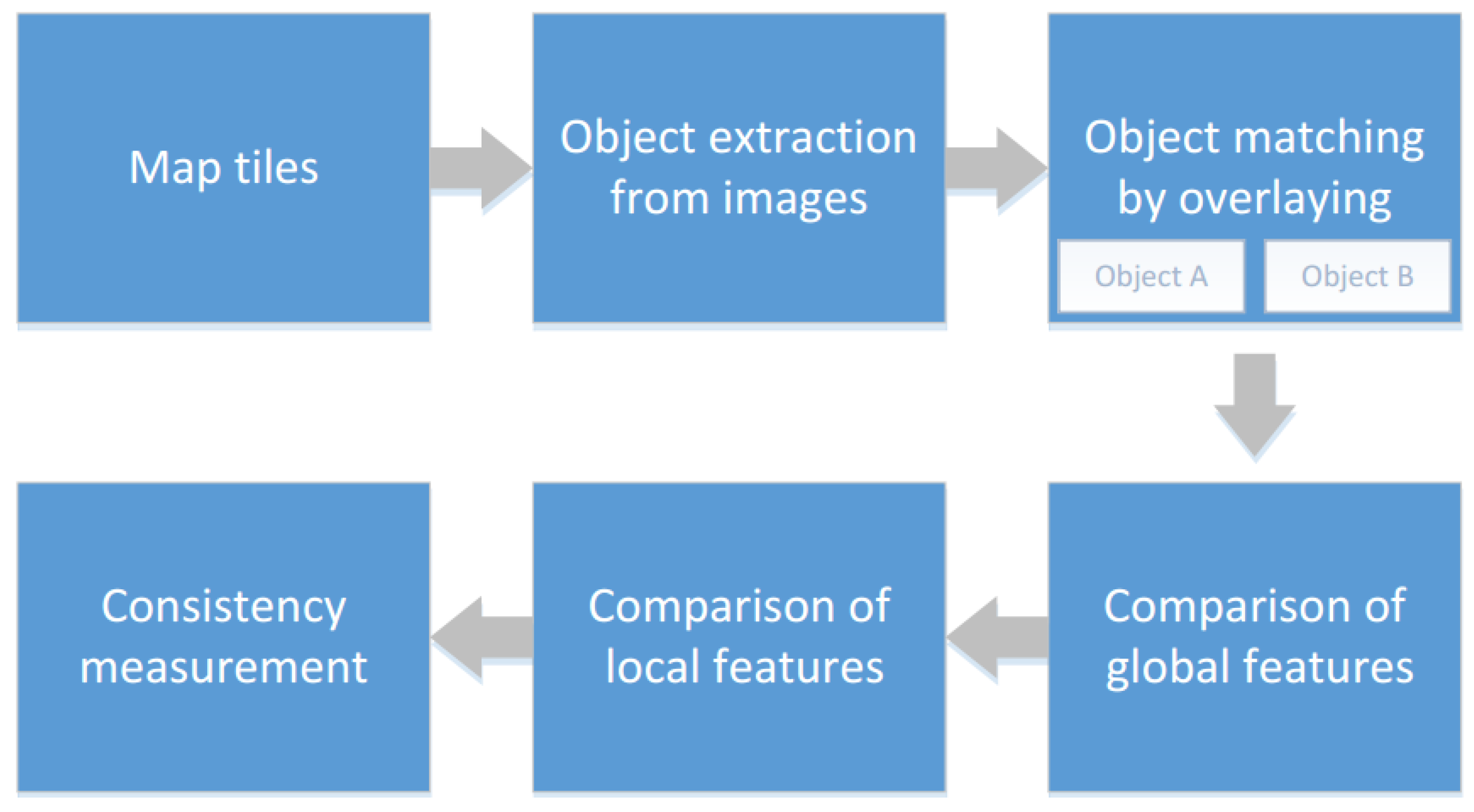
2. Framework of Hierarchical Consistency Assessment for Water Areas
Framework for Measuring Consistency
3. Measuring the Consistency of Water Areas
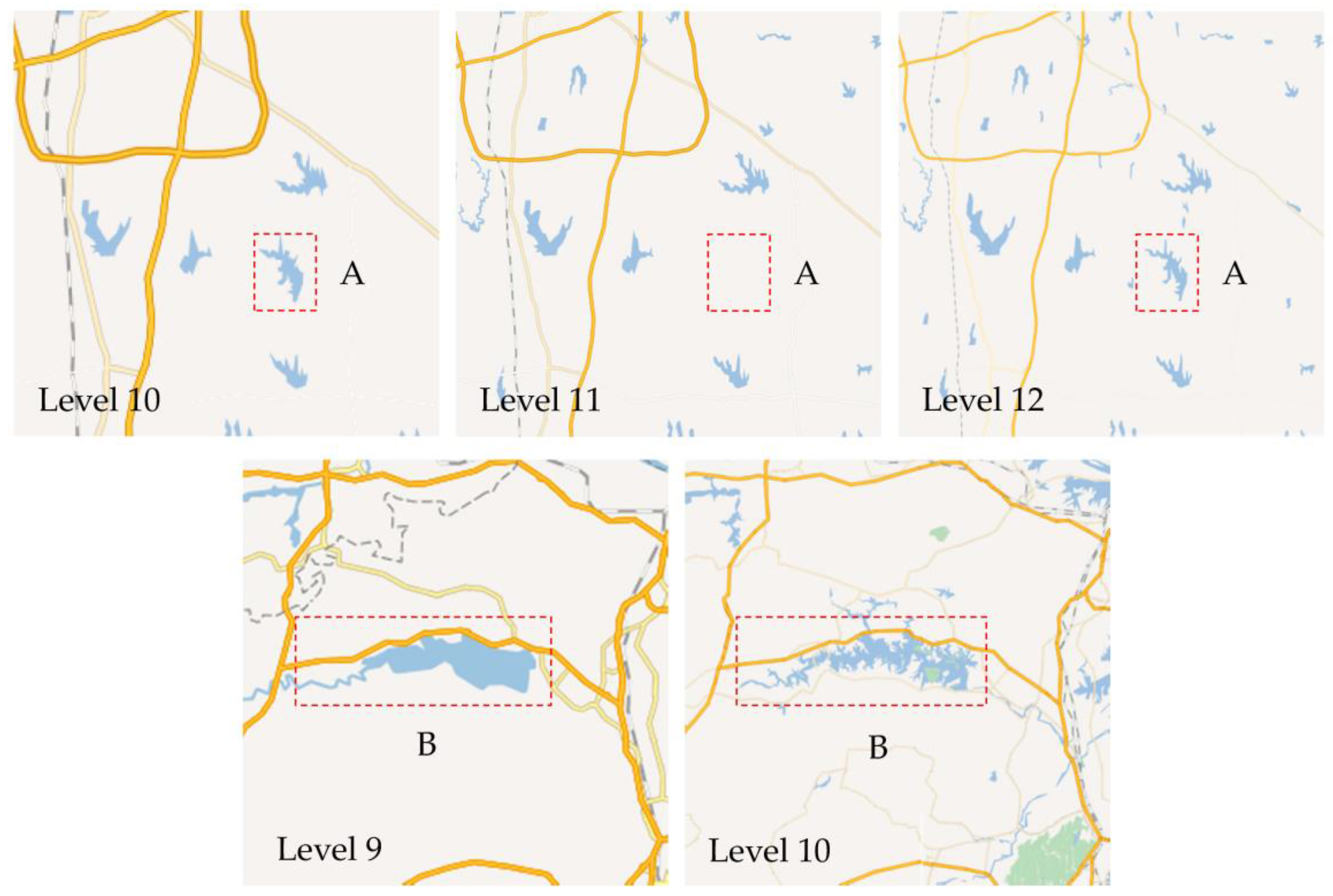
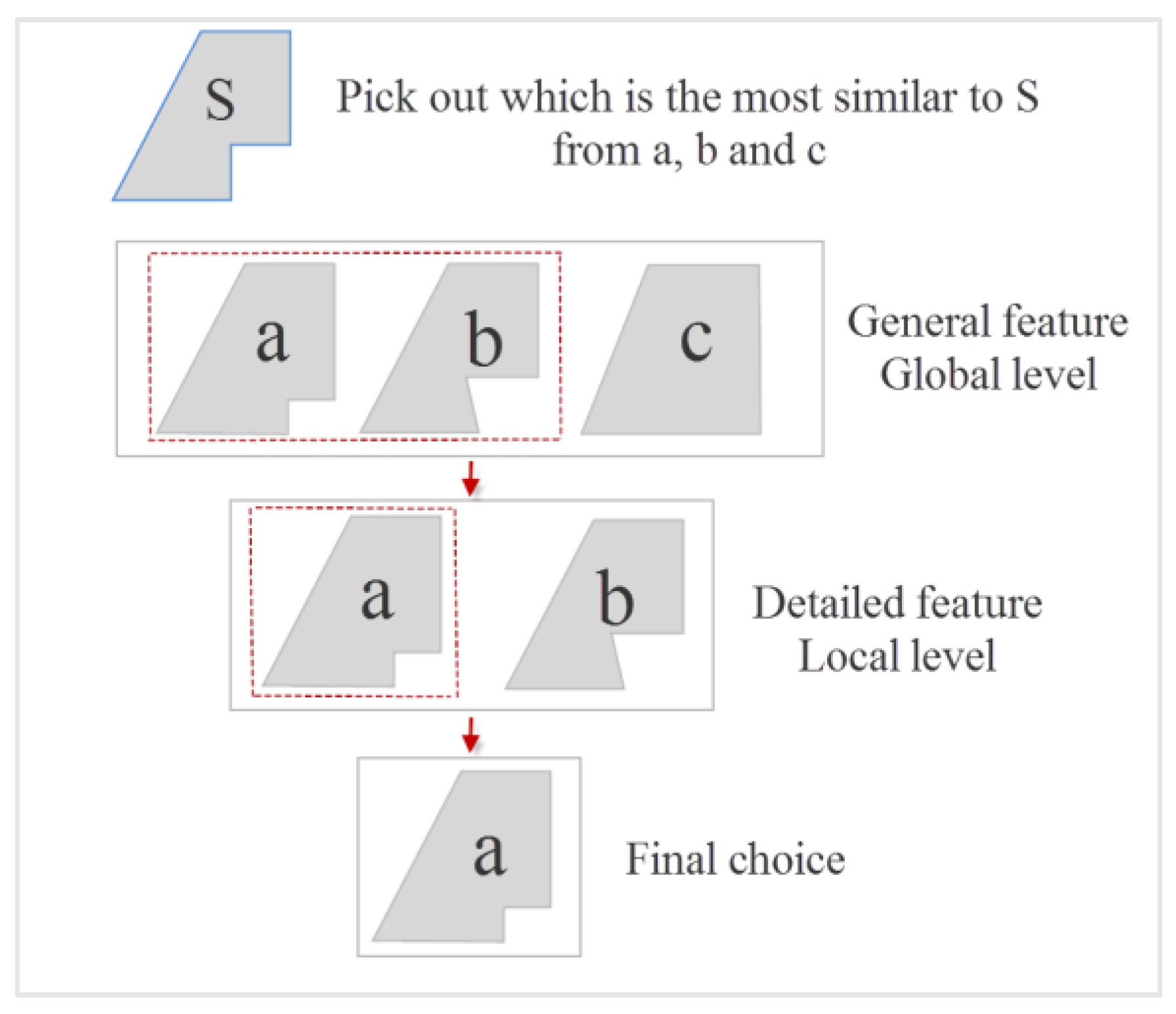
3.1. Feature Classification and the Degree of Consistency
3.1.1. Degree of Global Feature Consistency
- (1)
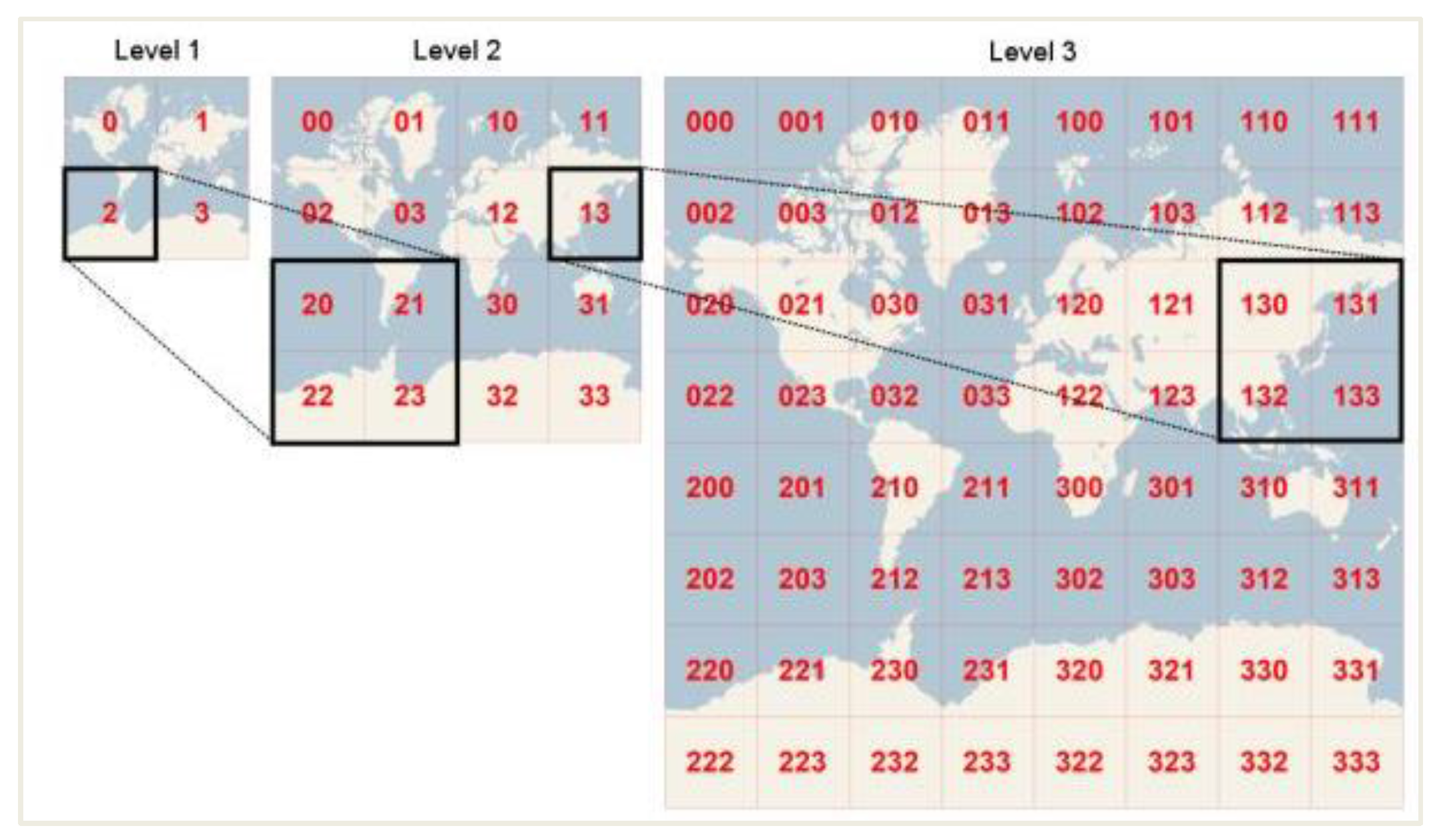
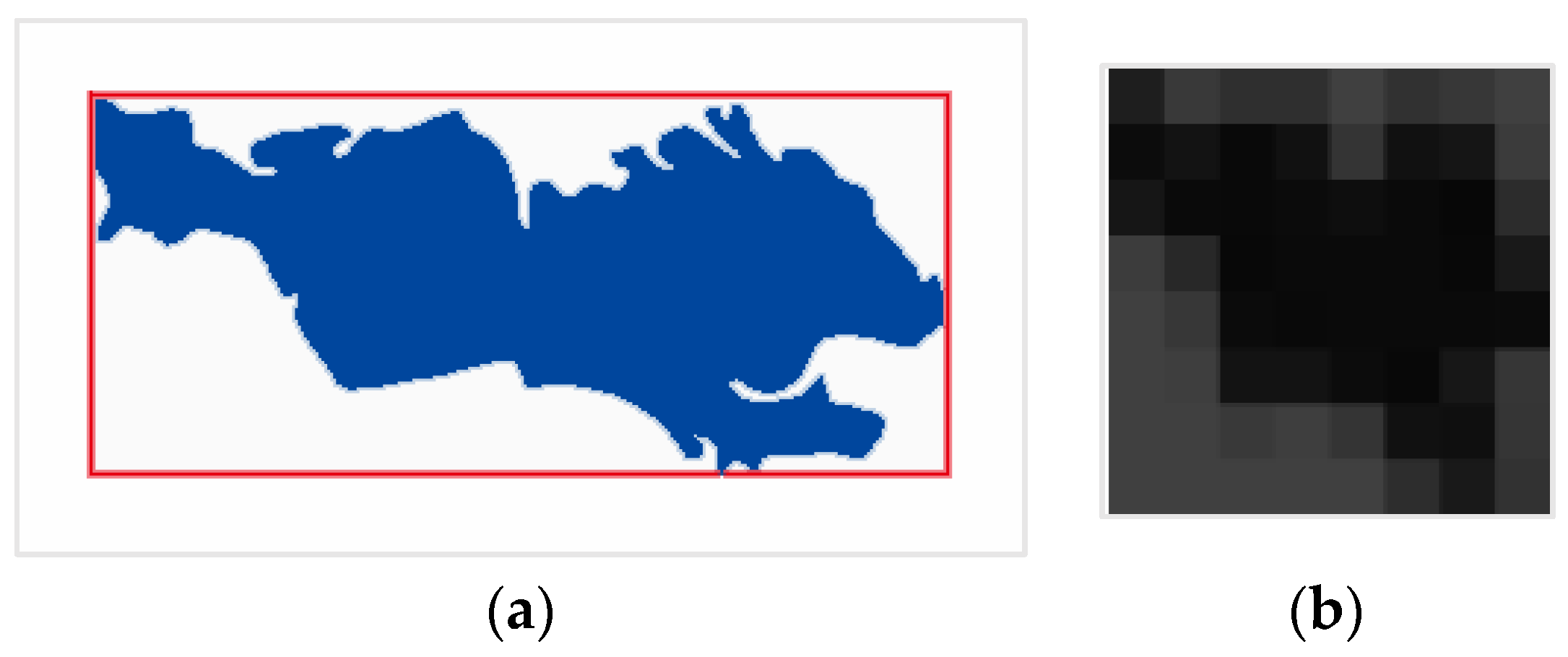
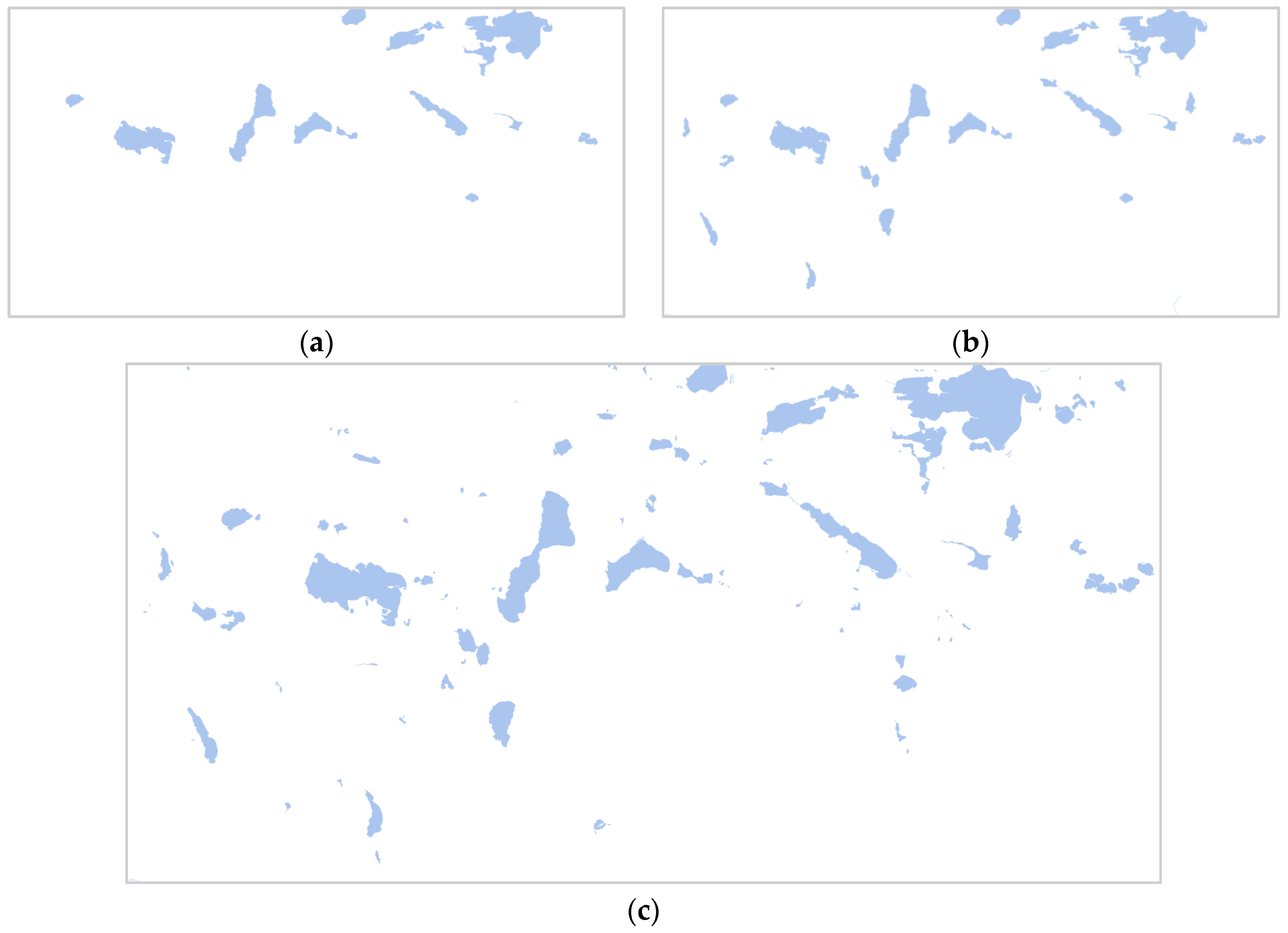
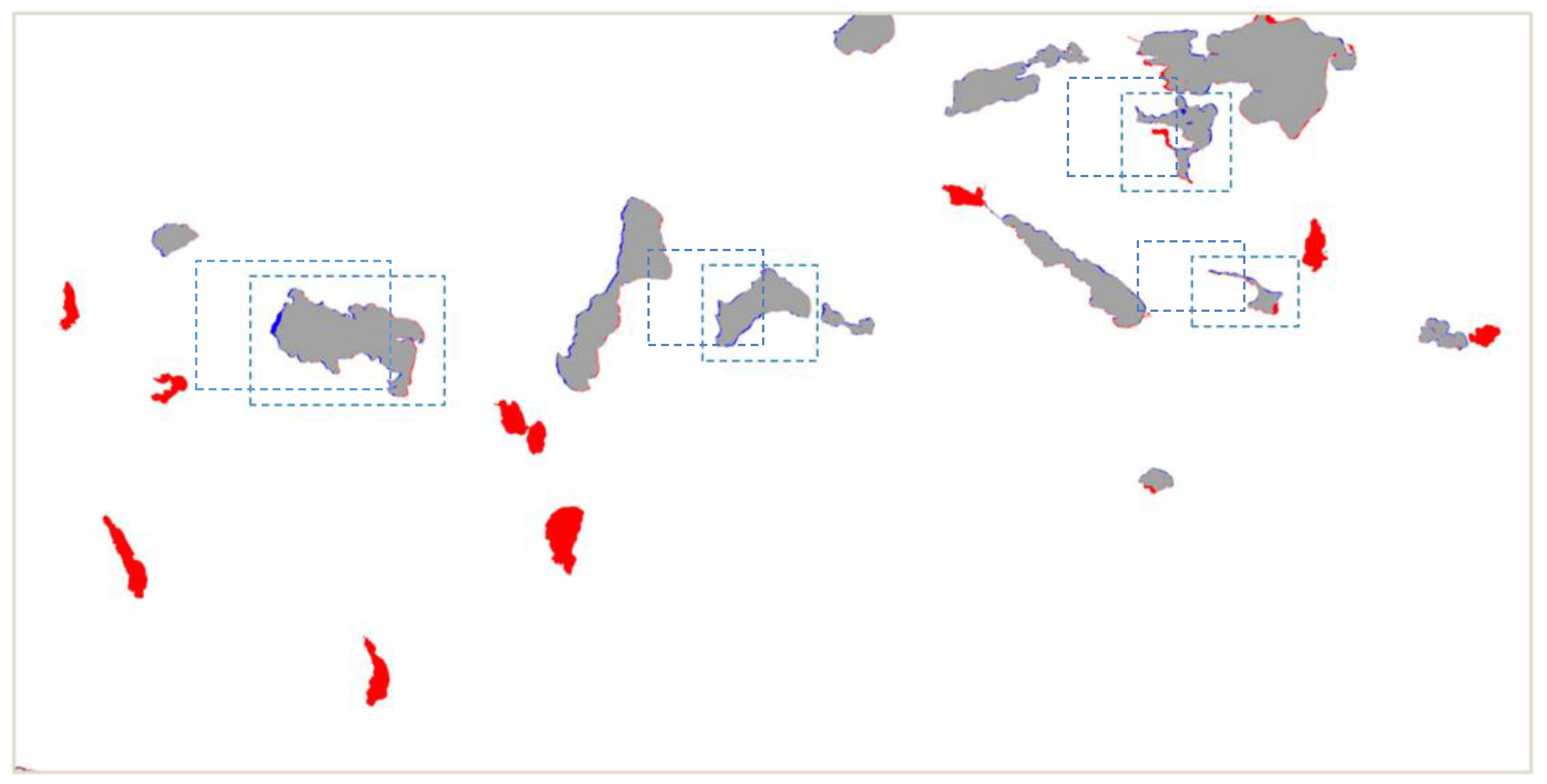
- Determine the calculation region. A reasonable calculation region should be identified before feature extraction. In this paper, we consider the minimum bounding rectangle of the object to be the effective calculation region, as shown in Figure 5a.
- (2)
- Reduce the size. Shrinking is performed to retain sketchy information and remove the high frequencies in an image. In this circumstance, we shrink the image to 8 × 8, yielding a total of 64 pixels. The aspect ratio does not need to be maintained, and features can be condensed to fit into an 8 × 8 square. Thus, the hash algorithm can be applied to assess any changes in the image without considering the scale or aspect ratio.
- (3)
- Reduce and average the colours. A small 8 × 8 picture is transformed to a grayscale image, as shown in Figure 5b, and the average gray value of the 64 pixels is calculated.
- (4)
- Calculate the bits. Each bit is characterized depending on whether its colour value is above or below the mean.
- (5)
- Construct the hash. The 64 bits are set to a 64-bit integer. The order does not matter, as long as consistency is maintained. For example, bits can be set from left to right or from top to bottom using the big-endian approach.
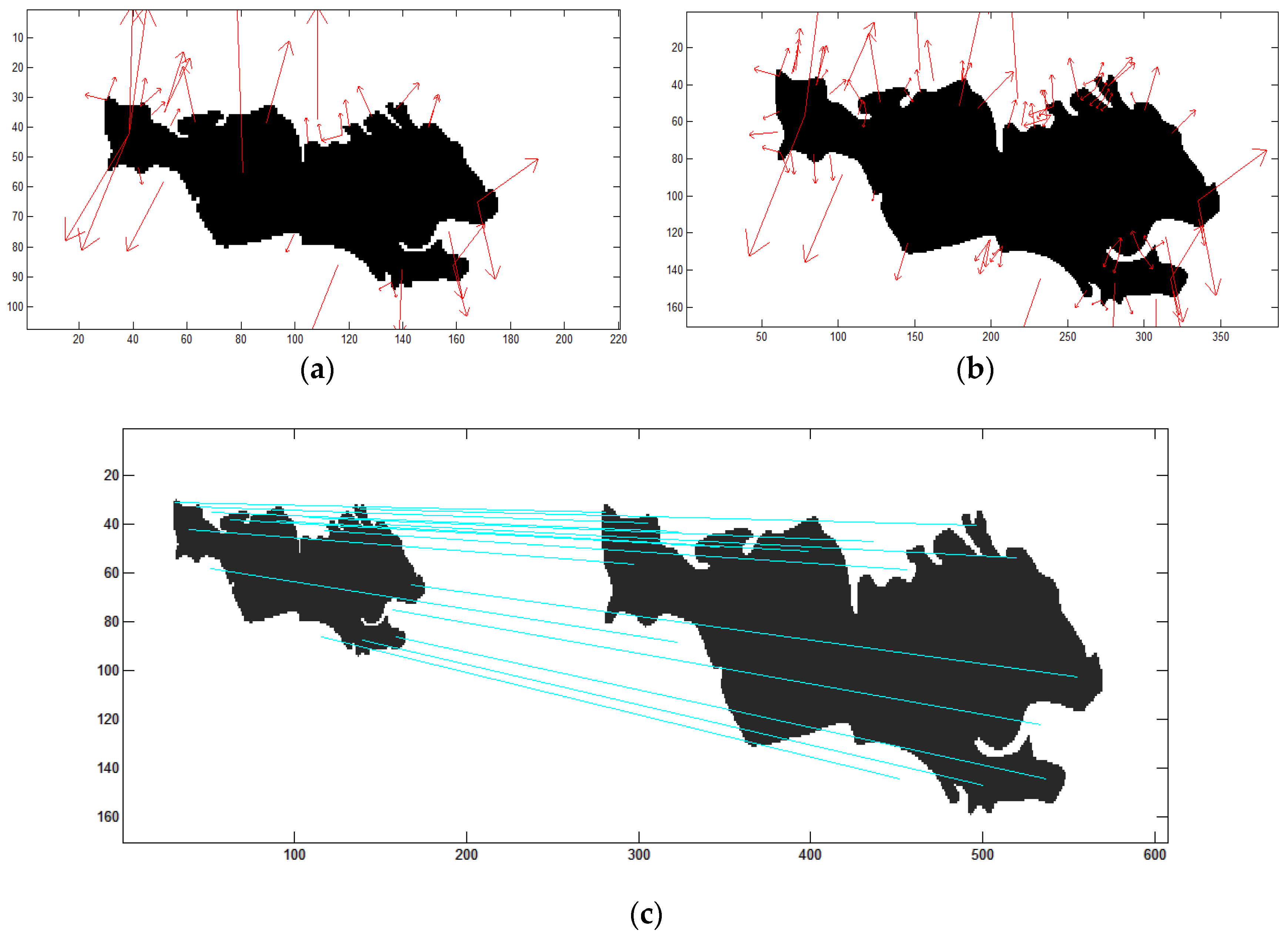
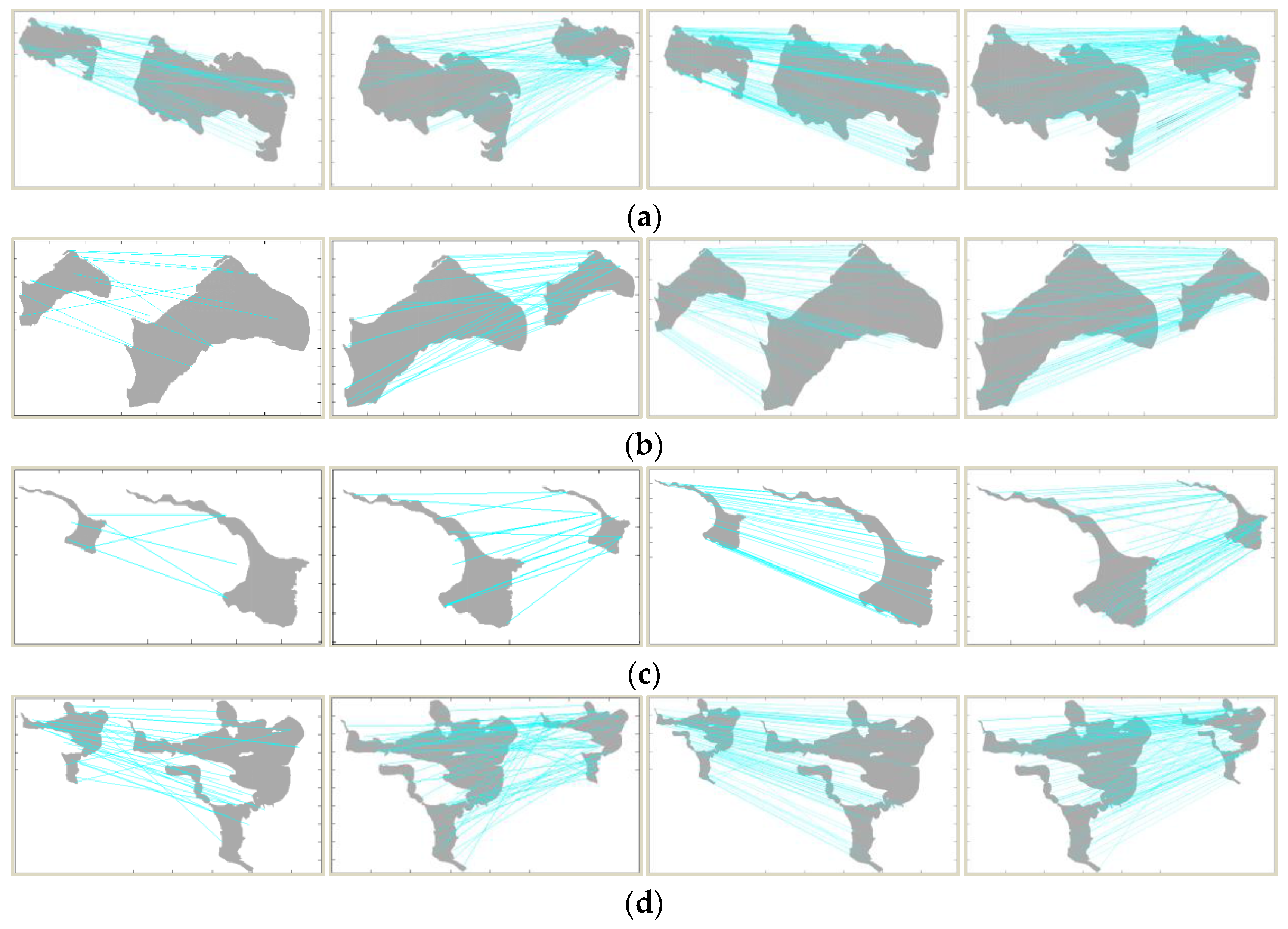
3.1.2. Degree of Local Feature Consistency
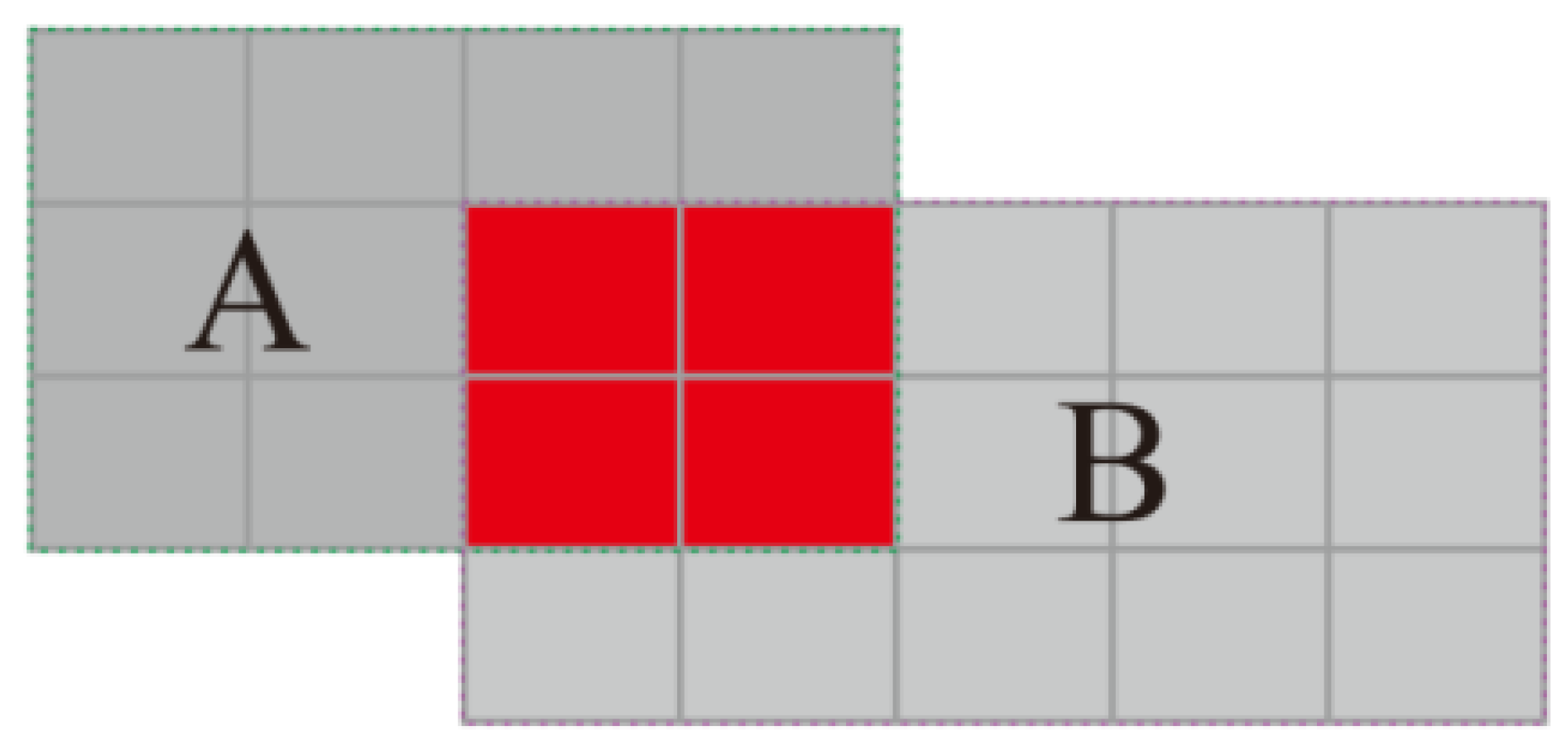
3.1.3. Degree of Overlap
3.2. Definition of Degrees of Consistency
4. Experiments and Analysis
4.1. Methods
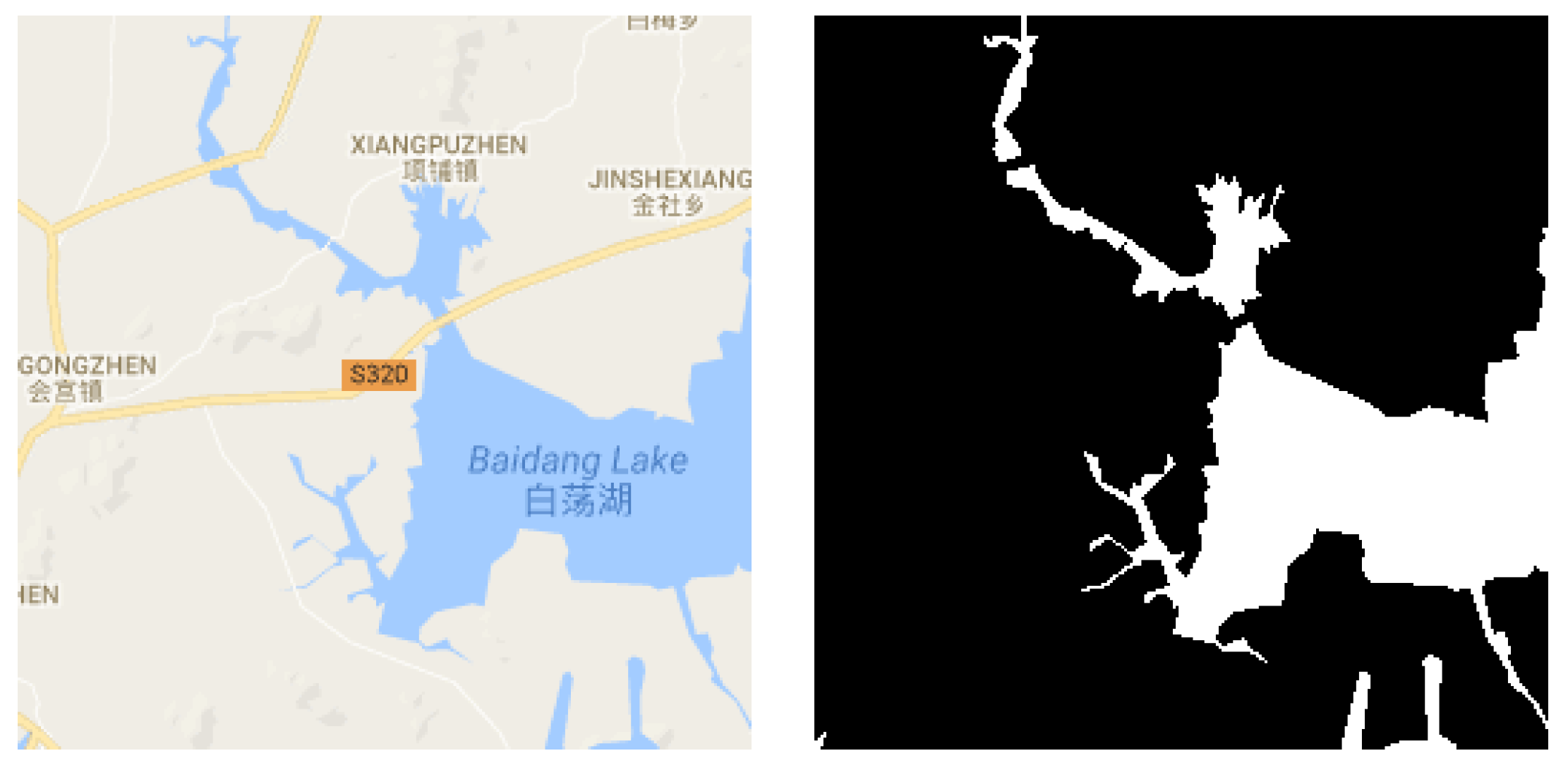
4.1.1. Extract Water Areas via Colour Segmentation
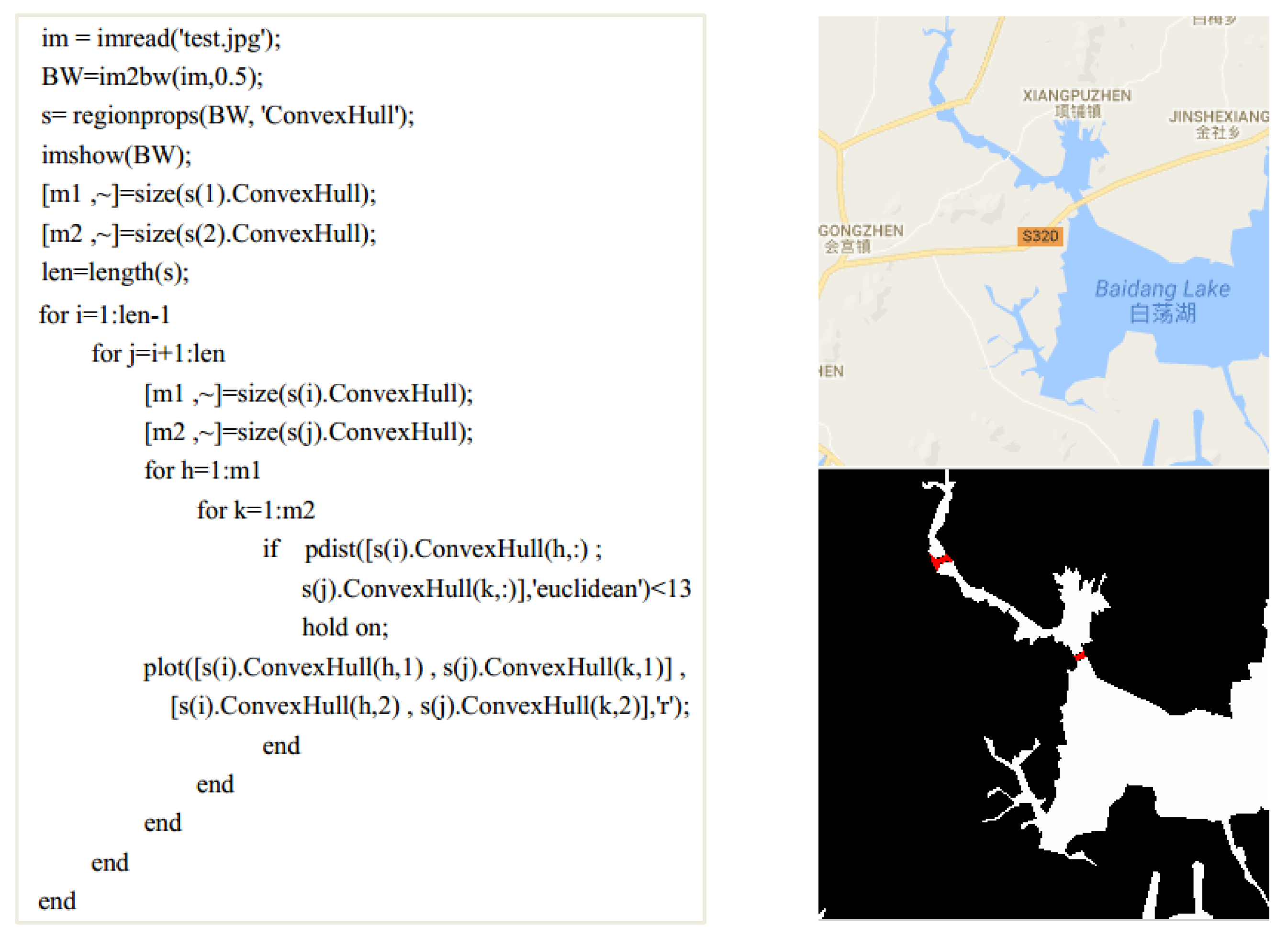
4.1.2. Connection of Fractured Water Areas
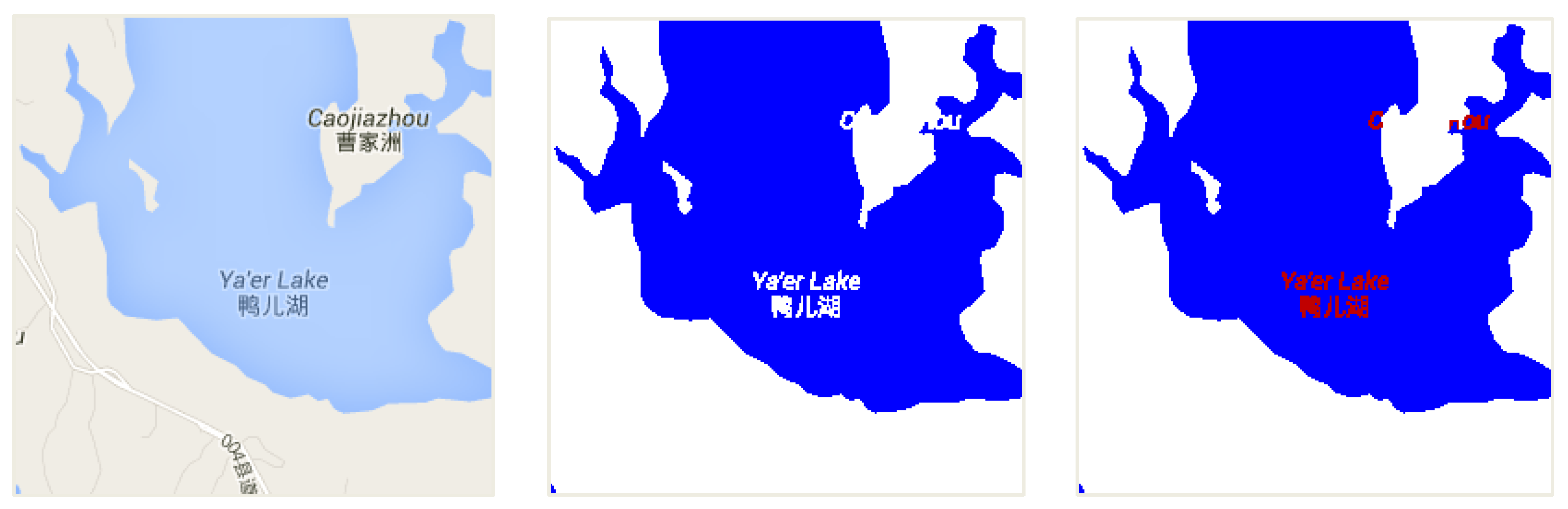
4.1.3. Filling Holes in Water Areas
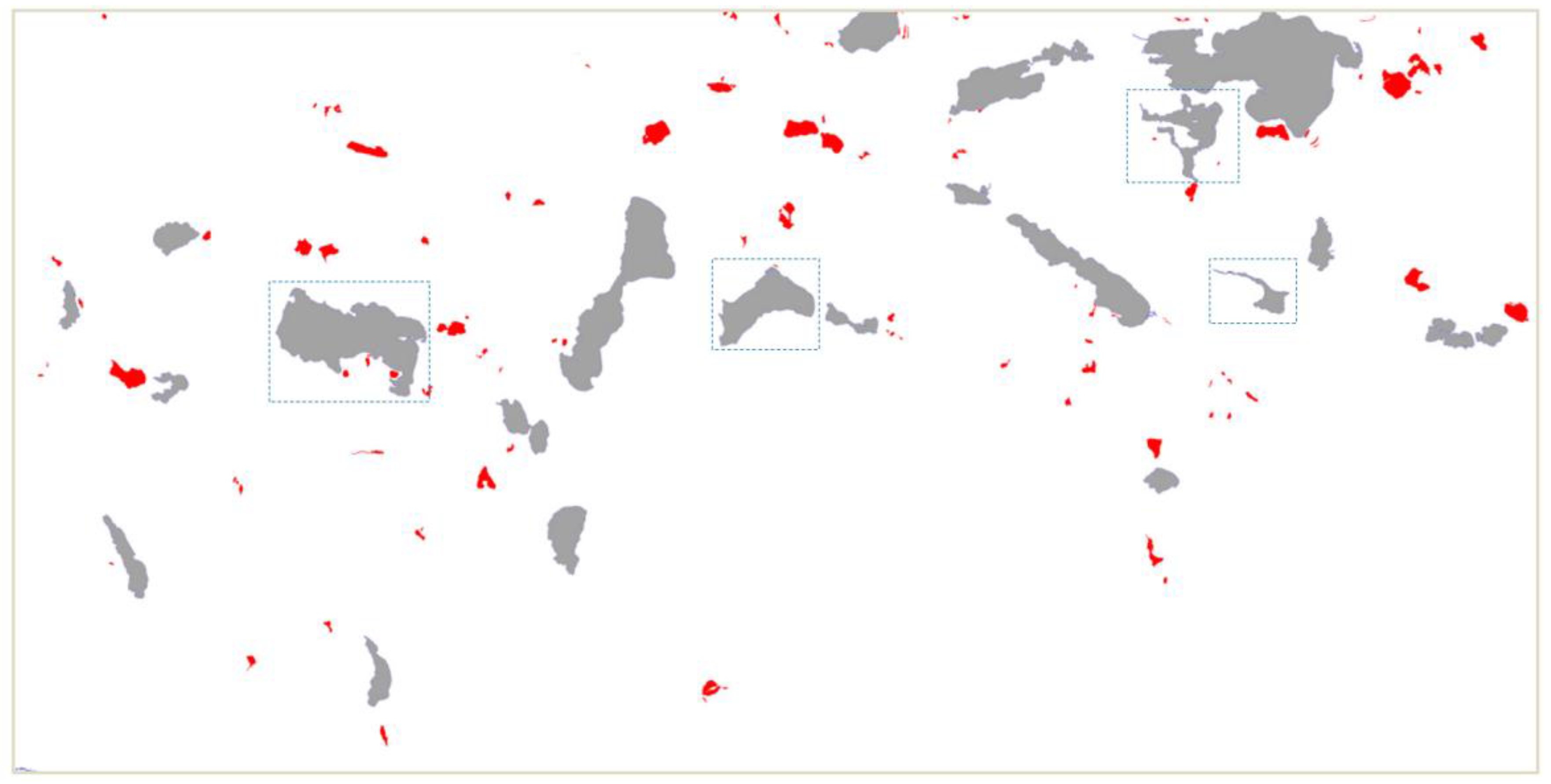
4.2. Study Area
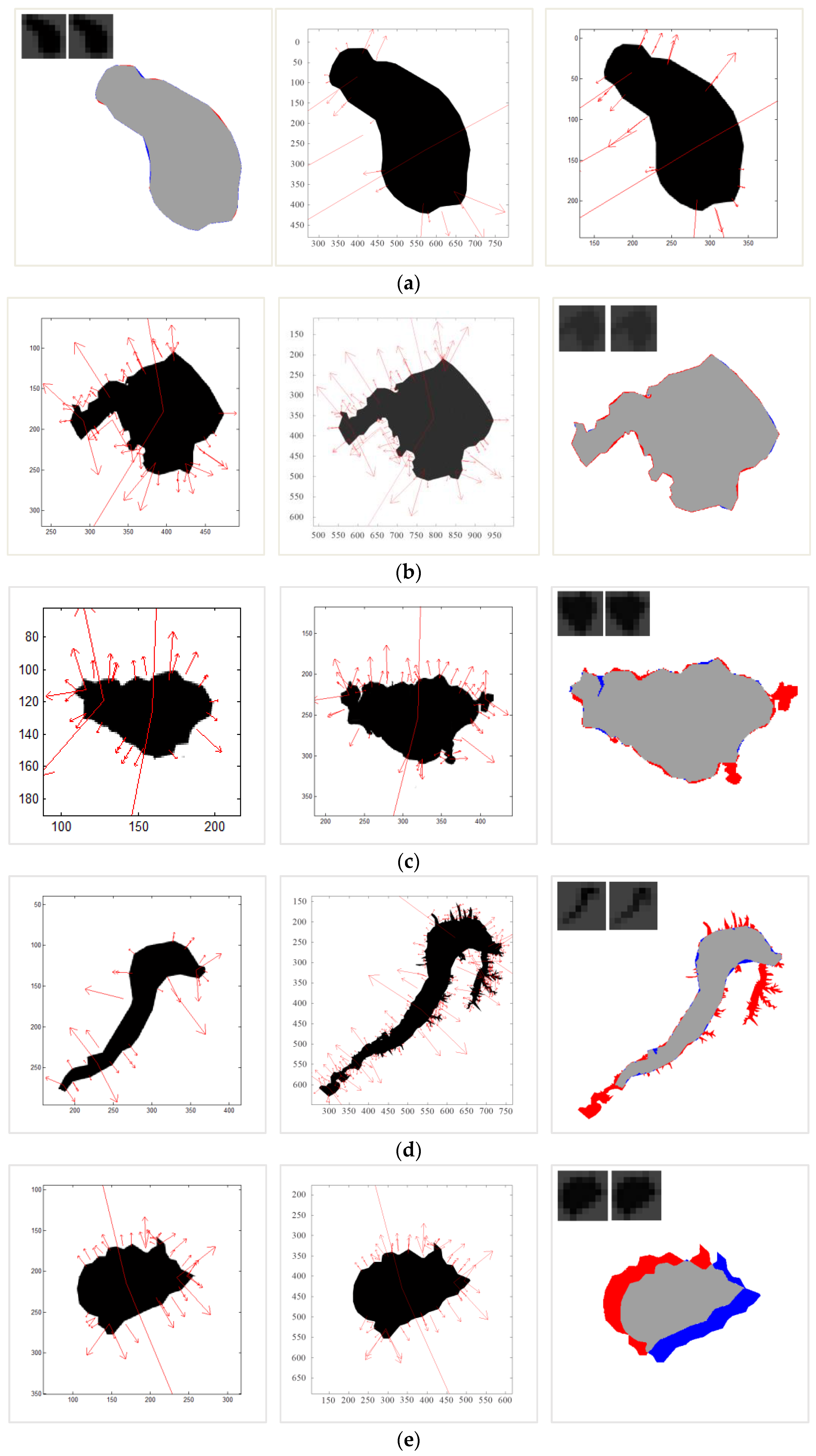
4.3. Results and Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Goodchild, M.F.; Li, L. Assuring the quality of volunteered geographic information. Spat. Stat. 2012, 1, 110–120. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Muller, J.C. Issues of Quality and Uncertainty. In Advances in Cartography; Muller, J.-C., Ed.; Elsevier: London, UK, 1991; pp. 113–139. [Google Scholar]
- Bertolotto, M.; Egenhofer, M.J. Progressive transmission of vector data over the World Wide Web. GeoInformatica 2001, 5, 345–373. [Google Scholar] [CrossRef]
- Parent, C.; Spaccapietra, S.; Zimanyi, E. The MurMur project: Modeling and querying multi-representation spatio-temporal databases. Inf. Syst. 2006, 5, 733–769. [Google Scholar] [CrossRef]
- Duckham, M.; Lingham, J.; Mason, K.; Worboys, M. Qualitative reasoning about consistency in geographic information. Inf. Sci. 2006, 176, 601–627. [Google Scholar] [CrossRef]
- Goodchild, M.F. Citizens as sensors: The world of volunteered geography. GeoJournal 2007, 69, 211–221. [Google Scholar] [CrossRef]
- Du, H.; Anand, S.; Alechina, N.; Morley, J.; Hart, G.; Leibovici, D.; Jackson, M.; Ware, M. Geospatial information integration for authoritative and crowd sourced road vector data. Trans. GIS 2012, 16, 455–476. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, Y.; Luan, X. A probabilistic relaxation approach for matching road networks. Int. J. Geogr. Inf. Sci. 2012, 27, 319–338. [Google Scholar] [CrossRef]
- Koukoletsos, T.; Haklay, M.; Ellul, C. Assessing data completeness of VGI through an automated matching procedure for linear data. Trans. GIS 2012, 16, 477–498. [Google Scholar] [CrossRef]
- Abdelmoty, A.I.; Jones, C.B. Towards Maintaining Consistency of Spatial Databases. In Proceedings of the Sixth International Conference on Information and Knowledge Management, Las Vegas, NV, USA, 10–14 November 1997; pp. 293–300. [Google Scholar]
- Dettori, G.; Puppo, E. How Generalization Interacts with the Topological and Metric Structure of Maps. In Proceedings of the 7th International Symposium on Spatial Data Handling, London, UK, 12–16 August 1996; pp. 9–27. [Google Scholar]
- Delis, V.; Hadzilacos, T. On the Assessment of Generalisation Consistency. In Proceedings of the International Symposium on Advances in Spatial Databases, Berlin, Germany, 15–18 July 1997; pp. 321–335. [Google Scholar]
- Du, S. Evaluating structural and topological consistency of complex regions with broad boundaries in multi-resolution spatial databases. Inf. Sci. 2008, 178, 52–68. [Google Scholar] [CrossRef]
- Rodríguez, A. Inconsistency issues in spatial databases. In Inconsistency Tolerance, 1st ed.; Bertossi, L., Hunter, A., Schaub, T., Eds.; Lecture Notes in Computer Science 3300; Springer: Berlin/Heidelberg, Germany, 2005; pp. 237–269. [Google Scholar]
- Egenhofer, M.J.; Sharma, J. Topological Consistency. In Proceedings of the Fifth International Symposium on Spatial Data Handling, Charleston, SC, USA, 3–7 August 1992; pp. 335–343. [Google Scholar]
- Tryfona, N.; Egenhofer, M.J. Multi-resolution Spatial Databases: Consistency among Networks. In Proceedings of the Sixth International Workshop on Foundations of Models and Languages for Data and Objects, Schloss Dagstuhl, Germany, 16–20 September 1996; pp. 119–132. [Google Scholar]
- Tryfona, N.; Egenhofer, M.J. Consistency among parts and aggregates: A computational model. Trans. GIS 1996, 1, 189–206. [Google Scholar] [CrossRef]
- Kang, H.K.; Kim, T.W.; Li, K.J. Topological Consistency for Collapse Operation in Multiscale Databases. In Proceedings of the 23rd International Conference on Conceptual Modeling, Berlin, Germany, 8–12 November 2004; pp. 91–102. [Google Scholar]
- Du, S.; Guo, L.; Wang, Q. A scale-explicit model for checking directional consistency in multiresolution spatial data. Int. J. Geogr. Inf. Sci. 2010, 24, 465–485. [Google Scholar] [CrossRef]
- Rodríguez, M.A.; Brisaboa, N.; Meza, J.; Luaces, M.R. Measuring Consistency with Respect to Topological Dependency Constraints. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 182–191. [Google Scholar]
- Brisaboa, N.R.; Luaces, M.R.; Andrea Rodríguez, M.; Seco, D. An inconsistency measure of spatial data sets with respect to topological constraints. Int. J. Geogr. Inf. Sci. 2014, 28, 56–82. [Google Scholar] [CrossRef]
- Ang, Y.H.; Li, Z.; Ong, S.H. Image Retrieval based on Multidimensional Feature Properties. In Proceedings of the Symposium on Electronic Imaging: Science & Technology, San Jose, CA, USA, 23 March 1995; pp. 47–57. [Google Scholar]
- Zahn, C.T.; Roskies, R.Z. Fourier descriptors for plane closed curves. IEEE Trans. Comput. 1972, 100, 269–281. [Google Scholar] [CrossRef]
- Veltkamp, R.C. Shape Matching: Similarity Measures and Algorithms. In Proceedings of the SMI 2001 International Conference on Shape Modeling and Applications, San Jose, CA, USA, 7–11 May 2001; pp. 188–197. [Google Scholar]
- Lee, D.J.; Antani, S.; Long, L.R. Similarity Measurement Using Polygon Curve Representation and Fourier Descriptors for Shape-based Vertebral Image Retrieval. In Proceedings of the SPIE on Medical Imaging 2003: International Society for Optics and Photonics, San Diego, CA, USA, 16 May 2003; pp. 1283–1291. [Google Scholar]
- Mortara, M.; Spagnuolo, M. Similarity measures for blending polygonal shapes. Comput. Graph. 2001, 25, 13–27. [Google Scholar] [CrossRef]
- Latecki, L.J.; Lakamper, R. Shape similarity measure based on correspondence of visual parts. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1185–1190. [Google Scholar] [CrossRef]
- McMaster, R.B.; Shea, K.S. Generalization in Digital Cartography; Association of American Geographers: Washington, DC, USA, 1992. [Google Scholar]
- Goodchild, M.; Jeansoulin, R. Data Quality in Geographic Information: From Error to Uncertainty, 1st ed.; Hermes: Paris, France, 1998. [Google Scholar]
- Egenhofer, M.J.; Clemeentini, E.; Felice, P.D. Evaluating inconsistencies among multiple representations. In Proceedings of the 6th International Symposium on Spatial Data Handling, Edinburgh, UK, 5–9 September 1994; pp. 901–920. [Google Scholar]
- Sheeren, D.; Mustière, S.; Zucker, J.D. Consistency Assessment between Multiple Representations of Geographical Databases: A Specification-based Approach. In Developments in Spatial Data Handling, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 617–628. [Google Scholar]
- Ai, T.; Ke, S.; Yang, M.; Li, J. Envelope generation and simplification of polylines using Delaunay triangulation. Int. J. Geogr. Inf. Sci. 2017, 31, 297–319. [Google Scholar] [CrossRef]
- Ai, T.; Li, J. A DEM generalization by minor valley branch detection and grid filling. ISPRS J. Photogramm. Rem. Sens. 2010, 65, 198–207. [Google Scholar] [CrossRef]
- Müler, J.C.; Zeshen, W. Area-patch generalisation: A competitive approach. Cartogr. J. 1992, 29, 137–144. [Google Scholar] [CrossRef]
- Sheeren, D.; Mustière, S.; Zucker, J.D. A data-mining approach for assessing consistency between multiple representations in spatial databases. Int. J. Geogr. Inf. Sci. 2009, 23, 961–992. [Google Scholar] [CrossRef]
- Schneider, M.; Chang, S.F. A Robust Content Based Digital Signature for Image Authentication. In Proceedings of the 3rd IEEE International Conference on Image Processing, Lausanne, Switzerland, 19 September 1996; pp. 227–230. [Google Scholar]
- Swaminathan, A.; Mao, Y.; Wu, M. Robust and secure image hashing. IEEE Trans. Inf. Forensics Secur. 2006, 1, 215–230. [Google Scholar] [CrossRef]
- Li, Y.; Lu, Z.; Zhu, C.; Niu, X. Robust image hashing based on random gabor filtering and dithered lattice vector quantization. IEEE Trans. Image Process. 2012, 21, 1963–1980. [Google Scholar] [PubMed]
- Zhao, Y.; Wang, S.; Zhang, X.; Yao, H. Robust hashing for image authentication using zernike moments and local features. IEEE Trans. Inf. Forensics Secur. 2013, 8, 55–63. [Google Scholar] [CrossRef]
- Lowe, D.G. Object Recognition from Local Scale-Invariant Features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 1150–1157. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
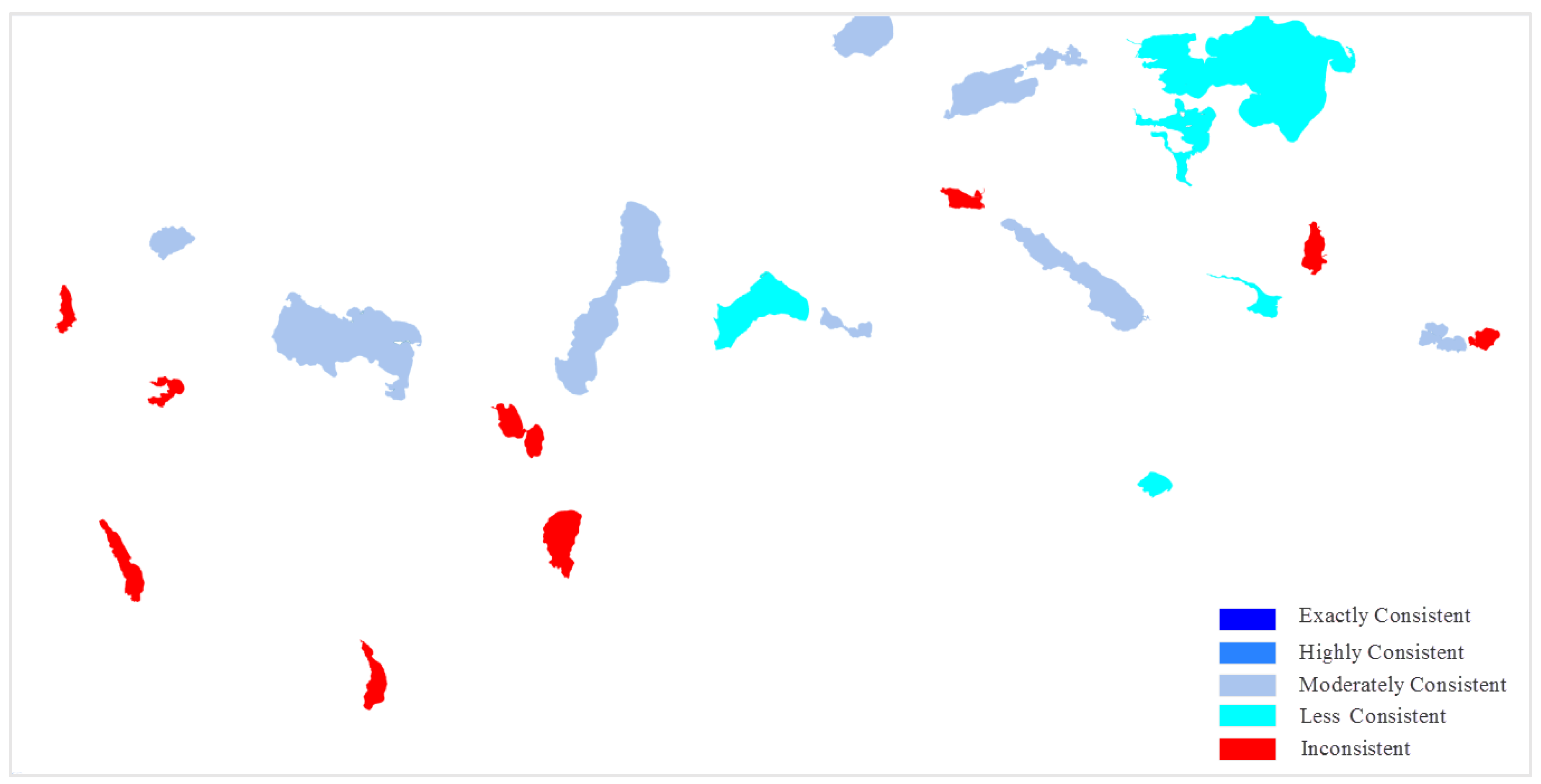
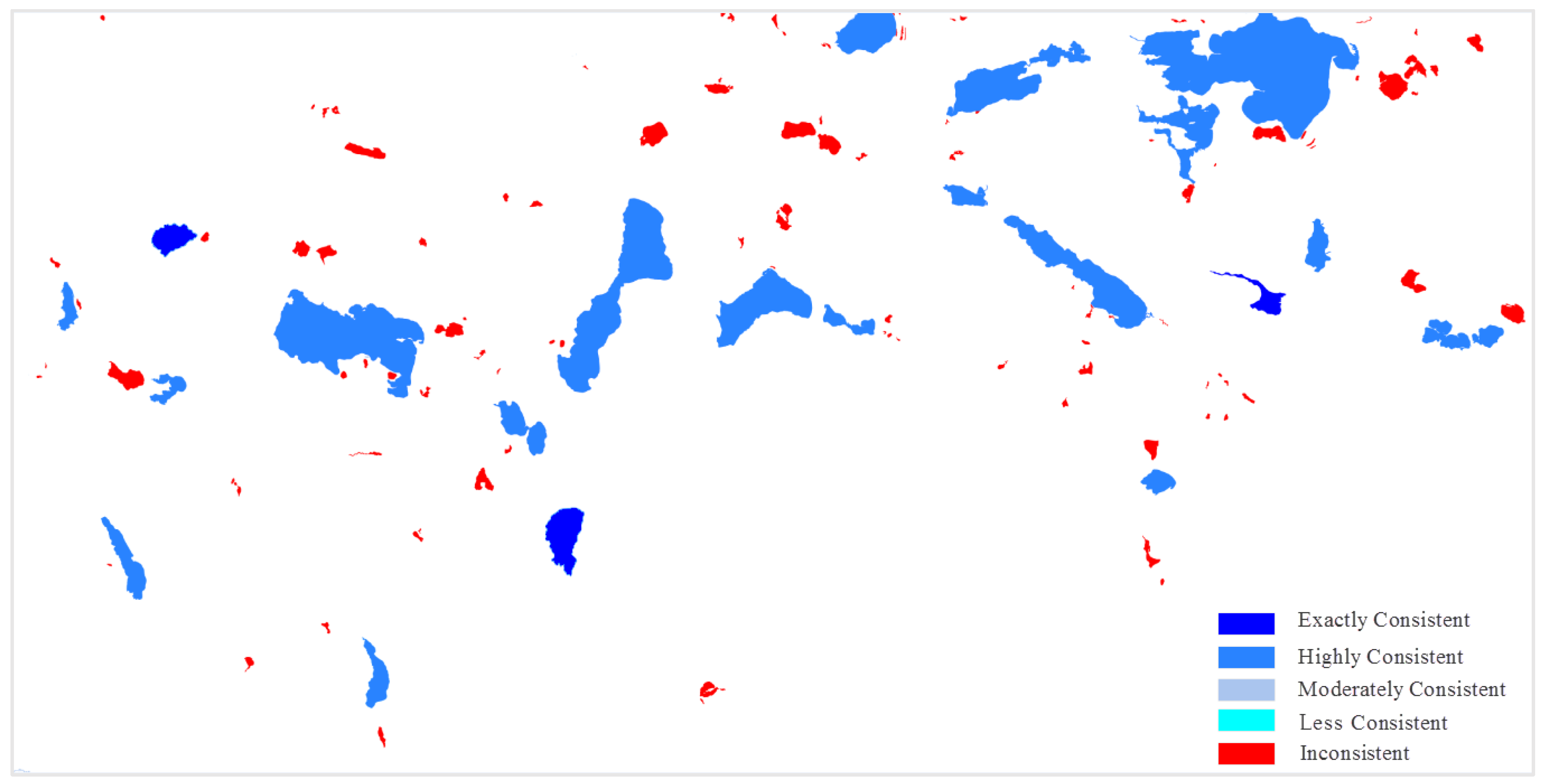
| Exactly consistent | Highly consistent | Moderately consistent | Less consistent | Inconsistent | |
| Highly consistent | Moderately consistent | Less consistent | Inconsistent | Inconsistent | |
| Moderately consistent | Less consistent | Inconsistent | Inconsistent | Inconsistent | |
| Less consistent | Inconsistent | Inconsistent | Inconsistent | Inconsistent | |
| Inconsistent | Inconsistent | Inconsistent | Inconsistent | Inconsistent |
| Level | Keypoints | Matches | LC | GC | OD | C | Grade | |
|---|---|---|---|---|---|---|---|---|
| a | 10–11 | 109/212 | 55/91 | 0.46 | 0.9 | 0.96 | 0.77 | Moderately |
| 11–12 | 212/313 | 155/181 | 0.65 | 1 | 0.99 | 0.89 | Highly | |
| b | 10–11 | 51/106 | 16 /40 | 0.35 | 0.9 | 0.95 | 0.74 | Less |
| 11–12 | 106/140 | 71 /89 | 0.65 | 1 | 0.99 | 0.89 | Highly | |
| c | 10–11 | 23/60 | 6/15 | 0.26 | 0.9 | 0.90 | 0.71 | Low |
| 11–12 | 60/100 | 44 /66 | 0.70 | 1 | 0.99 | 0.91 | Exactly | |
| d | 10–11 | 65/205 | 33 /71 | 0.43 | 0.8 | 0.92 | 0.70 | Less |
| 11–12 | 205/301 | 137/165 | 0.61 | 1 | 0.99 | 0.88 | Highly |
| Grade | Total (10–11) | Percentage (10–11) | Total (11–12) | Percentage (11–12) |
|---|---|---|---|---|
| Exactly | 0 | 0% | 3 | 2.4% |
| Highly | 0 | 0% | 19 | 15.0% |
| Moderately | 8 | 36.4% | 0 | 0% |
| Less | 5 | 22.7% | 0 | 0% |
| Inconsistent | 9 | 40.9% | 105 | 82.6% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Ai, T. A Hierarchical Approach for Measuring the Consistency of Water Areas between Multiple Representations of Tile Maps with Different Scales. ISPRS Int. J. Geo-Inf. 2017, 6, 240. https://doi.org/10.3390/ijgi6080240
Shen Y, Ai T. A Hierarchical Approach for Measuring the Consistency of Water Areas between Multiple Representations of Tile Maps with Different Scales. ISPRS International Journal of Geo-Information. 2017; 6(8):240. https://doi.org/10.3390/ijgi6080240
Chicago/Turabian StyleShen, Yilang, and Tinghua Ai. 2017. "A Hierarchical Approach for Measuring the Consistency of Water Areas between Multiple Representations of Tile Maps with Different Scales" ISPRS International Journal of Geo-Information 6, no. 8: 240. https://doi.org/10.3390/ijgi6080240
APA StyleShen, Y., & Ai, T. (2017). A Hierarchical Approach for Measuring the Consistency of Water Areas between Multiple Representations of Tile Maps with Different Scales. ISPRS International Journal of Geo-Information, 6(8), 240. https://doi.org/10.3390/ijgi6080240







