1. Introduction
State of the art indoor localization systems use a fusion of multiple (smartphone) sensors to infer the pedestrian’s current location within a building based on a variety of sensor observations. Among those, the internal IMU, namely accelerometer and gyroscope, is often used as a core component that provides accurate relative movement information like step and turn detection. However, this requires the pedestrian’s initial position to be well known, e.g., using a GPS-fix just before entering the building. Additionally, the sensor’s error will sum up over time [
1].
Depending on the used fusion method, the latter can be addressed using a movement model for the pedestrian that prevents unlikely movements and locations. However, this will obviously work only to some extent and still requires the initial position to be at least vaguely known. Thus, indoor localization systems incorporate the knowledge of sensors that provide absolute location information, like Wi-Fi and iBeacons. The signal strength of nearby transmitters, received by the smartphone, yields vague information about the distance towards it. While the provided accuracy is relatively low, it can be stabilized by the IMU and vice versa.
The downside of this approach is that both Wi-Fi and iBeacons require additional prior knowledge to work. To infer the probability of the pedestrian currently residing at an arbitrary location, the signal strengths received by the smartphone are compared with the signal strengths that should be received at this location (prior knowledge). As radio frequency (RF) signals are highly dependent on the surroundings, those values can change rapidly within meters. That is why fingerprinting became popular, where the required prior knowledge is gathered by manually scanning each location within the building, e.g., using cells of ≈2 m in size. This usually leads to a very high accuracy due to actual measurements of the real situation. However, the amount of work for the initial setup and the maintenance, when transmitters are changed or renovations take place, is very high.
Setup and maintenance effort can be prevented by using models to predict the signal strengths that should be received at some arbitrary location. Depending on the used model, only a few parameters and the locations of the transmitters within the building are required. For newer installations, the latter is often available and tagged within the building’s floor plan. Obviously, simple models will represent the real signal strengths only to some extent, as not all ambient conditions, such as walls, are considered. Furthermore, the choice of the model’s parameters depends on the actual architecture and Wi-Fi setup: Parameters that work within Building A might not work out within Building B.
Thus, a compromise comes to mind: instead of using several hundreds of fingerprints, a few reference measurements used for a model setup might be a valid tradeoff between resulting accuracy and necessary setup time.
Within this work, we will focus on simple signal strength prediction models that do not incorporate knowledge of nearby walls, but can be used for real-time applications on commercial smartphones. To mitigate the issues of those signal strength predictors, we propose a new model that is a combination of several simple ones. It is more accurate, requires only minor additional computations and thus is well suited for use in mobile applications. The to-be-expected accuracy (in dB and m) of all models is analyzed for various setups ranging from just empirical parameters (no setup time when transmitter positions are known) to optimized parameters, where no prior knowledge is necessary and a few reference measurements suffice.
Besides analyzing the Wi-Fi performance on its own, we will also have a closer look at the resulting performance changes within a fully-featured smartphone-based indoor localization system using a movement model based on the building’s floor plan, together with various other sensors and recursive state estimation based on a particle filter.
2. Related Work
Indoor localization based on Wi-Fi and received signal strength indications (RSSI) dates back to the year 2000 and the work of Bahl and Padmanabhan [
2]. During a one-time offline phase, a multitude of reference measurements are conducted. During the online phase, where the pedestrian walks along the building, those prior measurements are compared against live readings. The pedestrian’s location is inferred using the
k-nearest neighbor(s) based on the Euclidean distance between currently received signal strengths and the readings during the offline phase.
Inspired by this initial work, Youssef et al. [
3] proposed a more robust, probabilistic approach. Their fingerprints were placed every
m and estimated by scanning each location 100 times. The resulting signal strength distribution for each location is hereafter encoded by a histogram. The latter can be compared against live measurements to infer its matching probability. The center of mass among the
k highest probabilities, including their weight, describes the pedestrian’s current location. In [
4], a similar approach is used and compared against nearest neighbor, kernel density estimation and machine learning. Furthermore, they mention potential issues of (temporarily) invisible transmitters and describe a simple heuristic of how to handle such cases.
Meng et al. [
5] discuss several fingerprinting issues like environmental changes after the fingerprints were recorded. They propose an outlier detection based on RANSAC to remove potentially distorted measurements and thus improve the matching process.
Despite a very high accuracy—up to an average error of 1 m—due to real-world comparisons, the aforementioned approaches suffer from tremendous setup and maintenance times. Using robots instead of human workforce to accurately gather the necessary fingerprints might thus be a viable choice [
6]. Being less expensive and more accurate, this technique can also be combined with SLAM for cases where the floor plan is unavailable.
Besides real-world measurements via fingerprinting, model predictions can be used to determine signal strengths for arbitrary locations. Propagation models are a well-established field of research, initially used to determine the Wi-Fi-coverage for new installations. While many of them are intended for outdoor and line-of-sight purposes, they are often applied to indoor use cases, as well [
7,
8,
9].
The model-based approach presented by Chintalapudi et al. [
10] works without any prior knowledge. During the setup phase, pedestrians just walk within the building and transmit all observations to a central server. Some GPS fixes with well-known position (e.g., entering and leaving the building) observed by the pedestrians are used as reference points. A genetic optimization algorithm hereafter estimates both, the parameters for a signal strength prediction model and the pedestrian’s locations during the walk. The estimated parameters can be refined using additional walks and may hereafter be used for the indoor localization process. Likewise, it is possible to apply a global optimization that also determines a vague floor plan for the building [
11].
While signal strength models are used to predict a signal strength given the distance from the transmitter, some also allow one to infer the distance based on a known signal strength. Given several signal strength measurements from transmitters at known locations, it is thus possible to perform trilateration. Such an approach is presented in [
12], where the pedestrian’s 2D location and one model parameter are optimized using a non-linear least squares approach. Optimizing the location and model parameter together yields a setup that is invariant to temporal environmental changes affecting the signal strength propagation. However, all transmitters are assumed to have the same optimized model parameter, which is an oversimplification for most environments. This issue is addressed in [
13], where this parameter is estimated per transmitter to increase the accuracy. However, due to the used optimized strategy, it is hard to include additional constraints, such as knowledge given by a floor plan that would prevent the estimation from returning unreachable areas within a building. Likewise, the approach will not work smoothly for 3D location estimation, as the corresponding signal strength propagation models are usually non-continuous due to the impact of floors/ceilings.
As the presented drawbacks denote, using just Wi-Fi signal strengths as location estimation is erroneous. It thus makes sense to combine several other sensors via sensor fusion, to leverage the positive aspects of each individual source. Recursive state estimation, e.g., based on an (extended) Kalman filter, allows for combining absolute Wi-Fi location information, absolute landmarks and relative pedestrian dead reckoning (PDR), as presented in [
14,
15].
Besides signal strengths, other RF characteristics like the signal’s time of arrival (TOA) and time difference of arrival (TDOA), as used within the GPS, or its angle of arrival (AOA) can be used. They are more accurate and mostly invariant to architectural obstacles [
16,
17]. Especially signal runtimes are unaffected by walls and thus allow for stable distance estimations, if the used components support measuring time delays down to a few picoseconds. This is why those techniques often need special (measurement) hardware to estimate parameters like signal runtime or signal phase shifts. Those requirements only allow for a limited number of use cases.
We therefore focus on the RSSI that is available on each commercial smartphone and use a simple signal strength prediction model to estimate the most probable location given the phone’s observations. Furthermore, we propose a new model based on multiple simple ones, which will reduce the prediction error. Several strategies to optimize simple models and the resulting accuracies are hereafter evaluated and discussed. Finally, we include additional smartphone sensors using sensor fusion via recursive state estimation to enhance the system’s accuracy.
3. Indoor Positioning System
Our smartphone-based indoor localization system estimates a pedestrian’s current location and heading using recursive density estimation [
18,
19] seen in Equation (
1).
The pedestrian’s hidden state
is given by:
where
represent its position in 3D space and
his/her current (absolute) heading.
The corresponding observation vector, given by the smartphone’s sensors, is defined as:
contains the signal strength measurements of all access-points (APs) currently visible to the phone,
describes the number of steps detected since the last filter-step,
the (relative) angular change since the last filter-step,
the vague absolute heading as provided by the magnetometer,
the ambient pressure in hPa and
the current location given by the GPS. If the latter is currently not available, this is indicated by a special value combination, which is checked within the evaluation.
Assuming statistical independence, the state evaluation density from Equation (
1) can be written as:
Besides the evaluation, a movement model, based on random walks on a graph, samples only those transitions (= pedestrian movements) that are allowed by the building’s floor plan. The smartphone’s accelerometer, gyroscope, magnetometer, GPS- and Wi-Fi-module provide the observations for both the transition and the following evaluation step to infer the hidden state, namely the pedestrian’s location and heading [
20,
21].
Absolute location information is provided by and , if available. Otherwise, their probability is uniformly distributed (same likelihood for any location). The vague absolute heading provided by the smartphone’s magnetometer is included using a simple heuristic for . Finally, the barometer is used to distinguish between normal walking and climbing stairs within by comparing relative pressure changes. This makes the barometer invariant to long-term pressure fluctuations due to temperature and humidity.
Furthermore, the smartphone’s IMU is used to infer the number of steps and the relative turn angle the pedestrian has taken since the last filter update. While those values could be used within the evaluation Equation (
4), we apply them within the transition model (see [
1,
20]) to estimate the pedestrian’s potential movement
within the building. Using real values to perform this movement-update instead of just scattering randomly along the floor plan followed by downvoting within the evaluation Equation (
4) provides a more stable result.
As this work focuses on Wi-Fi optimization, not all parts of the localization system were discussed in detail. For missing explanations and further details on the aforementioned practices, please refer to [
20]. Compared to this reference, absolute heading and GPS have been added as additional sensors to further enhance the localization. Within Equation (
5), we favor movements (model transitions Equation (
1)) with a heading
around the heading
indicated by the smartphone’s compass. As this sensor is usually inaccurate, we use
to just prevent walks in the opposite direction. The result is normalized using
. A normal distribution in Equation (
6) is used to model GPS uncertainty. The difference between the GPS estimation and potential state
is given by the Euclidean 2D
in Equation (
6).
The GPS sensor should enhance scenarios where multiple, unconnected buildings are involved and the pedestrian is required to move outdoors to enter the next facility. Indoors, the GPS will usually not provide viable location estimations, and the system has to solely rely on the smartphone’s Wi-Fi observations. Therefore, it is crucial for the Wi-Fi component to supply location estimations that are as accurate as possible, while the component itself must be easy to set up and maintain.
4. WiFi Location Estimation
The Wi-Fi sensor infers the pedestrian’s current location based on a comparison between live observations (the smartphone continuously scans for nearby access-points) and fingerprints or signal strength predictions for well-known locations. The location that fits the observations best is the pedestrian’s current location. Assuming statistical independence of all transmitters installed within a building, the matching probability
for a location
can be written as:
where matching a single signal strength observation
against the reference is given by:
In Equation (
8),
and
denote the average signal strength and corresponding standard deviation for the AP identified by
i, which should be measurable given the location
. Those two values can be determined using various methods. Most common and accurate, as of today, is fingerprinting, where hundreds of locations throughout the building are scanned beforehand. The received access-points including their (average) signal strength and deviation denote each location’s fingerprint. To prevent the time-consuming setup process, we use a model to predict the average signal strength for each location, based on the AP’s position
and a few additional parameters.
4.1. Signal Strength Prediction Model
The log distance model [
22,
23] in Equation (
9) is a commonly-used signal strength prediction model that is intended for line-of-sight predictions. However, depending on the surroundings, the model is versatile enough to also serve for indoor purposes. It predicts an access-point’s signal strength for an arbitrary location, given the distance
d between both and two environmental parameters: The AP’s signal strength
measurable at a known distance
(usually 1 m) and the signal’s depletion over distance
, which depends on the AP’s surroundings like walls and other obstacles.
is a zero-mean Gaussian noise and models the uncertainty.
As
depends on the architecture around the transmitter, the model is bound to homogenous surroundings like one floor, solely divided by drywall of the same thickness and material. The log normal shadowing or wall attenuation factor model [
24] is a slight modification to adapt the log distance model to indoor use cases. It introduces an additional parameter that considers obstacles between (line-of-sight) the AP and the location in question by attenuating the signal with a constant value. Depending on the use case, this value describes the number and type of walls, ceilings, floors, etc., between both positions. For obstacles, this requires an intersection test of each obstacle with the line-of-sight, which is costly for larger buildings. For real-time use on a smartphone, a (discretized) model pre-computation might thus be necessary [
25].
Throughout this work, we thus use a tradeoff between both models, where walls are ignored and only floors/ceilings are considered. Assuming buildings with even floor levels, the number of floors/ceilings between two position can be determined without costly intersection checks and thus allows for real-time use cases running on smartphones.
In Equation (
10), a constant attenuation factor
is multiplied by the number
n of floors/ceilings between the sender and the location in question. The attenuation
(per element) depends on the building’s architecture, and for common, steel-reenforced concrete floors,
is a viable choice [
26].
4.2. Model Parameters
As previously mentioned, for the prediction model to work, it is necessary to know the location
for every permanently-installed access-point
i within the building to derive the distance
d, plus its environmental parameters
,
and
. While it is possible to use empiric values for those environmental parameters [
27], the positions are mandatory.
For many buildings, there should be floor plans that include the locations of all installed transmitters. If so, a model setup takes only several minutes to (vaguely) position the APs within a virtual map and assign some fixed, empirically-chosen parameters for , and . Depending on the building’s architecture, this might already provide enough accuracy for some use cases, where vague location information is sufficient.
4.3. Model Parameter Optimization
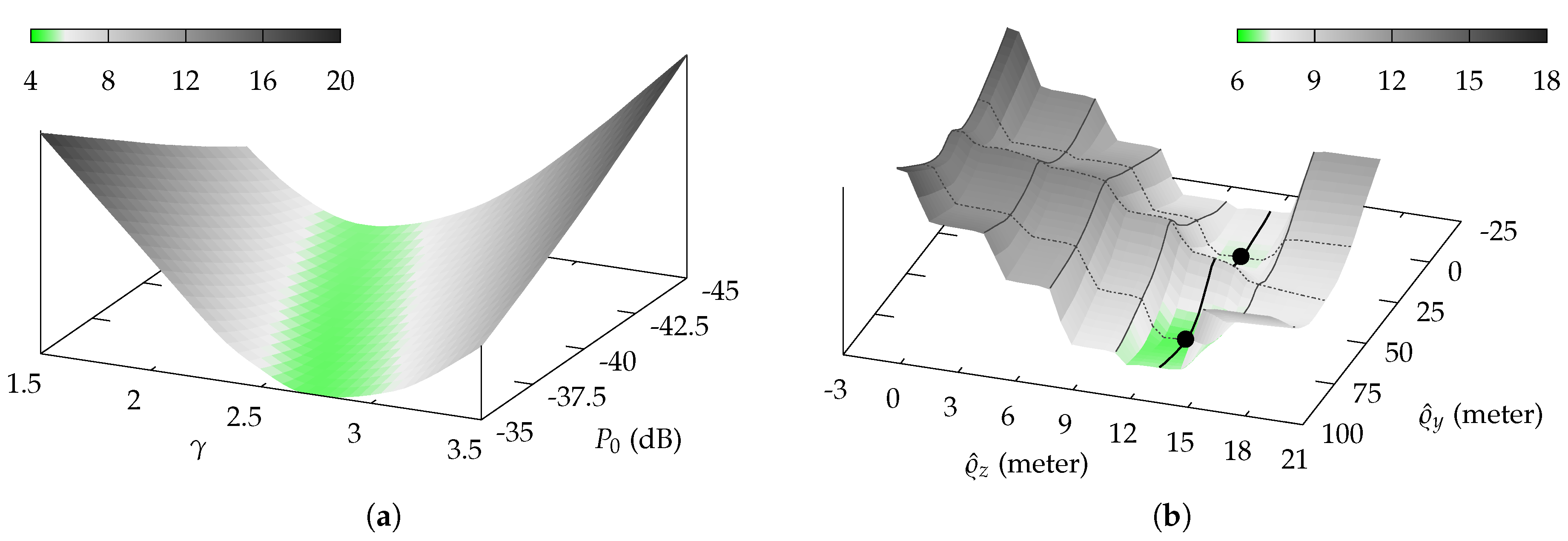
For systems that demand a higher accuracy, one can choose a compromise between fingerprinting and the aforementioned pure empiric model parameters by optimizing those parameters based on a few reference measurements throughout the building. The more parameters are staged for optimization (), the more reference measurements are necessary to provide a stable result. Depending on the desired accuracy, setup time and whether the transmitter positions are known or unknown, several optimization strategies arise, where not all six parameters are optimized, but only some of them.
The target function Equation (
11) optimizes the model-parameters for one access-point by reducing the squared error between reference measurements
with well-known location
and corresponding model predictions
. The number of floors between
and the transmitter’s location
is
.
Just optimizing
and
with constant
and known transmitter position usually means optimizing a convex function, as can be seen in
Figure 1a. For such error functions, algorithms like gradient descent and simplex [
28,
29,
30] are well suited and will provide the global minimum.
However, optimizing an unknown transmitter position usually means optimizing a non-convex, discontinuous function, especially when the
z-coordinate, which influences the number of attenuating floors/ceilings, is involved. While the latter can be mitigated by introducing a continuous function for the number
n, e.g., a sigmoid, the function is not necessarily convex.
Figure 1b depicts two local minima and only one of both also is a global one.
Such functions demand for optimization algorithms, that are able to deal with non-convex functions. We thus used a genetic algorithm to perform this task [
31]. However, initial tests indicated that while being superior to simplex and similar algorithms, the results were not yet satisfying, as the optimization often did not converge.
As the range of the six to-be-optimized parameters is known (
within the building,
,
,
within a sane interval around empiric values), we slightly modified the genetic algorithm: The initial population is now uniformly sampled from the known range. During each iteration, the best 25% of the population are kept, and the remaining entries are re-created by modifying the best entries with uniform random values within ±10% of the known range. Inspired by cooling, known from simulated annealing [
32], the result is stabilized by narrowing the allowed modification range over time.
4.4. Modified Signal Strength Model
As the used model tradeoff does not consider walls, it is expected to provide erroneous values for regions that are heavily shrouded, e.g., by steel-reenforced concrete or metalized glass.
Instead of using only one optimized model per access-point, we use several instances with different parameters that are limited to some region within the building. By reducing the area that the model has to describe, we expect the limited number of model parameters to provide better (local) results.
model per floor will use one model for each story, which is optimized using only the fingerprints that belong to the corresponding floor. During evaluation, the
z-value from
in Equation (
8) is used to select the correct model for this location’s signal strength estimation.
model per region works similarly, except that each model is limited to a predefined, axis-aligned bounding box. This approach allows for an even more refined distinction between several areas like in- and out-door regions or locations that are expected to highly differ from their surroundings.
Especially the second model imposes a potential issue we need to address: If an AP is seen only once or twice within such a bounding box, it is impossible to optimize its parameters, just like a line cannot be defined using one single point. However, due to Equation (
8), we need each model to provide the same number of access-points. Otherwise, regions with less known transmitters would automatically be more likely than others. We therefore use fixed model parameters,
,
and
for every transmitter with less than three reference measurements per region. This yields a model that always returns
dBm, independent of the distance from the transmitter. While this most probably is not the correct reading for all locations, it works for most cases, as usual smartphones are unable to measure signals below this threshold.
4.5. Wi-Fi Quality Factor
Evaluations within previous works showed that there are many situations where the overall Wi-Fi location estimation is highly erroneous. Either when the signal strength prediction model does not match real-world conditions or the received measurements are ambiguous and there is more than one location within the building that matches those readings. Both cases can occur e.g., in areas surrounded by concrete walls, where the model does not match the real-world conditions as those walls are not considered, and the smartphone barely receives APs due to the high attenuation.
If such a sensor error occurs only for a short time period, the recursive density estimation from Equation (
1) is able to compensate using other observations and the transition model. However, if the sensor fault persists for a longer time period, such an error will slowly distort the posterior distribution. As our movement model depends on the actual floor plan, the density might get trapped, e.g., within a room if the other sensors are unable to compensate for the Wi-Fi error.
Thus, we try to determine the quality of received measurements, which allows for temporarily disabling Wi-Fi’s contribution within the evaluation Equation (
4) if the quality is insufficient.
In Equation (
12), we use the average signal strength
among all access-points seen within one measurement
and scale this value to match a region of
depending on an upper and lower bound. Using this scaled region allows for using the quality factor as a probability measure to reduce/increase the impact of the Wi-Fi component [
33]. Within this work, a simple binary good/bad decision was used instead: If the returned quality is below a certain threshold, Wi-Fi is completely ignored within the evaluation. The lower and upper bound are chosen empirically by looking at the usual range of Wi-Fi signal strengths that still provide persistent data-connections to clients. Likewise, the threshold is determined by examining the scaled output of Equation (
12) for some places with good and bad Wi-Fi location estimations, respectively.
4.6. Virtual Access Points
Assuming normal conditions, the received signal strength at one location will also (strongly) vary over time due to environmental conditions like temperature, humidity, open/closed doors and RF interference. Fast variations can be addressed by averaging several consecutive measurements at the expense of a delay in time. To prevent this delay, we use the fact that many buildings use so-called virtual access points where one physical hardware access-point provides more than one virtual network to connect to. They can usually be identified, as only the last digit of the MAC address is altered among the virtual networks. As those normally share the same frequency, they are unable to transmit at the same instant in time. When scanning for APs, one will thus receive several responses from the same hardware, all with a very small delay (micro- to milli-seconds). Such measurements may be grouped using some aggregate function like average, median or maximum instead of using each single measurement.
Furthermore, VAP grouping can be used to suppress unlikely observations: If a physical hardware is known to provide six virtual networks, it is unlikely for the smartphone to only see one of those networks. This is due to temporal effects or multipath signal propagation, and the received signal strength will often be far from the normal average. It thus makes sense to just omit such unlikely observations, focusing on the remaining, stable ones.
5. Experiments
Within our experiments, we will first have a look at model optimizations to reduce the error (in dB) between the signal strengths predicted by the models and real-world conditions in
Section 5.1. This optimization is based on 121 reference measurements conducted at known locations. Likewise, we will examine the impact of using less reference measurements for this process.
Hereafter, in
Section 5.2, we examine the resulting accuracy (in m) when using the optimized models for localization solely by the Wi-Fi component without additional sensors, assumptions or filtering. This evaluation uses smartphone data from 13 walks within the buildings and corresponding ground truth for error estimations.
Finally, all models are evaluated in the context of our indoor localization system Equation (
1), using additional smartphone sensors and the building’s floor plan in
Section 5.3.
For simplicity reasons, all calculations have been performed using desktop hardware. However, the setup is able to run on commercial smartphones, as well as it uses C++ code: the presented system participated as the winner in the IPIN 2016 Indoor Localization Competition using a Motorola Nexus 6 smartphone. It took around 90 min to perform reference measurements within the area of the competition (the floor plan was known beforehand) followed by one minute of calculation time for the optimization 3 strategy. Using 5000 particles for the particle filter, it took around 100 ms for each transition/evaluation step. Those updates were scheduled every 500 ms.
All optimizations and evaluations conducted within this work took place within two adjacent buildings (four and two floors, respectively) and two connected outdoor regions (entrance and inner courtyard), 110 m × 60 m in size.
Within all Wi-Fi observations, we only consider the access-points that are permanently installed and can be identified by their well-known MAC address. Temporal and movable transmitters like smart TVs or smartphone hotspots are ignored as they might cause estimation errors.
The Wi-Fi quality factor from
Section 4.5 was configured with a lower bound of
dBm, an upper bound of
dBm and a threshold of
.
Unfortunately, due to legal reasons, our institution does not allow depicting the actual location of installed transmitters within the following figures.
5.1. Model Optimization
As the signal strength prediction model is the core of the absolute positioning component described in
Section 3, we start with the model parameter optimization (see
Section 4).
,
and
will be estimated based on some reference measurements using various optimization strategies. The results of those optimization strategies are compared with each other and an empiric parameter choice:
=
dBm @ 1 m (defined by the usual AP transmit power for Europe), a path loss exponent
and
per floor/ceiling (made of reinforced concrete) [
7,
24,
26].
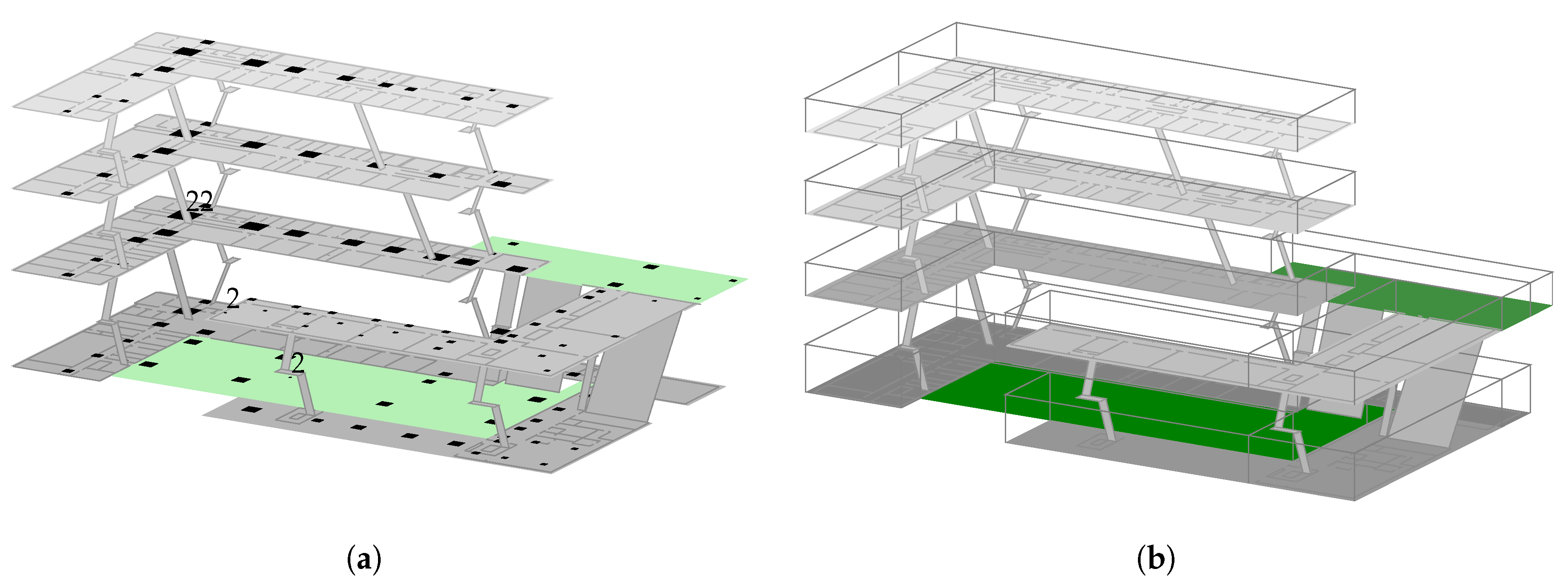
Figure 2a depicts the location of the used 121 reference measurements. Each location was scanned 30 times (≈25 s scan time); non-permanent access-points were removed; the values were grouped per physical transmitter (see
Section 4.6) and aggregated to form the average signal strength per transmitter.
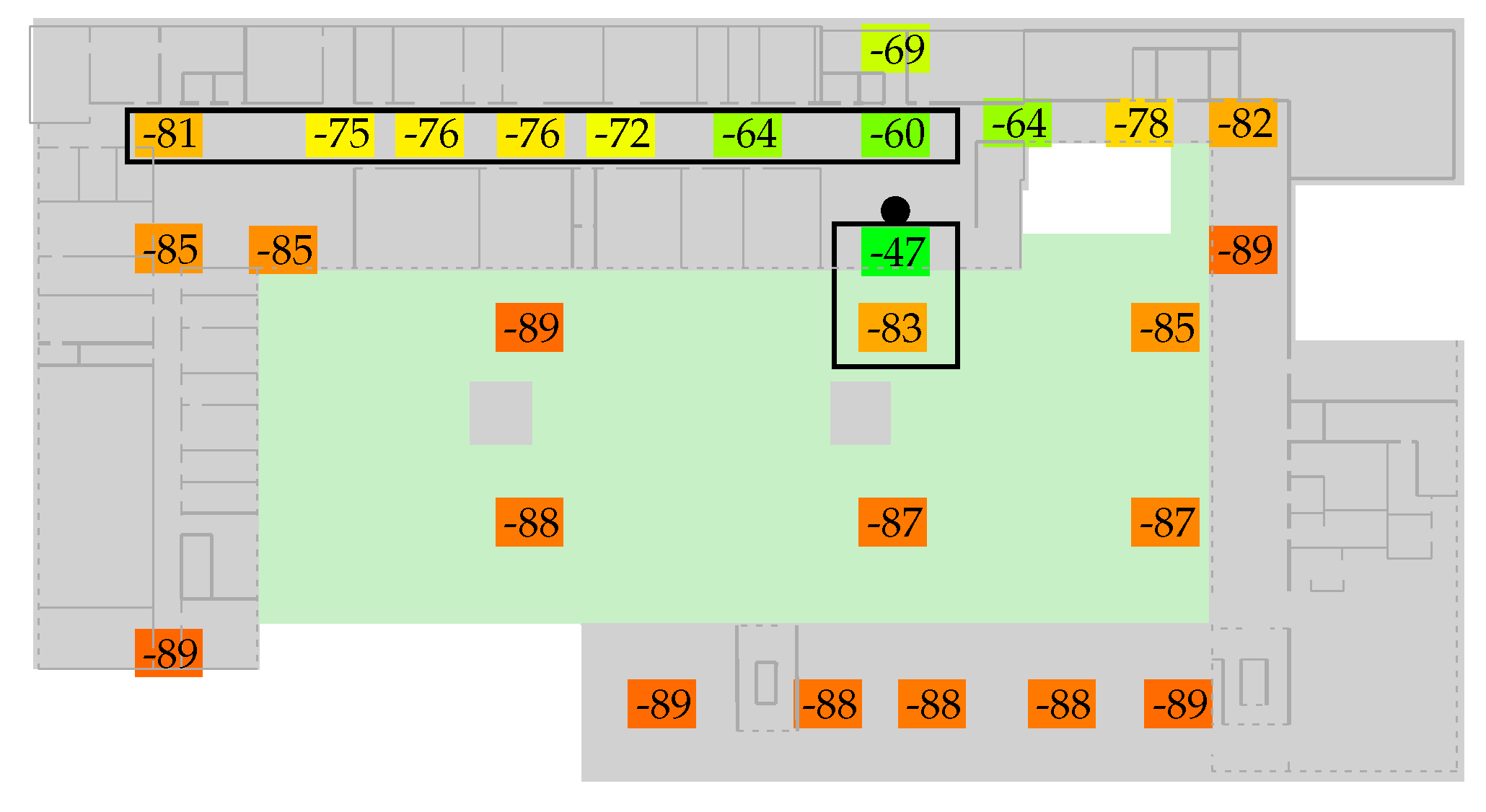
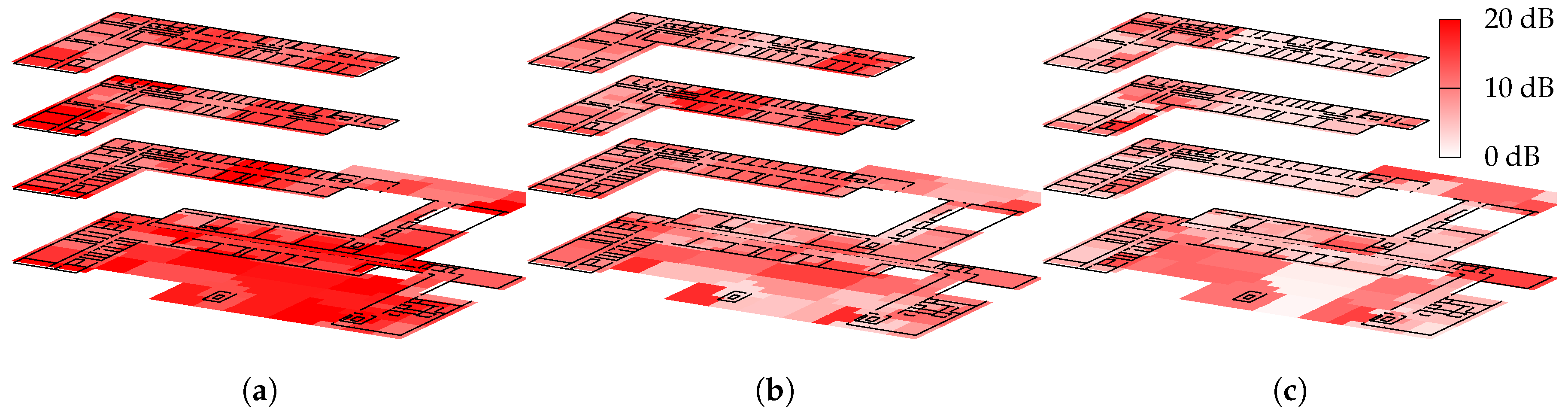
Figure 3 depicts the to-be-expected issues by examining the signal strength values of the reference measurements for one access-point. Even though the transmitter is only 5 m away from the reference measurement (small box), the metalized windows attenuate the signal as much as 50 m of corridor (wide rectangle). The model described in
Section 4.1 will not be able to match such situations due to the lack of obstacle information. We will thus look at various optimization strategies and the error between the resulting estimation model and our reference measurements:
empiric params uses the same three empiric parameters , , for each AP in combination with its position, which is well known from the floor plan.
optimization 1 is the same as above, except that the three parameters are optimized using the reference measurements (convex function). All transmitters share the same three parameters.
optimization 2 optimizes the three parameters per access-point instead of using the same parameters for all. This still denotes a convex function per transmitter.
optimization 3 does not need any prior knowledge and will optimize all six parameters (3D position, , , ) based on the reference measurements (non-convex function).
model per floor and model per region are just like optimization 3 except that there are several sub-models, each of which is optimized for one floor/region instead of the whole building. The chosen bounding boxes and resulting sub-models are depicted in
Figure 2b.
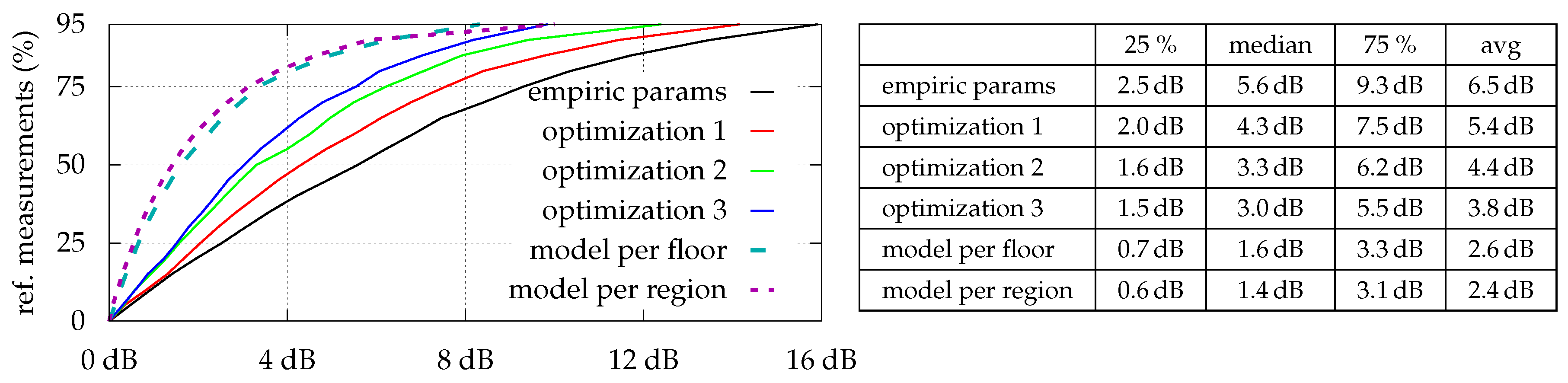
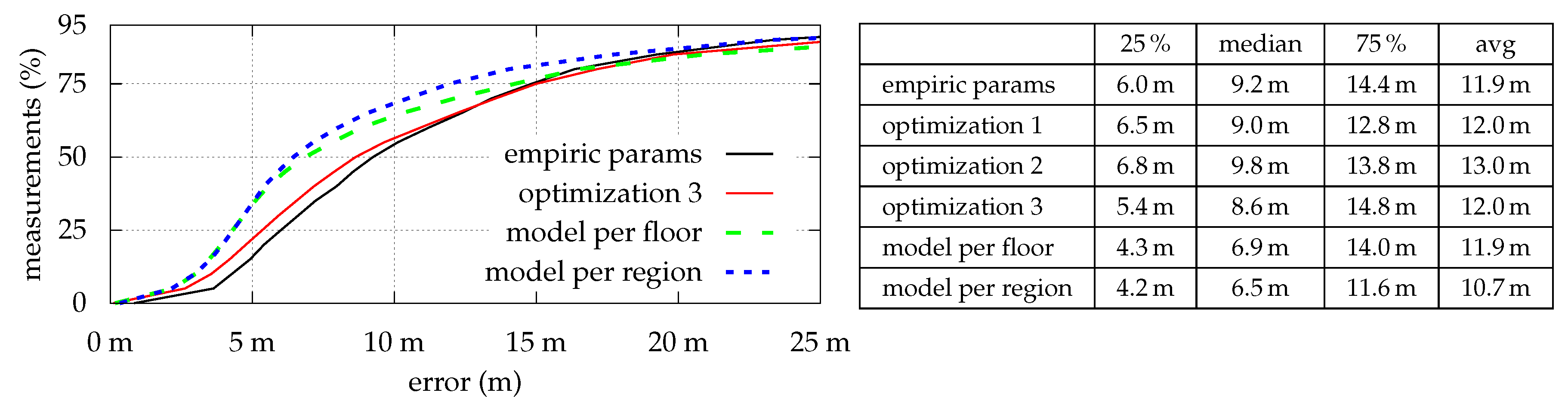
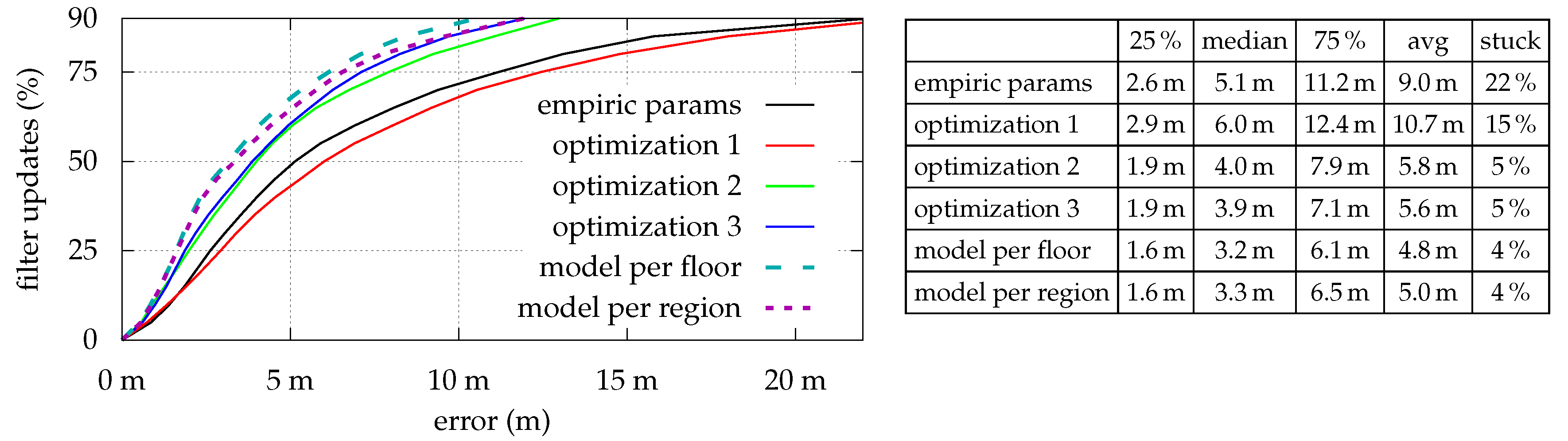
Figure 4 shows the optimization results for all strategies which are as expected: The estimation error is indirectly proportional to the number of optimized parameters. However, while median- and average-errors are fine, maximal errors sometimes are relatively high. As depicted in
Figure 5, even with model per region, some locations simply do not fit the model, and thus lead to high (local) errors. Looking at the optimization results for
,
and
supports this finding. While the median for those values based on all optimized transmitters is totally sane (
dBm,
,
dB), the minimum and maximum values are far beyond the physically possible range.
The same holds for the estimated transmitter position when using optimization 3: The median distance between estimated and real position is ~8 m and the maximum ~27 m. For 68% of all installed transmitters, the estimated floor-number matched the real location.
While model per region is able to overcome the indoor vs. outdoor issues depicted in
Figure 3, by using a separate bounding box just for the outdoor area, it obviously requires a profound prior knowledge to correctly select the individual regions for the sub-model.
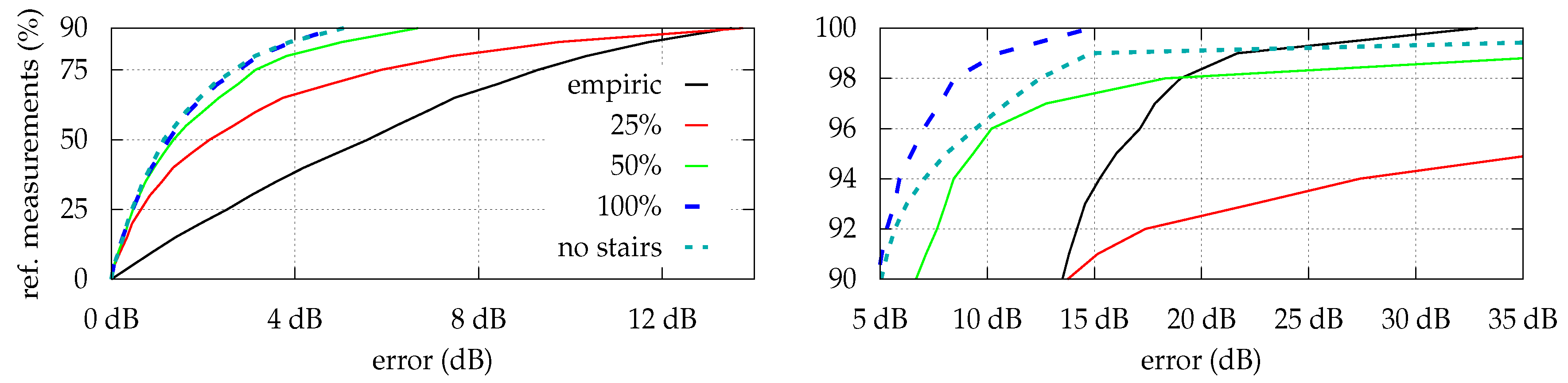
As we try to minimize the system’s setup time as much as possible, we need to determine the amount of necessary reference measurements for the optimization to produce robust model parameters. Depending on the chosen model, and thus the number of to-be-optimized parameters, more measurements will be required.
While there was almost no difference between using 121 or 30 reference measurements for optimization 1 and optimization 2 (average error changed from to dB and to dB, respectively), model per region is highly affected (average error changed from to dB), as it needs at least a certain number of measurements within each region for the optimization to converge.
Figure 6 depicts the impact of reducing the number of reference measurements during the optimization process for the model per region strategy. The error is determined by using the (absolute) difference between expected signal strength and the optimized model’s corresponding prediction for all of the 121 reference measurements. Considering only 60 of the 121 scans (50%) yields a slightly increasing model error but still provides good results. While using only 25% of the reference measurements increases the error rapidly, for 75% of the 121 considered error-values, the estimation is still better than using just empiric values without optimization.
Additionally we examined the impact of skipping reference measurements for difficult locations, like staircases surrounded by steel-enforced concrete. While this slightly decreases the estimation error for all other positions (hallway, etc.) as expected, the error within the skipped locations is dramatically increasing (see right half of
Figure 6). It is thus highly recommended to also perform reference measurements for locations, that are expected to strongly deviate (signal strength) from their surroundings.
5.2. Wi-Fi Location Estimation Error
Having optimized several signal strength prediction models, we can now examine the resulting localization accuracy (in m) for each. For now, this will just cover the Wi-Fi component itself. The impact of fusing additional sensors and a adding prior knowledge provided by a transition model will be evaluated later.
The position
within the building that best fits some Wi-Fi signal strength measurements
received by the smartphone is the one that maximizes
. Omitting prior knowledge and normalization, this can be rewritten as:
Following Equations (
7) and (
8), the best location
given
is the one that satisfies:
In Equation (
14)
is the signal strength for access-point
i, installed at location
, returned from the to-be-examined prediction model. For all comparisons, we use a constant uncertainty of
, which is an empirical choice based on prior experiments.
The quality of the estimated location is determined by using the Euclidean distance between estimation and the pedestrian’s ground truth position at the time the scan has been received.
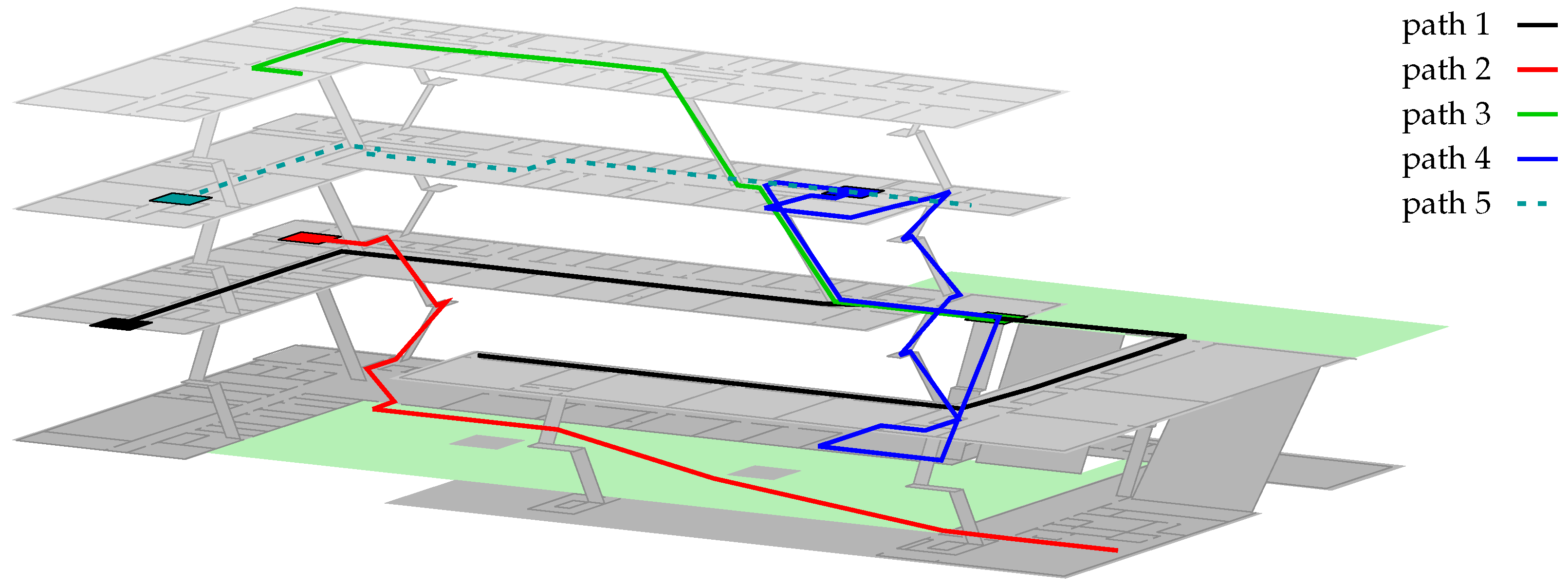
We therefore conducted 13 walks on 5 different paths within our building, each of which is defined by connecting marker points at well known positions (see
Figure 7). Whenever the pedestrian reached such a marker, the current time was recorded. Due to constant walking speeds, the ground truth for any timestamp can be approximated using linear interpolation between adjacent markers.
The position estimation for each Wi-Fi measurement within the recorded walks (3756 scans in total) is compared against its corresponding ground truth, indicating the 3D distance error. This is the Euclidean distance (in
) between estimation and ground truth, calculated for every Wi-Fi measurement (approximately every 600 ms). The resulting cumulative error distribution can be seen in
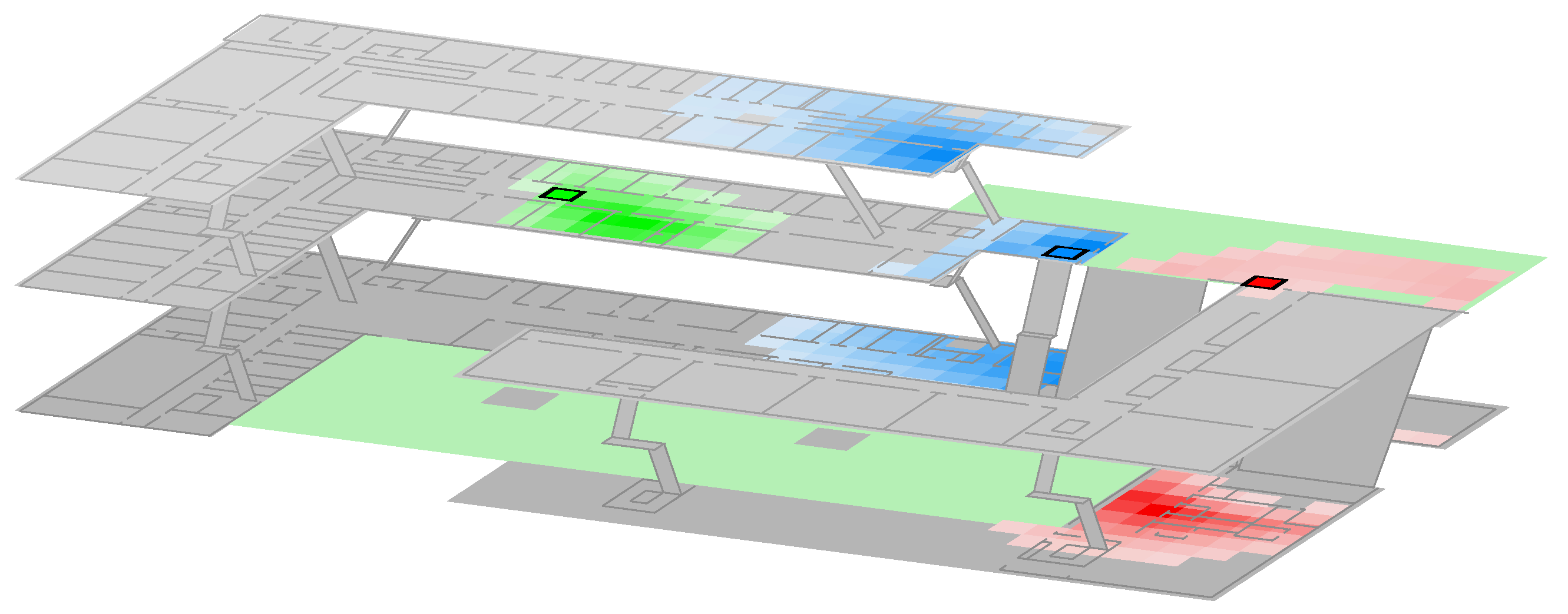
Figure 8. The quality of the location estimation directly scales with the quality of the signal strength prediction model. However, as discussed earlier, the maximal estimation error might increase for some setups. Either due to multi-modalities, where more than one area matches the recent Wi-Fi observation, or optimization yielded an over-adaption where the average signal strength prediction error is small, but the maximum error is dramatically increased for some regions.
Figure 9 depicts aforementioned issues of multimodal (blue) or wrong (red) location estimations. Filtering (Equation (
1)) thus is highly recommended, as minor errors are compensated using other sensors or a movement model that prevents the estimation from leaping within the building. However, if wrong sensor values are observed for longer time periods, even filtering will produce erroneous results and might get stranded (density is trapped e.g., within a room), as the movement model is constrained by the actual floor plan.
To reduce the amount of such misclassifications, where other locations within the building are as likely as the pedestrian’s actual location, we examined various approaches. Unfortunately, most of which did not provide a viable enhancement under all conditions for the performed walks.
The misclassification-rate is determined by counting the amount of (random) locations within the building that produce a similar probability Equation (
8) compared to the actual ground truth position.
One possibility to dissolve such an equal Wi-Fi-likelihood between two (or more) locations is, to not only consider the APs seen by the smartphone, but also the APs not seen by the smartphone. This additional information can be used to rule out all locations where this unseen access-point should have be received (high signal strength from the prediction model). While this works in theory, evaluations revealed several issues:
There is a chance that even a nearby AP is unseen during a scan due to packet collisions or temporal effects within the surrounding. It thus might make sense to opt-out other locations only, if at least two APs are missing. On the other hand, this obviously demands for (at least) two APs to actually be different between the two locations, and requires a lot of permanently installed transmitters to work out.
Furthermore, this requires the signal strength prediction model to be fairly accurate. Within our testing walks, several places are surrounded by concrete walls, which cause a harsh, local drop in signal strength. The models used within this work will not accurately predict the signal strength for such locations.
To sum up, while some situations, e.g., outdoors could be improved, many other situations are deteriorated, especially when some transmitters are (temporarily) attenuated by ambient conditions like concrete walls.
We therefore examined variations of the probability calculation from Equation (
8). Contrary to the results shown in [
34], removing weak APs from
did not work out. While some estimations were improved, the overall error increased for our walks, as there are many situations where only a handful access-points can be seen. Removing this (valid) information will increase the error for such situations.
However, incorporating additional knowledge provided by virtual access-points (see
Section 4.6) mitigated this issues. If, e.g., only one out of six virtual networks is seen, this observation is likely to be erroneous, no matter what the corresponding signal strength indicates. As those occasions are relatively seldom, the impact is a minor one. Nevertheless, depending on the used prediction model, a handful of major estimation errors were prevented. Additionally, among all examined models and walks, there was none where this approached lead to increased error values.
Using a smaller
or a stricter exponential distribution for the model vs. scan comparison in Equation (
8) had a positive effect on the misclassification error for some of the walks, but also slightly increased the overall estimation error. Due to those negative side-effects, the final localization system (Equation (
1)) is unlikely to profit from such changes.
5.3. Filtered Location Estimation Error
After examining the Wi-Fi component on its own, we will now analyze the impact of previously discussed model optimizations on our smartphone-based indoor localization system described in
Section 3, based on Equation (
1).
Due to transition constraints from the building’s floor plan, we expect the posterior density to often get stuck when the Wi-Fi component provides erroneous estimations due to bad signal strength predictions or observations (see
Figure 9):
A pedestrian walks along a hallway, but bad model values indicate that his most likely position is within a room right next to the hallway. If the density (described by the particles) is dragged (completely) into this room, the IMU indicates no change in direction (pedestrian walks straight), and the room has only one single door, the density is trapped within this room. While such problems can often be solved by simply using more particles to describe the posterior, smartphone use cases are usually performance- and battery limited.
As particle filtering from Equation (
1) is a random process with varying output, we calculated each combination of the 13 walks and six optimization strategies, 25 times, using 5000, 7500 and 10,000 particles resulting in 75 runs per walk, 975 per strategy and 5850 in total.
Figure 10 depicts the cumulative error distribution per optimization strategy, resulting from all executions for each conducted walk.
While most values represent the expected results (more optimization yields better results), the values for optimization 1 and model per region do not. The increased error for both strategies can be explained by having a closer look at the walked paths and relates to exceptional regions like outdoors. In both cases there is some sort of model over-adaption. As mentioned earlier, a single, simple model is unable to accurately estimate the signal strength for both buildings and adjacent outdoor regions. Due to metalized glass (see
Figure 3), in- and out-door conditions strongly differ. The model’s optimization builds a compromise among all locations and renders indoor places unnecessarily bad: Previous discussions showed that outdoor regions do not provide viable Wi-Fi signals at all. It thus makes sense to just omit badly covered regions from the model optimization process, as the filter’s evaluation will simply omit Wi-Fi when the quality is insufficient (see
Section 4.5).
While model per region does not suffer from such issues due to separated optimization regions for in- and outdoor, its increased error relates to movements between such adjacent regions, as there often is a huge model difference. While this difference is perfectly fine, as it also exists within real-world conditions, the filtering process suffers at such model-boundaries: The model prevents the particles from moving e.g., from inside the building towards outdoor regions, as the outdoor-model does not yet match. Due to sensor delays and issues with the absolute heading near in- and outdoor boundaries (metal-framed doors) the error is slightly increased and retained for some time until the density stabilizes itself.
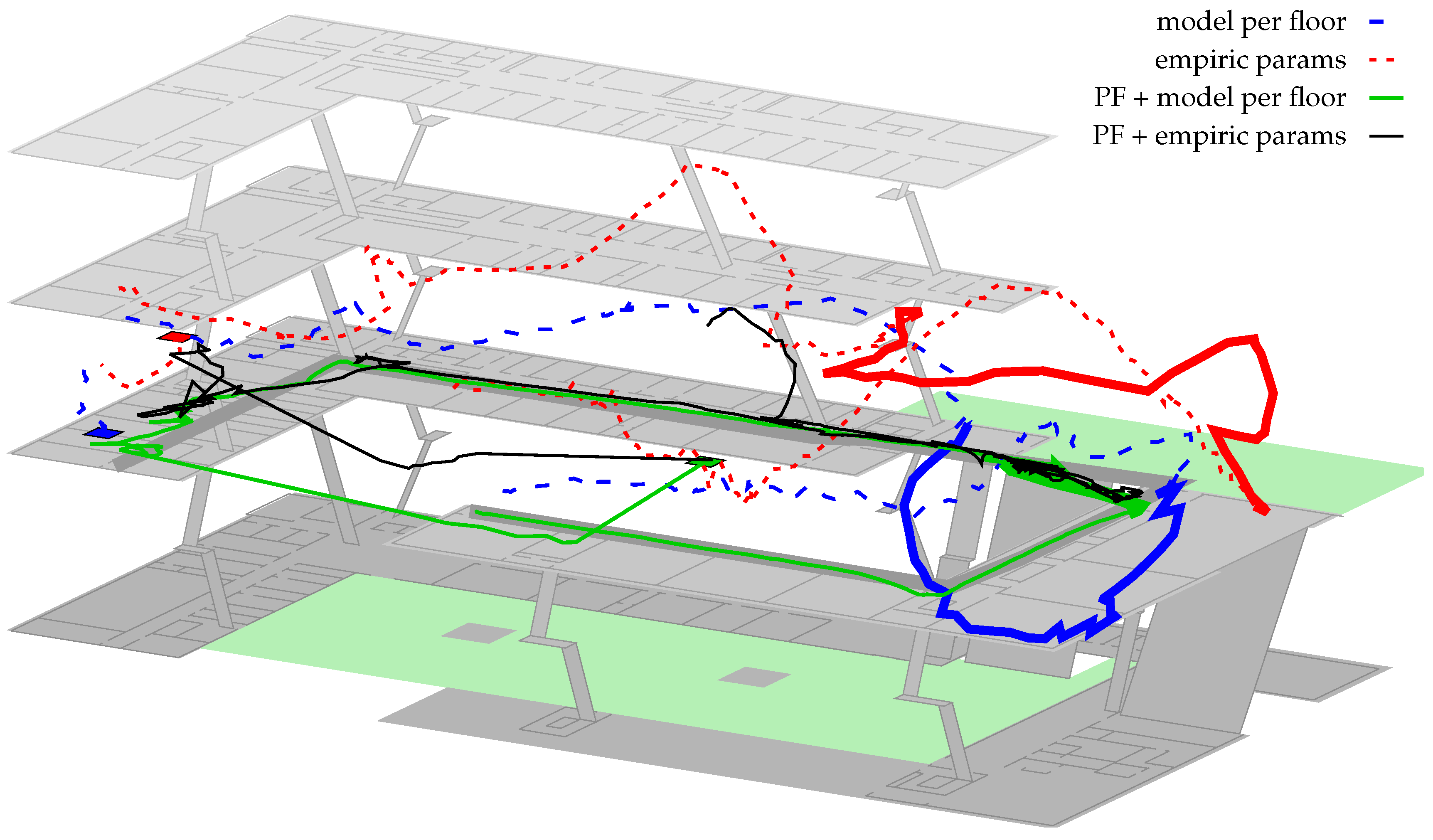
Especially for Path 1, the particle-filter often got stuck within the upper right outdoor area between both buildings (see
Figure 11). Using the empirical parameters, 40% of all runs for this path got stuck at this location. optimization 1 already reduced the risk to 20% and all other optimization strategies did not get stuck at all. Increasing the number of particles from 5000 to 10,000 indicated only a minor increase in accuracy and slightly decreased the risk of getting stuck. For battery- and performance-constrained use cases on the smartphone 5000 thus seems to be sufficient.
Issues while moving from the inside out or vice versa, should also be mitigated by incorporating the smartphone’s GPS sensor. However, within our testing walks, the GPS did rarely provide accurate measurements, as the outdoor time often was too short for the sensor to receive a valid fix. The accuracy indicated by the GPS usually was ≥50 m and thus did not provide useful information.
However, comparing the error results within
Figure 8 and
Figure 10, one can denote the positive impact of fusing multiple sensors with a transition model based on the building’s actual floor plan. Even within outdoor regions and staircases that suffer from erroneous Wi-Fi estimations due to a bad signal strength coverage. The quality metric described in
Section 4.5 was able to detect such cases and Wi-Fi was temporarily ignored. The remaining sensors, like the IMU, and the floor plan were able to keep the pedestrian’s heading until the signal quality reached sane levels again.
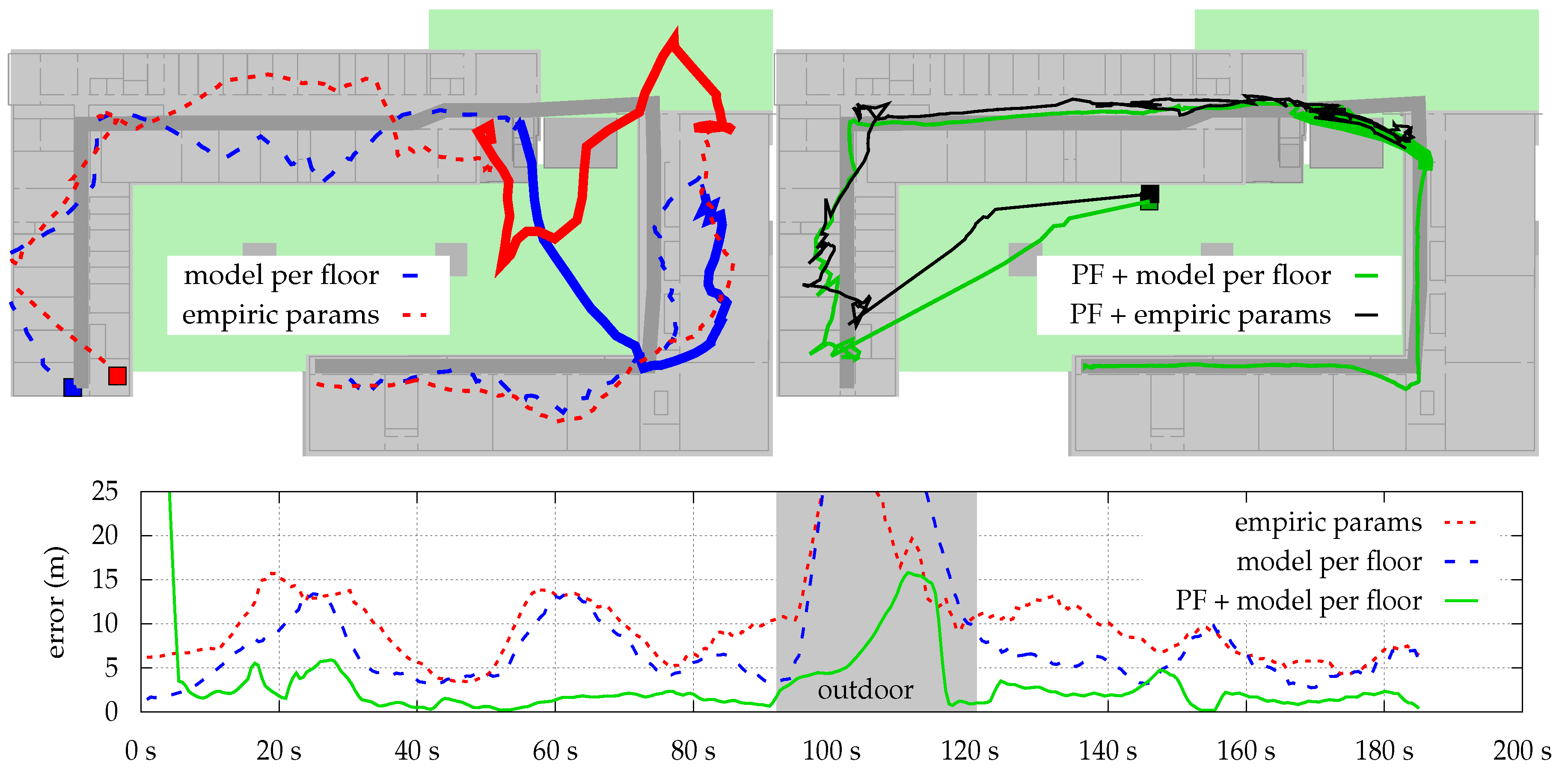
Finally,
Figure 11 depicts all of the previously discussed improvements and issues by examining Path 1 from
Figure 7. For better visibility within path- and error-plots, the unfiltered estimations were smoothed, using a moving average of ten consecutive values (≈7 s). As can be seen, optimizing the Wi-Fi model yields an improvement for indoor situations, as the estimation is closer to the ground truth, and the starting position (indicated by the rectangle) is more accurate. For the depicted walk, the error outdoors is increased, as the likeliest position is shifted. Adding the particle filter (Equation (
1)) on top of the optimized model, fixes this issue. What cannot be seen within the figure: while the likeliest position is deteriorated by the optimization, the likelihood of the region around the pedestrian’s ground truth is actually increased. Thus, combined with transition model and other sensors, the system is able to stay right on track. The filter fails for empiric params, as one AP near the entry of the second building prevents the density from entering, due to a very high difference between model and real-world conditions.
6. Conclusions and Future Work
As denoted within the previous evaluations and discussions, the accuracy of indoor localization systems based on Wi-Fi depends on a manifold of parameters, and even minor adjustments can yield visible improvements. Depending on required accuracy and acceptable setup and maintenance times, several approaches are conceivable:
If the use case does not require utmost accuracy and the locations of permanently-installed transmitters are already well known, just using empiric model parameters is a viable choice for many situations.
However, when combined with (particle) filtering, a heavily constrained movement model might be a potential issue, as it can get stuck when sensor observations or model predictions are too erroneous.
Using a small number of reference measurements to optimize the model parameters will already suffice to improve such errors. Furthermore, it also removes the need for prior knowledge about transmitter locations, as those can be estimated via optimization.
For the best accuracy, more complex signal strength propagation models are required, which in turn demand for more reference measurements. However, while using several instances of a simple propagation model for different regions within a building is able to decrease the estimation error, this approach might require prior guessing of where to place those regions. As indicated by the error plots, just using one model for every floor within the building seems to be a viable alternative.
More complex models that include information about walls and other obstacles should be able to reduce the maximum error, which remains for some locations, at the cost of additional computations. Special data structures for pre-computation combined with online interpolation might be a viable choice for utmost accuracy that is still able to run on a commercial smartphone in real-time.
While we were able to improve the performance of the Wi-Fi sensor component, the filtering process should be more robust against erroneous observations. Getting stuck should be prevented, independent of minor changes in quality for the signal strength prediction model [
33].
Our Wi-Fi quality metric often was able to determine situations that would yield multimodal or bad Wi-Fi estimations, and temporarily ignoring this sensor prevented additional errors. Still, there were some cases where the metric failed to correctly determine a potentially bad observation, which leaves room for future improvements.