An Improved Hybrid Method for Enhanced Road Feature Selection in Map Generalization
Abstract
:1. Introduction
2. An Improved Method of Road Selection
2.1. An Improved Stroke Generation Method
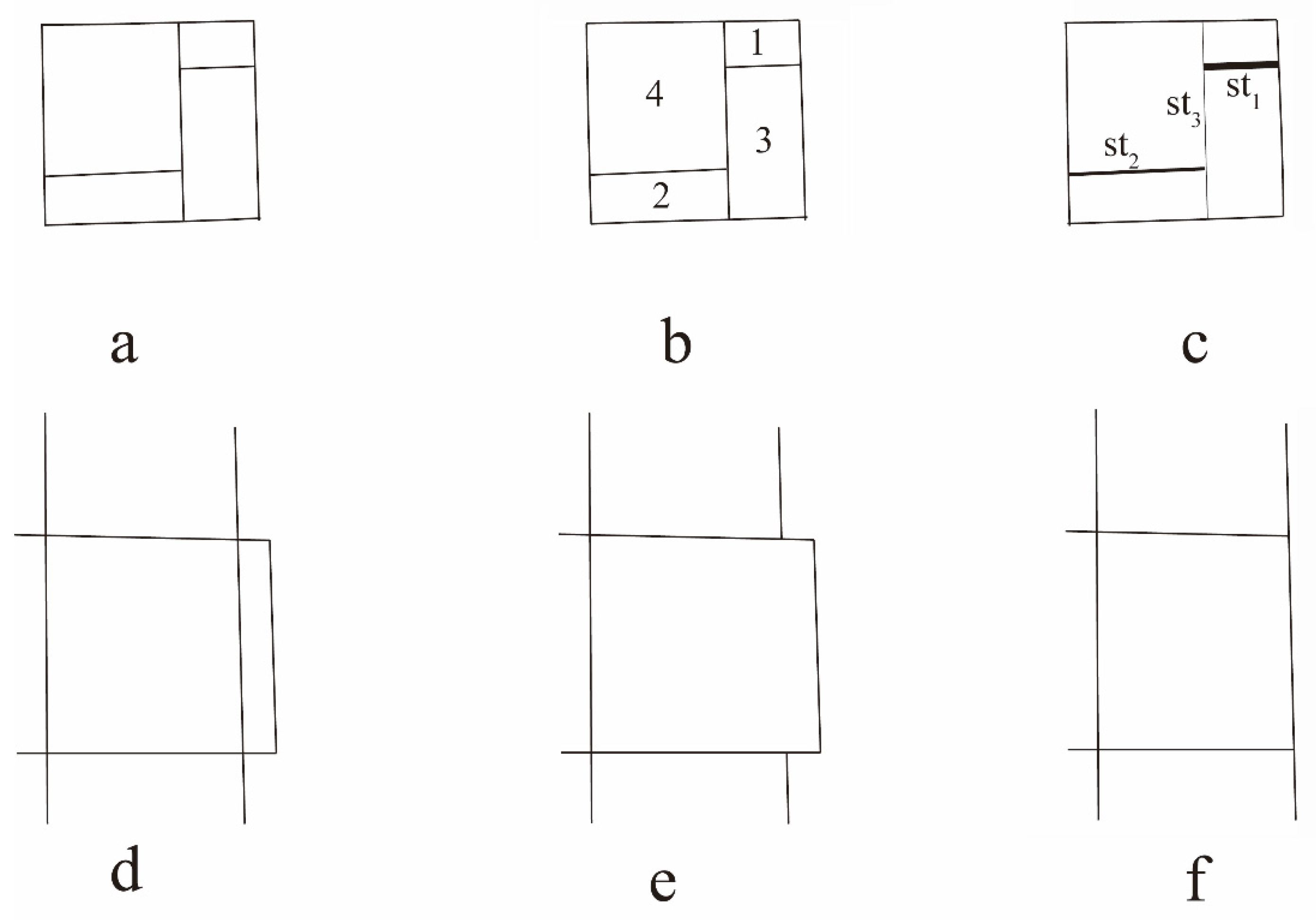
2.1.1. Overall Stroke Connection Rules
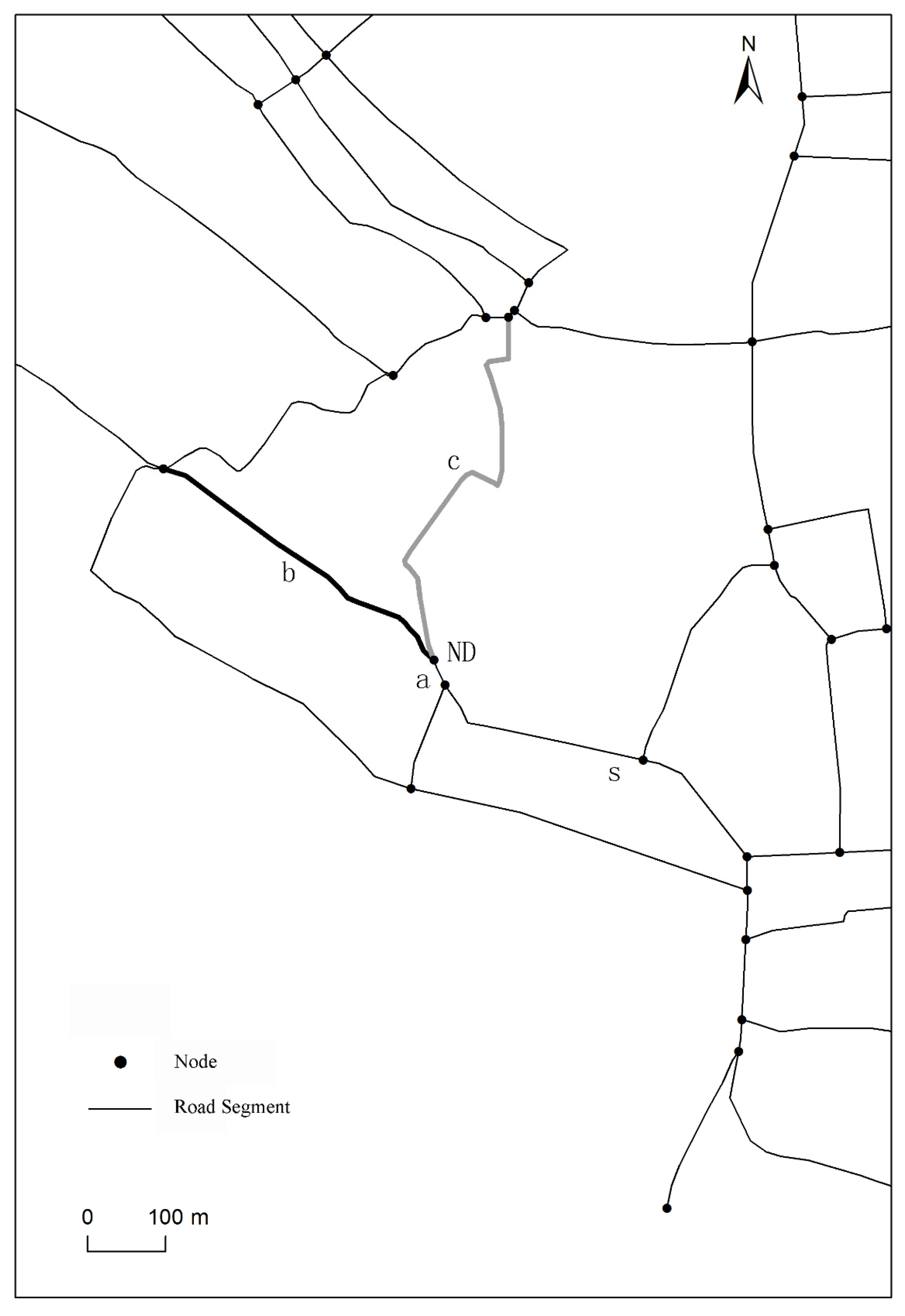
2.1.2. A Connection Strategy Based on Road Importance
2.2. Stroke Order Based on Stroke Importance
2.3. Road Density Based on a Weighted Voronoi Diagram
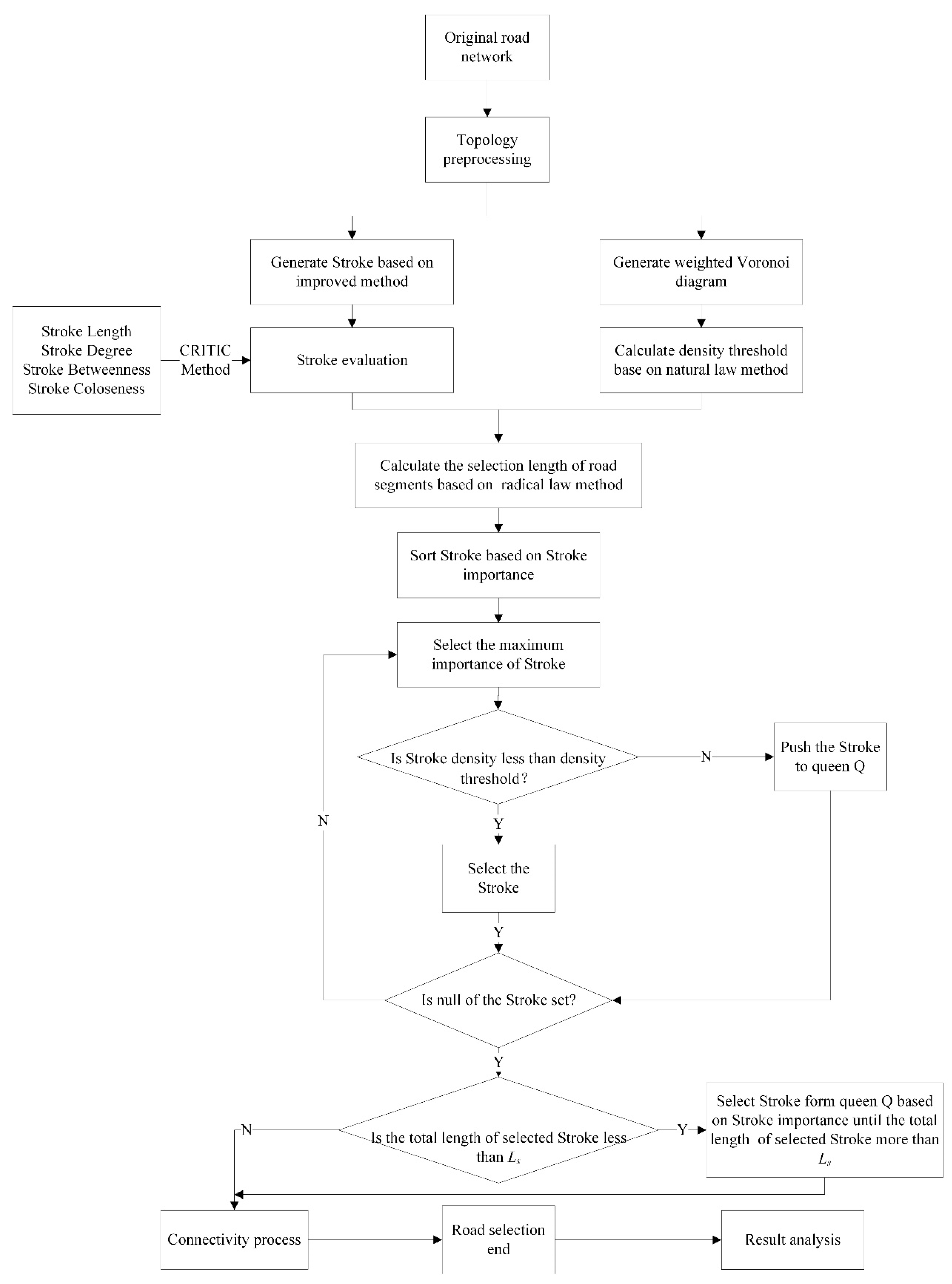
3. Road Selection Based on Stroke and Voronoi Diagrams
- (1)
- Generate a stroke using the improved stroke algorithm and compute stroke importance using the CRITIC method based on the evaluation indicators in Table 2. Then sort strokes based on stroke importance.
- (2)
- Generate a weighted Voronoi diagram to partition the road network and calculate stroke density based on the partition. Then calculate a density threshold using the natural principle method.
- (3)
- Calculate the total length Ls of the road selection using the radical law method.
- (4)
- Make stroke a selection unit used to select road segments based on stroke importance as well as stroke density. The strokes were sorted based on stroke importance and selected the strokes according to order, from high to low. If a stroke density is lower than the density threshold, the stroke is selected. The selected algorithm continues until the total length of the selected stroke is larger than Ls. If the total length of the selected stroke is still smaller than Ls when all strokes are processed using the selected algorithm, the strokes whose densities are lower than the density threshold are continually selected based on stroke importance until the total length of selected strokes is larger than Ls.
- (5)
- If the selected road network is disconnected, then a minimum spanning tree method is used to connect the road network by adding a minimum number of nodes [33]. In order to ensure overall connectivity of the road network after selection, the shortest path is selected to connect pseudo nodes to newly added nodes until all pseudo nodes have been processed.
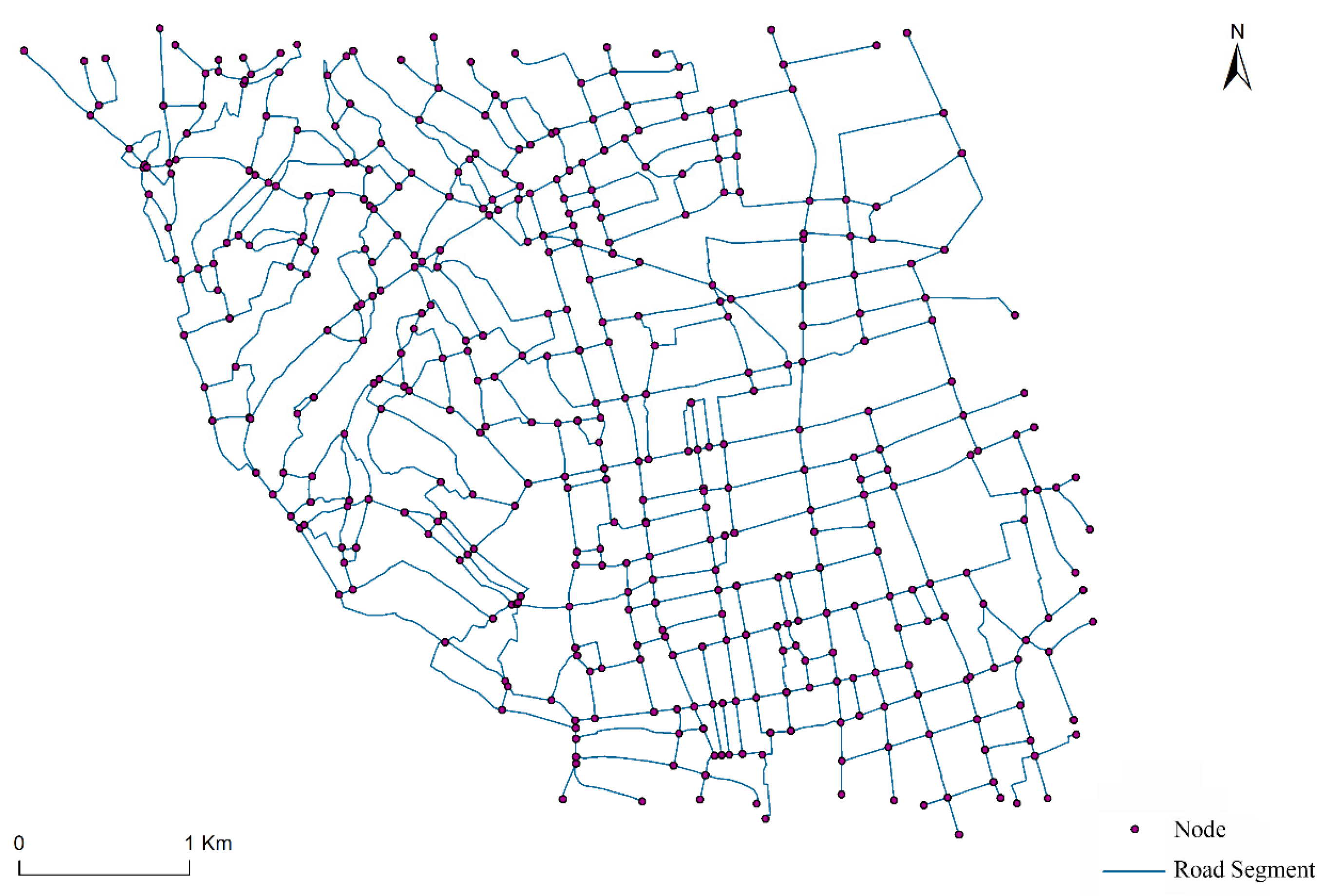
4. A Case Study
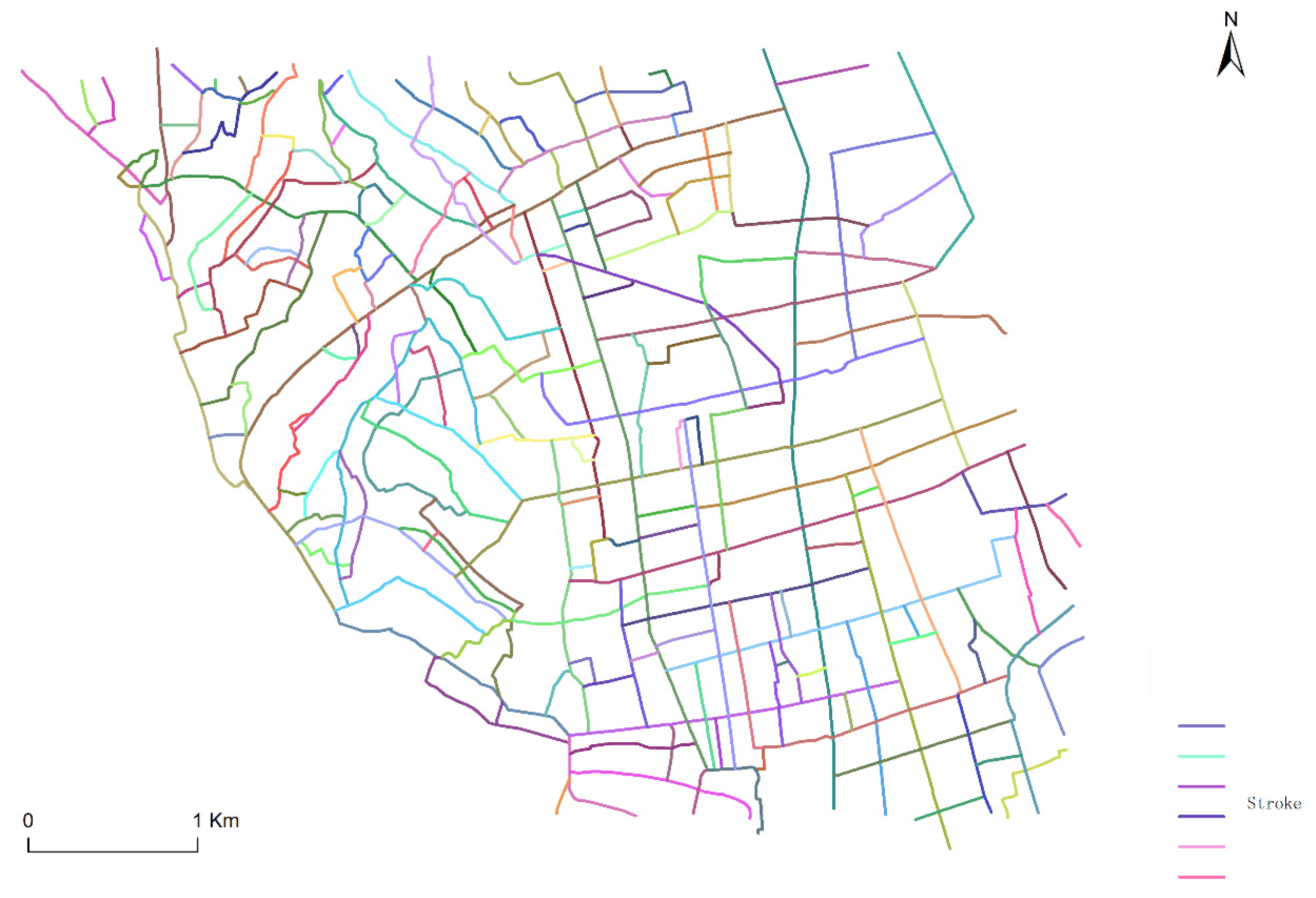
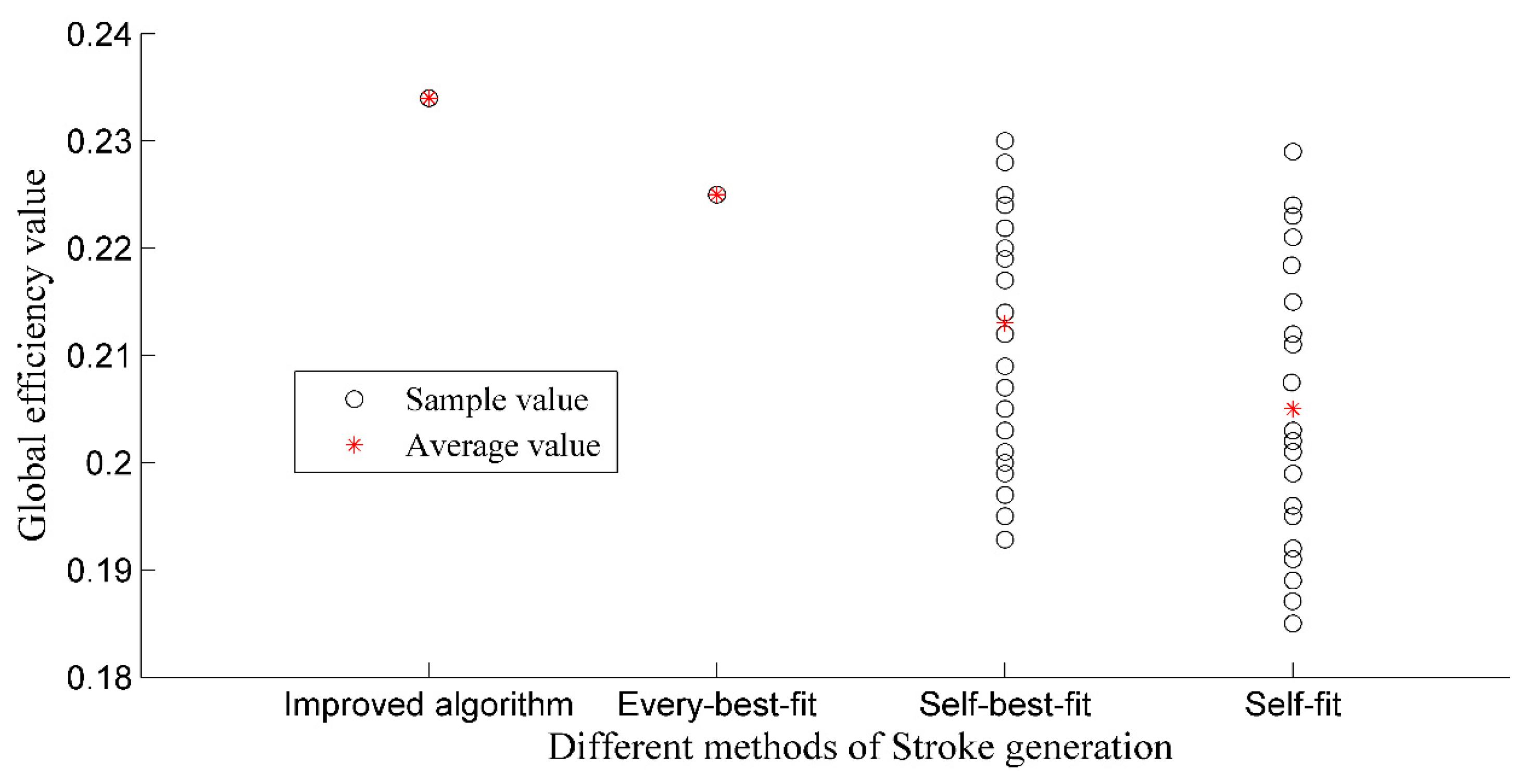
4.1. Analysis of Stroke Generation Results
4.2. Road Density Result Analysis
4.3. Results Analysis for Road Selection
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhou, Q.; Li, Z. How Many Samples are Needed? An Investigation of Binary Logistic Regression for Selective Omission in a Road Network. Cartogr. Geogr. Inf. Sci. 2016, 43, 405–416. [Google Scholar] [CrossRef]
- Suba, R.; Meijers, M.; Oosterom, P. Continuous Road Network Generalization throughout All Scales. ISPRS Int. J. Geo-Inf. 2016, 5, 145. [Google Scholar] [CrossRef]
- Dijk, T.C.; Haunert, J.H.; Oehrlein, J. Location-dependent generalization of road networks based on equivalent destinations. Comput. Gr. Forum 2016, 35, 451–460. [Google Scholar] [CrossRef]
- Thomson, R.; Brook, R. Generalisation of Geographical Networks. In Generalisation Geographic Information: Cartographic Modelling and Applications; Elsevier: Amsterdam, The Netherlands, 2007; pp. 255–268. [Google Scholar]
- Thomson, R.C.; Richardson, D.E. The Good Continuation Principle of Perceptual Organisation Applied to the Generalisation of Road Networks. In Proceedings of the 19th International Cartographic Conference, 11th General Assembly of ICA, Ottawa, ON, Canada, 14–21 August 1999; pp. 1215–1223. [Google Scholar]
- Jiang, B.; Claramunt, C. A Structural Approach to the Model Generalisation of an Urban Street Network. GeoInformatic 2004, 8, 157–171. [Google Scholar] [CrossRef]
- Touya, G. A Road Network Selection Process Based on Data Enrichment and Structure Detection. Trans. GIS 2010, 14, 595–614. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, C.; Zhang, H. Road Selection Based on Evaluation of Stroke Network Functionality. Acta Geod. Cartogr. Sin. 2012, 41, 769–776. [Google Scholar]
- Yang, B.; Luan, X.; Li, Q. Generating Hierarchical Strokes from Urban Street Networks Based on Spatial Pattern Recognition. Int. J. Geogr. Inf. Sci. 2011, 25, 2025–2050. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, Z. A Comparative Study of Various Strategies to Concatenate Road Segments into Strokes for Map Generalization. Int. J. Geogr. Inf. Sci. 2012, 26, 691–715. [Google Scholar] [CrossRef]
- Hh, H.; Qian, H.; Liu, H.; Wang, X.; Hu, H. Road Network Selection Based on Road Hierarchical Structure Control. Acta Geod. Cartogr. Sin. 2015, 44, 453–461. [Google Scholar]
- Hu, Y.; Chen, J.; Li, Z.; Zhao, R. Selective Omission of Road Features Based on Mesh Density for Digital Map Generalization. Acta Geod. Cartogr. Sin. 2007, 36, 351–357. [Google Scholar]
- Wanning, P.; Muller, J.C. A Dynamic Decision Tree Structure Supporting Urban Road Network Automated Generalization. Cartogr. J. 1996, 33, 5–10. [Google Scholar]
- Tian, J.; Ma, M.; Yang, X.C. An Approach to Constraint Based Urban Street Network Automated Generalization. Sci. Surv. Mapp. 2008, 33, 158–160. [Google Scholar]
- Chen, J.; Hu, Y.; Li, Z.; Zhao, R.; Meng, L. Selective Omission of Road Features Based on Mesh Density for Automatic Map Generalization. Int. J. Geogr. Inf. Sci. 2009, 23, 1013–1032. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, Q. Integration of Linear and Areal Hierarchies for Continuous Multiscale Representation of Road Networks. Int. J. Geogr. Inf. Sci. 2012, 26, 855–880. [Google Scholar] [CrossRef]
- Benz, A.; Weibel, R. Road network selection for medium scales using an extended stroke-mesh combination algorithm. Cartogr. Geogr. Inf. Sci. 2014, 41, 323–339. [Google Scholar] [CrossRef]
- Liu, X.; Zhan, F.; Ai, T. Road Selection Based on Voronoi Diagrams and “Strokes” in Map Generalization. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 194–202. [Google Scholar] [CrossRef]
- Tian, J.; Song, Z.H.; Ai, T.H. Grid Pattern Extraction in Road Networks with Graph. Geomat. Inf. Sci. Wuhan Univ. 2012, 37, 724–727. [Google Scholar]
- Chen, B.; Wu, F.; Qian, H.Z. Study on Road Networks Auto_selection Algorithms. J. Image Gr. 2008, 13, 2388–2393. [Google Scholar]
- Borruso, G. Network Density and the Delimitation of Urban Areas. Trans. GIS 2003, 7, 177–191. [Google Scholar] [CrossRef]
- Li, S.; Zhou, Q.; Wang, L. Road Construction and Landscape Fragmentation in China. J. Geogr. Sci. 2004, 15, 123–128. [Google Scholar] [CrossRef]
- Liu, X.; Ai, T.; Liu, Y. Road Density Analysis Based on Skeleton Partitioning for Road Generalization. Geo-Spat. Inf. Sci. 2009, 12, 110–116. [Google Scholar] [CrossRef]
- Tian, J.; Ren, C.; Wang, Y.; Xiong, F.; Lei, Y. Improvement of Self-Best-Fit Strategy for Stroke Building. Geomat. Inf. Sci. Wuhan Univ. 2015, 40, 1209–1214. [Google Scholar]
- Jiang, B.; Zhao, S.; Yin, J. Self-organized natural roads for predicting traffic flow: A sensitivity study. J. Stat. Mech. 2008. [Google Scholar] [CrossRef]
- Tian, J.; He, Q.S.; Yan, F. Formalization and New Algorithm of Stroke Generation in Road Networks. Geomat. Inf. Sci. Wuhan Univ. 2014, 39, 556–560. [Google Scholar]
- Diakoulaki, D.; Mavritas, G.; Papayannakis, L. Determining Objective Weights in Multiple Criteria Problems: The CRITIC Method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Ge, R. The Design and Implementation of Add-in Generating Voronoi Diagram with Multiple Weighted Generators Based on ArcObjects; Resources Environment and Earth Science of Yunnan University: Kunming, China, 2015. [Google Scholar]
- Li, Z.L.; Openshaw, S. Algorithm for automated line generalization based on a natural principle of objective generalization. Int. J. Geogr. Inf. Syst. 1992, 6, 373–389. [Google Scholar] [CrossRef]
- Li, Z.L.; Openshaw, S. A natural principle for objective generalization of digital map data. Cartogr. Geogr. Inf. Syst. 1993, 20, 19–29. [Google Scholar] [CrossRef]
- Müller, J. Optimum point density and compaction rates for the representation of graphic lines. Proc. AutoCarto 1987, 8, 221–230. [Google Scholar]
- Töpfer, F.; Pillewizer, W. The Principles of Selection: a Means of Cartographic Generalization. Cartogr. J. 1966, 3, 10–16. [Google Scholar] [CrossRef]
- Kruskal, J. On the Shortest Spanning Subtree of a Graph and the Travelling Salesman Problem. Am. Math. Soc. 1956, 7, 48–50. [Google Scholar] [CrossRef]
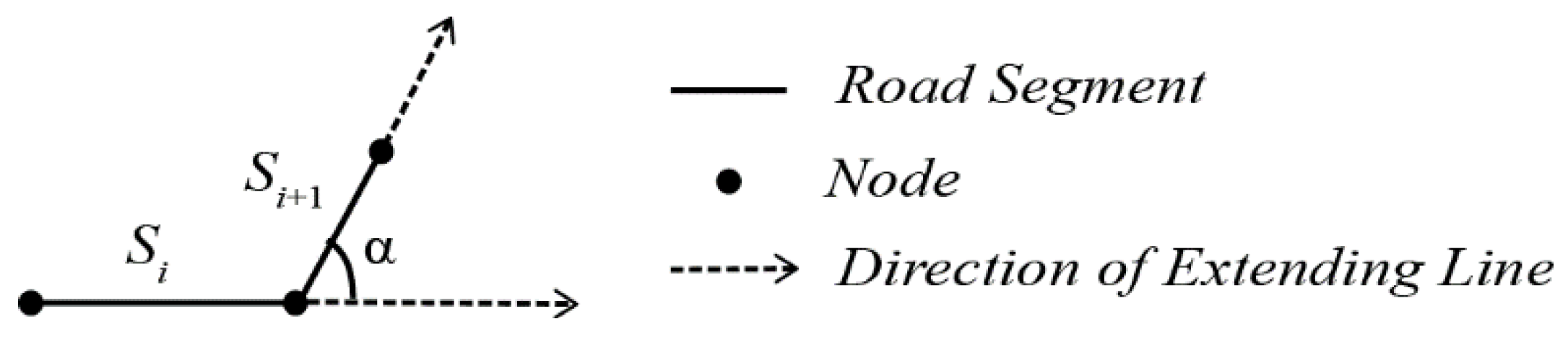
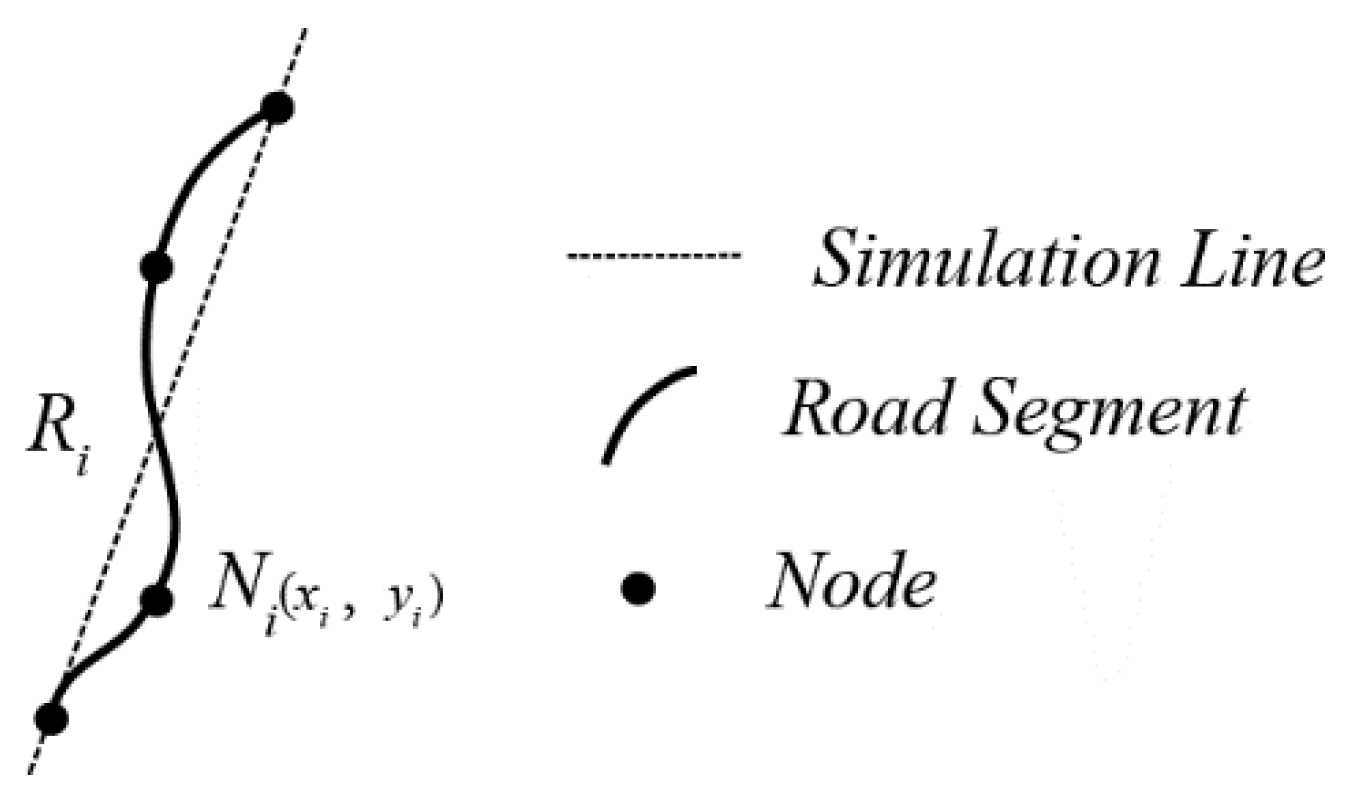
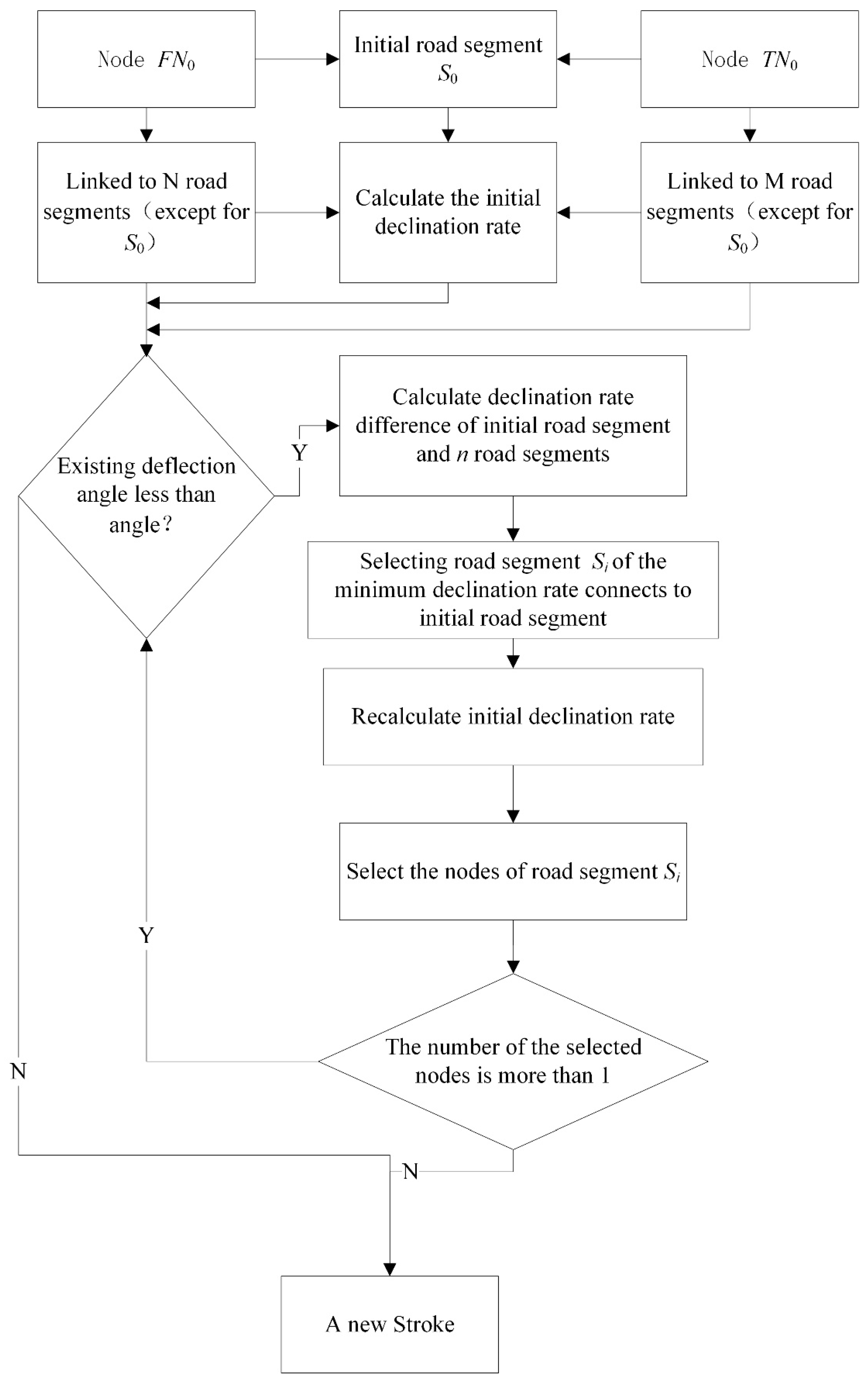
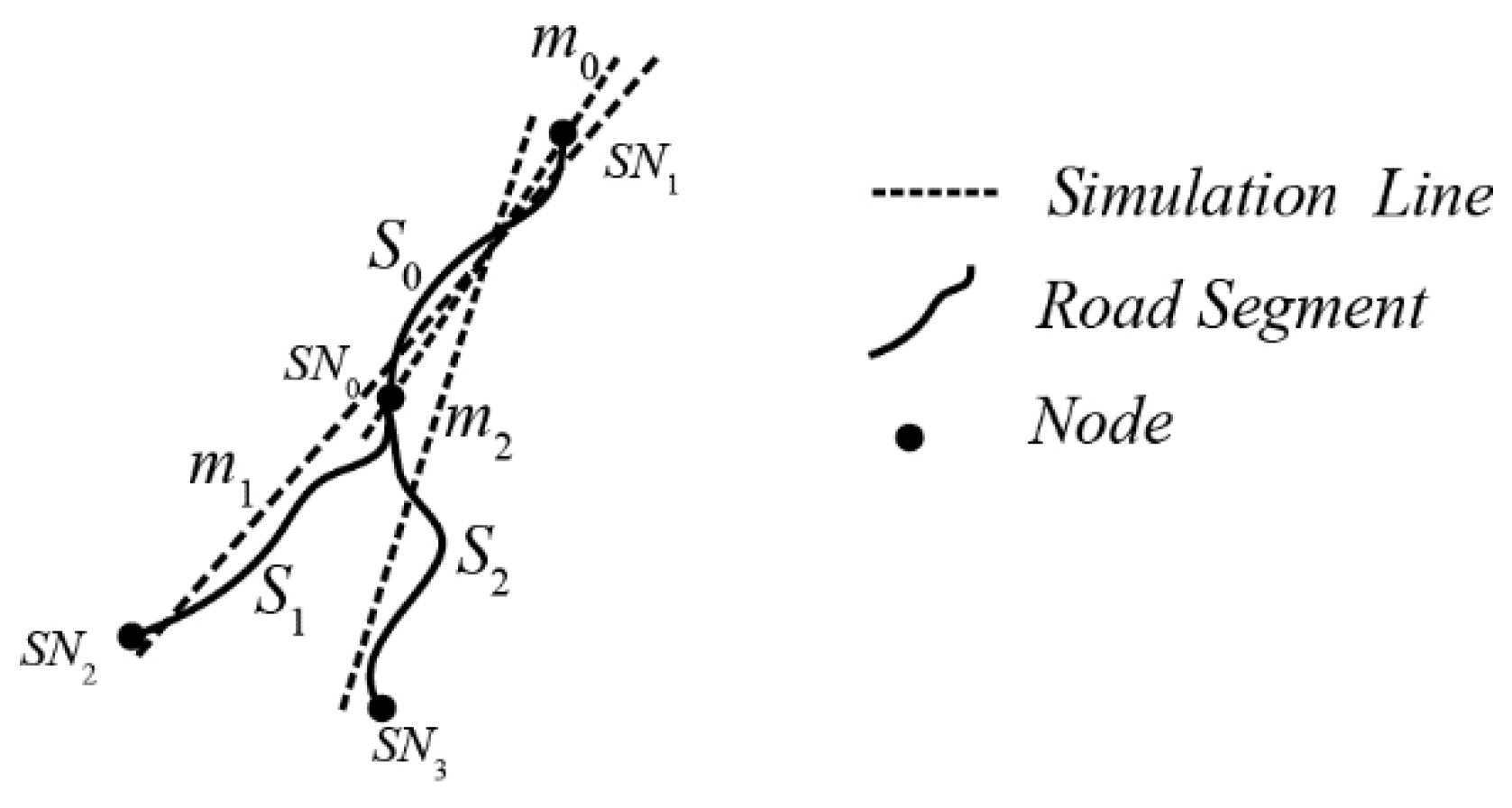
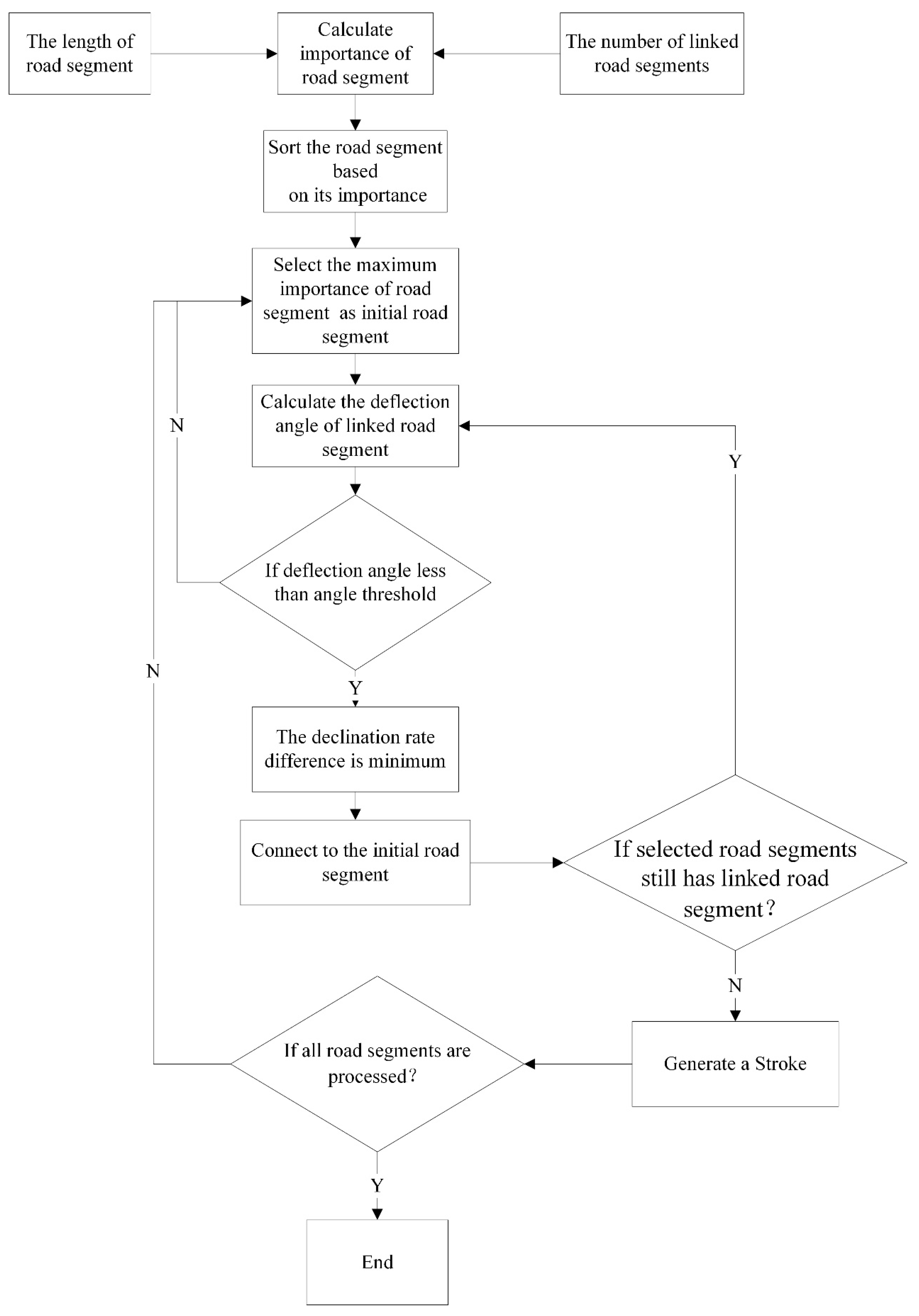



| Set S = Sort (Isegment); //Sort the importance of road segment If (S! == NULL) { Bool IsSelected = False; Initial segment = max (S); //Select road segment that has the maximum importance as the initial road segment Initial segment_IsSelected = True; //Set the property of initial road segment as True. IsLinked (Initial segment); Update S (); } IsLinked (Initial segment) //Judge whether road segment connects { Get the neighbor segments’ number of Initial segment; //Get the linked road segment of initial segment If (k = 0) Set ST = ST + Initial segment; //Build a new Stroke For neighbor segment = 1 to k //k is the number of linked road segments Calculate the deflection angle; //Calculate deflection angle If (deflection angle <= θ) Δ m = |msegment - mInitial segment|; Else Return; Linked segment = min (Δ m) segment; Linked segment_IsSelected = True; //Mark the connected road segment Set Initial segment = Linked segment; } Update S () //Update the road network { Set S_selected = Initial segment; S = S - S_selected; } |
| Stroke Evaluation Indicator | Explanation | Calculated Equation |
|---|---|---|
| Stroke Length (L) | The total length of road segments formed by stroke | , is the length of kth road segment of ith Stroke. |
| Stroke Degree (D) | The total number of road segment formed by stroke | If road segment is part of Stroke then = 1, or = 0. |
| Stroke Betweenness (B) | The probability of a stroke lying in the other strokes | , (j ≠ k; j, k ≠ i), N is the number of node; is the number of shortest paths between node j and node k; is the number of shortest paths between node j and node k that contains node i. |
| Stroke Closeness (C) | The minimal connection number of a stroke to other stroke, reflecting the probability of a stroke being close to the another stroke | , represents the shortest distance of Stroke and Stroke . |
| Method | Number of Correct Types | Number of False Types | Sample Size | Accuracy Rate (%) |
|---|---|---|---|---|
| Improved algorithm | 92/178 | 8/22 | 100/200 | 92/90 |
| Every-best-fit | 83/158 | 17/42 | 100/200 | 83/79 |
| Self-best-fit | 79/150 | 21/50 | 100/200 | 79/75 |
| Self-fit | 72/138 | 28/62 | 100/200 | 72/69 |
| Sum | 326/624 | 74/176 | 400/800 | 82/78 |
| Sample Size | Chi-Square | Degrees of Freedom | Significance |
|---|---|---|---|
| 100 | 15.2 | 3 | 13.8 > 7.82, Yes |
| 200 | 24.7 | 3 | 24.7 > 7.82, Yes |
| Methods | Absolute Difference | Critical Range | Significance |
|---|---|---|---|
| Improved algorithm and Every-best-fit | 0.09/0.11 | 0.065/0.051 | Yes/Yes |
| Improved algorithm and Self-best-fit | 0.13/0.15 | 0.078/0.059 | Yes/Yes |
| Improved algorithm and Self-fit | 0.20/0.21 | 0.087/0.063 | Yes/Yes |
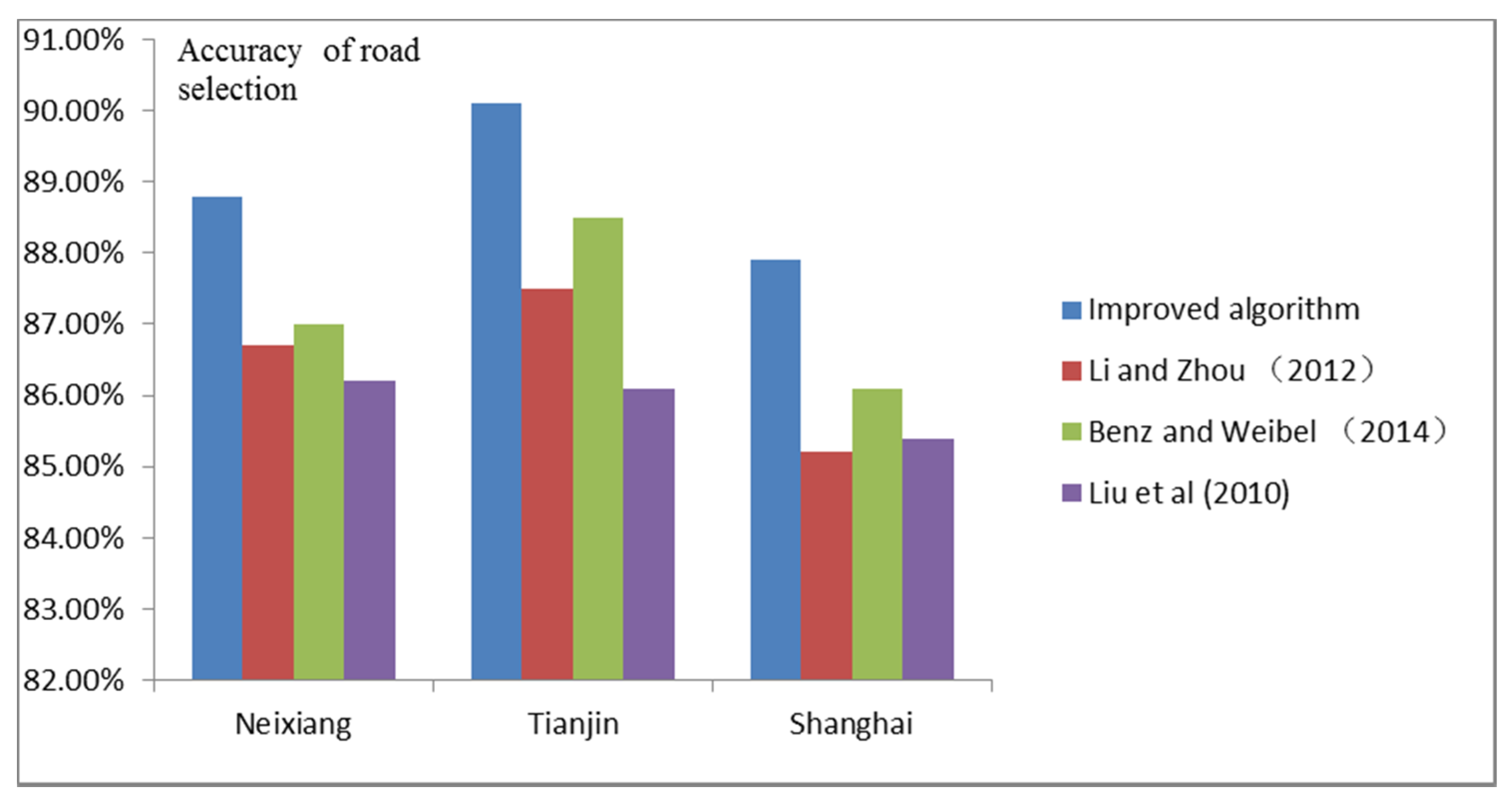
| Study Area | Stroke Generation Method | Length of Selected Road Segment (Km) | Length of Identical Strokes with Existing Map (Km) | Length of Identical Road Segments/Existing Map (%) | Length of Identical Road Segments/Automated Algorithm Result (%) | Accuracy of Road Selection (%) |
|---|---|---|---|---|---|---|
| Neixiang County (The length of existing map is 72.3 (Km)) | Improved Method | 74.8 | 65.4 | 90.1 | 87.4 | 88.8 |
| Every-best-fit | 76.1 | 62.2 | 86.0 | 81.8 | 83.9 | |
| Self-best-fit | 77.4 | 60.8 | 84.1 | 78.5 | 81.3 | |
| Self-fit | 79.2 | 58.0 | 80.2 | 73.2 | 76.7 | |
| Tianjin City (The length of existing map is 108.7 (Km)) | Improved Method | 111.4 | 96.4 | 88.7 | 86.5 | 87.6 |
| Every-best-fit | 113.7 | 89.6 | 82.4 | 78.8 | 80.6 | |
| Self-best-fit | 114.2 | 86.7 | 79.8 | 75.9 | 77.9 | |
| Self-fit | 110.5 | 93.0 | 85.6 | 84.2 | 84.9 | |
| Shanghai City (The length of existing map is 214.5 (Km)) | Improved Method | 217.7 | 185.5 | 86.5 | 85.2 | 85.9 |
| Every-best-fit | 216.3 | 174.1 | 81.2 | 80.5 | 80.9 | |
| Self-best-fit | 220.2 | 181.7 | 84.7 | 82.5 | 83.6 | |
| Self-fit | 218.4 | 171.2 | 79.8 | 78.4 | 79.6 |
| Road Selection Method | Length of Selected Road Segment (The length of Selected Road Segment by Manual Selection is 72.3 (Km)) | Length of Identical Strokes with Manual Results | Length of Identical Road Segments/Manual Result (%) | Number of Identical Road Segments/Automated Algorithm Result (%) | Accuracy of Road Selection (%) |
|---|---|---|---|---|---|
| Stroke-Based Method | 78.9 | 60.9 | 84.2 | 77.2 | 80.7 |
| Mesh Density-Based Method | 76.7 | 61.2 | 80.2 | 79.8 | 78.5 |
| Improved Method | 74.8 | 65.4 | 90.1 | 87.4 | 88.8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wang, Y.; Zhao, W. An Improved Hybrid Method for Enhanced Road Feature Selection in Map Generalization. ISPRS Int. J. Geo-Inf. 2017, 6, 196. https://doi.org/10.3390/ijgi6070196
Zhang J, Wang Y, Zhao W. An Improved Hybrid Method for Enhanced Road Feature Selection in Map Generalization. ISPRS International Journal of Geo-Information. 2017; 6(7):196. https://doi.org/10.3390/ijgi6070196
Chicago/Turabian StyleZhang, Jianchen, Yanhui Wang, and Wenji Zhao. 2017. "An Improved Hybrid Method for Enhanced Road Feature Selection in Map Generalization" ISPRS International Journal of Geo-Information 6, no. 7: 196. https://doi.org/10.3390/ijgi6070196
APA StyleZhang, J., Wang, Y., & Zhao, W. (2017). An Improved Hybrid Method for Enhanced Road Feature Selection in Map Generalization. ISPRS International Journal of Geo-Information, 6(7), 196. https://doi.org/10.3390/ijgi6070196






