1. Introduction
Following both the rapid development and popularization of geographic information and the enhancement of data collection, data with temporal and spatial attributes are quickly accumulated and form large numbers of spatio-temporal datasets [
1]; however, missing data are extremely common; for example, missing data on air quality monitoring sensor readings, missing data on floating car track points or the absence of mobile phone signaling records. If these gaps in data cannot be accurately filled, subsequent analysis and modeling of the data can lead to inaccurate results and unreasonable inference [
2]. Simply deleting records containing missing data would lead to significant loss of original information and would be a waste of data resources [
3]; therefore, methods to accurately and efficiently interpolate missing data are urgently needed.
In past decades, a large number of interpolation methods has been proposed to solve the problem of spatio-temporal missing data [
4,
5,
6,
7,
8,
9,
10]. These methods can be roughly divided into three categories: spatial interpolation, temporal interpolation and spatio-temporal interpolation.
Spatial interpolation methods mainly use spatial correlation among data to interpolate missing data. Traditional methods (e.g., inverse distance weighting (IDW)) simply assume that the data distribution obeys the first law of geography, namely the closer data are in spatial distribution, the greater the contribution they make to missing data interpolation. During interpolation, each site is assumed to be independent of the others, and weights are calculated by computing the distance between missing data and the surrounding site [
11,
12]. Most approaches use kriging, a linear regression method that utilizes minimum mean square error and does not treat each site independently. The method assumes consistent sample mean and variance to meet second order stationarity and assumes that the covariance between any two spatio-temporal points is only associated with the distance (i.e., the absolute position of time and space is irrelevant) [
13,
14]. However, due to the existence of spatial and temporal heterogeneity, the data distribution can show uneven characteristics and relationships according to different regions [
15]; therefore, the accuracy of interpolation results obtained by existing methods remains unsatisfactory if data are not homogeneously distributed. To solve this problem [
16] considered spatial autocorrelation and heterogeneity in a study area and proposed a point estimation model of biased hospital-based area disease estimation (P-BSHADE). The P-BSHADE method calculates the covariance and correlation coefficient of historical observational data and uses the expectation between surrounding stations and interpolation sites to get an optimal linear unbiased estimator. However, in cases of continuous missing data, the method leads to a singular value of the missing data matrix, which results in large interpolation error. At the same time, this method does not consider the heterogeneity of the time dimension [
2].
Time series prediction methods typically use historical data for a given location to build a prediction framework for predicting the values of missing data points at the same site. The autoregressive integrated moving-average (ARIMA) model [
17] and simple exponential smoothing (SES) [
18] are two representative examples of this approach. However, this approach fails to address two major problems. First, many prediction models do not fully utilize the essential characteristics of spatio-temporal data, which can degrade performance; second, if a consecutive series of data is all lost, prediction methods often cannot achieve complete reconstruction [
19].
Given that single dimension interpolation methods only consider spatial or temporal dimensions, achieving satisfactory interpolation results is challenging. In recent years, a number of studies have extended single dimension interpolation methods to consider both space and time; for example, spatio-temporal probabilistic principal component regression (ST-PCR), spatio-temporal IDW (ST-IDW), spatio-temporal kriging (ST-kriging) and the spatio-temporal heterogeneous covariance method (ST-HC) [
2,
3,
7,
9,
10,
20,
21,
22]. ST-PCR [
9] is a statistical learning-based method, which takes advantage of the statistical feature of observed data. However, it often needs a strong hypothesis over the data. ST-IDW [
23] defined a three-dimensional space-time distance, which then applied IDW to estimate missing values; however, due to the existing problems with the IDW method, application of ST-IDW remains limited and fails to achieve unbiased estimation. The ST-kriging method [
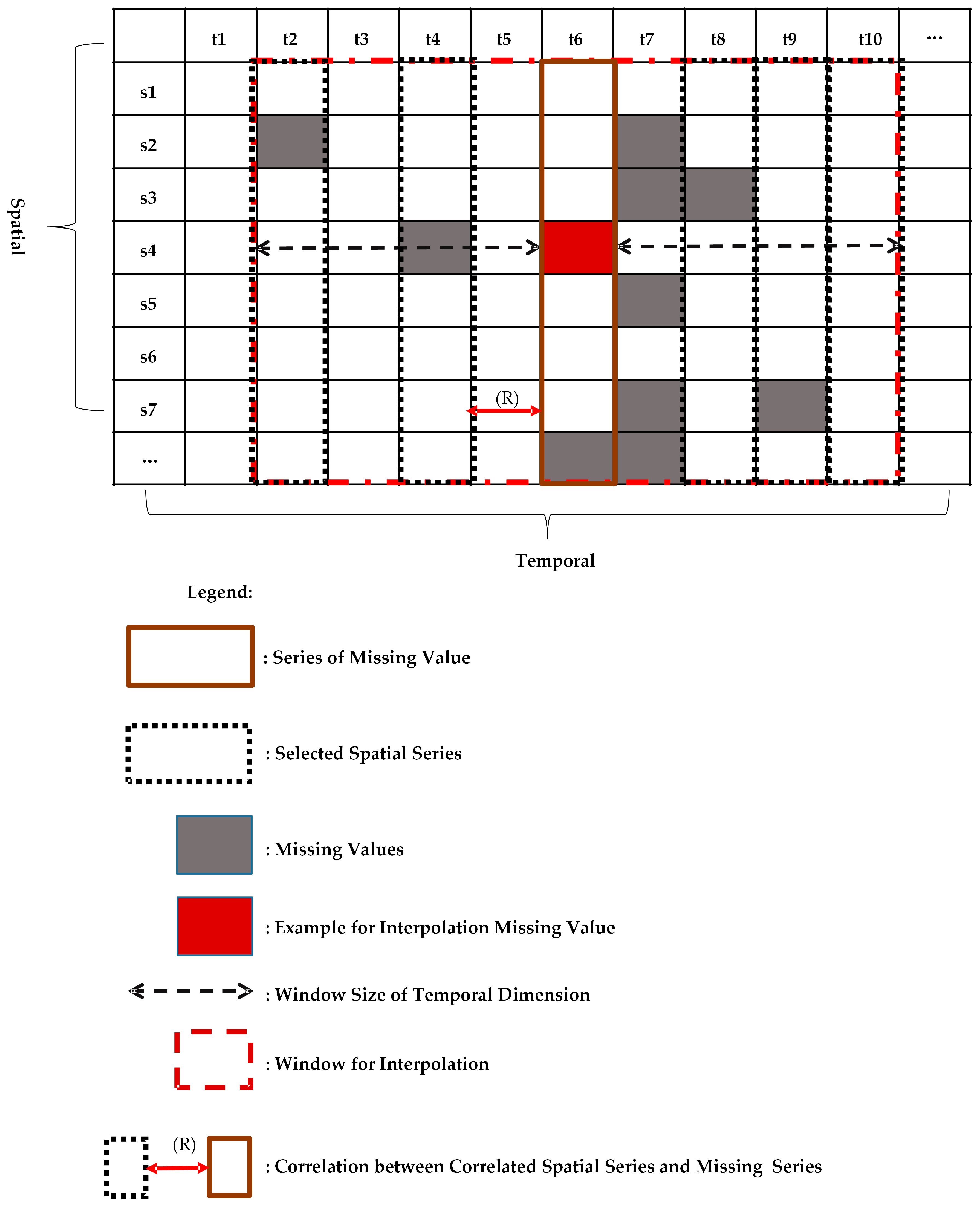
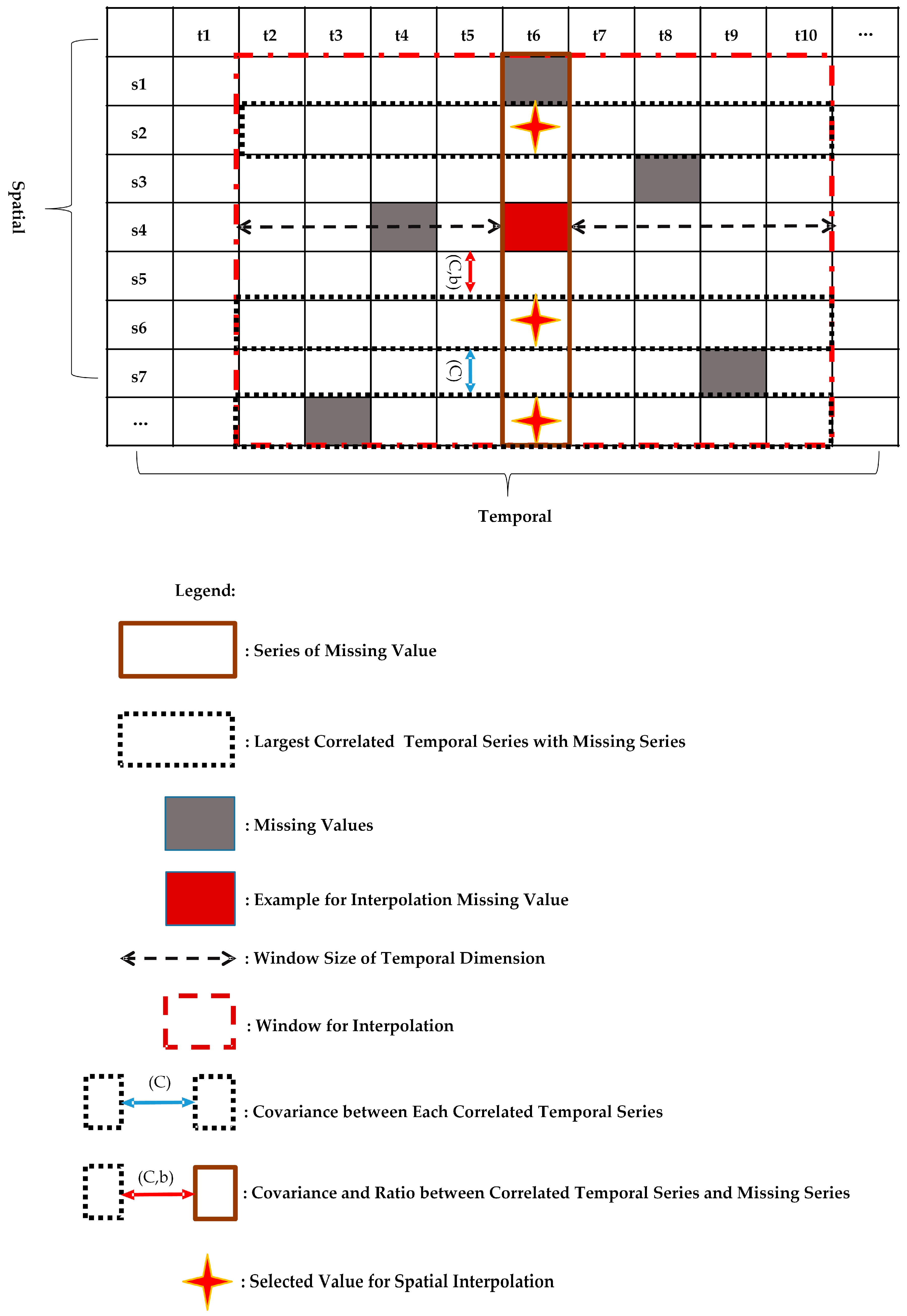
14] estimates the interpolation function by adopting a spatio-temporal covariance function, but it does not take into account the effects of spatial and temporal heterogeneity on interpolation results. To address this issue, the ST-HC method, which is an extension of P-BSHADE, estimates missing data by considering temporal and spatial heterogeneity. Missing datasets are firstly partitioned into homogenous spatial regions, and then, the most correlated spatial sampling and time sampling series are selected for the partition of missing data. According to the P-BSHADE algorithm, both spatial and temporal contribution weights are calculated to obtain the best linear unbiased estimates in spatial and temporal dimensions. Finally, using the correlation coefficient to determine the spatial and temporal weights, estimated values in spatial and temporal dimensions are integrated to obtain overall estimated values of missing data [
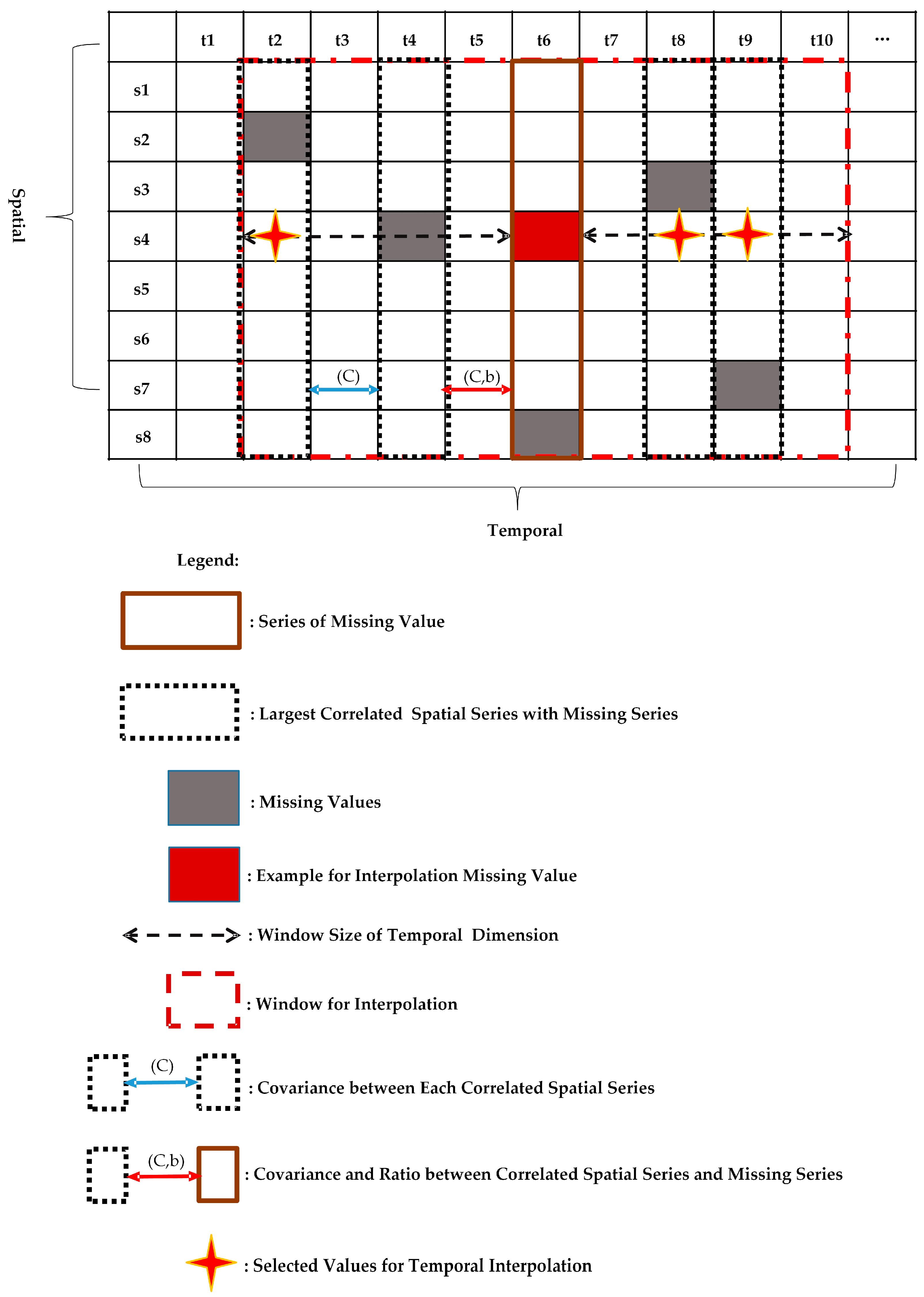
2]. However, this method requires the whole dataset to participate in computation, which leads to high computational complexity and a large volume of redundant data. For example, when the time span of the dataset is large, including the n dimensional space sequence, both n
2 covariance and the correlation coefficient need to be calculated for each missing data point. In addition, when data are missing continuously, interpolation accuracy is low, and it may even be impossible to obtain a final interpolation result.
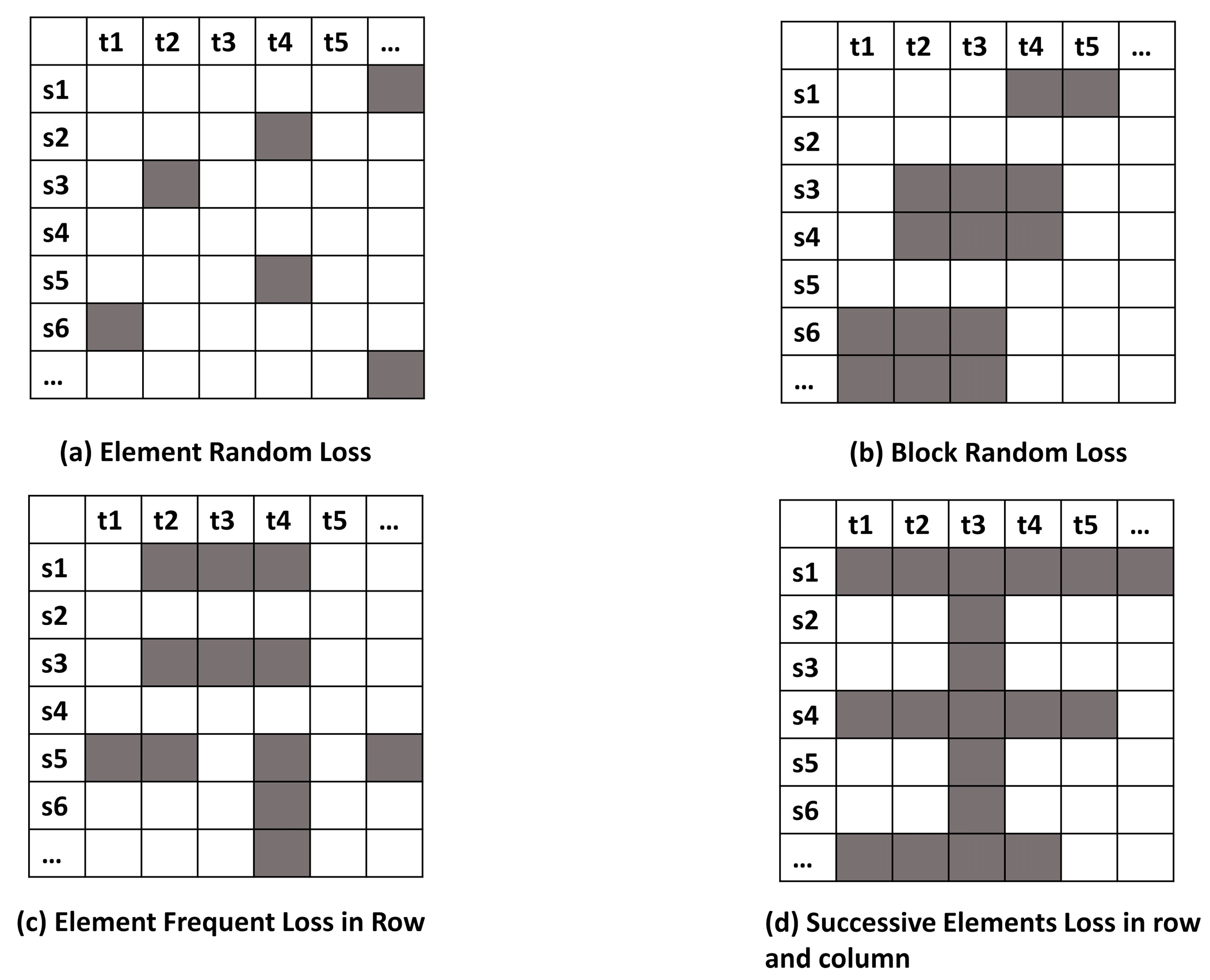
Missing data reconstruction methods are further challenged by the variation in patterns of missing data [
24,
25]; for example, missing data completely at random, non-random missing data [
26], or whole blocks of missing data [
27] (
Figure 1). The work in [
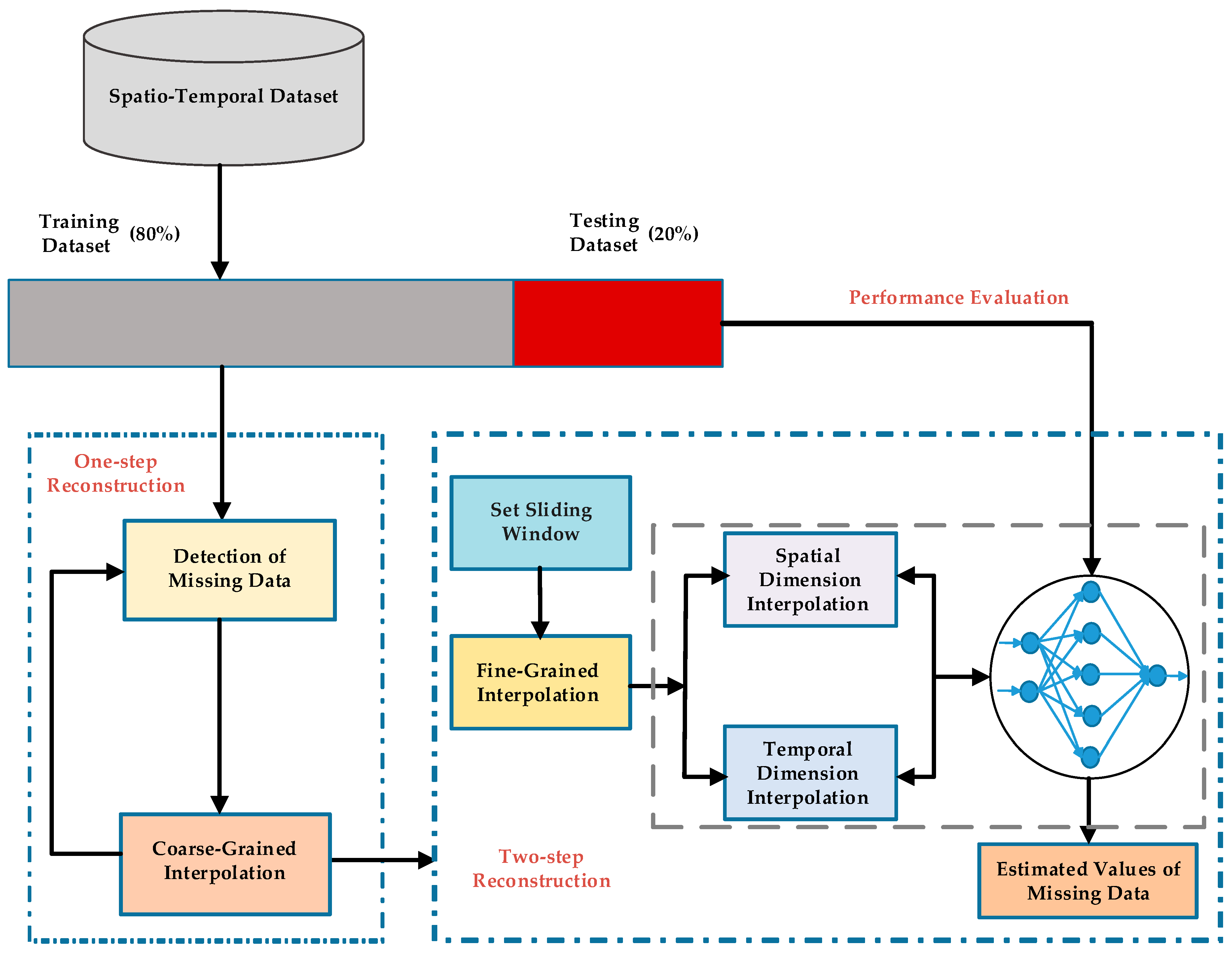
10] formulates the spatio-temporal sensory data as a high-dimensional tensor, using the tensor completion method to recover missing values. However, when a whole temporal or spatial dimension of the data is missing, this method may fail. The same problem exists for other spatio-temporal interpolation methods (e.g., IDW, kriging, P-BSHADE, ST-IDW, ST-kriging, ST-HC). Furthermore, most existing methods assume a linear relationship between spatial and temporal data (e.g., ST-HC, ST-IDW, ST-kriging); however, the relationship between spatial and temporal data may be linear or nonlinear. To address these issues, in this study, we developed a new two-step method to reconstruct missing spatio-temporal data (ST-2SMR).