A Standard Indoor Spatial Data Model—OGC IndoorGML and Implementation Approaches
Abstract
:1. Introduction
2. Related Work on Indoor Spatial Data Models and Standards
2.1. Indoor Spatial Data Models
2.2. Standards for Indoor Spatial Information
3. Requirements for Indoor Spatial Data Models
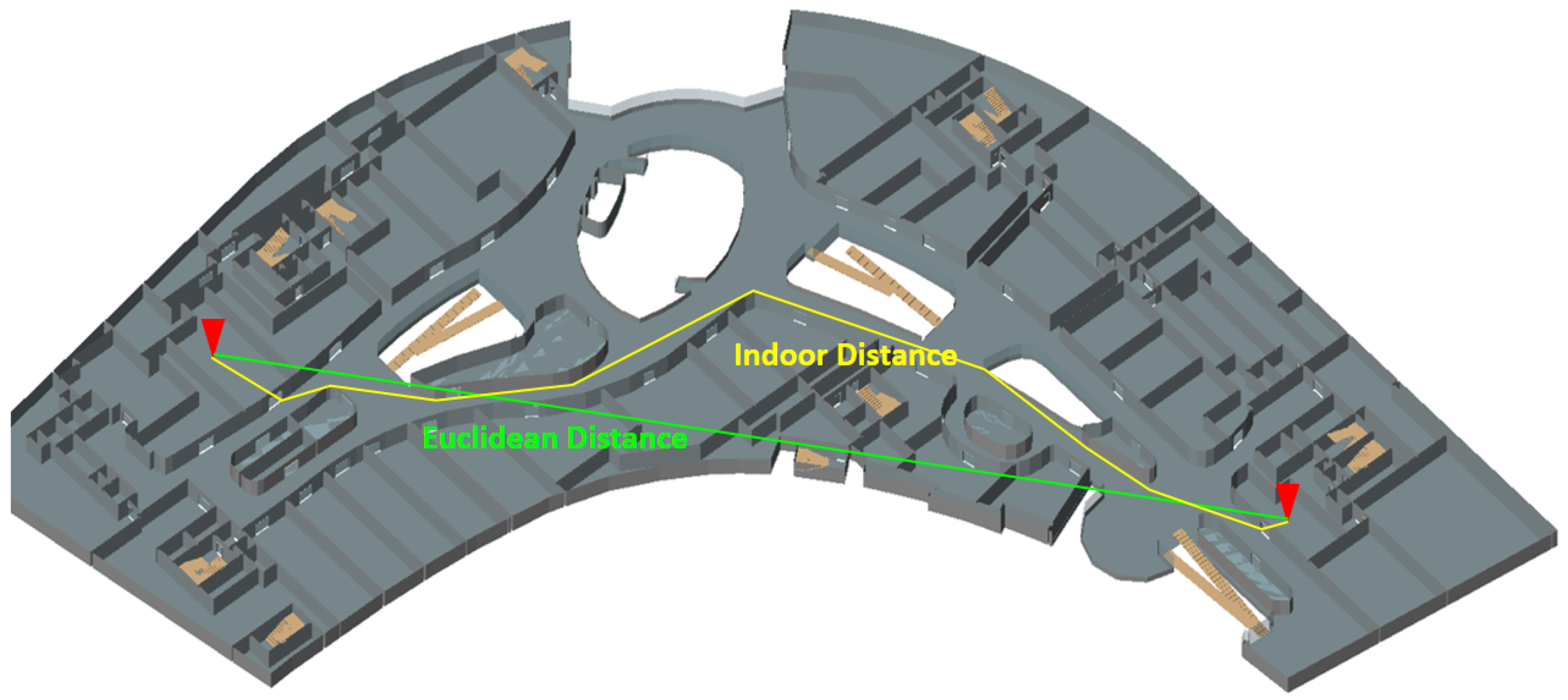
3.1. Indoor Distance
3.2. Complex Structures of Indoor Space
3.3. Cell-Based Context Awareness
3.4. Integrating Multiple Datasets
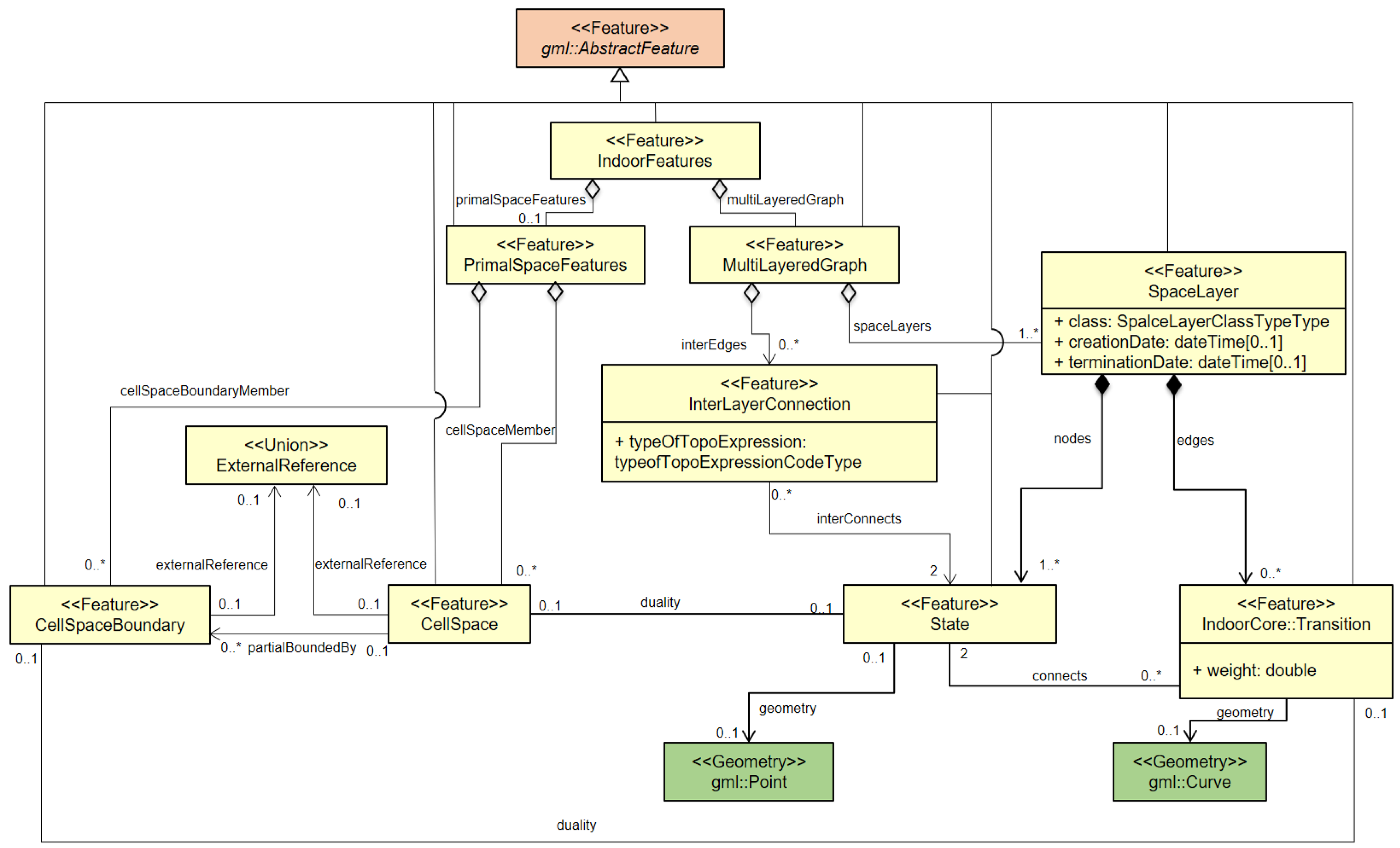
4. Basic Concepts of IndoorGML
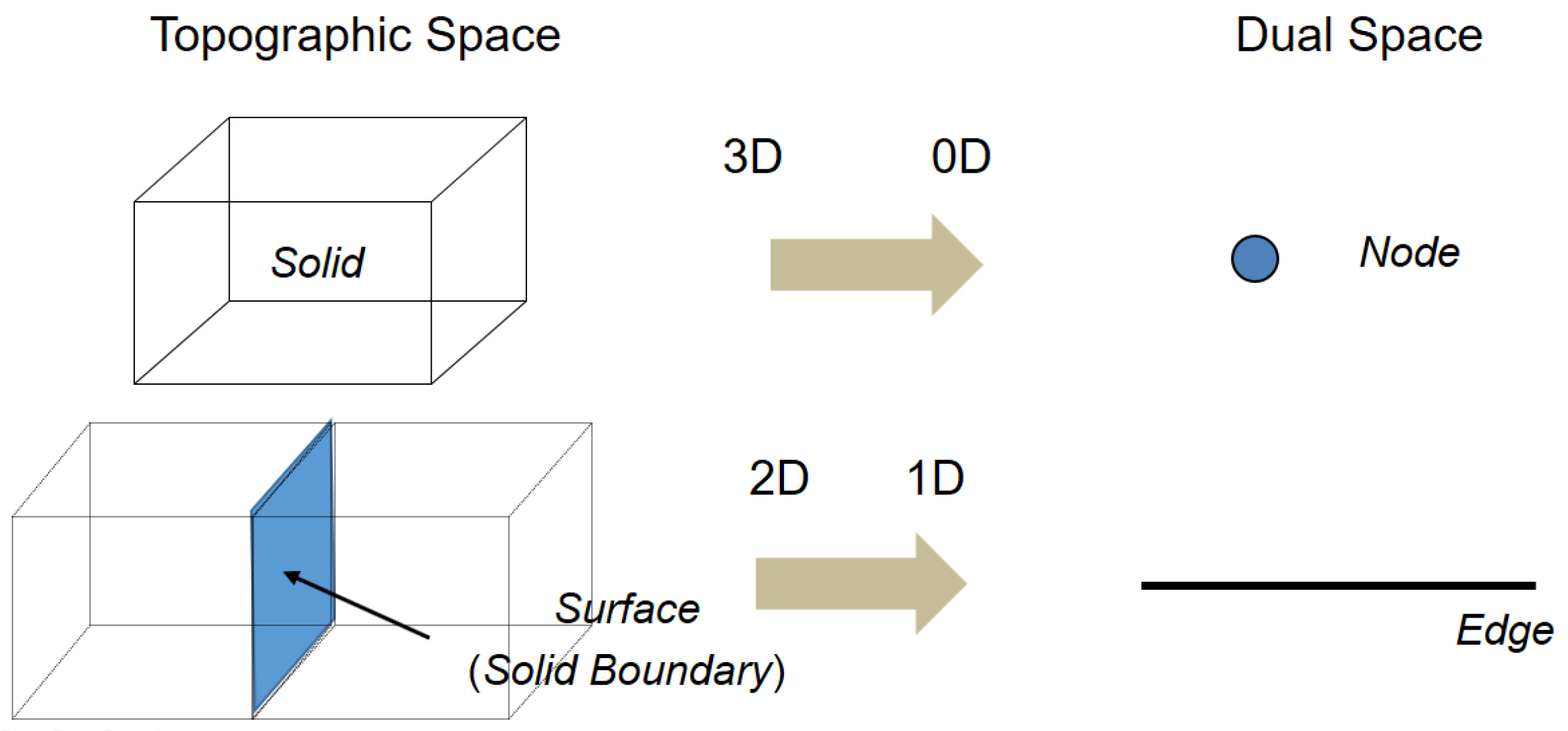
4.1. Cellular Space Model
- 1.
- ,
- 2.
- ⋃ and
- 3.
- each cell c has its cell identifier .
4.2. Cell Geometry
- Option 1, no geometry: The first option is to exclude any geometric properties from IndoorGML data and to include only topological relationships between cells, which will be explained in the next subsection.
- Option 2, geometry in IndoorGML: The second option is to represent its geometry within IndoorGML data by geometric types defined in ISO 19107. For example, the three-dimensional geometry of a cell is defined as a solid of ISO 19107. Note that the geometry of the cell is an open primitive as defined in ISO 19107, which means that the boundary of the cell geometry does not belong to the cell. This definition is consistent with the non-overlapping condition of the cellular space defined in Section 4.1.
- Option 3, external reference: The third option is to include external references to the object in another dataset that contains geometric data. For example, a cell in IndoorGML data only points to an object in CityGML via the GML identifier that contains geometric properties.
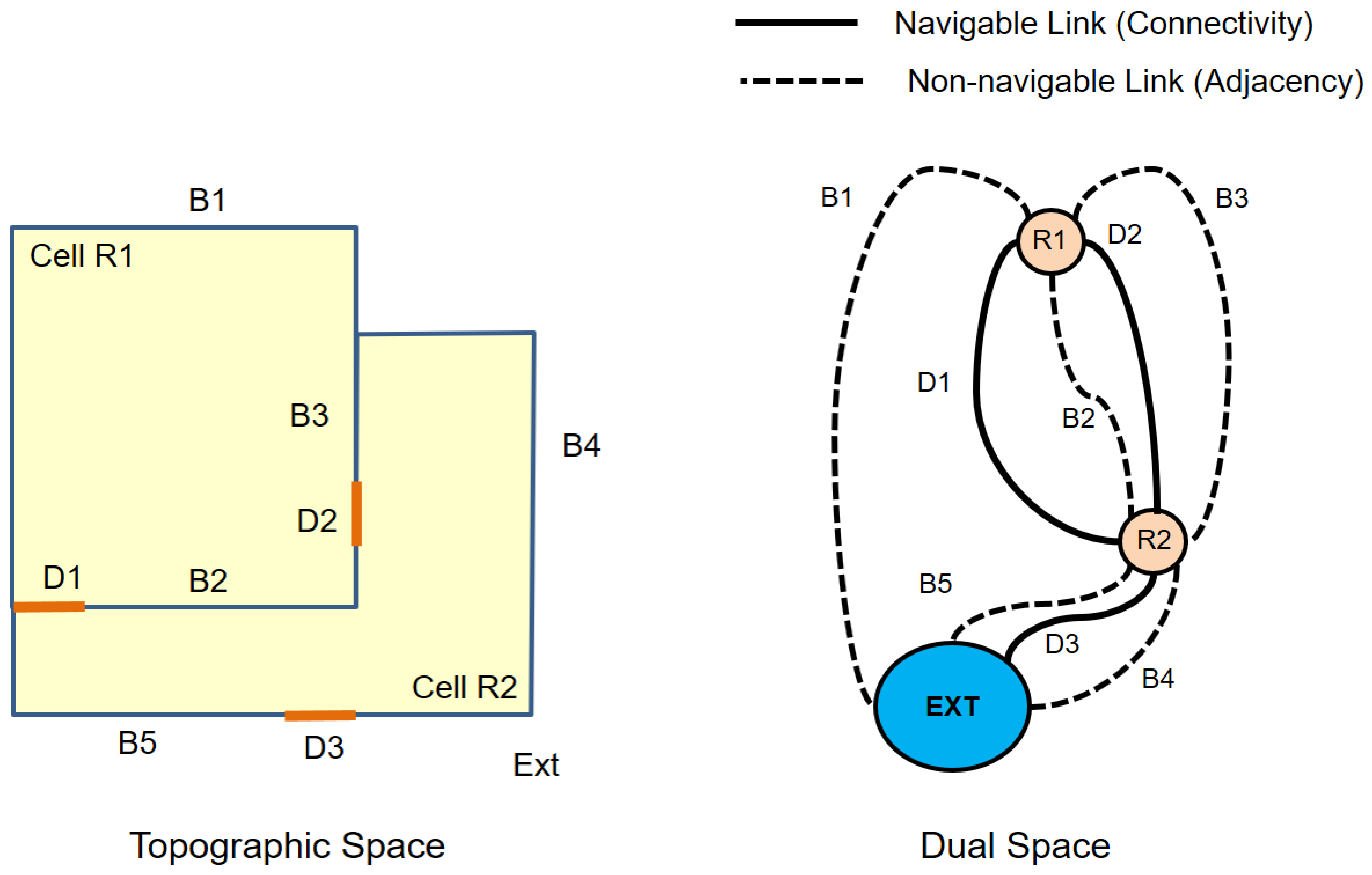
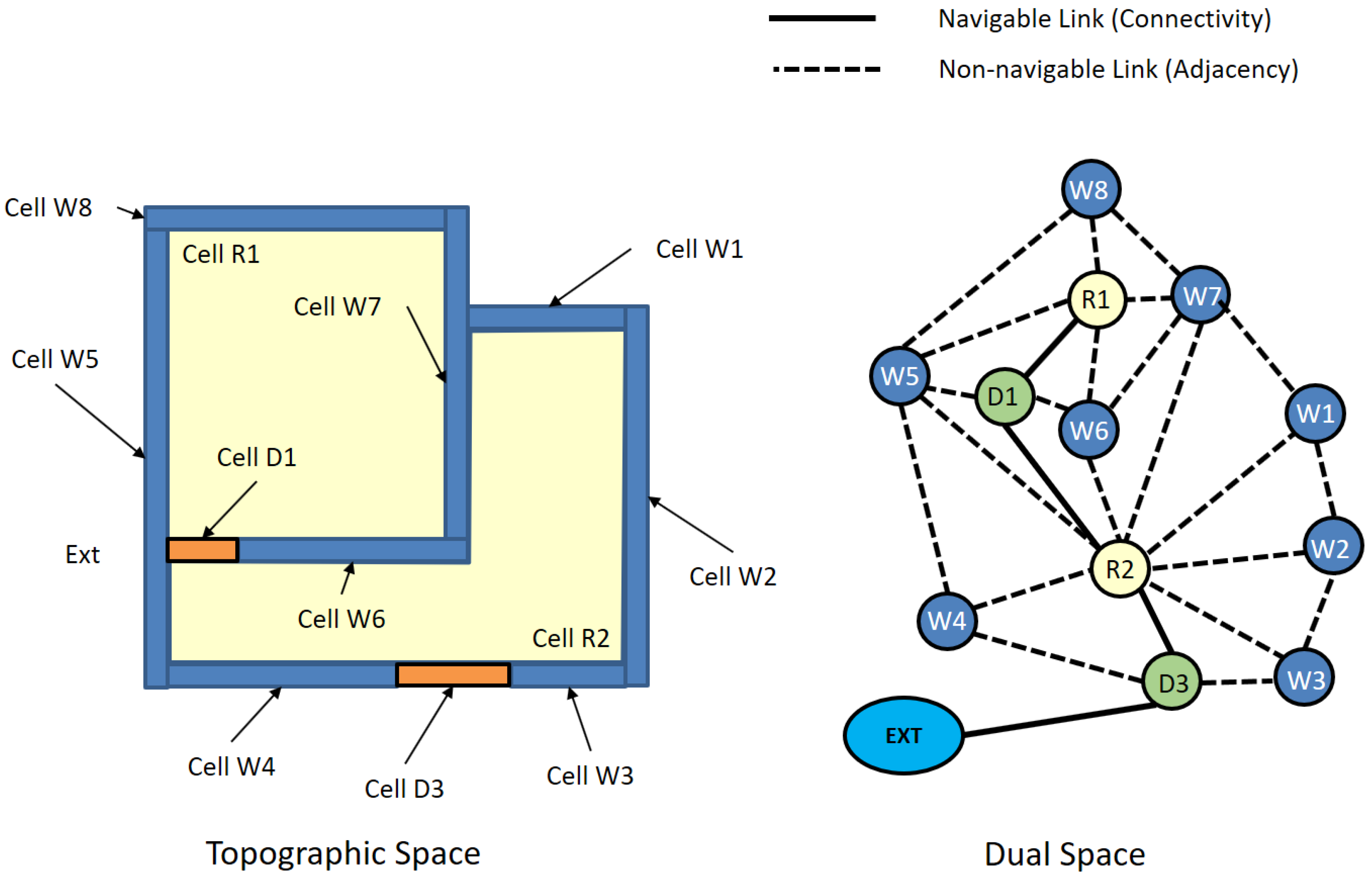
4.3. Topology between Cells
4.4. Cell Semantics
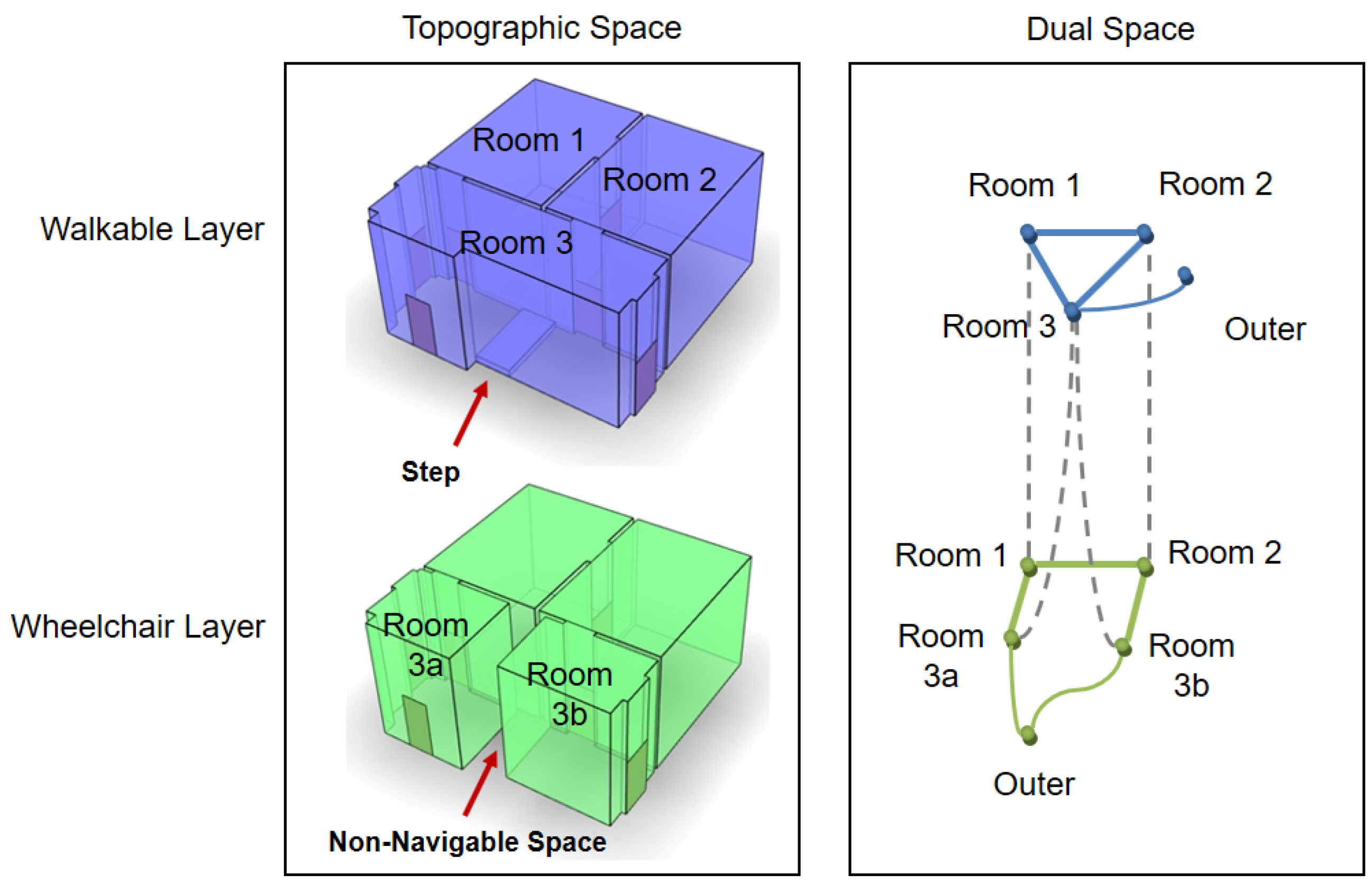
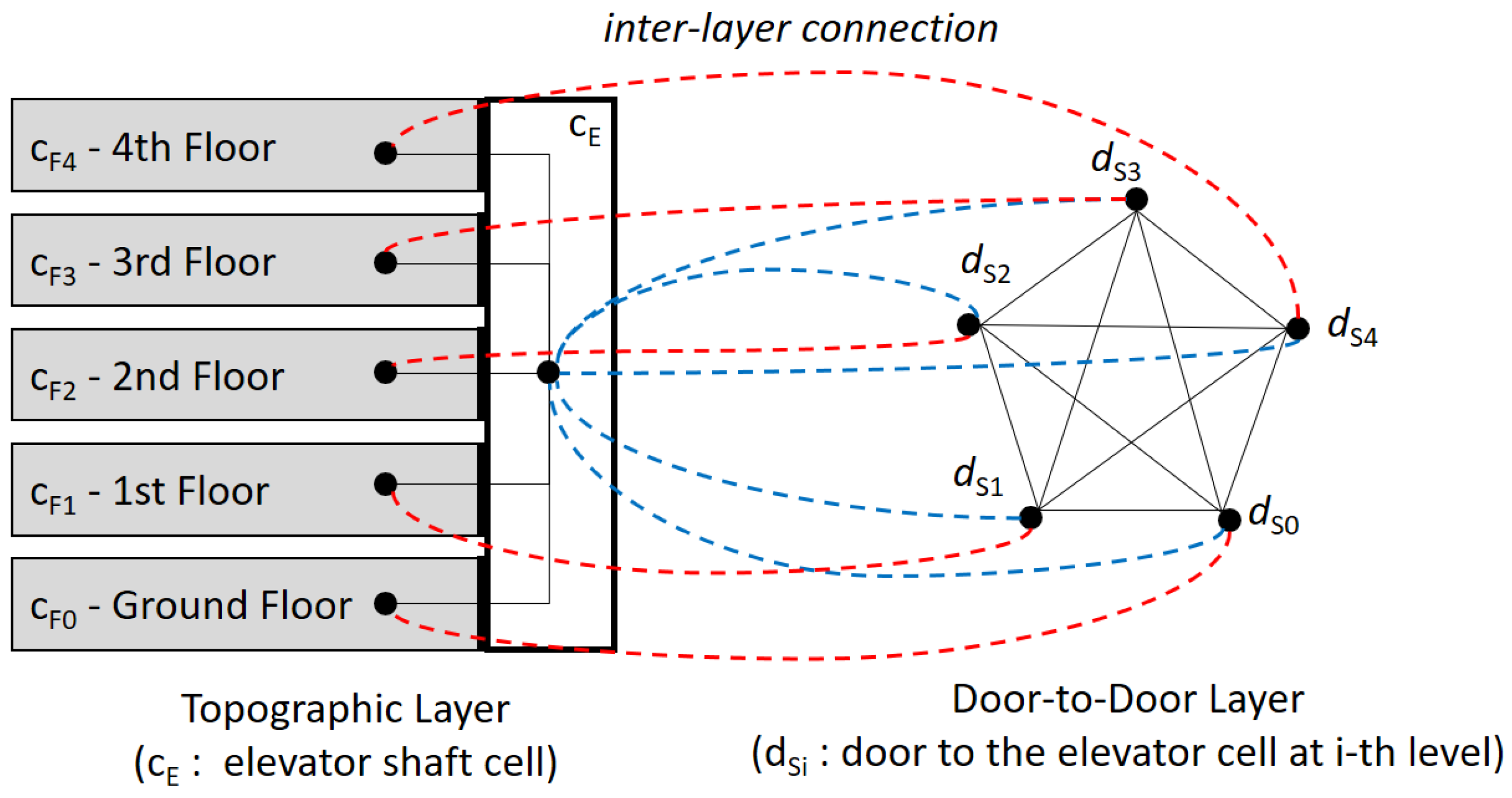
4.5. Multi-Layered Space Model
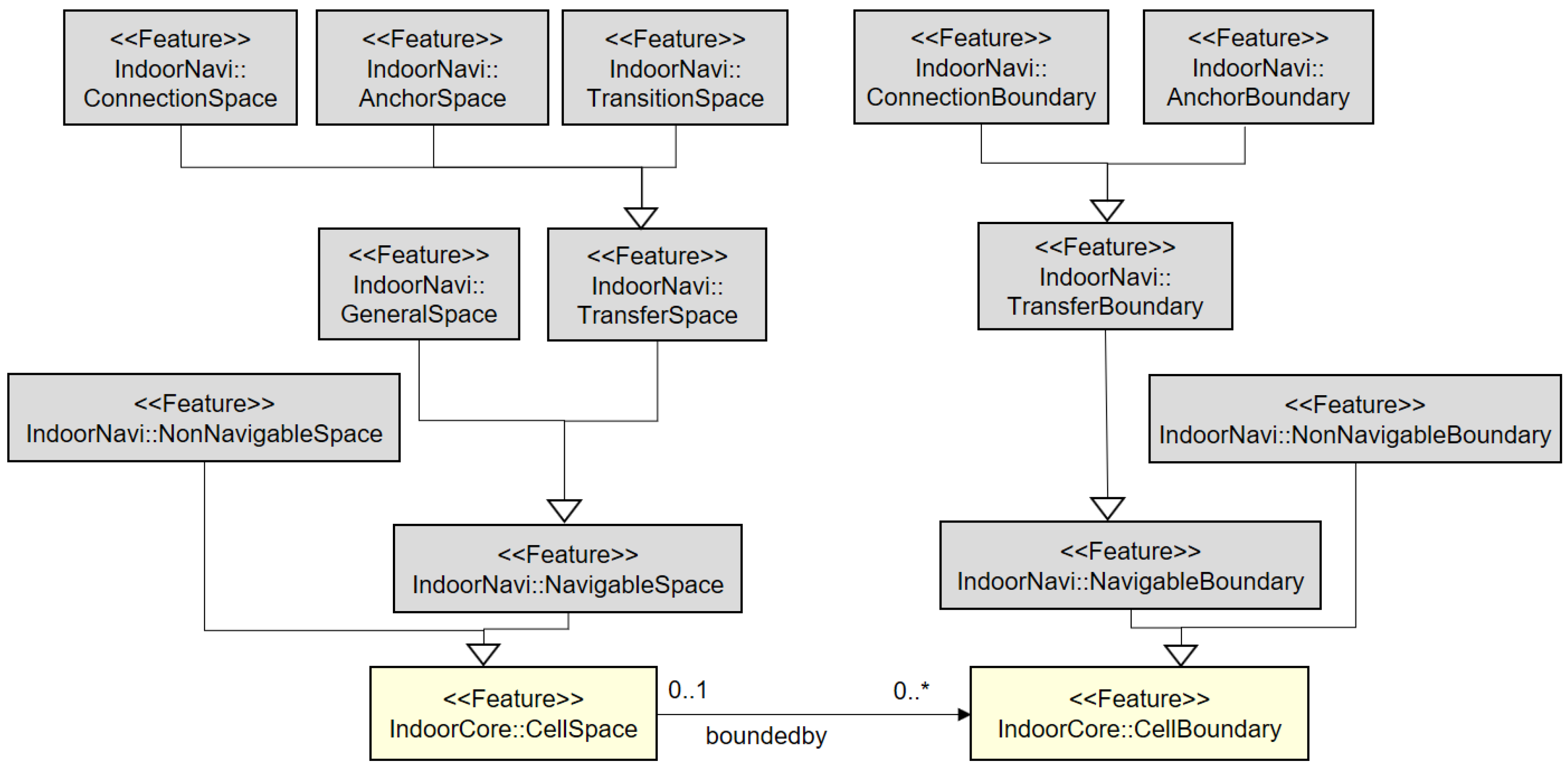
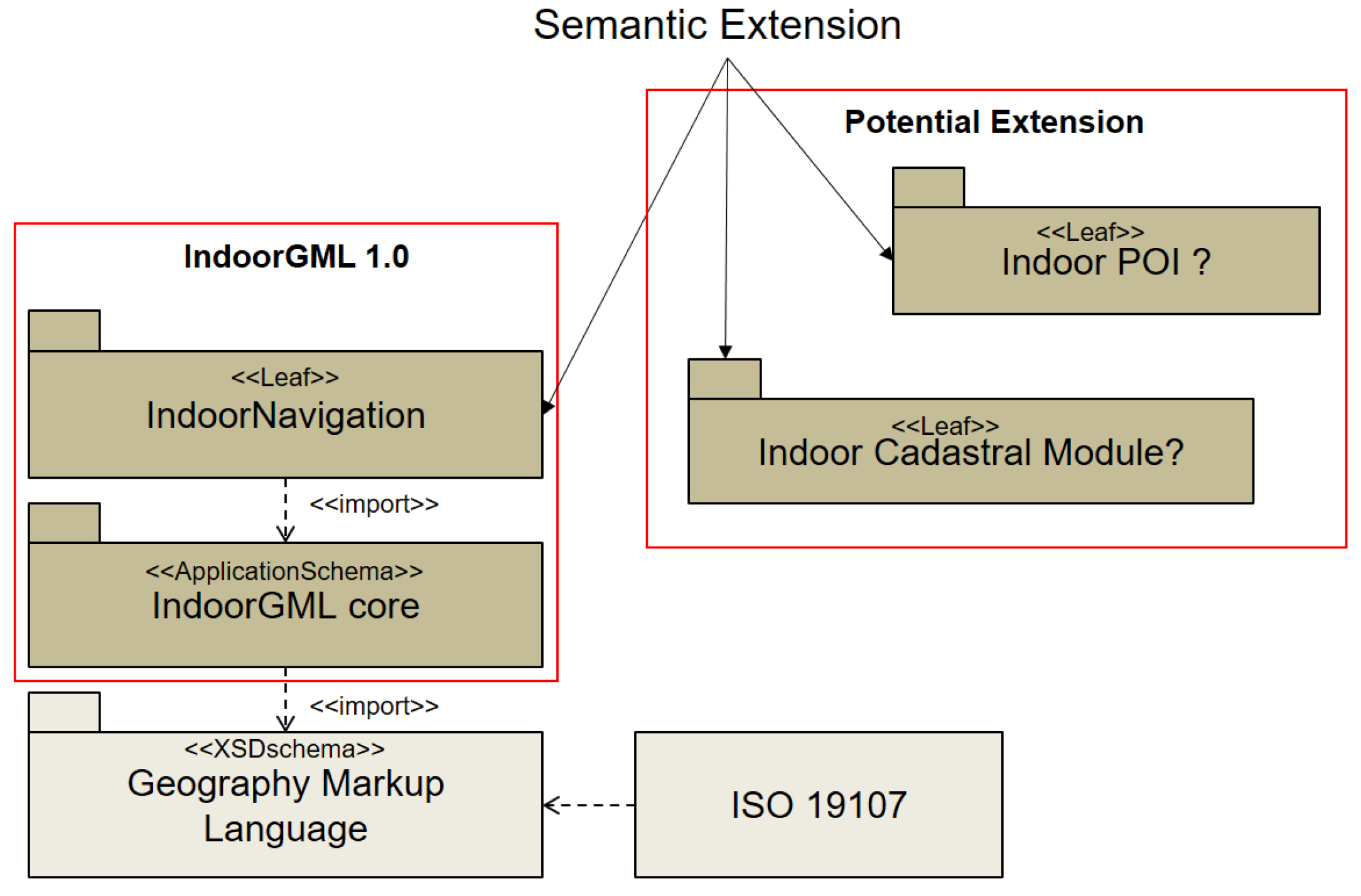
4.6. Modular Structure of IndoorGML
4.7. Implementation of IndoorGML Core Module
5. Cell Determination in IndoorGML
5.1. Cell Determination and Subspacing
- different properties: if a space has different properties such as kitchen area and living room, it is desirable to partition it into two cells with virtual boundaries.
- big space as a cell: if a space is too big, like a long hall-wall or a big convention hall, it is recommended to split it into smaller subspaces.
- sensor coverages: it is also possible to divide a space in terms of sensor coverage, such as CCTV viewshed or WiFi and RFID coverages [29].
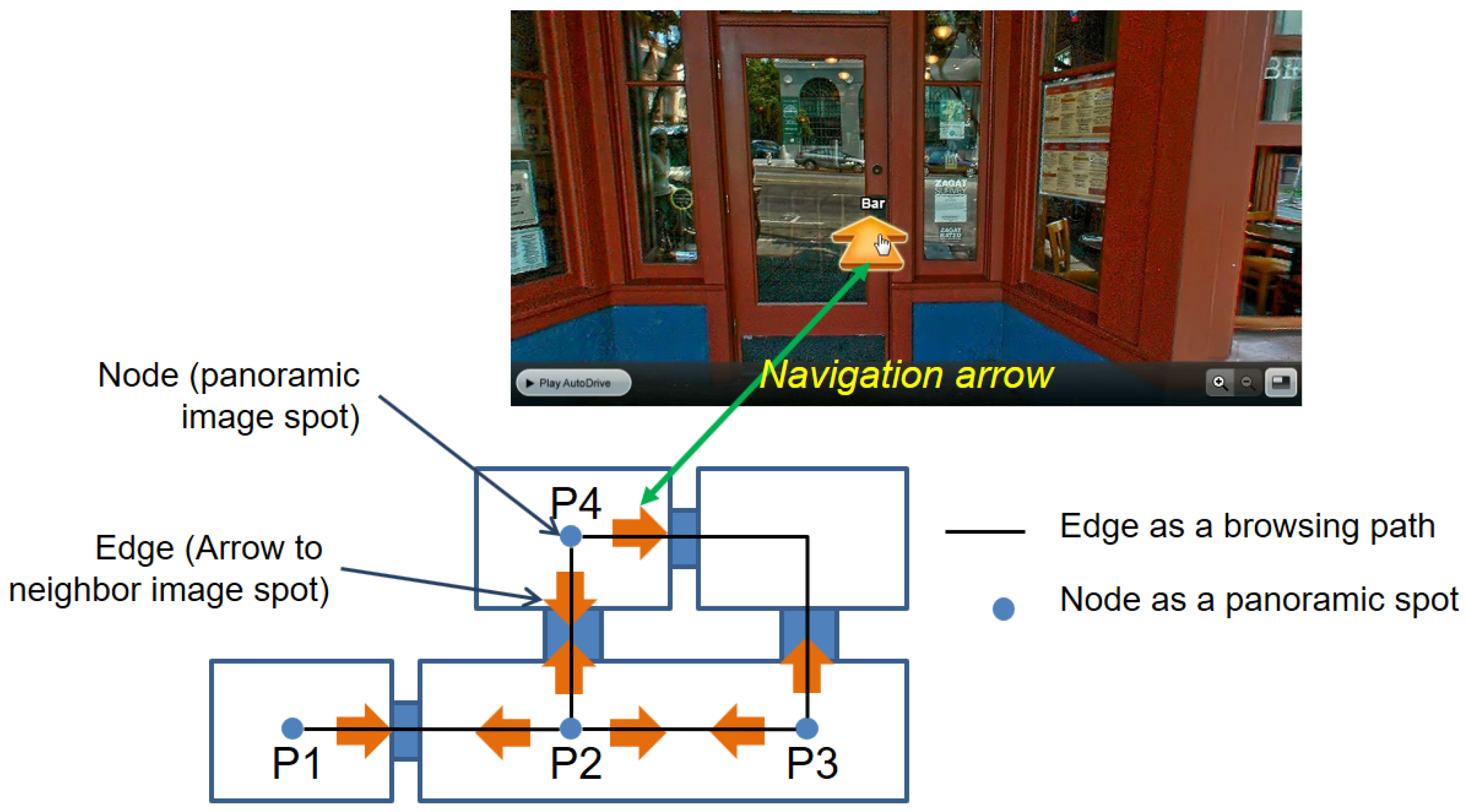
- cell without spatial extent: while cells have spatial extents in most cases, there are also cases where no spatial extent is necessarily required except a point. For example, each image spot in a panoramic image service shown in Figure 13 is represented as a cell without spatial extent except a point. Note that the panorama spot image layer is defined as a separate space layer of IndoorGML, and we define inter-layer connections with the cells in the topographic layer. We also assume that each navigation arrow connecting two image spots is considered as an edge in the connectivity graph for the panorama spot image layer, as in Figure 13.
5.2. Thick-Wall Model vs. Thin-Wall Model
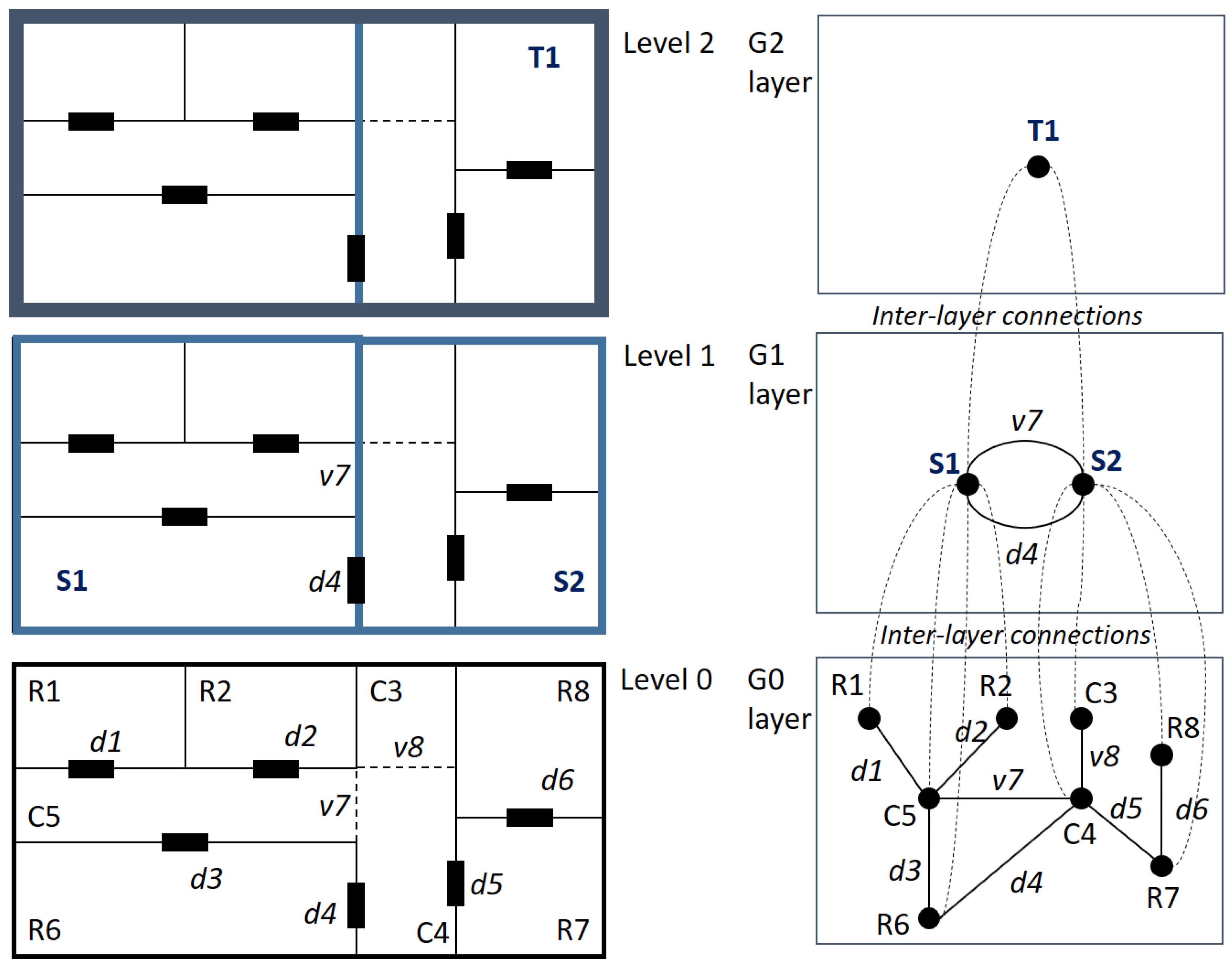
5.3. Representing Hierarchical Structures
- -
- and
- -
- .
- -
- ,
- -
- , and
- -
- .
- -
- ,
- -
- ,
- -
- ,
- -
- If
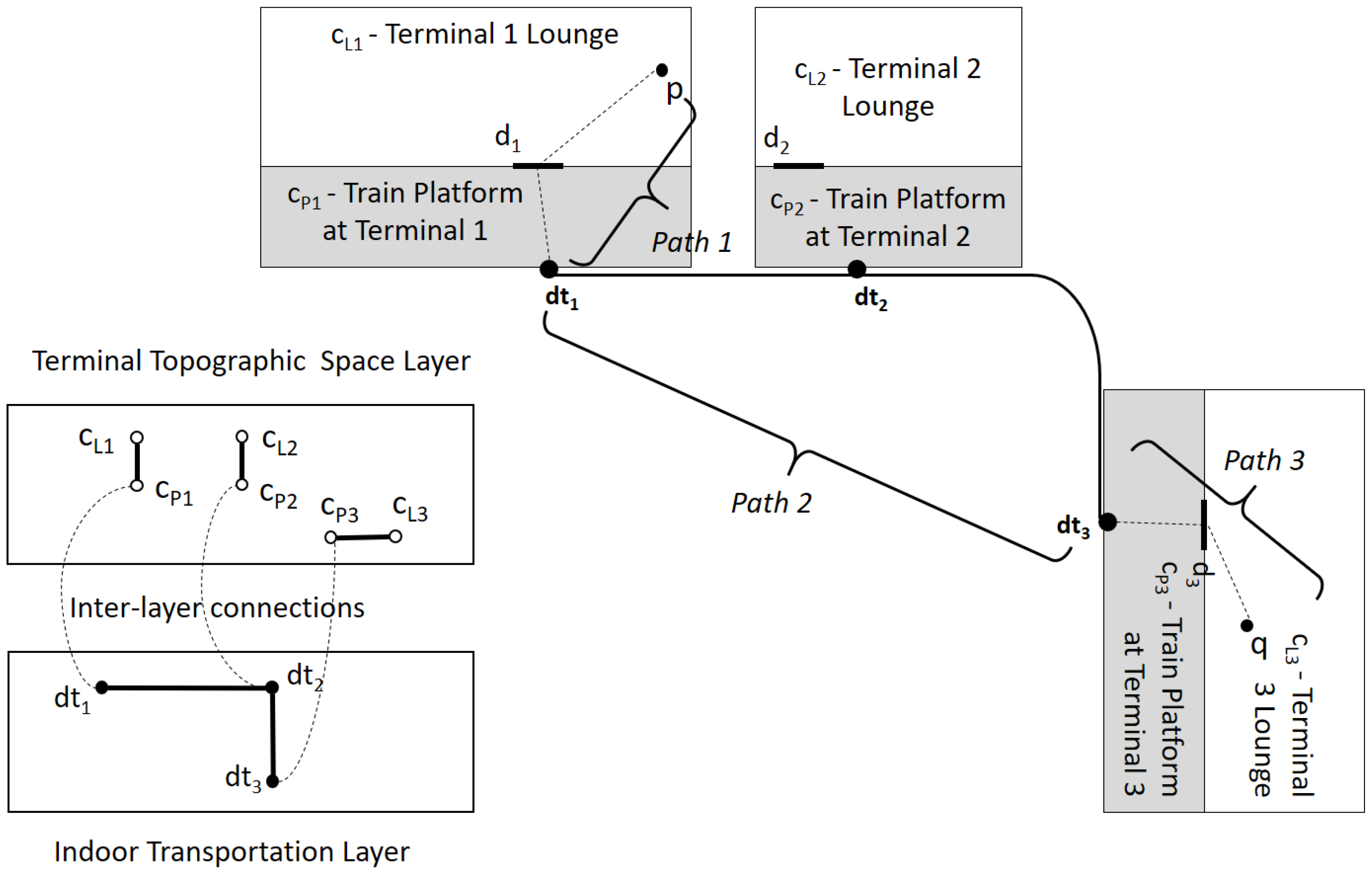
6. Computing Indoor Distance Using IndoorGML
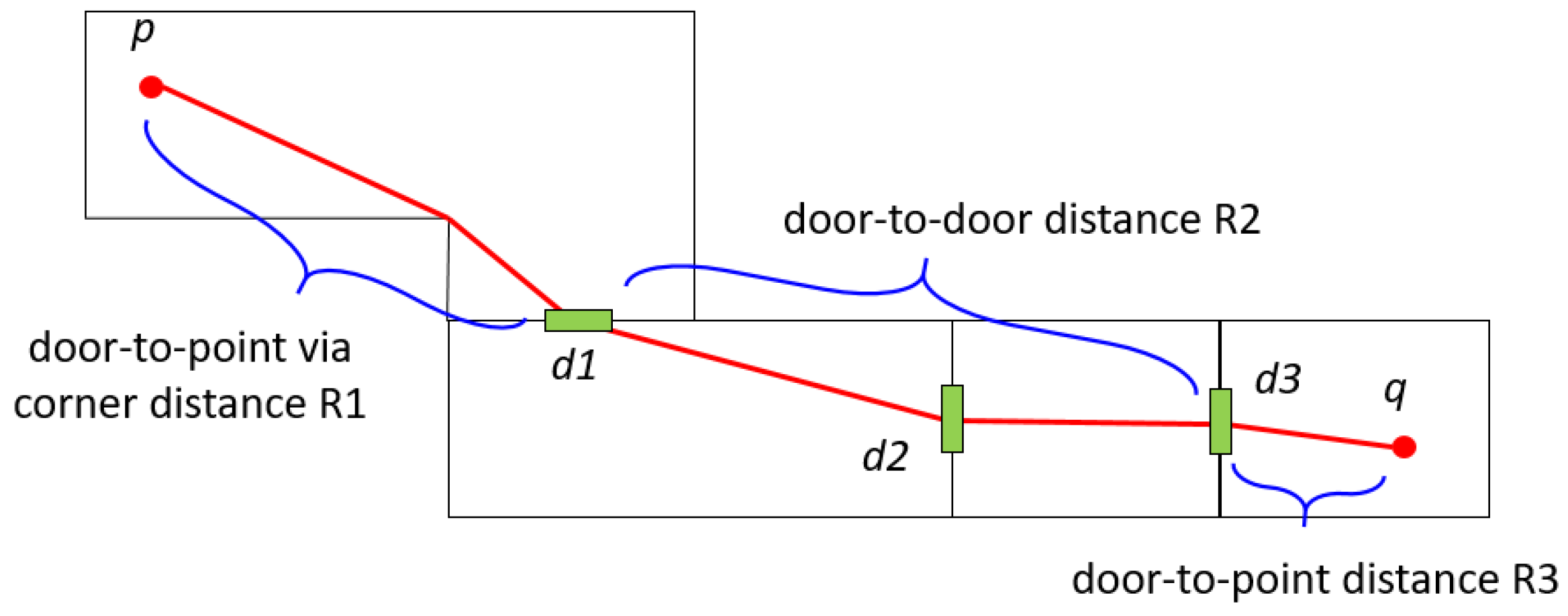
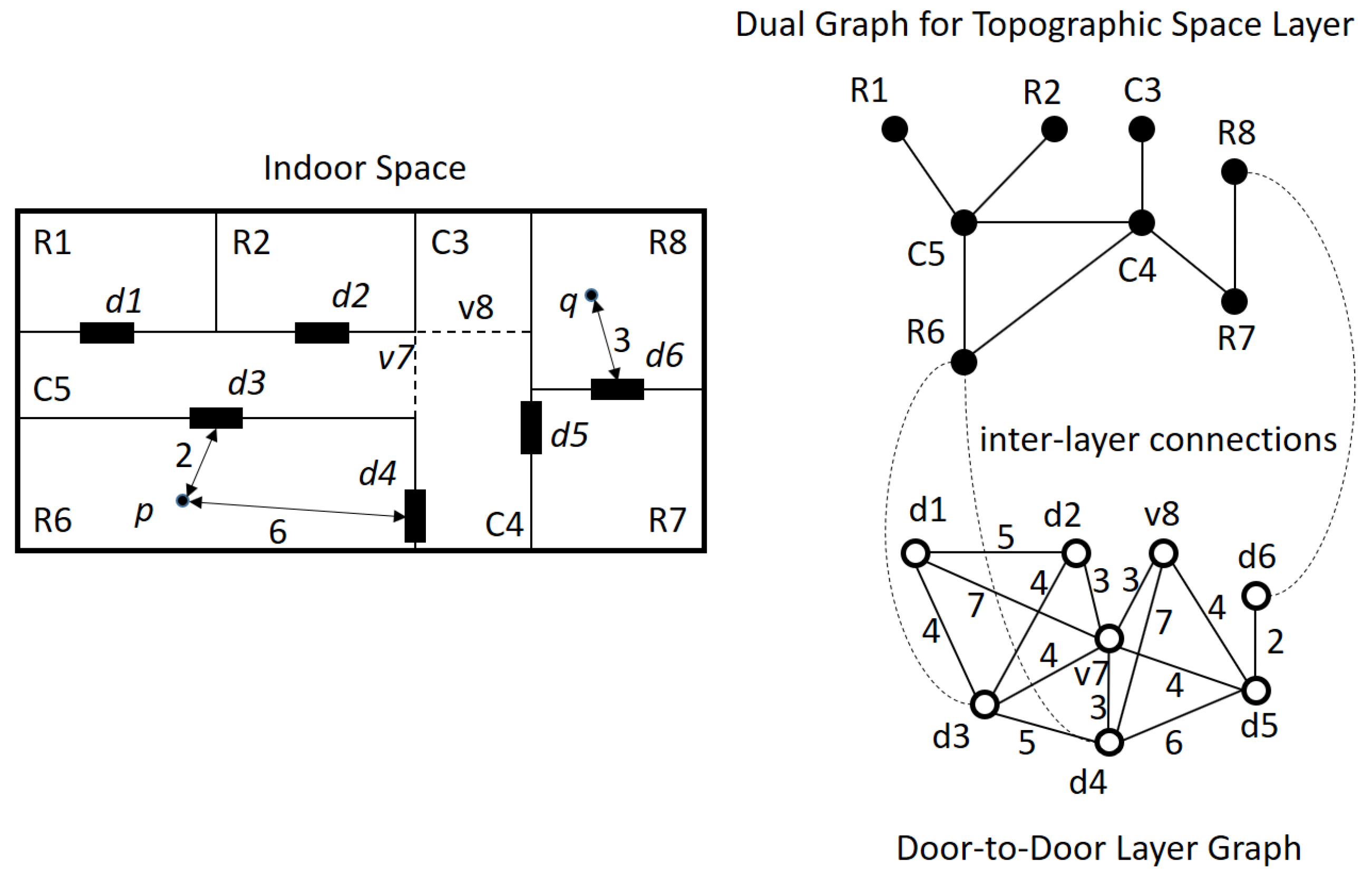
6.1. Horizontal Distance
| Algorithm 1. Indoor_Distance () |
| Input: |
| - topographic layer C: set of indoor cells with cell geometry, |
| - door-to-door (D2D) layer graph , |
| - multi-layered space model graph , and |
| - starting and ending points |
| Output: horizontal indoor distance |
| Begin |
| 1. the cell containing point p; |
| 2. the cell containing point q; |
| 3. where L is the set of inter-layer connections; |
| 4. ; |
| 5. ; |
| 6. ; |
| 7. is the shortest path from to from D2D layer graph; |
| 8. where , and ; |
| 9. return ; |
| End |
6.2. Vertical Distance
6.3. Multi-Modal Distance
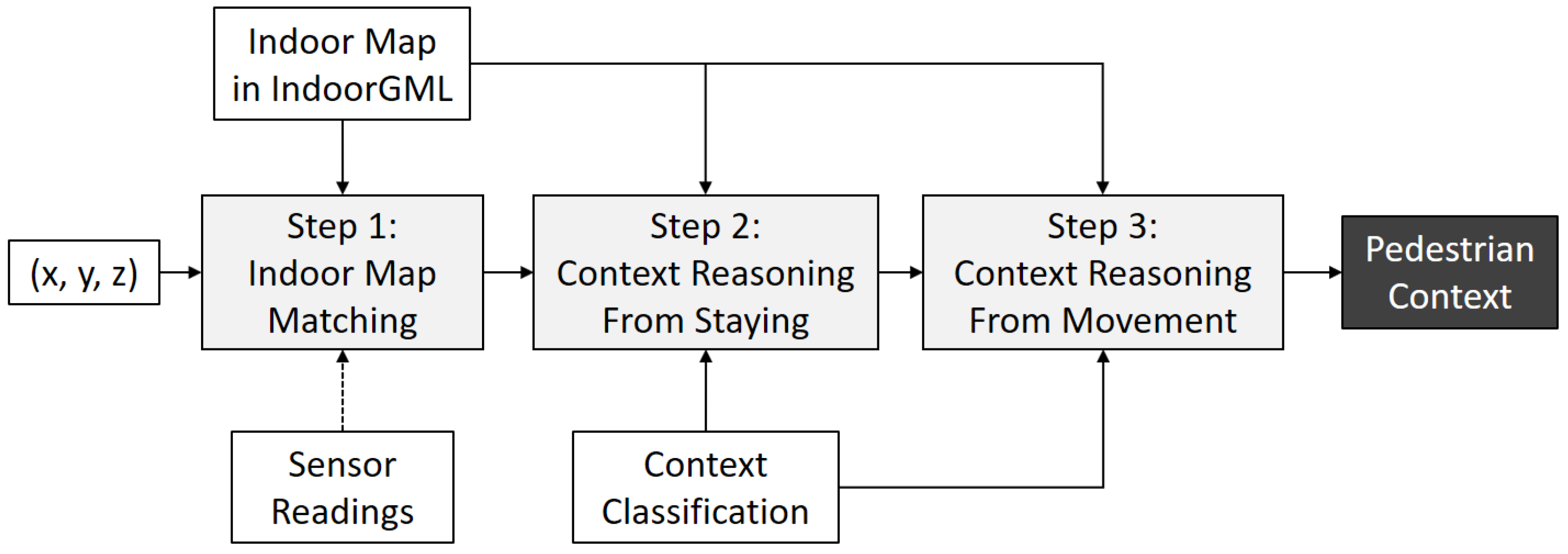
7. Context-Awareness by IndoorGML
- Step 1: indoor map matching:
- Step 2: context reasoning from staying interval:
- Step 3: context reasoning from visit sequence:
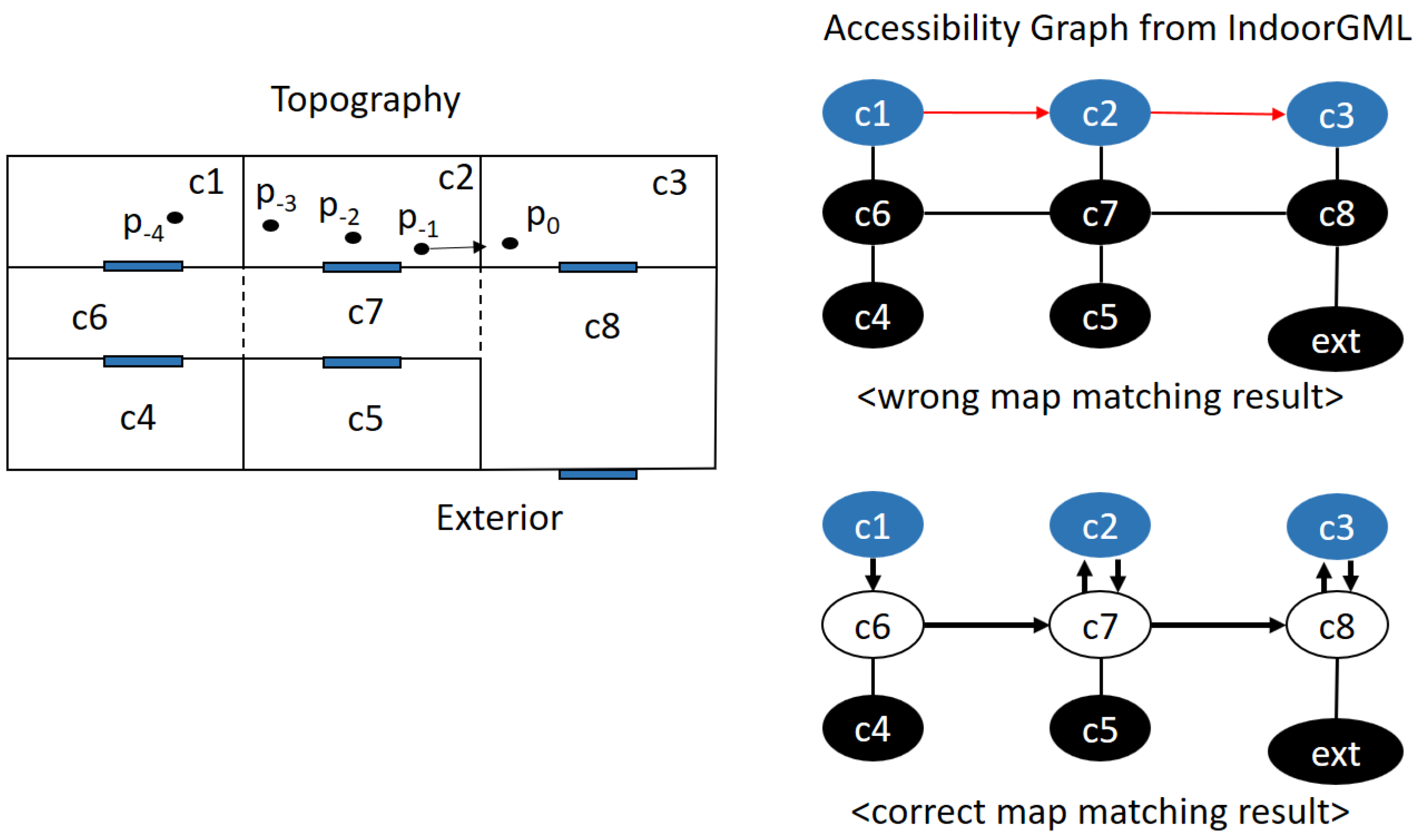
7.1. Indoor Map Matching by IndoorGML
| Algorithm 2. Indoor_Map_Matching_From_Point () |
| Input: |
| - topographic layer C: set of indoor cells with cell geometry, |
| - accessibility graph , |
| - current point and past trajectory , and |
| - sensor readings S. |
| Output: current cell c |
| Begin |
| 1. Find containing ; |
| 2. Correct by analyzing the past trajectory and accessibility graph ; |
| 3. Improve by analyzing other sensor readings; |
| 4. return c; |
| End |
7.2. Context Reasoning from the Staying and Visit Sequence
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Afyouni, I.; Cyril, R.; Christophe, C. Spatial models for context-aware indoor navigation systems: A survey. J. Spat. Inf. Sci. 2012, 10, 85–123. [Google Scholar] [CrossRef]
- BuildingSMART, IFC Standard. Available online: http://www.buildingsmart-tech.org/specifications/ifc-overview (accessed on 12 April 2017).
- OGC, OGC CityGML Encoding Standard, Document No. 12-019, 2012. Available online: http://www.opengeospatial.org/standards/citygml (accessed on 12 April 2017).
- OGC, OGC IndoorGML, Document No. 14-005r4, 2014. Available online: http://www.opengeospatial.org/standards/indoorgml (accessed on 12 April 2017).
- ISO/TC211, Geographic Information—Spatial Schema; ISO 19107:2003; ISO: Geneva, Switzerland, 2003.
- Stadler, A.; Kolbe, T.H. Spatio-semantic coherence in the integration of 3D city models. In Proceedings of the 5th International Symposium on Spatial Data Quality, Enschede, The Netherlands, 13–15 June 2007. [Google Scholar]
- Hughes, J.F.; Van Dam, A.; Foley, J.D.; Feiner, S.K. Computer Graphics: Principles and Practice; Pearson Education: Upper Saddle River, NJ, USA, 2014. [Google Scholar]
- Laurini, R.; Thompson, D. Fundamentals of Spatial Information Systems; Academic Press: London, UK, 1992; pp. 217–256. [Google Scholar]
- Tsui, P.H.; Brimicombe, A.J. The hierarchical tessellation model and its use in spatial analysis. Trans. GIS 1997, 2, 267–279. [Google Scholar] [CrossRef]
- Hu, H.; Lee, D.L. Semantic location modeling for location navigation in mobile environment. In Proceedings of the 5th IEEE International Conference on Mobile Data Management, Berkeley, CA, USA, 19–22 January 2004; pp. 52–61. [Google Scholar]
- Brumitt, B.; Shafer, S. Topological world modeling using semantic spaces. In Proceedings of the Workshop on Location Modeling for Ubiquitous Computing, Atlanta, GA, USA, 30 September–2 October 2001; pp. 55–62. [Google Scholar]
- Yuan, W.; Schneider, M. Supporting continuous range queries in indoor space. In Proceedings of the 11th International Conference on Mobile Data Management, Kansas City, MO, USA, 23–26 May 2010; pp. 209–214. [Google Scholar]
- Lu, H.; Cao, X.; Jensen, C.S. A foundation for efficient indoor distance-aware query processing. In Proceedings of the 28th International Conference on Data Engineering, Arlington, VA, USA, 1–5 April 2012; pp. 438–449. [Google Scholar]
- Li, K.J.; Yoo, S.J.; Han, Y. Geo-coding scheme for multimedia in indoor space. In Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Orlando, FL, USA, 5–8 November 2013; pp. 424–427. [Google Scholar]
- Ryu, H.G.; Kim, T.; Li, K.J. Indoor navigation map for visually impaired people. In Proceedings of the Sixth ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness, Dallas, TX, USA, 4–7 November 2014; pp. 32–35. [Google Scholar]
- Stoffel, E.P.; Schoder, K.; Ohlbach, H.J. Applying hierarchical graphs to pedestrian indoor navigation. In Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Irvine, GA, USA, 5–7 November 2008; pp. 54–57. [Google Scholar]
- ISO/TC184, Industry Foundation Classes (IFC) for Data Sharing in the Construction and Facility Management Industries; ISO 16739:2013; ISO: Geneva, Switzerland, 2013.
- OGC, OGC GML, Document No. 07-036, 2007. Available online: http://www.opengeospatial.org/standards/gml (accessed on 12 April 2017).
- Zhu, Q.; Li, Y.; Xiong, Q.; Zlatanova, S.; Ding, Y.; Zhang, Y.; Zhou, Y. Indoor Multi-Dimensional Location GML and Its Application for Ubiquitous Indoor Location Services. ISPRS Int. J. Geo-Inf. 2016, 5, 220. [Google Scholar] [CrossRef]
- Li, K.J.; Ryu, H.G.; Kim, H.C.; Lee, J.H.; Lee, J.H. Comparing CityGML and IndoorGML Based on a Use Case at Lotte World Mall; Document No. 16-012r1; OGC Discussion Paper: Wayland, MA, USA, 2016. [Google Scholar]
- Wang, H. Sensing Information Modelling for Smart City. In Proceedings of the IEEE International Conference on Smart City/SocialCom/SustainCom, Chengdu, China, 19–21 December 2015; pp. 40–45. [Google Scholar]
- Civilis, A.; Jensen, C.S.; Pakalnis, S. Techniques for efficient road-network-based tracking of moving objects. IEEE Trans. Knowl. Data Eng. 2005, 17, 698–712. [Google Scholar] [CrossRef]
- Li, D.; Lee, D.L. A topology-based semantic location model for indoor applications. In Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Irvine, CA, USA, 5–7 November 2008. [Google Scholar]
- Xie, X.; Lu, H.; Pederson, T.B. Distance-aware join for indoor moving objects. IEEE Trans. Knowl. Data Eng. 2015, 27, 428–442. [Google Scholar] [CrossRef]
- Schilit, B.; Adams, N.; Want, R. Context-aware computing applications. In Proceedings of the Workshop on Mobile Computing Systems and Applications, Santa Cruz, CA, USA, 8–9 December 1994; pp. 85–90. [Google Scholar]
- Mautz, R. Indoor Positioning Technologies. Habilitation Thesis, Institute of Geodesy and Photogrammetry, ETH Zurich, Switzerland, 2012. Available online: http://dx.doi.org/10.3929/ethz-a-007313554 (accessed on 12 April 2017).
- Lee, J. A Spatial Access-Oriented Implementation of a 3-D GIS Topological Data Model for Urban Entities. Geoinformatica 2004, 8, 237–264. [Google Scholar] [CrossRef]
- ISO/TC59/SC13, Building Construction—Organization of Information about Construction Works—Part 2: Framework for Classification; ISO 12006-2:2015; ISO: Geneva, Switzerland, 2015.
- Becker, T.; Nagel, C.; Kolbe, T.H. A Multilayered Space-Event Model for Navigation in Indoor Spaces. In Proceedings of the 3rd International Workshop on 3D Geo-Information Sciences, Seoul, Korea, 13–14 November 2008; pp. 61–77. [Google Scholar]
- Zlatanova, S.; Van Oosterom, P.J.M.; Lee, J.; Li, K.J.; Lemmen, C.H.J. LADM and IndoorGML for Support of Indoor Space Identification. ISPRS Ann. 2016, 4, 257–263. [Google Scholar] [CrossRef]
- Kruminaite, M.; Zlatanova, S. Indoor space subdivision for indoor navigation. In Proceedings of the Sixth ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness, Dallas, TX, USA, 4–7 November 2014; pp. 25–31. [Google Scholar]
- Zlatanova, S.; Liu, L.; Sithole, G.; Zhao, J. Space Subdivision for Indoor Applications; Technical Report; GISt Report No. 66; Delft University of Technology, OTB Research Institute for the Built Environment: Delft, The Netherlands, 2014. [Google Scholar]
- Goetz, M.; Zipf, A. Formal definition of a user-adaptive and length-optimal routing graph for complex indoor environments. Geo-Spat. Inf. Sci. 2011, 14, 119–128. [Google Scholar] [CrossRef]
- Liu, L.; Zlatanova, S. An Approach for Indoor Path Computation among Obstacles that Considers User Dimension. ISPRS Int. J. Geo-Inf. 2015, 4, 2821–2841. [Google Scholar] [CrossRef]
- Kim, J.S.; Li, K.J. Location K-anonymity in indoor spaces. Geoinformatica 2016, 20, 119–128. [Google Scholar] [CrossRef]
- Guibas, L.J.; Hershberger, J. Optimal shortest path queries in a simple polygon. In Proceedings of the Third Annual Symposium on Computational Geometry, Waterloo, ON, Canada, 8–10 June 1987; pp. 50–63. [Google Scholar]
- Mathew, W.; Raposo, R.; Martins, B. Predicting future locations with hidden Markov models. In Proceedings of the 2012 ACM Conference on Ubiquitous Computing, Pittsburg, PA, USA, 5–9 September 2012; pp. 911–918. [Google Scholar]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, H.-K.; Li, K.-J. A Standard Indoor Spatial Data Model—OGC IndoorGML and Implementation Approaches. ISPRS Int. J. Geo-Inf. 2017, 6, 116. https://doi.org/10.3390/ijgi6040116
Kang H-K, Li K-J. A Standard Indoor Spatial Data Model—OGC IndoorGML and Implementation Approaches. ISPRS International Journal of Geo-Information. 2017; 6(4):116. https://doi.org/10.3390/ijgi6040116
Chicago/Turabian StyleKang, Hae-Kyong, and Ki-Joune Li. 2017. "A Standard Indoor Spatial Data Model—OGC IndoorGML and Implementation Approaches" ISPRS International Journal of Geo-Information 6, no. 4: 116. https://doi.org/10.3390/ijgi6040116
APA StyleKang, H.-K., & Li, K.-J. (2017). A Standard Indoor Spatial Data Model—OGC IndoorGML and Implementation Approaches. ISPRS International Journal of Geo-Information, 6(4), 116. https://doi.org/10.3390/ijgi6040116




