Linking Neighborhood Characteristics and Drug-Related Police Interventions: A Bayesian Spatial Analysis
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Dependent Variable
2.3. Independent Variables
3. Design and Analysis
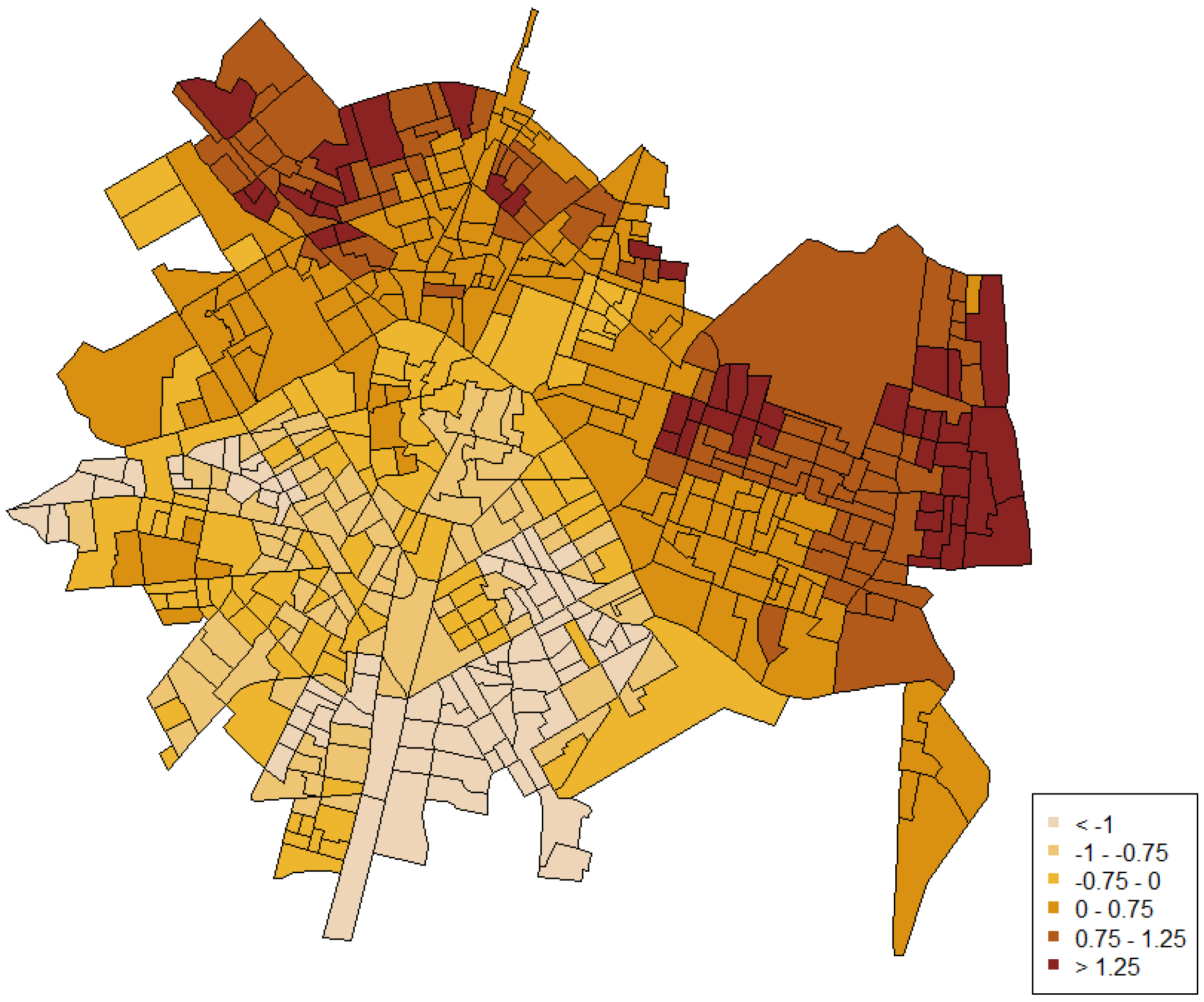
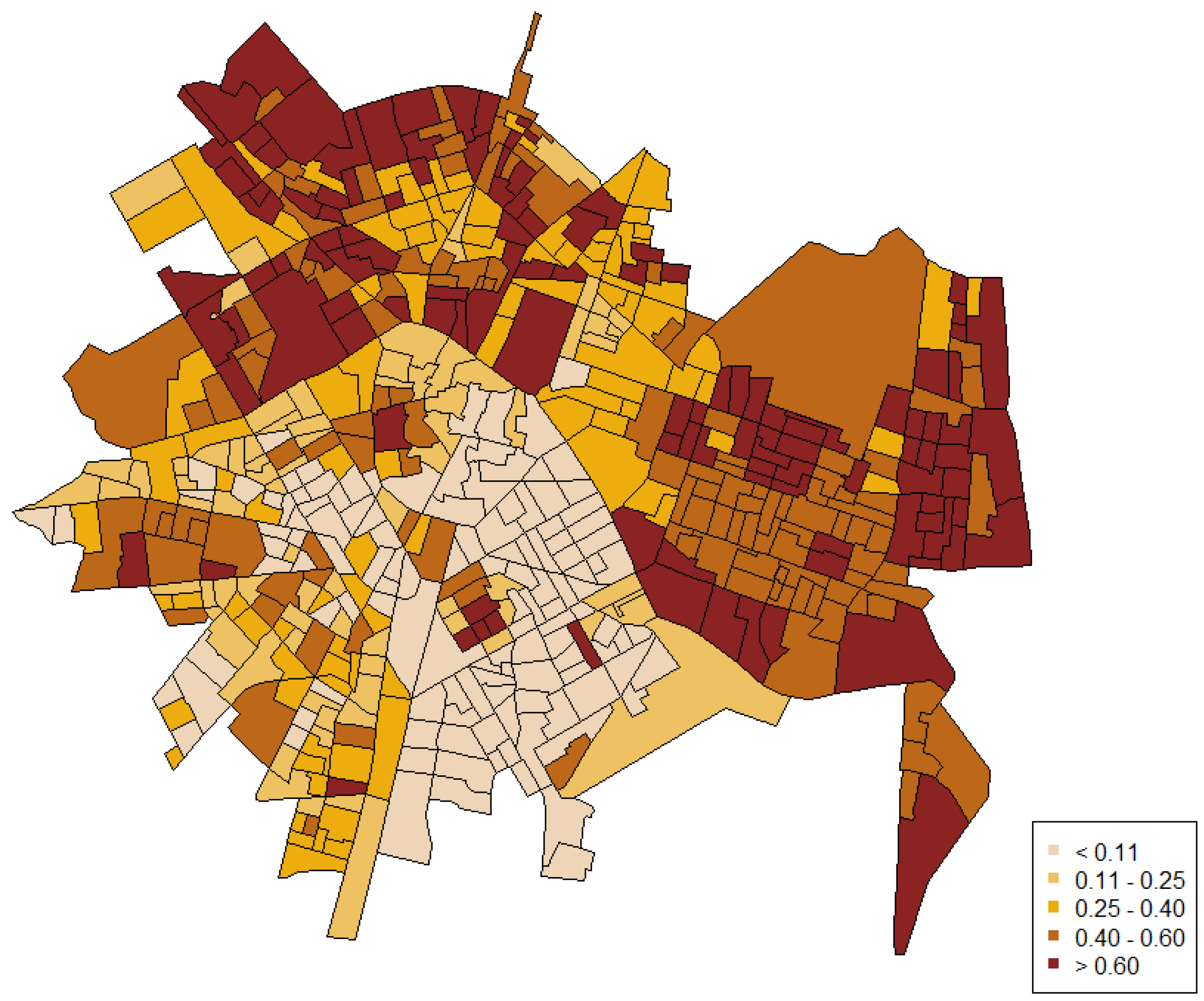
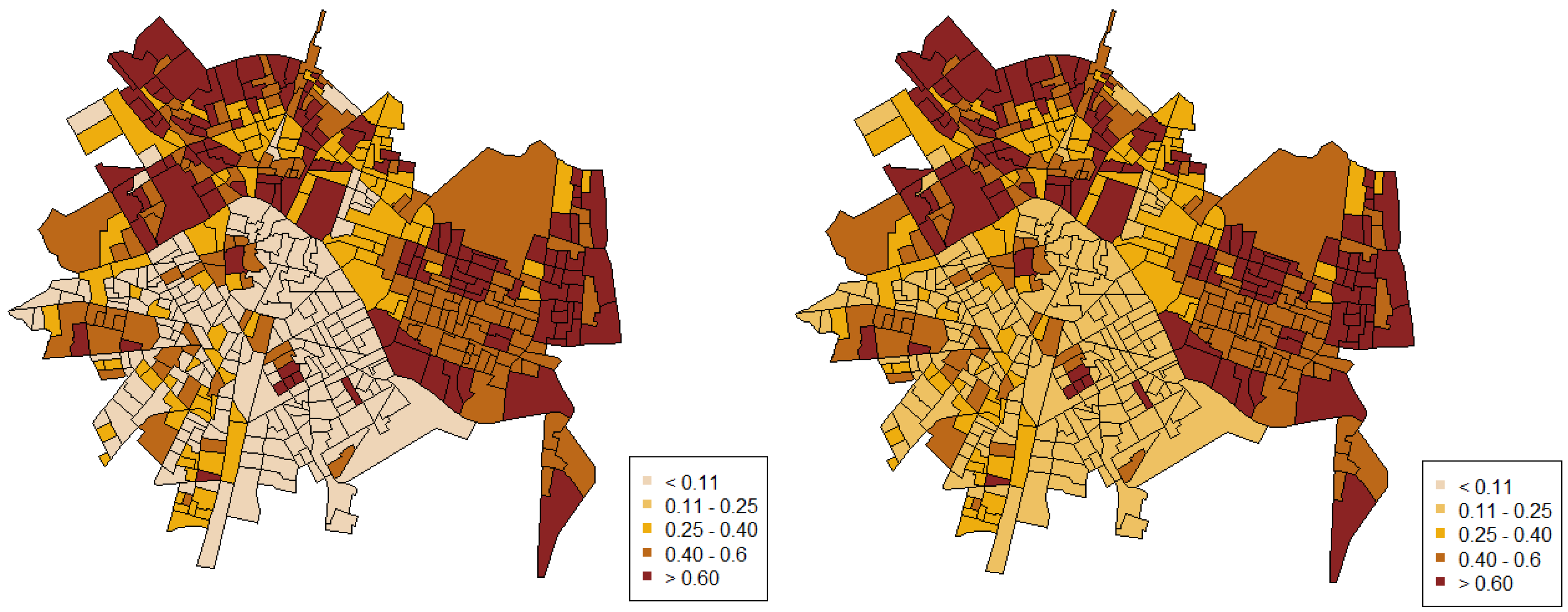
4. Results
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. WinBUGS Code
References
- Sampson, R.J.; Raudenbush, S.W.; Earls, F. Neighborhoods and violent crime: A multilevel study of collective efficacy. Science 1997, 277, 918–924. [Google Scholar] [CrossRef] [PubMed]
- Sampson, R.J.; Groves, W.B. Community structure and crime: Testing social-disorganization theory. Am. J. Sociol. 1989, 94, 774–802. [Google Scholar] [CrossRef]
- Shaw, C.R.; McKay, H.D. Juvenile Delinquency and Urban Areas; University of Chicago Press: Chicago, IL, USA, 1942. [Google Scholar]
- Peterson, R.D.; Krivo, L.J. Segregated spatial locations, race-ethnic composition, and neighborhood violent crime. Ann. Am. Acad. Political Soc. Sci. 2009, 623, 93–107. [Google Scholar] [CrossRef]
- Kubrin, C.E.; Weitzer, R. New directions in social disorganization theory. J. Res. Crime Delinq. 2003, 40, 374–402. [Google Scholar] [CrossRef]
- Morenoff, J.D.; Sampson, R.J.; Raudenbush, S.W. Neighborhood inequality, collective efficacy, and the spatial dynamics of urban violence. Criminology 2001, 39, 517–558. [Google Scholar] [CrossRef]
- Wilson, W.J. The Truly Disadvantaged: The Inner City, the Underclass and Public Policy; University of Chicago Press: Chicago, IL, USA, 1987. [Google Scholar]
- Thompson, S.K.; Gartner, R. The spatial distribution and social context of homicide in Toronto’s Neighborhoods. J. Res. Crime Delinq. 2013, 51, 88–118. [Google Scholar] [CrossRef]
- Gracia, E.; López-Quílez, A.; Marco, M.; Lladosa, S.; Lila, L. Exploring neighborhood influences on small-area variations in intimate partner violence risk: A Bayesian random-Effects modeling approach. Int. J. Environ. Res. Public Health 2014, 11, 866–882. [Google Scholar] [CrossRef] [PubMed]
- Gracia, E.; López-Quílez, A.; Marco, M.; Lladosa, S.; Lila, L. The spatial epidemiology of intimate partner violence: Do neighborhoods matter? Am. J. Epidemiol. 2015, 182, 58–66. [Google Scholar] [CrossRef] [PubMed]
- Bursik, R.J., Jr.; Webb, J. Community change and patterns of delinquency. Am. J. Sociol. 1982, 88, 24–42. [Google Scholar] [CrossRef]
- Sampson, R.J. Collective efficacy theory. In Encyclopedia of Criminological Theory; Cullen, F.T., Wilcox, P., Eds.; SAGE: Thousand Oaks, CA, USA, 2010; pp. 802–812. [Google Scholar]
- Townsley, N.; Homel, R.; Chaseling, J. Repeat burglary victimization: Spatial and temporal patterns. Aust. N. Z. J. Criminol. 2000, 33, 37–63. [Google Scholar] [CrossRef]
- Johnson, S.D.; Bowers, K.J. The stability of space-time clusters of burglary. Eur. J. Criminol. 2005, 2, 67–92. [Google Scholar] [CrossRef]
- Johnson, S.D.; Bernasco, W.; Bowers, K.J.; Elffers, H.; Ratcliffe, J.H.; Rengert, G.F.; Townsley, M. Space-time patterns of risk: A cross national assessment of residential burglary victimization. J. Quant. Criminol. 2007, 23, 201–219. [Google Scholar] [CrossRef]
- Law, J.; Quick, M. Exploring links between juvenile offenders and social disorganization at a large map scale: A Bayesian spatial modeling approach. J. Geogr. Syst. 2013, 15, 89–113. [Google Scholar] [CrossRef]
- Browning, C.R.; Byron, R.A.; Calder, C.A.; Krivo, L.J.; Kwan, M.; Lee, J.Y.; Peterson, R.D. Commercial density, residential concentration, and crime: Land use patterns and violence in neighborhood context. J. Res. Crime Delinq. 2010, 47, 329–357. [Google Scholar] [CrossRef]
- Sampson, R.J.; Raudenbush, S.W. Systematic social observation of public spaces: A new look at disorder in urban neighborhoods. Am. J. Sociol. 1999, 105, 603–651. [Google Scholar] [CrossRef]
- Capowich, G.E. The conditioning effects of neighborhood ecology on burglary victimization. Crim. Justice Behav. 2003, 30, 39–61. [Google Scholar] [CrossRef]
- Wright, E.M.; Benson, M.L. Clarifying the effects of neighbourhood context on violence ‘behind closed doors’. Justice Q. 2011, 28, 775–798. [Google Scholar] [CrossRef]
- Freisthler, B.; Merrit, D.H.; LaScala, E.A. Understanding the ecology of child maltreatment: A review of the literature and directions for future research. Child Maltreat. 2006, 11, 263–280. [Google Scholar] [CrossRef] [PubMed]
- Hibdon, J.; Groff, E.R. What you find depends on where you look: Using emergency medical services call data to target illicit drug use hot spots. J. Contemp. Crim. Justice 2014, 30, 169–185. [Google Scholar] [CrossRef]
- Martinez, R.; Rosenfeld, R.; Mares, D. Social disorganization, drug market activity, and neighborhood violent crime. Urban Aff. Rev. 2008, 43, 846–874. [Google Scholar] [CrossRef] [PubMed]
- Dunlap, E. Impact of drugs on family life and kin networks in the inner-city African-American single parent household. In Drugs, Crime, and Social Isolation: Barriers to Urban Opportunity; Harrell, A., Peterson, G., Eds.; Urban Institute Press: Washington, DC, USA, 1992; pp. 181–207. [Google Scholar]
- Johnson, B.D.; Williams, T.; Dei, K.A.; Sanabria, H. Drug abuse in the inner city: Impact on hard-drug users and the community. In Drugs and Crime; Tonry, M., Wilson, J.Q., Eds.; University of Chicago Press: Chicago, IL, USA, 1990; pp. 9–67. [Google Scholar]
- Lum, C. The geography of drug activity and violence: Analyzing crime event types. Subst. Use Misuse 2008, 43, 195–218. [Google Scholar] [CrossRef] [PubMed]
- Taniguchi, T.A.; Ratcliffe, J.H.; Taylor, R.B. Gang set space, drug markets, and crime around drug corners in Camden. J. Res. Crime Delinq. 2011, 48, 327–363. [Google Scholar] [CrossRef]
- Haining, R.; Law, J. Combining police perceptions with police records of serious crime areas: A modelling approach. J. R. Stat. Soc. Ser. A Stat. Soc. 2007, 170, 1019–1034. [Google Scholar] [CrossRef]
- Sparks, C.S. Violent crime in San Antonio, Texas: An application of spatial epidemiological methods. Spat. Spatiotemporal Epidemiol. 2011, 2, 301–309. [Google Scholar] [CrossRef] [PubMed]
- Bruinsma, G.J.N.; Pauwels, L.J.R.; Weerman, F.M.; Bernasco, W. Social disorganization, social capital, collective efficacy and the spatial distribution of crime and offenders: An empirical test of six neighbourhood models for a Dutch city. Br. J. Criminol. 2013, 53, 942–963. [Google Scholar] [CrossRef]
- Bernardinelli, L.; Clayton, D.; Pascutto, C.; Montomoli, C.; Ghislandi, M.; Songini, M. Bayesian analysis of space–time variation in disease risk. Stat. Med. 1995, 14, 2433–2443. [Google Scholar] [CrossRef] [PubMed]
- Van de Schoot, R.; Denissen, J.; Neyer, F.J.; Kaplan, D.; Asendorpf, J.B.; Van Aken, M.A.G. A gentle introduction to Bayesian analysis: Applications to developmental research. Child Dev. 2014, 85, 842–860. [Google Scholar] [CrossRef] [PubMed]
- Anselin, L. From SpaceStat to CyberGIS: Twenty years of spatial data analysis software. Int. Reg. Sci. Rev. 2012, 35, 131–157. [Google Scholar] [CrossRef]
- Lawson, A.B. Bayesian Disease Mapping: Hierarchical Modeling in Spatial Epidemiology; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Haining, R.; Law, J.; Griffith, D. Modelling small area counts in the presence of overdispersion and spatial autocorrelation. Comput. Stat. Data Anal. 2009, 53, 2923–2937. [Google Scholar] [CrossRef]
- Gruenewald, P.J. Geospatial analysis of alcohol and drug problems: Empirical needs and theoretical foundations. GeoJournal 2013, 78, 443–450. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, A.; LaScala, E.; Gruenewald, P.J.; Freisthler, B.; Treno, A.; Remer, L.G. Social disorganization, alcohol, and drug markets and violence. In Geography and Drug Addiction; Thomas, Y.F., Richardson, D., Cheung, I., Eds.; Springer: Dordrecht, The Netherlands, 2008; pp. 117–130. [Google Scholar]
- Marco, M.; Gracia, E.; Tomás, J.M.; López-Quílez, A. Assessing neighborhood disorder: Validation of a three-factor observational scale. Eur. J. Psychol. Appl. Leg. Context 2015, 7, 81–89. [Google Scholar] [CrossRef]
- Ratcliffe, J.H.; McCullagh, M.J. Chasing ghosts? Police perception of high crime areas. Br. J. Criminol. 2001, 41, 330–341. [Google Scholar] [CrossRef]
- Rengert, G.F.; Pelfrey, W.V. Cognitive mapping of the city center: Comparative perceptions of dangerous places. In Crime Mapping and Crime Prevention; Weisburd, D., McEwen, J.T., Eds.; Criminal Justice Press: Monsey, NY, USA, 1997; pp. 193–218. [Google Scholar]
- Ferrari, S.L.P.; Cribari-Neto, F. Beta regression for modelling rates and proportions. J. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Kieschnick, R.; McCullough, B.D. Regression analysis of variates observed on (0, 1): Percentages, proportions and fractions. Stat. Model. 2003, 3, 193–213. [Google Scholar] [CrossRef]
- Anselin, L. Spatial Econometrics: Methods and Models; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Tu, Y.; Yu, S.; Sun, H. Transaction-based office price indexes: A spatiotemporal modeling approach. Real Estate Econ. 2004, 32, 297–328. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.; Stern, H.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Besag, J.; York, J.; Molliè, A. Bayesian image restoration, with two applications in spatial statistics. Ann. Inst. Stat. Math. 1991, 43, 1–20. [Google Scholar] [CrossRef]
- Congdon, P. Assessing the impact of socioeconomic variables on small area variations in suicide outcomes in England. Int. J. Environ. Res. Public Health 2013, 10, 158–177. [Google Scholar] [CrossRef] [PubMed]
- Lum, C. Violence, drug markets and racial composition: Challenging stereotypes through spatial analysis. Urban Stud. 2011, 48, 2715–2732. [Google Scholar] [CrossRef] [PubMed]
- Gruenewald, P.J.; Freisthler, B.; Remer, L.; LaScala, E.A.; Treno, A. Ecological models of alcohol outlets and violent assaults: Crime potentials and geospatial analysis. Addiction 2006, 101, 666–677. [Google Scholar] [CrossRef] [PubMed]
- Graif, C.; Sampson, R.J. Spatial heterogeneity in the effects of immigration and diversity on neighborhood homicide rates. Homicide Stud. 2009, 13, 242–260. [Google Scholar] [CrossRef] [PubMed]
- Sampson, R.J.; Morenoff, J.D.; Raudenbush, S.W. Social anatomy of racial and ethnic disparities in violence. Am. J. Public Health 2005, 95, 224–232. [Google Scholar] [CrossRef] [PubMed]
- Freisthler, B.; Gruenewald, P.J.; Johnson, F.W.; Treno, A.J.; LaScala, E.A. An exploratory study examining the spatial dynamics of illicit drug availability and rates of drug use. J. Drug Educ. 2005, 35, 15–27. [Google Scholar] [CrossRef] [PubMed]
- Anderson, E. Code of the Street: Decency, Violence, and the Moral Life of the Inner City; W.W. Norton and Company: New York, NY, USA, 1999. [Google Scholar]
- Pinchevsky, G.M.; Wright, E.M. The impact of neighborhoods on intimate partner violence and victimization. Trauma Violence Abus. 2012, 13, 112–132. [Google Scholar] [CrossRef] [PubMed]
- Sampson, R.J. Disparity and diversity in the contemporary city: Social (dis)order revisited. Br. J. Sociol. 2009, 60, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Maguire, M.; Morgan, R.; Reiner, R. The Oxford Handbook of Criminology; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Rengert, G. The Geography of Illegal Drugs; Westview Press: Boulder, CO, USA, 1998. [Google Scholar]
- Weisburd, D.; Bernasco, W.; Bruinsma, G.J.N. Units of analysis in geographic criminology: Historical development, critical issues, and open questions. In Putting Crime in Its Place: Units of Analysis in Geographic Criminology; Weisburd, D., Bernasco, W., Bruinsma, G.J.N., Eds.; Springer: New York, NY, USA, 2009; pp. 3–31. [Google Scholar]
- Sampson, R.J.; Wikström, P. The social order of violence in Chicago and Stockholm neighborhoods: A comparative inquiry. In Order, Conflict and Violence; Kalyvas, S., Shapiro, I., Masoud, T., Eds.; Cambridge University Press: Cambridge, UK, 2008; pp. 97–119. [Google Scholar]
- Le Galès, P.; Zagrodzki, M. Cities Are Back in Town: The US/Europe Comparison; Report for the Centre d’Etudes Européennes, Report no. 05/06; Sciences Po: Paris, France, 2006. [Google Scholar]
- Summers, A.A.; Cheshire, P.C.; Senn, L. Urban Change in the United States and Western Europe: Comparative Analysis and Policy; The Urban Institute Press: Washington, DC, USA, 1999. [Google Scholar]


| Variable | Mean | SD | Minimum | Maximum |
|---|---|---|---|---|
| Socioeconomic status | 0 | 0.98 | −1.69 | 4.22 |
| Cadastral value | 250.10 | 74.61 | 111.50 | 590.70 |
| High-end cars (%) | 5.75 | 3.62 | 1.30 | 24.80 |
| Financial business (%) | 18.15 | 7.77 | 0 | 43.20 |
| Commercial business (%) | 34.03 | 9.21 | 7.50 | 66.40 |
| Education level | 3.15 | 0.33 | 2.39 | 3.86 |
| Immigrant concentration (%) | 13.45 | 6.53 | 1.90 | 40.20 |
| Physical decay (0–20) | 5.83 | 3.61 | 0 | 20 |
| Residential instability (per 1000) | 268 | 87.98 | 91.10 | 649.80 |
| Distance to police station (km) | 0.75 | 0.38 | 0 | 2.10 |
| Drug-related police interventions (0–1) | 0.34 | 0.32 | 0 | 1 |
| Explanatory Variables | Mean | Std. Error | 95% CrI |
|---|---|---|---|
| Intercept | −1.285 | 0.217 | −1.712, −0.893 |
| Socioeconomic status | −0.127 * | 0.074 | −0.279, 0.020 |
| Physical decay | 0.038 * | 0.018 | 0.005, 0.072 |
| Immigrant concentration | 0.015 * | 0.013 | −0.012, 0.043 |
| Residential instability | 0.000 | 0.001 | −0.002, 0.002 |
| Distance to police stations | 0.403 * | 0.178 | 0.059, 0.730 |
| σs | 0.776 | 0.037 | 0.901, 0.999 |
| σu | 0.973 | 0.026 | 0.703, 0.844 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marco, M.; Gracia, E.; López-Quílez, A. Linking Neighborhood Characteristics and Drug-Related Police Interventions: A Bayesian Spatial Analysis. ISPRS Int. J. Geo-Inf. 2017, 6, 65. https://doi.org/10.3390/ijgi6030065
Marco M, Gracia E, López-Quílez A. Linking Neighborhood Characteristics and Drug-Related Police Interventions: A Bayesian Spatial Analysis. ISPRS International Journal of Geo-Information. 2017; 6(3):65. https://doi.org/10.3390/ijgi6030065
Chicago/Turabian StyleMarco, Miriam, Enrique Gracia, and Antonio López-Quílez. 2017. "Linking Neighborhood Characteristics and Drug-Related Police Interventions: A Bayesian Spatial Analysis" ISPRS International Journal of Geo-Information 6, no. 3: 65. https://doi.org/10.3390/ijgi6030065
APA StyleMarco, M., Gracia, E., & López-Quílez, A. (2017). Linking Neighborhood Characteristics and Drug-Related Police Interventions: A Bayesian Spatial Analysis. ISPRS International Journal of Geo-Information, 6(3), 65. https://doi.org/10.3390/ijgi6030065








