Recent Advances of Structures Monitoring and Evaluation Using GPS-Time Series Monitoring Systems: A Review
Abstract
1. Introduction
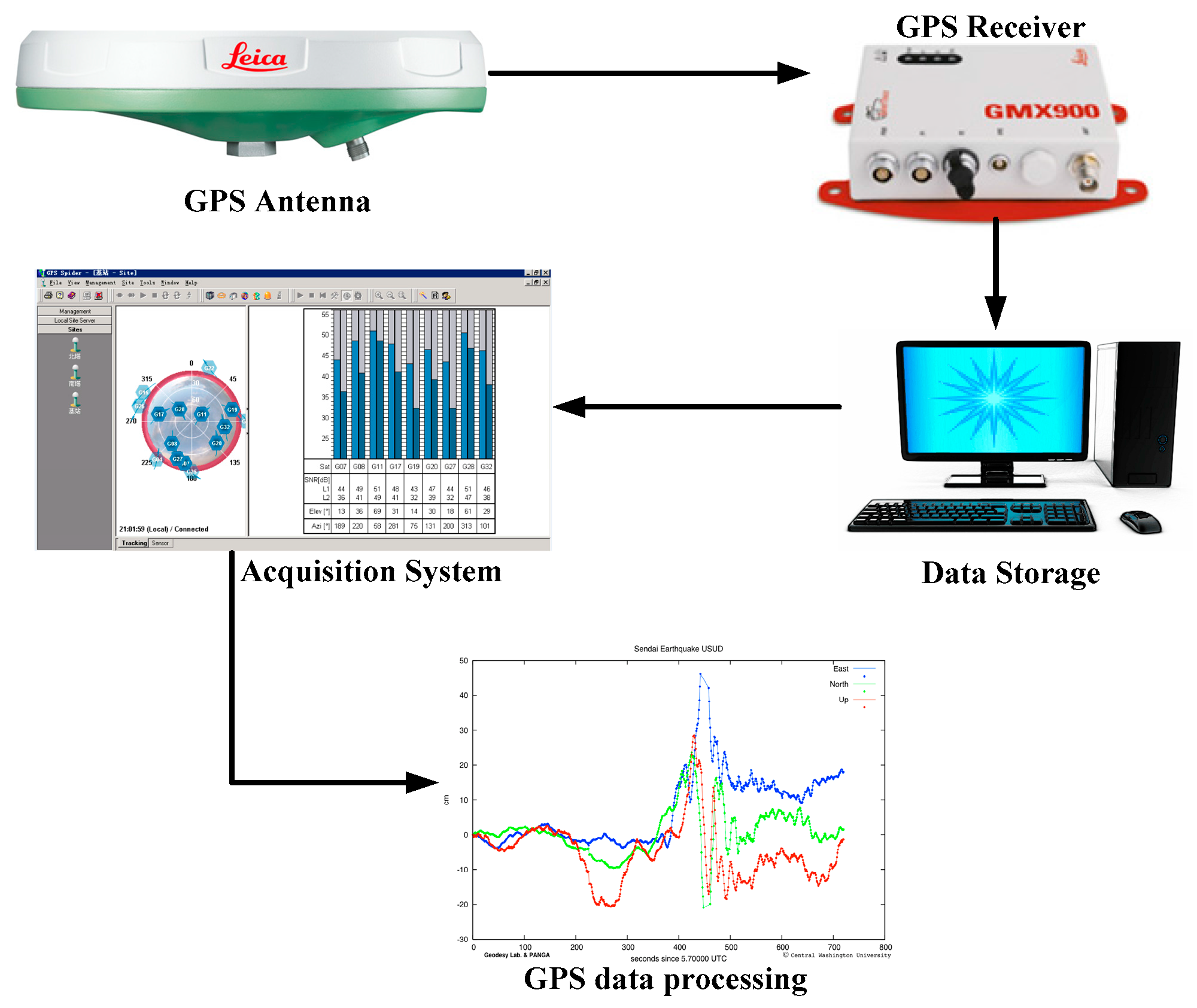
2. GPS Measurement Theory, Errors and Recent Developments
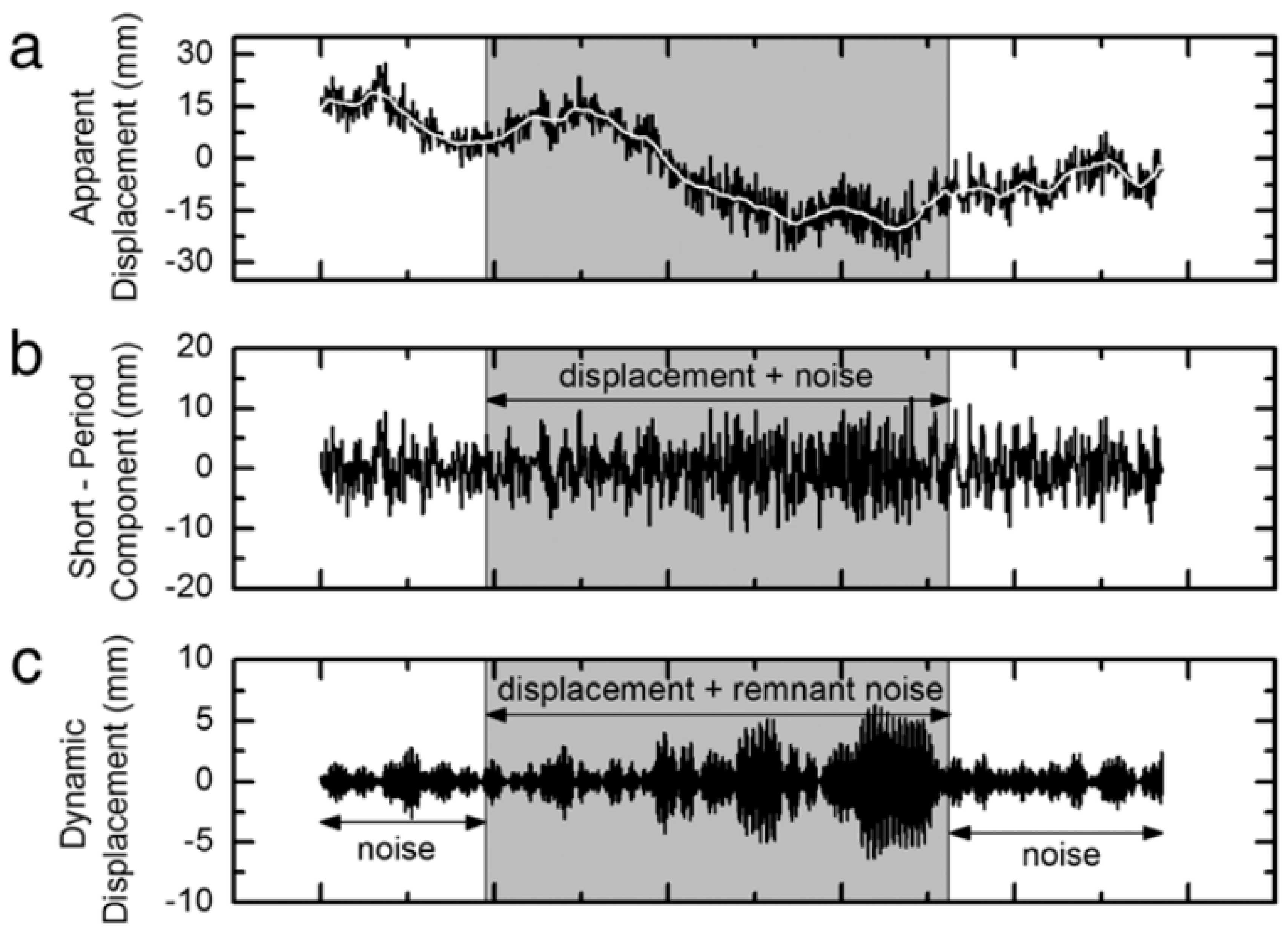
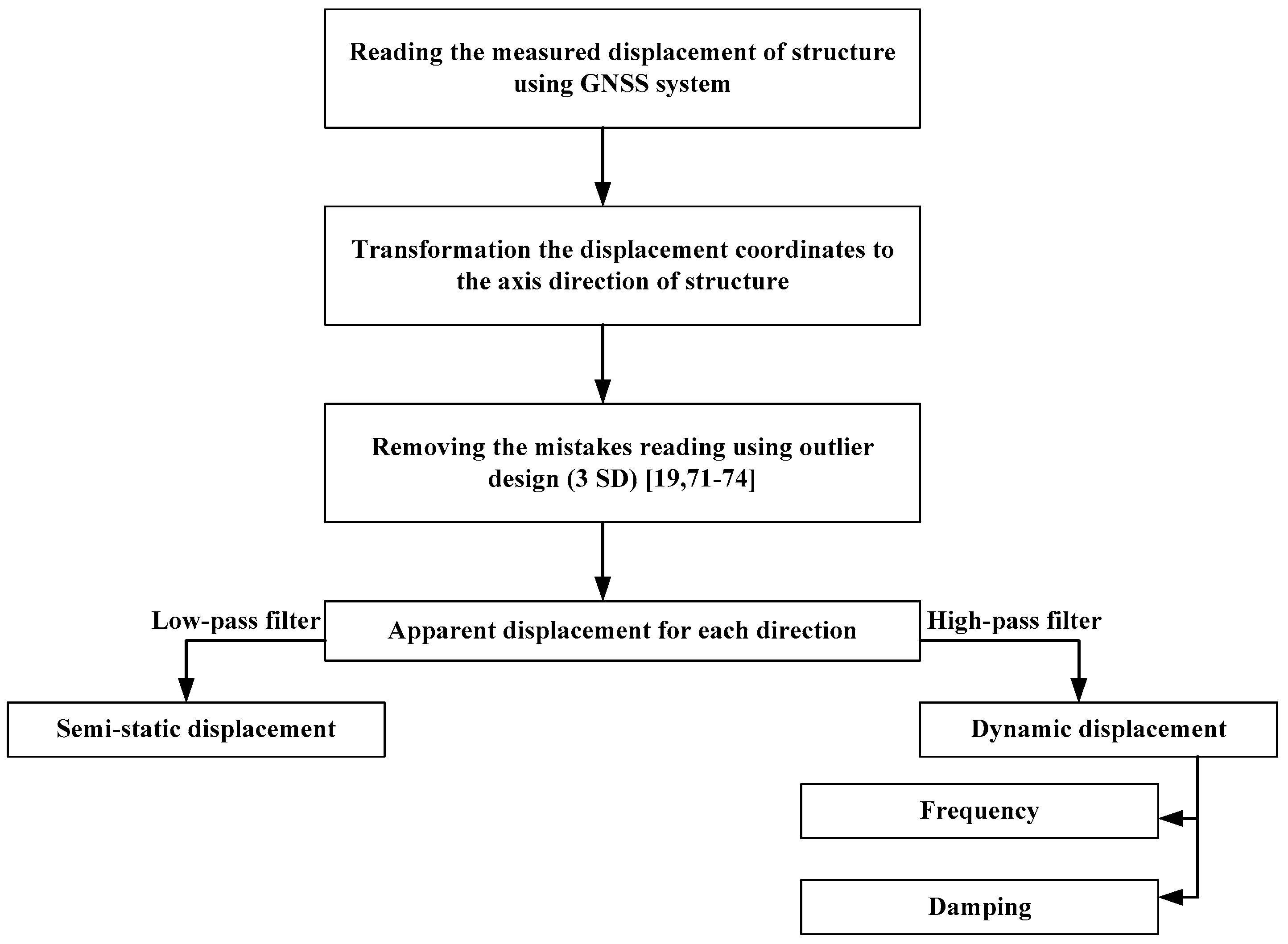
- The static trial was conducted to investigate both the frequencies and amplitudes of the receivers’ background noise. The minimum, maximum and mean values of the GPS measurements displayed very low-frequency drifts of relatively small amplitude, though on average, the mean of the measurements tends to zero. The standard deviation (SD), skewness and kurtosis analysis of the results show that the background noise follows, to some extent, Gaussian distribution. Also, the standard Gaussian distributions provide a conservative measure of the spread of the background noises, which captures the majority of the background noises within three SD from the mean. The power spectrum density (PSD) reveals that the background noise demonstrates broadband nature and the dominant noise energy distributes over a relatively low-frequency range without a distinct periodic tendency.
- Data analytical results prove that the wavelet packet-based filtering scheme based on denoising procedure method is simple and effective to remove the background noise of GPS high-rate measurements.
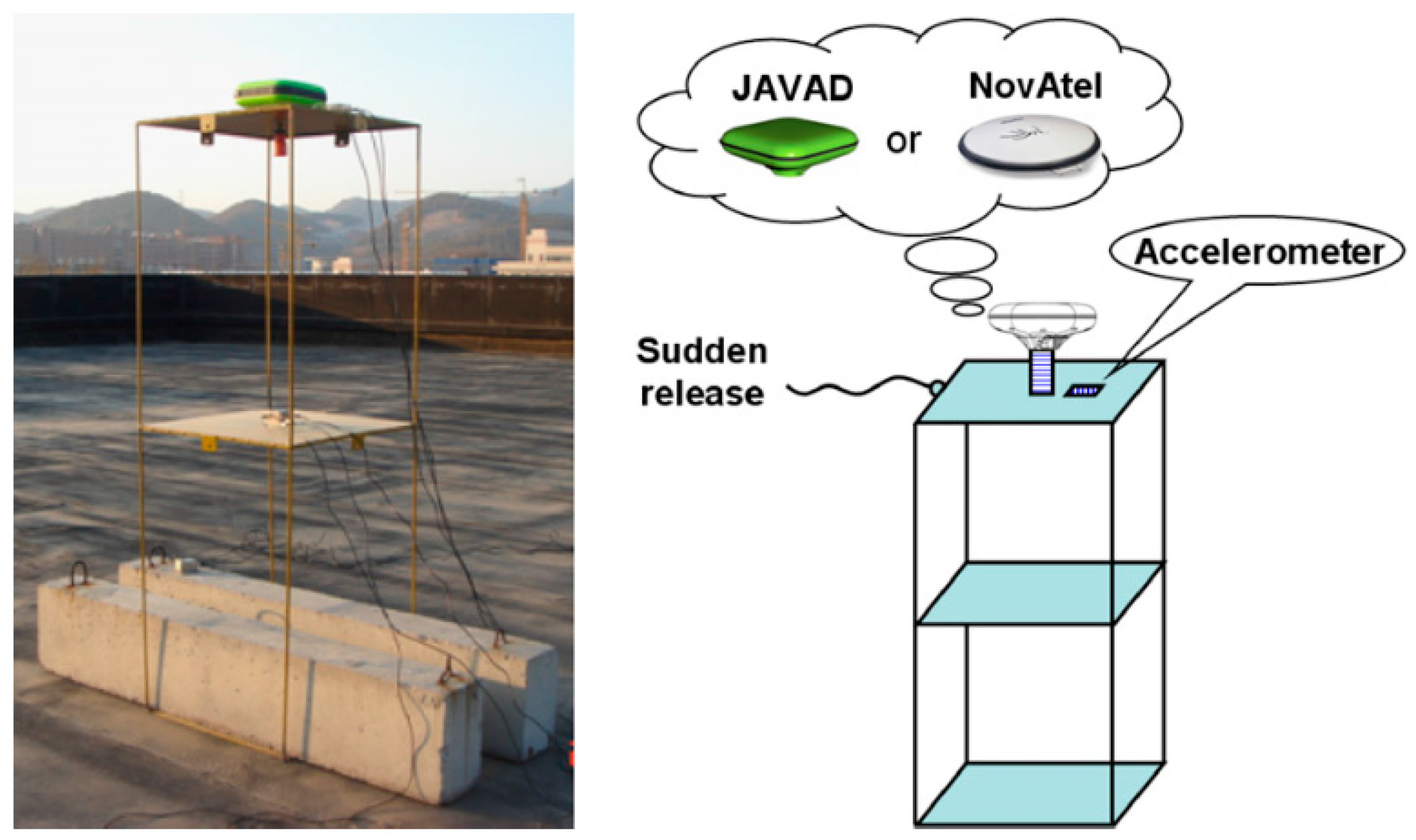
- A major output of this study is the potential of using high-rate GPS to measure stiff structures’ high frequencies up to 10 Hz. GPS receivers with high logging rates can directly provide data in high-frequency range comparable with accelerometer data accuracy. However, it is not desirable to replace an accelerometer network completely; geodetic sensors could provide important information to allow fast determination of structural modal parameters for bridge online health monitoring.
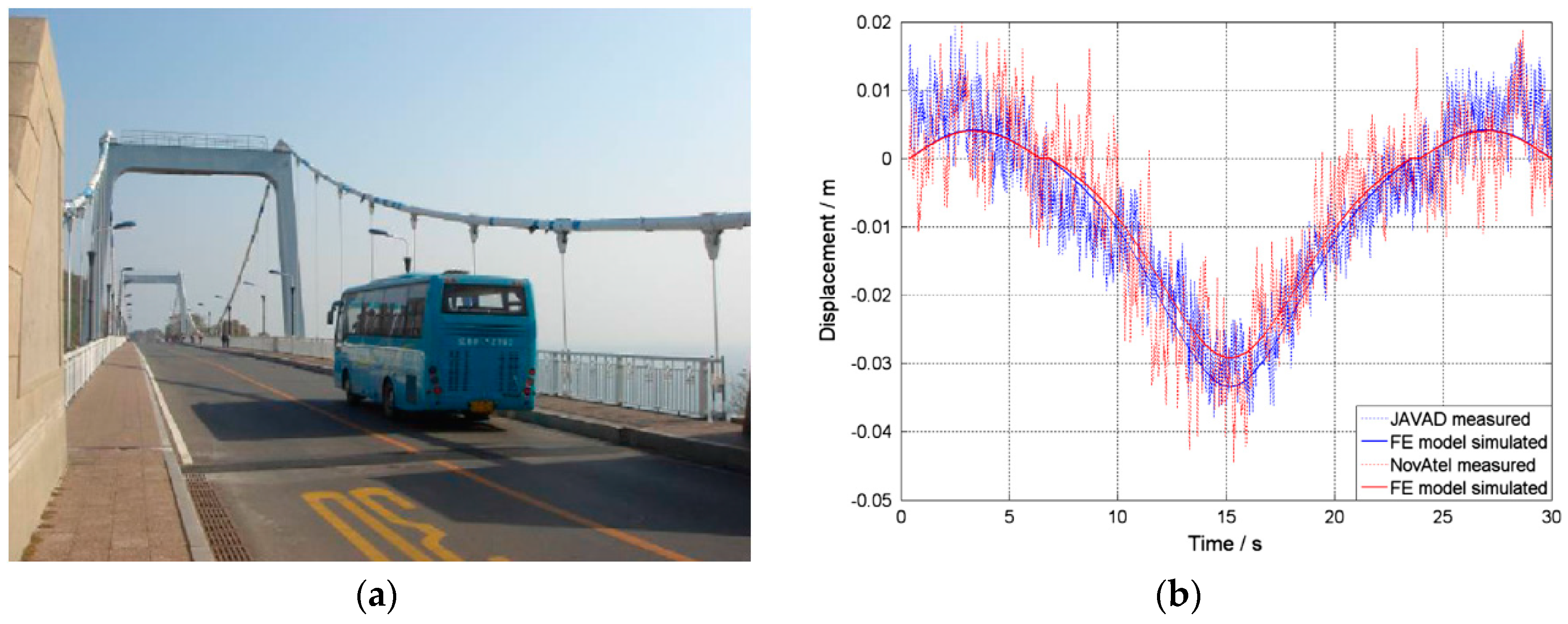
- The results show that high-rate GPS receivers can successfully quantify both environmental induced bridge displacements and vehicles’ transient motion, which are in good agreement with the predictions from the developed finite element (FE) model, as presented in Table 3. The displacement responses caused by vehicle loading after statistical analysis may be adopted for identifying the vehicle classes with different weight, as presented in Figure 4.
3. GPS Monitoring Techniques
3.1. Methodology for Assessment of DGPS
3.2. Methodology for Assessment of PPP
4. Recent Dynamic Behavior Assessment of Structures
5. Summary and Conclusions
- The GPS sampling rate has, until now, been developed to reach 100 Hz, and this sampling rate gives flexibility to measure the high accurate real-time positions of monitoring points in static and dynamic measurements. This reveals that the stiff and flexible of structures can be assessed, and the behavior of structures can be measured in time and frequency domains with high accuracy.
- RTK monitoring systems assess the behavior of structures, but their cost is greatly increased when increasing the sampling rate. Therefore, recently, two systems have been developed: the NRTK and PPP-GNSS systems, which are now effectively used to measure highly accurate positions of the monitoring points at low cost. Moreover, some developments for the GPS receivers have been established, but the accuracy is still limited.
- By increasing the sampling rate of GPS monitoring techniques and developing low-cost monitoring systems, the dynamic behavior of structures (frequency and damping) can be extracted based on the random decrement method, with the denoising of the GPS data. The wavelet analysis methods are effectively used to denoise signals when coupled with advanced GPS instruments. Currently, RTK monitoring systems are used to detect the dynamic behavior, while the PPP is still under study to measure the full behavior of structures.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sohn, H.; Farrar, C.R.; Hemez, F.M.; Czarnecki, J.J. A Review of Structural Health Monitoring Literature: 1996–2001. Struct. Health Monit. 2003, LA-13976-M, 1996–2001. [Google Scholar]
- Li, H.-N.; Yi, T.-H.; Ren, L.; Li, D.-S.; Huo, L.-S. Reviews on innovations and applications in structural health monitoring for infrastructures. Struct. Monit. Maint. 2014, 1, 1. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. Measurement of the dynamic displacements and of the modal frequencies of a short-span pedestrian bridge using GPS and an accelerometer. Eng. Struct. 2011, 33, 10–17. [Google Scholar] [CrossRef]
- Gikas, V. Ambient vibration monitoring of slender structures by microwave interferometer remote sensing. J. Appl. Geod. 2012, 6, 167–176. [Google Scholar] [CrossRef]
- Psimoulis, P.; Stiros, S. Measuring deflections of a short-span‚ railway bridge using a Robotic Total Station. J. Bridge Eng. 2013, 18, 182–185. [Google Scholar] [CrossRef]
- Rainieri, C.; Fabbrocino, G.; Cosenza, E. Integrated seismic early warning and structural health monitoring of critical civil infrastructures in seismically prone areas. Struct. Health Monit. 2011, 10, 291–308. [Google Scholar] [CrossRef]
- Vagnoli, M.; Remenyte-Prescott, R.; Andrews, J. Railway bridge structural health monitoring and fault detection: State-of-the-art methods and future challenges. Struct. Health Monit. 2017. [Google Scholar] [CrossRef]
- Housner, G.W.; Bergman, L.A.; Caughey, T.K.; Chassiakos, A.G.; Claus, R.O.; Masri, S.F.; Skelton, R.E.; Soong, T.T.; Spencer, B.F.; Yao, J.T.P. Structural Control: Past, Present, and Future. J. Eng. Mech. 1997, 123, 897–971. [Google Scholar] [CrossRef]
- Seo, J.; Hu, J.W.; Lee, J. Summary Review of Structural Health Monitoring Applications for Highway Bridges. J. Perform. Constr. Facil. 2016, 30, 4015072. [Google Scholar] [CrossRef]
- Yi, T.H.; Li, H.N.; Gu, M. Recent research and applications of GPS-based monitoring technology for high-rise structures. Struct. Control Health Monit. 2013, 20, 649–670. [Google Scholar] [CrossRef]
- Chowdhury, F.H.; Raihan, M.T.; Islam, G.M.S. Application of different structural health monitoring system on bridges: An overview. In Proceedings of the IABSE-JSCE Joint Conference on Advances in Bridge Engneering-III, Dhaka, Bangladesh, 21–22 August 2015; pp. 978–984. [Google Scholar]
- Annamdas, V.G.M.; Bhalla, S.; Soh, C.K. Applications of structural health monitoring technology in Asia. Struct. Health Monit. 2017, 16, 324–346. [Google Scholar] [CrossRef]
- Ou, J.; Li, H. Structural Health Monitoring in mainland China: Review and Future Trends. Struct. Health Monit. 2010, 9, 219–231. [Google Scholar]
- Gangadharan, R.; Prasanna, G.; Bhat, M.R.; Murthy, C.R.L.; Gopalakrishnan, S. Acoustic emission source location and damage detection in a metallic structure using a graph-theory-based geodesic approach. Smart Mater. Struct. 2009, 18, 115022. [Google Scholar] [CrossRef]
- Im, S.B.; Hurlebaus, S.; Kang, Y.J. Summary Review of GPS Technology for Structural Health Monitoring. J. Struct. Eng. 2013, 139, 1653–1664. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. Dynamic Deflections of a Stiff Footbridge Using 100-Hz GNSS and Accelerometer Data. J. Surv. Eng. 2015, 141, 4015003. [Google Scholar] [CrossRef]
- Çelebi, M.; Sanli, A. GPS in pioneering dynamic monitoring of long-period structures. Earthq. Spectra 2002, 18, 47–61. [Google Scholar] [CrossRef]
- Behr, J.A.; Hudnut, K.W.; King, N.E. Continuous GPS Monitoring of Structural Deformation at Pacoima Dam. Int. Tech. Meet. Satell. Div. Inst. Navig. 1998, 69, 59–68. [Google Scholar]
- Kaloop, M.R.; Hu, J.W. Dynamic Performance Analysis of the Towers of a Long-Span Bridge Based on GPS Monitoring Technique. J. Sens. 2016, 2016. [Google Scholar] [CrossRef]
- Casciati, F.; Fuggini, C. Monitoring a steel building using GPS sensors. Smart Struct. Syst. 2011, 7, 349–363. [Google Scholar] [CrossRef]
- Yigit, C.O. Experimental assessment of post-processed kinematic Precise Point Positioning method for structural health monitoring. Geomat. Nat. Hazards Risk 2014, 7, 360–383. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Hu, J.W. Stayed-Cable Bridge Damage Detection and Localization Based on Accelerometer Health Monitoring Measurements. Shock Vib. 2015, 2015. [Google Scholar] [CrossRef]
- Moschas, F.; Avallone, A.; Saltogianni, V.; Stiros, S. Strong motion displacement waveforms using 10-Hz precise point positioning GPS: An assessment based on free oscillation experiments Fanis. Int. Assoc. Earthq. Eng. 2015, 44, 657–675. [Google Scholar] [CrossRef]
- Yigit, C.O.; Gurlek, E. Experimental testing of high-rate GNSS precise point positioning (PPP) method for detecting dynamic vertical displacement response of engineering structures. Geomat. Nat. Hazards Risk 2017, 1–12. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Kim, D. GPS-structural health monitoring of a long span bridge using neural network adaptive filter. Surv. Rev. 2014, 46, 7–14. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. Noise characteristics of high-frequency, short-duration GPS records from analysis of identical, collocated instruments. Meas. J. Int. Meas. Confed. 2013, 46, 1488–1506. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Kim, D. De-noising of GPS structural monitoring observation error using wavelet analysis. Geomat. Nat. Hazards Risk 2016, 7, 804–825. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. PLL bandwidth and noise in 100 Hz GPS measurements. GPS Solut. 2014, 19, 173–185. [Google Scholar] [CrossRef]
- Yi, T.H.; Li, H.N.; Gu, M. Experimental assessment of high-rate GPS receivers for deformation monitoring of bridge. Meas. J. Int. Meas. Confed. 2013, 46, 420–432. [Google Scholar] [CrossRef]
- Zhao, X.; Ri, K.; Han, R.; Yu, Y.; Li, M.; Ou, J. Experimental Research on Quick Structural Health Monitoring Technique for Bridges Using Smartphone. Adv. Mater. Sci. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Ozer, E.; Feng, M.Q. Direction-sensitive smart monitoring of structures using heterogeneous smartphone sensor data and coordinate system transformation. Smart Mater. Struct. 2017, 26, 45026. [Google Scholar] [CrossRef]
- Jo, H.; Sim, S.H.; Tatkowski, A.; Spencer, B.F.; Nelson, M.E. Feasibility of displacement monitoring using low-cost GPS receivers. Struct. Control Health Monit. 2013, 20, 1240–1254. [Google Scholar] [CrossRef]
- Ozer, E. Multisensory Smartphone Applications in Vibration-Based Structural Health Monitoring; Columbia University: New York, NY, USA, 2016. [Google Scholar]
- Zhao, X.; Han, R.; Ding, Y.; Yu, Y.; Guan, Q.; Hu, W.; Li, M.; Ou, J. Portable and convenient cable force measurement using smartphone. J. Civ. Struct. Health Monit. 2015, 5, 481–491. [Google Scholar] [CrossRef]
- Ding, Y.; Han, R.; Yu, Y.; Liu, H.; Li, S.; Zhao, X. Bridge inspection and management system based on smart phone. In Proceedings of the ASME 2016 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Stowe, VT, USA, 28–30 September 2016; pp. 1–5. [Google Scholar]
- Larocca, A.P.C.; de Araujo Neto, J.O.; Alves Trabanco, J.L.; dos Santos, M.C.; Barros Barbosa, A.C. First Steps Using Two GPS Satellites for Monitoring the Dynamic Behavior of a Small Concrete Highway Bridge. J. Surv. Eng. 2016, 142, 1–8. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Collins, J. GPS-Global Positioning System. Theory and Practice; Springer: Wien, Austria, 1997. [Google Scholar]
- University of Princetown. Global Navigation Satellite System (GNSS). University of Princetown, 2005. Available online: https://www.princeton.edu/~alaink/Orf467F07/GNSS.pdf (accessed on 7 November 2017).
- Montillet, J.; Szeliga, W.M.; Melbourne, T.I.; Flake, R.M.; Schrock, G. Critical Infrastructure Monitoring with Global Navigation Satellite Systems. J. Surv. Eng. 2016, 142, 4016014. [Google Scholar] [CrossRef]
- Kim, R.E.; Li, J.; Spencer, B.F.; Nagayama, T.; Mechitov, K.A. Synchronized sensing for wireless monitoring of large structures. Smart Struct. Syst. 2016, 18, 885–909. [Google Scholar] [CrossRef]
- Kumberg, T.; Schneid, S.; Reindl, L. A Wireless Sensor Network Using GNSS Receivers for a Short-Term Assessment of the Modal Properties of the Neckartal Bridge. Appl. Sci. 2017, 7, 626. [Google Scholar] [CrossRef]
- Casciati, F.; Casciati, S.; Chen, Z.-C.; Faravelli, L.; Vece, M. Collecting data from a sensor network in a single-board computer. J. Phys. Conf. Ser. 2015, 628, 12113. [Google Scholar] [CrossRef]
- Casciati, S.; Chen, Z.C.; Faravelli, L.; Vece, M. Synergy of monitoring and security. Smart Struct. Syst. 2016, 17, 743–751. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Hu, J.W. Optimizing the de-noise neural network model for GPS time-series monitoring of structures. Sensors 2015, 15, 24428–24444. [Google Scholar] [CrossRef] [PubMed]
- Ogundipe, O.; Roberts, G.W.; Brown, C.J. GPS monitoring of a steel box girder viaduct. Struct. Infrastruct. Eng. 2014, 10, 25–40. [Google Scholar] [CrossRef]
- Kuan, C.-M. Generalized Least Squares Theory. In Statistics: Concepts and Methods, 2nd ed.; Huatai Publisher: Taipei, Taiwan, 2004; pp. 77–110. [Google Scholar]
- Breuer, P.; Chmielewski, T.; Górski, P.; Konopka, E.; Tarczyński, L. Monitoring horizontal displacements in a vertical profile of a tall industrial chimney using Global Positioning System technology for detecting dynamic characteristics. Struct. Control Health Monit. 2015, 22, 1002–1023. [Google Scholar] [CrossRef]
- Kaloop, M.R. GPS-Bridge Health Monitoring Case-Study: Analysis and Assessment; LAP Lambert Academic: Düsseldorf, Germany, 2015. [Google Scholar]
- Peppa, I.; Psimoulis, P.; Meng, X. Using the signal-to-noise ratio of GPS records to detect motion of structures. Struct. Control Health Monit. 2017, e2080. [Google Scholar] [CrossRef]
- Menezes, E.; Trevisan, T. First prospects in a new approach for structure monitoring from GPS multipath effect and wavelet spectrum. Adv. Space Res. 2017, 59, 2536–2547. [Google Scholar]
- Nakamura, S. GPS Measurement of Wind-Induced Suspension Bridge Girder Displacements. J. Struct. Eng. 2000, 126, 1413–1419. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Li, H. Multi input-single output models identification of tower bridge movements using GPS monitoring system. Meas. J. Int. Meas. Confed. 2014, 47, 531–539. [Google Scholar] [CrossRef]
- Ren, L.; Yuan, C.-L.; Li, H.-N.; Yi, T.-H. Structural Health Monitoring System Developed for Dalian Stadium. Int. J. Struct. Stab. Dyn. 2016, 16, 1640018. [Google Scholar] [CrossRef]
- Li, D.; Ho, S.-C.M.; Song, G.; Ren, L.; Li, H. A review of damage detection methods for wind turbine blades. Smart Mater. Struct. 2015, 24, 33001. [Google Scholar] [CrossRef]
- Wang, J.; Meng, X.; Qin, C.; Yi, J. Vibration frequencies extraction of the forth road bridge using high sampling GPS data. Shock Vib. 2016, 2016. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Hu, J.W.; Elbeltagi, E. Adjustment and Assessment of the Measurements of Low and High Sampling Frequencies of GPS Real-Time Monitoring of Structural Movement. ISPRS Int. J. Geo-Inf. 2016, 5, 222. [Google Scholar] [CrossRef]
- Kijewski-correa, T.; Kochly, M.; Stowell, J. On the Emerging Role of GPS in Structural Health Monitoring. In Proceedings of the Council on Tall Buildings and Urban Habitat, Seuol, Korea, 10–13 October 2004; pp. 144–151. [Google Scholar]
- Lepadatu, A.; Tiberius, C. GPS for structural health monitoring—Case study on the Basarab overpass cable-stayed bridge Loading tests. J. Appl. Geod. 2014, 8, 65–85. [Google Scholar]
- Yu, J.; Yan, B.; Meng, X.; Shao, X.; Ye, H. Measurement of Bridge Dynamic Responses Using Network-Based Real-Time Kinematic GNSS Technique. J. Surv. Eng. 2016, 142, 4015013. [Google Scholar] [CrossRef]
- Chan, W.S.; Xu, Y.L.; Ding, X.L.; Xiong, Y.L.; Dai, W.J. Assessment of dynamic measurement accuracy of GPS in three directions. J. Surv. Eng. 2006, 132, 108–117. [Google Scholar] [CrossRef]
- Kuter, N.; Kuter, S. Accuracy comparison between GPS and DGPS: A field study at METU campus. Ital. J. Remote Sens. 2010, 42, 3–14. [Google Scholar] [CrossRef]
- Ge, L.; Han, S.; Rizos, C.; Ishikawa, Y.; Hoshiba, M.; Yoshida, Y.; Izawa, M.; Hashimoto, N.; Himori, S. GPS seismometers with up to 20 Hz sampling rate. Earth Planets Space 2000, 52, 881–884. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. Dynamic multipath in structural bridge monitoring: An experimental approach. GPS Solut. 2014, 18, 209–218. [Google Scholar] [CrossRef]
- Casciati, F.; Fuggini, C. Engineering vibration monitoring by GPS: Long duration records. Earthq. Eng. Eng. Vib. 2009, 8, 459–467. [Google Scholar] [CrossRef]
- Breuer, P.; Chmielewski, T.; Górski, P.; Konopka, E.; Tarczyński, L. The Stuttgart TV Tower—Displacement of the top caused by the effects of sun and wind. Eng. Struct. 2008, 30, 2771–2781. [Google Scholar] [CrossRef]
- Calle, D.; Navarro, P.; Mozo, A.; Píriz, R.; Rodríguez, D.; Tobías, G. A novel device for autonomous real-time precise positioning with global coverage. In Proceedings of the 24th International Technical Meeting of the Satellite Division of the Institute of Navigation 2011, ION GNSS 2011, Portland, OR, USA, 19–23 September 2011; Volume 1, pp. 699–706. [Google Scholar]
- Kaloop, M.R.; Rabah, M. Time and frequency domains response analyses of April 2015 Greece’s earthquake in the Nile Delta based on GNSS-PPP. Arab. J. Geosci. 2016, 9, 316. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Lichten, S.M.; Border, J.S. Strategies for high-precision Global Positioning System orbit determination. J. Geophys. Res. 1987, 92, 751–762. [Google Scholar] [CrossRef]
- Dach, R.; Hugentobler, U.; Fridez, P.; Meindl, M. Bernese GPS Software Version 5.0 User Manual; Astronomical Institute, University of Bern: Bern, Switzerland, 2007; Volume 640. [Google Scholar]
- Elnabwy, M.T.; Kaloop, M.R.; Elbeltagi, E. Talkha steel highway bridge monitoring and movement identification using RTK-GPS technique. Meas. J. Int. Meas. Confed. 2013, 46, 4282–4292. [Google Scholar] [CrossRef]
- Psimoulis, P.A.; Houli, N.; Michel, C.; Meindl, M.; Rothacher, M. Long-period surface motion of the multipatch Mw9.0 Tohoku-Oki earthquake. Geophys. J. Int. 2015, 199, 968–980. [Google Scholar] [CrossRef][Green Version]
- Psimoulis, P.; Houlié, N.; Meindl, M.; Rothacher, M. Consistency of PPP GPS and strong-motion records: Case study of Mw9.0 Tohoku-Oki 2011 earthquake. Smart Struct. Syst. 2015, 16, 347–366. [Google Scholar] [CrossRef]
- Górski, P. Investigation of dynamic characteristics of tall industrial chimney based on GPS measurements using Random Decrement Method. Eng. Struct. 2015, 83, 30–49. [Google Scholar] [CrossRef]
- Casciati, F.; Casciati, S.; Faravelli, L.; Vece, M. Validation of a Data-fusion Based Solution in view of the Real-Time Monitoring of Cable-Stayed Bridges. Procedia Eng. 2017, 199, 2288–2293. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, X.; Lv, C.; Wu, J.; Li, L.; Ding, D. An innovative information fusion method with adaptive Kalman filter for integrated INS/GPS navigation of autonomous vehicles. Mech. Syst. Signal Process. 2018, 100, 605–616. [Google Scholar] [CrossRef]
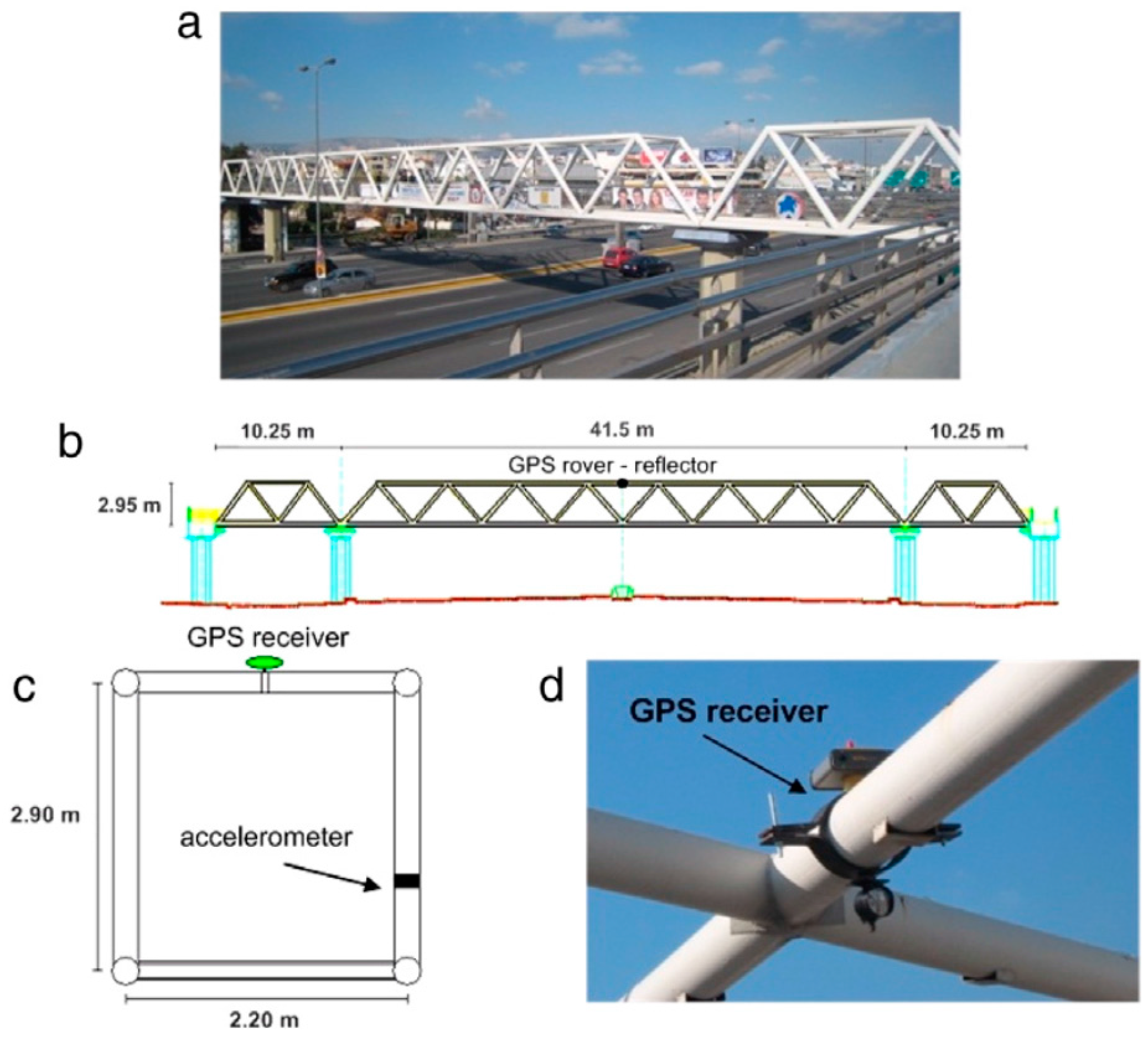
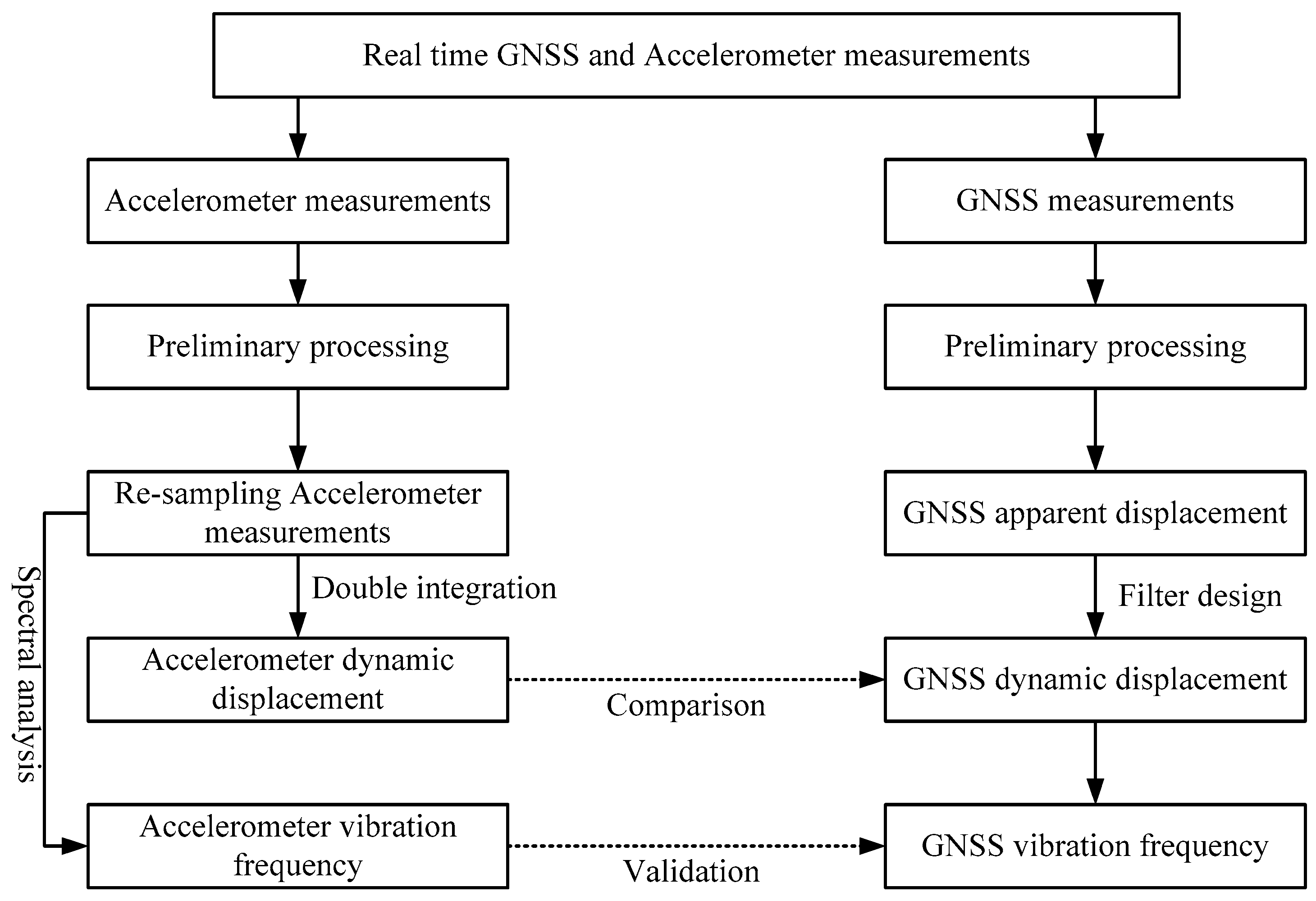
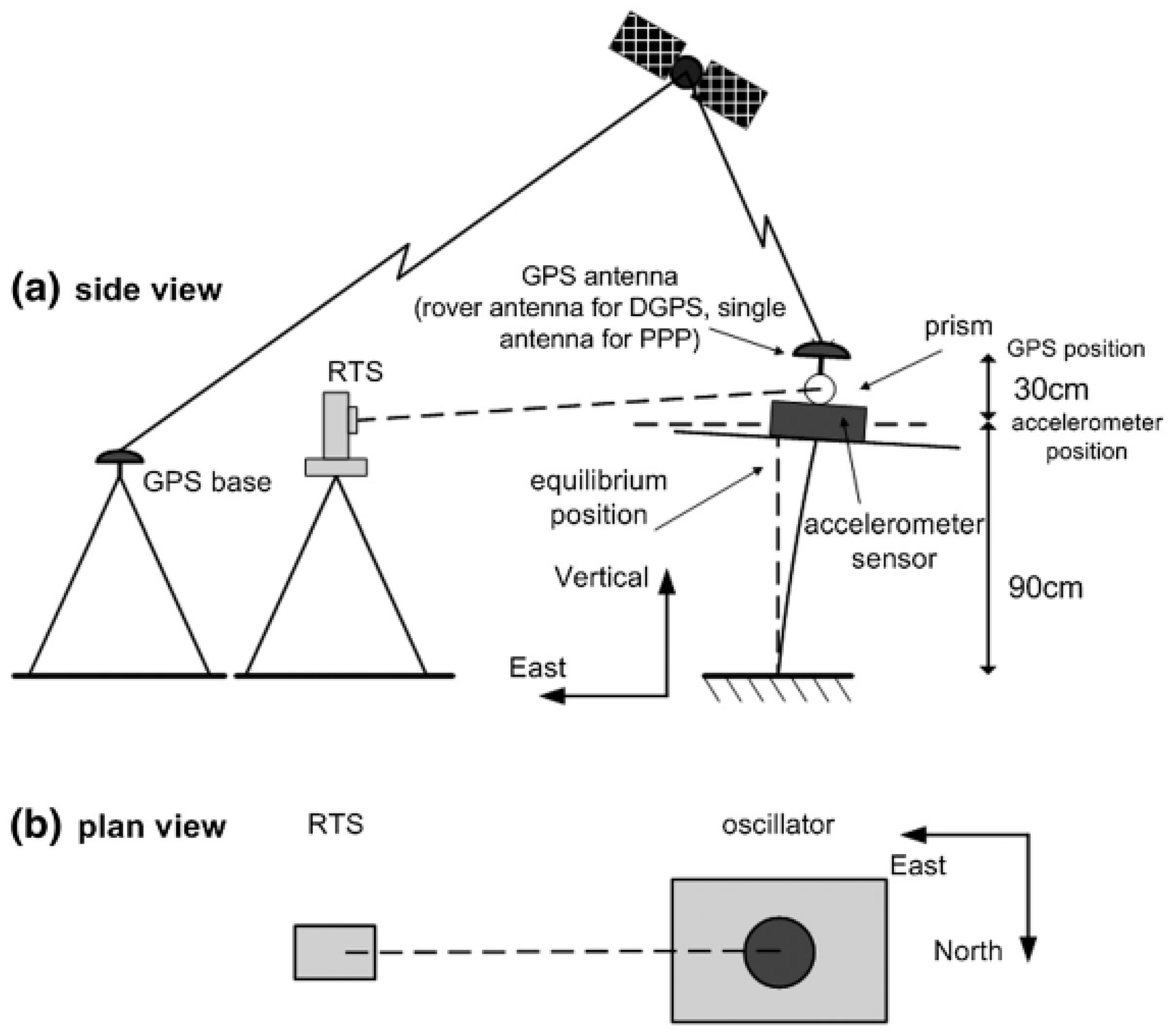
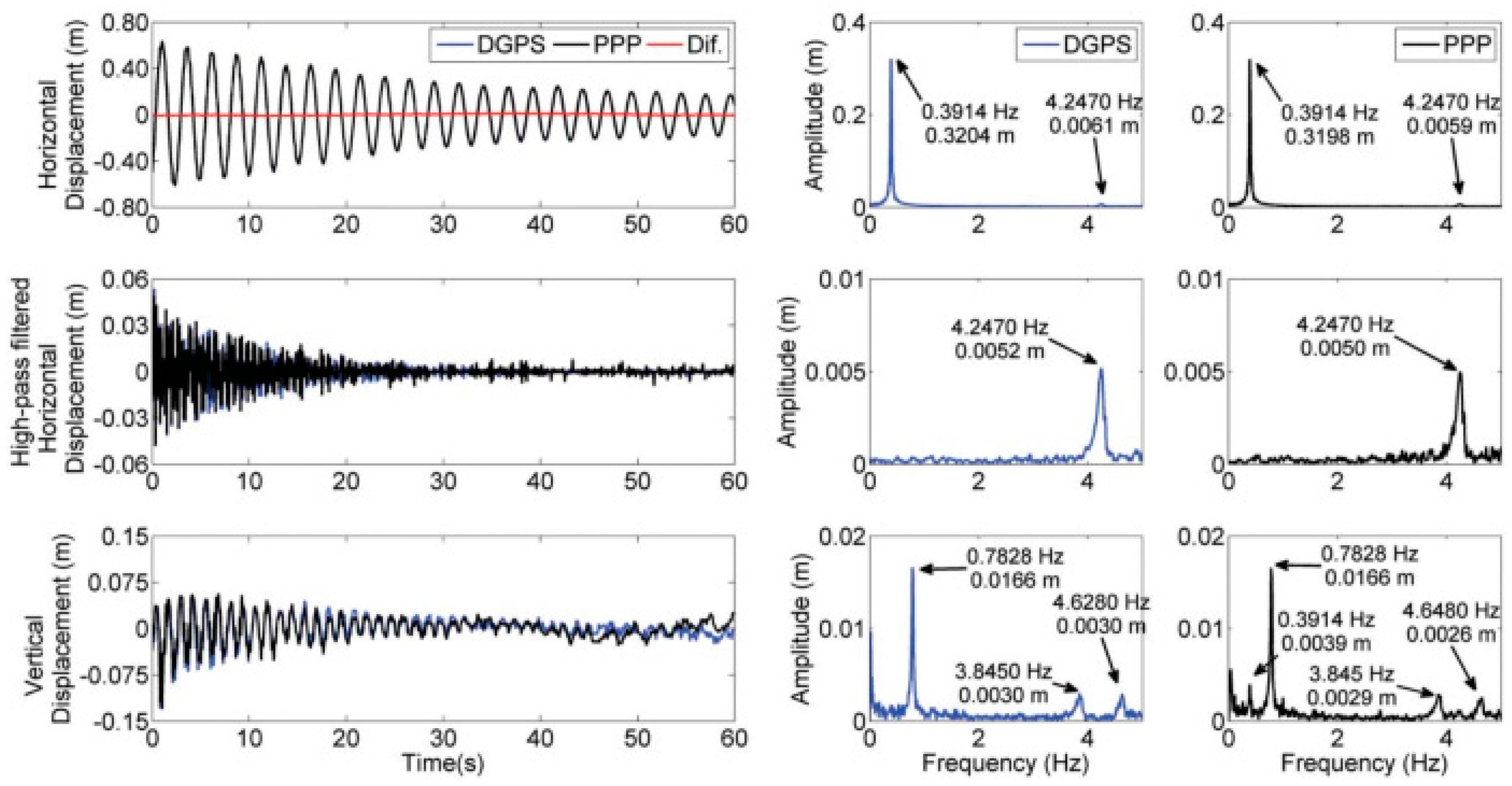
| Duration | Sampling Frequency | Noise Type |
|---|---|---|
| 12.5 years | Weekly solution | White + flicker noise (FN) |
| 10 to 13 years | Daily solution | White + FN |
| 7 years | 30 s | 1st order Gauss-Markov + white noise |
| 6 years | Daily solutions | White + FN + random walk noise |
| 3 years | Daily solutions | White + FN |
| 3 years | Daily solutions | White + FN + random walk noise |
| 2.5 years | Daily solutions | White + FN |
| Up to 1.5 years | Daily solutions | White + FN + walk noise |
| 0.3 years | 1 Hz | White + FN |
| 0.2 years | 30 s | White + FN |
| 2 h | 1 Hz | White + FN |
| ~1 h–121 days | 1–50 Hz | Random walk + white noise |
| ~15 min | 1 Hz | FN |
| ~1 h | 1 Hz | Time-correlated noise + white noise |
| 3.3 h | 1 Hz | Colored noise + white noise |
| Manufacturer | Model | Direction | Accuracy | Sampling Frequency (Hz) | |
|---|---|---|---|---|---|
| Fast Static (mm ± ppm) | RTK (mm ± ppm) | ||||
| Leica | Viva GS15 | H | 5 ± 0.5 | 10 ± 1 | 20 |
| V | 10 ± 0.5 | 20 ± 1 | |||
| Javad | Triumph-1 | H | 3 ± 0.5 × baseline | 10 ± 1 × baseline | 100 |
| V | 5 ± 0.5 × baseline | 15 + 1 × baseline | |||
| NovCom | SF-3050 | H | ---- | 10 ± 0.5 | 100 |
| V | ---- | 20 ± 1 | |||
| NovAtel | ProPak-V3 | H | ---- | 10 ± 1 | 50 |
| V | ---- | ---- | |||
| Septentrio | AsteRx2e | H | ---- | 6 ± 0.5 | 25 |
| V | ---- | 10 ± 1 | |||
| Sokkia | GRX1 | H | 3 ± 0.5 | 10 ± 1 | 20 |
| V | 5 ± 0.5 | 15 ± 1 | |||
| Topcon | GR-5 | H | 3 ± 0.5 | 10 ± 1 | 100 |
| V | 5 ± 0.5 | 15 ± 1 | |||
| Trimble | NetR9 | H | 3 ± 0.1 | 8 ± 1 | 20 |
| V | 4 ± 0.4 | 15 ± 1 | |||
| Mode | FH (Hz) | GPS (Hz) | Relative Change (%) | ||
|---|---|---|---|---|---|
| NovAtel | JAVAD | NovAtel | JAVAD | ||
| 1 | 0.66 | 0.68 | 0.68 | 3.03 | 3.03 |
| 2 | 1.08 | 1.01 | 1.02 | 6.48 | 5.56 |
| 3 | 1.48 | 1.42 | 1.42 | 4.05 | 4.05 |
| 4 | 1.58 | 1.77 | 1.76 | 12.03 | 11.39 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaloop, M.R.; Elbeltagi, E.; Hu, J.W.; Elrefai, A. Recent Advances of Structures Monitoring and Evaluation Using GPS-Time Series Monitoring Systems: A Review. ISPRS Int. J. Geo-Inf. 2017, 6, 382. https://doi.org/10.3390/ijgi6120382
Kaloop MR, Elbeltagi E, Hu JW, Elrefai A. Recent Advances of Structures Monitoring and Evaluation Using GPS-Time Series Monitoring Systems: A Review. ISPRS International Journal of Geo-Information. 2017; 6(12):382. https://doi.org/10.3390/ijgi6120382
Chicago/Turabian StyleKaloop, Mosbeh R., Emad Elbeltagi, Jong Wan Hu, and Ahmed Elrefai. 2017. "Recent Advances of Structures Monitoring and Evaluation Using GPS-Time Series Monitoring Systems: A Review" ISPRS International Journal of Geo-Information 6, no. 12: 382. https://doi.org/10.3390/ijgi6120382
APA StyleKaloop, M. R., Elbeltagi, E., Hu, J. W., & Elrefai, A. (2017). Recent Advances of Structures Monitoring and Evaluation Using GPS-Time Series Monitoring Systems: A Review. ISPRS International Journal of Geo-Information, 6(12), 382. https://doi.org/10.3390/ijgi6120382








