Optimizing Cruising Routes for Taxi Drivers Using a Spatio-Temporal Trajectory Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Sources
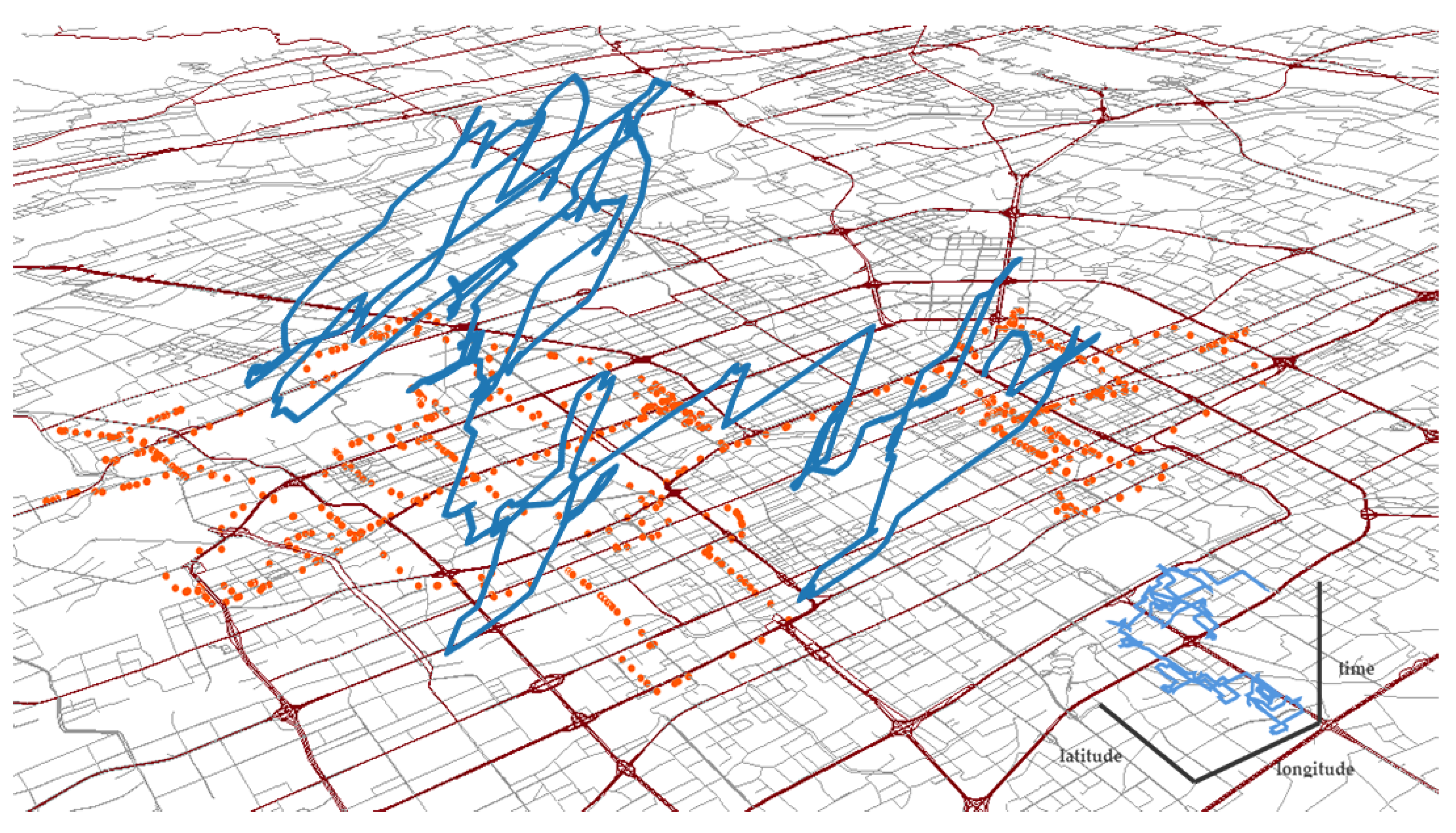
2.2. Data Preprocessing
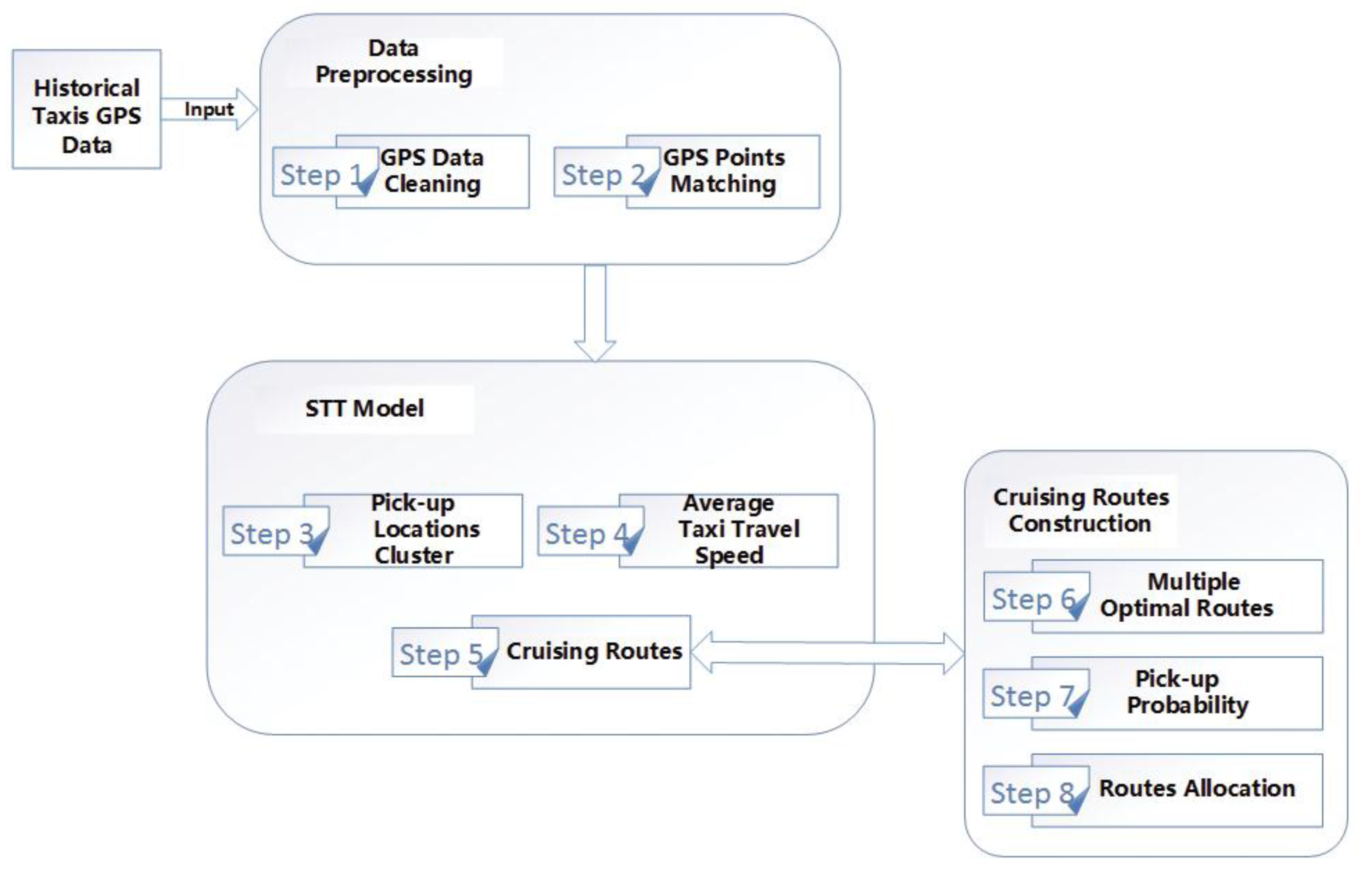
3. Spatio-Temporal Trajectory Model
3.1. Cluster of Pick-Up Locations
3.2. Average Taxi Travel Speed and Travel Time
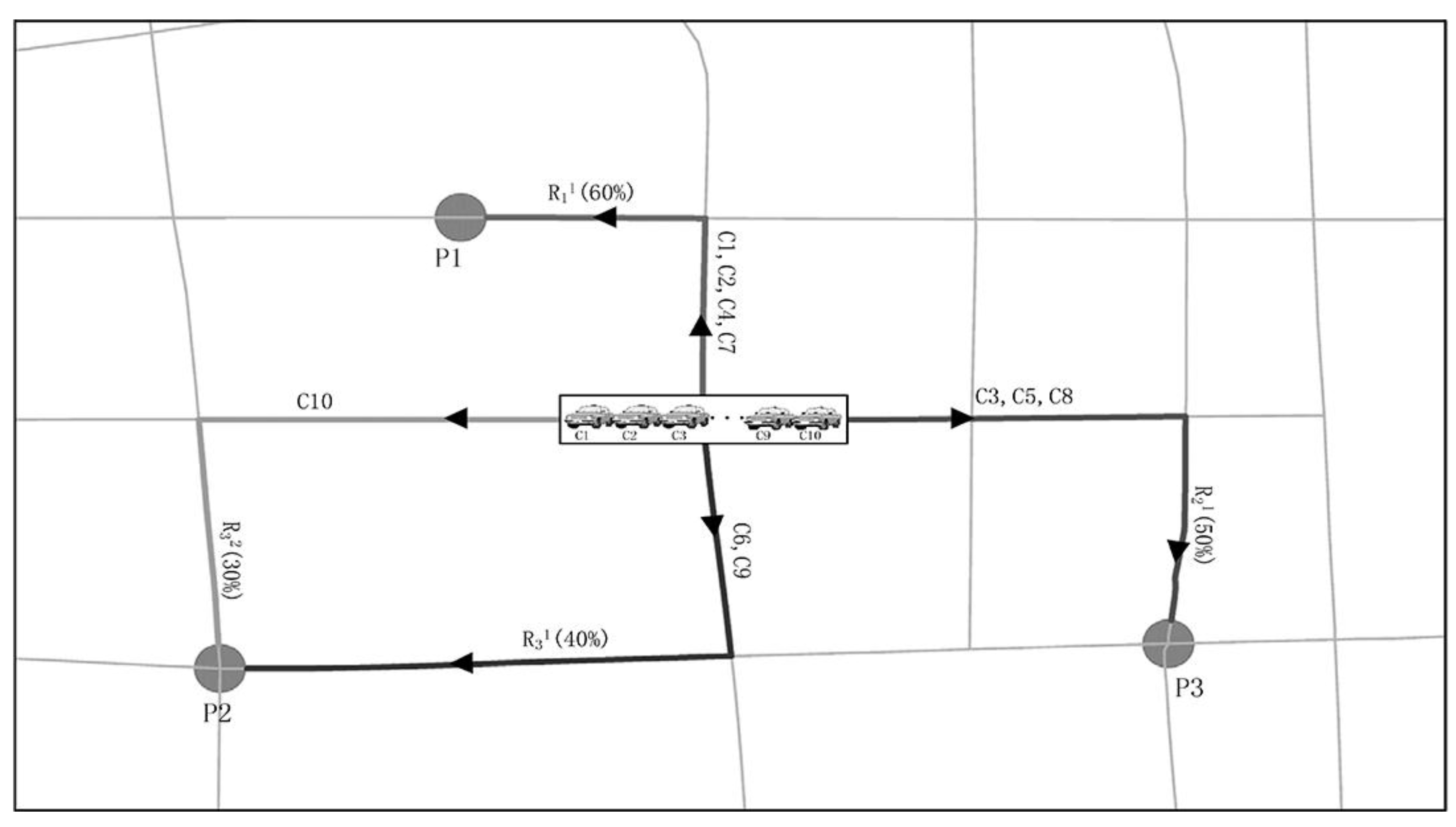
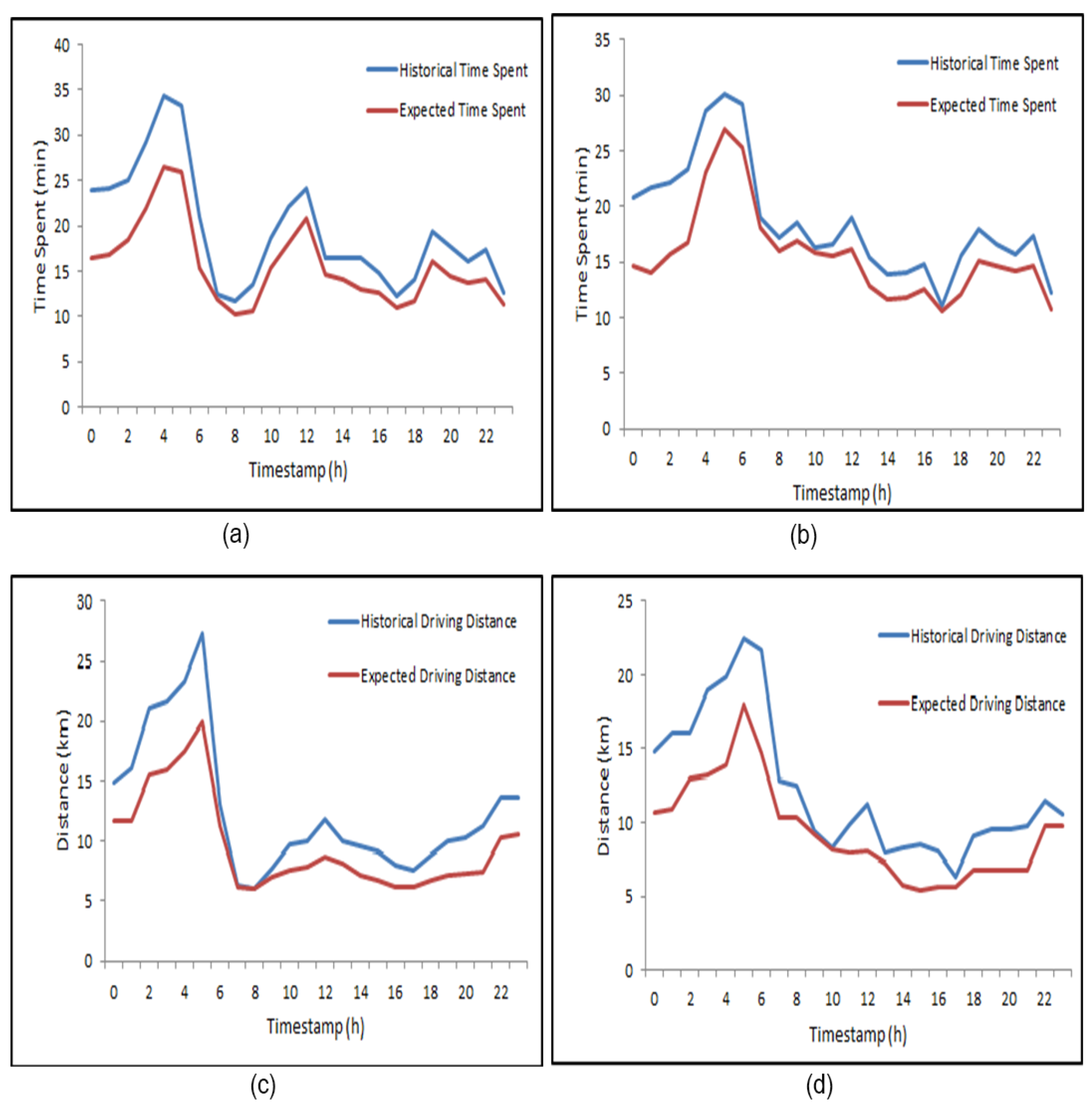
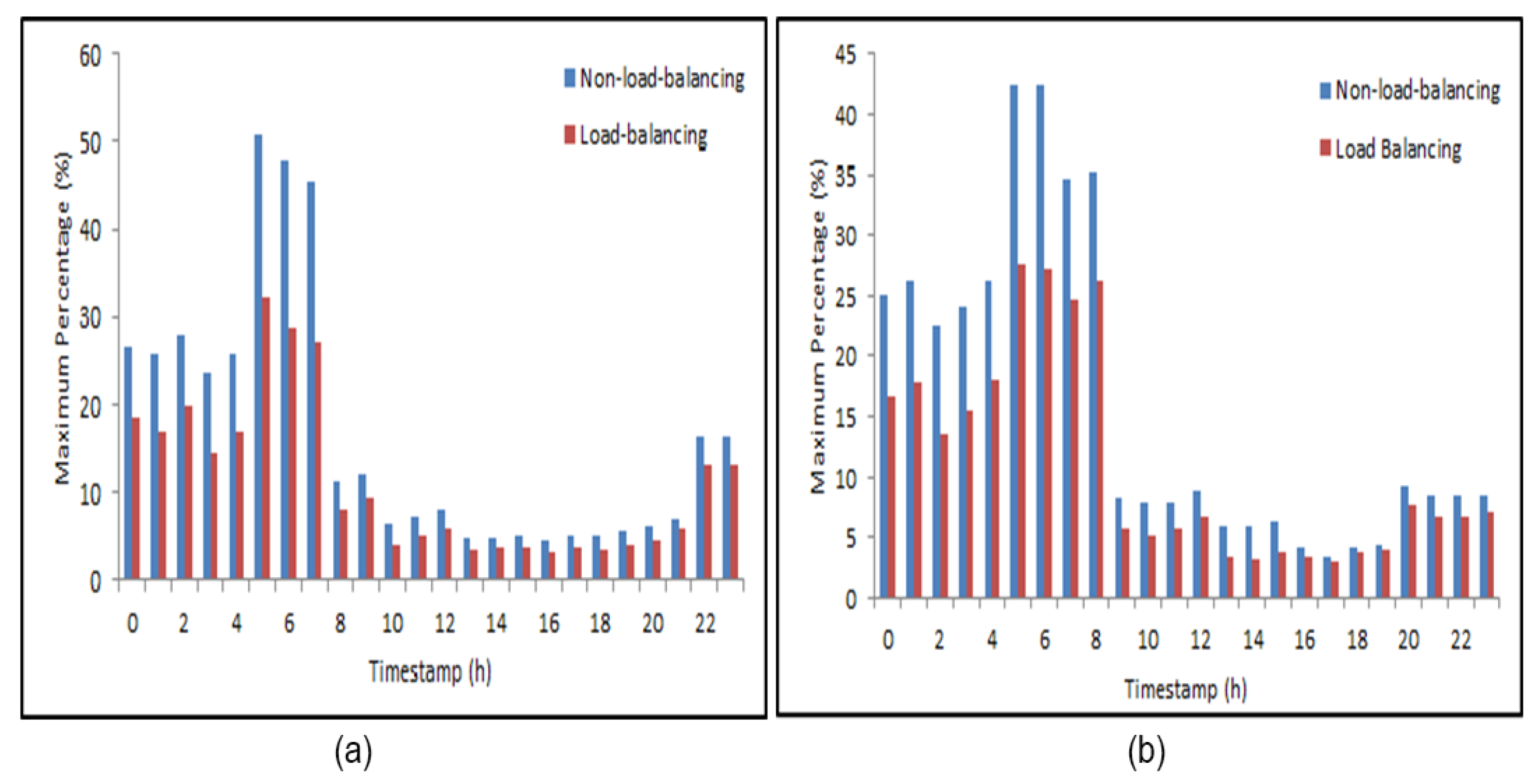
3.3. Cruising Routes
| Algorithm 1: The Weighted Round-Robin Scheduling Algorithm |
| Inputs: Candidate cruising routes set as ; indicates the probability of picking up a new passenger at ; indicates the route selected last time, and is initialized with −1; is the current weight in scheduling and is initialized with 0; is the maximum weight of all the routes in ; is the greatest common divisor of all route weights in . Output: The distributed server 1: while true do 2: ← () mod ; 3: If then 4: ← − ; 5: If then 6: ← ; 7: if then 8: return NULL; 9: end if 10: end if 11: end if 13: if then 14: return ; 15: end if 16: end |
4. Results
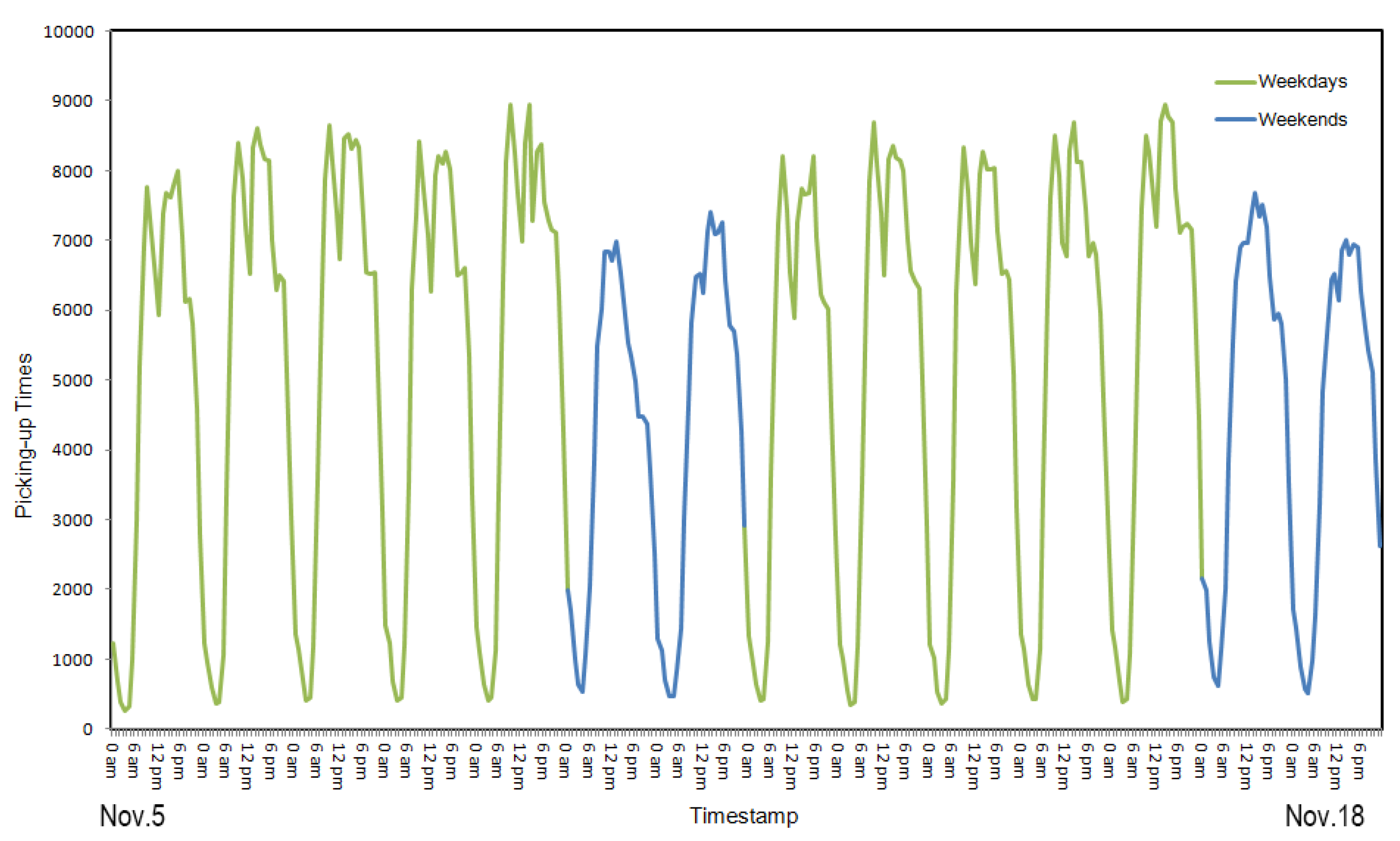
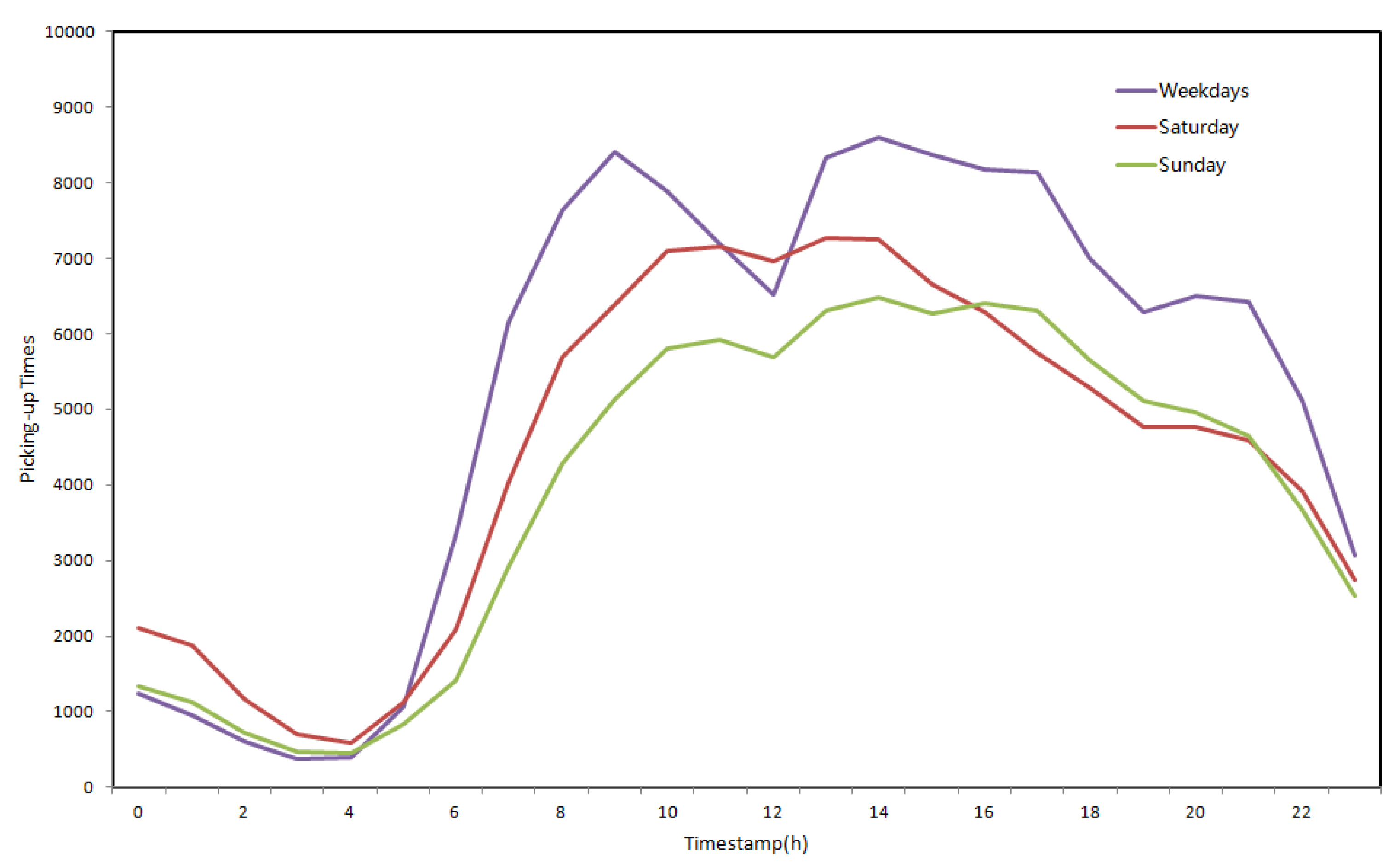
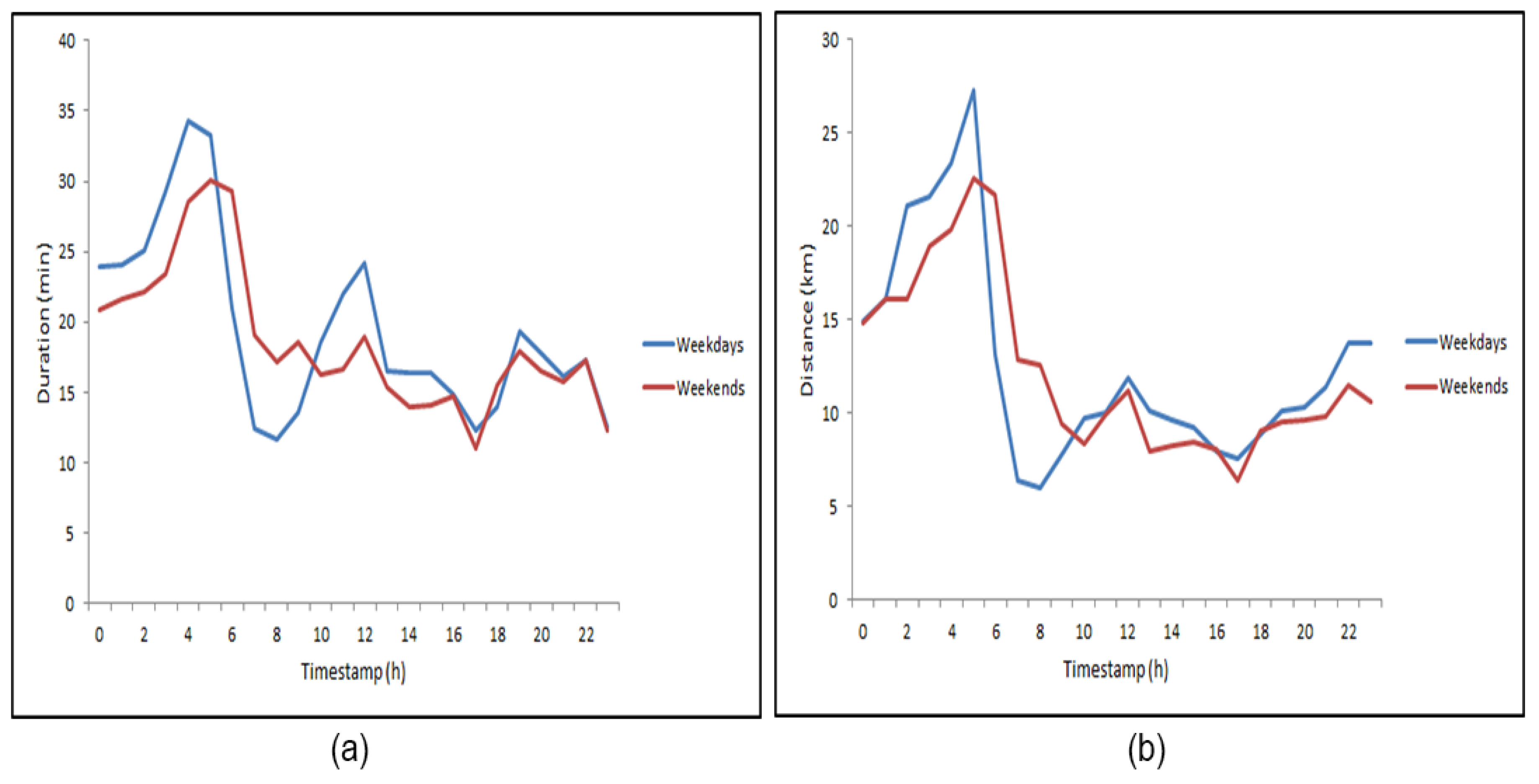
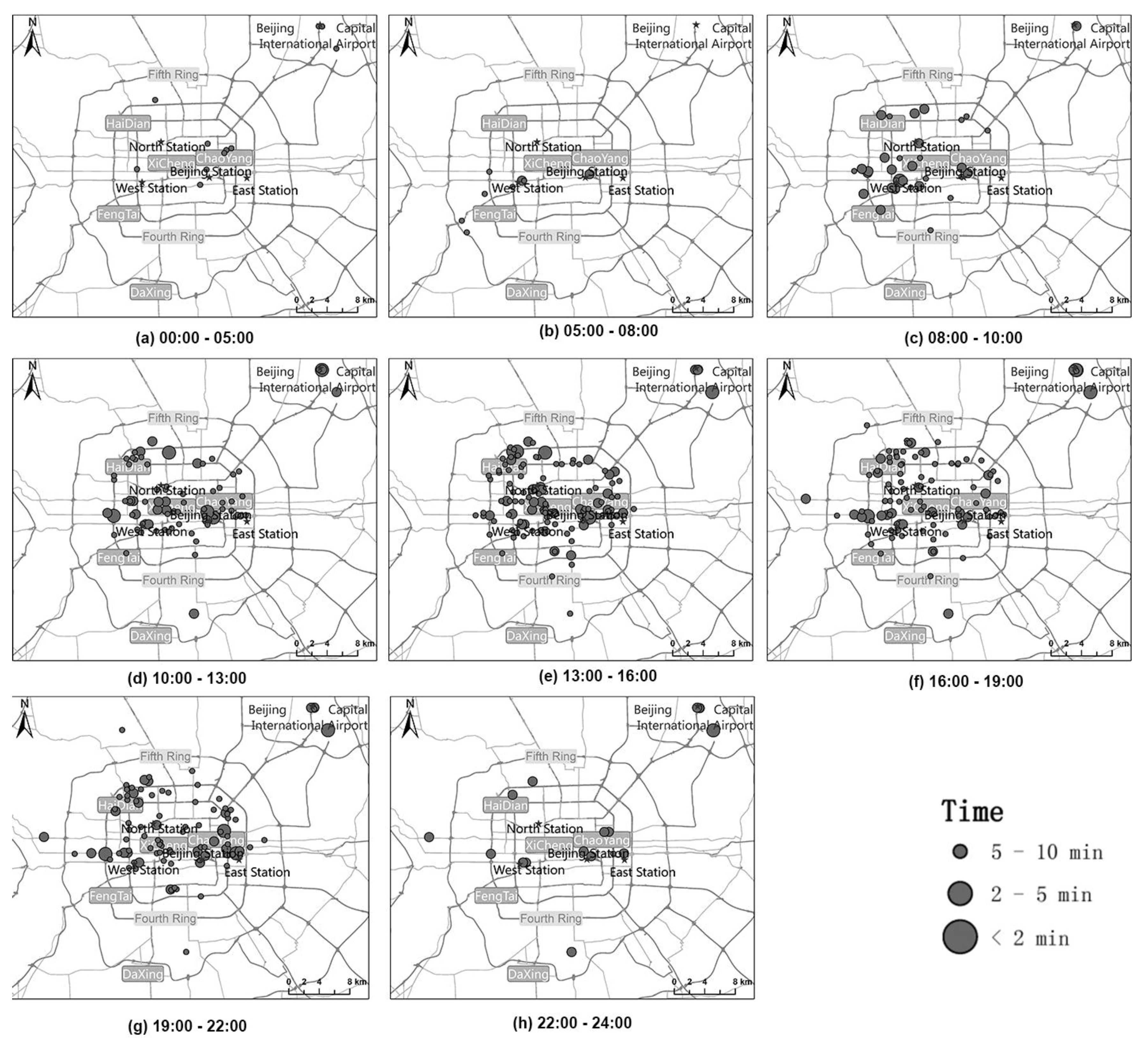
- In the early morning, high-demand areas were mainly in the Dongcheng District and Chaoyang District on weekdays (Figure 7a) and especially on weekends (Figure 8a). Eastern Beijing has both foreign affairs areas and business districts, and as many business centers are there, taxi demand occurred in the early morning. Moreover, as people go out for longer on weekends, there was also greater demand on weekends.
- Later in the day, the number of high-demand areas began to increase. Chaoyang is the largest district in terms of population, followed by the Haidian District and Fengtai District. Approximately 45.6% of Beijing’s population lives in these districts. Figure 7 and Figure 8 show that high-demand areas were concentrated in these areas. There are many good colleges and high schools in the Haidian District. Manufacturing and scientific research groups are concentrated between West Second Ring Road and West Third Ring Road. Moreover, most of the population is employed in the Haidian District and Fengtai District. Therefore, during the day, the number of high-demand areas in the Haidian District and Fengtai District were greater than that in the Chaoyang District; this difference was particularly pronounced on the weekends (Figure 7c–e and Figure 8c,d).
- During the evening, the number of high-demand areas in the Chaoyang District changed more slowly than in the Haidian District and Fengtai District, particularly on the weekends. The major reason might be because there are several catering and entertainment businesses in the Chaoyang District (Figure 7f–h and Figure 8e,f).
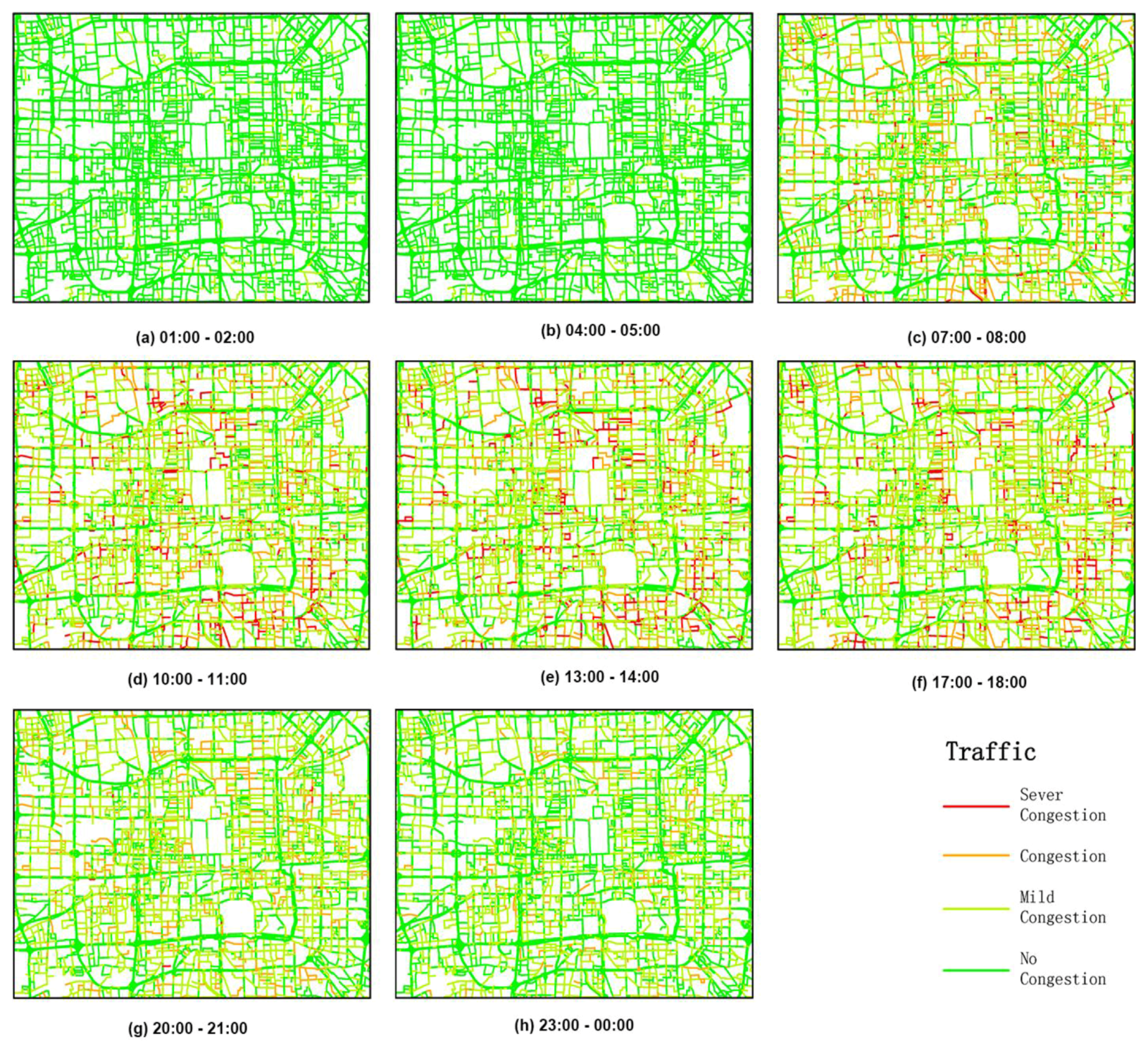
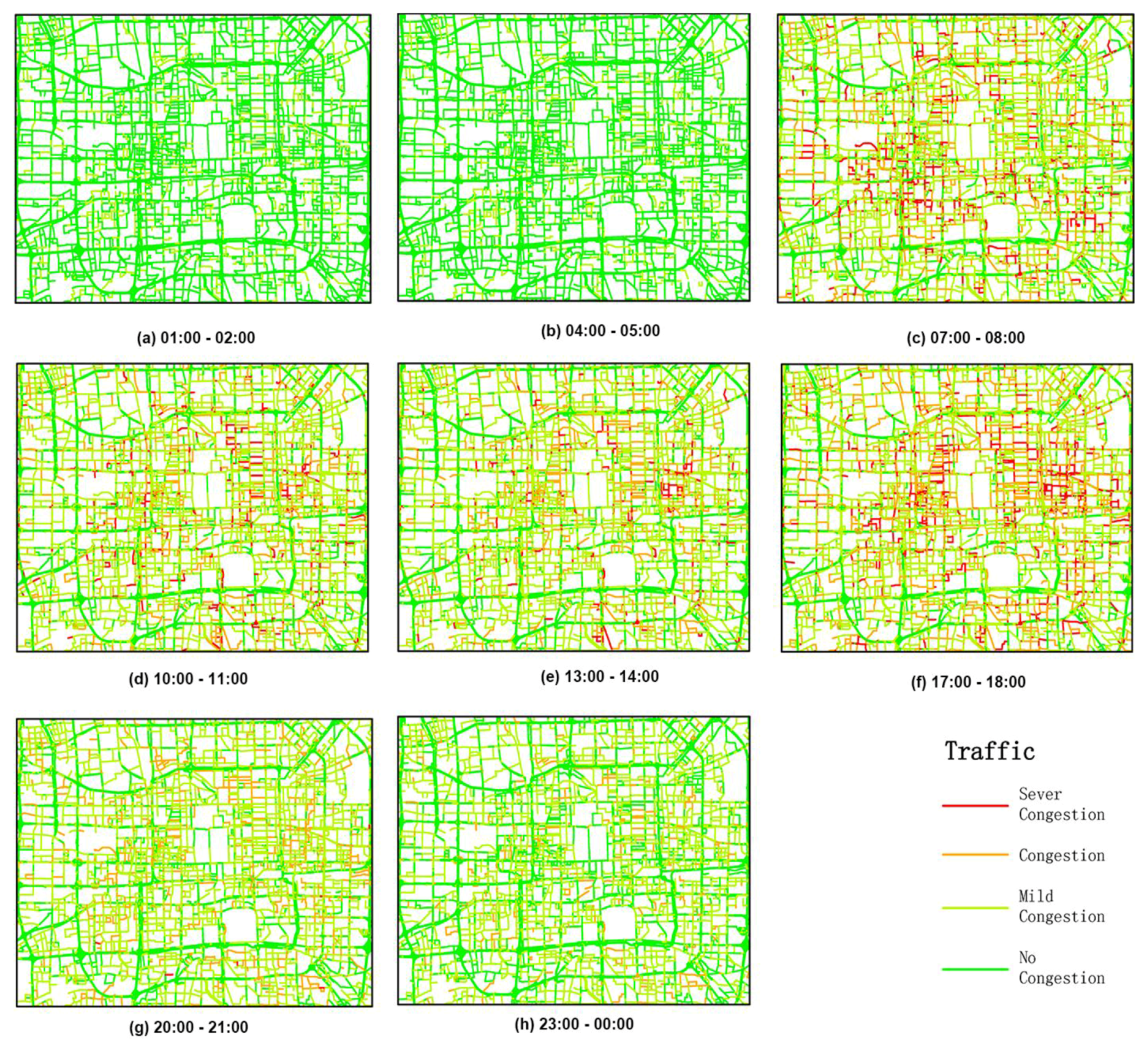
- 5. According to the Evaluation Index System of Urban Road Traffic Management provided by the Ministry of Public Security, a travel speed of >30 km/h indicates no congestion, a travel speed of between 20 km/h and 30 km/h indicates mild congestion, a travel speed of between 10 km/h and 20 km/h indicates congestion, and a travel speed of <10 km/h indicates strong congestion. We observed that before 5 a.m., traffic transportation showed the best conditions no matter which day of the week. Almost all the roads were clear (Figure 9a,b and Figure 10a,b), because during this period, there were fewer people and cars going out. Moreover, on weekdays, roads became increasingly congested from 6 a.m. onwards. During the peak morning hours, the average speed was approximately 25 km/h (Figure 9c). However, the traffic conditions were slightly better in the early afternoon (Figure 9d,e). In the period of the evening peak (5 p.m. to 7 p.m.), roads again became congested, and the congestion worsened (Figure 9f); the average speed was only approximately 22.9 km/h. After the evening peak, the traffic began to clear, and at midnight, there were no jammed roads (Figure 9g,h). On the weekends, traffic transportation showed better conditions than that on weekdays. There was no morning peak or evening peak (Figure 10c,f), but the traffic conditions were still congested during the day (Figure 10d,e). After the evening peak, the traffic began to clear. This pattern shows that people’s activities have impacts on traffic transportation conditions.
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Qian, X.; Ukkusuri, S.V. Spatial variation of the urban taxi ridership using gps data. Appl. Geogr. 2015, 59, 31–42. [Google Scholar] [CrossRef]
- Moreira-Matias, L.; Gama, J.; Ferreira, M.; Mendes-Moreira, J.; Damas, L. Predicting taxi-passenger demand using streaming data. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1393–1402. [Google Scholar] [CrossRef]
- Yuan, N.J.; Zheng, Y.; Zhang, L.H.; Xie, X. T-finder: A recommender system for finding passengers and vacant taxis. IEEE Trans. Knowl. Data Eng. 2013, 25, 2390–2403. [Google Scholar] [CrossRef]
- Wong, R.C.P.; Szeto, W.Y.; Wong, S.C. A cell-based logit-opportunity taxi customer-search model. Transp. Res. Part C Emerg. Technol. 2014, 48, 84–96. [Google Scholar] [CrossRef]
- Castro, P.S.; Zhang, D.Q.; Chen, C.; Li, S.J.; Pan, G. From taxi gps traces to social and community dynamics: A survey. ACM Comput. Surv. (CSUR) 2013, 46, 17. [Google Scholar] [CrossRef]
- Ge, Y.; Xiong, H.; Tuzhilin, A.; Xiao, K.; Gruteser, M.; Pazzani, M. An energy-efficient mobile recommender system. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010; pp. 899–908. [Google Scholar]
- Chen, B.Y.; Yuan, H.; Li, Q.Q.; Lam, W.H.K.; Shaw, S.L.; Yan, K. Map-matching algorithm for large-scale low-frequency floating car data. Int. J. Geogr. Inf. Sci. 2014, 28, 22–38. [Google Scholar] [CrossRef]
- Zhang, D.Q.; Sun, L.; Li, B.; Chen, C.; Pan, G.; Li, S.J.; Wu, Z.H. Understanding taxi service strategies from taxi gps traces. IEEE Trans. Intell. Transp. Syst. 2015, 16, 123–135. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Y.; Ni, L.M.; Fan, J.; Li, M. Towards mobility-based clustering. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010; pp. 919–928. [Google Scholar]
- Yuan, J.; Zheng, Y.; Xie, X. Discovering regions of different functions in a city using human mobility and pois. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 186–194. [Google Scholar]
- Jiang, B.; Yin, J.J.; Zhao, S.J. Characterizing the human mobility pattern in a large street network. Phys. Rev. E 2009, 80, 021136. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.R.; Zheng, C.Y.; Tian, Y.; Liang, R.H. Large-scale taxi o/d visual analytics for understanding metropolitan human movement patterns. J. Vis. 2015, 18, 185–200. [Google Scholar] [CrossRef]
- Wang, Z.C.; Lu, M.; Yuan, X.R.; Zhang, J.P.; van de Wetering, H. Visual traffic jam analysis based on trajectory data. IEEE Trans. Vis. Comput. Gr. 2013, 19, 2159–2168. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.S.; Liu, H.B.; Yu, R.J.; Deng, B.; Chen, X.H.; Wu, B. Exploring operating speeds on urban arterials using floating car data: Case study in shanghai. J. Transp. Eng. 2014, 140, 04014044. [Google Scholar] [CrossRef]
- Liu, X.L.; Lu, F.; Zhang, H.C.; Qiu, P.Y. Intersection delay estimation from floating car data via principal curves: A case study on beijing’s road network. Front. Earth Sci. 2013, 7, 206–216. [Google Scholar] [CrossRef]
- Herring, R.; Hofleitner, A.; Abbeel, P.; Bayen, A. Estimating arterial traffic conditions using sparse probe data. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010; pp. 929–936. [Google Scholar]
- Yuan, J.; Zheng, Y.; Xie, X.; Sun, G. T-drive: Enhancing driving directions with taxi drivers’ intelligence. IEEE Trans. Knowl. Data Eng. 2013, 25, 220–232. [Google Scholar] [CrossRef]
- Sun, D.; Zhang, C.; Zhang, L.; Chen, F.; Peng, Z.-R. Urban travel behavior analyses and route prediction based on floating car data. Transport. Lett. 2014, 6, 118–125. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, D.Q.; Li, N.; Zhou, Z.H. B-planner: Planning bidirectional night bus routes using large-scale taxi gps traces. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1451–1465. [Google Scholar] [CrossRef]
- Tang, L.L.; Li, Q.Q.; Chang, X.M.; Shaw, S.L.; Zhao, Z.L. Modeling of taxi drivers’ experience for routing applications. Sci. China Technol. Sci. 2010, 53, 44–51. [Google Scholar] [CrossRef]
- Liu, L.; Andris, C.; Ratti, C. Uncovering cabdrivers’ behavior patterns from their digital traces. Comput. Environ. Urban Syst. 2010, 34, 541–548. [Google Scholar] [CrossRef]
- Yuan, J.; Zheng, Y.; Zhang, L.; Xie, X.; Sun, G. Where to find my next passenger. In Proceedings of the 13th International Conference on Ubiquitous Computing, Beijing, China, 17–21 September; ACM: New York, NY, USA, 2011; pp. 109–118. [Google Scholar]
- Hu, X.; An, S.; Wang, J. Exploring urban taxi drivers: Activity distribution based on gps data. Math. Probl. Eng. 2014, 2014, 13. [Google Scholar] [CrossRef]
- Li, B.; Zhang, D.; Sun, L.; Chen, C.; Li, S.; Qi, G.; Yang, Q. Hunting or waiting? Discovering passenger-finding strategies from a large-scale real-world taxi dataset. In Proceedings of the 2011 IEEE International Conference on Pervasive Computing and Communications Workshops (PERCOM Workshops), Seattle, WA, USA, 21–25 March 2011; pp. 63–68. [Google Scholar]
- Yang, C.; Gonzales, E.J. Modeling taxi trip demand by time of day in new york city. Transp. Res. Rec. 2014, 110–120. [Google Scholar] [CrossRef]
- Wong, R.C.P.; Szeto, W.Y.; Wong, S.C.; Yang, H. Modelling multi-period customer-searching behaviour of taxi drivers. Transp. B Trans. Dyn. 2014, 2, 40–59. [Google Scholar] [CrossRef]
- Zong, F. Understanding taxi driver’s cruising behavior with zip model. J. Cent. South Univ. 2014, 21, 3404–3410. [Google Scholar] [CrossRef]
- Liu, S.; Wang, S.; Liu, C.; Krishnan, R. Understanding taxi drivers’ routing choices from spatial and social traces. Front. Comput. Sci. 2015, 9, 200–209. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, Z.; Qingquan, L.; Qingzhou, M. Mining time-dependent attractive areas and movement patterns from taxi trajectory data. In Proceedings of the 2009 17th International Conference on Geoinformatics, Fairfax, VA, USA, 12–14 August 2009; pp. 1–6. [Google Scholar]
- Hwang, R.H.; Hsueh, Y.L.; Chen, Y.T. An effective taxi recommender system based on a spatio-temporal factor analysis model. Inf. Sci. 2015, 314, 28–40. [Google Scholar] [CrossRef]
- Database of Beijing City Government Data Resources. Available online: http://www.bjdata.gov.cn/ (accessed on 17 November 2017).
- Quddus, M.A.; Ochieng, W.Y.; Noland, R.B. Current map-matching algorithms for transport applications: State-of-the art and future research directions. Transp. Res. C Emerg. Technol. 2007, 15, 312–328. [Google Scholar] [CrossRef]
- Velaga, N.R.; Quddus, M.A.; Bristow, A.L. Developing an enhanced weight-based topological map-matching algorithm for intelligent transport systems. Transp. Res. C Emerg. Technol. 2009, 17, 672–683. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, T.; Li, J.; Lian, X. Synthetic fuzzy evaluation method of trajectory similarity in map-matching. J. Intell. Transp. Syst. 2011, 15, 193–204. [Google Scholar] [CrossRef]
- Quddus, M.A.; Noland, R.B.; Ochieng, W.Y. A high accuracy fuzzy logic based map matching algorithm for road transport. J. Intell. Transp. Syst. 2006, 10, 103–115. [Google Scholar] [CrossRef]
- Skog, I.; Handel, P. In-car positioning and navigation technologies: A survey. IEEE Trans. Intell. Transp. Syst. 2009, 10, 4–21. [Google Scholar] [CrossRef]
- Wang, X.F.; Huang, D.S. A novel density-based clustering framework by using level set method. IEEE Trans. Knowl. Data Eng. 2009, 21, 1515–1531. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters a density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, Oregon, 2–4 August 1996; AAAI Press: Palo Alto, CA, USA, 1996; pp. 226–231. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Wimmer, M.; Xu, X. Incremental clustering for mining in a data warehousing environment. In Proceedings of the 24rd International Conference on Very Large Data Bases, New York, NY, USA, 24–27 August 1998; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1998; pp. 323–333. [Google Scholar]
- Kalnis, P.; Mamoulis, N.; Bakiras, S. On discovering moving clusters in spatio-temporal data. In Advances in Spatial and Temporal Databases, Proceedings of the 9th International Symposium, SSTD 2005, Angra dos Reis, Brazil, 22–24 August 2005. ; Bauzer Medeiros, C., Egenhofer, M.J., Bertino, E., Eds.; Springer: Berlin/Heidelberg, Gernamy, 2005; pp. 364–381. [Google Scholar]
- Birant, D.; Kut, A. St-dbscan: An algorithm for clustering spatial–temporal data. Data Knowl. Eng. 2007, 60, 208–221. [Google Scholar] [CrossRef]
- Erman, J.; Arlitt, M.; Mahanti, A. Traffic classification using clustering algorithms. In Proceedings of the 2006 SIGCOMM Workshop on Mining Network Data, Pisa, Italy, 11–15 September 2006; ACM: New York, NY, USA, 2006; pp. 281–286. [Google Scholar]
- Cherkassky, B.V.; Goldberg, A.V.; Radzik, T. Shortest paths algorithms: Theory and experimental evaluation. Math. Program. 1996, 73, 129–174. [Google Scholar] [CrossRef]
- Topkis, D.M. A k shortest path algorithm for adaptive routing in communications networks. IEEE Trans. Commun. 1988, 36, 855–859. [Google Scholar] [CrossRef]
- Eppstein, D. Finding the k shortest paths. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 154–165. [Google Scholar]
- Iqbal, M.A.; Saltz, J.H.; Bokhart, S.H. Performance Tradeoffs in Static and Dynamic Load Balancing Strategies; NASA Langley Research Center: Hampton, VA, USA, 1986.
- Cardellini, V.; Colajanni, M.; Yu, P.S. Dynamic load balancing on web-server systems. IEEE Int. Comput. 1999, 3, 28–39. [Google Scholar] [CrossRef]
- Katevenis, M.; Sidiropoulos, S.; Courcoubetis, C. Weighted round-robin cell multiplexing in a general-purpose atm switch chip. IEEE J. Sel. Areas Commun. 1991, 9, 1265–1279. [Google Scholar] [CrossRef]
- Saidu, I.; Subramaniam, S.; Jaafar, A.; Zukarnain, Z.A. A load-aware weighted round-robin algorithm for ieee 802.16 networks. EURASIP J. Wirel. Commun. Netw. 2014, 2014, 226. [Google Scholar] [CrossRef]
- Moreira-Matias, L.; Fernandes, R.; Gama, J.; Ferreira, M.; Mendes-Moreira, J.; Damas, L. An online recommendation system for the taxi stand choice problem (Poster). In Proceedings of the Vehicular NETWORKING Conference, Seoul, Korea, 14–16 November 2013; pp. 173–180. [Google Scholar]
- Kong, X.; Xia, F.; Wang, J.; Rahim, A.; Das, S.K. Time-location-relationship combined service recommendation based on taxi trajectory data. IEEE Trans. Ind. Inf. 2017, 13, 1202–1212. [Google Scholar] [CrossRef]
- Qian, S.; Zhu, Y.; Li, M. Smart recommendation by mining large-scale gps traces. In Proceedings of the 2012 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 1–4 April 2012; pp. 3267–3272. [Google Scholar]
- Pei, T.; Zhu, A.X.; Zhou, C.H.; Li, B.L.; Qin, C.Z. A new approach to the nearest-neighbour method to discover cluster features in overlaid spatial point processes. Int. J. Geogr. Inf. Sci. 2006, 20, 153–168. [Google Scholar] [CrossRef]

| TaxiID | Timestamp | Longitude (°) | Latitude (°) | Speed (km/h) | Directions (°) | Occupied Tag |
|---|---|---|---|---|---|---|
| 001140 | 20121101001504 | 117.109 | 40.153 | 75 | 136 | 1 |
| Eps (m) | MinPts | |
|---|---|---|
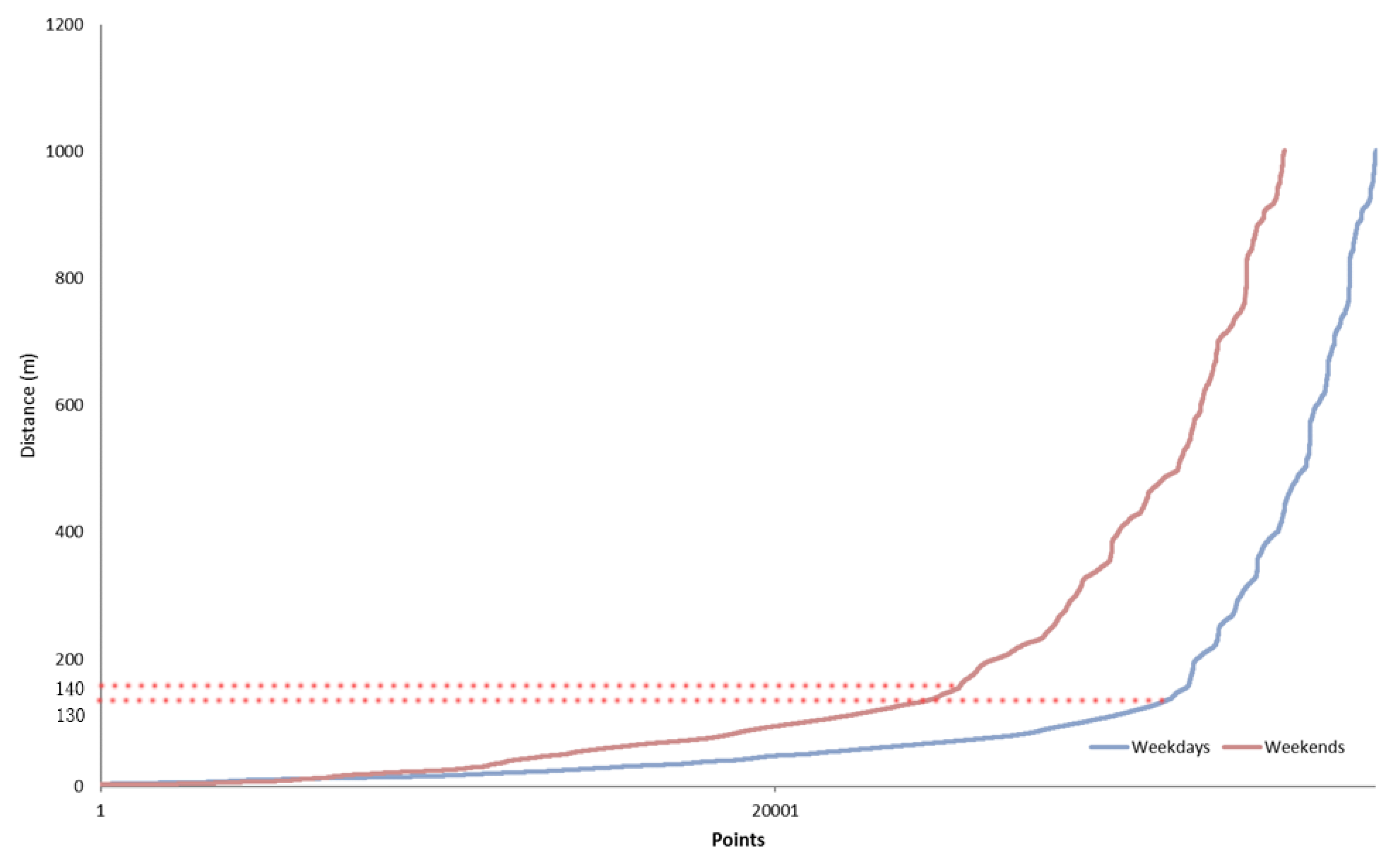
| Weekdays | 130 | 20 |
| Weekends | 140 | 25 |
| Weekdays | Count | Workdays | Count |
|---|---|---|---|
| 0 a.m.–5 a.m. | 12 | 0 a.m.–5 a.m. | 20 |
| 5 a.m.–8 a.m. | 8 | 5 a.m.–9 a.m. | 8 |
| 8 a.m.–10 a.m. | 33 | 9 a.m.–1 p.m. | 90 |
| 10 a.m.–1 p.m. | 75 | 1 p.m.–4 p.m. | 56 |
| 1 p.m.–4 p.m. | 127 | 4 p.m.–8 p.m. | 91 |
| 4 p.m.–7 p.m. | 101 | 8 p.m.–0 a.m. | 55 |
| 7 p.m.–10 p.m. | 95 | ||
| 10 p.m.–0 a.m. | 17 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Hu, S.; Yin, L.; Wang, Y.; Chen, Z.; Guo, M.; Chen, H.; Xie, Z. Optimizing Cruising Routes for Taxi Drivers Using a Spatio-Temporal Trajectory Model. ISPRS Int. J. Geo-Inf. 2017, 6, 373. https://doi.org/10.3390/ijgi6110373
Wu L, Hu S, Yin L, Wang Y, Chen Z, Guo M, Chen H, Xie Z. Optimizing Cruising Routes for Taxi Drivers Using a Spatio-Temporal Trajectory Model. ISPRS International Journal of Geo-Information. 2017; 6(11):373. https://doi.org/10.3390/ijgi6110373
Chicago/Turabian StyleWu, Liang, Sheng Hu, Li Yin, Yazhou Wang, Zhanlong Chen, Mingqiang Guo, Hao Chen, and Zhong Xie. 2017. "Optimizing Cruising Routes for Taxi Drivers Using a Spatio-Temporal Trajectory Model" ISPRS International Journal of Geo-Information 6, no. 11: 373. https://doi.org/10.3390/ijgi6110373
APA StyleWu, L., Hu, S., Yin, L., Wang, Y., Chen, Z., Guo, M., Chen, H., & Xie, Z. (2017). Optimizing Cruising Routes for Taxi Drivers Using a Spatio-Temporal Trajectory Model. ISPRS International Journal of Geo-Information, 6(11), 373. https://doi.org/10.3390/ijgi6110373






