Evaluation of Empirical and Machine Learning Algorithms for Estimation of Coastal Water Quality Parameters
Abstract
:1. Introduction
2. Datasets
2.1. Satellite Data
2.2. In Situ Chl-a and SS Concentrations Data
3. Methodology
3.1. Satellite Imagery Pre-Processing
- Lsatλ = At-satellite spectral radiance/TOA radiance for band λ (W/(m2 sr μm));
- Qcalλ = Quantized calibrated pixel value for band λ (DN);
- Qcalmin = Minimum quantized calibrated pixel value corresponding to Lminλ (DN);
- Qcalmax = Maximum quantized calibrated pixel value corresponding to Lmaxλ (DN);
- Lminλ = Spectral at-sensor radiance, scaled to Qcalmin for band λ (W/(m2 sr μm)); and
- Lmaxλ = Spectral at-sensor radiance, scaled to Qcalmax for band λ (W/(m2 sr μm)).
- DNλ = Quantized calibrated pixel value for band λ;
- Gλ = Band-specific gain factor [DN/(W/(m2 sr μm)] for band λ; and
- L0λ = Band-specific bias factor [W/(m2 sr μm)] for band λ.
3.2. Cross-Comparison of Sensors
3.3. Atmospheric Correction
3.4. Satellite and In Situ Data Matching
3.5. Modeling of Chl-a and SS Concentrations
- Regional Models—a single model for the entire coastal area of Hong Kong; and
- Local Models—a separate model for each of the water class defined by [11].
3.5.1. Empirical Predictive Modeling (EPM)
3.5.2. Neural Network Modeling (NN)
3.6. Performance Evaluation
4. Results
4.1. Regional Modeling of Chl-a and SS Concentrations
4.1.1. Empirical Predictive Modeling
4.1.2. Neural Network Modeling
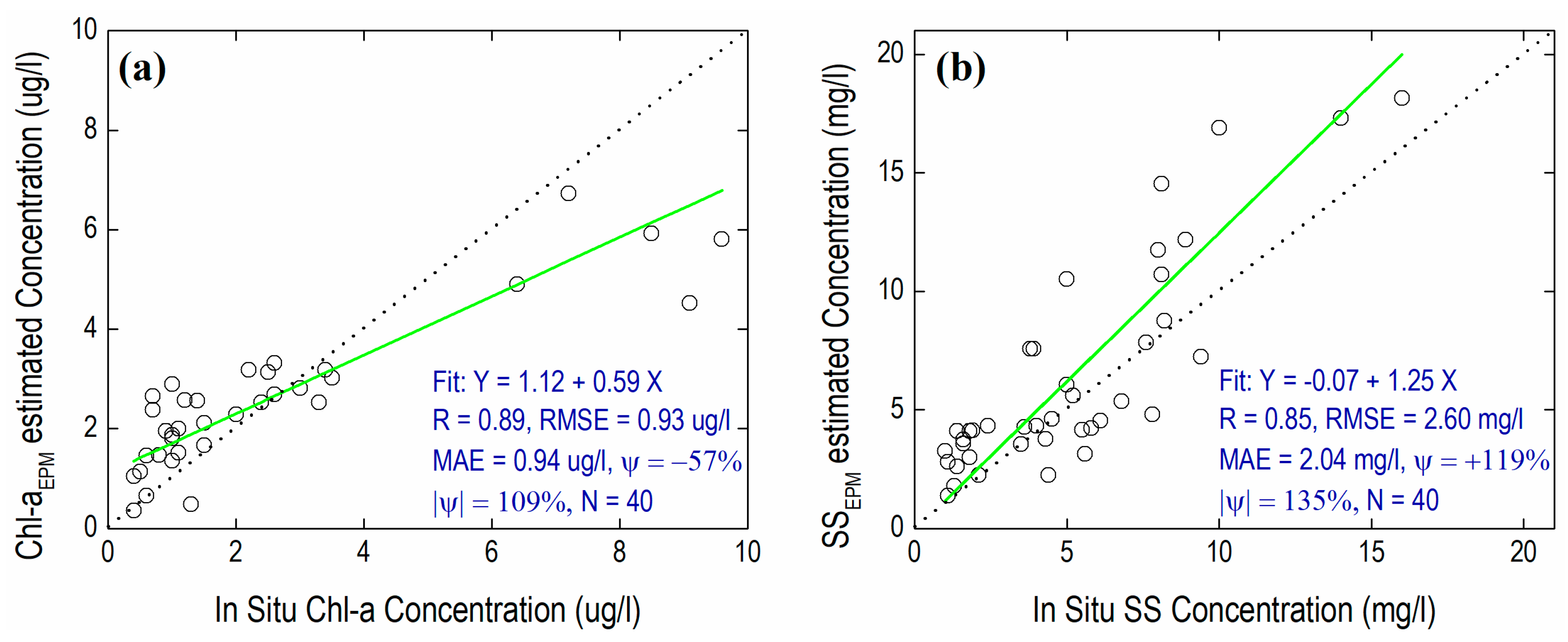
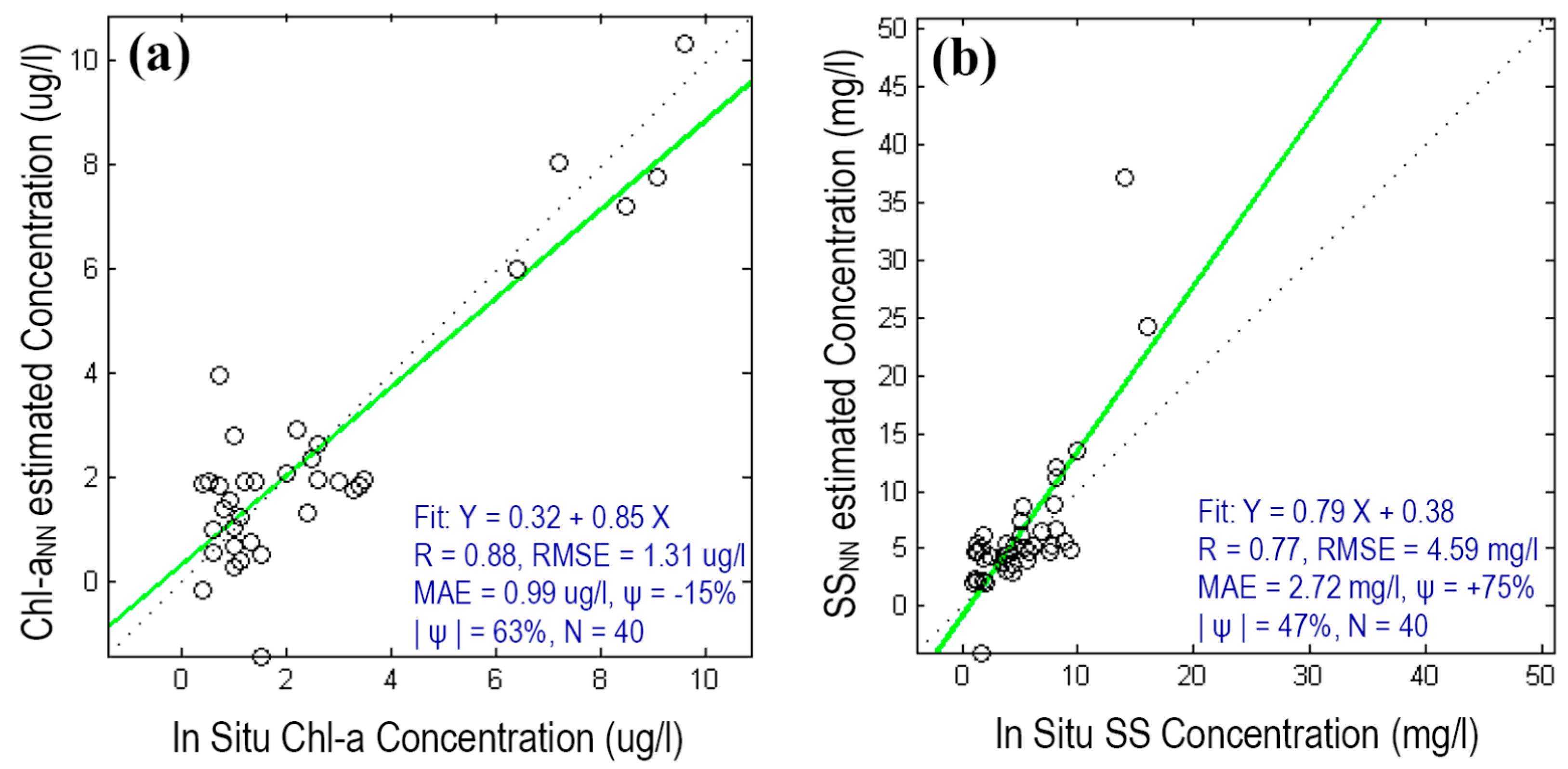
4.1.3. Validation of Regional EPM and NN Models
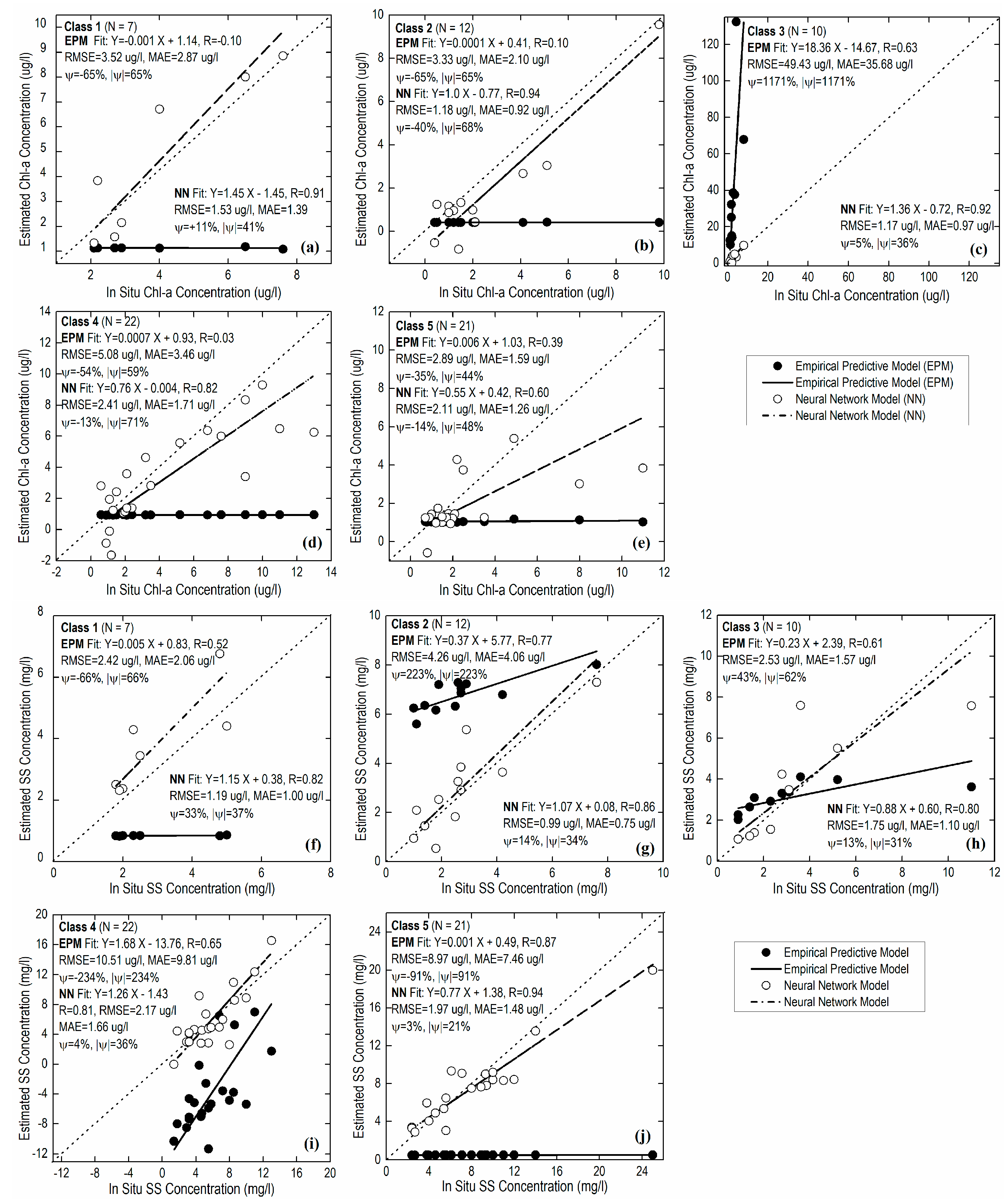
4.2. Class-Specific (Local) Modeling of Chlorophyll-a (Chl-a) and Suspended Solid (SS) Concentrations
4.2.1. Empirical Predictive Modeling
4.2.2. Neural Network Modeling
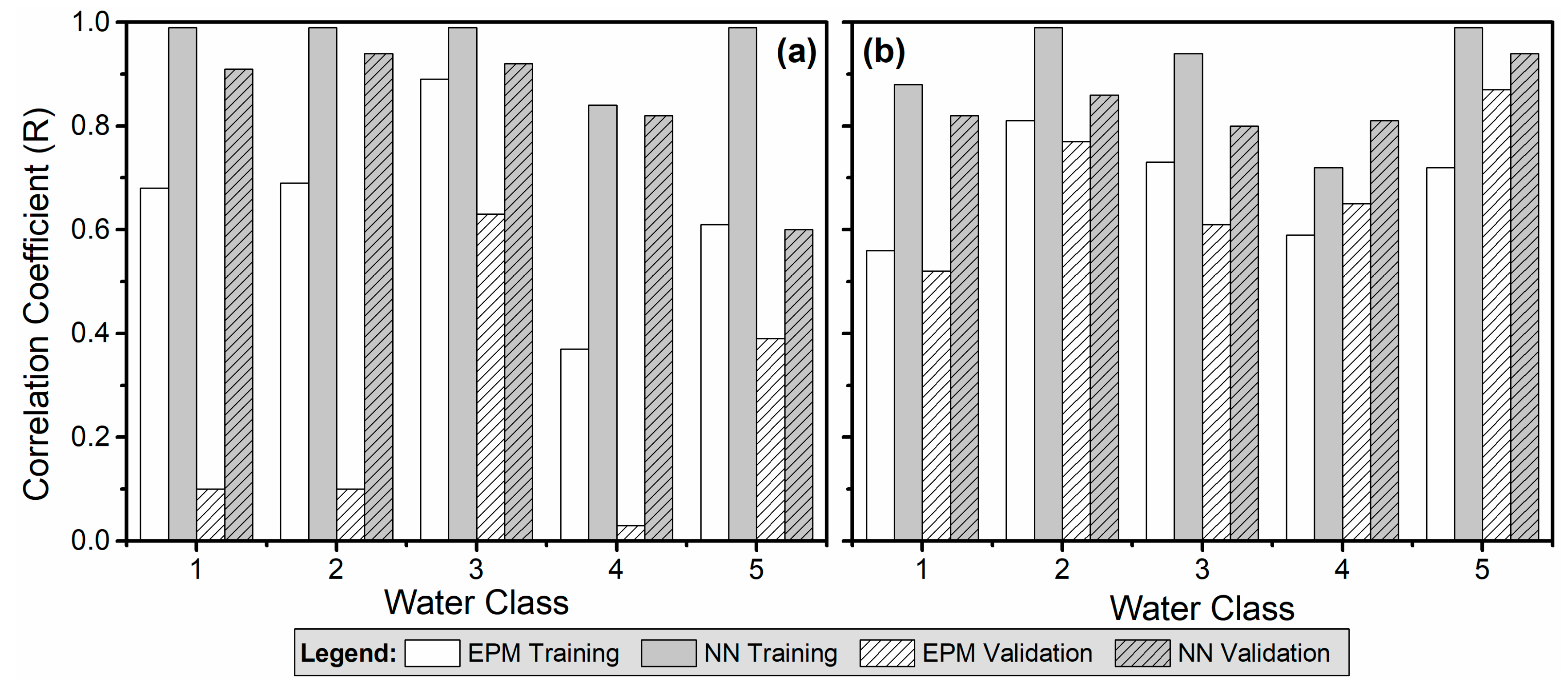
4.2.3. Validation of the Class-Specific (Local) Models
4.3. Statistical Performance Measures
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Neumann, B.; Vafeidis, A.T.; Zimmermann, J.; Nicholls, R.J. Future coastal population growth and exposure to sea-level rise and coastal flooding--A global assessment. PLoS ONE 2015, 10, e0118571. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Guo, H.; Liu, L. Quantitative identification and source apportionment of anthropogenic heavy metals in marine sediment of Hong Kong. Environ. Geol. 2007, 53, 295–305. [Google Scholar] [CrossRef]
- Derraik, J.G. The pollution of the marine environment by plastic debris: A review. Mar. Pollut. Bull. 2002, 44, 842–852. [Google Scholar] [CrossRef]
- Gorgoglione, A.; Gioia, A.; Iacobellis, V.; Piccinni, A.F.; Ranieri, E. A Rationale for Pollutograph Evaluation in Ungauged Areas, Using Daily Rainfall Patterns: Case Studies of the Apulian Region in Southern Italy. Appl. Environ. Soil Sci. 2016, 2016, 1–16. [Google Scholar] [CrossRef]
- IOCCG. Remote Sensing of Ocean Colour in Coastal, and Other Optically-Complex, Waters; Reports of the International Ocean-Colour Coordinating Group: Dartmouth, NS, Canada, 2000. [Google Scholar]
- Nazeer, M.; Wong, M.S.; Nichol, J.E. A new approach for the estimation of phytoplankton cell counts associated with algal blooms. Sci. Total Environ. 2017, 590–591, 125–138. [Google Scholar] [CrossRef] [PubMed]
- Butt, M.J.; Nazeer, M. Landsat ETM+ Secchi Disc Transparency (SDT) retrievals for Rawal Lake, Pakistan. Adv. Space Res. 2015, 56. [Google Scholar] [CrossRef]
- Mohammad, A.; Price, K.P.; Buddemeier, R.; Fautin, D.G.; Egbert, S. Mapping Spatial and Temporal Distributions of Kuwait SST Using MODIS Remotely Sensed Data. Appl. Remote Sens. J. 2012, 2, 1–16. [Google Scholar]
- Chen, J.; Cui, T.; Qiu, Z.; Lin, C. A three-band semi-analytical model for deriving total suspended sediment concentration from HJ-1A/CCD data in turbid coastal waters. ISPRS J. Photogramm. Remote Sens. 2014, 93, 1–13. [Google Scholar] [CrossRef]
- Ha, N.T.T.; Thao, N.T.P.; Koike, K.; Nhuan, M.T. Selecting the Best Band Ratio to Estimate Chlorophyll-a Concentration in a Tropical Freshwater Lake Using Sentinel 2A Images from a Case Study of Lake Ba Be (Northern Vietnam). ISPRS Int. J. Geo-Inf. 2017, 6, 290. [Google Scholar] [CrossRef]
- Nazeer, M.; Nichol, J.E. Improved water quality retrieval by identifying optically unique water classes. J. Hydrol. 2016, 541, 1119–1132. [Google Scholar] [CrossRef]
- Bian, C.; Jiang, W.; Song, D. Terrigenous transportation to the Okinawa Trough and the influence of typhoons on suspended sediment concentration. Cont. Shelf Res. 2010, 30, 1189–1199. [Google Scholar] [CrossRef]
- Grashorn, S.; Lettmann, K.A.; Wolff, J.-O.; Badewien, T.H.; Stanev, E.V. East Frisian Wadden Sea hydrodynamics and wave effects in an unstructured-grid model. Ocean Dyn. 2015, 65, 419–434. [Google Scholar] [CrossRef]
- Brivio, P.A.; Giardino, C.; Zilioli, E. Determination of chlorophyll concentration changes in Lake Garda using an image-based radiative transfer code for Landsat TM images. Int. J. Remote Sens. 2001, 22, 487–502. [Google Scholar] [CrossRef]
- Duan, H.; Zhang, Y.; Zhang, B.; Song, K.; Wang, Z. Assessment of chlorophyll-a concentration and trophic state for Lake Chagan using Landsat TM and field spectral data. Environ. Monit. Assess. 2007, 129, 295–308. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Jordan, K.J. Estimating and mapping chlorophyll-a concentration in Pensacola Bay, Florida using Landsat ETM+ data. Int. J. Remote Sens. 2005, 26, 5245–5254. [Google Scholar] [CrossRef]
- Kabbara, N.; Benkhelil, J.; Awad, M.; Barale, V. Monitoring water quality in the coastal area of Tripoli (Lebanon) using high-resolution satellite data. ISPRS J. Photogramm. Remote Sens. 2008, 63, 488–495. [Google Scholar] [CrossRef]
- Mahasandana, S.; Tripathi, N.K.; Honda, K. Sea surface multispectral index model for estimating chlorophyll a concentration of productive coastal waters in Thailand. Can. J. Remote Sens. 2009, 35, 287–296. [Google Scholar] [CrossRef]
- Wang, F.; Han, L.; Kung, H.-T.; Van Arsdale, R.B. Applications of Landsat-5 TM imagery in assessing and mapping water quality in Reelfoot Lake, Tennessee. Int. J. Remote Sens. 2006, 27, 5269–5283. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, H.; Chen, C.; Chen, L.; Zhang, B.; Gitelson, A. a Estimation of chlorophyll-a concentration in estuarine waters: Case study of the Pearl River estuary, South China Sea. Environ. Res. Lett. 2011, 6, 24016. [Google Scholar] [CrossRef]
- Xi, H.; Zhang, Y. Total suspended matter observation in the Pearl River estuary from in situ and MERIS data. Environ. Monit. Assess. 2011, 177, 563–574. [Google Scholar] [CrossRef] [PubMed]
- Tian, L.; Wai, O.; Chen, X.; Liu, Y.; Feng, L.; Li, J.; Huang, J. Assessment of Total Suspended Sediment Distribution under Varying Tidal Conditions in Deep Bay: Initial Results from HJ-1A/1B Satellite CCD Images. Remote Sens. 2014, 6, 9911–9929. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.S.; Liu, Z.; Yin, K.; Li, Z.; Wai, O.W.; King, B. Integration of multi-source data for water quality classification in the Pearl River estuary and its adjacent coastal waters of Hong Kong. Cont. Shelf Res. 2004, 24, 1827–1843. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.-S.; Liu, Z.; Li, Z.; Wai, O.W.; King, B. Water quality management in the estuary of Pearl River and Hong Kong’s coastal waters based on SeaWiFS, Landsat TM sensor data and in situ water quality sampling data. In Third International Asia-Pacific Environmental Remote Sensing Remote Sensing of the Atmosphere, Ocean, Environment, and Space; Frouin, R.J., Yuan, Y., Kawamura, H., Eds.; International Society for Optics and Photonics: Washington, DC, USA, 2003; pp. 589–599. [Google Scholar]
- Le, C.; Hu, C.; Cannizzaro, J.; Duan, H. Long-term distribution patterns of remotely sensed water quality parameters in Chesapeake Bay. Estuar. Coast. Shelf Sci. 2013, 128, 93–103. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Nazeer, M.; Nichol, J.E.; Yung, Y.-K. Evaluation of atmospheric correction models and Landsat surface reflectance product in an urban coastal environment. Int. J. Remote Sens. 2014. [Google Scholar] [CrossRef]
- HKEPD. Marine Water Quality in Hong Kong in 2015. Hong Kong, 2016. Available online: http://wqrc.epd.gov.hk/pdf/water-quality/annual-report/MarineReport2015eng.pdf (accessed on 12 October 2017).
- Li, G.; Li, X.; Li, G.; Wen, W.; Wang, H.; Chen, L.; Yu, J.; Deng, F. Comparison of Spectral Characteristics Between China HJ1-CCD and Landsat 5 TM Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 139–148. [Google Scholar] [CrossRef]
- Nazeer, M.; Nichol, J.E. Combining Landsat TM/ETM+ and HJ-1 A/B CCD Sensors for Monitoring Coastal Water Quality in Hong Kong. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1898–1902. [Google Scholar] [CrossRef]
- Song, C.; Woodcock, C.E.; Seto, K.C.; Lenney, M.P.; Macomber, S.A. Classification and Change Detection Using Landsat TM Data. Remote Sens. Environ. 2001, 75, 230–244. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanré, D.; DeuzéHerman, J.L.; Herman, M.; Morcrette, J.J.; Kotchenova, S.Y. Second Simulation of a Satellite Signal in the Solar Spectrum—Vector (6SV), 6S User Guide, Version 3. 2006. Available online: https://pdfs.semanticscholar.org/4cff/1aa6101a41a3d6fca21805f8e4d756846f40.pdf (accessed on 10 August 2017).
- Acker, J. G.; Leptoukh, G. Online Analysis Enhances Use of NASA Earth Science Data. Eos Trans. Am. Geophys. Union 2007, 88, 14. [Google Scholar] [CrossRef]
- Bailey, S.; Werdell, P. A multi-sensor approach for the on-orbit validation of ocean color satellite data products. Remote Sens. Environ. 2006, 102, 12–23. [Google Scholar] [CrossRef]
- Nazeer, M.; Nichol, J.E. Development and application of a remote sensing-based Chlorophyll-a concentration prediction model for complex coastal waters of Hong Kong. J. Hydrol. 2016, 532. [Google Scholar] [CrossRef]
- Dorji, P.; Fearns, P.; Broomhall, M. A Semi-Analytic Model for Estimating Total Suspended Sediment Concentration in Turbid Coastal Waters of Northern Western Australia Using MODIS-Aqua 250 m Data. Remote Sens. 2016, 8, 556. [Google Scholar] [CrossRef]
- Zibordi, G.; Mélin, F.; Berthon, J.-F.; Canuti, E. Assessment of MERIS ocean color data products for European seas. Ocean Sci. 2013, 9, 521–533. [Google Scholar] [CrossRef]
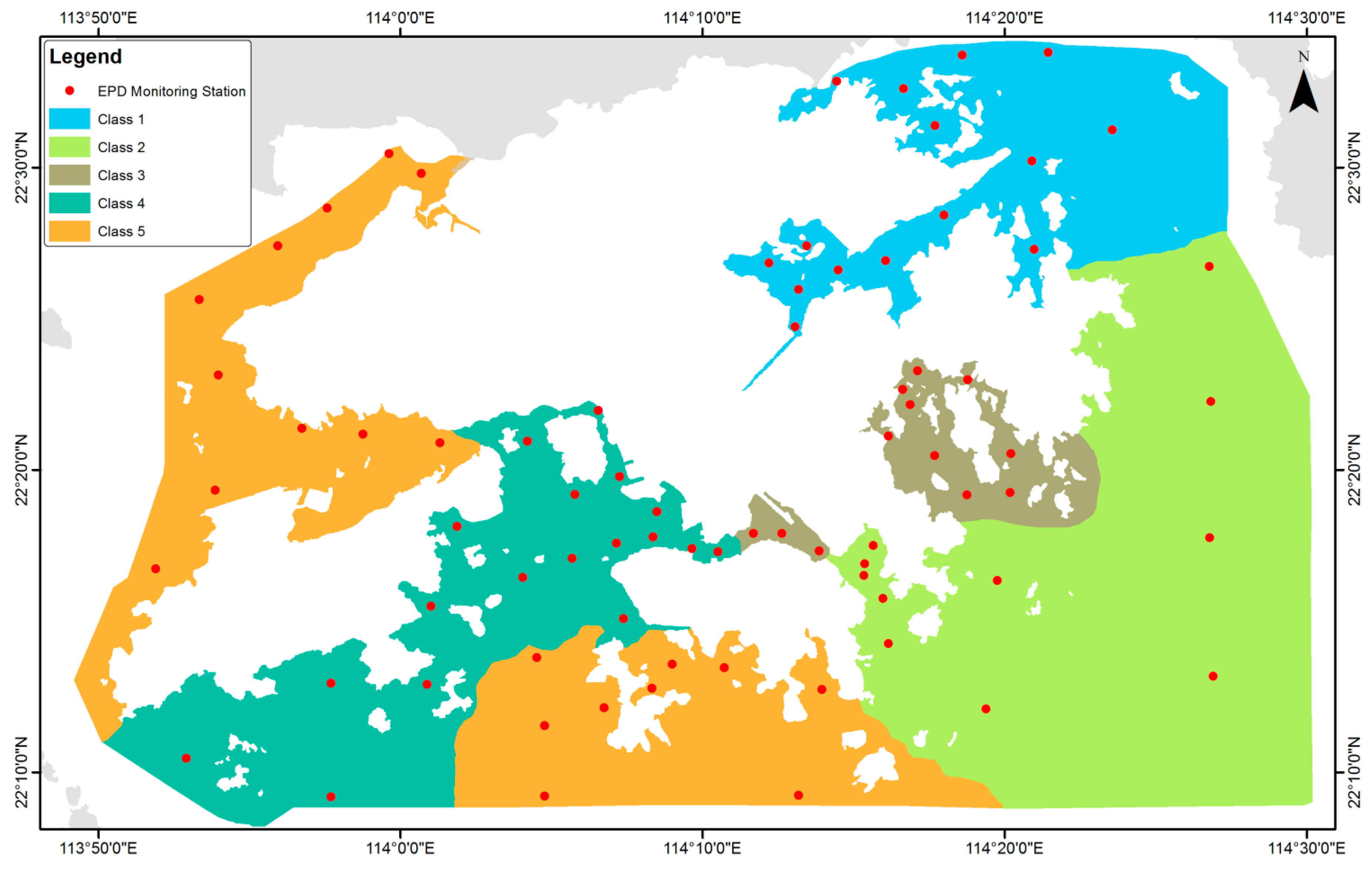
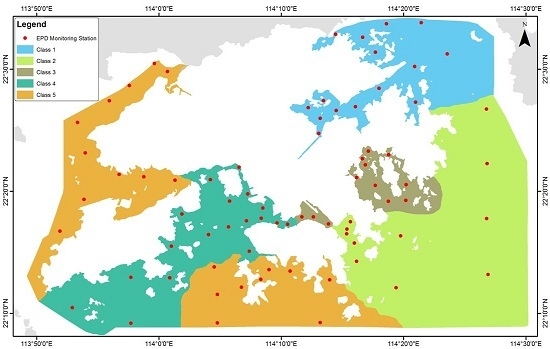
| Variable | Max | Min | Median | Average | StDev |
|---|---|---|---|---|---|
| Chl-a (μg/L) | 13.00 | 0.30 | 1.90 | 2.98 | 2.84 |
| SS (mg/L) | 56.00 | 0.50 | 4.40 | 5.73 | 6.07 |
| Water Class | No. of Match-Ups | Chl-a Range (µg/L) | SS Range (mg/L) |
|---|---|---|---|
| Class 1 | 24 | 0.4–8.1 | 1.1–5.0 |
| Class 2 | 40 | 0.3–12.0 | 1.0–7.6 |
| Class 3 | 33 | 0.7–11.0 | 0.5–11.0 |
| Class 4 | 74 | 0.5–13.0 | 0.7–22.0 |
| Class 5 | 69 | 0.6–12.0 | 2.0–56.0 |
| Total | 240 | 0.3–13.0 | 0.5–56.0 |
| Water Class | N | For Chl-a Concentrations | For SS Concentrations | ||
|---|---|---|---|---|---|
| Chl-a = | R | SS = | R | ||
| Class 1 | 17 | −0.15 × √(B4/B3) + 1.26 | 0.68 | 0.11 × (B2/B1) + 0.73 | 0.56 |
| Class 2 | 28 | 0.04 × (B3/B2) + 0.39 | 0.69 | 0.58 × (B2) + 3.64 | 0.81 |
| Class 3 | 23 | 3.48 × (B2×B4) + 0.13 | 0.89 | 0.56 × Av (B1, B3) + 1.45 | 0.73 |
| Class 4 | 52 | 0.06 × (B2/B1) + 0.87 | 0.37 | 3.43 × B3/(B4)2 − 15.93 | 0.59 |
| Class 5 | 48 | 0.12 × (B2/B1) + 0.90 | 0.61 | 0.02 × (B3/B1) + 0.49 | 0.72 |
| Water Class | N | R (for Chl-a) | R (for SS) |
|---|---|---|---|
| Class 1 | 17 | 0.99 | 0.88 |
| Class 2 | 28 | 0.99 | 0.99 |
| Class 3 | 23 | 0.99 | 0.94 |
| Class 4 | 52 | 0.84 | 0.72 |
| Class 5 | 48 | 0.99 | 0.99 |
| Model | N | R | RMSE | MAE | ψ | |ψ| |
|---|---|---|---|---|---|---|
| Chl-aEPM | 40 | 0.89 | 0.93 (µg/L) | 0.94 (µg/L) | −57 (%) | 109 (%) |
| Chl-aNN | 40 | 0.88 | 1.31 (µg/L) | 0.99 (µg/L) | −15 (%) | 63 (%) |
| SSEPM | 40 | 0.85 | 2.60 (mg/L) | 2.04 (mg/L) | 119 (%) | 135 (%) |
| SSNN | 40 | 0.77 | 4.59 (mg/L) | 2.72 (mg/L) | 75 (%) | 47 (%) |
| Water Class | N | For Chl-a (SS) Concentrations | ||||
|---|---|---|---|---|---|---|
| R | RMSE | MAE | ψ (%) | |ψ| (%) | ||
| Class 1 | 7 | −0.10 (0.52) | 3.52 (2.42) | 2.87 (2.06) | −65 (−66) | 65 (66) |
| 0.91 (0.82) | 1.53 (1.19) | 1.39 (1.00) | 11 (33) | 41 (37) | ||
| Class 2 | 12 | 0.10 (0.77) | 3.33 (4.26) | 2.10 (4.06) | −65 (223) | 65 (223) |
| 0.94 (0.86) | 1.18 (0.99) | 0.92 (0.75) | −40 (14) | 68 (34) | ||
| Class 3 | 10 | 0.63 (0.61) | 49.43 (2.53) | 35.68 (1.57) | 1171 (43) | 1171 (62) |
| 0.92 (0.80) | 1.17 (1.75) | 0.97 (1.10) | 5 (13) | 36 (31) | ||
| Class 4 | 22 | 0.03 (0.65) | 5.08 (10.51) | 3.46 (9.81) | −54 (−234) | 59 (234) |
| 0.82 (0.81) | 2.41 (2.17) | 1.71 (1.66) | −13 (4) | 71 (36) | ||
| Class 5 | 21 | 0.39 (0.87) | 2.89 (8.97) | 1.59 (7.46) | −35 (−91) | 44 (91) |
| 0.60 (0.94) | 2.11 (1.97) | 1.26 (1.48) | −14 (3) | 48 (21) | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazeer, M.; Bilal, M.; Alsahli, M.M.M.; Shahzad, M.I.; Waqas, A. Evaluation of Empirical and Machine Learning Algorithms for Estimation of Coastal Water Quality Parameters. ISPRS Int. J. Geo-Inf. 2017, 6, 360. https://doi.org/10.3390/ijgi6110360
Nazeer M, Bilal M, Alsahli MMM, Shahzad MI, Waqas A. Evaluation of Empirical and Machine Learning Algorithms for Estimation of Coastal Water Quality Parameters. ISPRS International Journal of Geo-Information. 2017; 6(11):360. https://doi.org/10.3390/ijgi6110360
Chicago/Turabian StyleNazeer, Majid, Muhammad Bilal, Mohammad M. M. Alsahli, Muhammad Imran Shahzad, and Ahmad Waqas. 2017. "Evaluation of Empirical and Machine Learning Algorithms for Estimation of Coastal Water Quality Parameters" ISPRS International Journal of Geo-Information 6, no. 11: 360. https://doi.org/10.3390/ijgi6110360
APA StyleNazeer, M., Bilal, M., Alsahli, M. M. M., Shahzad, M. I., & Waqas, A. (2017). Evaluation of Empirical and Machine Learning Algorithms for Estimation of Coastal Water Quality Parameters. ISPRS International Journal of Geo-Information, 6(11), 360. https://doi.org/10.3390/ijgi6110360