WLAN Fingerprint Indoor Positioning Strategy Based on Implicit Crowdsourcing and Semi-Supervised Learning
Abstract
1. Introduction
2. Related Work
3. System Components and Methods
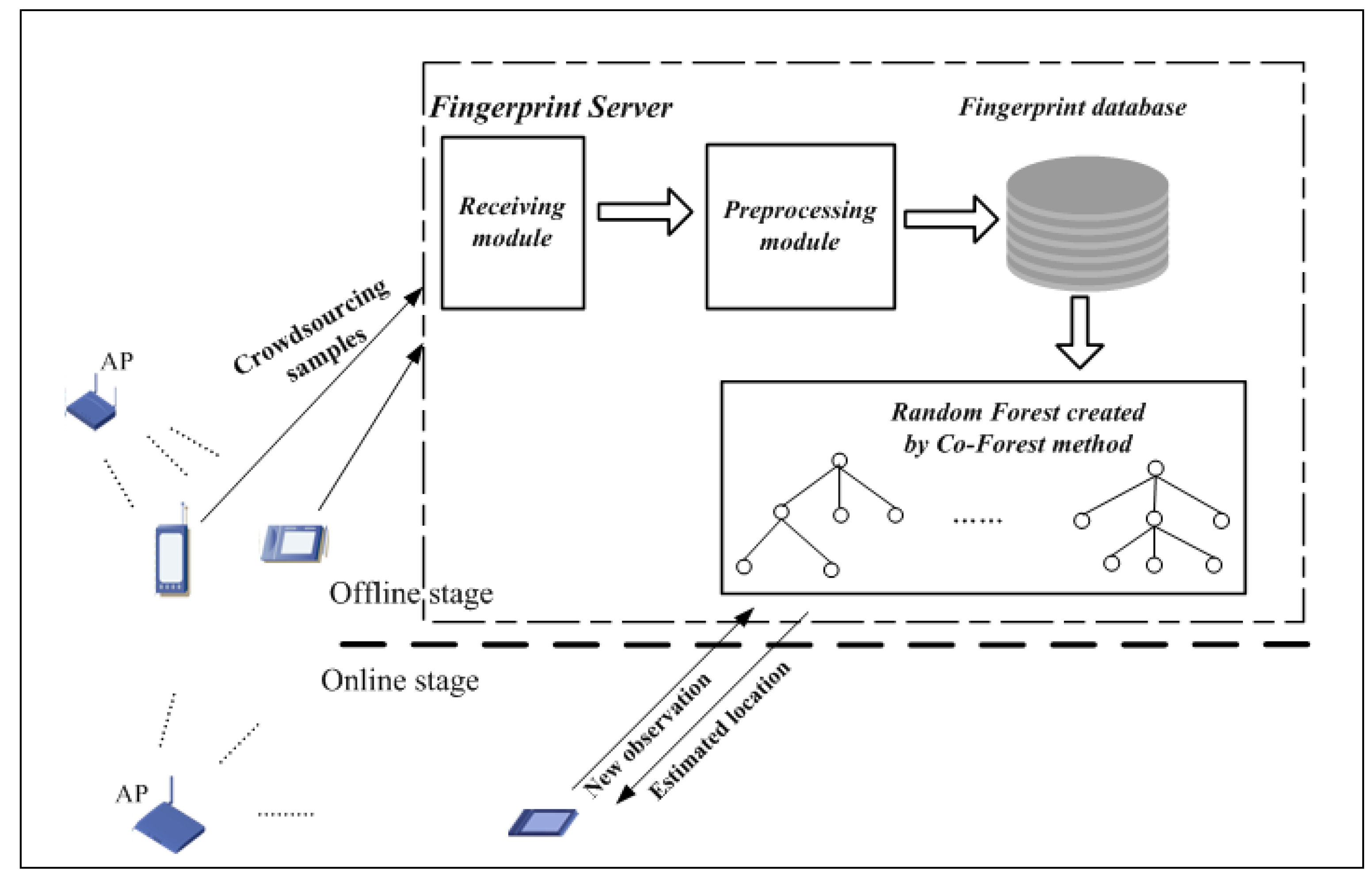
3.1. Components of the Proposed Positioning System
3.2. Preprocessing Method for Crowdsourcing RSS Samples
3.3. Semi-Supervised Learning Method for Indoor Fingerprint Positioning
| Algorithm 1 Co-Forest |
| Input: set of labeled RSS samples set of unlabeled RSS samples count of random trees confidence threshold Output: refined random trees C 1. create the initial Random forest composed of N tree classifiers from ; 2. ; 3. for to do { 4. 5. } 6. while (there are some random trees changing ) do { 7. ; 8. for to do { 9. (); 10. ; 11. if () 12. ; 13. for each unlabeled fingerprint in do { 14. if () 15. =; 16. } 17. } 18. for to do { 19. if () 20. 21. } 22. } 23. return C |
4. Experiments and Analysis
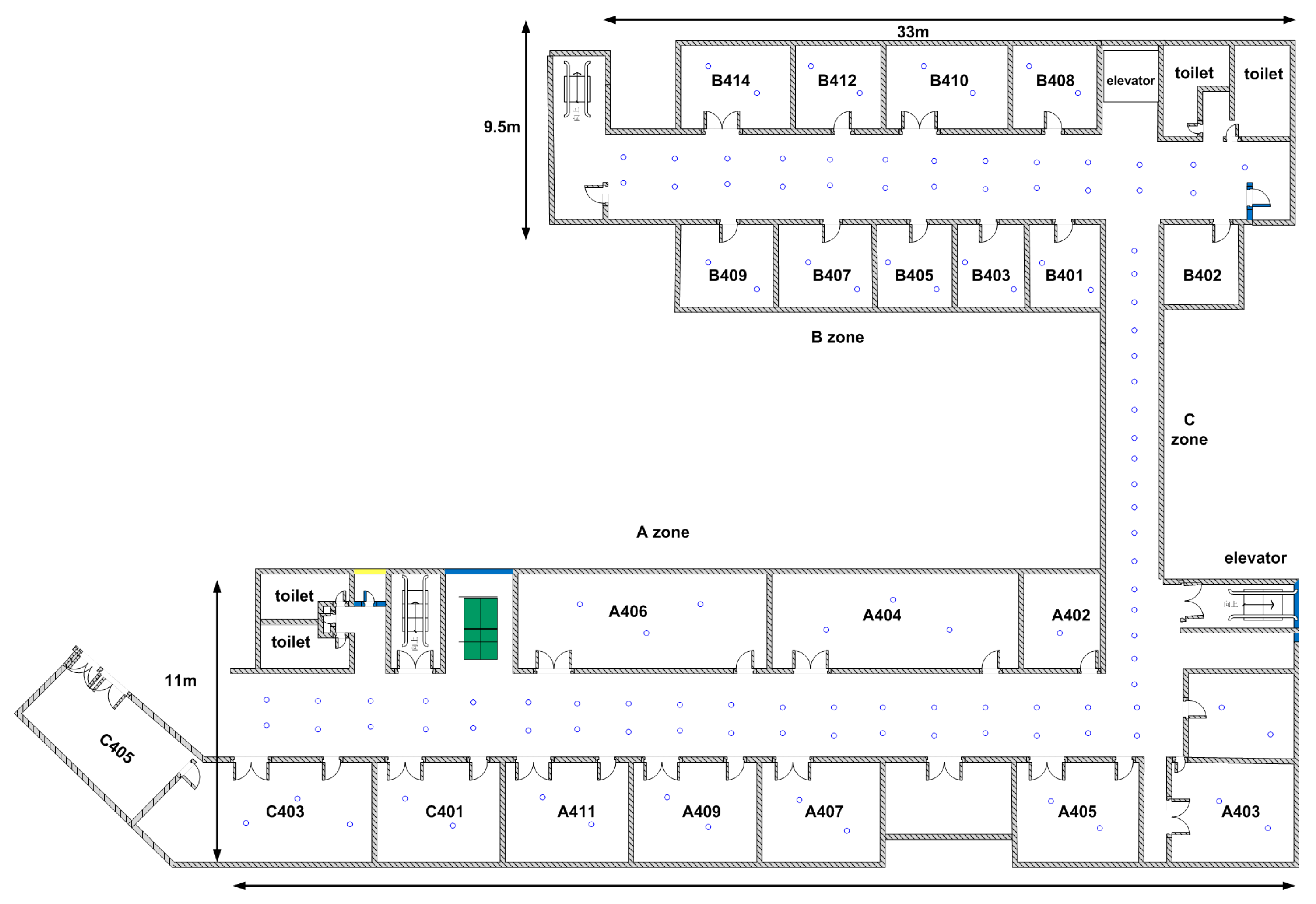
4.1. Experimental Setup
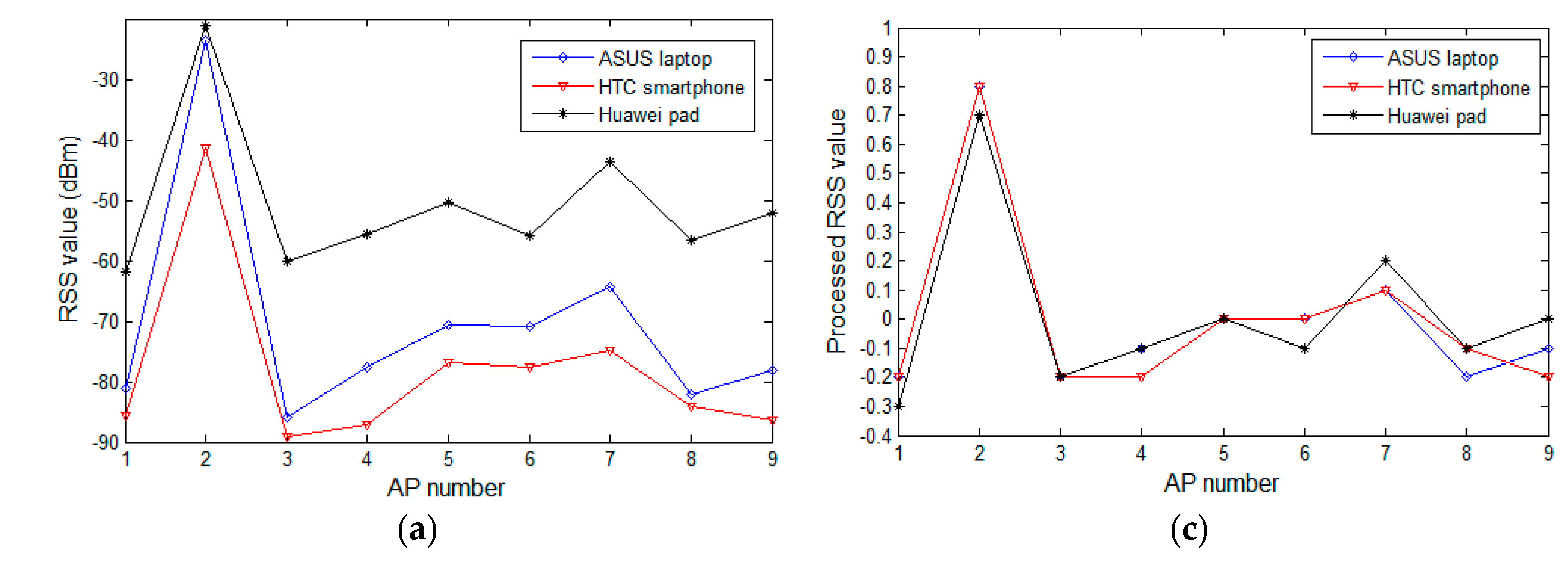
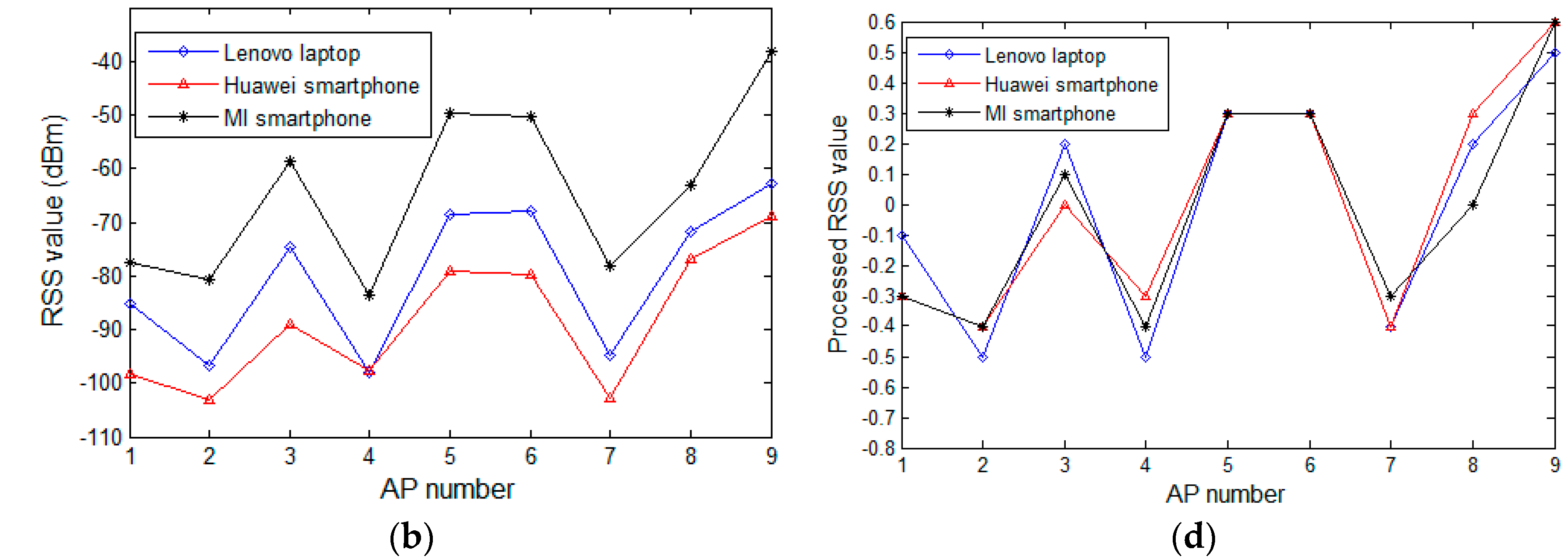
4.2. Experimental Analysis on the Difference in RSS Samples of Heterogeneous Devices and Comparison between Processed and Raw Samples
4.3. Effect of Preprocessing Method on Tackling Device Heterogeneity
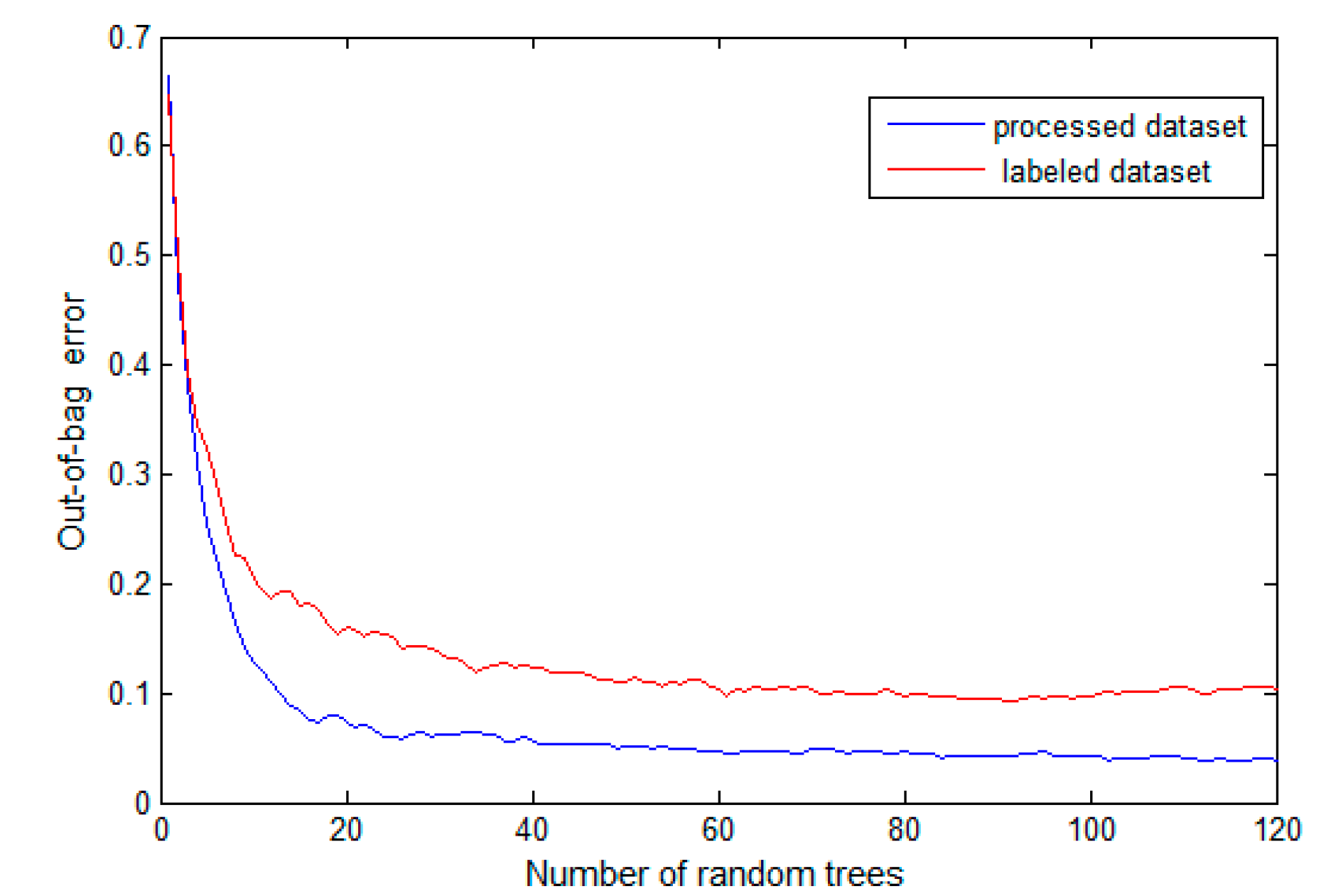
4.4. Selection of the Number of Trees in the Random Forest
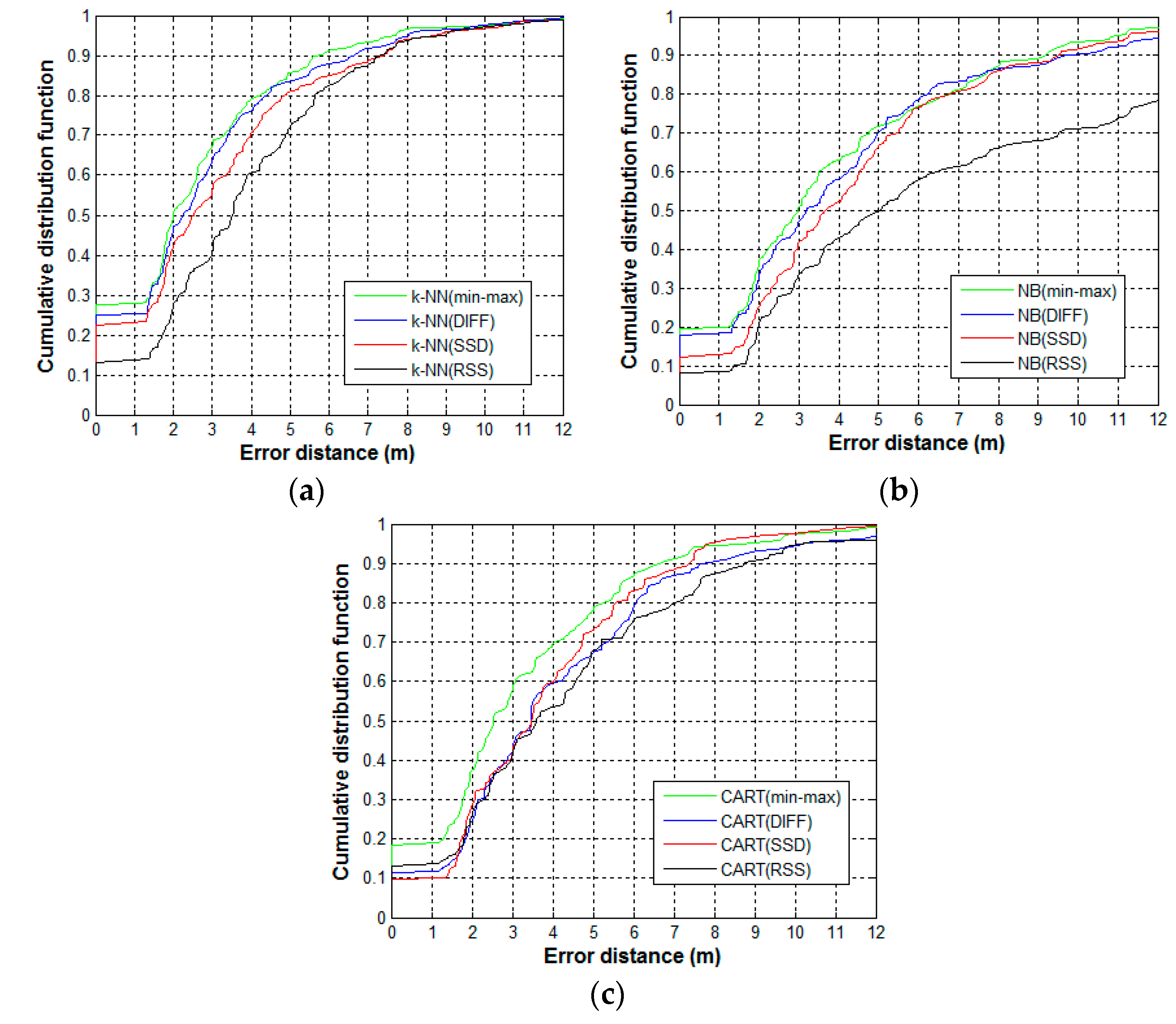
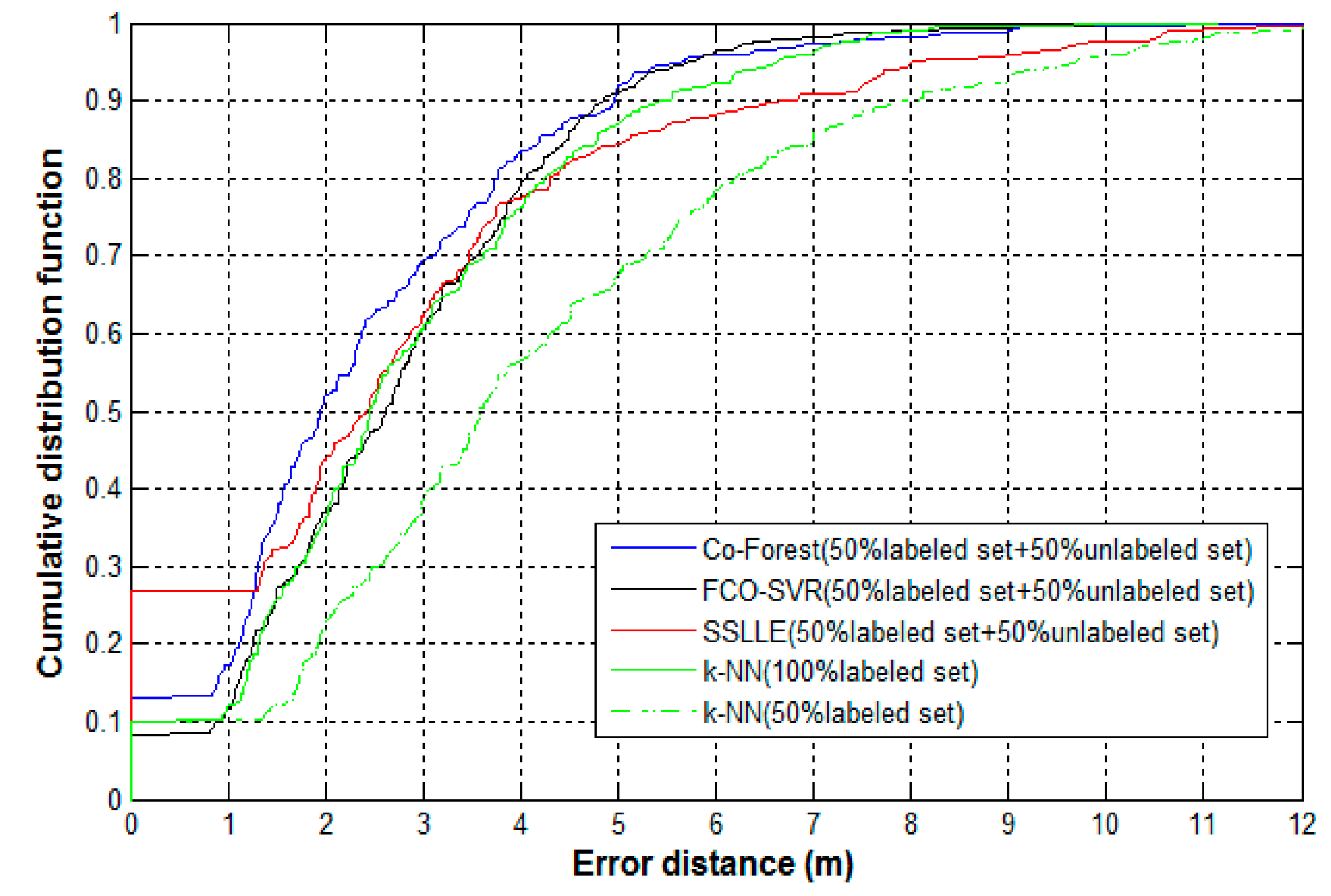
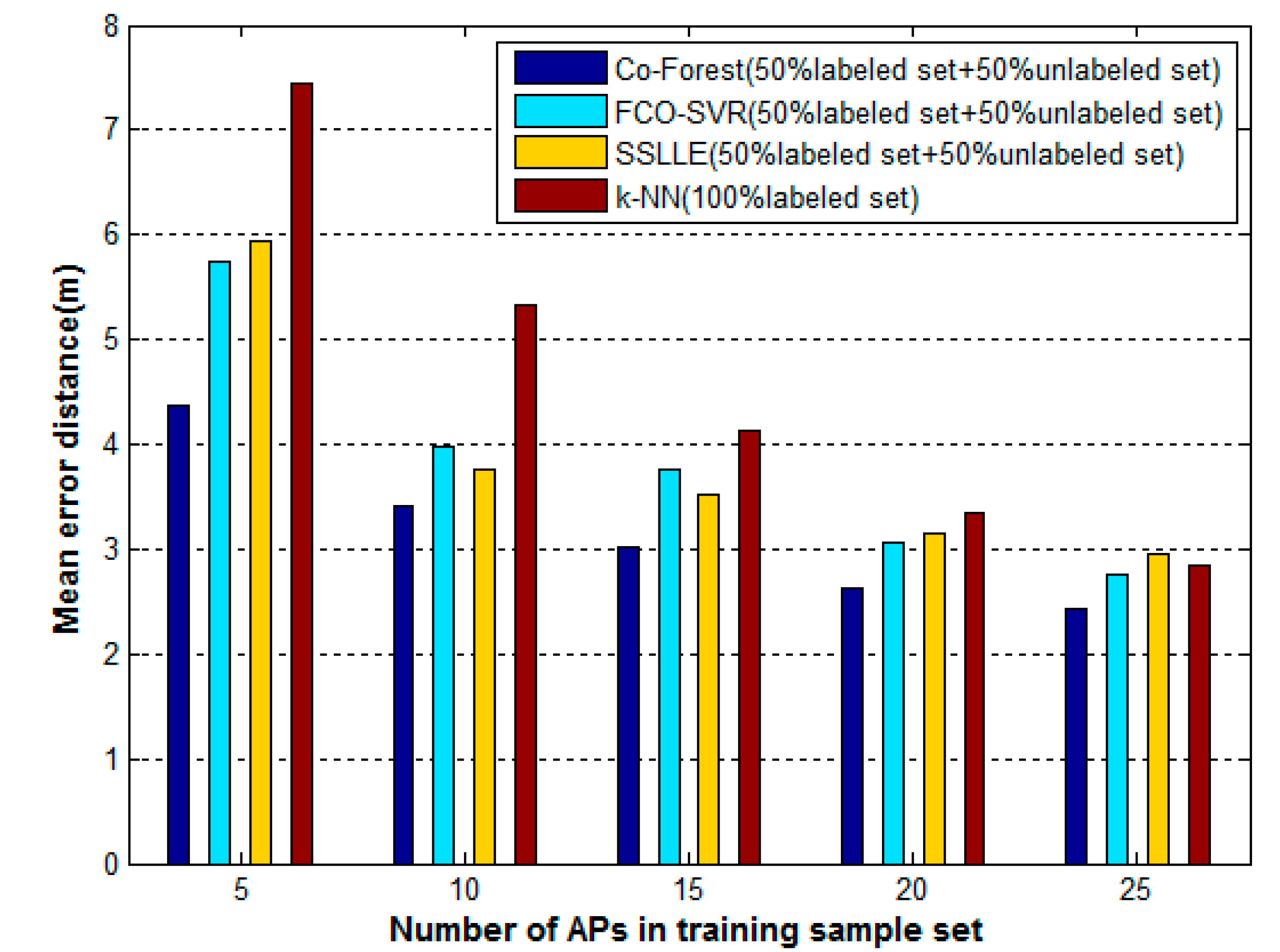
4.5. Positioning Accuracy Comparison of Co-Forest and Classical Algorithms
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hightower, J.; Borriello, G. A survey and taxonomy of location systems for ubiquitous computing. IEEE Comput. 2001, 34, 57–66. [Google Scholar] [CrossRef]
- Liu, H.; Darabi, H.; Banerjee, P.; Liu, J. Survey of wireless indoor positioning techniques and systems. IEEE Trans. Syst. Man Cybern. C 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
- He, S.N.; Chan, S.H.G. Wi-Fi fingerprint-based indoor positioning: Recent advances and comparisons. IEEE Commun. Surv. Tutor. 2016, 18, 466–490. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Liu, C.; Zhang, L.; Li, Z. Integrated WiFi/PDR/smartphone using an adaptive system noise extended Kalman filter algorithm for indoor localization. ISPRS Int. J. Geo-Inf. 2016, 5, 8. [Google Scholar] [CrossRef]
- Xia, S.X.; Liu, Y.; Yuan, G.; Zhu, M.; Wang, Z. Indoor Fingerprint Positioning based on Wi-Fi: An Overview. ISPRS Int. J. Geo-Inf. 2017, 6, 135. [Google Scholar] [CrossRef]
- Hossain, A.K.M.; Soh, W.-S. A survey of calibration-free indoor positioning systems. Comput. Commun. 2015, 66, 1–13. [Google Scholar] [CrossRef]
- Dong, F.; Chen, Y.; Liu, J.; Ning, Q.; Piao, S. A calibration-free localization solution for handling signal strength variance. In Proceedings of the International Conference on Mobile Entity Localization and Tracking in Gps-Less Environments, Orlando, FL, USA, 30 September 2009; pp. 79–90. [Google Scholar]
- Bolliger, P. Redpin-adaptive, zero-configuration indoor localization through user collaboration. In Proceedings of the ACM International Workshop on Mobile Entity Localization and Tracking in Gps-Less Environments, San Francisco, CA, USA, 19 September 2008; pp. 55–60. [Google Scholar]
- Luo, Y.; Hoeber, O.; Chen, Y. Enhancing Wi-Fi fingerprinting for indoor positioning using human-centric collaborative feedback. Hum.-Cen. Comput. Inf. Sci. 2013, 3, 2. [Google Scholar] [CrossRef]
- Hossain, A.K.M.; Van, H.N.; Soh, W.-S. Utilization of user feedback in indoor positioning system. Perv. Mob. Comput. 2010, 6, 467–481. [Google Scholar] [CrossRef]
- Ledlie, J.; Park, J.G.; Curtis, D.; Cavalcante, A. Mole: A scalable, user-generated WiFi positioning engine. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Guimaraes, Portugal, 21–23 September 2011; pp. 1–10. [Google Scholar]
- Park, J.G.; Charrow, B.; Curtis, D.; Battat, J.; Minkov, E.; Hicks, J. Growing an organic indoor location system. In Proceedings of the International Conference on Mobile Systems, Applications, and Services, San Francisco, CA, USA, 15–18 June 2010; pp. 271–284. [Google Scholar]
- Hossain, A.K.M.; Jin, Y.; Soh, W.-S.; Van, H.N. SSD: A robust rf location fingerprint addressing mobile devices’ heterogeneity. IEEE Trans. Mob. Comput. 2013, 12, 65–77. [Google Scholar] [CrossRef]
- Kim, W.; Yang, S.; Gerla, M.; Lee, E.K. Crowdsource based Indoor Localization by Uncalibrated Heterogeneous Wi-Fi devices. Mob. Inf. Syst. 2016, 2016, 1–18. [Google Scholar] [CrossRef]
- Machaj, J.; Brida, P.; Piché, R. Rank based fingerprinting algorithm for indoor positioning. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Guimaraes, Portugal, 21–23 September 2011; pp. 1–6. [Google Scholar]
- Rai, A.; Chintalapudi, K.K.; Padmanabhan, V.N.; Sen, R. Zee: Zero-effort crowdsourcing for indoor localization. In Proceedings of the MobiCom’12, Istanbul, Turkey, 22–26 August 2012; pp. 293–304. [Google Scholar]
- Wu, C.; Yang, Z.; Liu, Y.; Xi, W. WILL: Wireless indoor localization without site survey. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 839–848. [Google Scholar]
- Wang, H.; Sen, S.; Mariakakis, A.; Youssef, M. Demo: Unsupervised indoor localization. In Proceedings of the International Conference on Mobile Systems, Applications, and Services, Lake District, UK, 26–29 June 2012; pp. 499–500. [Google Scholar]
- Jain, V.K.; Tapaswi, S.; Shukla, A. Location estimation based on semi-supervised locally linear embedding (sslle) approach for indoor wireless networks. Wirel. Pers. Commun. 2012, 67, 879–893. [Google Scholar] [CrossRef]
- Xia, Y.; Ma, L.; Zhang, Z.Z.; Zhou, C.F. Wlan Indoor Positioning Algorithm based on Semi-supervised Manifold Learning. J. Syst. Eng. Electron. 2014, 36, 1423–1427. [Google Scholar]
- Zhang, Y.; Zhi, X.L. Indoor Positioning Algorithm Based on Semi-supervised Learning. Comput. Eng. 2010, 36, 277–279. [Google Scholar]
- Xia, M. Semi-Supervised Learing Based Indoor WLAN Positioning. Ph.D. Thesis, Chongqing University of Posts and Telecommunications, Chongqing, China, 2016. [Google Scholar]
- Goswami, A.; Ortiz, L.E.; Das, S.R. Wigem: A learning-based approach for indoor localization. In Proceedings of the 7th International Conference on Emerging Networking Experiments and Technologies (CoNEXT), Tokyo, Japan, 6–9 December 2011; pp. 1–12. [Google Scholar]
- Laoudias, C.; Zeinalipour-Yazti, D.; Panayiotou, C.G. Crowdsourced indoor localization for diverse devices through radiomap fusion. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Montbeliard-Belfort, France, 28–31 October 2013; pp. 1–7. [Google Scholar]
- Cho, Y.; Ji, M.; Lee, Y.; Park, S. WiFi AP position estimation using contribution from heterogeneous mobile devices. In Proceedings of the IEEE/ION Position Location and Navigation Symposium (PLANS), Myrtle Beach, SC, USA, 24–26 April 2012; pp. 562–567. [Google Scholar] [CrossRef]
- Jain, Y.K.; Bhandare, S.K. Min Max Normalization Based Data Perturbation Method for Privacy Protection. Int. J. Comput. Commun. Technol. 2011, 2, 45–50. [Google Scholar]
- Gajera, V.; Shubham; Gupta, R.; Jana, P.K. An effective Multi-Objective task scheduling algorithm using Min-Max normalization in cloud computing. In Proceedings of the International Conference on Applied and Theoretical Computing and Communication Technology, Bengaluru, India, 21–23 July 2016; pp. 812–816. [Google Scholar]
- Song, C.J.; Wang, J.; Yuan, G. Hidden naive bayes indoor fingerprinting localization based on best-discriminating ap selection. ISPRS Int. J. Geo-Inf. 2016, 5, 189. [Google Scholar] [CrossRef]
- Li, M.; Zhou, Z.H. Improve Computer-Aided Diagnosis with Machine Learning Techniques Using Undiagnosed Samples. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2007, 37, 1088–1098. [Google Scholar] [CrossRef]
- Blum, A.; Mitchell, T. Combining labeled and unlabeled data with co-training. In Proceedings of the Eleventh Conference on Computational Learning Theory, Madison, WI, USA, 24–26 July 1998; pp. 92–100. [Google Scholar]
- Jedari, E.; Wu, Z.; Rashidzadeh, R.; Saif, M. Wi-Fi based indoor location positioning employing random forest classifier. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Banff, AB, Canada, 13–16 October 2015; pp. 1–5. [Google Scholar]
- Górak, R.; Luckner, M. Modified Random Forest Algorithm for Wi–Fi Indoor Localization System. In Proceedings of the First International Conference on Computer Communication and the Internet, Wuhan, China, 13–15 October 2016; pp. 147–157. [Google Scholar]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How many trees in a random forest? Lect. Notes Comput. Sci. 2012, 7376, 154–168. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
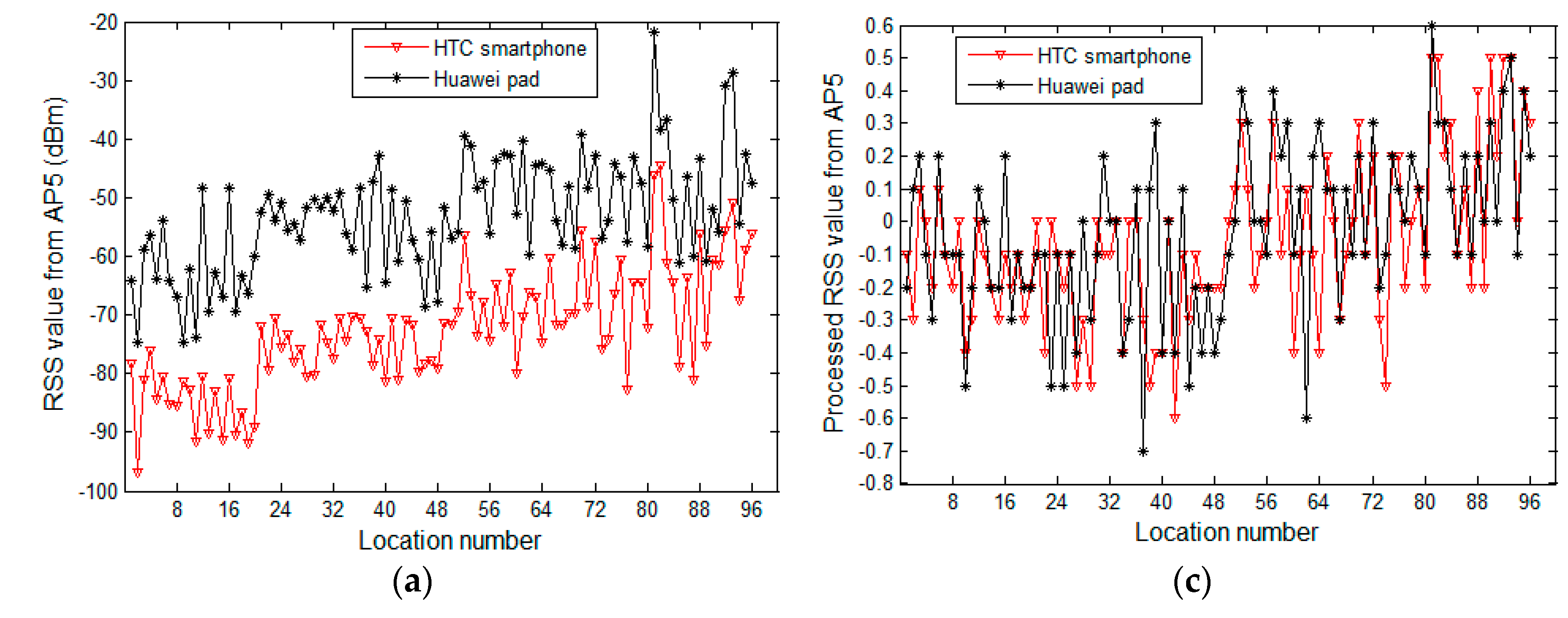
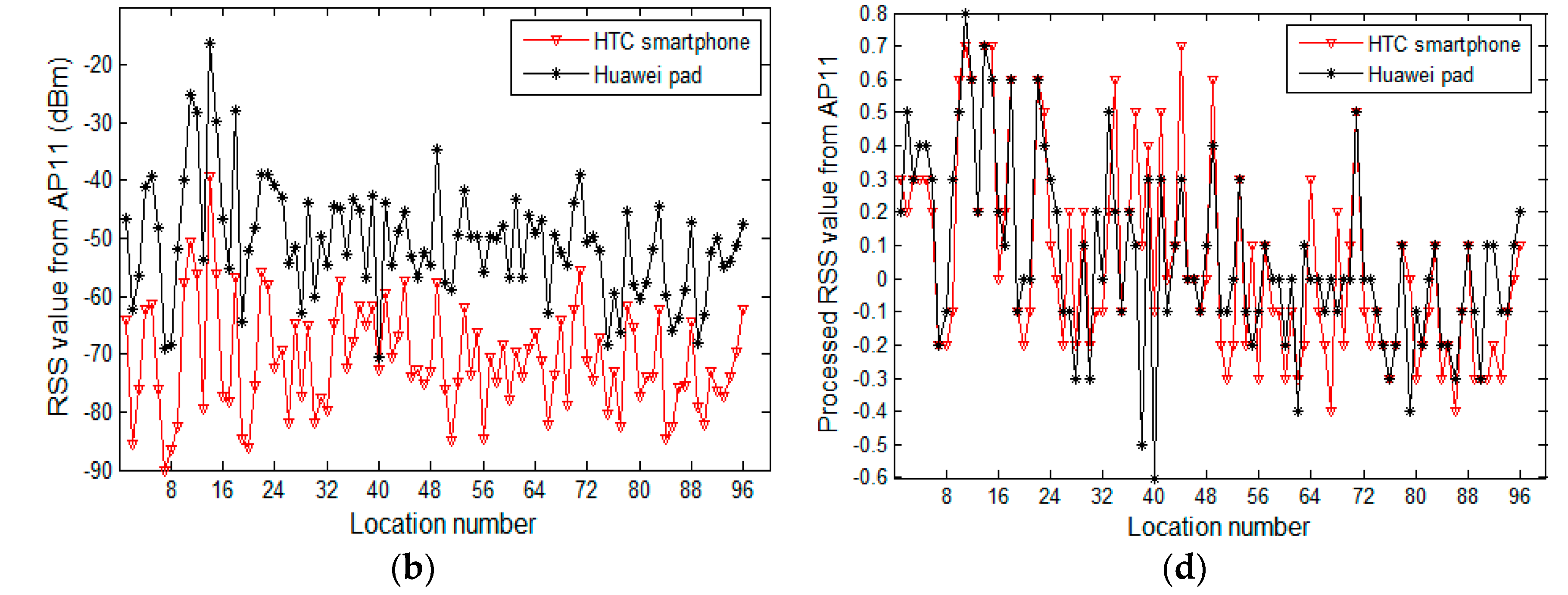
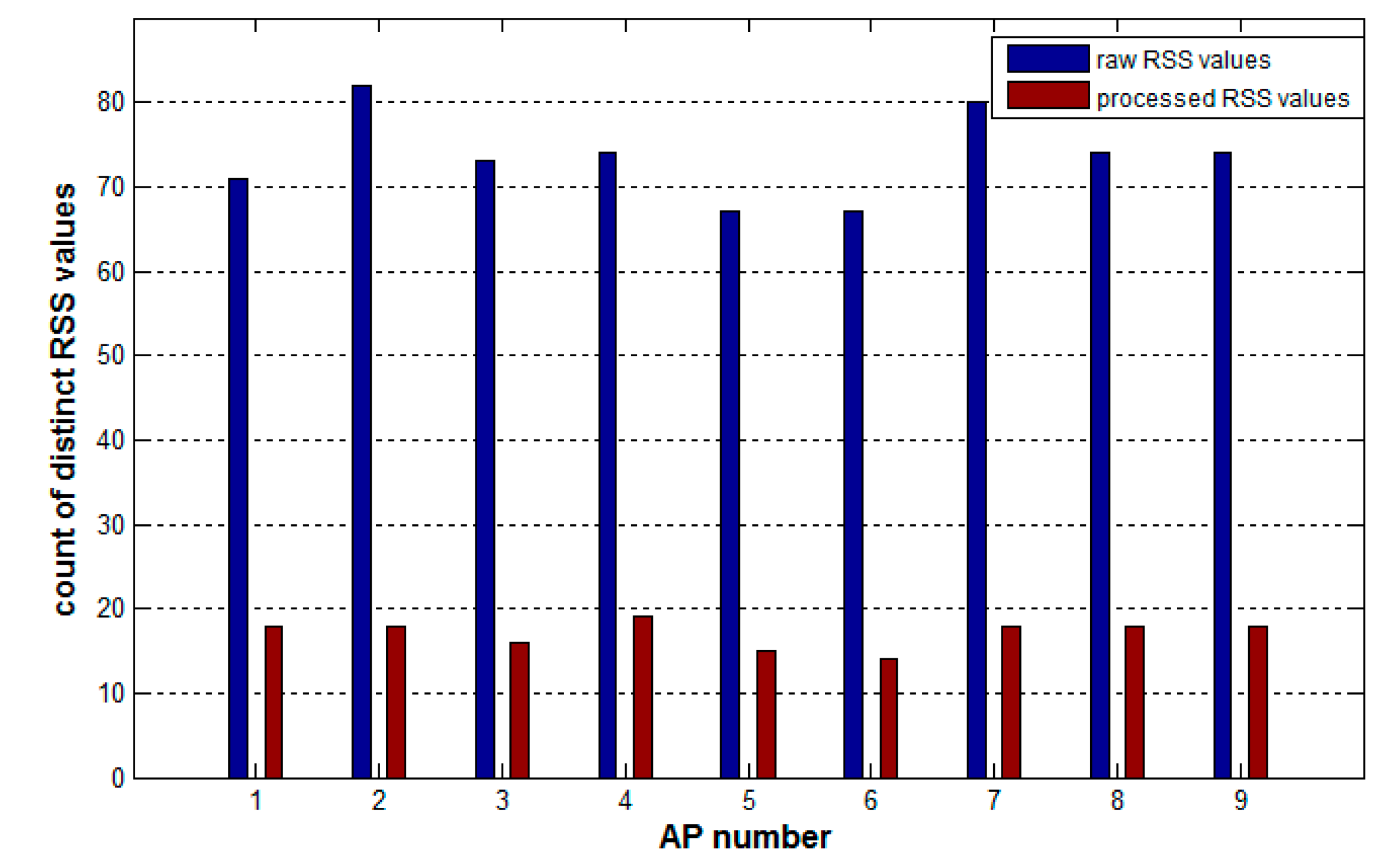
| Device | AP1 | AP2 | AP3 | AP4 | AP5 | AP6 |
|---|---|---|---|---|---|---|
| Device 1 | −85 | −42 | −89 | −77 | −76 | −89 |
| Device 2 | −81 | −35 | −76 | −70 | −77 | −85 |
| Device 3 | −83 | −40 | −85 | −84 | −72 | −90 |
| Device 4 | −67 | −18 | −64 | −61 | −53 | −67 |
| Device 5 | −79 | −35 | −87 | −72 | −73 | −81 |
| Device | AP1 | AP2 | AP3 | AP4 | AP5 | AP6 |
|---|---|---|---|---|---|---|
| Device 1 | −0.1 | 0.7 | −0.2 | 0.1 | 0.1 | −0.2 |
| Device 2 | −0.2 | 0.8 | −0.1 | 0.1 | −0.1 | −0.2 |
| Device 3 | −0.1 | 0.8 | −0.1 | −0.1 | 0.2 | −0.2 |
| Device 4 | −0.2 | 0.8 | −0.1 | −0.1 | 0.1 | −0.2 |
| Device 5 | −0.1 | 0.7 | −0.2 | 0.0 | 0.0 | −0.1 |
| AP1 | AP2 | AP3 | AP4 | AP5 | AP6 | AP7 | AP8 | AP9 | |
|---|---|---|---|---|---|---|---|---|---|
| Amount of Computation Saved | 64% | 78% | 69% | 67% | 63% | 64% | 75% | 68% | 68% |
| Algorithms | Mean Error (m) | Maximum Error (m) | Minimum Error (m) | Median Error (m) |
|---|---|---|---|---|
| k-NN (50% Labeled Set) | 4.05 | 11.95 | 0 | 3.59 |
| k-NN (100% Labeled Set) | 2.84 | 8.14 | 0 | 2.45 |
| SSLLE | 2.95 | 11.77 | 0 | 2.42 |
| FCO-SVR | 2.75 | 8.52 | 0.36 | 2.63 |
| Co-Forest | 2.42 | 8.03 | 0 | 1.95 |
| Algorithms | Mean Error (m) |
|---|---|
| k-NN (100% Labeled Set) | 5.31 |
| SSLLE | 5.69 |
| FCO-SVR | 4.51 |
| Co-Forest | 3.65 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, C.; Wang, J. WLAN Fingerprint Indoor Positioning Strategy Based on Implicit Crowdsourcing and Semi-Supervised Learning. ISPRS Int. J. Geo-Inf. 2017, 6, 356. https://doi.org/10.3390/ijgi6110356
Song C, Wang J. WLAN Fingerprint Indoor Positioning Strategy Based on Implicit Crowdsourcing and Semi-Supervised Learning. ISPRS International Journal of Geo-Information. 2017; 6(11):356. https://doi.org/10.3390/ijgi6110356
Chicago/Turabian StyleSong, Chunjing, and Jian Wang. 2017. "WLAN Fingerprint Indoor Positioning Strategy Based on Implicit Crowdsourcing and Semi-Supervised Learning" ISPRS International Journal of Geo-Information 6, no. 11: 356. https://doi.org/10.3390/ijgi6110356
APA StyleSong, C., & Wang, J. (2017). WLAN Fingerprint Indoor Positioning Strategy Based on Implicit Crowdsourcing and Semi-Supervised Learning. ISPRS International Journal of Geo-Information, 6(11), 356. https://doi.org/10.3390/ijgi6110356





