GIS-Based Evaluation of Spatial Interactions by Geographic Disproportionality of Industrial Diversity
Abstract
1. Introduction
2. Factors of Spatial Interactions
3. Materials and Methods
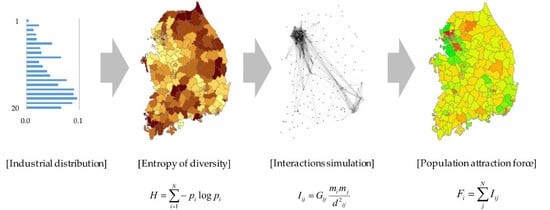
3.1. Fundamental Concepts
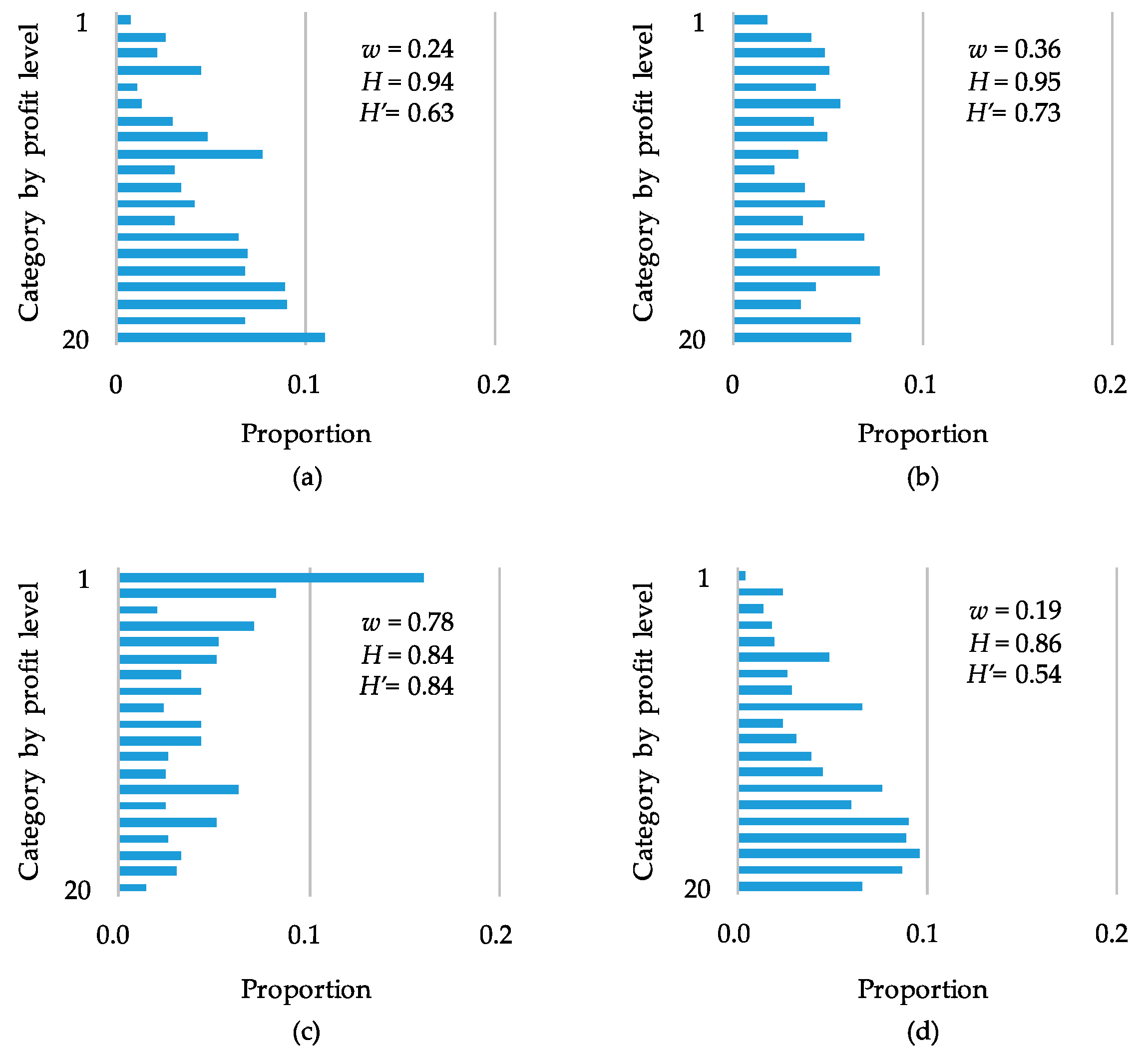
3.1.1. Industrial Diversity and Entropy
3.1.2. Evaluation of Spatial Interactions
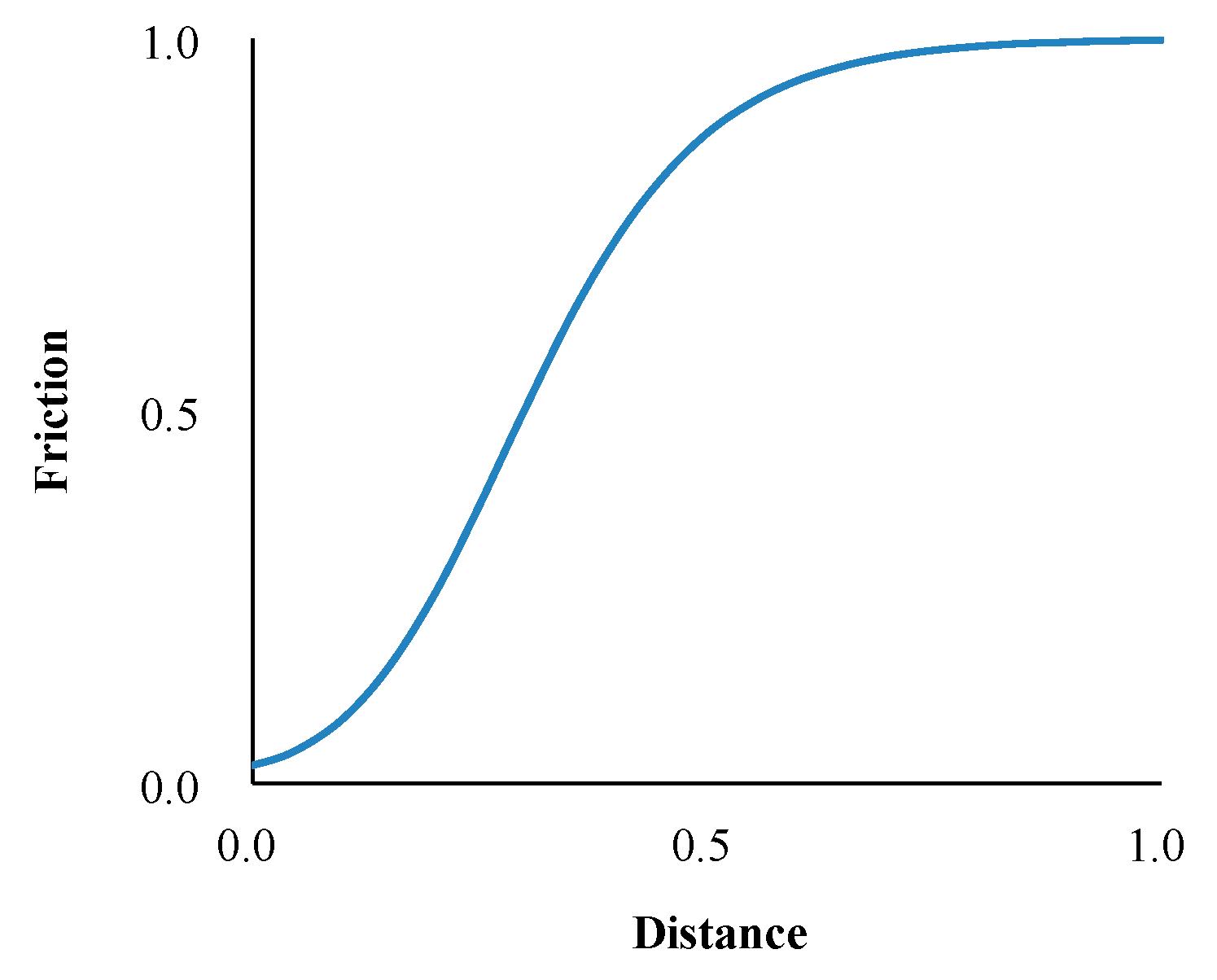
3.1.3. Virtual Interaction and Attraction Force
3.2. Data
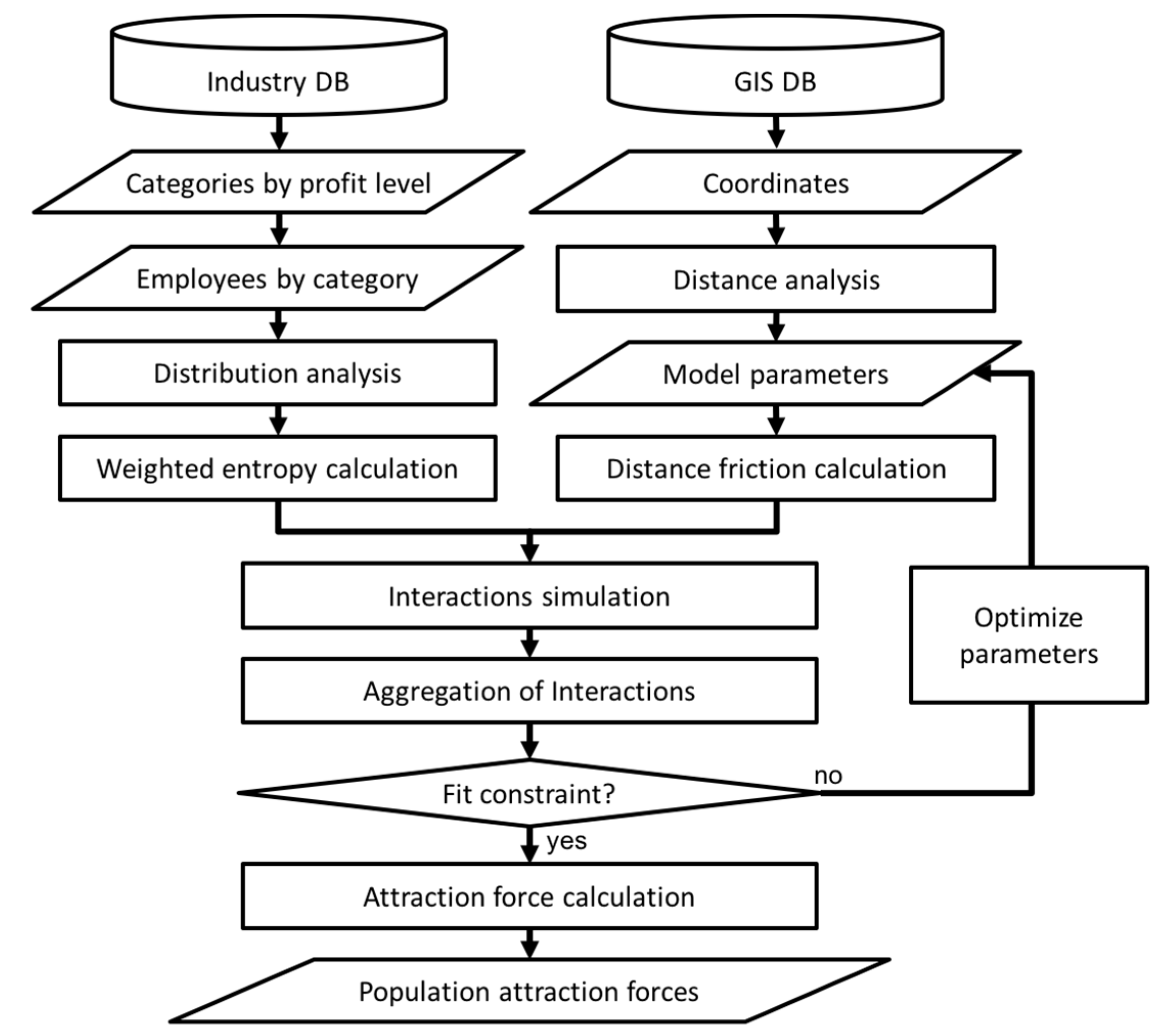
3.3. Methods
- Step 1: Analyzing the data;
- Step 2: Calculating the entropy of industrial diversity;
- Step 3: Simulating the spatial interactions;
- Step 4: Optimizing the parameters in the model; and
- Step 5: Evaluating the attraction force.
4. Results and Discussion
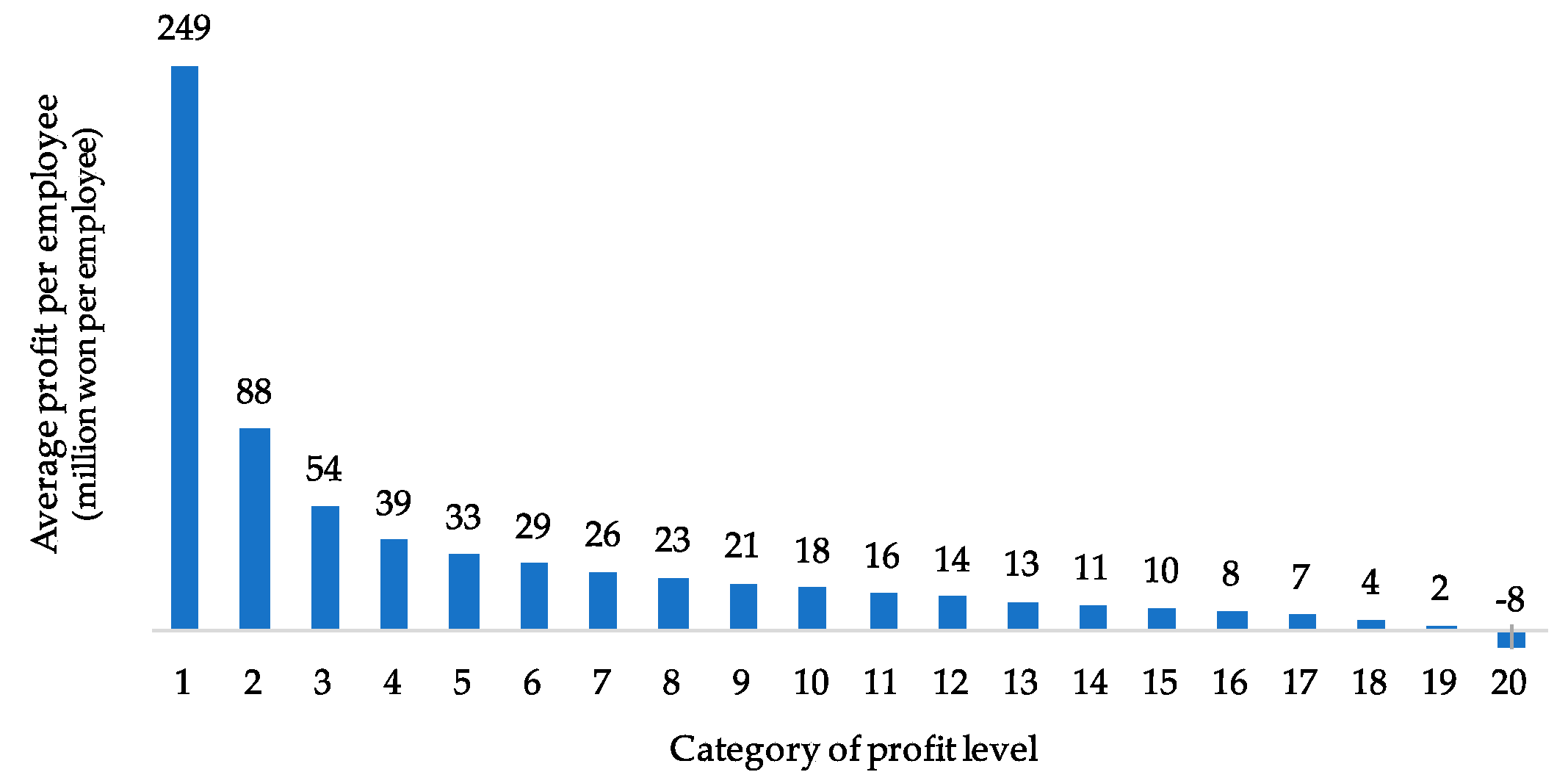
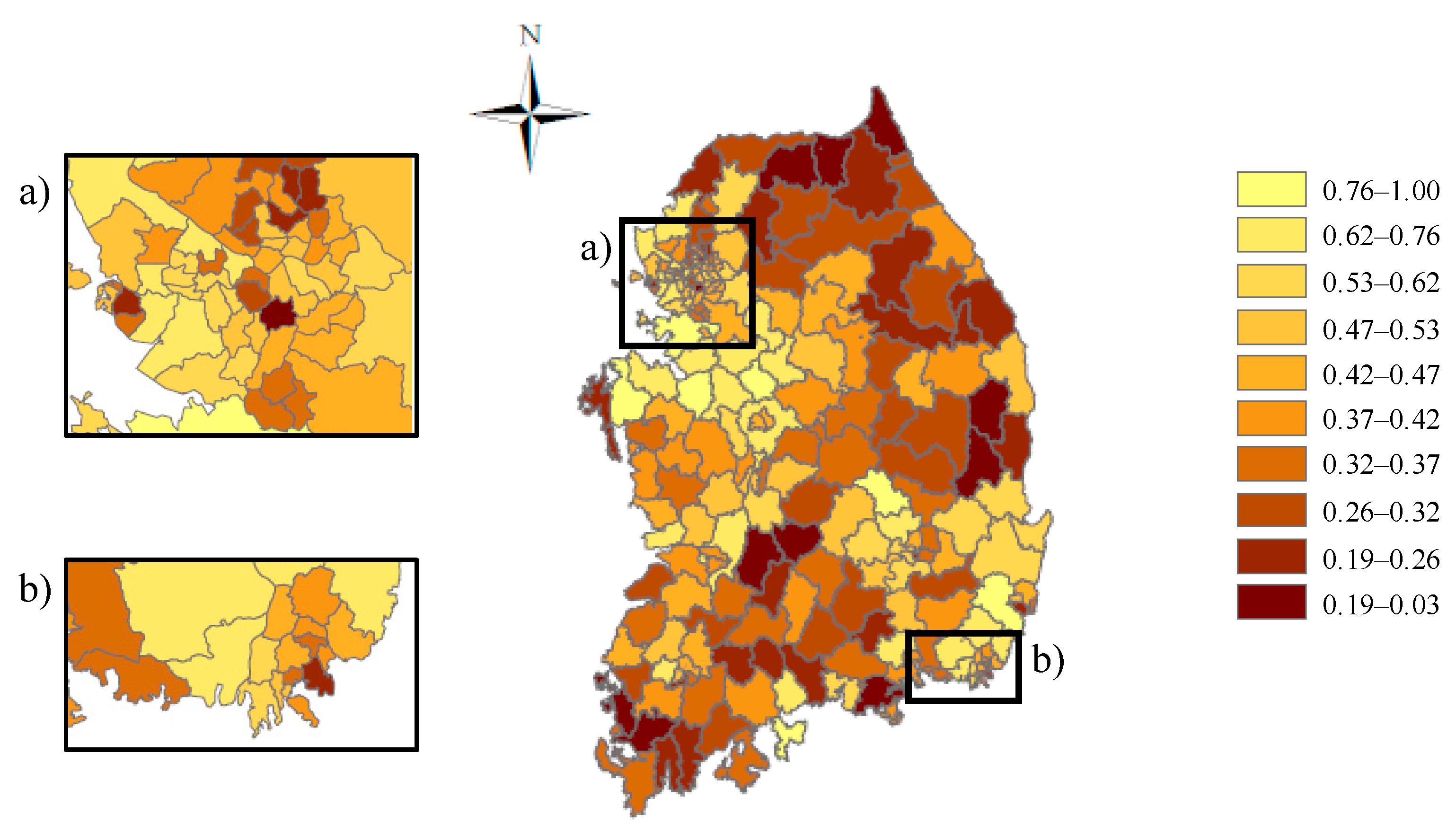
4.1. Industrial Distribution and Weighted Entropy
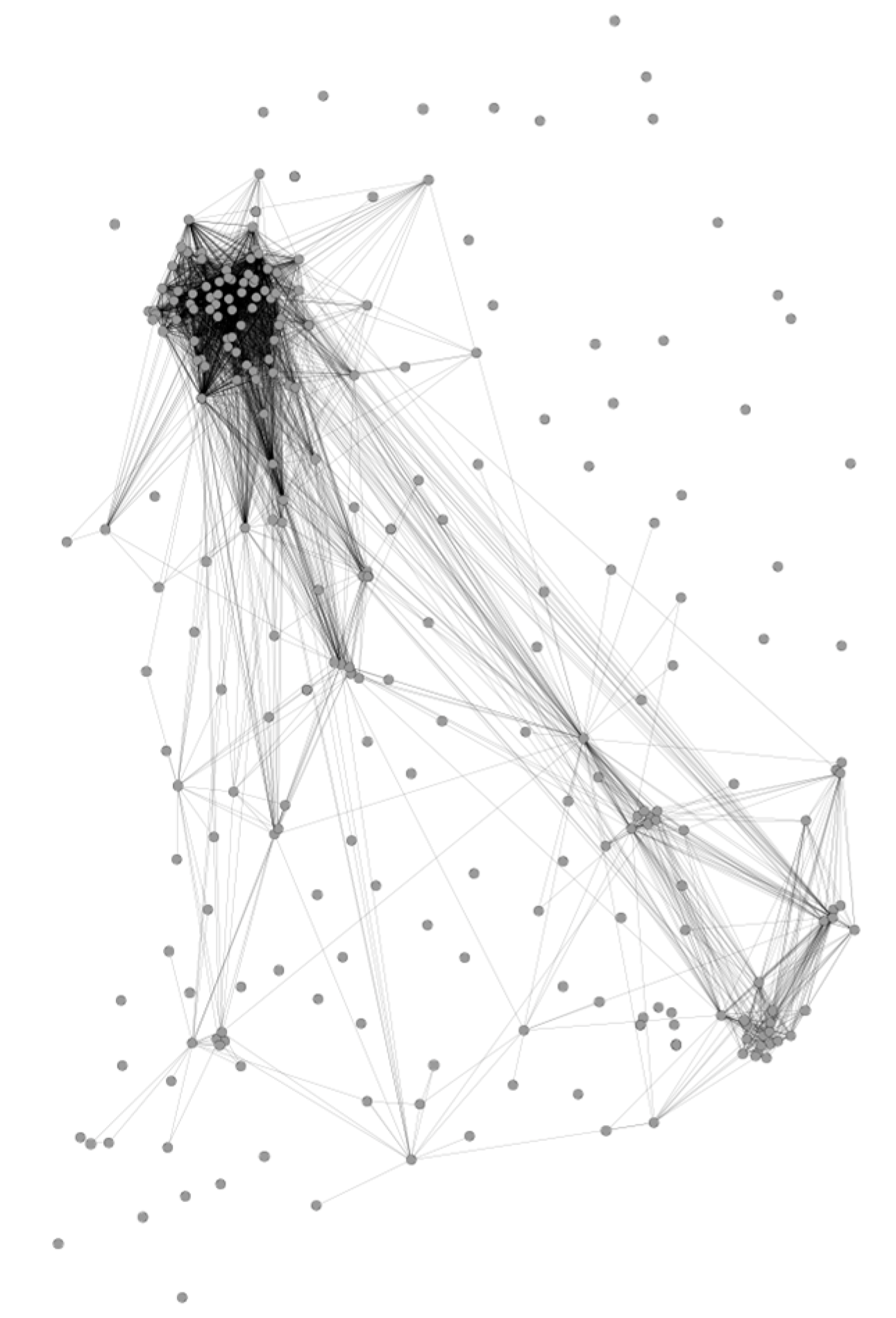
4.2. Spatial Interactions and Attraction Forces
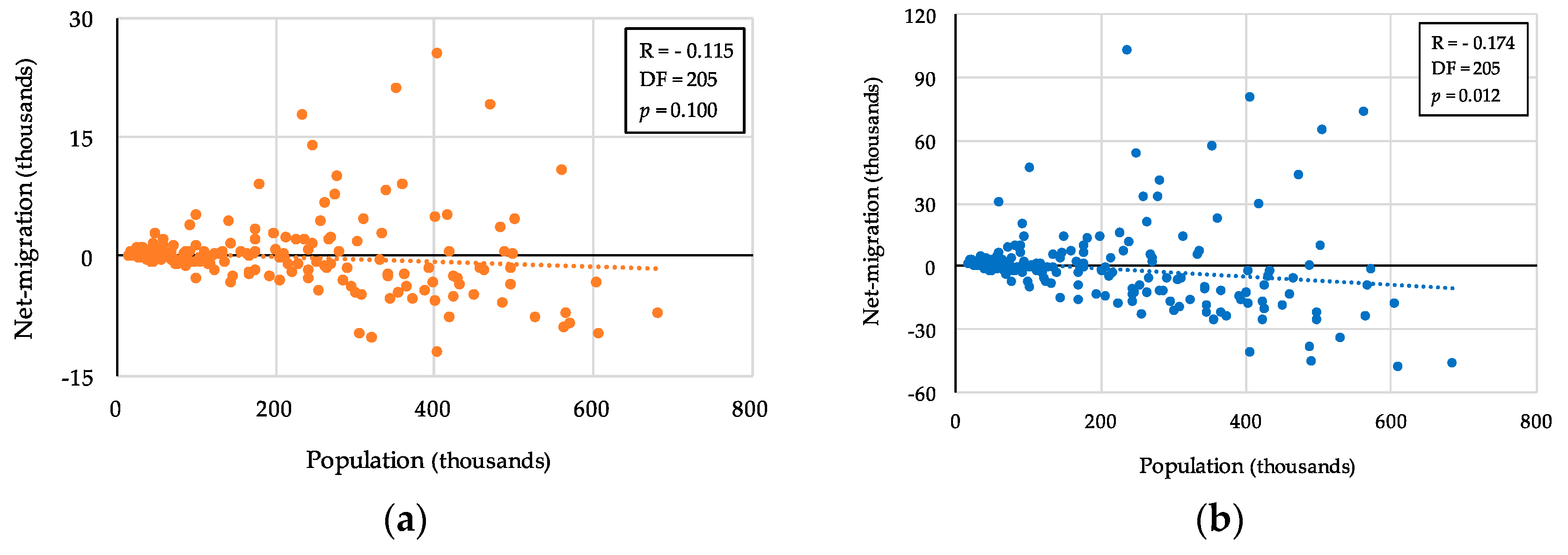
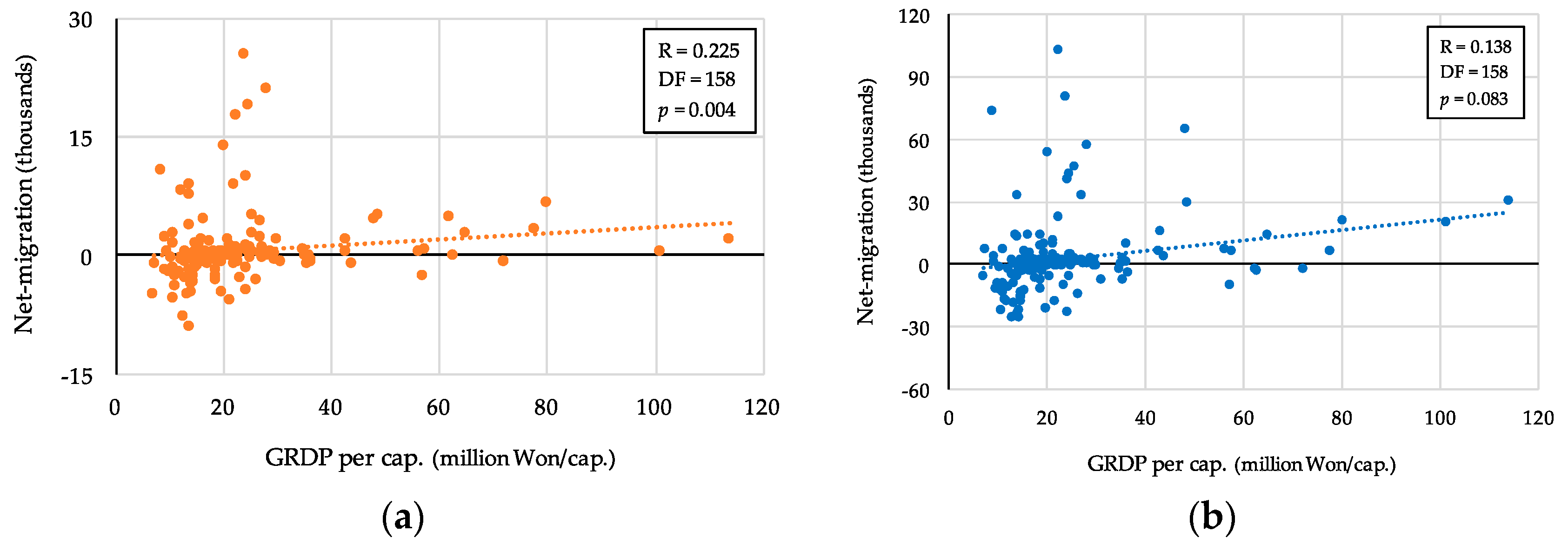
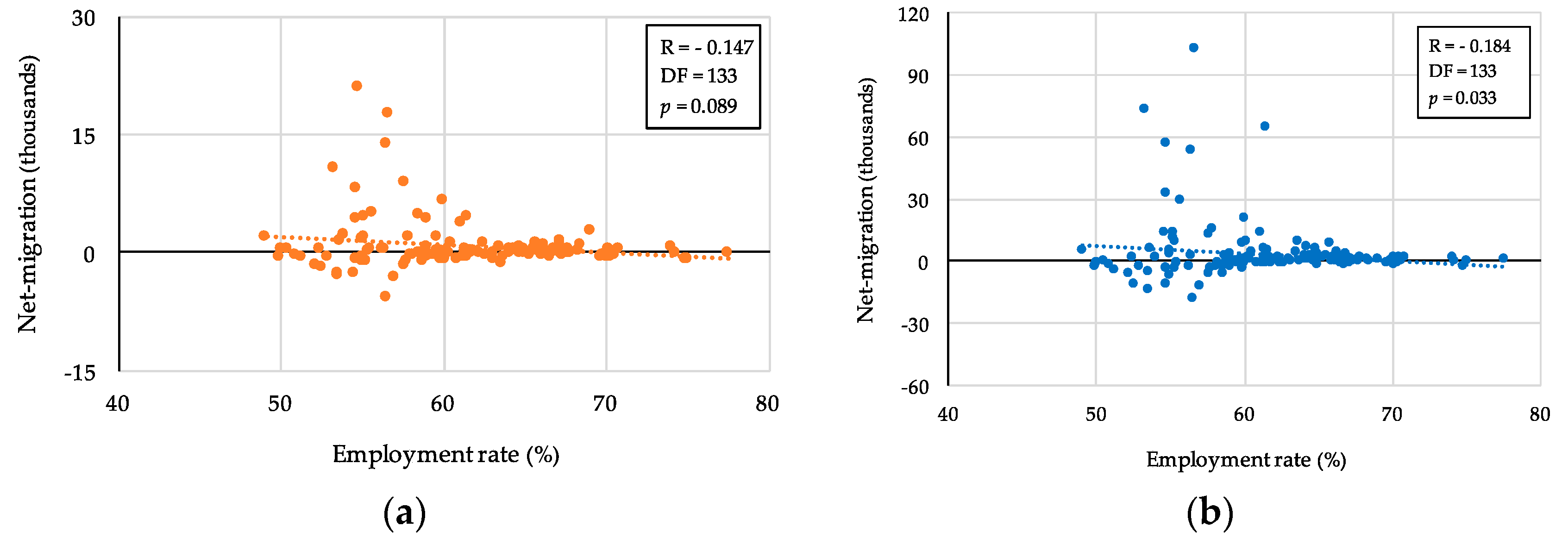
4.3. Evaluated Forces and Observed Migration
5. Conclusions
Supplementary Materials
Author Contributions
Conflicts of Interest
Appendix A

References
- David, W.E. Japan’s Shrinking Regions in the 21st Century: Contemporary Responses to Depopulation and Socioeconomic Decline. Reg. Stud. 2012, 46, 1275–1276. [Google Scholar] [CrossRef]
- Wegren, S.K. The Quest for Rural Sustainability in Russia. Sustainability 2016, 8, 602. [Google Scholar] [CrossRef]
- Farrell, K. The Rapid Urban Growth Triad: A New Conceptual Framework for Examining the Urban Transition in Developing Countries. Sustainability 2017, 9, 1407. [Google Scholar] [CrossRef]
- Li, Y.; López-Carr, D.; Chen, W. Factors Affecting Migration Intentions in Ecological Restoration Areas and Their Implications for the Sustainability of Ecological Migration Policy in Arid Northwest China. Sustainability 2014, 6, 8639–8660. [Google Scholar] [CrossRef]
- Mao, Y.; Liu, Y.; Wang, H.; Tang, W.; Kong, X. A Spatial-Territorial Reorganization Model of Rural Settlements Based on Graph Theory and Genetic Optimization. Sustainability 2017, 9, 1370. [Google Scholar] [CrossRef]
- Feser, E.; Sweeney, S. Out-migration, depopulation, and the geography of US economic distress. Int. Reg. Sci. Rev. 2003, 26, 38–67. [Google Scholar] [CrossRef]
- Puga, D. European regional policies in light of recent location theories. J. Econ. Geogr. 2002, 2, 373–406. [Google Scholar] [CrossRef]
- Bunting, T.; Filion, P. Uneven cities: Addressing rising inequality in the twenty-first century. Can. Geogr. 2001, 45, 126–131. [Google Scholar] [CrossRef]
- Commins, P. Socio-economic adjustments to rural depopulation. Reg. Stud. 1978, 12, 79–94. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.K. The Potential Possibility and Practical Policy Implements for Attracting Enterprises in Rural Areas. J. Agric. Ext. Community Dev. 2013, 20, 173–203. (In Korean) [Google Scholar] [CrossRef]
- Park, S.H.; Jung, Y.H.; Park, G.H. Shrinking population in cities and urban planning for policy action. KRIHS Policy Brief 2013, 422, 1–6. (In Korean) [Google Scholar]
- Keeble, D. Spatial Policy in Britain: Regional or Urban? Area 1977, 9, 3–8. [Google Scholar]
- Biswas, T.; McHardy, J.; Nolan, M.A. Inter-Regional Migration: The UK Experience; Department of Economics, University of Sheffield: Sheffield, UK, 2009; pp. 3–11. ISSN 1749-8368. [Google Scholar]
- Lehmer, F.; Ludsteck, J. The returns to job mobility and inter-regional migration: Evidence from Germany. Pap. Reg. Sci. 2011, 90, 549–571. [Google Scholar] [CrossRef]
- Simini, F.; González, M.C.; Maritan, A.; Barabási, A.L. A universal model for mobility and migration patterns. Nature 2012, 484, 96–100. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, C.B.; Moffitt, U. Migration, Sustainable Development and the Role of Business. UN Chron. 2013, 50, 22–25. [Google Scholar] [CrossRef]
- United Nations Conference on Sustainable Development (UNCSD). Migration and Sustainable Development. Rio+20 Issues Briefs 2012, 15, 1–7. [Google Scholar]
- Attaran, M. Industrial diversity and economic performance in U.S. areas. Ann. Reg. Sci. 1986, 20, 44–54. [Google Scholar] [CrossRef]
- Malizia, E.E.; Ke, S. The Influence of Economic Diversity on Unemployment and Stability. J. Reg. Sci. 1993, 33, 221–235. [Google Scholar] [CrossRef]
- Clarke, J.I. Population and Development Projects in Africa, 1st ed.; Cambridge University Press: Cambridge, UK, 2009; pp. 41–52. ISBN 978-0-521-12561-1. [Google Scholar]
- Yang, C.; Han, H.; Song, J. Spatial Distribution of Migration and Economic Development: A Case Study of Sichuan Province, China. Sustainability 2014, 6, 6509–6528. [Google Scholar] [CrossRef]
- Tan, R.; Zhou, K.; He, Q.; Xu, H. Analyzing the Effects of Spatial Interaction among City Clusters on Urban Growth—Case of Wuhan Urban Agglomeration. Sustainability 2016, 8, 759. [Google Scholar] [CrossRef]
- Rodrigue, J.P.; Comtois, C.; Slack, B. Transportation and Geography. In The Geography of Transport Systems, 3rd ed.; Routledge: New York, NY, USA, 2013; pp. 1–41. ISBN 978-0-415-48324-7. [Google Scholar]
- Haynes, K.E.; Fotheringham, A.S. Gravity and Spatial Interaction Models; Sage Publications: Beverly Hills, CA, USA, 1984; pp. 5–28. ISBN 978-0803923263. [Google Scholar]
- Reilly, W.J. The Law of Retail Gravity; William J. Reilly: New York, NY, USA, 1931; pp. 3–34. [Google Scholar]
- Alonso, W. A Theory of Movements. In Human Settlement Systems: International Perspectives on Structure, Change and Public Policy; Hansen, N.M., Ed.; Ballinger: Cambridge, MA, USA, 1978; pp. 197–211. ISBN 978-0884101765. [Google Scholar]
- Sen, A.; Smith, T.E. Gravity Models of Spatial Interaction Behavior; Springer: Berlin/Heidelberg, Germany, 1995; pp. 15–152. ISBN 978-3-642-79882-5. [Google Scholar]
- Westerlund, J.; Wilhelmsson, F. Estimating the gravity model without gravity using panel data. Appl. Econ. 2011, 43, 641–649. [Google Scholar] [CrossRef]
- De Vries, J.; Nijkamp, P.; Rietveld, P. Alonso’s Theory of Movements: Developments in Spatial Interaction Modeling. J. Geogr. Syst. 2001, 3, 233–256. [Google Scholar] [CrossRef]
- Griffith, D.A.; Fischer, M.M. Constrained variants of the gravity model and spatial dependence: Model specification and estimation issues. J. Geogr. Syst. 2013, 15, 291–317. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Attaran, M.; Zwick, M. Entropy and Other Measures of Industrial Diversification. Q. J. Bus. Econ. 1987, 26, 17–34. [Google Scholar]
- Fotheringham, A.S.; Webber, M.J. Spatial structure and the parameters of spatial interaction models. Geogr. Anal. 1980, 12, 33–46. [Google Scholar] [CrossRef]
- Champion, T.; Fotheringham, S.; Rees, P.; Boyle, P.; Stillwell, J. The Determinants of Migration Flows in England: A Review of Existing Data and Evidence; Report Prepared for the Department of the Environment, Transport and the Regions; The Department of Geography University of Newcastle upon Tyne: Newcastle upon Tyne, UK, 1998; pp. 31–128. ISBN 0-902155-39-3. [Google Scholar]
- Smith, S.K.; Tayman, J.; Swanson, D.A. State and Local Population Projections: Methodology and Analysis; Kluwer Academic: Norwell, MA, USA; Plenum Publishers: New York, NY, USA, 2001; pp. 97–136. ISBN 0-306-46493-4. [Google Scholar]
- Rogers, A. Demographic Modeling of the Geography of Migration and Population: A Multiregional Perspective. Geogr. Anal. 2008, 40, 276–296. [Google Scholar] [CrossRef]
- Ravenstein, E.G. The Laws of Migration. J. R. Stat. Soc. 1885, 48, 167–235. [Google Scholar] [CrossRef]
- Stouffer, S.A. Intervening opportunities: A theory relating mobility and distance. Am. Sociol. Rev. 1940, 5, 845–867. [Google Scholar] [CrossRef]
- Dodd, S.C. The interactance hypothesis: A gravity model fitting physical masses and human groups. Am. Sociol. Rev. 1950, 15, 245–256. [Google Scholar] [CrossRef]
- Rogerson, P.A.; Plane, D.A. Modeling Temporal Change in Flow Matrices. Pap. Reg. Sci. 1984, 54, 147–164. [Google Scholar] [CrossRef]
- Plane, D.A.; Rogerson, P.A. The Geographical Analysis of Population with Applications to Planning and Business, 1st ed.; Wiley: New York, NY, USA, 1994; pp. 91–126. ISBN 978-0471510147. [Google Scholar]
- Wilson, A.G. A statistical theory of spatial distribution models. Transp. Res. 1967, 1, 253–269. [Google Scholar] [CrossRef]
- Wilson, A.G. The use of entropy maximising models: In the theory of trip distribution, more split and route split. J. Transp. Econ. Policy 1969, 3, 108–126. [Google Scholar]
- Gordon, I.R. Entropy, Variety, Economics, and Spatial Interaction. Geogr. Anal. 2010, 42, 446–471. [Google Scholar] [CrossRef]
- O’Kelly, M.E. Entropy-based spatial interaction models for trip distribution. Geogr. Anal. 2010, 42, 472–487. [Google Scholar] [CrossRef]
- Constantin, D.L. The Use of Gravity Models for Spatial Interaction Analysis. Economy Inform. 2004, 1, 116–118. [Google Scholar]
- Li, J.; Qian, J.; Liu, Y. A Novel Analysis Method of Geographical Centrality Based on Space of Flows. ISPRS Int. J. Geo-Inf. 2017, 6, 153. [Google Scholar] [CrossRef]
- Wilson, A.G. Entropy in Urban and Regional Modelling: Retrospect and Prospect. Geogr. Anal. 2010, 42, 364–394. [Google Scholar] [CrossRef]
- Curry, L. A Spatial Analysis of Gravity Flows. Reg. Stud. 1972, 6, 131–147. [Google Scholar] [CrossRef]
- Plane, D.A. Migration space: Doubly constrained gravity model mapping of relative interstate separation. Ann. Assoc. Am. Geogr. 1984, 74, 244–256. [Google Scholar] [CrossRef]
- Boyle, P.J.; Flowerdew, R. Improving Distance Estimates between Areal Units in Migration Models. Geogr. Anal. 1997, 29, 93–107. [Google Scholar] [CrossRef]
- Statistics Korea (KOSTAT), Korean Statistical Information Service (KOSIS). Available online: http://kosis.kr/statisticsList/statisticsList_01List.jsp (accessed on 3 May 2017).
- Environmental Systems Research Institute (ESRI). ArcGIS Desktop: Release 10.3; Environmental Systems Research Institute: Redlands, CA, USA, 2014. [Google Scholar]
- Bastian, M.; Heymann, S.; Jacomy, M. Gephi: An open source software for exploring and manipulating networks. In Proceedings of the Third International AAAI Conference on Weblogs and Social Media, San Jose, CA, USA, 17–20 May 2009. [Google Scholar]
- Shmueli, G. To Explain or to Predict? Stat. Sci. 2010, 25, 289–310. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1988; pp. 109–143. ISBN 978-0-12-179060-8. [Google Scholar]
- Oswald, A.J.; Wu, S. Objective Confirmation of Subjective Measures of Human Well-Being: Evidence from the U.S.A. Science 2010, 327, 576–579. [Google Scholar] [CrossRef] [PubMed]
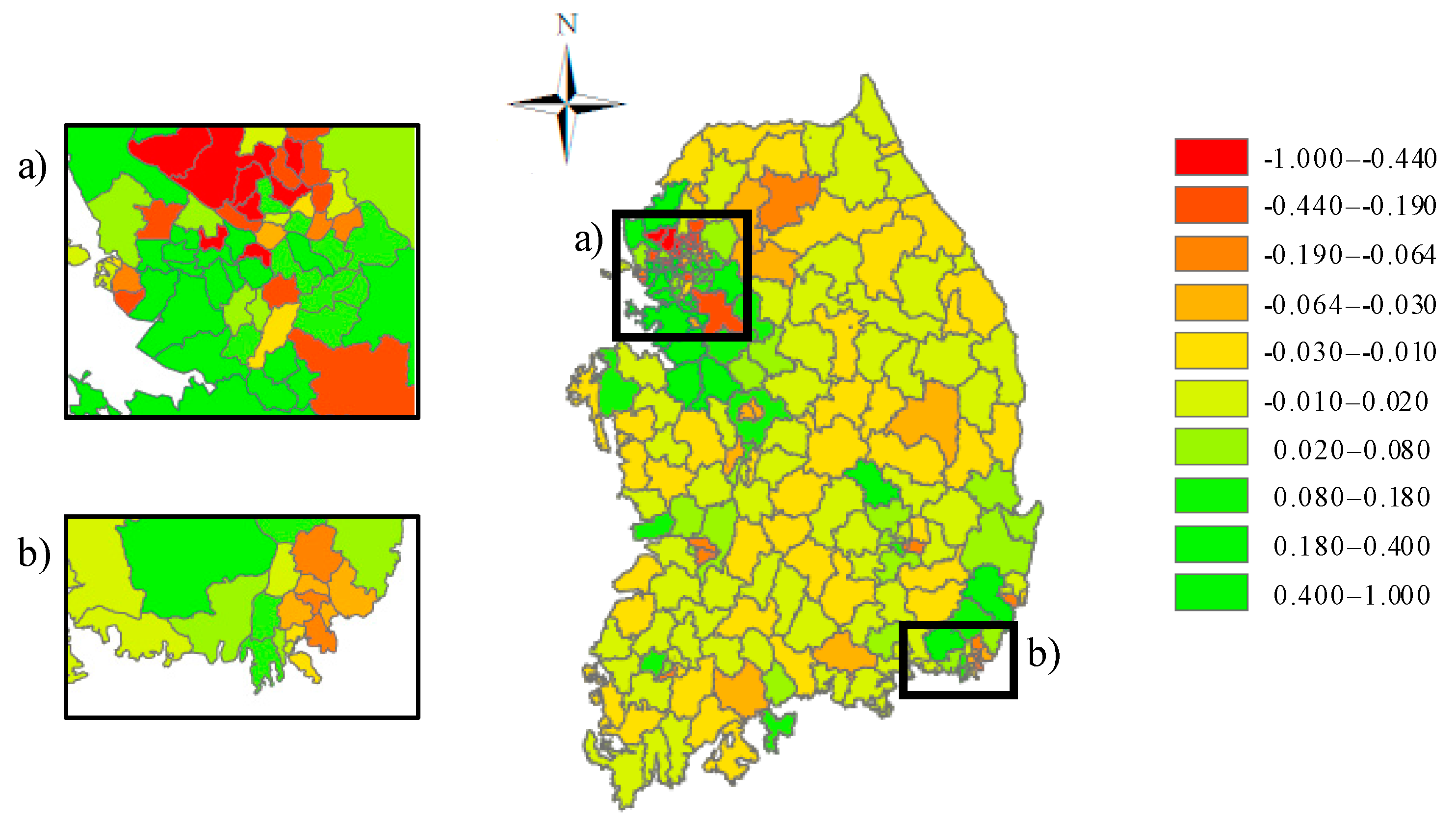
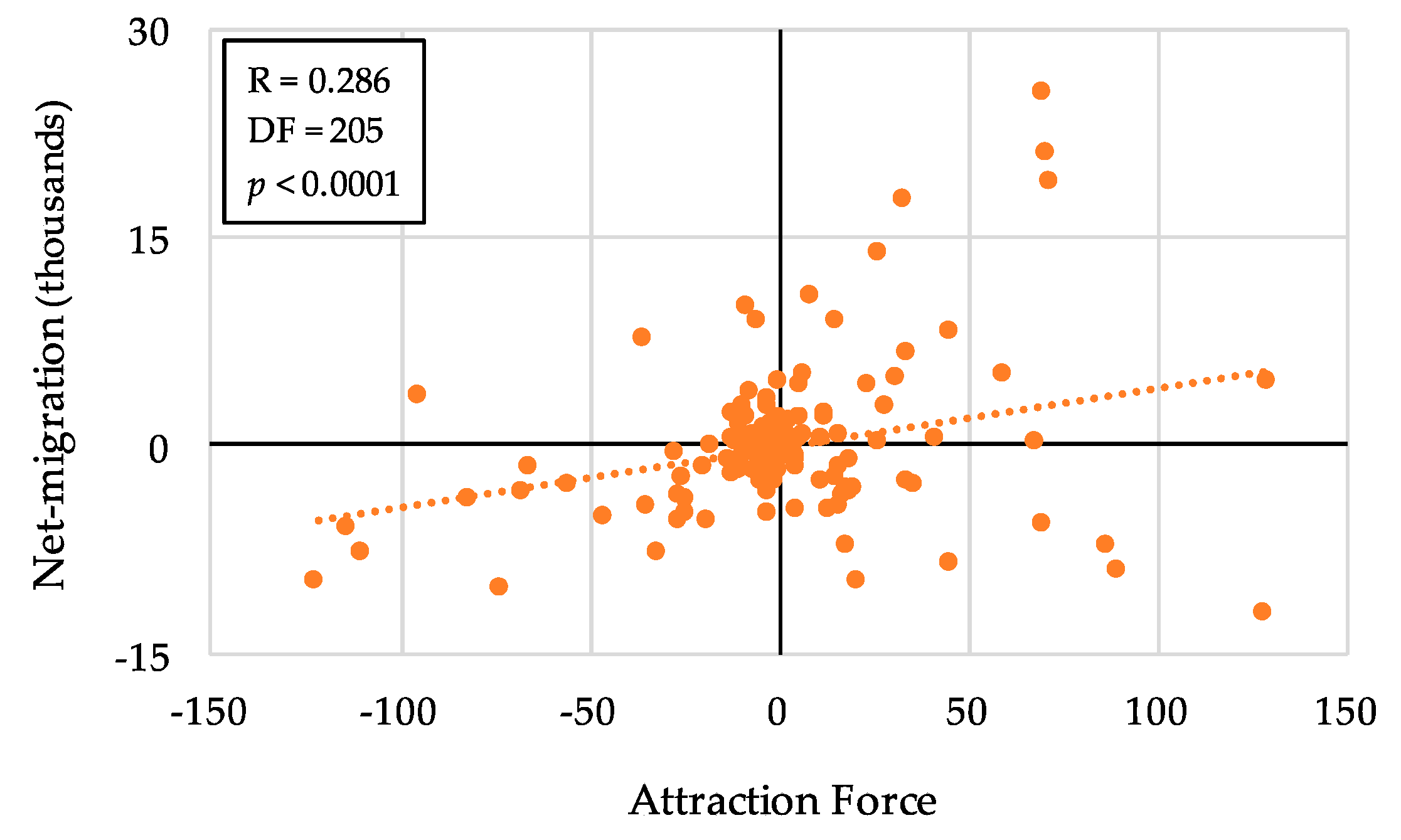
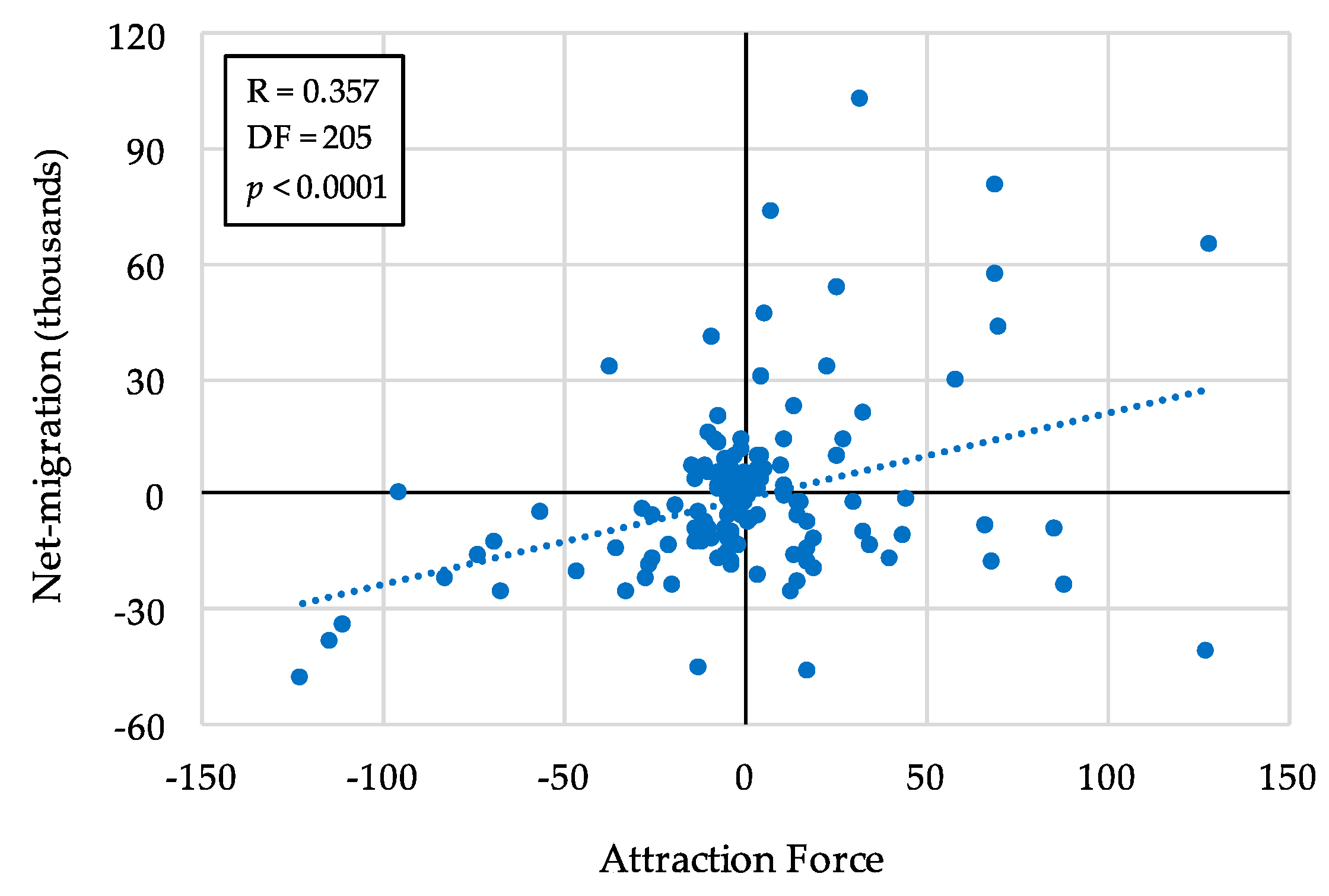
| Factors | D.F. | 2011 | 2011–2015 | ||
|---|---|---|---|---|---|
| R Coefficient | p-Value | R Coefficient | p-Value | ||
| Attraction Force (introduced) | 205 | 0.286 *** | (<0.0001) | 0.357 *** | (<0.0001) |
| Profit level (introduced) 1 | 205 | 0.179 ** | (0.010) | 0.195 *** | (0.005) |
| Entropy of dist. by p.l. (introduced) 2 | 205 | 0.139 ** | (0.045) | 0.139 *** | (0.045) |
| Entropy of dist. by SIC 3 | 204 | –0.018 | (0.793) | –0.061 | (0.381) |
| Population | 205 | –0.115 | (0.100) | –0.174 ** | (0.012) |
| GRDP level 4 | 158 | 0.138 * | (0.083) | 0.225 *** | (0.004) |
| Employment rate | 133 | –0.184 ** | (0.033) | –0.147 * | (0.089) |
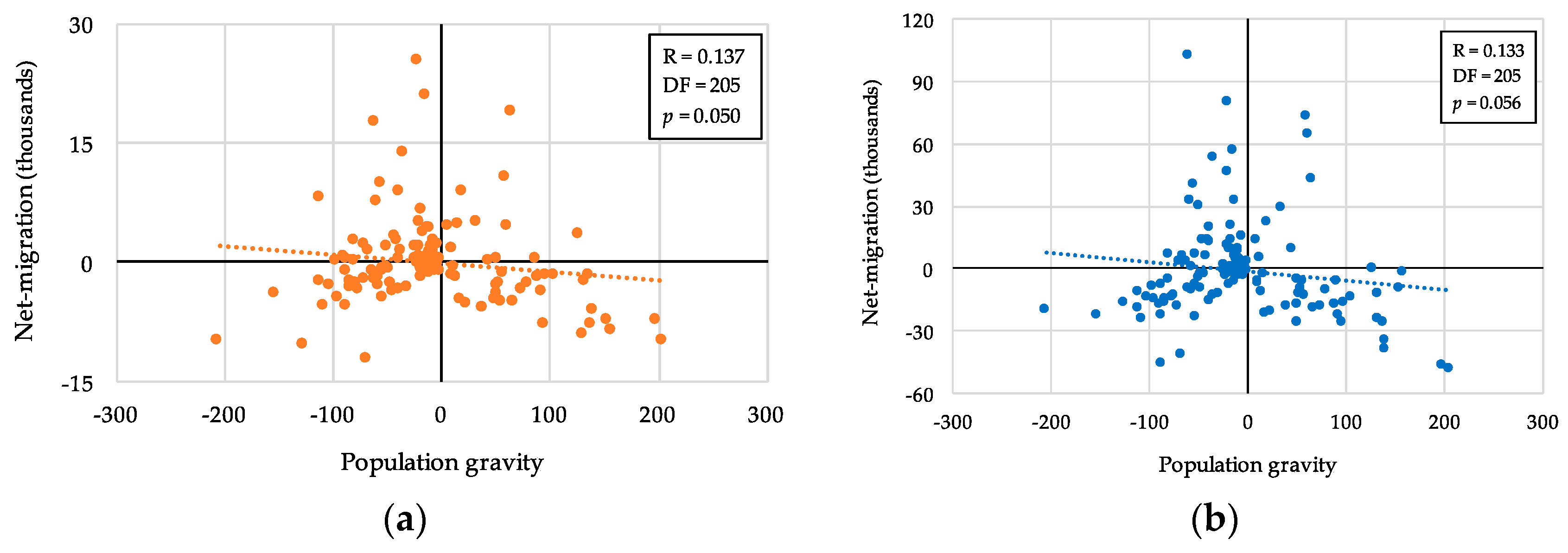
| Gravity model (pow. func.) 5 | 205 | 0.137 ** | (0.050) | 0.133 * | (0.056) |
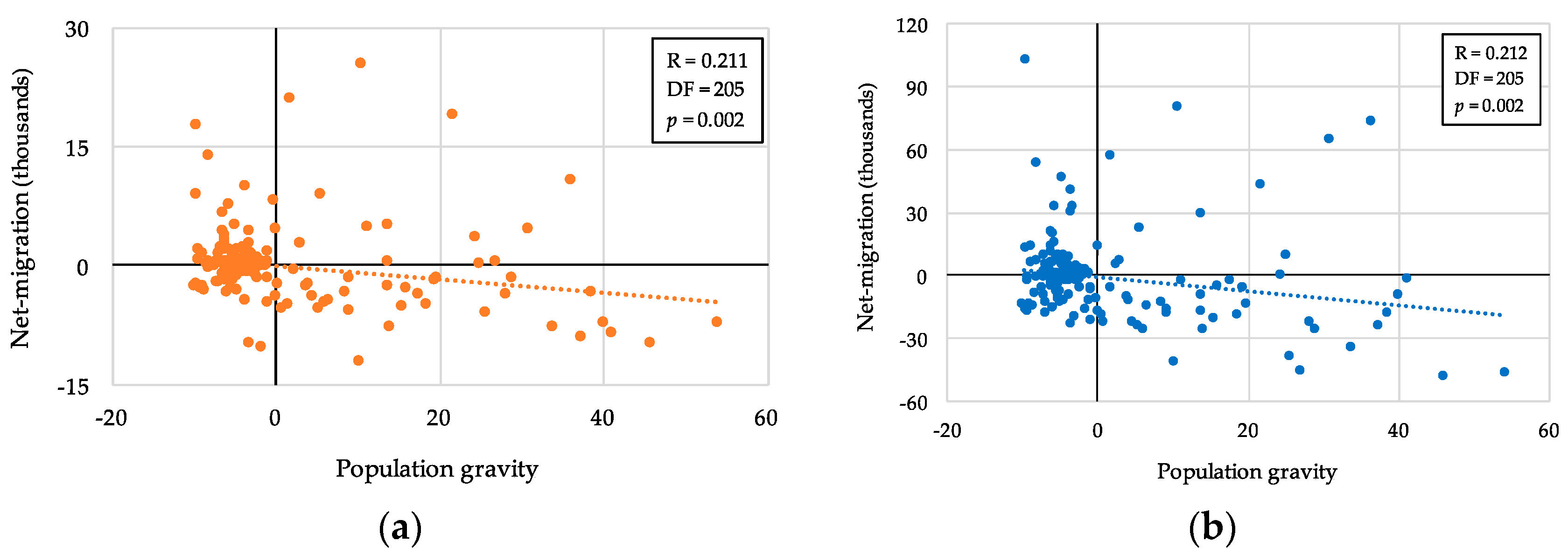
| Gravity model (exp. func.) 6 | 205 | 0.211 *** | (0.002) | 0.212 *** | (0.002) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Hoshino, S. GIS-Based Evaluation of Spatial Interactions by Geographic Disproportionality of Industrial Diversity. ISPRS Int. J. Geo-Inf. 2017, 6, 352. https://doi.org/10.3390/ijgi6110352
Lee J, Hoshino S. GIS-Based Evaluation of Spatial Interactions by Geographic Disproportionality of Industrial Diversity. ISPRS International Journal of Geo-Information. 2017; 6(11):352. https://doi.org/10.3390/ijgi6110352
Chicago/Turabian StyleLee, Jemyung, and Satoshi Hoshino. 2017. "GIS-Based Evaluation of Spatial Interactions by Geographic Disproportionality of Industrial Diversity" ISPRS International Journal of Geo-Information 6, no. 11: 352. https://doi.org/10.3390/ijgi6110352
APA StyleLee, J., & Hoshino, S. (2017). GIS-Based Evaluation of Spatial Interactions by Geographic Disproportionality of Industrial Diversity. ISPRS International Journal of Geo-Information, 6(11), 352. https://doi.org/10.3390/ijgi6110352