A Post-Rectification Approach of Depth Images of Kinect v2 for 3D Reconstruction of Indoor Scenes
Abstract
1. Introduction
2. Related Work
3. Kinect v2 Sensor Presentation
3.1. Characteristics of the Kinect v2
3.2. Pinhole Camera Model
3.3. Distortion Model of Camera Lens
3.4. Depth Sensor
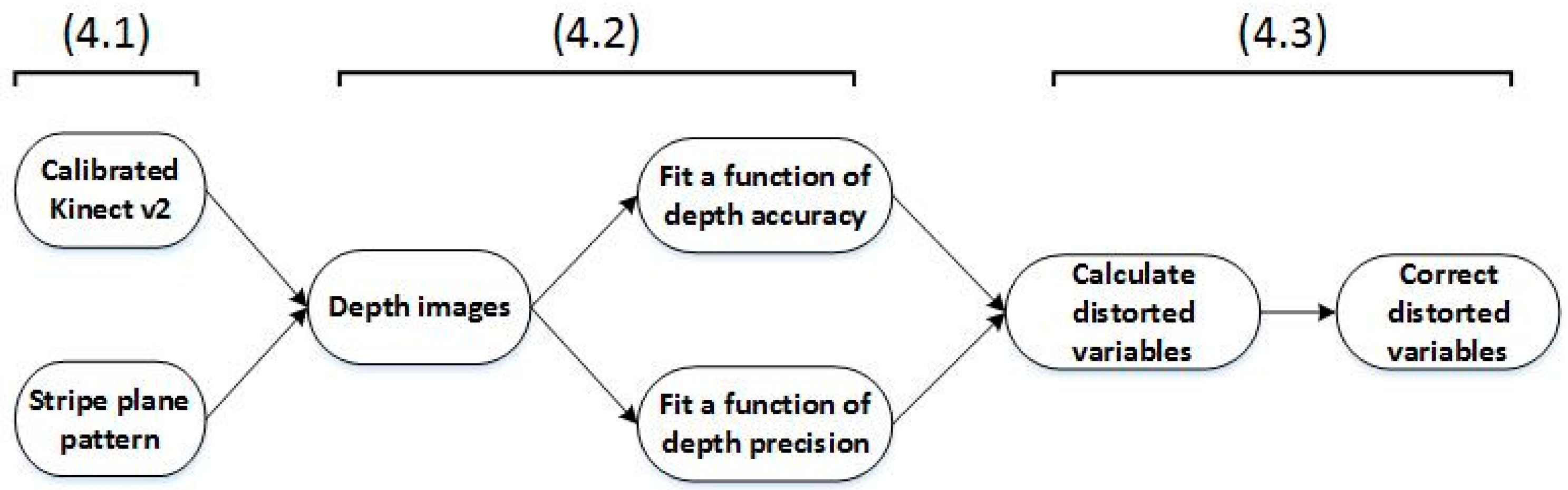
4. Method
4.1. Calibrate the Kinect v2 and Prepare the Stripe Plane Pattern
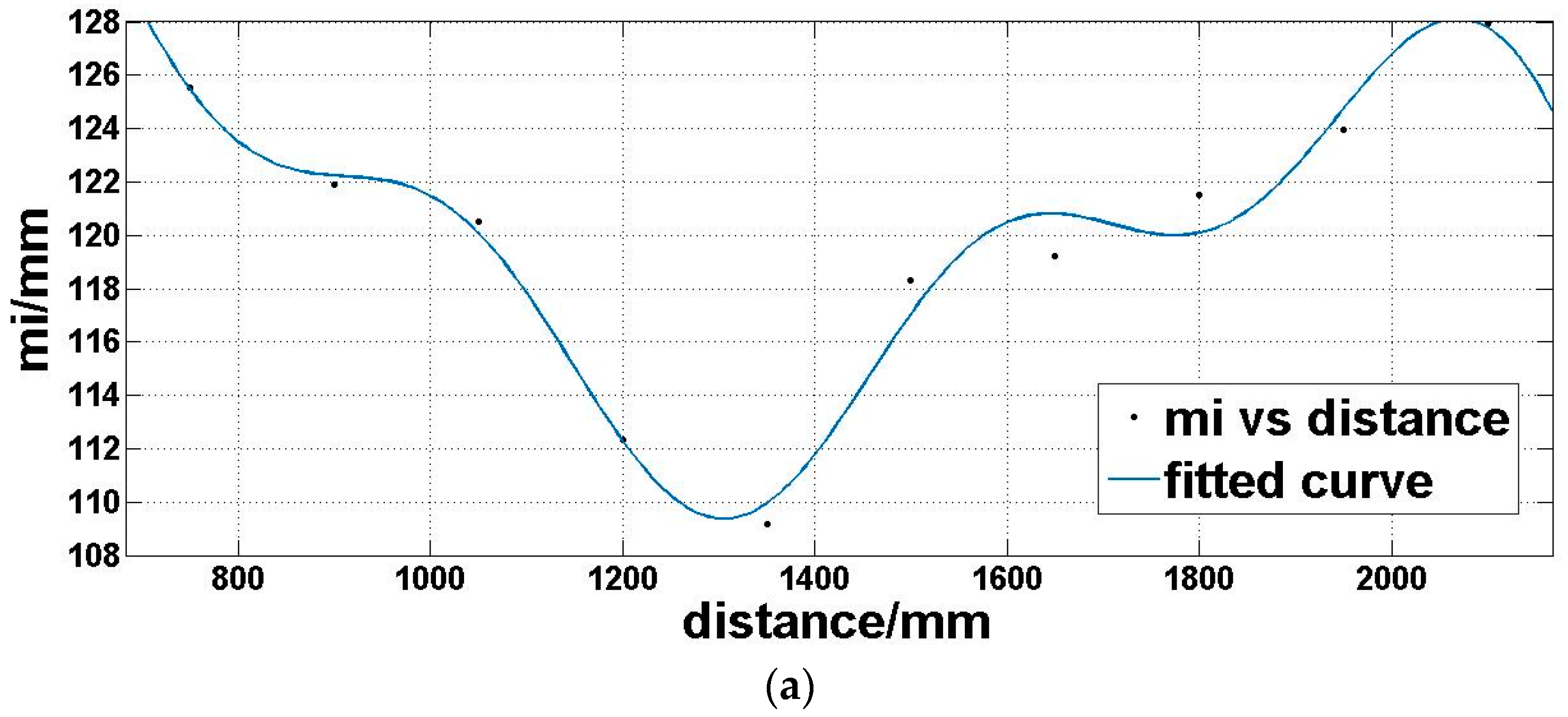
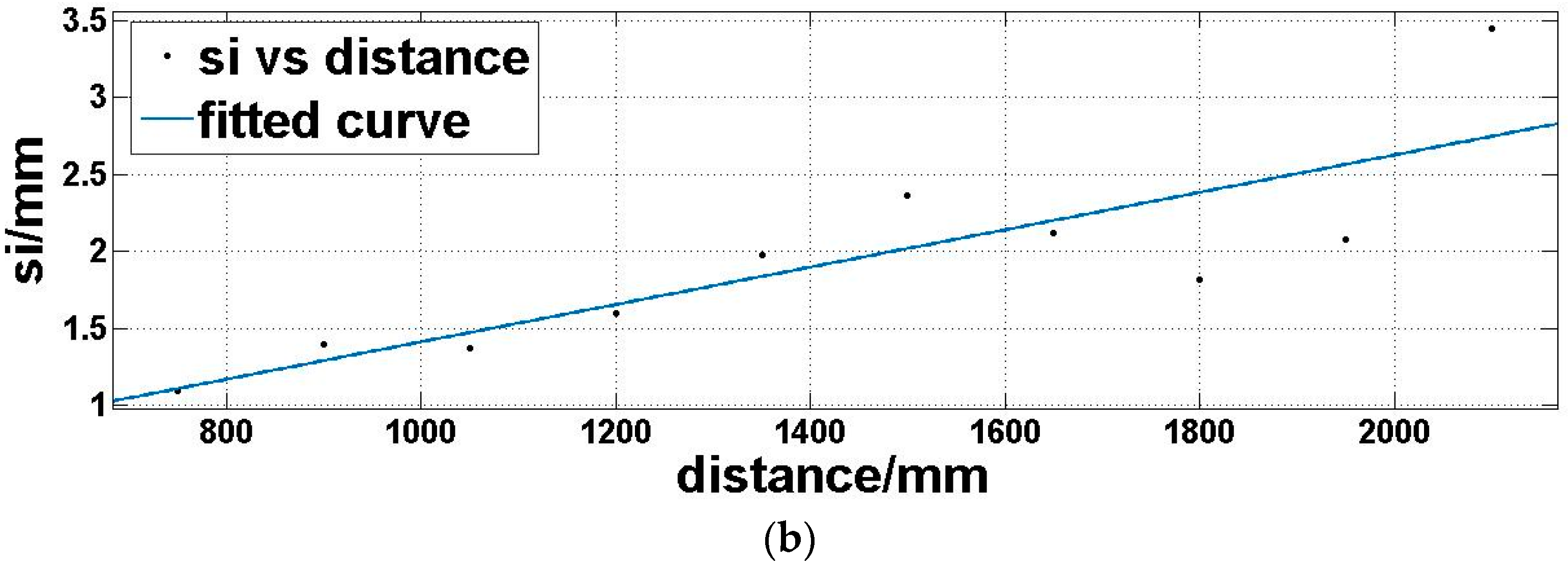
4.2. Capture Depth Images and Fit Functions of Depth Accuracy and Precision, Respectively
4.3. Correct Depth Images
5. Experiments and Results
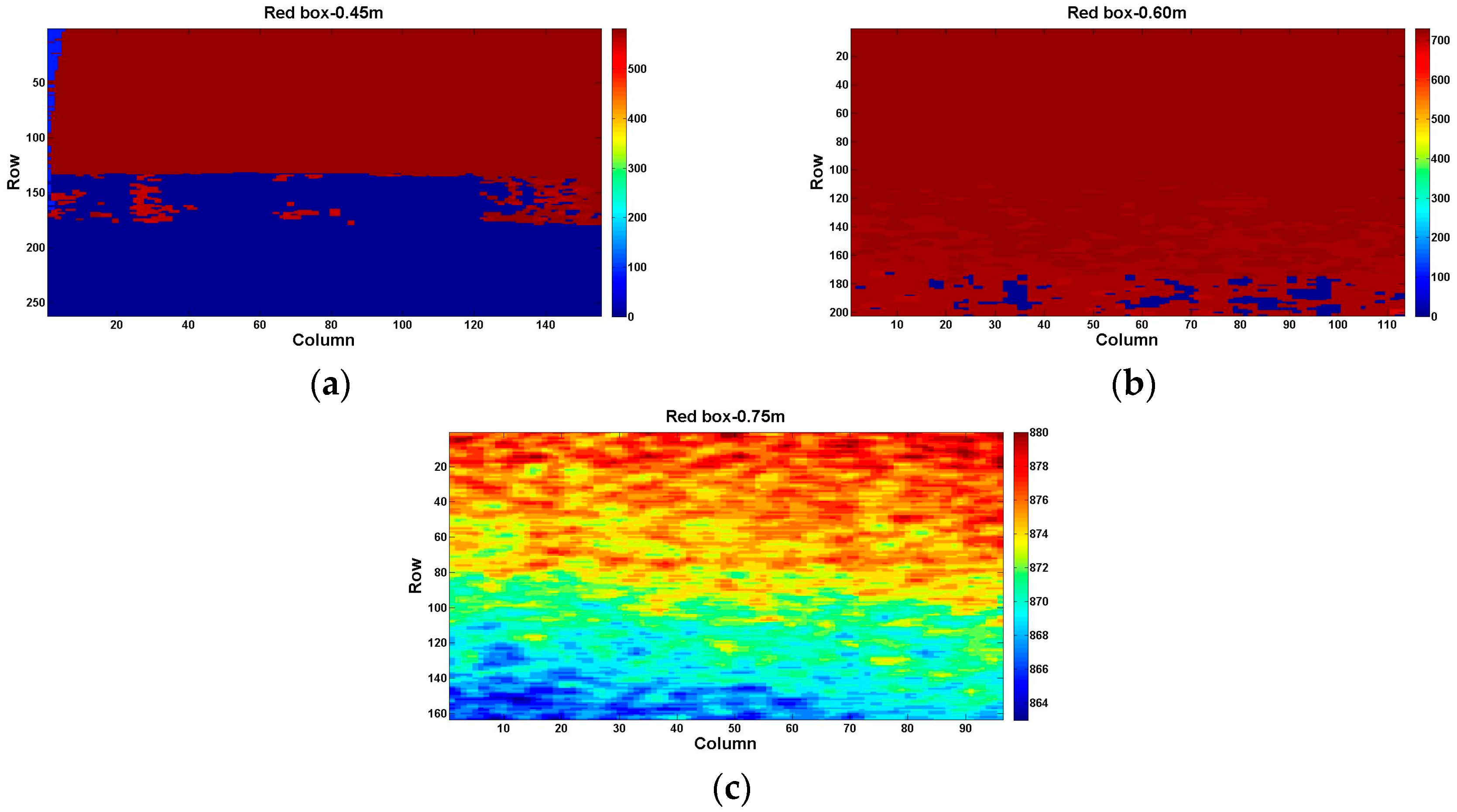
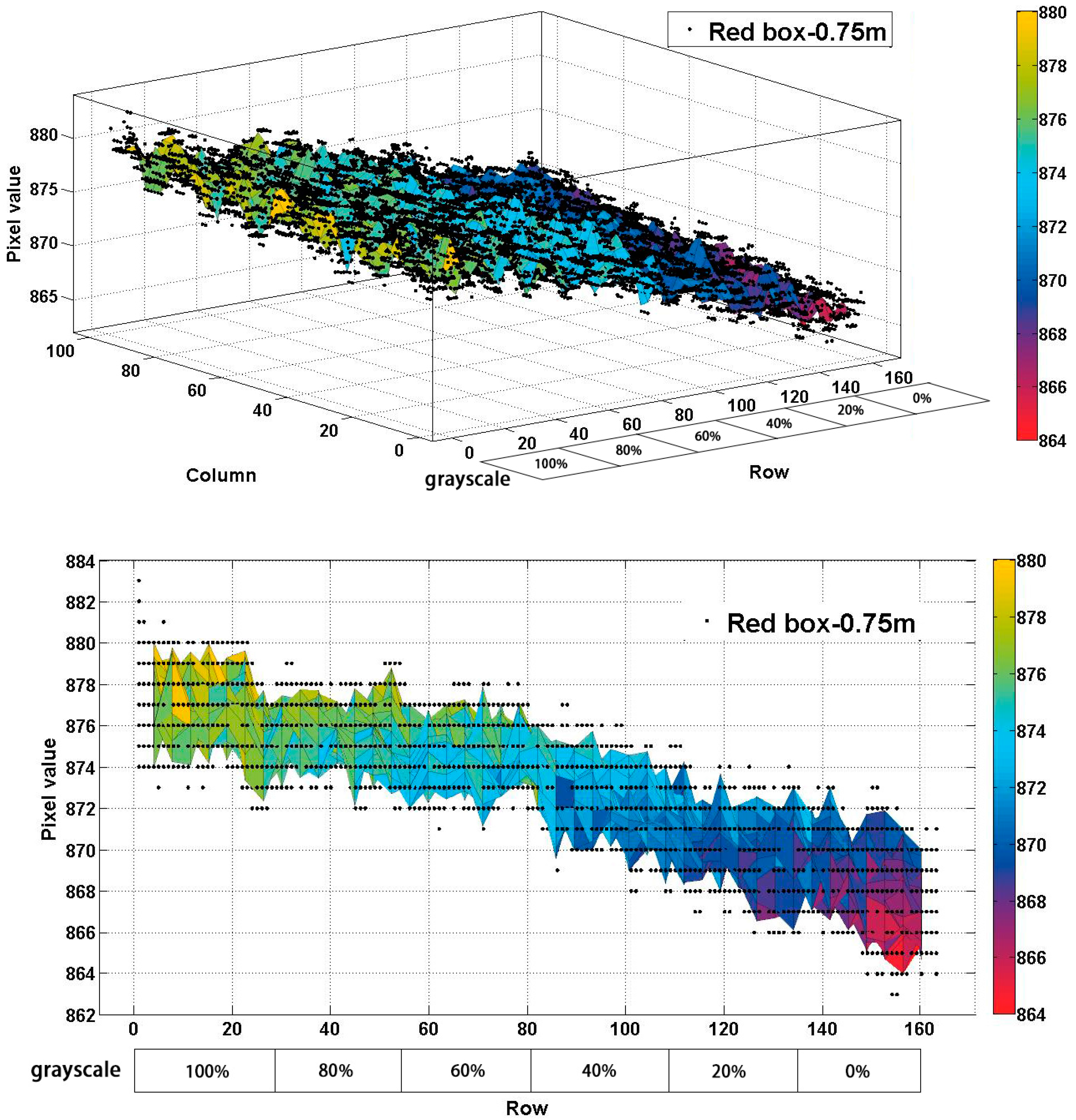
5.1. Same Distance, but Different Reflectivity
5.2. Same Reflectivity, but Different Distances
5.3. Application for RGB-D SLAM System
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wu, B.; Yu, B.; Wu, Q.; Yao, S.; Zhao, F.; Mao, W. A graph-based approach for 3D building model reconstruction from airborne LiDAR point clouds. Remote Sens. 2017, 9, 92. [Google Scholar] [CrossRef]
- Kuhnert, K.-D.; Stommel, M. Fusion of stereo-camera and pmd-camera data for real-time suited precise 3d environment reconstruction. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 4780–4785. [Google Scholar]
- Lachat, E.; Macher, H.; Mittet, M.; Landes, T.; Grussenmeyer, P. First experiences with Kinect v2 sensor for close range 3D modelling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40. [Google Scholar] [CrossRef]
- Lee, D. Optimizing Point Cloud Production from Stereo Photos by Tuning the Block Matcher. Available online: https://erget.wordpress.com/2014/05/02/producing-3d-point-clouds-from-stereo-photos-tuning-the-block-matcher-for-best-results/ (accessed on 20 August 2017).
- Henry, P.; Krainin, M.; Herbst, E.; Ren, X.; Fox, D. RGB-D mapping: Using Kinect-style depth cameras for dense 3D modeling of indoor environments. Int. J. Robot. Res. 2012, 31, 647–663. [Google Scholar] [CrossRef]
- Endres, F.; Hess, J.; Sturm, J.; Cremers, D.; Burgard, W. 3-D mapping with an RGB-D camera. IEEE Trans. Robot. 2014, 30, 177–187. [Google Scholar] [CrossRef]
- Valgma, L. 3d Reconstruction Using Kinect v2 Camera. Bachelor’s Thesis, University of Tartu, Tartu, Estonia, 2016. [Google Scholar]
- Konolige, K. Projected texture stereo. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–8 May 2010; pp. 148–155. [Google Scholar]
- PrimeSense. Light Coding Technology. Available online: https://en.wikipedia.org/wiki/PrimeSense (accessed on 20 March 2016).
- Canesta. Time-of-Flight Technology. Available online: https://en.wikipedia.org/wiki/Canesta (accessed on 17 January 2017).
- MESA Imaging. ToF (Time-of-Flight). Available online: https://en.wikipedia.org/wiki/MESA_Imaging (accessed on 20 August 2017).
- Butkiewicz, T. Low-cost coastal mapping using Kinect v2 time-of-flight cameras. Oceans-St. John’s 2014, 2014, 1–9. [Google Scholar]
- Lachat, E.; Macher, H.; Landes, T.; Grussenmeyer, P. Assessment and calibration of a RGB-D camera (kinect v2 sensor) towards a potential use for close-range 3D modeling. Remote Sens. 2015, 7, 13070–13097. [Google Scholar] [CrossRef]
- Fankhauser, P.; Bloesch, M.; Rodriguez, D.; Kaestner, R.; Hutter, M.; Siegwart, R. Kinect v2 for mobile robot navigation: Evaluation and modeling. In Proceedings of the 2015 International Conference on Advanced Robotics (ICAR), Istanbul, Turkey, 27–31 July 2015; pp. 388–394. [Google Scholar]
- Choi, S.; Zhou, Q.-Y.; Koltun, V. Robust reconstruction of indoor scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5556–5565. [Google Scholar]
- Wasenmüller, O.; Meyer, M.; Stricker, D. Augmented reality 3d discrepancy check in industrial applications. In Proceedings of the 2016 IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Merida, Mexico, 19–23 September 2016; pp. 125–134. [Google Scholar]
- Pagliari, D.; Pinto, L. Calibration of kinect for xbox one and comparison between the two generations of Microsoft sensors. Sensors 2015, 15, 27569–27589. [Google Scholar] [CrossRef] [PubMed]
- Wiedemeyer, T. Tools for Using the Kinect One (Kinect v2) in ROS. Available online: https://github.com/code-iai/iai_kinect2 (accessed on 20 August 2017).
- Sarbolandi, H.; Lefloch, D.; Kolb, A. Kinect range sensing: Structured-light versus time-of-flight kinect. Comput. Vis. Image Underst. 2015, 139, 1–20. [Google Scholar] [CrossRef]
- Wasenmüller, O.; Stricker, D. Comparison of Kinect v1 and v2 Depth Images in Terms of Accuracy and Precision. In Proceedings of the Asian Conference on Computer Vision Workshop (ACCV workshop), Taipei, Taiwan, 20–24 November 2016; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Lawin, F.J. Depth Data Processing and 3D Reconstruction Using the Kinect v2. Master’s Thesis, Linköping University, Linköping, Sweden, 2015. [Google Scholar]
- Gonzalez-Jorge, H.; Rodríguez-Gonzálvez, P.; Martínez-Sánchez, J.; González-Aguilera, D.; Arias, P.; Gesto, M. Metrological comparison between Kinect I and Kinect II sensors. Measurement 2015, 70, 21–26. [Google Scholar] [CrossRef]
- Lindner, M.; Kolb, A. Calibration of the intensity-related distance error of the PMD ToF-camera. Opt. East 2007, 2007, 67640W:1–67640W:8. [Google Scholar]
- Lindner, M.; Schiller, I.; Kolb, A.; Koch, R. Time-of-flight sensor calibration for accurate range sensing. Comput. Vis. Image Underst. 2010, 114, 1318–1328. [Google Scholar] [CrossRef]
- Rodríguez-Gonzálvez, P.; González-Aguilera, D.; González-Jorge, H.; Hernández-López, D. Low-Cost Reflectance-Based Method for the Radiometric Calibration of Kinect 2. IEEE Sens. J. 2016, 16, 1975–1985. [Google Scholar] [CrossRef]
- Blake, J.; Echtler, F.; Kerl, C. Open Source Drivers for the Kinect for Windows v2 Device. Available online: https://github.com/OpenKinect/libfreenect2 (accessed on 20 August 2017).
- Georgakis, G. Multiview RGB-D Dataset for Object Instance Detection. Available online: http://cs.gmu.edu/~robot/gmu-kitchens.html (accessed on 20 August 2017).
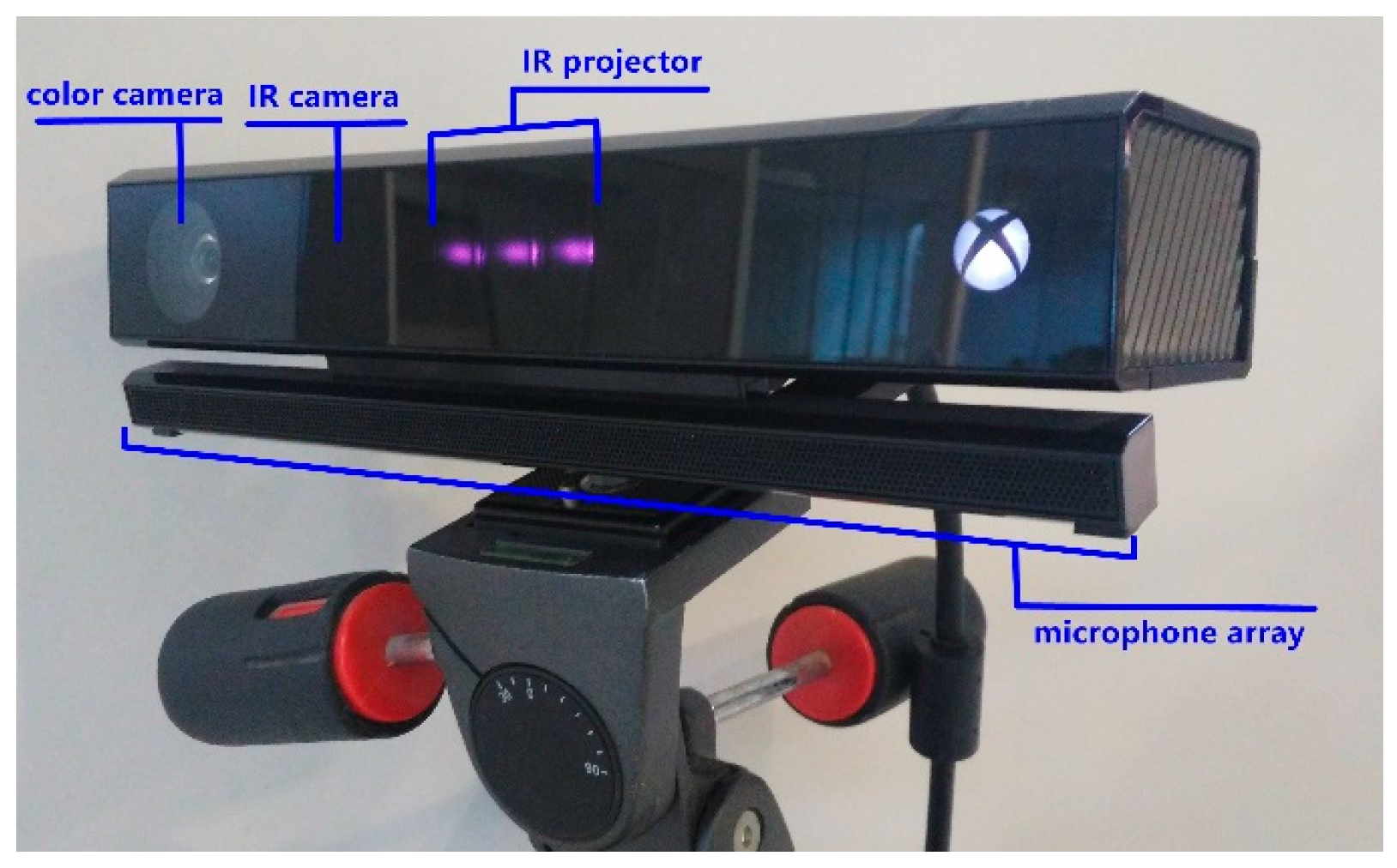






| Color | Camera Resolution | 1920 × 1080 pixels |
| Framerate | 30 frames per second | |
| Depth | Camera Resolution | 512 × 424 pixels |
| Framerate | 30 frames per second | |
| Field of VIEW (depth) | Horizontal | 70 degrees |
| Vertical | 60 degrees | |
| Operative Measuring Range | from 0.5 m to 4.5 m | |
| Depth Technology | Time-of-flight (ToF) | |
| Tilt Motor | No | |
| USB Standard | 3.0 | |
| Panel Level | Reflectivity |
|---|---|
| 0% | 0.9913 |
| 20% | 0.7981 |
| 40% | 0.6019 |
| 60% | 0.4125 |
| 80% | 0.1994 |
| 100% | 0.0011 |
| Depth Sensor | Kinect v1 | Kinect v2 | |
|---|---|---|---|
| Error Source | |||
| Ambient Background Light [7] | √ | √ | |
| Temperature Drift [19] | √ | √ | |
| Systematic Distance Error [19] | √ | √ | |
| Depth Inhomogeneity [7] | √ | √ | |
| Multi-Path Effects [20] | √ | √ | |
| Intensity-Related Distance Error [7] | × | √ | |
| Semitransparent and Scattering Media [20] | √ | √ | |
| Dynamic Scenery [20] | √ | √ | |
| Flying Pixel [7] | × | √ | |
| Distance (m) | 0.75 | 0.90 | 1.05 | 1.20 | 1.35 | 1.50 | 1.65 | 1.80 | 1.95 | 2.10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Value (mm) | ||||||||||||
| Item | ||||||||||||
| 100% black | ||||||||||||
| mcorr | 0.1607 | −0.4710 | 0.6894 | −0.2793 | −0.5033 | 1.0029 | −1.5421 | 1.1476 | −0.7082 | −0.0217 | ||
| Scorr | 2.0669 | 2.3116 | 2.4457 | 2.4295 | 3.2557 | 3.1760 | 3.9849 | 3.6780 | 5.1154 | 4.4273 | ||
| m | 127.6166 | 123.7936 | 122.8260 | 114.3370 | 111.3207 | 119.5455 | 121.4907 | 123.1732 | 124.5892 | 129.7157 | ||
| s | 2.0669 | 2.3116 | 2.4457 | 2.4295 | 3.2557 | 3.1760 | 3.9849 | 3.6780 | 5.1154 | 4.4273 | ||
| 80% black | ||||||||||||
| mcorr | 0.0873 | −0.3563 | 0.4352 | −0.0085 | −0.7791 | 1.2867 | −1.5841 | 1.4674 | −0.6622 | 0.2705 | ||
| Scorr | 1.0963 | 1.3948 | 1.3684 | 1.5997 | 1.9776 | 2.3625 | 2.1146 | 1.8148 | 2.0750 | 3.4419 | ||
| m | 125.5293 | 121.8862 | 120.5257 | 112.3133 | 109.1780 | 118.3241 | 119.2202 | 121.5227 | 123.9722 | 127.9327 | ||
| s | 1.0963 | 1.3948 | 1.3684 | 1.5997 | 1.9776 | 2.3625 | 2.1146 | 1.8148 | 2.0750 | 3.4419 | ||
| 60% black | ||||||||||||
| mcorr | 0.3129 | −0.6364 | 1.1514 | −0.6131 | −0.3607 | 1.0400 | −1.9007 | 1.4719 | −1.0410 | −0.0744 | ||
| Scorr | 1.2006 | 1.3411 | 1.4766 | 1.1424 | 1.4639 | 1.7628 | 1.9563 | 1.6953 | 1.7913 | 2.2094 | ||
| m | 124.6040 | 121.4815 | 120.6797 | 111.3145 | 109.1095 | 116.9787 | 118.4527 | 121.9892 | 123.6846 | 128.0617 | ||
| s | 1.2006 | 1.3411 | 1.4766 | 1.1424 | 1.4639 | 1.7628 | 1.9563 | 1.6953 | 1.7913 | 2.2094 | ||
| 40% black | ||||||||||||
| mcorr | 0.0478 | −0.0596 | 0.1218 | 0.0904 | −0.4571 | 0.6311 | −0.8309 | 0.6094 | −0.4894 | −0.0280 | ||
| Scorr | 1.4408 | 1.7909 | 1.4628 | 1.4888 | 1.2835 | 1.5967 | 1.2283 | 1.3882 | 2.8126 | 1.6514 | ||
| m | 122.3192 | 120.1545 | 117.1464 | 109.2976 | 107.1321 | 114.7480 | 116.7984 | 119.2528 | 123.7405 | 125.8464 | ||
| s | 1.4408 | 1.7909 | 1.4628 | 1.4888 | 1.2835 | 1.5967 | 1.2283 | 1.3882 | 2.8126 | 1.6514 | ||
| 20% black | ||||||||||||
| mcorr | 0.1038 | −0.7496 | 0.9256 | −0.5031 | −0.2778 | 1.0179 | −1.3685 | 1.6489 | −0.4917 | 0.4327 | ||
| Scorr | 1.3713 | 1.6607 | 1.6392 | 1.4375 | 1.5381 | 1.8762 | 1.4057 | 1.2839 | 1.4366 | 2.5210 | ||
| m | 120.0186 | 116.1750 | 116.2189 | 108.1833 | 106.1495 | 113.9487 | 115.8037 | 118.9490 | 121.4179 | 125.7333 | ||
| s | 1.3713 | 1.6607 | 1.6392 | 1.4375 | 1.5381 | 1.8762 | 1.4057 | 1.2839 | 1.4366 | 2.5210 | ||
| 0% black (100% white) | ||||||||||||
| mcorr | 0.6980 | 0.0054 | 1.3 | 0.3592 | −0.0831 | 1.8191 | −1.0919 | 2.2539 | −0.2420 | 0.7992 | ||
| Scorr | 1.6839 | 1.8881 | 1.7393 | 1.6467 | 1.7178 | 2.0895 | 1.3940 | 1.1620 | 1.4396 | 2.6236 | ||
| m | 117.5105 | 113.7644 | 113.7520 | 105.6693 | 103.2963 | 112.9783 | 114.3643 | 117.4583 | 120.2713 | 124.4468 | ||
| s | 1.6839 | 1.8881 | 1.7393 | 1.6467 | 1.7178 | 2.0895 | 1.3940 | 1.1620 | 1.4396 | 2.6236 | ||
| Camera | Intrinsic Parameters | ||||
| fx (mm) | fy (mm) | u0 (pixel) | v0 (pixel) | ||
| Color | 1144.361 | 1147.337 | 966.359 | 548.038 | |
| IR | 388.198 | 389.033 | 253.270 | 213.934 | |
| Camera | Distortion Coefficients | ||||
| k1 | k2 | k3 | p1 | p2 | |
| Color | 0.108 | −0.125 | 0.062 | −0.001 | −0.003 |
| IR | 0.126 | −0.329 | 0.111 | −0.001 | −0.002 |
| DepthShift (mm) | |||||
| IR | 60.358 | ||||
| Rotation Matrix | Translation Vector | ||||
| Color and IR | |||||
| Reflectivity | 0.9913 | 0.7981 | 0.6019 | 0.4125 | 0.1994 | 0.0011 | |
| Expectation (mm) | |||||||
| m | 107.3987 | 109.0536 | 109.8727 | 112.3605 | 113.0718 | 115.2330 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, J.; Yuan, L.; Tang, W.; Deng, Z.; Wu, Q. A Post-Rectification Approach of Depth Images of Kinect v2 for 3D Reconstruction of Indoor Scenes. ISPRS Int. J. Geo-Inf. 2017, 6, 349. https://doi.org/10.3390/ijgi6110349
Jiao J, Yuan L, Tang W, Deng Z, Wu Q. A Post-Rectification Approach of Depth Images of Kinect v2 for 3D Reconstruction of Indoor Scenes. ISPRS International Journal of Geo-Information. 2017; 6(11):349. https://doi.org/10.3390/ijgi6110349
Chicago/Turabian StyleJiao, Jichao, Libin Yuan, Weihua Tang, Zhongliang Deng, and Qi Wu. 2017. "A Post-Rectification Approach of Depth Images of Kinect v2 for 3D Reconstruction of Indoor Scenes" ISPRS International Journal of Geo-Information 6, no. 11: 349. https://doi.org/10.3390/ijgi6110349
APA StyleJiao, J., Yuan, L., Tang, W., Deng, Z., & Wu, Q. (2017). A Post-Rectification Approach of Depth Images of Kinect v2 for 3D Reconstruction of Indoor Scenes. ISPRS International Journal of Geo-Information, 6(11), 349. https://doi.org/10.3390/ijgi6110349





