Enhanced Map-Matching Algorithm with a Hidden Markov Model for Mobile Phone Positioning
Abstract
1. Introduction
2. Brief Review of Map-Matching Algorithms
3. HMM-Based Map-Matching
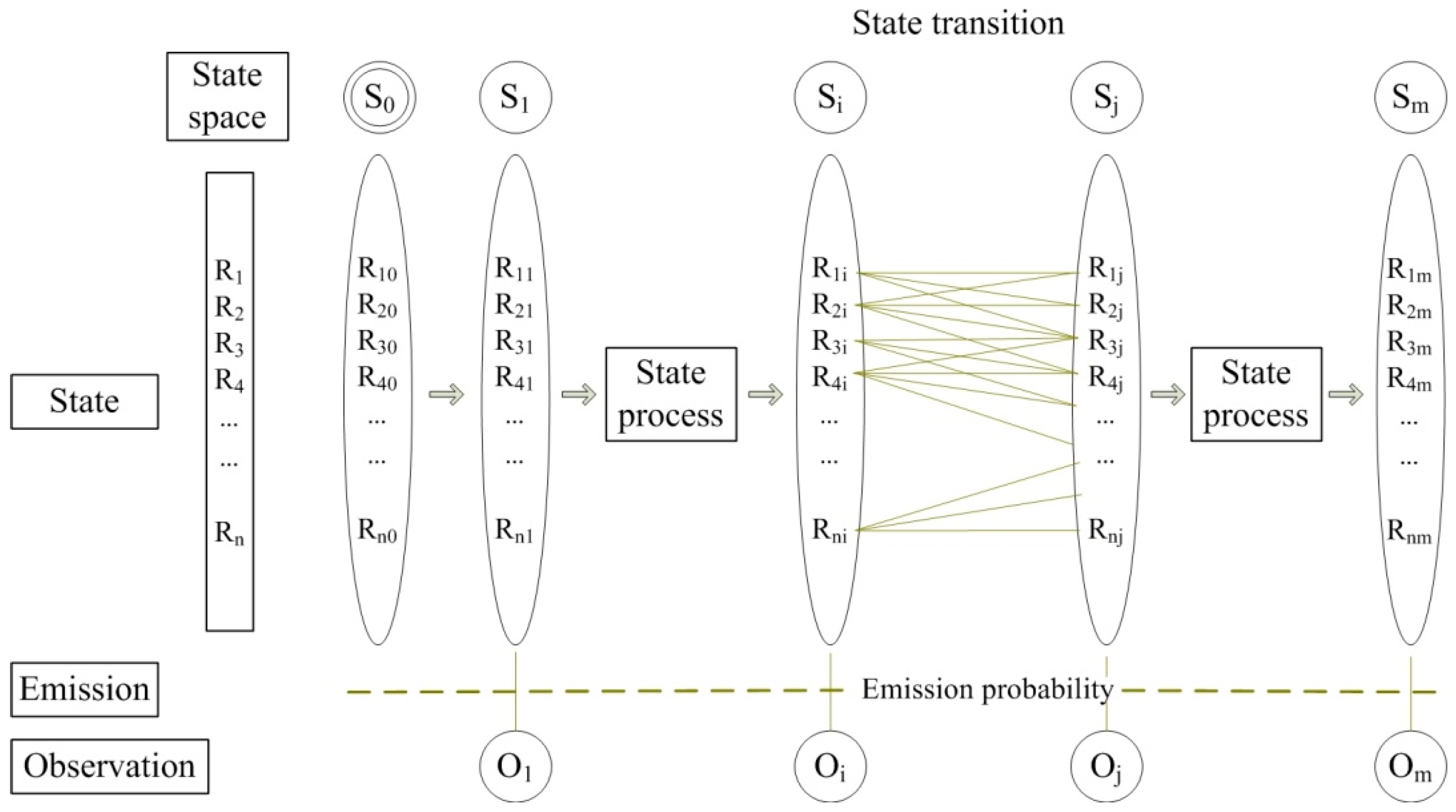
3.1. Hidden Markov Model and Its Five Parameters
3.2. Basics of Viterbi Algorithm
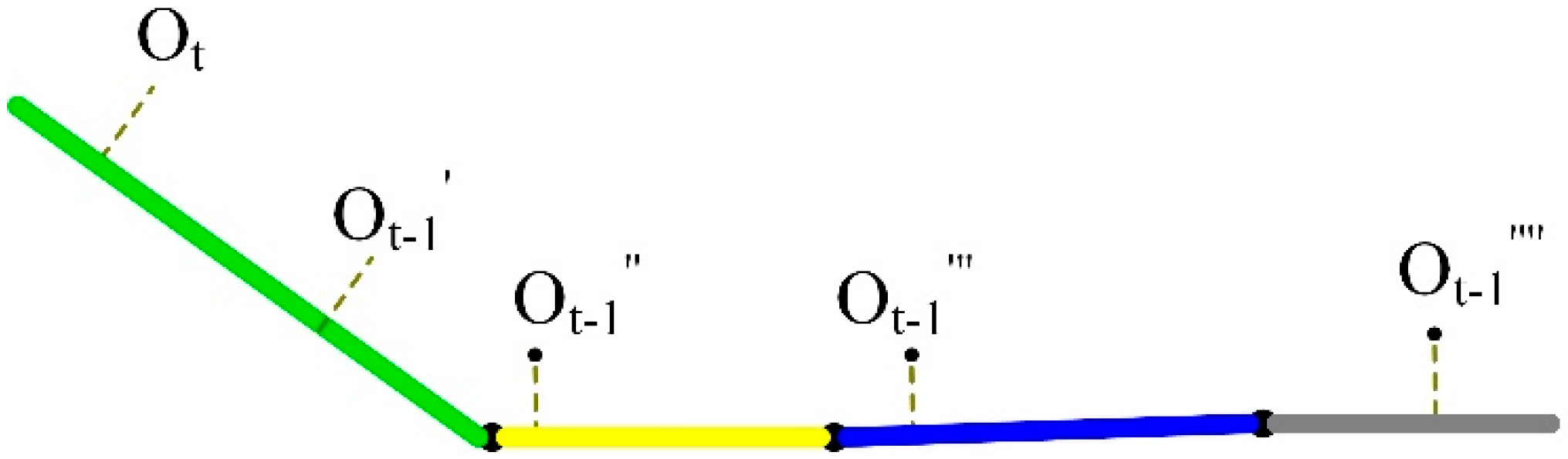
3.3. HMM-Based Map-Matching
3.4. Process
4. Experiment and Analysis
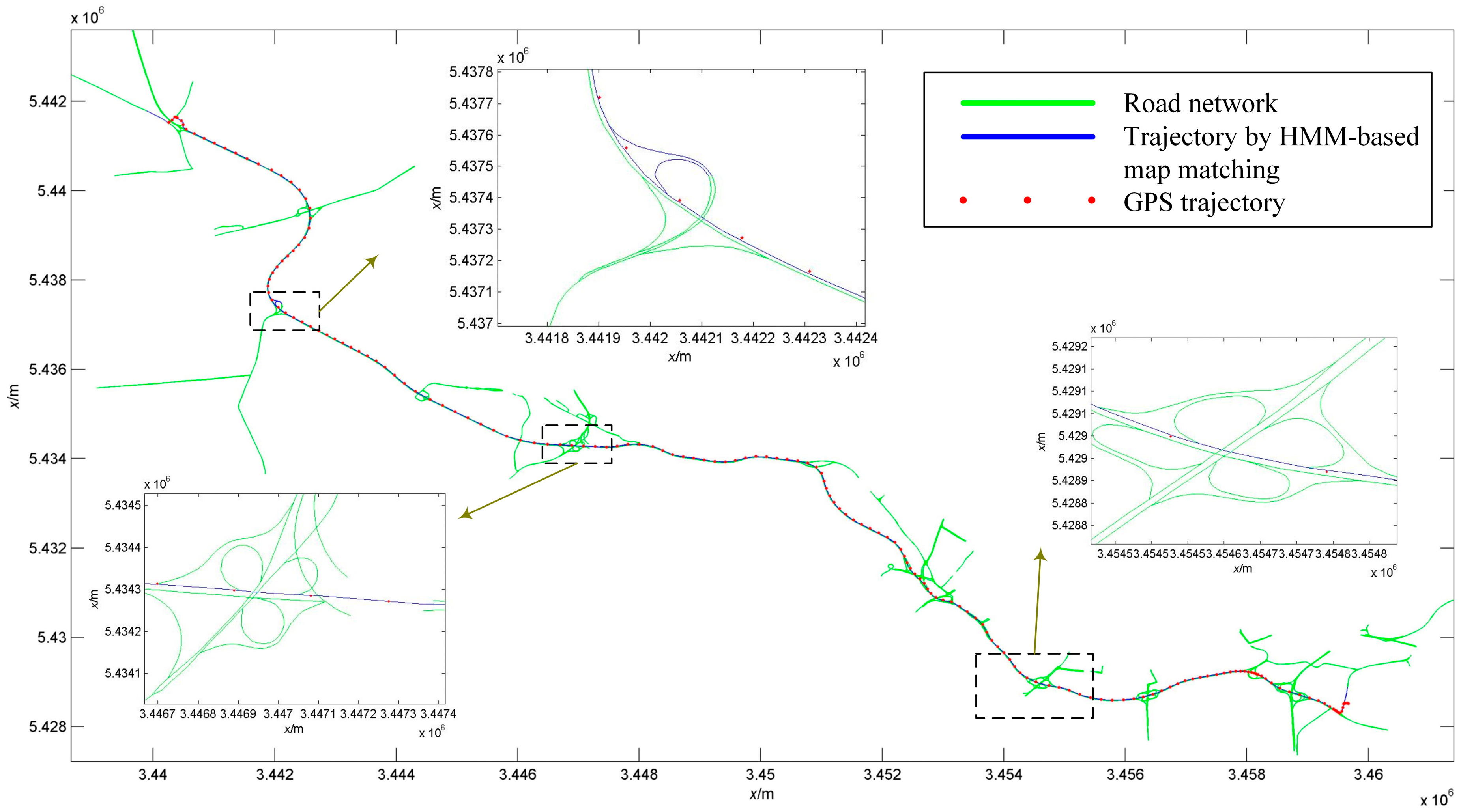
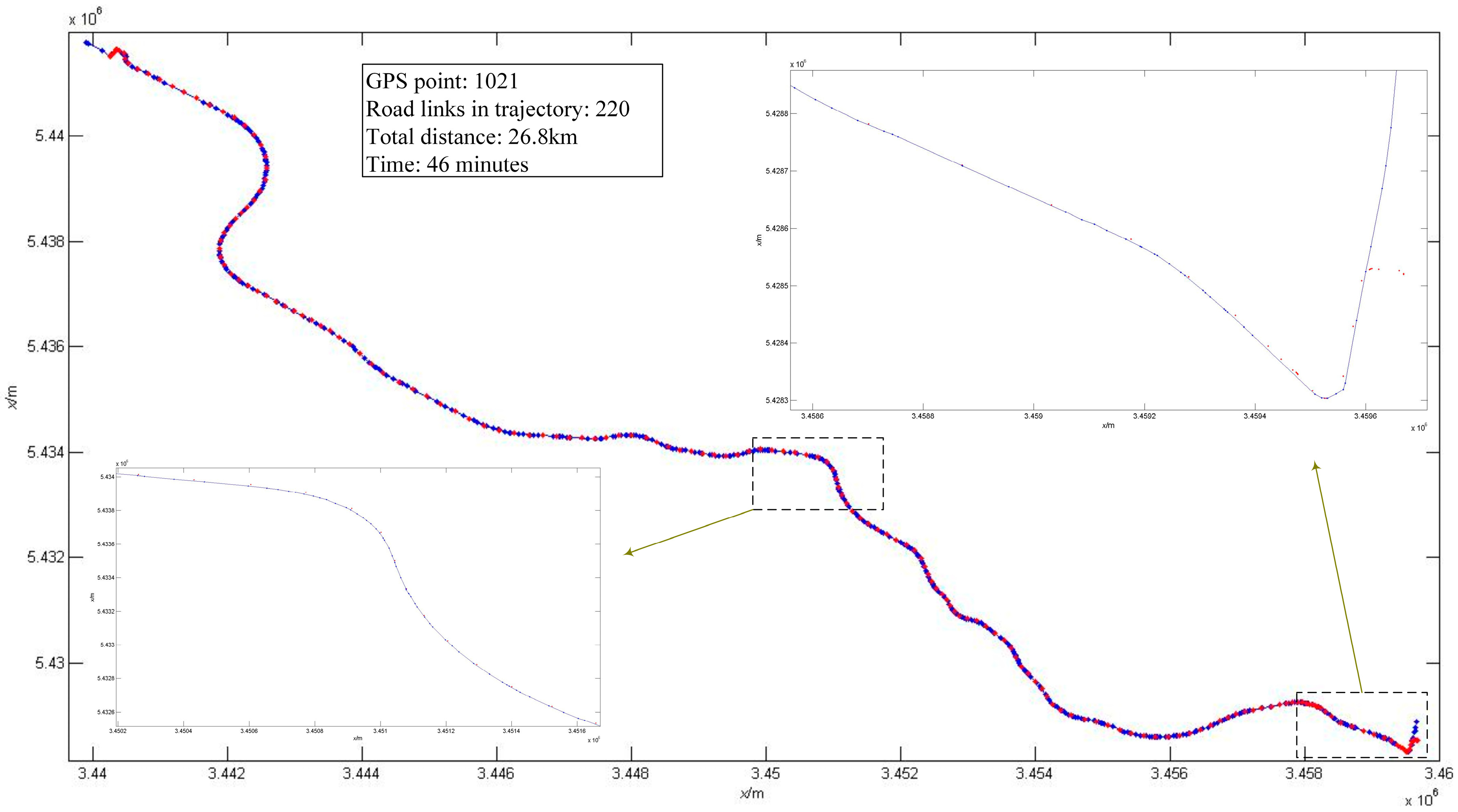
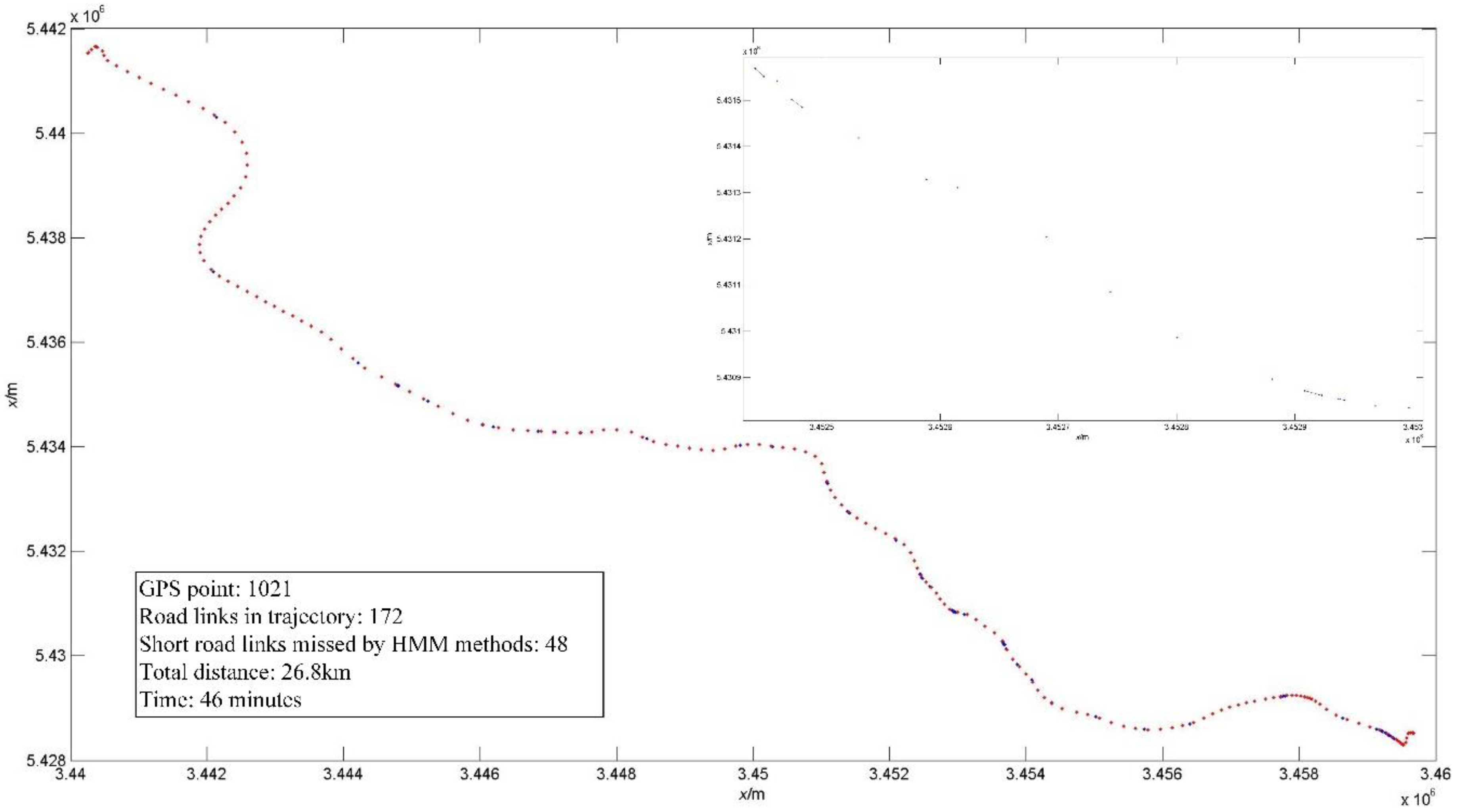
4.1. Map-Matching with HMM on GPS Positioning
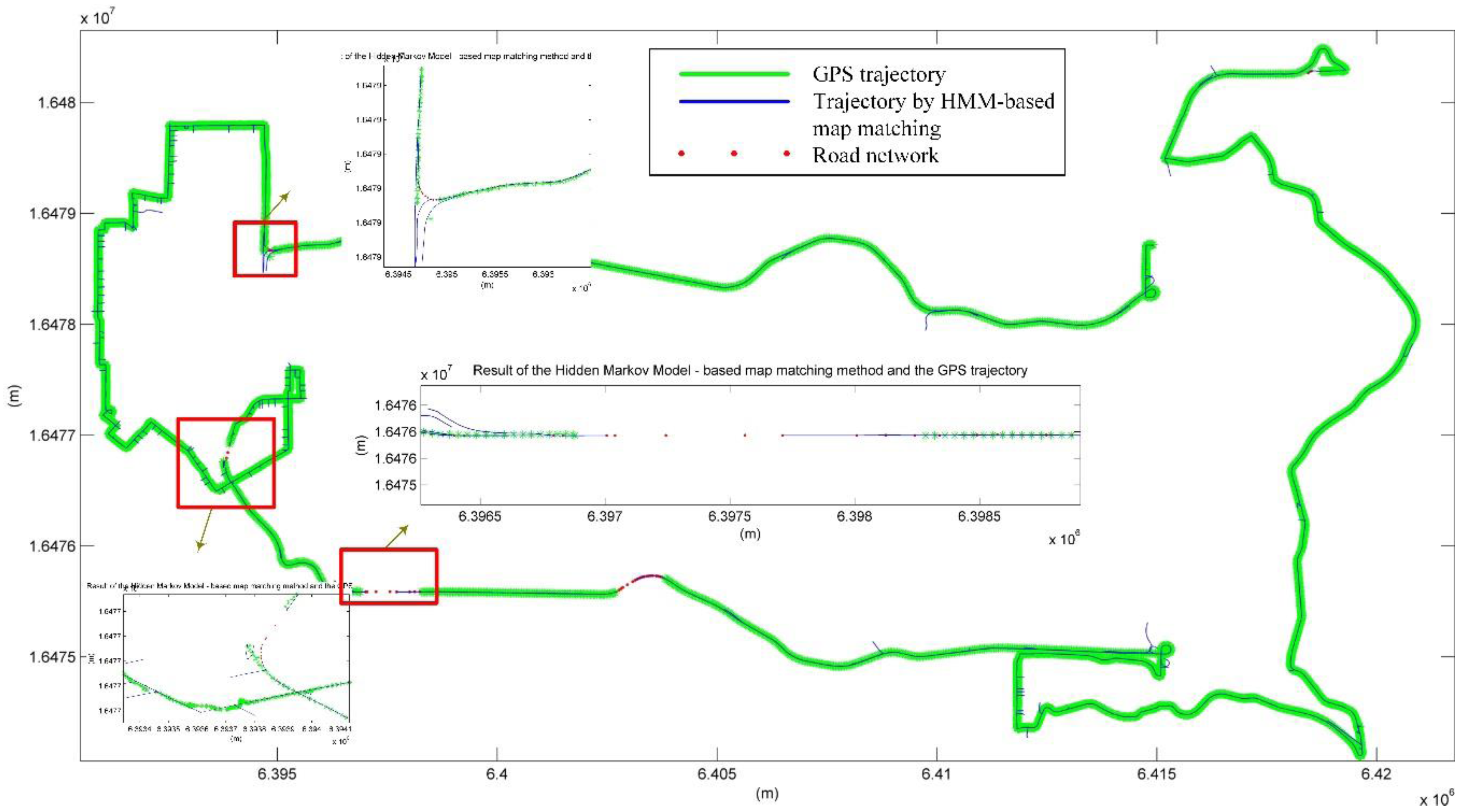
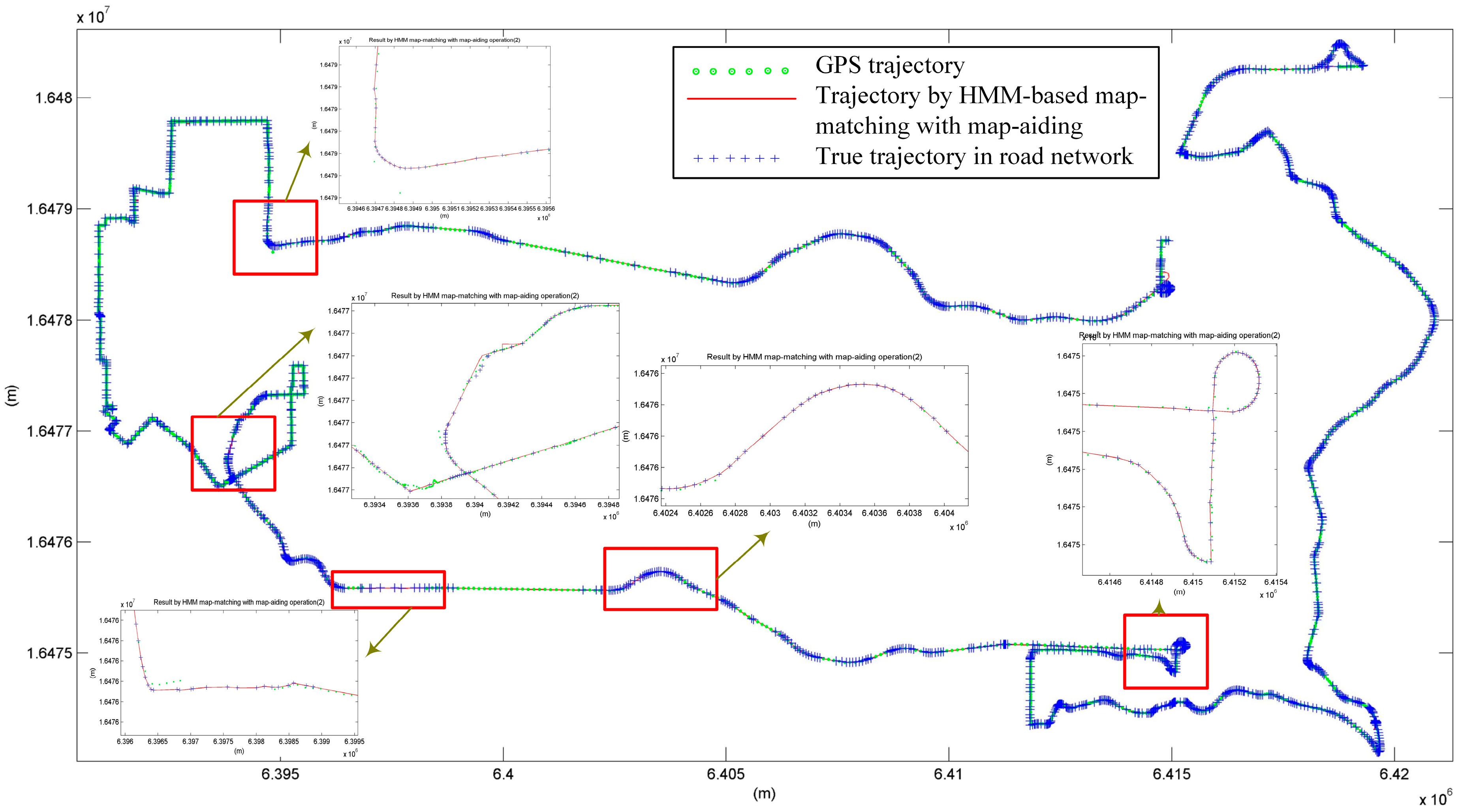
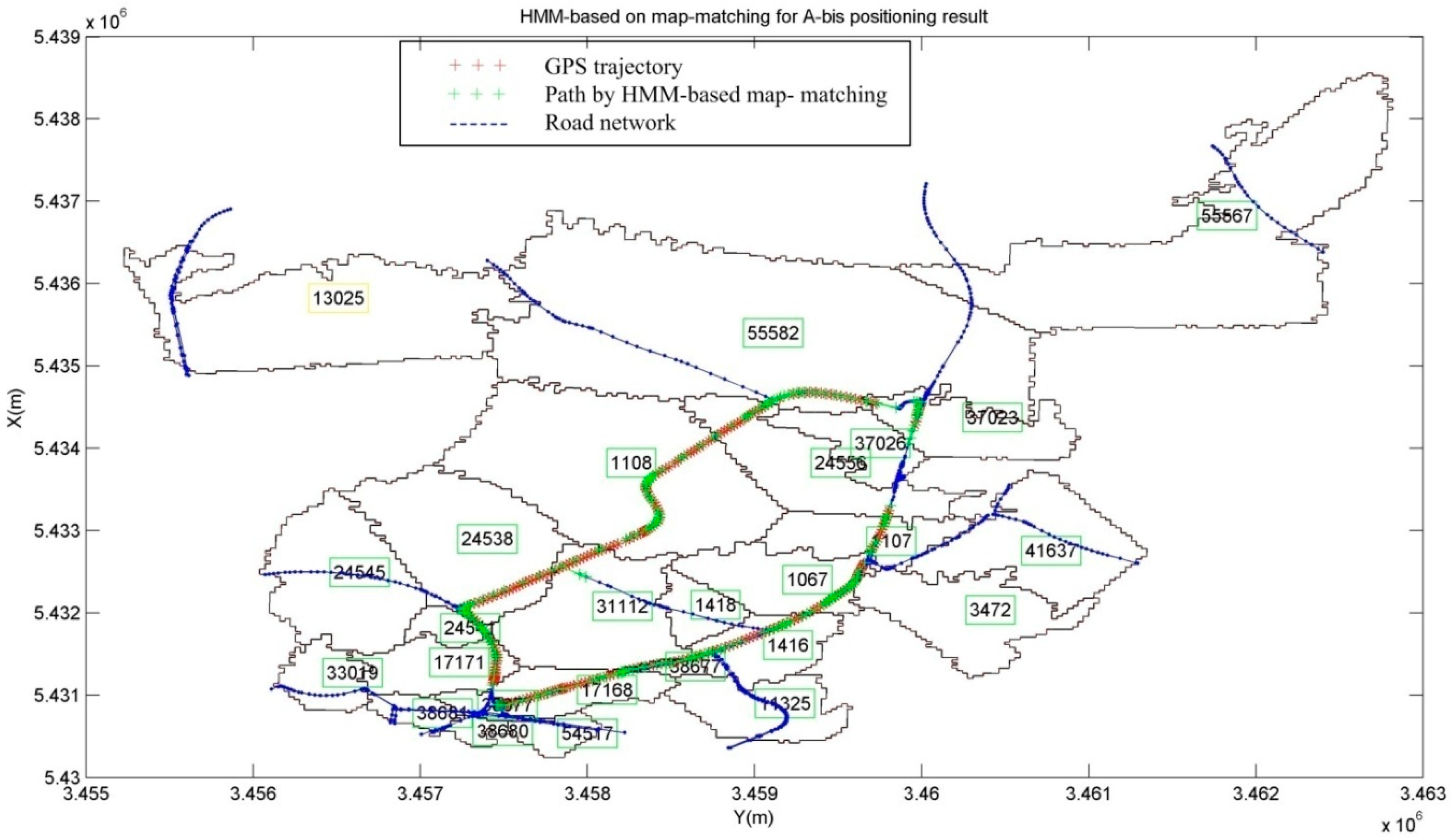
4.2. Map-Matching with HMM in Large Scale Road Network
4.3. Map-Matching with HMM on Low-Rate Positioning Data
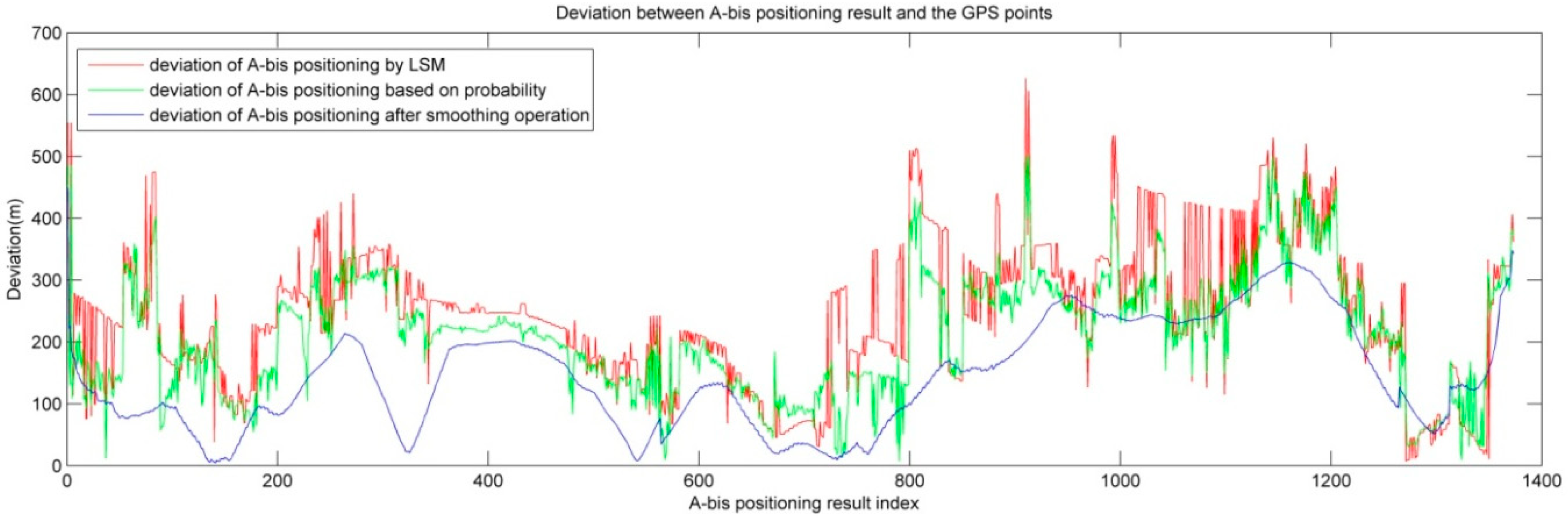
4.4. Map-Matching with HMM on Mobile Phone Positioning with Signal Strength
4.5. Summary of the Validation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bierlaire, M.; Chen, J.; Newman, J. A probabilistic map matching method for smartphone GPS data. Transp. Res. Part C Emerg. Technol. 2013, 26, 78–98. [Google Scholar] [CrossRef]
- Griffin, T.; Huang, Y.; Seals, S. Routing-based map matching for extracting routes from GPS trajectories. In Proceedings of the 2nd International Conference on Computing for Geospatial Research & Applications, Washington, DC, USA, 23–25 May 2011; p. 24. [Google Scholar]
- Kainz, W.; Christ, A.; Kellom, T.; Seidman, S.; Nikoloski, N.; Beard, B.; Kuster, N. Dosimetric comparison of the specific anthropomorphic mannequin (SAM) to 14 anatomical head models using a novel definition for the mobile phone positioning. Phys. Med. Biol. 2005, 50, 3423. [Google Scholar] [CrossRef] [PubMed]
- Katrin, R.; Volker, S. Mobile positioning for traffic state acquisition. J. Locat. Based Serv. 2007, 1, 133–144. [Google Scholar]
- Dalumpines, R.; Scott, D.M. GIS-based map-matching: Development and demonstration of a post processing map-matching algorithm for transportation research. In Advancing Geo-Information Science for a Changing World; Springer: Berlin/Heidelberg, Germany, 2011; pp. 101–120. [Google Scholar]
- Zhou, X.; Liu, J.; Yeh, A.G.O.; Yue, Y.; Li, W. The Uncertain Geographic Context Problem in Identifying Activity Centers Using Mobile Phone Positioning Data and Point of Interest Data. In Advances in Spatial Data Handling and Analysis; Springer International Publishing: Basel, Switzerland, 2015; pp. 107–119. [Google Scholar]
- Wiltschko, T.; Schwieger, V.; Möhlenbrink, W. Generating Floating Phone Data for Traffic Flow Optimization. In Proceedings of the 3rd International Symposium “Networks for Mobility”, Stuttgart, Germany, 5–6 October 2006. [Google Scholar]
- Hu, J.; Cao, W.; Luo, J.; Yu, X. Dynamic modeling of urban population travel behavior based on data fusion of mobile phone positioning data and FCD. In Proceedings of the 2009 17th International Conference on Geoinformatics, Fairfax, VA, USA, 12–14 August 2009; pp. 1–5. [Google Scholar]
- Quddus, M.; Ochieng, W.; Noland, R. Current map-matching algorithms for transport applications: State-of-the art and future research directions. Transp. Res. Part C Emerg. Technol. 2007, 15, 312–328. [Google Scholar] [CrossRef]
- Pink, O.; Hummel, B. A statistical approach to map-matching using road network geometry, topology and vehicular motion constraints. In Proceedings of the 11th International IEEE Conference on Intelligent Transportation Systems, Beijing, China, 12–15 October 2008; pp. 862–867. [Google Scholar]
- Weil, M. Drafting a new route planning system: Molson Coors Canada’s new delivery planning system taps routing, pallet building, and truck loading functionality to optimize shipment flow. Inbound Logist. 2014, 34, 293–296. [Google Scholar]
- Mahdi, H.; Hassan, A.K. A critical review of real-time map-matching algorithms: Current issues and future directions. Comput. Environ. Urban Syst. 2014, 48, 153–165. [Google Scholar]
- Yoonsik, B.; Jiyoung, K.; Kiyun, Y. An Improved Map-Matching Technique Based on the Fréchet Distance Approach for Pedestrian Navigation Services. Sensors 2016, 16, 1768. [Google Scholar] [CrossRef]
- Felipe, J.; Sergio, M.; Jose, E.N. Definition of an Enhanced Map-Matching Algorithm for Urban Environments with Poor GNSS Signal Quality. Sensors 2016, 16, 193. [Google Scholar] [CrossRef]
- Qinglin, T.; Zoran, S.; Kevin, I.W. A Hybrid Indoor Localization and Navigation System with Map Matching for Pedestrians Using Smartphones. Sensors 2015, 15, 30759–30783. [Google Scholar] [CrossRef]
- Sylvie, L.-P.; Nicolas, G.; Mehdi, B. A HMM map-matching approach enhancing indoor positioning performances of an inertial measurement system. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Banff, AB, Canada, 13–16 October 2015; pp. 1–4. [Google Scholar]
- Jagadeesh, G.R.; Srikanthan, T.; Zhang, X.D. A Map-matching Method for GPS Based Real-Time Vehicle Location. J. Navig. 2004, 57, 429–440. [Google Scholar] [CrossRef]
- Quddus, M.A.; Noland, R.B.; Ochieng, W.Y. Validation of map-matching algorithm using high precision positioning with GPS. J. Navig. 2004, 58, 257–271. [Google Scholar] [CrossRef]
- Jagadeesh, G.R.; Srikanthan, T. Probabilistic Map Matching of Sparse and Noisy Smartphone Location Data. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Las Palmas, Spain, 15–18 September 2015; pp. 812–817. [Google Scholar]
- Meng, Y. Improved Positioning of Land Vehicle in ITS Using Digital Map and Other Accessory Information. Ph.D. Thesis, Department of Land Surveying and Geoinformatics, Hong Kong Polytechnic University, Hong Kong, China, 2006. [Google Scholar]
- Quddus, M.A.; Ochieng, W.Y.; Zhao, L.; Noland, R.B. A general map-matching algorithm for transport telematics applications. GPS Solut. 2003, 7, 157–167. [Google Scholar] [CrossRef]
- Taylor, G.; Brunsdon, C.; Li, J.; Olden, A.; Steup, D.; Winter, M. GPS accuracy estimation using map-matching techniques: Applied to vehicle positioning and odometer calibration. Comput. Environ. Urban Syst. 2006, 30, 757–772. [Google Scholar] [CrossRef]
- Ren, M.; Karimi, H.A. A hidden Markov model-based map-matching algorithm for wheelchair navigation. J. Navig. 2009, 62, 383–395. [Google Scholar] [CrossRef]
- Ochieng, W.Y.; Quddus, M.A.; Noland, R.B. Map-matching in complex urban road networks. Rev. Bras. Cartogr. 2003, 5, 1–18. [Google Scholar]
- Chen, B.Y.; Yuan, H.; Li, Q.; Lam, W.H.; Shaw, S.L.; Yan, K. Map matching algorithm for large-scale low-frequency floating car data. Int. J. Geogr. Inf. Sci. 2014, 28, 22–38. [Google Scholar] [CrossRef]
- Krakiwsky, E.J.; Harris, C.B.; Wong, R.V.C. A Kalman filter for integrating dead reckoning, map matching and GPS positioning. In Proceedings of the IEEE PLANS’ 88—Position Location and Navigation Symposium Record: Navigation into the 21st Century, Orlando, FL, USA, 29 November–2 December 1988; pp. 39–46. [Google Scholar]
- Pyo, J.S.; Shin, D.H.; Sung, T.K. Development of a map matching method using the multiple hypothesis technique. In Proceedings of the 2001 IEEE Intelligent Transportation Systems, Oakland, CA, USA, 25–29 August 2001; pp. 23–27. [Google Scholar]
- Yuan, J.; Zheng, Y.; Zhang, C.; Xie, X.; Sun, G.Z. An interactive-voting based map matching algorithm. In Proceedings of the 2010 Eleventh International Conference on Mobile Data Management, Kansas City, MO, USA, 23–26 May 2010; pp. 43–52. [Google Scholar]
- Toledo-Moreo, R.; Bétaille, D.; Peyret, F. Lane-level integrity provision for navigation and map matching with GNSS, dead reckoning, and enhanced maps. IEEE Trans. Intell. Transp. Syst. 2010, 11, 100–112. [Google Scholar] [CrossRef]
- Shin, S.H.; Park, C.G.; Choi, S. New map-matching algorithm using virtual track for pedestrian dead reckoning. ETRI J. 2010, 32, 891–900. [Google Scholar] [CrossRef]
- Sajid, S.; Geoff, G.; Andrew, M. Fast State Discovery for HMM Model Selection and Learning. In Proceedings of the Eleventh International Conference on Artificial Intelligence and Statistics (AI-STATS), San Juan, Puerto Rico, 21–24 March 2007. [Google Scholar]
- Raymond, R.; Morimura, T.; Osogami, T.; Hirosue, N. Map-matching with hidden Markov model on sampled road network. In Proceedings of the 2012 21st International Conference on Pattern Recognition (ICPR), Tsukuba, Japan, 11–15 November 2012; pp. 2242–2245. [Google Scholar]
- Newson, P.; Krumm, J. Hidden Markov map matching through noise and sparseness. In Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 4–6 November 2009; pp. 336–343. [Google Scholar]
- Yin, H.; Wolfson, O. A weight-based map matching method in moving objects databases. In Proceedings of the 16th International Conference on Scientific and Statistical Database Management, Santorini Island, Greece, 23 June 2004; pp. 437–438. [Google Scholar]
- Lou, Y.; Zhang, C.; Zheng, Y.; Xie, X.; Wang, W.; Huang, Y. Map-matching for low-sampling-rate GPS trajectories. In Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 4–6 November 2009; pp. 352–361. [Google Scholar]
- Wang, Y.; Zhu, Y.; He, Z.; Yue, Y.; Li, Q. Challenges and Opportunities in Exploiting Large-Scale GPS Probe Data; Technical Report HPL-2011-109; HP Laboratories: Palo Alto, CA, USA, 2011. [Google Scholar]
- Paulo, S.; John, P.D. Adversarial Geospatial Abduction Problems. ACM Trans. Intell. Syst. Technol. 2012, 3, 1–35. [Google Scholar]
- Yankai, L.; Zhou, L. A novel algorithm of low sampling rate GPS trajectories on map-matching. J. Wirel. Commun. Netw. 2017, 2017, 30. [Google Scholar] [CrossRef]
- Forney, G.D. The Viterbi algorithm. Proc. IEEE 1973, 61, 268–278. [Google Scholar] [CrossRef]
- Viterbi, A.J. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans. Inf. Theory 1967, 13, 260–269. [Google Scholar] [CrossRef]
- Lawrence, R.R. A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition. Proc. IEEE 1989, 77, 257–287. [Google Scholar]
- Szwed, P.; Pekala, K. An Incremental Map-Matching Algorithm Based on Hidden Markov Model. In Proceedings of the 13th International Conference Artificial Intelligence and Soft Computing Volume 8468 of the Series Lecture Notes in Computer Science, ICAISC 2014, Zakopane, Poland, 1–5 June 2014; pp. 579–590. [Google Scholar]
- Xia, Y.; Liu, Y.; Ye, Z.; Wu, W.; Zhu, M. Quadtree-based domain decomposition for parallel map-matching on GPS data. In Proceedings of the 2012 15th International IEEE Conference on Intelligent Transportation Systems, Anchorage, AK, USA, 16–19 September 2012; pp. 808–813. [Google Scholar]
- Oran, A.; Jaillet, P. An HMM-based map matching method with cumulative proximity-weight formulation. In Proceedings of the 2013 International Conference on Connected Vehicles and Expo (ICCVE), Las Vegas, NV, USA, 2–6 December 2012; pp. 480–485. [Google Scholar]

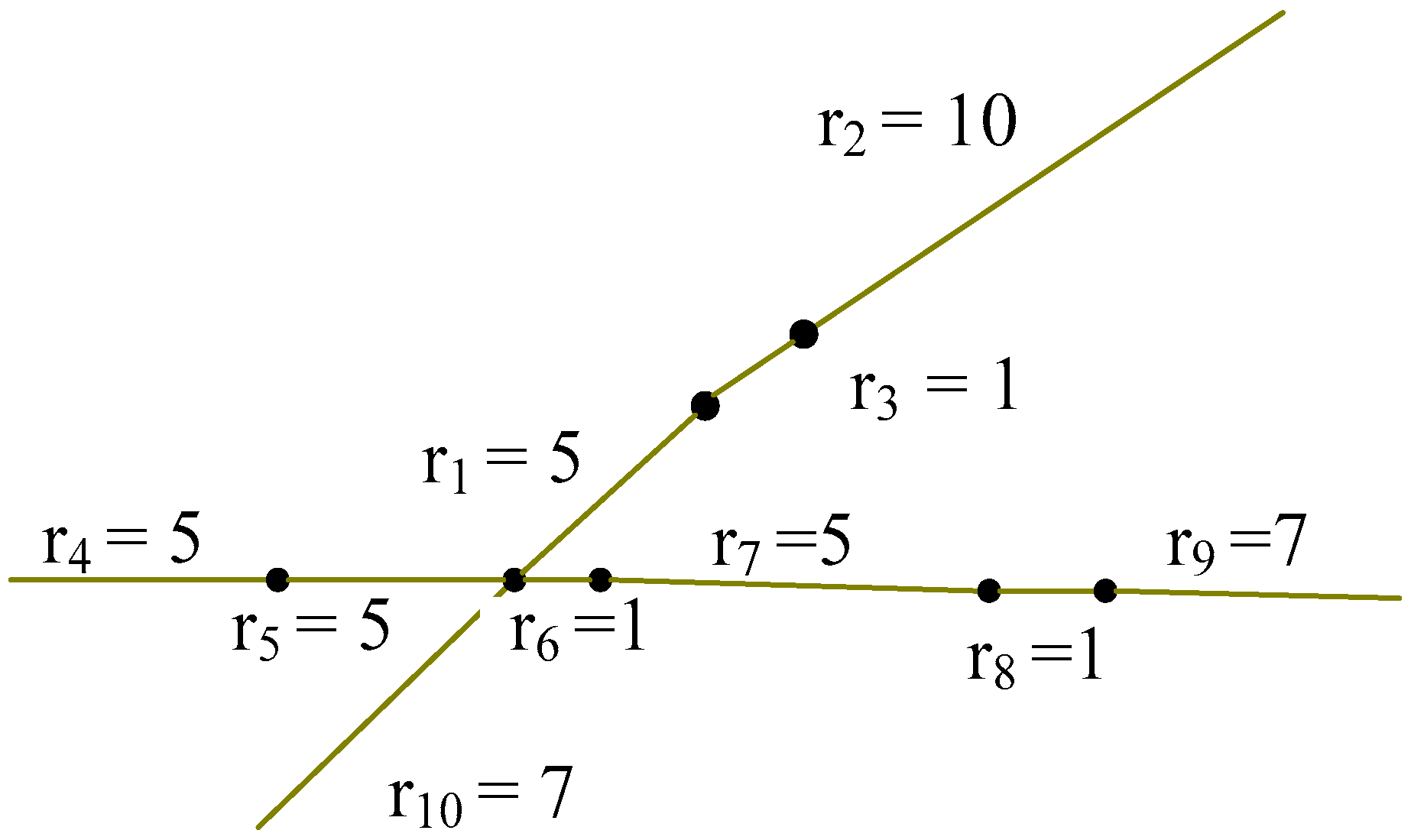



| r1 | r2 | r3 | r4 | r5 | r6 | r7 | r8 | r9 | r10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| r1 | 3/5 | 1/5 | 2/5 | 1/5 | 2/5 | 2/5 | 1/5 | 0 | 0 | 2/5 |
| r2 | 1/5 | 3/5 | 2/5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| r3 | 2/5 | 2/5 | 3/5 | 0 | 1/5 | 1/5 | 0 | 0 | 0 | 1/5 |
| r4 | 1/5 | 0 | 0 | 3/5 | 2/5 | 1/5 | 0 | 0 | 0 | 1/5 |
| r5 | 2/5 | 0 | 1/5 | 2/5 | 3/5 | 2/5 | 1/5 | 0 | 0 | 2/5 |
| r6 | 2/5 | 0 | 1/5 | 1/5 | 2/5 | 3/5 | 2/5 | 1/5 | 0 | 2/5 |
| r7 | 1/5 | 0 | 0 | 0 | 1/5 | 2/5 | 3/5 | 2/5 | 1/5 | 1/5 |
| r8 | 0 | 0 | 0 | 0 | 0 | 1/5 | 2/5 | 3/5 | 2/5 | 0 |
| r9 | 0 | 0 | 0 | 0 | 0 | 0 | 1/5 | 2/5 | 3/5 | 0 |
| r10 | 2/5 | 0 | 1/5 | 1/5 | 2/5 | 2/5 | 1/5 | 0 | 0 | 3/5 |
| Data Type | Number of Observations | Rate of Short Road Links to Total Trajectories by Length | Correct Rate with HMM after Map Aiding (%) | Trajectory Length (km) |
|---|---|---|---|---|
| GPS data route 1 | 1021 | 1.12% | 100% | 28.6 |
| GPS data route 2 | 7539 | 0.01% | 99.93% | 107.8 |
| A interface data route 3 | 1373 | 1.32% | 95.6% | 26.4 |
| GPS data route 3 | 1373 | 0.51% | 100% | 26.4 |
| A interface data route 4 | 1507 | 1.09% | 95.2% | 31.9 |
| GPS data route 4 | 1507 | 0.39% | 100% | 31.9 |
| GPS data route 4 (low sampling rate) | 301 | 3.64% | 100% | 31.2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, A.; Chen, S.; Xv, B. Enhanced Map-Matching Algorithm with a Hidden Markov Model for Mobile Phone Positioning. ISPRS Int. J. Geo-Inf. 2017, 6, 327. https://doi.org/10.3390/ijgi6110327
Luo A, Chen S, Xv B. Enhanced Map-Matching Algorithm with a Hidden Markov Model for Mobile Phone Positioning. ISPRS International Journal of Geo-Information. 2017; 6(11):327. https://doi.org/10.3390/ijgi6110327
Chicago/Turabian StyleLuo, An, Shenghua Chen, and Bin Xv. 2017. "Enhanced Map-Matching Algorithm with a Hidden Markov Model for Mobile Phone Positioning" ISPRS International Journal of Geo-Information 6, no. 11: 327. https://doi.org/10.3390/ijgi6110327
APA StyleLuo, A., Chen, S., & Xv, B. (2017). Enhanced Map-Matching Algorithm with a Hidden Markov Model for Mobile Phone Positioning. ISPRS International Journal of Geo-Information, 6(11), 327. https://doi.org/10.3390/ijgi6110327




