Towards Detecting the Crowd Involved in Social Events
Abstract
:1. Introduction
2. Methodology
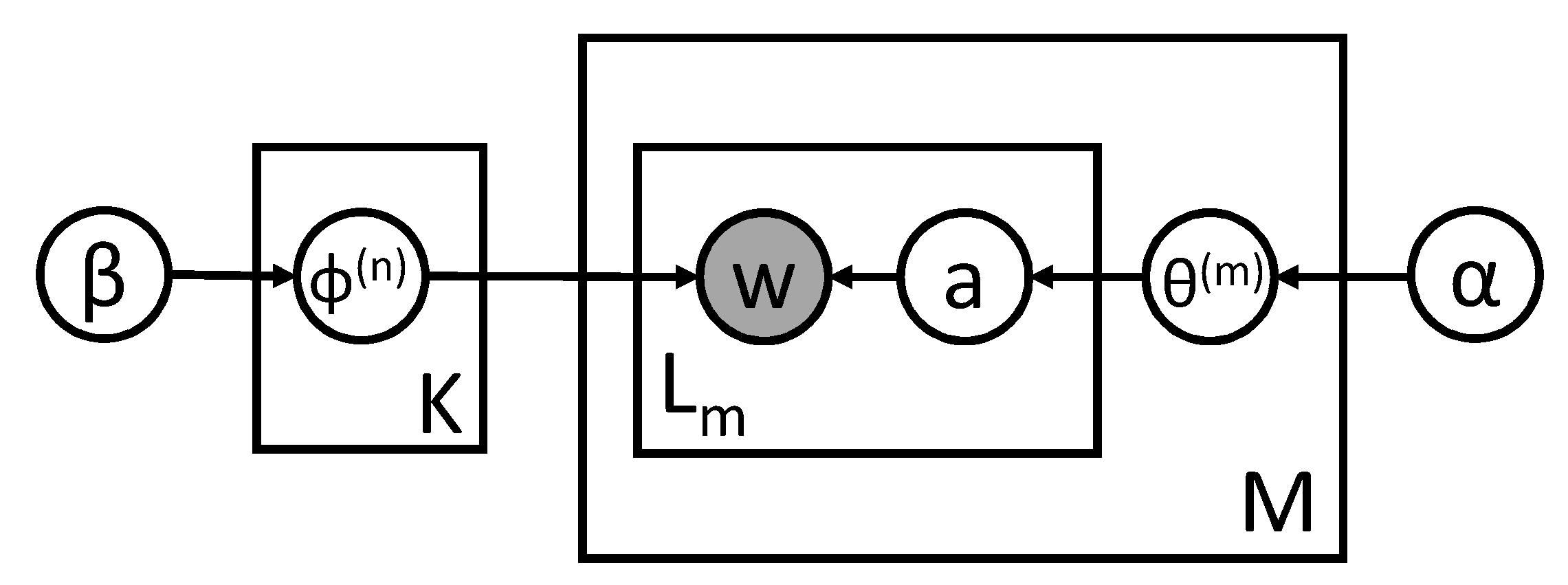
2.1. Preliminaries
2.2. Psychological Feature Modeling
2.3. Mental Unity Measuring
3. Case Study
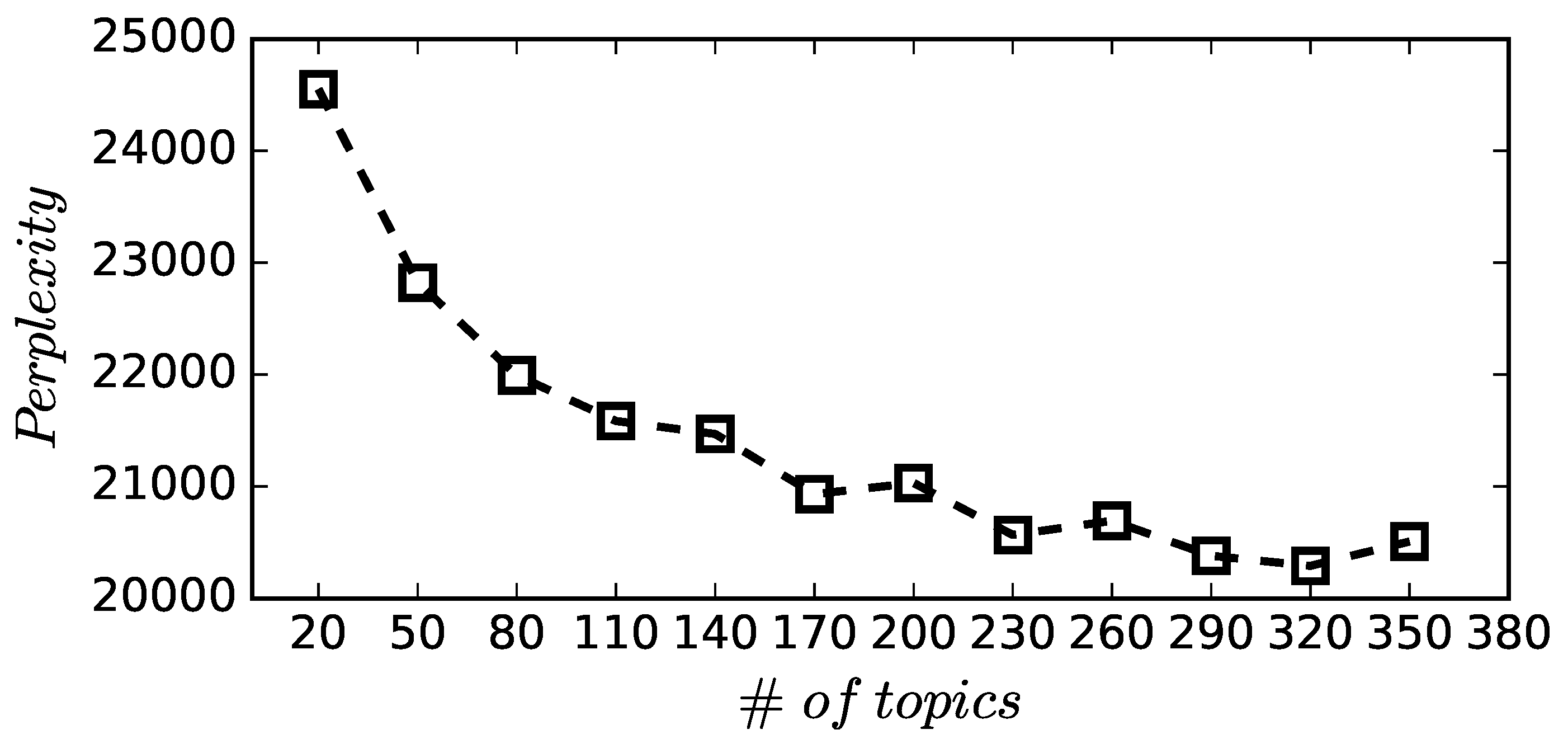
3.1. Data and Experiment Design
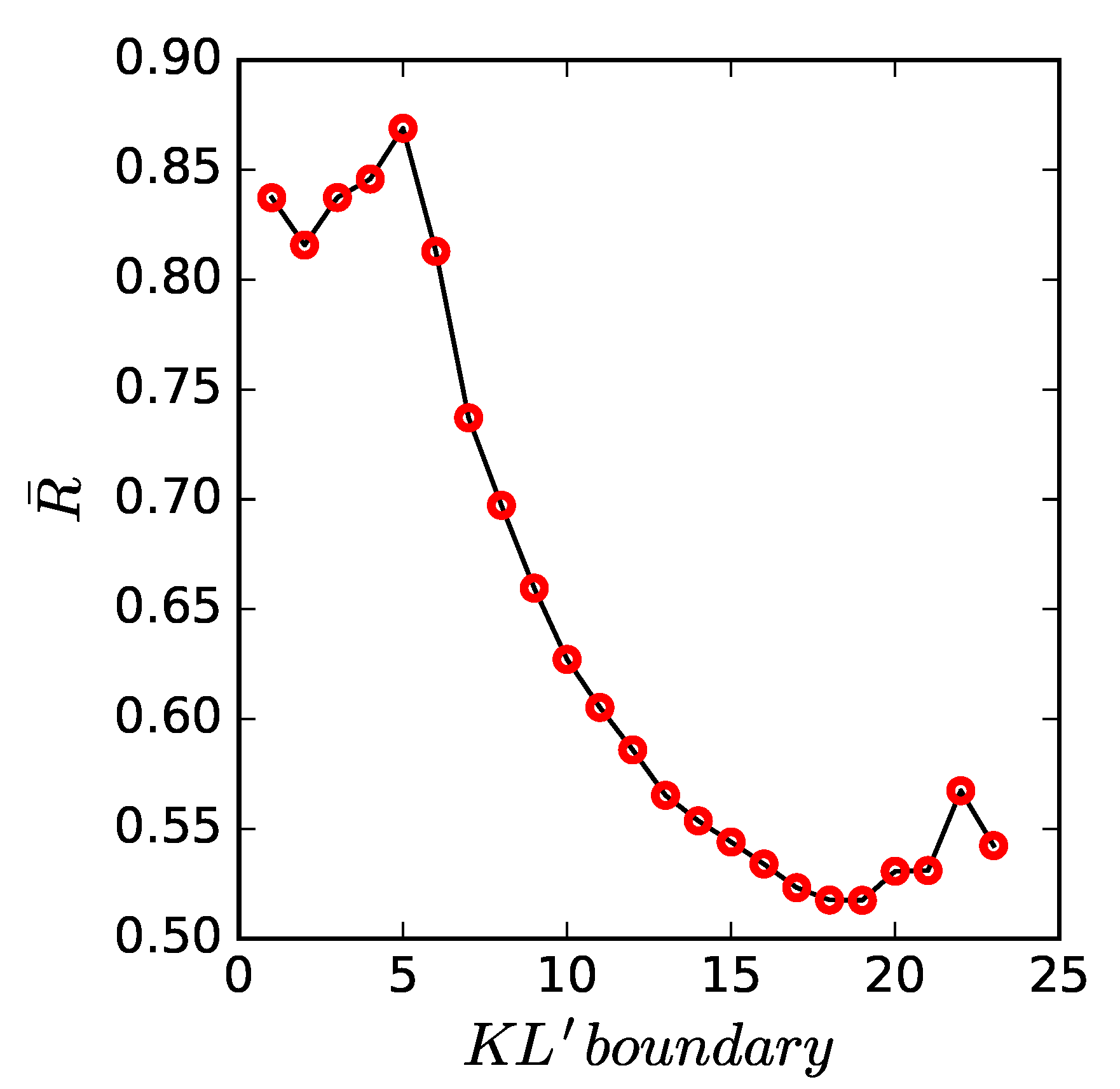
3.2. Psychological Feature Patterns
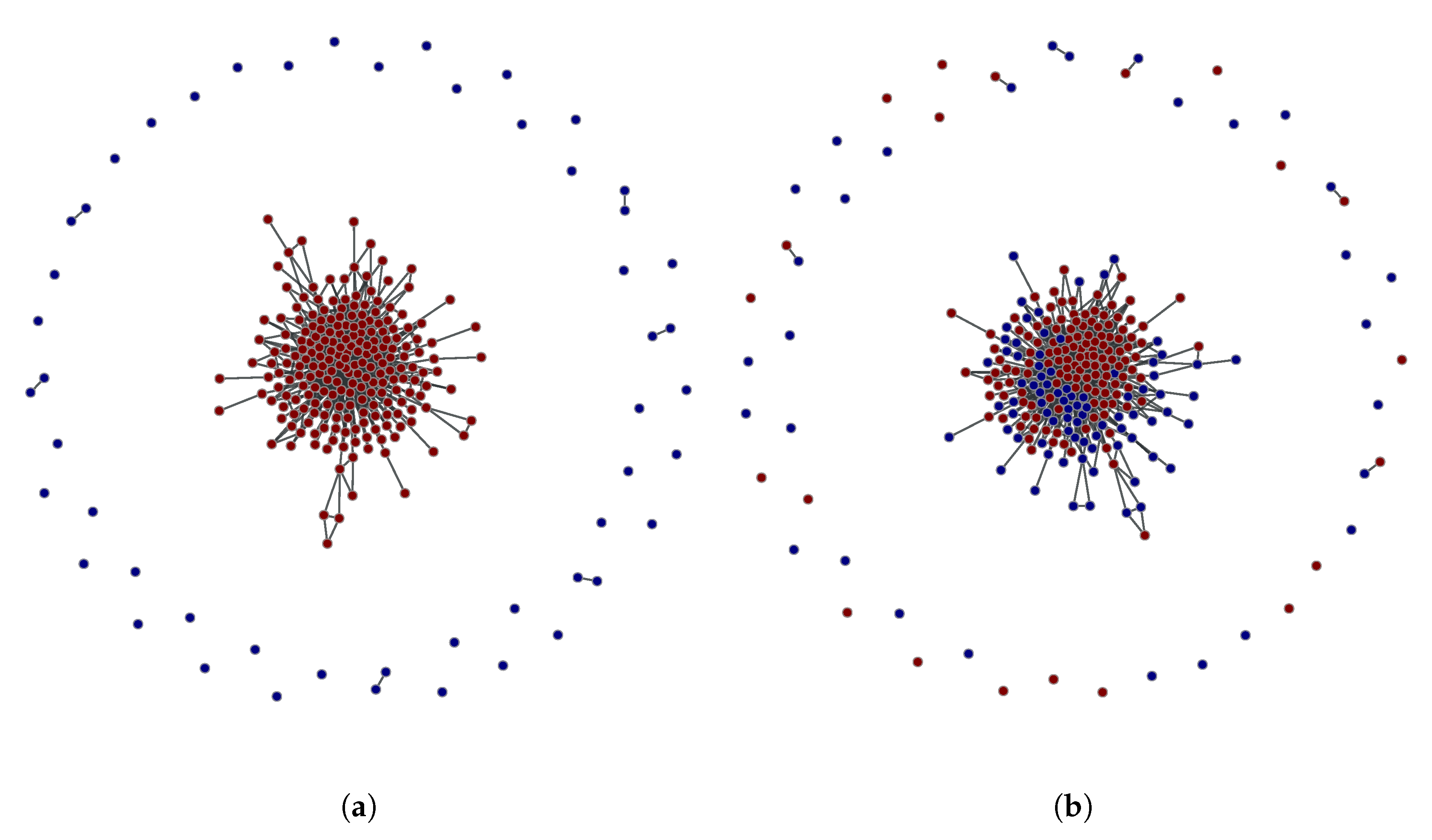
3.3. Detected Crowd
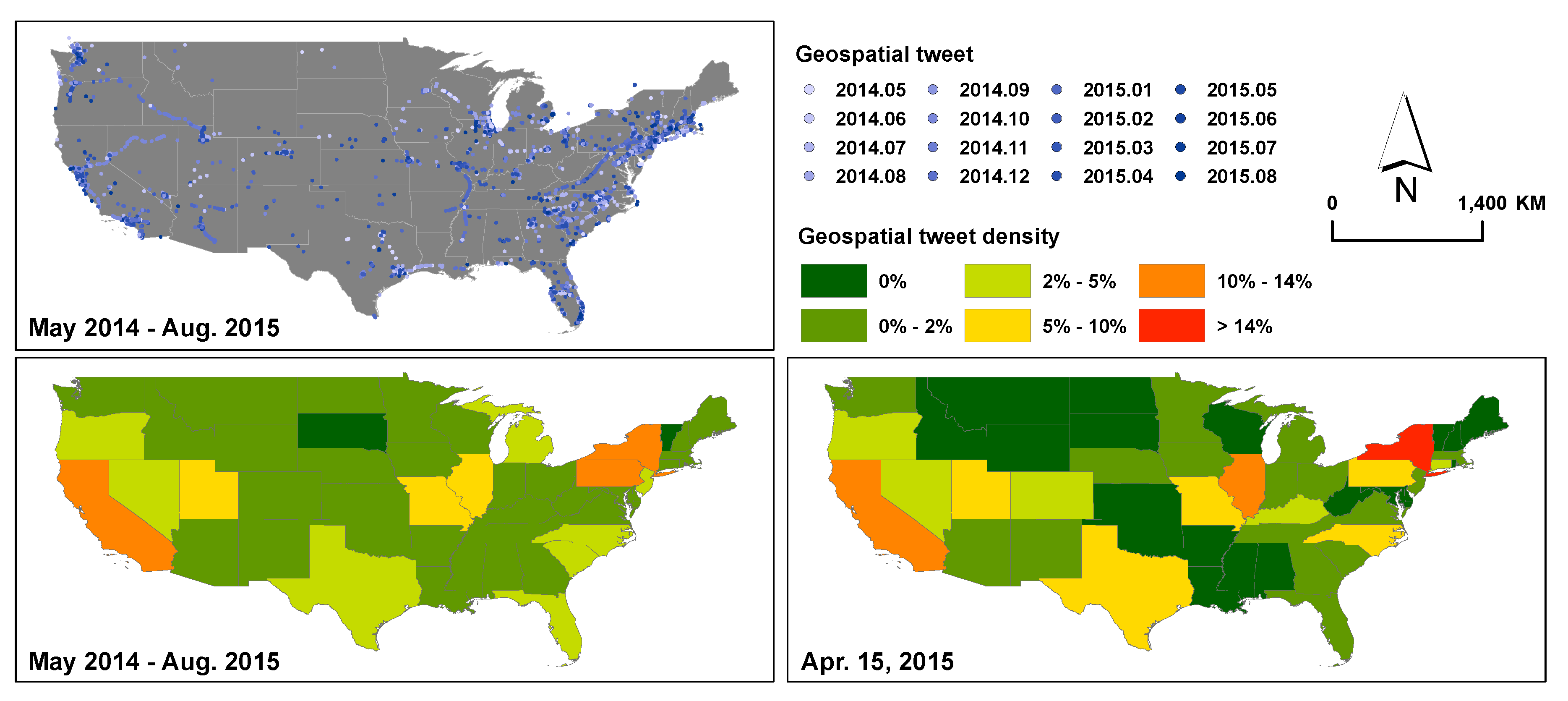
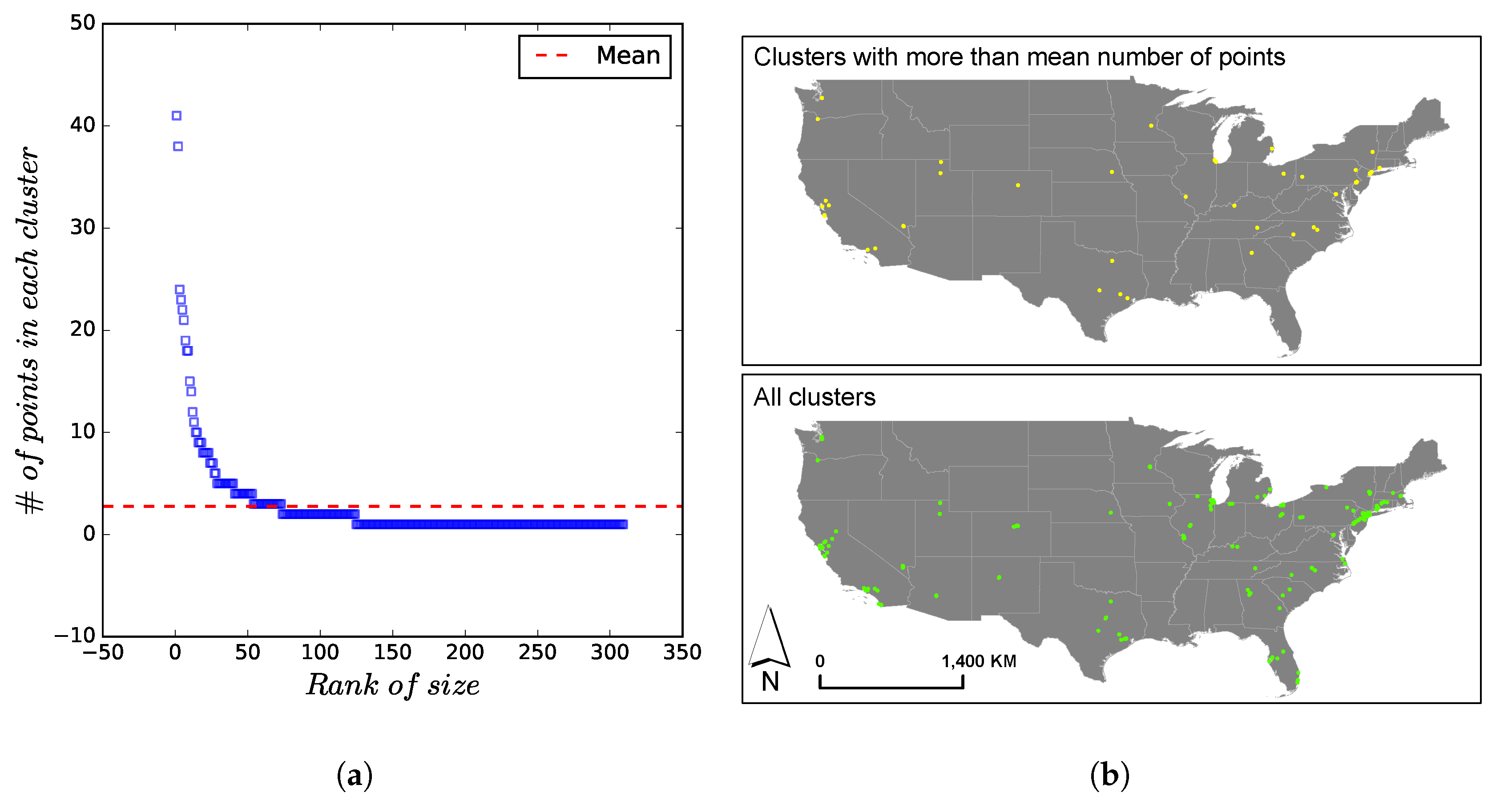
3.4. Geospatial Patterns
3.5. Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nye, R.A. The Origins of Crowd Psychology: Gustave LeBon and the Crisis of Mass Democracy in the Third Republic; Sage Publications: Beverly Hills, CA, USA; London, UK, 1975; Volume 2. [Google Scholar]
- Le Bon, G. The Crowd: A Study of the Popular Mind; Macmillan: New York, NY, USA, 1921. [Google Scholar]
- Turner, R.H.; Killian, L.M. Collective Behavior, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1987. [Google Scholar]
- Helbing, D.; Molnár, P.; Farkas, I.J.; Bolay, K. Self-organizing pedestrian movement. Environ. Plan. B Plan. Des. 2001, 28, 361–383. [Google Scholar] [CrossRef]
- Moussaïd, M.; Helbing, D.; Theraulaz, G. How simple rules determine pedestrian behavior and crowd disasters. Proc. Natl. Acad. Sci. USA 2011, 108, 6884–6888. [Google Scholar] [CrossRef] [PubMed]
- Sieben, A.; Schumann, J.; Seyfried, A. Collective phenomena in crowds—Where pedestrian dynamics need social psychology. PLoS ONE 2017, 12, e0177328. [Google Scholar] [CrossRef] [PubMed]
- Von Krüchten, C.; Schadschneider, A. Empirical study on social groups in pedestrian evacuation dynamics. Phys. A Stat. Mech. Appl. 2017, 475, 129–141. [Google Scholar] [CrossRef]
- Templeton, A.; Drury, J.; Philippides, A. From mindless masses to small groups: Conceptualizing collective behavior in crowd modeling. Rev. Gen. Psychol. 2015, 19, 215. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Axhausen, K.W.; Lee, D.H.; Huang, X. Understanding metropolitan patterns of daily encounters. Proc. Natl. Acad. Sci. USA 2013, 110, 13774–13779. [Google Scholar] [CrossRef] [PubMed]
- Järv, O.; Ahas, R.; Witlox, F. Understanding monthly variability in human activity spaces: A twelve-month study using mobile phone call detail records. Transp. Res. Part C Emerg. Technol. 2014, 38, 122–135. [Google Scholar] [CrossRef]
- Alexander, L.; Jiang, S.; Murga, M.; González, M.C. Origin-destination trips by purpose and time of day inferred from mobile phone data. Transp. Res. Part C Emerg. Technol. 2015, 58, 240–250. [Google Scholar] [CrossRef]
- Ferrara, E.; De Meo, P.; Catanese, S.; Fiumara, G. Detecting criminal organizations in mobile phone networks. Expert Syst. Appl. 2014, 41, 5733–5750. [Google Scholar] [CrossRef]
- Fast, S.M.; González, M.C.; Wilson, J.M.; Markuzon, N. Modelling the propagation of social response during a disease outbreak. J. R. Soc. Interface 2015, 12. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; González, M.C.; Hidalgo, C.A.; Barabási, A.L. Understanding the spreading patterns of mobile phone viruses. Science 2009, 324, 1071–1076. [Google Scholar] [CrossRef] [PubMed]
- González, M.C.; Hidalgo, C.A.; Barabasi, A.L. Understanding individual human mobility patterns. Nature 2008. [Google Scholar] [CrossRef]
- Song, C.; Qu, Z.; Blumm, N.; Barabási, A.L. Limits of predictability in human mobility. Science 2010, 327, 1018–1021. [Google Scholar] [CrossRef] [PubMed]
- Lima, A.; Stanojevic, R.; Papagiannaki, D.; Rodriguez, P.; González, M.C. Understanding individual routing behaviour. J. R. Soc. Interface 2016, 13. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Ferreira, J.; González, M.C. Activity-based human mobility patterns inferred from mobile phone data: A case study of Singapore. IEEE Trans. Big Data 2017, 3, 208–219. [Google Scholar] [CrossRef]
- Chaniotakis, E.; Antoniou, C.; Aifadopoulou, G.; Dimitriou, L. Inferring activities from social media data. In Proceedings of the 96th Transportation Research Board Annual Meeting, Washington, DC, USA, 8–12 January 2017. [Google Scholar]
- Guellil, I.; Boukhalfa, K. Social big data mining: A survey focused on opinion mining and sentiments analysis. In Proceedings of the 12th IEEE International Symposium on Programming and Systems (ISPS), Algiers, Algeria, 28–30 April 2015; pp. 1–10. [Google Scholar]
- Liao, L.; Fox, D.; Kautz, H. Extracting places and activities from gps traces using hierarchical conditional random fields. Int. J. Robot. Res. 2007, 26, 119–134. [Google Scholar] [CrossRef]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent dirichlet allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Griffiths, T.; Steyvers, M. A probabilistic approach to semantic representation. In Proceedings of the 24th Annual Conference of the Cognitive Science Society, Fairfax, VA, USA, 8–10 August 2002; pp. 381–386. [Google Scholar]
- Griffiths, T.; Steyvers, M. Prediction and semantic association. In Advances in Neural Information Processing Systems 15; MIT Press: Cambridge, MA, USA, 2002; pp. 11–18. [Google Scholar]
- Griffiths, T.L.; Steyvers, M. Finding scientific topics. Proc. Natl. Acad. Sci. USA 2004, 101, 5228–5235. [Google Scholar] [CrossRef] [PubMed]
- Steyvers, M.; Griffiths, T. Probabilistic topic models. In Handbook of Latent Semantic Analysis; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2007; Volume 427, pp. 424–440. [Google Scholar]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Fight for $15: Workers Across US Protest to Raise Minimum Wage–As It Happened. Available online: https://www.theguardian.com/us-news/2015/apr/15/fight-for-15-minimum-wage-protests-new-york-los-angeles-atlanta-boston (accessed on 15 April 2015).
- Fight for $15 Organization. Available online: https://fightfor15.org/about-us/ (accessed on 29 November 2012).
- Twitter Developer Documents. Available online: https://developer.twitter.com/en/docs (accessed on 1 January 2017).
- Jurdak, R.; Zhao, K.; Liu, J.; AbouJaoude, M.; Cameron, M.; Newth, D. Understanding human mobility from Twitter. PLoS ONE 2015, 10, e0131469. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Li, S. Understanding human activity patterns based on space-time-semantics. ISPRS J. Photogramm. Remote Sens. 2016, 121, 1–10. [Google Scholar] [CrossRef]
- Atefeh, F.; Khreich, W. A survey of techniques for event detection in twitter. Comput. Intell. 2015, 31, 132–164. [Google Scholar] [CrossRef]
- Sakaki, T.; Okazaki, M.; Matsuo, Y. Earthquake shakes Twitter users: Real-time event detection by social sensors. In Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010; ACM: New York, NY, USA, 2010; pp. 851–860. [Google Scholar]
- Taxidou, I.; Fischer, P.M. Online analysis of information diffusion in twitter. In Proceedings of the 23rd International Conference on World Wide Web, Seoul, Korea, 7–11 April 2014; ACM: New York, NY, USA, 2014; pp. 1313–1318. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]


| Topic ID | |
|---|---|
| 60 | 0.217 |
| 176 | 0.152 |
| 156 | 0.149 |
| 198 | 0.148 |
| 38 | 0.12 |
| 92 | 0.112 |
| 179 | 0.037 |
| 190 | 0.029 |
| 87 | 0.005 |
| 84 | 0.002 |
| Topic #74 | Topic #176 | Topic #187 | |||
|---|---|---|---|---|---|
| Word | Word | Word | |||
| walmart | 0.031 | workers | 0.06 | wage | 0.014 |
| walmart strikers | 0.027 | fight for | 0.038 | awww | 0.008 |
| oakland | 0.026 | wage | 0.035 | brilliant | 0.008 |
| hellaodub | 0.019 | #fightfor15 | 0.021 | demon | 0.007 |
| live | 0.018 | worker | 0.021 | greed | 0.007 |
| black | 0.017 | strike fast food | 0.021 | crooks and liars | 0.007 |
| our walmart | 0.014 | union | 0.021 | elected | 0.007 |
| blend | 0.013 | seiu | 0.018 | segment | 0.006 |
| hella | 0.012 | fight | 0.014 | gag | 0.006 |
| love | 0.01 | wages | 0.013 | laughable | 0.005 |
| All Clusters | Selected Clusters | |
|---|---|---|
| # of clusters | 309 | 53 |
| # of users | 170 | 75 |
| Users posting off-site tweets before event (a) | 51 | 18 |
| Users posting on-site tweets before event (b) | 119 | 57 |
| a:b | 0.43 | 0.31 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Fan, H.; Zipf, A. Towards Detecting the Crowd Involved in Social Events. ISPRS Int. J. Geo-Inf. 2017, 6, 305. https://doi.org/10.3390/ijgi6100305
Huang W, Fan H, Zipf A. Towards Detecting the Crowd Involved in Social Events. ISPRS International Journal of Geo-Information. 2017; 6(10):305. https://doi.org/10.3390/ijgi6100305
Chicago/Turabian StyleHuang, Wei, Hongchao Fan, and Alexander Zipf. 2017. "Towards Detecting the Crowd Involved in Social Events" ISPRS International Journal of Geo-Information 6, no. 10: 305. https://doi.org/10.3390/ijgi6100305
APA StyleHuang, W., Fan, H., & Zipf, A. (2017). Towards Detecting the Crowd Involved in Social Events. ISPRS International Journal of Geo-Information, 6(10), 305. https://doi.org/10.3390/ijgi6100305






